2021年高考数学二轮复习重难点突破—解三角形问题
高考数学二轮复习 专题2 三角函数、三角变换、解三角形、平面向量 第一讲 三角函数的图象与性质 理-

专题二 三角函数、三角变换、解三角形、平面向量第一讲 三角函数的图象与性质1.角的概念.(1)终边相同的角不一定相等,相等的角终边一定相同(填“一定”或“不一定”). (2)确定角α所在的象限,只要把角α表示为α=2k π+α0[k ∈Z,α0∈[0,2π)],判断出α0所在的象限,即为α所在象限.2.诱导公式.诱导公式是求三角函数值、化简三角函数的重要依据,其记忆口诀为:奇变偶不变,符号看象限.1.三角函数的定义:设α是一个任意大小的角,角α的终边与单位圆交于点P (x ,y ),则sin α=y ,cos α=x ,tan α=yx.2.同角三角函数的基本关系. (1)sin 2α+cos 2α=1. (2)tan α=sin αcos α.判断下面结论是否正确(请在括号中打“√”或“×”).(1)角α终边上点P 的坐标为⎝ ⎛⎭⎪⎫-12,32,那么sin α=32,cos α=-12;同理角α终边上点Q 的坐标为(x 0,y 0),那么sin α=y 0,cos α=x 0.(×)(2)锐角是第一象限角,反之亦然.(×) (3)终边相同的角的同一三角函数值相等.(√)(4)常函数f (x )=a 是周期函数,它没有最小正周期.(√) (5)y =cos x 在第一、二象限上是减函数.(×) (6)y =tan x 在整个定义域上是增函数.(×)1.(2015·某某卷)若sin α=-513,且α为第四象限角,则tan α的值等于(D )A.125 B .-125 C.512 D .-512解析:解法一:因为α为第四象限的角,故cos α=1-sin 2α=1-(-513)2=1213,所以tan α=sin αcos α=-5131213=-512. 解法二:因为α是第四象限角,且sin α=-513,所以可在α的终边上取一点P (12,-5),则tan α=y x =-512.故选D.2.已知α的终边经过点A (5a ,-12a ),其中a <0,则sin α的值为(B ) A .-1213 B.1213 C.513 D .-5133.(2014·新课标Ⅰ卷)在函数①y =cos|2x |,②y =|cos x |,③y =cos ⎝⎛⎭⎪⎫2x +π6,④y=tan ⎝⎛⎭⎪⎫2x -π4中,最小正周期为π的所有函数为(A ) A .①②③ B .①③④C .②④D .①③解析:①中函数是一个偶函数,其周期与y =cos 2x 相同,T =2π2=π;②中函数y =|cos x |的周期是函数y =cos x 周期的一半,即T =π;③T =2π2=π;④T =π2.故选A.4.(2015·某某卷)如图,某港口一天6时到18时的水深变化曲线近似满足函数y =3sin(π6x +φ)+k .据此函数可知,这段时间水深(单位:m)的最大值为(C )A .5B .6C .8D .10解析:根据图象得函数的最小值为2,有-3+k =2,k =5,最大值为3+k =8.一、选择题1.若sin(α-π)=35,α为第四象限角,则tan α=(A )A .-34B .-43C.34D.43 解析:∵sin(α-π)=35,∴-sin α=35,sin α=-35.又∵α为第四象限角, ∴cos α= 1-sin 2α= 1-⎝ ⎛⎭⎪⎫-352=45, tan α=sin αcos α=-3545=-34.2. 定义在R 上的周期函数f (x ),周期T =2,直线x =2是它的图象的一条对称轴,且f (x )在[-3,-2]上是减函数,如果A ,B 是锐角三角形的两个内角,则(A )A .f (sin A )>f (cosB ) B .f (cos B )>f (sin A )C .f (sin A )>f (sin B )D .f (cos B )>f (cos A )解析:由题意知:周期函数f (x )在[-1,0]上是减函数,在[0,1]上是增函数.又因为A ,B 是锐角三角形的两个内角,A +B >π2,得:sin A >cos B ,故f (sin A )>f (cos B ).综上知选A.3.函数y =2sin ⎝⎛⎭⎪⎫πx 6-π3(0≤x ≤9)的最大值与最小值之和为(A )A .2- 3B .0C .-1D .-1- 3解析:用五点作图法画出函数y =2sin ⎝⎛⎭⎪⎫πx 6-π3(0≤x ≤9)的图象,注意0≤x ≤9知,函数的最大值为2,最小值为- 3.故选A.4. 把函数y =cos 2x +1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图象是(A )解析:y =cos 2x +1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的解析式为y =cos (x +1).故选A.5.(2015·新课标Ⅰ卷)函数f (x )=cos(ωx +φ)的部分图象如图所示,则f (x )的单调递减区间为(D )A.⎝⎛⎭⎪⎫k π-14,k π+34,k ∈ZB.⎝⎛⎭⎪⎫2k π-14,2k π+34,k ∈Z C.⎝ ⎛⎭⎪⎫k -14,k +34,k ∈ZD.⎝⎛⎭⎪⎫2k -14,2k +34,k ∈Z 解析:由图象知周期T =2⎝ ⎛⎭⎪⎫54-14=2,∴2πω=2,∴ω=π.由π×14+φ=π2+2k π,k ∈Z ,不妨取φ=π4,∴f (x )=cos ⎝⎛⎭⎪⎫πx +π4.由2k π<πx +π4<2k π+π,得2k -14<x <2k +34,k ∈Z ,∴f (x )的单调递减区间为⎝⎛⎭⎪⎫2k -14,2k +34,k ∈Z.故选D.6.已知函数f (x )=A sin(ωx +φ)(x ∈R,A >0,ω>0,|φ|<π2)的图象(部分)如图所示,则f (x )的解析式是(A )A .f (x )=2sin ⎝ ⎛⎭⎪⎫πx +π6(x ∈R)B .f (x )=2sin ⎝ ⎛⎭⎪⎫2πx +π6(x ∈R)C .f (x )=2sin ⎝ ⎛⎭⎪⎫πx +π3(x ∈R)D .f (x )=2sin ⎝⎛⎭⎪⎫2πx +π3(x ∈R) 解析:由图象可知其周期为:4⎝ ⎛⎭⎪⎫56-13=2,∵2πω=2,得ω=π,故只可能在A ,C 中选一个,又因为x =13时达到最大值,用待定系数法知φ=π6.二、填空题7.若sin θ=-45,tan θ>0,则cos θ=-35.8.已知角α的终边经过点(-4,3),则cos α=-45.解析:由题意可知x =-4,y =3,r =5,所以cos α=x r =-45.三、解答题9. (2014·某某卷)已知函数f (x )=2cos x (sin x +cos x ). (1)求f ⎝⎛⎭⎪⎫5π4的值;(2)求函数f (x )的最小正周期及单调递增区间.分析:思路一 直接将5π4代入函数式,应用三角函数诱导公式计算.(2)应用和差倍半的三角函数公式,将函数化简2sin ⎝ ⎛⎭⎪⎫2x +π4+1. 得到T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,解得k π-3π8≤x ≤k π+π8,k ∈Z.思路二 先应用和差倍半的三角函数公式化简函数f (x )=2sin x cos x +2cos 2x =2sin ⎝⎛⎭⎪⎫2x +π4+1.(1)将5π4代入函数式计算;(2)T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,解得k π-3π8≤x ≤k π+π8,k ∈Z.解析:解法一 (1)f ⎝⎛⎭⎪⎫5π4=2cos 5π4⎝ ⎛⎭⎪⎫sin 5π4+cos 5π4=-2cos π4⎝ ⎛⎭⎪⎫-sin π4-cos π4=2.(2)因为f (x )=2sin x cos x +2cos 2x =sin 2x +cos 2x +1 =2sin ⎝ ⎛⎭⎪⎫2x +π4+1. 所以T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,得k π-3π8≤x ≤k π+π8,k ∈Z ,所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-3π8,k π+π8,k ∈Z.解法二 因为f (x )=2sin x cos x +2cos 2x =sin 2x +cos 2x +1 =2sin ⎝ ⎛⎭⎪⎫2x +π4+1.(1)f ⎝⎛⎭⎪⎫5π4=2sin 11π4+1=2sin π4+1=2. (2)T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,得k π-3π8≤x ≤k π+π8,k ∈Z ,所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-3π8,k π+π8,k ∈Z.10.函数f (x )=A sin ⎝ ⎛⎭⎪⎫ωx -π6+1(A >0,ω>0)的最大值为3, 其图象相邻两条对称轴之间的距离为π2.(1)求函数f (x )的解析式;word(2)设α∈⎝ ⎛⎭⎪⎫0,π2,则f ⎝ ⎛⎭⎪⎫α2=2,求α的值. 解析:(1)∵函数f (x )的最大值为3,∴A +1=3,即A =2.∵函数图象的相邻两条对称轴之间的距离为π2, ∴最小正周期为 T =π,∴ω=2,故函数f (x )的解析式为y =2sin ⎝ ⎛⎭⎪⎫2x -π6+1. (2)∵f ⎝ ⎛⎭⎪⎫α2=2sin ⎝⎛⎭⎪⎫α-π6+1=2, 即sin ⎝⎛⎭⎪⎫α-π6=12, ∵0<α<π2,∴-π6<α-π6<π3. ∴α-π6=π6,故α=π3. 11.(2015·卷)已知函数f (x )=2sin x 2cos x 2-2sin 2x 2. (1)求f (x )的最小正周期;(2)求f (x )在区间[-π,0]上的最小值.解析:(1)由题意得f (x )=22sin x -22(1-cos x )=sin ⎝ ⎛⎭⎪⎫x +π4-22,所以f (x )的最小正周期为2π.(2)因为-π≤x ≤0,所以-3π4≤x +π4≤π4. 当x +π4=-π2,即x =-3π4时,f (x )取得最小值. 所以f (x )在区间[-π,0]上的最小值为f ⎝ ⎛⎭⎪⎫-3π4=-1-22.。
高考数学二轮复习——突破爪型【三角形】八大妙手

突破爪型三角形的八大“妙手”爪型三角形是解三角形中非常重要的一种构型,人教版教材中也多次出现相关例题,很多此处不再逐一列举,教材必修二53页到54页中这样的例子比比皆是.本节我将给出关于爪型三角形处理的一些重要手段,例如找补角,或者等面积思想,以及利用上述思想结合正余弦定理推出处理爪型三角形的一些重要结论:斯特瓦尔特定理,角平分线定理等. 一.基本原理1.爪型三角形的几何特征基本几何特征:如图, π=∠+∠APC APB .例1.(2022全国甲卷)已知ABC ∆中,点D 在边BC 上,120ADB ∠=︒,2AD =,2CD BD =.当ACAB取得最小值时,BD = . 解析:设BD x =,2CD x =,在三角形ACD 中,2244222cos60b x x =+−⋅⋅⋅︒,可得:22444b x x =−+,在三角形ABD 中,22422cos120c x x =+−⋅⋅⋅︒,可得:2224c x x =++,要使得ACAB 最小,即22b c 最小,222244412432411b x x c x x x x −+==−+++++,其中31231x x +++,此时22423bc−,当且仅当1x +时,即1x =1.例 2.(2021新高考1卷)记ABC 是内角A ,B ,C 的对边分别为a ,b ,c .已知2b ac =,点D 在边AC 上,sin sin BD ABC a C ∠=.(1)证明:BD b =;(2)若2AD DC =,求cos ABC ∠解析:(1)由题设,sin sin a C BD ABC =∠,由正弦定理知:sin sin c b C ABC =∠,即sin sin C cABC b=∠,.∴acBD b=,又2b ac =,∴BD b =,得证. (2)由题意知:2,,33b b BD b AD DC ===, ∴22222241399cos 24233b b bc cADB b b b +−−∠==⋅,同理2222221099cos 2233b b b a a CDB b b b +−−∠==⋅,∵ADB CDB π∠=−∠,∴2222221310994233b bc a b b −−=,整理得2221123b a c +=,又2b ac =, ∴42221123b b a a +=,整理得422461130a a b b −+=,解得2213a b =或2232a b =,由余弦定理知:222224cos 232a c b a ABC ac b +−∠==−,当2213a b =时,7cos 16ABC ∠=>不合题意;当2232a b =时,7cos 12ABC ∠=;综上,7cos 12ABC ∠=.2.中线公式与向量方法若已知顶角BAC 的大小,且→→⋅=BC BP λ时,可利用向量共线的基本结论求得.例3(广州市2023届高三一模)在ABC 中,内角,,A B C 的对边分别为,,a b c ,2,2sin 3sin2c b A C ==.(1)求sin C ; (2)若ABC的面积为2,求AB 边上的中线CD 的长. 解析:(1)因为2sin 3sin2A C =,所以2sin 6sin cos A C C =,所以26cos a c C =,即3cos a c C =, 所以cos 3a C c =,由余弦定理及2c b =得:2222222243cos 222a b c a b b a b C ab ab ab+−+−−===,又cos 36a a C c b ==,所以222232926a b a a b ab b −=⇒=,即2a =,2cos 664b a C b b ===sin C == (2)由214374211sin2ABCSab Cab,所以ab =1)2a =, 所以2,b a ==,因为CD 为AB 边上的中线,所以()12CD CA CB =+,所以()222124CD CA CB CA CB =++⋅()2212cos 4b a ab C =⨯++1418224⎛=⨯++⨯⨯ ⎝⎭7=,所以7CD =,所以AB 边上的中线CD .例4.(湖北省七市(州)2023届高三下学期3月联合统一调研测试)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2cos 2b C a c =+. (1)求B ;(2)设9b =,若点M 是边AC 上一点,2AM MC =,且MAB MBA ∠=∠,求BMC △的面积.【详解】(1)2π3B =. (2)如图所示:因为2AM MC =,所以3AM =,6MC =.又MAB MBA ∠=∠,所以3BM AM ==. 在ABC 中,由余弦定理得2222cos b a c ac B =+−,即2281a c ac ++=.① 又2AM MC =,所以2133BM BA BC =+,两边平方得222414999BM BA BC BA BC =++⋅,即224149cos 999c a ac B =++,所以224281a c ac +−=.②,②-①得233c ac =,所以a c=,代入①得a c ==BMC △中,(22222336BM BC MC +=+==,所以BMC △是以MBC ∠为直角的三角形,所以BMC △的面积为132⨯⨯3.AP 为角平分线:角平分线定理如图,可设θ=∠=∠CAM BAM ,这样可得)1.......(sin 21sin 21⎪⎪⎩⎪⎪⎨⎧⋅⋅⋅=⋅⋅⋅=∆∆θθAM AC S AM AB S ACM ABM .另一方面,设ABC ∆的高为h ,则)2.......(2121⎪⎪⎩⎪⎪⎨⎧⋅⋅=⋅⋅=∆∆h CM S h BM S ACM ABM ,联立上面两式可得:MCBMAC AB =,即角平分线性质定理.例5.(2015全国2卷)ABC ∆中,D 是BC 上的点,AD 平分BAC ∠,ABD ∆面积是ADC ∆面积的2倍. (1) 求sin sin BC; (2) 若AD =1,DC =22求BD 和AC 的长. 解析:(1)1sin 2ABDS AB AD BAD =∠,1sin 2ADCS AC AD CAD =∠ 因为ABDADCSS=,BAD CAD ∠=∠,所以2AB AC =,由正弦定理可得sin 1sin 2B AC C AB ∠==∠.(2)因为::ABDADCSSBD DC =,所以BD =ABD 和ADC 中,由余弦定理知2222cos AB AD BD AD BD ADB =+−∠,2222cos AC AD DC AD DC ADC =+−∠故222222326AB AC AD BD DC +=++=,由(1)知2AB AC =,所以1AC =.4.斯特瓦尔特定理斯特瓦尔特定理:设P 为ABC ∆的BC 边上异于C B ,的任一点,则有CB PC BP BC AP BP AC PC AB ⋅⋅+⋅=⋅+⋅222.证明:由余弦定理,可得:APC PC AP PC AP AC ∠⋅⋅−+=cos 2222①)cos(2222APC PB AP PB AP AB ∠−⋅⋅−+=π②,将上述两式分别乘CP BP ,后相加整理,可得.注:可以看到,斯特瓦尔特定理的证明关键是利用爪型三角形中两角互补,即: 这个隐含条件,而这个条件是处理爪型三角形的一个重要技巧. 推论1.当设P 为ABC ∆的BC 边中点时,222241)(21BC AC AB AP −+=. 注:该结论还可由)(21→→→+=AC AB AP 证得.推论2.当设P 为BAC ∠的角平分线时,PC BP AC AB AP ⋅−⋅=2.推论3.当设P 满足→→⋅=BC BP λ时,2222)1()1(AC AB BC AP λλλλ+−+−=. 例6. 记ABC 是内角A ,B ,C 的对边分别为a ,b ,c .已知2b ac =,点D 在边AC 上,sin sin BD ABC a C ∠=. (1)证明:BD b =;(2)若2AD DC =,求cos ABC ∠解析:(2)由斯特瓦特定理,得. 由b BD =及DC AD 2=,得2222923231b a c b −+=.化简变形,得2223611c a b +=. 因为ac b =2,所以0311622=+−c ac a .即0)32)(3(=−−c a c a .解得a c 3=或a c 32=..ACDCAC AD AC AC AD BC AC DC BA BD ⋅⋅−⋅+⋅=2222当a c 3=时,223a b =.由余弦定理,得(不合题意,舍去). 当a c 32=时,2232a b =.由余弦定理,得.所以127cos =∠ABC . 5.张角定理在ABC ∆中,D 是BC 上的一点,连结AD ,那么ADBACAB CAD AC BAD ∠=∠+∠sin sin sin .证明:因为ACD ABD ABC S S S ∆∆∆+=,由三角形面积公式可得DAC AC AD BAD AD AB BAC AC AB ∠⋅⋅+∠⋅⋅=∠⋅⋅sin 21sin 21sin 21 两边同除AD AC AB ⋅⋅,得到ADBACAB CAD AC BAD ∠=∠+∠sin sin sin例7 (2018年江苏卷)在ABC ∆中,角C B A ,,的对边分别为c b a ,,,︒=∠120ABC ,ABC ∠的平分线交AC 于点D ,且1=BD ,则c a +4的最小值为________.解 由张角定理有BC ABD AB CBD BD ABC ∠+∠=∠sin sin sin ,即ac ︒︒︒+=60sin 60sin 1120sin , 整理得111=+ac .所以.当且仅当a c 2=,即3,23==c a 时取得最小值9.6.等面积思想.设AM 为A ∠的平分线,则设θ=∠=∠CAM BAM ,那么有等面积可得:θθsin )(212sin 21⋅⋅+=⋅=∆AM c b bc S ABC ,进一步可得:AM c b bc ⋅+=⋅)(cos 2θ,于是可以看到,倘若我们知道角θ与角平分线AM 的长度,则可得到c b bc +↔的转化关系,配合均值不等式就可得到一些范围问题. 例8.(2022成都一诊)在ABC 中,已知角2π3A =,角A 的平分线AD 与边BC 相交于点D ,AD =2.则AB +2AC 的最小值为___________.解析:,,,2AB c AC b BC a AD ====,依题意AD 是角A 的角平分线, 由三角形的面积公式得1π1π12π2sin 2sin sin 232323c b bc ⨯⨯⨯+⨯⨯⨯=⨯⨯,672cos 222=−+=∠ac b c a ABC )(1272cos 222凌晨讲数学=−+=∠ac b c a ABC )(945)11)(4(4凌晨讲数学≥++=++=+c a a c a c c a c a化简得22c b bc +=,1112b c +=,()112222223c b AB AC c b c b b c b c ⎛⎫⎛⎫+=+=++=++ ⎪ ⎪⎝⎭⎝⎭236⎛≥+=+ ⎝当且仅当2,c bc b c ==,22,22b b b c +===时等号成立.故答案为:6+例9(江苏省南通市2023届高三下学期第一次调研测试)在ABC 中,,,A B C 的对边分别为(),,,cos 2cos 2cos a b c a B a C c b A −=−. (1)若c =,求cos B 的值;(2)若1,b BAC ∠=的平分线AD 交BC 于点D ,求AD 长度的取值范围. 解析:(1)已知()cos 2cos 2cos a B a C c b A −=−,由正弦定理可得()sin cos 2sin cos 2sin sin cos A B A C C B A −=−,sin cos cos sin 2sin cos 2cos sin A B A B A C A C ∴+=+, ()()sin 2sin A B A C ∴+=+,sin 2sin C B ∴=,2,c b c ∴=,即b ,22222233cos 2a a a a c b B ac +−+−∴=== (2)由(1)知2c b =,由1b =,则2c =.设BAD θ∠=,1112sin22sin 1sin 222ABCSAD AD θθθ=⋅⋅=⋅⋅⋅+⋅⋅⋅,4cos 3AD θ∴=,0,2πθ⎛⎫∈ ⎪⎝⎭, 40,3AD ⎛⎫∴∈ ⎪⎝⎭.例10.(2021新高考1卷)在ABC ∆中,ac b =2,点D 在边AC 上,C a ABC BD sin sin =∠.(1)证明:b BD =;(2)若DC AD 2=,求ABC ∠cos .解析:(1)设ABC 的外接圆半径为R ,由正弦定理,得sin sin ,22b cR ABC C R==∠, 因为sin sin BD ABC a C ∠=,所以22b cBD a R R⋅=⋅,即BD b ac ⋅=.又因为2b ac =,所以BD b =.方法2.(等面积思想)(2)如图,已知2AD DC =,则23ABD ABC S S =△△, 即21221sin sin 2332b ac AD A B BC ⨯=⨯⨯∠∠,而2b ac =,即sin sin ADB ABC ∠=∠,故有ADB ABC ∠=∠,从而ABD C ∠=∠.由2b ac =,即b ca b =,即CA BA CB BD=,即ACB ABD ∽,故AD AB AB AC =,又2b ac =,所以23c a =,则2227cos 212c a b ABC ac +−==∠.7.三角形相似如图,在三角形ABC 中,已知角A 的大小,D 为BC 边上一点.那么我们可利用初中的相似三角形来求解一些这种条件下的爪型三角形问题,简直妙!如下图,过点B 做AC 的平行线交AD 延长线于E ,则CDA BDE ∆∆~,且由平行的性质可知:BED CAD ∠=∠,于是,已知角A 的大小即可得ABE ∠的大小,倘若我们进一步指导AD 的长度,以及点D 为BC 边上的具体位置,那么在ABE ∆中可以解决很多问题,下面通过例题来分析.例11.(2022成都一诊)在ABC ∆中,已知角32π=A ,角A 的平分线AD 与边BC 相交于D ,2=AD ,则AC AB 2+的最小值为________. 解析:如上图,由于BED CAD ∠=∠,故由32π=A 可得3π=∠ABE ,再加之AD 为角A的平分线,则3π=∠=∠=∠BAE BEA ABE ,于是ABE ∆为等边,则2,−==c DE c BE ,最后由于CDA BDE ∆∆~,可得:bc c b c b c AD ED AC BE =+⇒−=⇒=)(222. 由于246)2()11(2)2(21222+≥+⋅+=+⋅⋅=+=+c b c b b c b c AC AB ,等号成立当且仅当b c 2=.注:用辅助线加相似的方法来做这些题目非常容易,比起向量法简单的多.前面的例题读者也可尝试能否用几何方法思考,此处不再赘述.8.坐标法例12.记ABC 是内角A ,B ,C 的对边分别为a ,b ,c .已知2b ac =,点D 在边AC 上,sin sin BD ABC a C ∠=.(1)证明:BD b =;(2)若2AD DC =,求cos ABC ∠.解析:以D 为坐标原点,AC 所在直线为x 轴,过点D 垂直于AC 的直线为y 轴,DC 长为单位长度建立直角坐标系,如图所示,则()()()0,0,2,0,1,0D A C −.由(1)知,3BD b AC ===,所以点B 在以D 为圆心,3为半径的圆上运动.设()(),33B x y x −<<,则229x y +=.⑤由2b ac =知,2BA BC AC ⋅=,9=.⑥,联立⑤⑥解得74x =−或732x =≥(舍去),29516y =,代入⑥式得||||32a BC c BAb =====,由余弦定理得2227cos 212ac b ABC ac +−∠==.。
高考数学二轮复习考点知识与题型专题讲解19---三角恒等变换与解三角形

高考数学二轮复习考点知识与题型专题讲解第19讲 三角恒等变换与解三角形[考情分析] 1.三角恒等变换主要考查化简、求值,解三角形主要考查求边长、角度、面积等,三角恒等变换作为工具,将三角函数与三角形相结合考查求解最值、范围问题.2.三角恒等变换以选择题、填空题为主,解三角形以解答题为主,中等难度.考点一 三角恒等变换 核心提炼1.两角和与差的正弦、余弦、正切公式(1)sin(α±β)=sin αcos β±cos αsin β;(2)cos(α±β)=cos αcos β∓sin αsin β;(3)tan(α±β)=tan α±tan β1∓tan αtan β.2.二倍角的正弦、余弦、正切公式(1)sin 2α=2sin αcos α;(2)cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α;(3)tan 2α=2tan α1-tan 2α.例1 (1)(2022·新高考全国Ⅱ)若sin(α+β)+cos(α+β)=22cos ⎝⎛⎭⎫α+π4sin β,则() A .tan(α-β)=1B .tan(α+β)=1C .tan(α-β)=-1D .tan(α+β)=-1答案 C解析 由题意得sin αcos β+cos αsin β+cos αcos β-sin αsin β=22×22(cos α-sin α)sin β,整理,得sin αcos β-cos αsin β+cos αcos β+sin αsin β=0,即sin(α-β)+cos(α-β)=0,所以tan(α-β)=-1.(2)(2021·全国甲卷)若α∈⎝⎛⎭⎫0,π2,tan 2α=cos α2-sin α,则tan α等于( ) A.1515 B.55 C.53 D.153答案 A解析 方法一因为tan 2α=sin 2αcos 2α=2sin αcos α1-2sin 2α, 且tan 2α=cos α2-sin α, 所以2sin αcos α1-2sin 2α=cos α2-sin α,解得sin α=14. 因为α∈⎝⎛⎭⎫0,π2, 所以cos α=154,tan α=sin αcos α=1515. 方法二 因为tan 2α=2tan α1-tan 2α=2sin αcos α1-sin 2αcos 2α=2sin αcos αcos 2α-sin 2α=2sin αcos α1-2sin 2α, 且tan 2α=cos α2-sin α, 所以2sin αcos α1-2sin 2α=cos α2-sin α,解得sin α=14. 因为α∈⎝⎛⎭⎫0,π2, 所以cos α=154,tan α=sin αcos α=1515. 规律方法 三角恒等变换的“4大策略”(1)常值代换:特别是“1”的代换,1=sin 2θ+cos 2θ=tan 45°等;(2)项的拆分与角的配凑:如sin 2α+2cos 2α=(sin 2α+cos 2α)+cos 2α,α=(α-β)+β等;(3)降幂与升幂:正用二倍角公式升幂,逆用二倍角公式降幂;(4)弦、切互化:一般是切化弦.跟踪演练1 (1)(多选)(2022·张家口模拟)已知sin θcos θ+3cos 2θ=cos θ+32,θ∈⎝⎛⎭⎫0,π2,则θ等于( ) A.π3 B.π6 C.π12 D.π18答案 BD解析 sin θcos θ+3cos 2θ =12sin 2θ+3×1+cos 2θ2=cos ⎝⎛⎭⎫2θ-π6+32=cos θ+32, 故cos ⎝⎛⎭⎫2θ-π6=cos θ, 所以2θ-π6=θ+2k π或2θ-π6=-θ+2k π(k ∈Z ), 故θ=π6+2k π或θ=π18+2k π3(k ∈Z ). 又θ∈⎝⎛⎭⎫0,π2,所以θ=π6或π18. (2)已知函数f (x )=sin x -2cos x ,设当x =θ时,f (x )取得最大值,则cos θ=________.答案 -255解析 f (x )=sin x -2cos x =5sin(x -φ),其中cos φ=55,sin φ=255, 则f (θ)=5sin(θ-φ)=5,因此θ-φ=π2+2k π,k ∈Z ,则cos θ=cos ⎝⎛⎭⎫φ+π2+2k π=-sin φ=-255. 考点二 正弦定理、余弦定理核心提炼1.正弦定理:在△ABC 中,a sin A =b sin B =c sin C=2R (R 为△ABC 的外接圆半径). 变形:a =2R sin A ,b =2R sin B ,c =2R sin C ,sin A =a 2R ,sin B =b 2R ,sin C =c 2R ,a ∶b ∶c =sin A ∶sin B ∶sin C 等.2.余弦定理:在△ABC 中,a 2=b 2+c 2-2bc cos A .变形:b 2+c 2-a 2=2bc cos A ,cos A =b 2+c 2-a 22bc . 3.三角形的面积公式:S =12ab sin C =12ac sin B =12bc sin A .例2 (1)(2022·济南模拟)若△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,已知b sin 2A =a sin B ,且c =2b ,则a b等于( ) A .3 B.13 C.33D. 3 答案 D解析 因为b sin 2A =a sin B ,所以2b sin A cos A =a sin B ,利用正弦定理可得2ab cos A =ab , 所以cos A =12,又c =2b , 所以cos A =b 2+c 2-a 22bc =b 2+4b 2-a 24b 2=12, 解得a b= 3.(2)(2022·全国乙卷)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin C sin(A -B )=sin B sin(C -A ).①证明:2a 2=b 2+c 2;②若a =5,cos A =2531,求△ABC 的周长. ①证明 方法一由sin C sin(A -B )=sin B sin(C -A ),可得sin C sin A cos B -sin C cos A sin B=sin B sin C cos A -sin B cos C sin A ,结合正弦定理a sin A =b sin B =c sin C, 可得ac cos B -bc cos A =bc cos A -ab cos C ,即ac cos B +ab cos C =2bc cos A (*).由余弦定理可得ac cos B =a 2+c 2-b 22, ab cos C =a 2+b 2-c 22,2bc cos A =b 2+c 2-a 2, 将上述三式代入(*)式整理,得2a 2=b 2+c 2.方法二 因为A +B +C =π,所以sin C sin(A -B )=sin(A +B )sin(A -B )=sin 2A cos 2B -cos 2A sin 2B=sin 2A (1-sin 2B )-(1-sin 2A )sin 2B=sin 2A -sin 2B ,同理有sin B sin(C -A )=sin(C +A )sin(C -A )=sin 2C -sin 2A .又sin C sin(A -B )=sin B sin(C -A ),所以sin 2A -sin 2B =sin 2C -sin 2A ,即2sin 2A =sin 2B +sin 2C ,故由正弦定理可得2a 2=b 2+c 2.②解 由①及a 2=b 2+c 2-2bc cos A 得,a 2=2bc cos A ,所以2bc =31.因为b 2+c 2=2a 2=50,所以(b +c )2=b 2+c 2+2bc =81,得b +c =9,所以△ABC 的周长l =a +b +c =14.规律方法 正、余弦定理的适用条件(1)“已知两角和一边”或“已知两边和其中一边的对角”应采用正弦定理.(2)“已知两边和这两边的夹角”或“已知三角形的三边”应采用余弦定理.注意:应用定理要注意“三统一”,即“统一角、统一函数、统一结构”.跟踪演练2 (1)在△ABC 中,若cos C =79,b cos A +a cos B =2,则△ABC 外接圆的面积为() A.49π8 B.81π8 C.81π49 D.81π32答案 D解析 根据正弦定理可知b =2R sin B ,a =2R sin A ,得2R sin B cos A +2R sin A cos B=2R sin(A +B )=2,因为sin(A +B )=sin(π-C )=sin C =1-cos 2C =429,所以R =928,所以△ABC 外接圆的面积S =πR 2=81π32.(2)(2022·衡水中学模拟)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且tan A tan B =2c -bb .①求角A 的大小;②若a =2,求△ABC 面积的最大值及此时边b ,c 的值.解 ①在△ABC 中,由正弦定理得,c =2R sin C ,b =2R sin B ,则tan A tan B =2c b -1=2sin C sin B -1,tan A tan B +1=2sin C sin B, 化简得cos A sin B +sin A cos B =2sin C cos A .即sin(A +B )=2sin C cos A ,∵A +B =π-C ,∴sin(A +B )=sin C ≠0,∴cos A =12, ∵0<A <π,∴A =π3. ②由余弦定理得a 2=b 2+c 2-2bc cos A ,又A =π3,∴b 2+c 2-bc =4, 又b 2+c 2≥2bc ,∴bc ≤4,则S △ABC =12bc sin A ≤12×4×32=3,当且仅当b =c =2时,等号成立, ∴△ABC 面积的最大值为3,此时b =2,c =2.考点三 解三角形的实际应用核心提炼解三角形应用题的常考类型(1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.(2)实际问题经抽象概括后,已知量与未知量涉及两个或两个以上的三角形,这时需作出这些三角形,先解够条件的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.例3 (1)滕王阁,位于江西省南昌市西北部沿江路赣江东岸,始建于唐朝永徽四年,因唐代诗人王勃的诗句“落霞与孤鹜齐飞,秋水共长天一色”而流芳后世.如图,小明同学为测量滕王阁的高度,在滕王阁的正东方向找到一座建筑物AB ,高为12 m ,在它们的地面上的点M (B ,M ,D 三点共线)测得楼顶A 、滕王阁顶部C 的仰角分别为15°和60°,在楼顶A 处测得滕王阁顶部C 的仰角为30°,则小明估算滕王阁的高度为(精确到1 m)()A .42 mB .45 mC .51 mD .57 m答案 D解析 由题意得,在Rt △ABM 中,AM =AB sin 15°, 在△ACM 中,∠CAM =30°+15°=45°,∠AMC =180°-15°-60°=105°,所以∠ACM =30°,由正弦定理得AM sin ∠ACM =CM sin ∠CAM, 所以CM =sin ∠CAM sin ∠ACM·AM =2AB sin 15°, 又sin 15°=sin(45°-30°) =22×32-22×12=6-24, 在Rt △CDM 中,CD =CM sin 60°=6AB 2sin 15°=1262×6-24=36+123≈57(m). (2)雷达是利用电磁波探测目标的电子设备,电磁波在大气中大致沿直线传播,受地球表面曲率的影响,雷达所能发现目标的最大直视距离L =(R +h 1)2-R 2+(R +h 2)2-R 2=2Rh 1+h 21+2Rh 2+h 22(如图),其中h 1为雷达天线架设高度,h 2为探测目标高度,R 为地球半径.考虑到电磁波的弯曲、折射等因素,R等效取8 490 km,故R远大于h1,h2.假设某探测目标高度为25 m,为保护航母的安全,须在直视距离412 km外探测到目标,并发出预警,则舰载预警机的巡航高度至少约为(参考数据:2×8.49≈4.12)()A.6 400 m B.8 100 mC.9 100 m D.1 000 m答案 C解析根据题意可知L=412 km,R=8 490 km,h2=0.025 km,因为L=(R+h1)2-R2+(R+h2)2-R2=2Rh1+h21+2Rh2+h22,即412=(8 490+h1)2-8 4902+(8 490+0.025)2-8 4902≈(8 490+h1)2-8 4902+20.6,解得h1≈9.02(km)≈9 100(m).所以舰载预警机的巡航高度至少约为9 100 m.规律方法解三角形实际问题的步骤跟踪演练3(1)如图,已知A,B,C,D四点在同一条直线上,且平面P AD与地面垂直,在山顶P点测得点A ,C ,D 的俯角分别为30°,60°,45°,并测得AB =200 m ,CD =100 m ,现欲沿直线AD 开通穿山隧道,则隧道BC 的长为()A .100(3+1)mB .200(3+1)mC .200 3 mD .100 3 m答案 C解析 由题意可知A =30°,D =45°,∠PCB =60°,所以∠PCD =120°,∠APC =90°,∠DPC =15°,因为sin 15°=sin(45°-30°) =22×32-22×12=6-24, 所以在△PCD 中,由正弦定理得CD sin ∠DPC =PC sin D, 即1006-24=PC 22, 解得PC =100(3+1)m ,所以在Rt △P AC 中,AC =2PC =200(3+1)m ,所以BC =AC -AB =2003(m).(2)如图是建党百年展览的展馆——国家博物馆.现欲测量博物馆正门柱楼顶部一点P 离地面的高度OP (点O 在柱楼底部).现分别从地面上的两点A ,B 测得点P 的仰角分别为30°,45°,且∠ABO =60°,AB =60 2 米,则OP 等于( )A.40米B.30米C.30 2 米D.30 3 米答案 C解析如图所示,设OP=h,由题意知∠OAP=30°,∠OBP=45°.在Rt△AOP中,OA=OPtan 30°=3h,在Rt△BOP中,OB=h.在△ABO中,由余弦定理,得OA2=AB2+OB2-2AB·OB cos 60°,代入数据计算得到h=302(米).即OP=302(米).专题强化练一、单项选择题1.(2021·全国甲卷)在△ABC中,已知B=120°,AC=19,AB=2,则BC等于() A.1 B. 2 C. 5 D.3答案 D解析 由余弦定理AC 2=AB 2+BC 2-2AB ·BC cos B ,得BC 2+2BC -15=0,解得BC =3或BC =-5(舍去).2.(2021·全国乙卷)cos 2π12-cos 25π12等于( ) A.12 B.33 C.22 D.32答案 D解析 cos 2π12-cos 25π12=1+cos π62-1+cos 5π62=1+322-1-322=32. 3.(2022·榆林模拟)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若△ABC 的面积为3154,b -c =1,cos A =14,则a 等于( ) A .10 B .3 C.10 D. 3答案 C解析 因为cos A =14,所以sin A =154, 又S △ABC =12bc sin A =158bc =3154, 所以bc =6,又b -c =1,可得b =3,c =2,所以a 2=b 2+c 2-2bc cos A =10,即a =10.4.已知cos α=55,sin(β-α)=-1010,α,β均为锐角,则β等于( ) A.π12B.π6C.π4D.π3答案 C解析 ∵α,β均为锐角,即α,β∈⎝⎛⎭⎫0,π2, ∴β-α∈⎝⎛⎭⎫-π2,π2, ∴cos(β-α)=1-sin 2(β-α)=31010, 又sin α=1-cos 2α=255, ∴cos β=cos[(β-α)+α]=cos(β-α)cos α-sin(β-α)sin α =31010×55-⎝⎛⎭⎫-1010×255=22, 又β∈⎝⎛⎭⎫0,π2,∴β=π4. 5.故宫是世界上现存规模最大、保存最为完整的木质结构古建筑群,故宫宫殿房檐设计恰好使北房在冬至前后阳光满屋,夏至前后屋檐遮阴.已知北京地区夏至前后正午太阳高度角约为75°,冬至前后正午太阳高度角约为30°.图1是顶部近似为正四棱锥、底部近似为正四棱柱的宫殿,图2是其示意图,则其出檐AB 的长度(单位:米)约为( )A .3米B .4米C .6(3-1)米D .3(3+1)米答案 C解析 如图,根据题意得∠ACB =15°,∠ACD =105°,∠ADC =30°,∠CAD =45°,CD =24米,所以∠CAD =45°,在△ACD 中,由正弦定理得CDsin ∠CAD =ACsin ∠ADC ,即24sin 45°=AC sin 30°,解得AC =122(米),在Rt △ACB 中,sin ∠ACB =AB AC ,即sin 15°=AB122,解得AB =122sin 15°=122sin(60°-45°)=122×⎝⎛⎭⎫32×22-12×22 =122×6-24=32(6-2)=6(3-1)米.6.(2022·济宁模拟)已知sin α-cos β=3cos α-3sin β,且sin(α+β)≠1,则sin(α-β)的值为() A .-35B.35C .-45D.45答案 C解析 由sin α-cos β=3cos α-3sin β得,sin α-3cos α=cos β-3sin β=sin ⎝⎛⎭⎫π2-β-3cos ⎝⎛⎭⎫π2-β,设f (x )=sin x -3cos x =10⎝⎛⎭⎫110sin x -310cos x=10sin(x -φ), 其中cos φ=110,sin φ=310,φ为锐角,已知条件即为f (α)=f ⎝⎛⎭⎫π2-β,所以π2-β=2k π+α,或π2-β-φ+α-φ=2k π+π,k ∈Z ,若π2-β=2k π+α,k ∈Z ,则α+β=-2k π+π2,k ∈Z ,sin(α+β)=sin π2=1与已知矛盾,所以π2-β-φ+α-φ=2k π+π,k ∈Z ,α-β=2k π+π2+2φ,k ∈Z ,则sin(α-β)=sin ⎝⎛⎭⎫2k π+π2+2φ =sin ⎝⎛⎭⎫π2+2φ=cos 2φ=2cos 2φ-1=-45.二、多项选择题7.(2022·张家口质检)下列命题中,正确的是( )A .在△ABC 中,若A >B ,则sin A >sin BB .在锐角△ABC 中,不等式sin A >cos B 恒成立C .在△ABC 中,若a cos A =b cos B ,则△ABC 是等腰直角三角形D .在△ABC 中,若B =π3,b 2=ac ,则△ABC 必是等边三角形 答案 ABD解析 对于A ,由A >B ,可得a >b ,利用正弦定理可得sin A >sin B ,正确;对于B ,在锐角△ABC 中,A ,B ∈⎝⎛⎭⎫0,π2, ∵A +B >π2, ∴π2>A >π2-B >0, ∴sin A >sin ⎝⎛⎭⎫π2-B =cos B ,因此不等式sin A >cos B 恒成立,正确;对于C ,在△ABC 中,a cos A =b cos B ,利用正弦定理可得sin A cos A =sin B cos B ,∴sin 2A =sin 2B ,∵A ,B ∈(0,π),∴2A =2B 或2A =π-2B ,∴A =B 或A +B =π2, ∴△ABC 是等腰三角形或直角三角形,错误;对于D ,由于B =π3,b 2=ac ,由余弦定理可得 b 2=ac =a 2+c 2-ac ,可得(a -c )2=0,解得a =c ,则A =C =B =π3, ∴△ABC 必是等边三角形,正确.8.函数f (x )=sin x (sin x +cos x )-12,若f (x 0)=3210,x 0∈⎝⎛⎭⎫0,π3,下列结论正确的是( ) A .f (x )=22sin ⎝⎛⎭⎫2x -π4 B .直线x =π4是f (x )图象的一条对称轴C .f (x )在⎝⎛⎭⎫0,π3上的最小值为-22D .cos 2x 0=210答案 AD解析 f (x )=sin 2x +sin x cos x -12 =1-cos 2x2+12sin 2x -12=12(sin 2x -cos 2x )=22sin ⎝⎛⎭⎫2x -π4,故A 正确;当x =π4时,sin ⎝⎛⎭⎫2x -π4=22,∴x =π4不是f (x )的对称轴,故B 错误;当x ∈⎝⎛⎭⎫0,π3时,2x -π4∈⎝⎛⎭⎫-π4,5π12,∴f (x )在⎝⎛⎭⎫0,π3上单调递增,∴f (x )在⎝⎛⎭⎫0,π3上无最小值,故C 错误;∵f (x 0)=3210,∴sin ⎝⎛⎭⎫2x 0-π4=35, 又2x 0-π4∈⎝⎛⎭⎫-π4,5π12, ∴cos ⎝⎛⎭⎫2x 0-π4=45, ∴cos 2x 0=cos ⎣⎡⎦⎤⎝⎛⎭⎫2x 0-π4+π4 =22⎣⎡⎦⎤cos ⎝⎛⎭⎫2x 0-π4-sin ⎝⎛⎭⎫2x 0-π4=210, 故D 正确.三、填空题9.(2022·烟台模拟)若sin α=cos ⎝⎛⎭⎫α+π6,则tan 2α的值为________. 答案 3解析 由sin α=cos ⎝⎛⎭⎫α+π6, 可得sin α=cos αcos π6-sin αsin π6 =32cos α-12sin α,则tan α=33, tan 2α=2tan α1-tan 2α=2×331-⎝⎛⎭⎫332= 3. 10.(2022·泰安模拟)已知sin ⎝⎛⎭⎫π3-α=14,则sin ⎝⎛⎭⎫π6-2α=________. 答案 -78解析 sin ⎝⎛⎭⎫π6-2α=sin ⎣⎡⎦⎤2⎝⎛⎭⎫π3-α-π2 =-cos ⎣⎡⎦⎤2⎝⎛⎭⎫π3-α =-⎣⎡⎦⎤1-2sin 2⎝⎛⎭⎫π3-α=-⎝⎛⎭⎫1-18=-78. 11.(2022·开封模拟)如图,某直径为55海里的圆形海域上有四个小岛,已知小岛B 与小岛C 相距5海里,cos ∠BAD =-45.则小岛B 与小岛D 之间的距离为________海里;小岛B ,C ,D 所形成的三角形海域BCD 的面积为________平方海里.答案 35 15解析 由圆的内接四边形对角互补,得cos ∠BCD =cos(π-∠BAD )=-cos ∠BAD=45>0, 又∠BCD 为锐角,所以sin ∠BCD =1-cos 2∠BCD =35, 在△BCD 中,由正弦定理得BD sin ∠BCD =BD 35=55,则BD =35(海里). 在△BCD 中,由余弦定理得 (35)2=CD 2+52-2×CD ×5×45, 整理得CD 2-8CD -20=0,解得CD =10(负根舍去).所以S △BCD =12×10×5×35=15(平方海里). 12.(2022·汝州模拟)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,a =2,cos 2C =cos 2A +4sin 2B ,则△ABC 面积的最大值为________.答案23解析 由cos 2C =cos 2A +4sin 2B 得,1-2sin 2C =1-2sin 2A +4sin 2B ,即sin 2A =sin 2C +2sin 2B ,由正弦定理得a 2=c 2+2b 2=4,由余弦定理得a 2=b 2+c 2-2bc cos A =4,∴c 2+2b 2=b 2+c 2-2bc cos A ,即cos A =-b 2c<0, ∵A ∈(0,π),∴sin A =1-b 24c 2, ∴S △ABC =12bc sin A =12b 2c 2⎝⎛⎭⎫1-b 24c 2 =12b 2c 2-14b 4, ∵c 2+2b 2=4,∴c 2=4-2b 2,∴S △ABC =12b 2(4-2b 2)-14b 4 =12-94b 4+4b 2, 则当b 2=89时, ⎝⎛⎭⎫-94b 4+4b 2max =-94×6481+4×89=169, ∴(S △ABC )max =12×43=23. 四、解答题13.(2022·新高考全国Ⅱ)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,分别以a ,b ,c 为边长的三个正三角形的面积依次为S 1,S 2,S 3.已知S 1-S 2+S 3=32,sin B =13. (1)求△ABC 的面积;(2)若sin A sin C =23,求b . 解 (1)由S 1-S 2+S 3=32, 得34(a 2-b 2+c 2)=32, 即a 2-b 2+c 2=2,又a 2-b 2+c 2=2ac cos B ,所以ac cos B =1.由sin B =13, 得cos B =223或cos B =-223(舍去), 所以ac =322=324, 则△ABC 的面积S =12ac sin B =12×324×13=28. (2)由sin A sin C =23,ac =324及正弦定理知 b 2sin 2B =ac sin A sin C =32423=94, 即b 2=94×19=14,得b =12. 14.(2022·抚顺模拟)在①(2c -a )sin C =(b 2+c 2-a 2)sin B b ;②cos 2A -C 2-cos A cos C =34;③3c b cos A=tan A +tan B 这三个条件中,任选一个,补充在下面问题中,问题:在△ABC 中,a ,b ,c 分别为角A ,B ,C 所对的边,b =23,________.(1)求角B ;(2)求2a -c 的取值范围.解 (1)选择①:∵(2c -a )sin C =(b 2+c 2-a 2)sin B b, ∴由正弦定理可得(2c -a )c =b 2+c 2-a 2=2bc cos A ,∴2c -a =2b cos A ,可得cos A =2c -a 2b, ∴由余弦定理可得cos A =2c -a 2b =b 2+c 2-a 22bc , 整理可得c 2+a 2-b 2=ac ,∴cos B =c 2+a 2-b 22ac =ac 2ac =12, ∵B ∈(0,π),∴B =π3. 选择②:∵cos 2A -C 2-cos A cos C =1+cos (A -C )2-cos A cos C =1-cos A cos C +sin A sin C 2=1-cos (A +C )2=34, ∴cos(A +C )=-12, ∴cos B =-cos(A +C )=12, 又∵B ∈(0,π),∴B =π3. 选择③: 由正弦定理可得3c b cos A =3sin C sin B cos A,又tan A +tan B =sin A cos A +sin Bcos B=sin A cos B +cos A sin Bcos A cos B =sin Ccos A cos B , 由3cb cos A =tan A +tan B , 可得3sin Csin B cos A =sin Ccos A cos B ,∵sin C >0,∴tan B =3, ∵B ∈(0,π),∴B =π3.(2)在△ABC 中,由(1)及b =23, 得b sin B =a sin A =c sin C =2332=4,故a =4sin A ,c =4sin C ,2a -c =8sin A -4sin C=8sin A -4sin ⎝⎛⎭⎫2π3-A=8sin A -23cos A -2sin A =6sin A -23cos A=43sin ⎝⎛⎭⎫A -π6,∵0<A <2π3,则-π6<A -π6<π2,-12<sin ⎝⎛⎭⎫A -π6<1,-23<43sin ⎝⎛⎭⎫A -π6<43﹒∴2a -c 的取值范围为()-23,43.。
高考数学二轮复习考点知识讲解与练习29---三角函数与解三角形热点问题
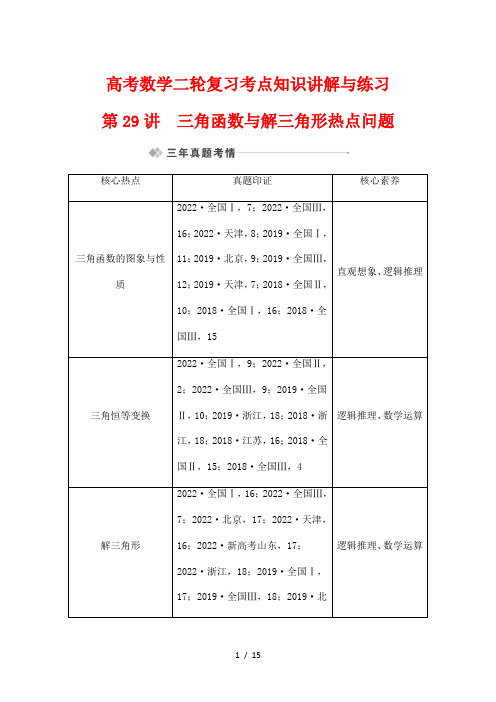
高考数学二轮复习考点知识讲解与练习第29讲三角函数与解三角形热点问题核心热点真题印证核心素养三角函数的图象与性质2022·全国Ⅰ,7;2022·全国Ⅲ,16;2022·天津,8;2019·全国Ⅰ,11;2019·北京,9;2019·全国Ⅲ,12;2019·天津,7;2018·全国Ⅱ,10;2018·全国Ⅰ,16;2018·全国Ⅲ,15直观想象、逻辑推理三角恒等变换2022·全国Ⅰ,9;2022·全国Ⅱ,2;2022·全国Ⅲ,9;2019·全国Ⅱ,10;2019·浙江,18;2018·浙江,18;2018·江苏,16;2018·全国Ⅱ,15;2018·全国Ⅲ,4逻辑推理、数学运算解三角形2022·全国Ⅰ,16;2022·全国Ⅲ,7;2022·北京,17;2022·天津,16;2022·新高考山东,17;2022·浙江,18;2019·全国Ⅰ,17;2019·全国Ⅲ,18;2019·北逻辑推理、数学运算京,15;2019·江苏,15;2018·全国Ⅰ,17三角函数的图象与性质(必修4P147复习参考题A 组第9题、第10题)题目9 已知函数y =(sin x +cos x )2+2cos 2x . (1)求它的递减区间; (2)求它的最大值和最小值.题目10 已知函数f (x )=cos 4x -2sin x cos x -sin 4x . (1)求f (x )的最小正周期;(2)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,求f (x )的最小值及取得最小值时x 的集合.[试题评析]两个题目主要涉及三角恒等变换和三角函数的性质,题目求解的关键在于运用二倍角公式及两角和公式化为y =A sin(ωx +φ)+k 的形式,然后利用三角函数的性质求解. 【教材拓展】 已知函数f (x )=4tan x sin ⎝ ⎛⎭⎪⎫π2-x ·cos ⎝ ⎛⎭⎪⎫x -π3- 3.(1)求f (x )的定义域与最小正周期; (2)讨论f (x )在区间⎣⎢⎡⎦⎥⎤-π4,π4上的单调性.解 (1)f (x )的定义域为{x |x ≠π2+k π,k ∈Z}, f (x )=4tan x cos x cos ⎝⎛⎭⎪⎫x -π3- 3=4sin x cos ⎝ ⎛⎭⎪⎫x -π3- 3=4sin x ⎝ ⎛⎭⎪⎫12cos x +32sin x - 3=2sin x cos x +23sin 2x - 3 =sin 2x -3cos 2x =2sin ⎝⎛⎭⎪⎫2x -π3.所以f (x )的最小正周期T =2π2=π. (2)由-π2+2k π≤2x -π3≤π2+2k π(k ∈Z),得-π12+k π≤x ≤5π12+k π(k ∈Z).设A =⎣⎢⎡⎦⎥⎤-π4,π4,B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |-π12+k π≤x ≤5π12+k π,k ∈Z ,易知A ∩B =⎣⎢⎡⎦⎥⎤-π12,π4. 所以当x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,f (x )在区间⎣⎢⎡⎦⎥⎤-π12,π4上单调递增,在区间⎣⎢⎡⎦⎥⎤-π4,-π12上单调递减.探究提高 1.将f (x )变形为f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π3是求解的关键,(1)利用商数关系统一函数名称;(2)活用和、差、倍角公式化成一复角的三角函数.2.把“ωx +φ”视为一个整体,借助复合函数性质求y =A sin(ωx +φ)+B 的单调性及奇偶性、最值、对称性等问题.【链接高考】(2019·浙江卷)设函数f (x )=sin x ,x ∈R. (1)已知θ∈[0,2π),函数f (x +θ)是偶函数,求θ的值;(2)求函数y =⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫x +π122+⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫x +π42的值域.解 (1)因为f (x +θ)=sin(x +θ)是偶函数, 所以,对任意实数x 都有sin(x +θ)=sin(-x +θ), 即sin x cos θ+cos x sin θ=-sin x cos θ+cos x sin θ, 故2sin x cos θ=0,所以cos θ=0. 又θ∈[0,2π),因此θ=π2或3π2. (2)y =⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫x +π122+⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫x +π42=sin 2⎝ ⎛⎭⎪⎫x +π12+sin 2⎝⎛⎭⎪⎫x +π4=12⎣⎢⎡⎦⎥⎤1-cos ⎝ ⎛⎭⎪⎫2x +π6+12⎣⎢⎡⎦⎥⎤1-cos ⎝ ⎛⎭⎪⎫2x +π2=1-12⎝ ⎛⎭⎪⎫32cos 2x -32sin 2x=1-32cos ⎝⎛⎭⎪⎫2x +π3.由于x ∈R ,知cos ⎝ ⎛⎭⎪⎫2x +π3∈[-1,1],因此,所求函数的值域为⎣⎢⎡⎦⎥⎤1-32,1+32.三角函数与平面向量【例题】(2021·湘赣十四校联考)已知向量m =(sin x ,-1),n =(3,cos x ),且函数f (x )=m ·n .(1)若x ∈⎝⎛⎭⎪⎫0,π2,且f (x )=23,求sin x 的值;(2)在锐角三角形ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .若a =7,△ABC 的面积为332,且f ⎝⎛⎭⎪⎫A +π6=73b sin C ,求△ABC 的周长.[自主解答]解 (1)f (x )=m ·n =(sin x ,-1)·(3,cos x ) =3sin x -cos x =2sin ⎝ ⎛⎭⎪⎫x -π6.∵f (x )=23,∴sin ⎝⎛⎭⎪⎫x -π6=13.又∵x ∈⎝ ⎛⎭⎪⎫0,π2,∴x -π6∈⎝ ⎛⎭⎪⎫-π6,π3,∴cos ⎝⎛⎭⎪⎫x -π6=223.∴sin x =sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫x -π6+π6=13×32+223×12=3+226. (2)∵f ⎝⎛⎭⎪⎫A +π6=73b sin C , ∴2sin A =73b sin C ,即6sin A =7b sin C . 由正弦定理可知6a =7bc . 又∵a =7,∴bc =6.由已知△ABC 的面积等于12bc sin A =332,∴sin A =32. 又∵A ∈⎝⎛⎭⎪⎫0,π2,∴A =π3.由余弦定理,得b 2+c 2-2bc cos A =a 2=7,故b 2+c 2=13, ∴(b +c )2=25,∴b +c =5, ∴△ABC 的周长为a +b +c =5+7.探究提高 1.破解平面向量与“三角”相交汇题的常用方法是“化简转化法”,即先利用三角公式对三角函数式进行“化简”;然后把以向量共线、向量垂直、向量的数量积运算等形式出现的条件转化为三角函数式;再活用正、余弦定理对边、角进行互化. 2.这种问题求解的难点一般不是向量的运算,而是三角函数性质、恒等变换及正、余弦定理的应用,只不过它们披了向量的“外衣”.【尝试训练】(2021·沧州质检)已知a =(53cos x ,cos x ),b =(sin x,2cos x ),函数f (x )=a ·b +|b |2.(1)求函数f (x )的最小正周期; (2)求函数f (x )的单调减区间;(3)当π6≤x ≤π2时,求函数f (x )的值域.解 f (x )=a ·b +|b |2=53cos x sin x +2cos 2x +sin 2x +4cos 2x =53sin x cos x +sin 2x +6cos 2x =532sin 2x +1-cos 2x 2+3(1+cos 2x ) =532sin 2x +52cos 2x +72=5sin ⎝⎛⎭⎪⎫2x +π6+72.(1)f (x )的最小正周期T =2π2=π. (2)由2k π+π2≤2x +π6≤2k π+3π2(k ∈Z)得k π+π6≤x ≤k π+2π3(k ∈Z).∴f (x )的单调减区间为⎣⎢⎡⎦⎥⎤k π+π6,k π+2π3(k ∈Z).(3)∵π6≤x ≤π2,∴π2≤2x +π6≤7π6,∴-12≤sin ⎝⎛⎭⎪⎫2x +π6≤1, ∴1≤5sin ⎝⎛⎭⎪⎫2x +π6+72≤172. ∴当π6≤x ≤π2时,函数f (x )的值域为⎣⎢⎡⎦⎥⎤1,172.解三角形【例题】(12分)(2022·全国Ⅱ卷)△ABC 中,sin 2A -sin 2B -sin 2C =sin B sin C .(1)求A ;(2)若BC =3,求△ABC 周长的最大值. [规范解答]解 (1)由正弦定理和已知条件得用正弦定理化角为边BC 2-AC 2-AB 2=AC ·AB .①2′由余弦定理得BC 2=AC 2+AB 2-2AC ·AB cos A .② 由①②得cos A =-12. 用余弦定理化边为角4′因为0<A <π,所以A =2π3.6′ (2)由正弦定理及(1)得AC sin B=AB sin C=BC sin A=23,8′从而AC =23sin B ,AB =23sin(π-A -B )=3cos B -3sin B . 故BC +AC +AB =3+3sin B +3cos B=3+23sin ⎝ ⎛⎭⎪⎫B +π3. 两角和正弦公式的逆用10′又0<B <π3,所以当B =π6时,△ABC 周长取得最大值3+2 3. 三角函数性质的应用12′❶写全得步骤分:对于解题过程中得分点的步骤有则给分,无则没分,所以得分点步骤一定要写全,如第(1)问中只要写出0<A <π就有分,没写就扣1分,第(2)问中0<B <π3也是如此.❷写明得关键分:对于解题过程中的关键点,有则给分,无则没分,所以在答题时要写清得分关键点,如第(1)问中由正弦定理得BC 2-AC 2-AB 2=AC ·AB ,由余弦定理得BC 2=AC 2+AB 2-2AC ·AB ·cos A ,第(2)问中ACsin B=AB sin C=BC sin A=23等.❸保证正确得计算分:解题过程中计算准确,是得满分的根本保证,如第(1)问中,cos A =-12,若计算错误,则第(1)问最多2分;再如第(2)问3+3sin B +3cos B =3+23sin ⎝⎛⎭⎪⎫B +π3化简如果出现错误,则第(2)问最多得2分.……利用正弦、余弦定理,对条件式进行边角互化……由三角函数值及角的范围求角……由正弦、余弦定理及条件式实现三角恒等变换……利用角的范围和三角函数性质求出最值……检验易错易混,规范解题步骤得出结论【规范训练】(2022·浙江卷)在锐角△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知2b sin A -3a =0. (1)求角B 的大小;(2)求cos A +cos B +cos C 的取值范围. 解 (1)由正弦定理,得2sin B sin A =3sin A ,故sin B =32,由题意得B =π3. (2)由A +B +C =π,得C =2π3-A . 由△ABC 是锐角三角形,得A ∈⎝ ⎛⎭⎪⎫π6,π2 .由cos C =cos ⎝⎛⎭⎪⎫2π3-A =-12cos A +32sin A ,得 cos A +cos B +cos C =32sin A +12cos A +12=sin ⎝⎛⎭⎪⎫A +π6+12∈⎝⎛⎦⎥⎤3+12,32. 故cos A +cos B +cos C 的取值范围是⎝ ⎛⎦⎥⎤3+12,32.1.(2019·天津卷)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知b +c =2a , 3c sin B =4a sin C . (1)求cos B 的值; (2)求sin ⎝ ⎛⎭⎪⎫2B +π6的值.解 (1)在△ABC 中,由正弦定理b sin B=c sin C,得b sin C =c sin B .又由3c sin B =4a sin C , 得3b sin C =4a sin C ,即3b =4a . 因为b +c =2a ,所以b =43a ,c =23a . 由余弦定理可得cos B =a 2+c 2-b 22ac =a 2+49a 2-169a 22·a ·23a =-14. (2)由(1)可得sin B =1-cos 2B =154, 从而sin 2B =2sin B cos B =-158, cos 2B =cos 2B -sin 2B =-78, 故sin ⎝⎛⎭⎪⎫2B +π6=sin 2B cos π6+cos 2B sin π6 =-158×32-78×12=-35+716. 2.已知函数f (x )=a ·b ,其中a =(2cos x ,-3sin 2x ),b =(cos x,1),x ∈R.(1)求函数y =f (x )的单调递减区间;(2)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,f (A )=-1,a =7,且向量m =(3,sin B )与n =(2,sin C )共线,求边长b 和c 的值.解 (1)f (x )=2cos 2x -3sin 2x =1+cos 2x -3sin 2x =1+2cos ⎝⎛⎭⎪⎫2x +π3, 令2k π≤2x +π3≤2k π+π(k ∈Z), 解得k π-π6≤x ≤k π+π3(k ∈Z), ∴函数y =f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π-π6,k π+π3(k ∈Z). (2)∵f (A )=1+2cos ⎝⎛⎭⎪⎫2A +π3=-1, ∴cos ⎝⎛⎭⎪⎫2A +π3=-1,又π3<2A +π3<7π3, ∴2A +π3=π,即A =π3. ∵a =7,∴由余弦定理得a 2=b 2+c 2-2bc cos A =(b +c )2-3bc =7.①∵向量m =(3,sin B )与n =(2,sin C )共线,∴2sin B =3sin C ,由正弦定理得2b =3c ,②由①②得b =3,c =2.3.已知函数f (x )=cos x (cos x +3sin x ).(1)求f (x )的最小值;(2)在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若f (C )=1,S △ABC =334,c =7,求△ABC 的周长.解 (1)f (x )=cos x (cos x +3sin x )=cos 2x +3sin x cos x =1+cos 2x 2+32sin 2x =12+sin ⎝⎛⎭⎪⎫2x +π6. 当sin ⎝⎛⎭⎪⎫2x +π6=-1时,f (x )取得最小值-12. (2)f (C )=12+sin ⎝ ⎛⎭⎪⎫2C +π6=1,∴sin ⎝⎛⎭⎪⎫2C +π6=12, ∵C ∈(0,π),2C +π6∈⎝ ⎛⎭⎪⎫π6,13π6,∴2C +π6=5π6,∴C =π3.∵S △ABC =12ab sin C =334,∴ab =3. 又(a +b )2-2ab cos π3=7+2ab , ∴(a +b )2=16,即a +b =4,∴a +b +c =4+7, 故△ABC 的周长为4+7.4.(2021·东北三省三校联考)已知在△ABC 中,三个内角A ,B ,C 的对边分别为a ,b ,c ,若b 2tan A =a 2tan B ,2sin 2A +B 2=1+cos 2C .(1)求角A 的大小; (2)若点D 为AB 上一点,满足∠BCD =45°,且CD =32-6,求△ABC 的面积. 解 (1)由2sin 2A +B2=1+cos 2C 得1-cos(A +B )=2cos 2C ,即2cos 2C -cos C -1=0, 解得cos C =-12(cos C =1舍去),故C =120°. 因为asin A =bsin B ,b 2tan A =a 2tan B ,所以sin 2B sin A cos A =sin 2A sin B cos B, 即sin A ·cos A =sin B cos B ,故sin 2A =sin 2B ,因此A =B 或A +B =90°(舍去),故A =30°.(2)由(1)知△ABC 为等腰三角形,设BC =AC =m ,由S △ABC =S △ACD +S △BCD 得12m 2·sin 120°=12m · CD ·sin 45°+12m ·CD ·sin 75°,整理得32m=CD⎝⎛⎭⎪⎫22+2+64=()32-6×32+64,解得m=23,故S△ABC=12m2·sin 120°=3 3.5.(2021·郑州调研)已知△ABC的内角A,B,C所对的边分别是a,b,c,其面积S=b2+c2-a24.(1)若a=6,b=2,求cos B;(2)求sin(A+B)+sin B cos B+cos(B-A)的最大值.解(1)∵S=b2+c2-a24,∴12bc sin A=b2+c2-a24,即sin A=b2+c2-a22bc=cos A,则tan A=1,又A∈(0,π),∴A=π4.由正弦定理asin A =bsin B,得622=2sin B,∴sin B=66,又a>b,∴cos B=1-16=306.(2)由第(1)问可知,A=π4,sin(A +B )+sin B cos B +cos(B -A )=sin ⎝ ⎛⎭⎪⎫B +π4+sin B cos B +cos ⎝⎛⎭⎪⎫B -π4 =22sin B +22cos B +sin B cos B +22cos B +22sin B =2(sin B +cos B )+sin B cos B ,令t =sin B +cos B ,则t 2=1+2sin B cos B ,sin(A +B )+sin B cos B +cos(B -A )=2t +12(t 2-1), 令y =12t 2+2t -12=12(t +2)2-32,t ∈(0,2], ∴当t =2,即B =π4时, sin(A +B )+sin B cos B +cos(B -A )取得最大值52.。
第19题 解三角形-2021年高考数学真题逐题揭秘与以例及类(新高考全国Ⅰ卷)(含答案解析)

第19题 解三角形一、原题呈现【原题】记ABC 是内角A ,B ,C 的对边分别为a ,b ,c .已知2b ac =,点D 在边AC 上,sin sin BD ABC a C ∠=.(1)证明:BD b =;(2)若2AD DC =,求cos ABC ∠.解法一:(1)由sin sin BD ABC a C ∠=及正弦定理得2sin sin a C ac b BD b ABC b b ====∠(2)由余弦定理得22222223cos 2223b c b b c a A b c b c ⎛⎫+- ⎪+-⎝⎭==⨯⨯⨯⨯整理得22211203a c b +-=,即2211203a c ac +-=, 所以233c a c a ==或, 当3c a =时,由2b ac =得b =,此时)1a b a c +=<,不满足题意,当23c a =时,由2b ac =得3b a =, 所以2227cos 212ac b ABC ac +-∠==解法二:(1)由题设,sin sin a C BD ABC =∠,由正弦定理知:sin sin c bC ABC=∠,即sin sin C cABC b=∠,∴acBD b=,又2b ac =, ∴BD b =,得证.(2)由题意知:2,,33b b BD b AD DC ===, ∴22222241399cos 24233b b b c c ADB b b b +--∠==⋅,同理2222221099cos 2233b b b a a CDB b b b +--∠==⋅, ∵ADB CDB π∠=-∠, ∴2222221310994233b bc a b b --=,整理得2221123b a c +=,又2b ac =, ∴42221123b b a a +=,整理得422461130a a b b -+=,解得2213a b =或2232a b =,由余弦定理知:222224cos 232a c b a ABC ac b+-∠==-,当2213a b =时,7cos 16ABC ∠=>不合题意;当2232a b =时,7cos 12ABC ∠=;综上,7cos 12ABC ∠=. 【就题论题】本题第(1)问比较简单,利用正弦定理进行边角代换,即可得出结论.第(2)问求解的关键是利用正弦定理、余弦定理整理出,a b 的关系式,再利用余弦定理求cos ABC ∠.二、考题揭秘【命题意图】本题考查正弦定理及余弦定理的应用,考查数学运算与逻辑推理的核心素养.难度:中等偏易【考情分析】新教材高考,解三角形是必考题,一般以解答题形式考查,考查主要方式是利用正弦定理与余弦定理解三角形,有时还会涉及到三角形中的三角变换.【得分秘籍】(1)正弦定理是一个连比等式,只要知道其比值或等量关系就可以运用正弦定理通过约分达到解决问题的目的.(2)运用余弦定理时,要注意整体思想的运用.在已知三角形两边及其中一边的对角,求该三角形的其他边角的问题时,首先必须判断是否有解,如果有解,是一解还是两解,注意“大边对大角”在判定中的应用.(3)应用正弦、余弦定理的解题技巧①求边:利用公式a=sinsinb AB,b=sinsina BA,c=sinsina CA或其他相应变形公式求解.②求角:先求出正弦值,再求角,即利用公式sin A=sina Bb,sin B=sinb Aa,sin C=sinc Aa或其他相应变形公式求解.③已知两边和夹角或已知三边可利用余弦定理求解.④灵活利用式子的特点转化:如出现a2+b2-c2=λab形式用余弦定理,等式两边是关于边或角的正弦的齐次式用正弦定理.(4)判定三角形形状的途径:①化边为角,通过三角变换找出角之间的关系.②化角为边,通过代数变形找出边之间的关系,正(余)弦定理是转化的桥梁.(5)三角形面积公式的应用原则①对于面积公式S=ɑb sin C=ɑc sin B=bc sin A,一般是已知哪一个角就使用哪一个公式.②与面积有关的问题,一般要用到正弦定理和余弦定理进行边和角的转化.(6)应用解三角形知识解决实际问题需要下列三步:①根据题意,画出示意图,并标出条件;②将所求问题归结到一个或几个三角形中(如本例借助方位角构建三角形),通过合理运用正、余弦定理等有关知识正确求解;③检验解出的结果是否符合实际意义,得出正确答案.【易错警示】(1)已知两边及其中一边的对角解三角形时,注意要对解的情况进行讨论,讨论的根据一是所求的正弦值是否合理,当正弦值小于等于1时,还应判断各角之和与180°的关系;二是两边的大小关系.(2)等式两边都不要随意约掉公因式;要移项提取公因式,否则会有漏掉一种形状的可能.三、以例及类(以下所选试题均来自新高考Ⅰ卷地区2020年1-6月模拟试卷) 解答题(2021福建省厦门市高三三模)1. 锐角ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,满足4sin s sin sin in C B a B C +=. (1)求A ;(2)若4b =,ABC 的面积为D 是BC 上的点,AD 平分BAC ∠,求AD .【答案】(1)3A π=;(2)AD =. 【解析】【分析】(1)先利用正弦定理进行边化角并化简得到sin A =,再结合锐角三角形得到角A 即可;(2)先利用面积公式求得c 边,再结合角平分线,利用BAD CAD BAC S S S +=△△△和面积公式,列式计算求得AD 即可.【详解】解:(1)在ABC 中,由正弦定理得sin sin sin a b cA B C==,4sin s sin sin in C B a B C +=,sin sin 4sin sin sin B C C B A B C +=,即sin 4sin sin sin B C A B C =又因为sin sin 0B C ≠,所以4sin A =,即sin A =, 又因为ABC 为锐角三角形,所以3A π=;(2)由1sin 2ABCSbc A ==14sin 23c π⨯⨯=3c =,因为BAC ∠的角平分线为AD ,所以126BAD CAD BAC π∠∠∠===, 又因为BAD CAD BAC S S S +=△△△,所以11sin sin 2626c AD b AD ππ⋅+⋅=113sin 4sin 2626AD AD ππ⨯⋅+⨯⋅=,所以74AD =7AD =. 【点睛】思路点睛:一般地,解有关三角形的题目时,常运用正弦定理(或余弦定理)进行边角互化,要有意识地根据已知条件判断用哪个定理更合适. 如果式子中含有角的余弦或边的二次式时,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理.(2021福建省福州市高三5月二模) 2.ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,sin cos()6b A a B π=-.(1)求B ;(2)若D 是ABC 的外接圆的劣弧AC 上一点,且3a =,4c =,1AD =,求CD .【答案】(1)3π;(2)3. 【解析】【分析】(1)利用正弦定理边化角,再用差角的余弦公式展开化成正切即可得解; (2)利用余弦定理求出边b ,借助圆内接四边形性质求得ADC ∠,最后又由余弦定理建立方程得解.【详解】(1)ABC 中,由正弦定理有sin cos()sin sin sin cos()66b A a B B A A B ππ=-⇒=-,从而1sin sin sin sin )2B A A B B =+,化简得,1sin sin cos 22A B A B =,因为0A π<<,即sin 0A ≠,所以tan B =0B π<<,故3B π=.(2)在ABC 中,由余弦定理知,2222cos b a c ac B =+-2234234cos133π=+-⨯⨯⋅=,即 b =又由于A ,B ,C ,D 四点共圆,从而23ADC B ππ∠=-=, 在ADC 中,设DC x =,由余弦定理得,2222cos AC AD DC AD DC ADC =+-⋅⋅∠,即得22213121cos3x x π=+-⋅⋅⋅,化简得,2120x x +-=,解得3x =或 4x =-(舍去), 故3DC =.【点睛】思路点睛:已知两边及一边的对角求第三边的三角形问题,可用余弦定理建立关于第三边的一元二次方程求解. (广东省汕头市高三二模)3. 随着人们生活水平的不断提高,人们对餐饮服务行业的要求也越来越高,由于工作繁忙无法抽出时间来享受美食,这样网上外卖订餐应运而生.现有美团外卖送餐员小李在A 地接到两份外卖单,他须分别到B 地、D 地取餐,再将两份外卖一起送到C 地,运餐过程不返回A 地.A ,B ,C ,D 各地的示意图如图所示,2km BD =,AD =,120ABD ∠=︒,45DCB ∠=︒,30CDB ∠=︒,假设小李到达B 、D 两地时都可以马上取餐(取餐时间忽略不计),送餐过程一路畅通.若小李送餐骑行的平均速度为每小时20千米,请你帮小李设计出所有送餐路径(如:AB BD DB BC →→→),并计算各种送餐路径的路程,然后选择一条最快送达的送餐路径,并计算出最短送餐时间为多少分钟.(各数值保留3位小数)(参考数据:1.414≈ 1.732≈)【答案】答案见解析 【解析】【分析】根据正弦定理先求解出,BC CD 的值,再根据余弦定理求解出AB 的值,然后分析每条送餐路径的路程并确定出最短送餐路径对应的送餐时间.【详解】解:在BCD △中,由正弦定理可知:sin sin BC BDBDC BCD =∠∠,即:2sin 30sin 45BC =︒︒,解得:BC =由sin sin CD BDCBD BCD =∠∠,即:2sin105sin 45CD =︒︒,解得:1CD =(由余弦定理可得22cos BC BD CD BD CD CDB =+-⋅⋅∠,解得=1CD +或者1CD ,,CBD DCB CD BD ∠>∠∴>=1CD ∴)在ABD △中,由余弦定理可知:222cos 2AB BD AD ABDAB BD即2412cos1204AB AB+-︒=,解得2AB =或4AB =-(舍);①若送餐路径为:AB BD DB BC →→→,则总路程=67.414km +≈①若送餐路径为:AD DB BC →→,则总路程=2 6.878km ≈①若送餐路径为:AB BD DC →→,则总路程=221 6.732km ++≈①若送餐路径为:AD DB BD DC →→→,则总路程=22110.196km ++≈所以最短送餐路径为AB BD DC →→, 此路径的送餐时间为:6.7326020.19620⨯=(分钟). 【点睛】关键点点睛:本题是实际问题中解三角形的应用,解答问题的关键在于通过正余弦定理求解出每一段未知的线段长度,然后再去分析每一条路径对应的总路程并确定出最短路径以及送餐时间. (2021广东省广州市天河区高三三模)4. 在ABC 中,角,,A B C 所对的边分别是,,a b c ,已知22cos c b a B -=. (1)求角A 的值; (2)若ABC的面积S c ==sin sin B C 的值 【答案】(1)3π;(2)12.【解析】【分析】(1)由正弦定理化边为角,然后由诱导公式,两角和的正弦变形可求得A 角;(2)由三角形面积求得b ,由余弦定理求得a ,然后用正弦定理可得sin sin B C . 【详解】(1)因为22cos c b a B -=,由正弦定理得2sin sin 2sin cos C B A B -=,sin 2sin()2sin cos 2sin()2sin cos 2(sin cos cos sin )B A B A B A B A B A B A B π=---=+-=+2sin cos 2cos sin A B A B -=,又B 是三角形内角,sin 0B ≠,所以()1cos ,02A A π=∈,,3A π=; (2)11sin sin 223ABC S bc A b π===△,b =2222212cos 292a b c bc A =+-=+-⨯=,3a =,又3sin sin sin sin 3a b c A B C π==== sin 1B =,1sin 2C = 所以1sin sin 2B C =.【点睛】方法点睛:正弦定理、余弦定理、三角形面积是解三角形的常用公式,解题方法是利用正弦定理进行边角转换,化边为角,然后由诱导公式,两角和的正弦公式变形求角,然后再根据问题先用相应公式计算. (2021河北省张家口市高三三模)5. 在四边形ABCD 中,,1,2AB CD AB AC BD ===,且sin sin DBC DCB ∠∠=.(1)求AD 的长; (2)求ABC 的面积.【答案】(1)AD =(2 【解析】【分析】(1)在DBC △中,由sin sin DBC DCB ∠∠=及正弦定理可得 2.BD CD ==设.AD x =在ABD △和ACD △中,分别由余弦定理,列方程22144724x x x x+-+-=-,解得AD ;(2)在ACD △中,由222AD CD AC +=,得到AD CD ⊥,直接利用面积公式求出ABC 的面积.【详解】(1)因为在四边形ABCD 中,AB CD ,所以cos cos .CDA DAB ∠∠=- 在DBC △中,由sin sin DBC DCB ∠∠=及正弦定理可得 2.BD CD == 设.AD x =在ABD △和ACD △中,由1,AB AC ==22144724x x x x+-+-=-, 所以()()2221447.x x +-=-+-解得x =AD =.(2)在ACD △中,2AD AC CD ===,得222AD CD AC +=,所以AD CD ⊥,所以12ABCSAB AD =⋅=.所以ABC 【点睛】(1)在解三角形中,选择用正弦定理或余弦定理,可以从两方面思考:①从题目给出的条件,边角关系来选择;②从式子结构来选择. (2)平面四边形问题通常转化为解三角形来处理. (2021河北省唐山市高三三模)6. 如图所示,在梯形ABCD 中,//AB CD ,2BAD π∠=,点E 是AD 上一点,2=4DE AE =,2cos cos cos BC BEC BE EBC CE ECB ∠=∠+∠.(1)求BEC ∠的大小;(2)若BCE 的面积S 为BC .【答案】(1)∠BEC =3π;(2)BC = 【解析】【分析】(1)利用余弦定理将角化为边,从而可得1cos 2BEC ∠=,故可求其大小. (2)设AEB α∠=,由解直角三角形可得,BE CE ,根据面积可求α的值,利用余弦定理可求BC 的长.【详解】(1)∵2cos cos cos BC BEC BE EBC CE ECB ∠=∠+∠2222222•2•BE C BE BC CE CE BC BE BE BC CE E BC BC+-+-⋅⋅=+=∴1cos 2BEC ∠=,而BEC ∠为三角形内角,故3BEC π∠=. (2)设AEB α∠=,则23DEC πα∠=-,其中203πα<<, ∵DE =2AE =4, ∴2cos cos AE BE αα==,422cos()cos()33CE DE ππαα=--=, ∵△BCE的面积1sin 23cos cos()3S BE CE παα=⋅⋅=-==2sin(2)16πα==--,2sin(21)6α=--, ∴sin 216πα⎛⎫-= ⎪⎝⎭,因为72666πππα-<-<,故262ππα-=,即3πα=, 此时24cos BE α==,482cos()3CE πα==-, ∴在△BCE 中,由余弦定理得:2222cos 48BC BE CE BE CE BEC +⨯∠=-=,∴BC =(2021湖北省襄阳市高三下学期5月第二次模拟)7. 如图,设ABC 中角,,A B C 所对的边分别为,,a b c ,AD 为BC 边上的中线,已知1c =,12sin cos sin sin sin 4c A B a A b B b C =-+,cos 7BAD ∠=.(1)求b 边的长度;(2)求ABC 的面积.【答案】(1)4b =;(2)【解析】【分析】(1)角化边即可求解;(2)设,AB AC θ=,根据cos 7BAD ∠=列方程即可求解 【详解】(1)由条件12sin cos sin sin sin 4c A B a A b B b C =-+, 可得:2212cos 4ca B a b bc =-+,即222221224a c b ca a b bc ac +-⋅=-+, 化简可得:4c b =,因为1c =,所以4b =(2)因为D 为中点,所以()12AD AB AC =+, 设,AB AC θ=,由()()()22222211122cos 444AD AB AC AB AC AB AC c b c b θ=+=++⋅=++⋅ 得17||2AD =, 又()114cos 22AB AD AB AB AC θ+⋅=⋅+=,所以1cos 7||||17AB AD BAD AB AD ⋅=∠==⋅ 化简可得:228cos 8cos 110θθ+-=解得1cos 2θ=或11cos 14θ=-, 又14cos 0θ+>,所以1cos 2θ=,则sin θ==,所以ABC 的面积为11sin 14222bc A =⨯⨯⨯=【点睛】关键点点睛:计算线段长度,关键是找到基底,然后用基底表示,平方之后再开方即可.(2021湖北省武汉市高三下学期4月质量检测)8. 平面凸四边形ABCD 中,9034BAD BCD AD AB ∠=∠=︒==,,.(1)若45ABC ∠=︒,求CD ;(2)若BC =AC .【答案】(1)2;(2) 【解析】【分析】(1)先利用勾股定理求出BD ,利用差角公式求出sin DBC ∠,再利用直角三角形性质可求CD ;(2)先利用直角三角形及BC 求出sin cos 55CBD CBD ∠=∠=,再利用和角公式求出cos ABC ∠,结合余弦定理可得AC .【详解】(1)连接BD ,在Rt BAD 中,由4390AB AD BAD ==∠=︒,,. 得5BD =,①34sin cos 55ABD ABD ∠=∠=,. ∵45ABC ∠=︒,∴45DBC ABC ∠=︒-∠,①43sin sin 45cos cos 45sin 252510DBC ABD ABD ∠=︒⋅∠-︒⋅∠=⨯=-,在Rt BCD 中,由90BCD ∠=︒知:sin 5102CD BD DBC =⋅∠=⨯=.(2)连接AC ,由(1)知5BD =,在Rt ABD △中易知34sin cos 55ABD ABD ∠=∠=,.在Rt BCD 中,由5BC BD ==得CD =,易知sin cos CBD CBD ∠=∠= ①()cos cos cos cos sin sin ABC ABD CBD ABD CBD ABD CBD ∠=∠+∠=∠⋅∠-∠⋅∠4355=-=. 在ABC 中由余弦定理得:(222222cos 424205AC AB BC AB BC ABC =+-⋅∠=+-⨯⨯= ①AC =(2021湖南省衡阳市高三下学期毕业班联考)9. 如图,ABC 中,1302BD CD BAD =∠=︒,.(1)若AB AC =,求sin DAC ∠;(2)若AD BD =,求AC BC的值. 【答案】(1)sin 1DAC ∠=;(2)【解析】【分析】(1)利用三角形的面积比列方程,化简求得sin DAC ∠.(2)设AD x =,求得3BC x =,利用余弦定理列方程,求得AC =,从而求得AC BC. 【详解】(1)设BC 边上的高为h ,11sin 2211sin 22BAD CAD BD h AB AD BAD SS CD h AC AD CAD ⋅⋅⋅⋅∠==⋅⋅⋅⋅∠, 而1sin 302BD CD AB AC BAD ==∠=︒,,,∴sin 1DAC ∠=. (2)设AD x =,则3060AD BD x BAD ABD ADC ==∠=∠=︒∠=︒,,,2,3CD x BC x ==,在ADC 中,由余弦定理得:()()2222222cos603AC x x xx x =+-⋅︒=,∴AC =,∴33AC BC x ==. (2021湖南省株洲市高三下学期质量检测)10. 如图所示,在四边形ABCD中,tan tan BAD BAC ∠=-∠=(1)求DAC ∠的大小;(2)若2DC =,求ADC 周长的最大值.【答案】(1)3π;(2)6. 【解析】【分析】(1)根据DAC BAD BAC ∠=∠-∠,由()tan tan DAC BAD BAC ∠=∠-∠,利用两角差的正切公式求解;(2)利用正弦定理得到,in AD AC ACD ADC =∠=∠,则ADC 的周长为)22si n sin AD AC ACD ADC ++=+∠+∠,再根据23ACD ADC π∠+∠=,利用两角和与差的三角函数转化为22sin 64AD AC ACD π⎛⎫++=+∠+ ⎪⎝⎭,利用三角函数的性质求解. 【详解】(1)因为DAC BAD BAC ∠=∠-∠,且tan tan 2BAD BAC ∠=-∠= 所以()tan tan DAC BAD BAC ∠=∠-∠,tan tan 1tan BAD BAC BAD BAC∠-∠=+∠⋅∠,-== 因为()0,DAC π∠∈, 所以3DAC π∠=;(2)由正弦定理得sin si n s in DAC A DC A CD ADC D AC ∠=∠==∠所以,in 33AD AC ACD ADC =∠=∠,所以ADC 的周长为)22si n sin AD AC ACD ADC ++=+∠+∠,22sin s n 33i ACD ACD π⎛⎫⎛⎫=+∠+-∠ ⎪ ⎪⎝⎭⎝⎭,32sin cos 223ACD ACD ⎛⎫=+∠+∠ ⎪ ⎪⎝⎭, 2n 64si ACD π⎛⎫=+∠+ ⎪⎝⎭, 因为203ACD π<∠<, 所以5666ACD πππ<∠+<, 所以1sin 126ACD π⎛⎫<∠+≤ ⎪⎝⎭, 所以ADC 的周长的最大值为2416+⨯=.【点睛】方法点睛:三角形周长问题,一般地是利用公式a =2R sin A ,b =2R sin B ,c =2R sin C (R 为ABC 外接圆半径),将边转化为角的三角函数关系,然后利用三角函数知识进行化简,其中往往用到三角形内角和定理A +B +C =π,然后利用三角函数的性质求解.(2021江苏省扬州中学高三3月调研)11. 如图,某生态农庄内有一直角梯形区域ABCD ,//AB CD ,AB BC ⊥,3AB =百米,2CD =百米.该区域内原有道路AC ,现新修一条直道DP (宽度忽略不计),点P 在道路AC 上(异于A ,C 两点),6BAC π∠=,DPA θ∠=.(1)用θ表示直道DP 的长度;(2)计划在ADP △区域内种植观赏植物,在CDP 区域内种植经济作物.已知种植观赏植物的成本为每平方百米2万元,种植经济作物的成本为每平方百米1万元,新建道路DP 的成本为每百米1万元,求以上三项费用总和的最小值.【答案】(1)1sin DP θ=,566ππθ<<;(2) 【解析】【分析】(1)根据解三角形和正弦定理可得1sin DP θ=,566ππθ<<, (2)分别求出APD S △,ADC S △,可得DPC S △,设三项费用之和为f,可得()1cos 12sin 2f θθθ+=+,566ππθ<<,利用导数求出最值. 【详解】解:(1)过点D 作DD AB '⊥,垂足为D ,在Rt ABC 中,∵AB BC ⊥,6BAC π∠=,3AB =,∴BC =在Rt ADD '中,∵1AD '=,DD '=2AD =,∴sin DAD '∠=∴3DAD π'∠=, ∵6BAC π∠=, ∴6DAP π∠=, 在ADP △中,由正弦定理可得sin sin 6AD DP πθ=, ∴1sin DP θ=,566ππθ<<, (2)在ADP △中,由正弦定理可得sin sin AD AP ADPθ=∠,∴52sin6sinAPπθθ⎛⎫-⎪⎝⎭=,∴5sin16sin2sinAPDS AP PDπθθθ⎛⎫-⎪⎝⎭=⋅⋅=△,又11sin22222 ADCS AD DC ADC=⋅⋅∠=⨯⨯⨯=△∴5sin6sinDPC ADC APDS S Sπθθ⎛⎫-⎪⎝⎭=-=△△△,设三项费用之和为f,则()55sin sin1 66211 sin sin sinfπθπθθθθθ⎛⎫⎛⎫⎛⎫--⎪ ⎪⎪⎝⎭⎝⎭⎪=⨯+⨯+⨯⎪⎪⎝⎭5sin16sin sinπθθθ⎛⎫-⎪⎝⎭=+1cos12sinθθ+=+,566ππθ<<,∴()21cos2sinfθθθ-='-,令()0fθ'=,解得23πθ=,当2,63ππθ⎛⎫∈ ⎪⎝⎭时,()0fθ'<,函数f单调递减,当25,36ππθ⎛⎫∈ ⎪⎝⎭时,()0fθ'>,函数f单调递增,∴()min23f fπθ⎛⎫==⎪⎝⎭(2021江苏省南京师范大学《数学之友》高三下学期一模)12. 已知ABC中,D是AC边的中点,且①3BA=;①BC=①BD=①60A ∠=︒.(1)求AC 的长;(2)BAC ∠的平分线交BC 于点E ,求AE 的长.上面问题的条件有多余,现请你在①,①,①,①中删去一个,并将剩下的三个作为条件解答这个问题,要求答案存在且唯一.你删去的条件是___________,请写出用剩余条件解答本题的过程.【答案】删去条件见解析;(1)2;(2)5. 【解析】【分析】若删去①①,由余弦定理易得出两解,不满足题意.删①,在ABD △中和ABC 中分别利用余弦定理建立关系可求解,再利用ABE ACE ABC S S S +=可求AE的长;删①,在ABD △中,由余弦定理有2cosADB ∠=,在BCD △中,cosCDB ∠=,由cos cos ADB CDB ∠=-∠求得x ,利用ABE ACE ABC S S S +=可求AE 的长. 【详解】删①.(1)设,AD CD x BA y ===,在ABD △中,由余弦定理可得227x y xy +-=,在ABC 中,由余弦定理可得22427x y xy +-=,联立方程解得1,3x y ==,所以3,2BA AC ==;(2)设AE m =,则由ABE ACE ABC S S S +=得1113sin 302sin 3032sin 60222m m ⨯+⨯=⨯⨯,解得5m =; 删①,则在ABD △中,由余弦定理有2222cos BD AB AD AB AD A =+-⋅⋅,即2796cos60AD AD =+-⋅,解得1AD =或2AD =,则2AC =或4,有2解,不满足题意;删①,在ABC 中,由余弦定理可得2222cos BC AB AC AB AC A =+-⋅⋅,即2796cos60AC AC =+-⋅,解得1AC =或2,有2解,不满足题意; 删①.(1)设AD CD x ==,在ABD △中,由余弦定理有22222cos2BD AD AB ADB BD AD ∠+-===⋅, 同理,在BCD △中,cosCDB ∠=,cos cos ADB CDB ∠∠=-,2=1x =,2AC ∴=; (2)设AE m =,则由ABE ACE ABC S S S +=得1113sin 302sin 3032sin 60222m m ⨯+⨯=⨯⨯,解得m =. 【点睛】关键点睛:解决本题得关键是熟练应用余弦定理建立等量关系求解. (2021江苏省苏州市高三下学期三模)13. ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知11(0)k k a b c+=>.(1)若2k C π==,求A 的值;(2)若k =2,求当C 最大时ABC 的形状.【答案】(1)4A π=;(2)正三角形. 【解析】【分析】(1)由11a b c +=,结合2C π=,利用正弦定理化简得到c 1o 1sin s A A +=24A A π⎛⎫+= ⎪⎝⎭求解;(2)由112a b c +=,得到2ab c a b =+,由余弦定理得到222cos 2a b c C ab+-=()2142a b ab b a a b ⎡⎤=+-⎢⎥+⎢⎥⎣⎦,再利用基本不等式求解. 【详解】(1)11a b +=sin 11sin si 2n 2A A π⎛⎫- ⎪⎝==⎭+即c 1o 1sin s AA +=sin cos cos A A A A +=⋅,24A A π⎛⎫+= ⎪⎝⎭, 所以24A A π+=或24A A ππ+=-, 解得4A π=; (2)112a b c+=,即2a b ab c +=, 所以2ab c a b =+, 由余弦定理得2222222cos 22ab a b a b c a b C ab ab ⎛⎫+- ⎪+-+⎝⎭==, ()()22141412222a b ab ab b a a b ⎡⎤⎡⎤⎢⎥=+-≥-=⎢⎥⎢⎥+⎢⎥⎣⎦⎢⎥⎣⎦, 当且仅当a b =时,等号成立,此时3C π=,ABC 是正三角形.【点睛】方法点睛:在解有关三角形的题目时,要有意识地考虑用哪个定理更适合,或是两个定理都要用,要抓住能够利用某个定理的信息,一般地,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.(2021山东省泰安肥城市高三三模)14. 已知锐角ABC ∆的外接圆半径为1,内角,,A B C 的对边分别为,,a b c ,ABC ∆的面积为S2224)S c b =+-.(1)求C ;(2)求bc a的取值范围. 【答案】(1)3C π=;(2bc a<< 【解析】 【分析】(1)2224S c b =+-)2224a b c S +-=,根据余弦定理以及三角形的面积公式可得1cos 4sin 2C ab C =⨯,化简整理即可求出结果;(2)根据正弦定理把bc a变形为2sin 2sin B A,进而得到23sin A Aπ⎛⎫- ⎪⎝⎭然后以函数的思想根据角A 的范围求值域即可.【详解】解:(1)2224S c b =-)2224a b c S +-=∴1cos 4sin 2C ab C =⨯sin C C = ∵cos 0C ≠,∴tan C =又(0,)C π∈ ∴3C π=.(2)ABC ∆的外接圆半径为1 ∴2sin c C=,即2sin c C =又sin sin sin a b c A B C ==, ∴2sin a A =,2sin b B =∴bc a==23sin sin A B A Aπ⎛⎫- ⎪⎝⎭==1cos sin22sinA AA⎫+⎪⎝⎭=32tan A=+又因为ABC∆是锐角三角形∴22ABππ⎧<<⎪⎪⎨⎪<<⎪⎩,即2232AAπππ⎧<<⎪⎪⎨⎪<-<⎪⎩,∴62Aππ<<∴tan3>A,1tan A<<32tan2A<<,∴bca<<【点睛】解三角形中的求值域的问题,有两种解题思路:(1)找到边与边之间的关系,利用均值不等式求出最值,再结合三角形两边之和大于第三边,两边之差小于第三边来确定范围;(2)利用正弦定理,转化为关于某个角的函数,以函数的思想求值域,注意转化的角的范围是关键.(2021山东省潍坊市高三三模)15. 在ABC中,内角A,B,C的对边分别为a,b,c,M是AC上的点,BM平分ABC∠,ABM的面积是BCM面积的2倍.(1)求sinsinCA;(2)若1cos4B=,2b=,求ABC的面积.【答案】(1)2;(2)4.【解析】【分析】(1)由2ABM BCMS S=△△,ABM MBC∠=∠,得到2AB BC=,由正弦定理得sin2sinC ABA BC==;(2)由(1)知2c a =,代入满足1cos 4B =的余弦定理,求得a ,c ,并求得sin B ,则由面积公式1sin 2ABC S ac B =△即可求得三角形面积. 【详解】解:(1)1sin 2ABM AB S BM ABM =⋅∠△, 1sin 2BCM BC S BM MBC =⋅∠△. 因为2ABM BCM S S =△△,ABM MBC ∠=∠,所以2AB BC =. 由正弦定理得sin 2sin C AB A BC == (2)由sin 2sin C A=得2c a =, 由余弦定理得2222cos b a c ac B =+-, 又因为1cos 4B =,2b =, 所以2221444a a a +-⨯4=, 所以1a =,从而2c =. 又因为1cos 4B =且0πB <<,所以sin 4B =.因此 11sin 122244ABC a S c B ==⨯⨯⨯=△. 【点睛】关键点点睛:根据角平分线及面积关系求得2c a =,并利用正弦定理,余弦定理进行边角转化,解得三角形中的参数.。
2023年高考数学二轮复习第二篇经典专题突破专题一三角函数和解三角形第1讲三角函数的图象和性质

返回导航
专题一 三角函数和解三角形
高考二轮总复习 • 数学
所以 ω=-16+23k,k∈Z, 所以 ω=52,f(x)=sin 52x+π4+2, 所以 fπ2=sin 54π+π4+2=1. 故选 A.
返回导航
专题一 三角函数和解三角形
高考二轮总复习 • 数学
返回导航
2.(2022·全国甲卷)设函数 f(x)=sin ωx+π3在区间(0,π)恰有三个极
返回导航
【解析】 f′(x)=-sin x+sin x+(x+1)cos x=(x+1)cos x,所以 f(x) 在区间0,π2和32π,2π上 f′(x)>0,即 f(x)单调递增;在区间π2,32π上 f′(x)<0, 即 f(x)单调递减,又 f(0)=f(2π)=2,fπ2=π2+2,f32π=-32π+1+1=- 32π,所以 f(x)在区间[0,2π]上的最小值为-32π,最大值为π2+2.故选 D.
值点、两个零点,则 ω 的取值范围是
( C)
A.53,163
B.53,169
C.163,83
D.163,169
专题一 三角函数和解三角形
高考二轮总复习 • 数学
返回导航
【解析】 依题意可得 ω>0,因为 x∈(0,π),所以 ωx+π3∈π3,ωπ+π3,
要使函数在区间(0,π)恰有三个极值点、两个零点,
又 y=sin x,x∈π3,3π的图象如下所示:
则52π<ωπ+π3≤3π,解得163<ω≤83,即 ω∈163,83.故选 C.
专题一 三角函数和解三角形
高考二轮总复习 • 数学
返回导航
3.(2022·全国甲卷)将函数 f(x)=sin ωx+π3(ω>0)的图象向左平移π2个 单位长度后得到曲线 C,若 C 关于 y 轴对称,则 ω 的最小值是 ( C )
由考题定考向,探方法成策略——以2021年新高考全国Ⅰ卷解三角形问题为例

试题研究2023年6月上半月㊀㊀㊀由考题定考向,探方法成策略以2021年新高考全国I卷解三角形问题为例◉江苏省连云港市城头高级中学㊀程玲强㊀㊀1真题呈现,问题解析考题㊀(2021年新高考全国Ⅰ卷第19题)记әA B C的内角A,B,C的对边分别为a,b,c.已知b2=a c,点D在A C边长,B D s i nøA B C=a s i n C.(1)证明:B D=b;(2)若A D=2D C,求c o søA B C .图1解析:本题为解三角形问题,可先绘制辅助图形,如图1所示.(1)根据题设可知,B D=a s i n Cs i nøA B C.由正弦定理得cs i n C=bs i nøA B C,即s i n Cs i nøA B C=cb.所以B D=a cb,又知b2=a c,则推出B D=b,得证.(2)由A C=b,A D=2D C,可得A D=2b3,D C=b3.所以,在әA B D中,c o søA D B=13b29-c24b23.同理可得c o søC D B=10b29-a22b23.因为øA D B=π-øC D B,所以13b29-c24b23=a2-10b292b23,整理得2a2+c2=11b23.又b2=a c,所以2a2+b4a2=11b23,整理得6a4-11a2b2+3b4=0,解得a2b2=13或a2b2=32.在әA B C中,由余弦定理,可得c o søA B C=a2+c2-b22a c=43-a22b2.当a2b2=13时,c o søA B C=76>1,不符合题意;当a2b2=32时,c o søA B C=712.综上可知,c o søA B C=712.另解:对于第(2)问,还可以从向量视角来解析.已知A D=2D C,则D是三角形边A C的三等分点,则有B Dң=13B Aң+23B Cң,两边平方,可得|B Dң|2=19|B Aң|2+49|B Aң||B Cң|c o søA B C+49|B C|2.①在әA B C中,由余弦定理,可得c o søA B C=a2+c2-b22a c.结合题目条件有b2=9D C2=a c,B D=b=3D C.将上述式子代入①式,消去B D,c o søA B C和b,可初步得到6a2-11a c+3c2=0,则c=23a或c=3a.当c=3a时,b2=a c=3a2,由余弦定理,得c o søA B C=76>1,不符合题意;当c=23a时,b2=a c=23a2,可得c o søA B C=712.2命题揭秘,技巧探究上述考题为高考常见的解三角形问题,主要考查三角函数的核心知识,如正弦定理㊁余弦定理,以及利用定理度量三角形,对学生计算分析㊁利用知识解决实际问题的能力有较高的要求.下面深入解读考题的06Copyright©博看网. All Rights Reserved.2023年6月上半月㊀试题研究㊀㊀㊀㊀命题规律,以及常用的解题技巧.2.1命题规律探究正弦定理㊁余弦定理是高考的热点知识,也是解三角形的核心知识,它们常用来求解三角形的相关问题,如已知边求其他角,判断三角形的形状,求三角形的面积,等等.同时,考题中也常将两个定理与和差公式㊁倍角公式以及三角形的面积公式相结合,转化的技巧性极强.问题解答需要灵活运用正弦定理㊁余弦定理,并有效结合函数与方程思想㊁化归转化思想等.2.2解题技巧探究正弦定理㊁余弦定理是解三角形的核心知识,对应变形式的应用也极为广泛,也是需要重点掌握的知识;另外需要掌握以下几个解析技巧.(1)正弦定理的推广:a s i n A=b s i n B=c s i n C=2R,其中R为әA B C外接圆的半径.求解әA B C外接圆的面积或周长时,可利用正弦定理的推广式来求外接圆的半径.(2)三角形面积公式:S=12a b s i n C=12b c s i n A=12c a s i n B.对于上式,可从三角形内角与边来解读,即三角形的面积可表示为任意两边及其夹角正弦值乘积的一半.(3)正弦知识与三角形个数:利用正弦定理的变形式可判断满足条件的三角形个数.由正弦定理可变形出s i n B=b s i n A a.当s i n B=b s i n A a>1,则满足条件的三角形为0个,即无解;当s i n B=b s i n A a=1,则满足条件的三角形为1个;当s i n B=b s i n A a<1,则满足条件的三角形为1个或2个.(4)正弦定理的适用问题:已知两角和任意一边,求其他边和角;已知两边和其中一边的对角,求其他边和角.(5)利用正㊁余弦定理解题常用策略:利用两个定理解题常结合转化思想,即将边转化为角,或将角转化为边,最终目标是实现角或边的统一.对于三角形中的不等式问题,可利用两个定理来适当 放缩 .对于三角形的取值范围问题,若以余弦定理为切入点,则可将问题转化为不等式;若以正弦定理为切入点,则可将问题转化为三角函数.3关联探究,解题分析解三角形问题的类型十分多样,所涉知识考点也较为众多,结合图形理解条件把握三角形特征,活用定理是解题的关键.下面结合具体问题进行关联探究.3.1倍角公式转化,破解三角函数值问题涉及倍角的三角函数问题较为特殊,需用倍角公式构建倍角与三角形内角的关系,然后利用正弦定理㊁余弦定理加以运算突破.图2例1㊀如图2所示,用三个全等的әA B F,әB C D,әC A E拼成了一个等边三角形A B C,әD E F为等边三角形,且E F=2A E,设øA C E=θ,则s i n2θ的值为.解析:设A E=k(k>0),则E F=2k.由øA C E=θ,әA B F,әB C D,әC A E全等,可得øF A B=θ, C D=k,D E=2k.又әA B C为等边三角形,所以øC A E=π3-θ.在әC A E中,由正弦定理,可得A Es i nøA C E=C Es i nøC A E,即3s i nθ=32c o sθ-12s i nθ.整理得t a nθ=37,则s i n2θ=2t a nθt a n2θ+1=2ˑ37349+1=7326.评析:例1是关于倍角的三角函数问题,问题涉及了全等三角形和等边三角形,利用正弦定理来求解所涉内角的正弦值是解题的基础,而利用倍角公式构建三角形内角和倍角之间的关系则是解题的关键.3.2正弦定理转化,破解面积取值问题三角形面积取值问题十分常见,从三角函数视角分析,可灵活运用正弦定理来求解,对于其中取值范围的分析,则可结合角度和边长的大小关系.例2㊀在锐角三角形A B C中,内角A,B,C的对边分别为a,b,c.已知b s i n B+C2=a s i n B,且c=2,则锐角三角形A B C面积的取值范围为.解析:由b s i n B+C2=a s i n B,可得b c o s A2=a s i n B.由正弦定理,可得s i n B c o s A2=s i n A s i n B.由0<B<π2,可得s i n B>0,故c o s A2=s i n A,即c o s A2=2s i n A2c o s A2.又0<A<π2,所以0<A2<π4,则c o sA2>0.故s i nA2=12,进而可得A=π3.16Copyright©博看网. All Rights Reserved.试题研究2023年6月上半月㊀㊀㊀图3如图3所示,在әA B C中B C1ʅA C,B C2ʅA B,可知A C1=A Bc o sπ3=1,A C2=A Bc o sπ3=4.因为әA B C为锐角三角形,所以点C在线段C1C2上运动,但不包括端点,于是有A C1<b<A C2,即1<b<4.而әA B C的面积可表示为SәA B C=12b c s i n A=32b,结合b的取值可得32bɪ(32,23).故әA B C面积的取值范围为(32,23).评析:例2是求三角形面积的取值范围问题,解题的关键是构建三角形模型㊁确定b的取值范围.上述解题分两阶段突破.第一阶段,结合余弦定理确定内角A的大小;第二阶段,结合图形求解b的取值范围,进而由三角形面积公式求面积的取值范围.3.3两角和差转化,破解三角函数最值问题对于与两角相关的三角函数值问题,突破的核心是两角和与差的公式,即完成两角的统一化,构建单一变量,将问题转化为简单的函数问题,然后利用函数性质求最值.例3㊀在әA B C中,内角A,B,C的对边分别为a,b,c,其面积S可表示为S=b2+c2-a24,试回答下列问题.(1)如果a=6,b=2,求c o s B的值;(2)试求s i n(A+B)+s i n B c o s B+c o s(B-A)的最大值.解析:(1)简答.利用面积公式可得A=π4,结合正弦定理可得s i n B=b s i n A a=66,分析可知B为锐角,故c o s B=306.(2)由(1)可知A=π4,所以s i n(A+B)+s i n B c o s B+c o s(B-A)=22s i n B+22c o s B+s i n B c o s B+22s i n B+22c o s B=2(s i n B+c o s B)+s i n B c o s B.令t=s i n B+c o s B=2s i n(B+π4),由Bɪ(0,3π4),得B+π4ɪ(π4,π),则s i n(B+π4)ɪ(0,1],所以tɪ(0,2].故s i n(A+B)+s i n B c o s B+c o s(B-A)=2t+t2-12=12(t+2)2-32,tɪ(0,2].分析可知,当t=2,B=π4时,原式取得最大值,且最大值为52.评析:上述第(2)问可视为是两角和差的三角函数最值问题,突破的核心策略是角的转化,即通过内角的变换将问题转化为单一内角的三角函数问题.上述解析过程充分利用了两角和与差的公式㊁内角的三角函数基本关系等,问题的转化思想和运算技巧体现得极为充分.4解后反思,教学建议解三角形问题是高考数学的重要题型,探究命题规律,总结解题技巧是教学探究的重点,下面进一步进行反思教学.4.1理解定理内涵,正确认识定理正弦定理㊁余弦定理是破解 解三角形 问题的核心定理,充分理解定理内涵㊁正确认识定理是探究学习的关键.实际上两大定理揭示了三角形边角关系.如余弦定理体现了三角形三边长与一个角余弦值的关系,是对勾股定理的推广;而正弦定理则体现了三角形各边和所对角正弦值之比的关系.教学中要帮助学生理解该知识内涵,同时引导学生体验定理的探究过程,掌握定理的证明方法,强化学生的思辨思维,以从根本上掌握解三角形问题的知识核心.4.2开展思维训练,总结通性通法边化角 和 角化边 是解三角形问题常用的两种思路,总体而言就是为了实现问题条件的 边 或角 的统一.在教学中要重视学生的思维训练,促使学生充分掌握该类问题的通性通法,正确判断解决问题应选用的方法.4.3关注类型问题,总结破题技巧解三角形问题的类型十分多样,问题的综合性㊁拓展性极强,因此关注问题的多种类型,总结破题技巧十分关键[1].实际教学中,教师要帮助学生构建解三角形问题的体系,引导学生合理变式,灵活运用定理㊁公式来转化突破.同时注意拓展解法,提升学生的思维水平.参考文献:[1]景君.不畏浮云遮望眼 一道江苏联赛解三角形题的剖析[J].中学数学,2021(7):19G20.Z26Copyright©博看网. All Rights Reserved.。
高考数学(文)二轮复习专题一 三角函数和平面向量 第2讲 平面向量、解三角形 Word版含答案

第2讲 平面向量、解三角形【课前热身】第2讲 平面向量、解三角形(本讲对应学生用书第4~6页)1.(必修4 P76习题7改编)在矩形ABCD 中,O 是对角线的交点,若BC u u u r =e 1,DC u u u r =e 2,则OC u u u r= .【答案】12(e 1+e 2)【解析】因为O 是矩形ABCD 对角线的交点,BCu u u r =e 1,DCu u u r =e 2,所以OCu u u r =12(BC u u u r +DC u u u r)=12(e 1+e 2).2.(必修4 P90习题19改编)已知向量a =(6,-3),b =(2,x+1),若a ⊥b ,则实数x= . 【答案】3【解析】因为a ⊥b ,所以a ·b =0,所以12-3x-3=0,解得x=3.3.(必修5 P10练习2改编)在锐角三角形ABC 中,设角A ,B 所对的边分别为a ,b.若2a sin B=3b ,则角A= .【答案】π3【解析】在△ABC 中,由正弦定理及已知得2sin A·sin B=3sin B ,因为B 为△ABC的内角,所以sin B ≠0,所以sinA=32.又因为△ABC 为锐角三角形,所以A ∈π02⎛⎫ ⎪⎝⎭,,所以A=π3.4.(必修4 P80例5改编)已知向量a =(1,0),b =(2,1),则当k= 时,向量k a -b 与a +3b 平行.【答案】-13【解析】由题设知向量a 与b 不平行,因为向量k a -b 与a +3b 平行,所以1k =-13,即k=-13.5.(必修5 P16习题1(3)改编)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知a=7,b=43,c=13,则△ABC 最小的内角为 .【答案】π6【解析】因为13<43<7,所以C<B<A ,又因为cosC=222-2a b c ab +=2743⨯⨯=32,所以C=π6.【课堂导学】平面向量与三角函数综合例1 (2016·淮安5月信息卷)已知向量m =(cos α,sin α),n =(3,-1),α∈(0,π).(1)若m ⊥n ,求角α的大小; (2)求|m +n |的最小值.【解答】(1)因为m =(cos α,sin α),n =(3,-1),且m ⊥n ,所以3cos α-sin α=0,即tan α=3.又因为α∈(0,π),所以α=π3.(2)因为m +n =(cos α+3,sin α-1),所以|m +n |=22(cos 3)(sin -1)αα++=523cos -2sin αα+=π54cos 6α⎛⎫++ ⎪⎝⎭. 因为α∈(0,π),所以α+ππ7π666⎛⎫∈ ⎪⎝⎭,,故当α+π6=π,即α=5π6时,|m +n |取得最小值1.正弦定理、余弦定理的应用例2 (2016·苏州暑假测试)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c.已知sin2-2A B+sin A sin B=22+.(1)求角C 的大小;(2)若b=4,△ABC 的面积为6,求c 的值.【解答】(1)sin2-2A B+sin A sin B=1-cos(-)2A B+2sin sin2A B=1-cos cos-sin sin2A B A B+2sin sin2A B=1-cos cos sin sin2A B A B+=1-(cos cos-sin sin)2A B A B=1-cos()2A B+=1-cos(π-)2C=1cos2C+=22+,所以cos C=22.又0<C<π,所以C=π4.(2)因为S=12ab sin C=12a×4×sinπ4=2a=6,所以a=32.因为c2=a2+b2-2ab cos C=(32)2+42-2×32×4×22=10,所以c=10.变式1(2016·南通一调)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知(a+b-c)(a+b+c)=ab.(1)求角C的大小;(2)若c=2a cos B,b=2,求△ABC的面积.【解答】(1)在△ABC中,由(a+b-c)(a+b+c)=ab,得222-2a b cab+=-12,即cosC=-12.因为0<C<π,所以C=2π3.(2)方法一:因为c=2a cos B,由正弦定理,得sin C=2sin A cos B.因为A+B+C=π,所以sin C=sin(A+B ),所以sin(A+B )=2sin A cos B ,即sin A cos B-cos A sin B=0, 所以sin(A-B )=0.又-π3<A-B<π3,所以A-B=0,即A=B ,所以a=b=2. 所以△ABC 的面积为S △ABC =12ab sin C=12×2×2×sin 2π3=3.方法二:由c=2a cos B 及余弦定理,得c=2a×222-2a c b ac +,化简得a=b ,所以△ABC 的面积为S △ABC =12ab sin C=12×2×2×sin 2π3=3.变式2 (2016·南通、扬州、淮安、宿迁、泰州二调)在斜三角形ABC 中,tan A+tan B+tan A tan B=1.(1)求角C 的大小; (2)若A=15°,2,求△ABC 的周长.【解答】(1)因为tan A+tan B+tan A tan B=1, 即tan A+tan B=1-tan A tan B.因为在斜三角形ABC 中,1-tan A tan B ≠0,所以tan(A+B )=tan tan 1-tan tan A BA B +=1,即tan(180°-C )=1,tan C=-1. 因为0°<C<180°,所以C=135°.(2)在△ABC 中,A=15°,C=135°,则B=180°-A-C=30°.由正弦定理sin BC A =sin CAB =sin ABC ,得sin15BC o =°sin30CA=2=2,故BC=2sin 15°=2sin(45°-30°)=2(sin 45°cos 30°-cos 45°sin 30°)=6-2 2,CA=2sin 30°=1.所以△ABC的周长为AB+BC+CA=2+1+6-22=2622++.平面向量与解三角形综合例3(2016·无锡期末)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知向量a=(sin B-sin C,sin C-sin A),b=(sin B+sin C,sin A),且a⊥b.(1)求角B的大小;(2)若b=c·cos A,△ABC的外接圆的半径为1,求△ABC的面积.【解答】(1)因为a⊥b,所以a·b=0,即sin2B-sin2C+sin A(sin C-sin A)=0,即sin A sin C=sin2A+sin2C-sin2B,由正弦定理得ac=a2+c2-b2,所以cos B=222-2a c bac+=12.因为B∈(0,π),所以B=π3.(2)因为c·cos A=b,所以bc=222-2b c abc+,即b2=c2-a2,又ac=a2+c2-b2,b=2R sin3,解得a=1,c=2.所以S△ABC =12ac sin B=3.变式(2016·苏锡常镇二调)在△ABC中,内角A,B,C的对边分别是a,b,c,已知向量m=(cos B,cos C),n=(4a-b,c),且m∥n.(1)求cos C的值;(2)若c=3,△ABC的面积S=15,求a,b的值.【解答】(1)因为m∥n,所以c cos B=(4a-b)cos C,由正弦定理,得sin C cos B=(4sin A-sin B)cos C,化简得sin(B+C)=4sin A cos C.因为A+B+C=π,所以sin(B+C)=sin A.又因为A∈(0,π),所以sin A≠0,所以cos C=14.(2)因为C∈(0,π),cos C=14,所以sin C=21-cos C=11-16=15.因为S=12ab sin C=15,所以ab=2.①因为c=3,由余弦定理得3=a2+b2-12ab,所以a2+b2=4,②由①②,得a4-4a2+4=0,从而a2=2,a=2(a=-2舍去),所以a=b=2.【课堂评价】1.(2016·镇江期末)已知向量a=(-2,1),b=(1,0),则|2a+b|=. 【答案】13【解析】因为2a+b=(-3,2),所以|2a+b|=22(-3)2+=13.2.(2016·南京学情调研)已知向量a=(1,2),b=(m,4),且a∥(2a+b),则实数m=.【答案】2【解析】方法一:由题意得a=(1,2),2a+b=(2+m,8),因为a∥(2a+b),所以1×8-(2+m)×2=0,故m=2.方法二:因为a∥(2a+b),所以存在实数λ,使得λa=2a+b,即(λ-2)a=b,所以(λ-2,2λ-4)=(m,4),所以λ-2=m且2λ-4=4,解得λ=4,m=2.3.(2016·南京、盐城一模)在△ABC中,设a,b,c分别为内角A,B,C的对边,若a=5,A=π4,cos B=35,则c=.【答案】7【解析】因为cos B=35,所以B∈π2⎛⎫⎪⎝⎭,,从而sin B=45,所以sin C=sin(A+B)=sinA cos B+cos A sin B=2×35+2×45=72,又由正弦定理得sinaA=sincC,即52 =72c,解得c=7.4.(2016·全国卷Ⅲ)在△ABC中,B=π4,BC边上的高等于13BC,则cos A=.(第4题)【答案】-10【解析】如图,作AD ⊥BC交BC 于点D ,设BC=3,则AD=BD=1,AB=2,AC=5.由余弦定理得32=(2)2+(5)2-2×2×5×cos A ,解得cos A=-10.5.(2016·南通一调)已知在边长为6的正三角形ABC 中,BD u u u r =12BC u u u r ,AE u u u r=13AC u u u r ,AD 与BE 交于点P ,则PB u u u r ·PD u u ur 的值为 .(第5题)【答案】274【解析】如图,以BC 为x 轴,AD 为y 轴,建立平面直角坐标系,不妨设B (-3,0),C (3,0),则D (0,0),A (0,33),E (1,23),P 330⎛ ⎝⎭,,所以PB u u u r ·PD u u ur =|PD u u u r |2=233⎝⎭=274.温馨提示:趁热打铁,事半功倍.请老师布置同学们完成《配套检测与评估》第3~4页.【检测与评估】第2讲 平面向量、解三角形一、 填空题1.(2016·苏州暑假测试)设x ,y ∈R ,向量a =(x ,1),b =(2,y ),且a +2b =(5,-3),则x+y= .2.(2016·盐城三模)已知向量a ,b 满足a =(4,-3),|b |=1,|a -b |=21,则向量a ,b 的夹角为 .3.(2016·全国卷Ⅱ)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若cos A=45,cos C=513,a=1,则b= .4.(2016·天津卷)在△ABC 中,若AB=13,BC=3,∠C=120°,则AC= .5.(2016·南京三模)如图,在梯形ABCD 中,AB ∥CD ,AB=4,AD=3,CD=2,AM u u u u r =2MD u u u u r .若AC u u u r ·BM u u u u r =-3,则AB u u u r ·AD u u u r = .(第5题)6.(2016·无锡期末)已知平面向量α,β满足|β|=1,且α与β-α的夹角为120°,则α的模的取值范围为 .7.在锐角三角形ABC 中,角A ,B ,C 所对的边分别为a ,b ,c.若b a +ab =6cos C ,则tan tan C A +tan tan CB = .8.(2016·苏北四市摸底)在△ABC 中,AB=2,AC=3,角A 的平分线与AB 边上的中线交于点O ,若AO u u u r =x AB u u u r+y AC u u u r (x ,y ∈R ),则x+y 的值为 .二、 解答题9.(2016·苏北四市期末)已知在锐角三角形ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,sin A=35,tan(A-B )=-12.(1)求tan B 的值; (2)若b=5,求c 的值.10.(2016·徐州、连云港、宿迁三检)如图,在梯形ABCD 中,已知AD ∥BC ,AD=1,BD=210,∠CAD=π4,tan ∠ADC=-2.(1)求CD 的长; (2)求△BCD 的面积.(第10题)11.(2016·南京三模)在△ABC 中,已知a ,b ,c 分别为角A ,B ,C 的对边.若向量m =(a ,cos A ),向量n =(cos C ,c ),且m ·n =3b cos B.(1)求cos B 的值;(2)若a ,b ,c 成等比数列,求1tan A +1tan C 的值.【检测与评估答案】第2讲 平面向量、解三角形一、 填空题1. -1 【解析】由题意得a +2b =(x+4,1+2y )=(5,-3),所以4512-3x y +=⎧⎨+=⎩,,解得1-2x y =⎧⎨=⎩,,所以x+y=-1.2. π3【解析】设向量a ,b 的夹角为θ,由|a -b|=,得21=(a -b )2=a 2+b 2-2a ·b =25+1-2·5·cos θ,即cos θ=12,所以向量a ,b 的夹角为π3.3. 2113 【解析】因为cos A=45,cos C=513,且A ,C 为三角形的内角,所以sin A=35,sin C=1213,所以sin B=sin(A+C )=sin A cos C+cos A sin C=6365.由正弦定理得sin b B =sin aA ,解得b=2113.4. 1【解析】设AC=x,由余弦定理得cos 120°=29-13 23xx+⋅⋅=-12,即x2+3x-4=0,解得x=1或x=-4(舍去),所以AC=1.5.32【解析】方法一:设ABu u u r=4a,ADu u u r=3b,其中|a|=|b|=1,则DCu u u r=2a,AMu u u u r=2b.由ACu u u r·BMu u u u r=(ADu u u r+DCu u u r)·(BAu u u r+AMu u u u r)=-3,得(3b+2a)·(2b-4a)=-3,化简得a·b=18,所以ABu u u r·ADu u u r=12a·b=32.方法二:建立平面直角坐标系,使得A(0,0),B(4,0),设D(3cos α,3sin α),则C(3cos α+2,3sin α),M(2cos α,2sin α).由ACu u u r·BMu u u u r=-3,得(3cos α+2,3sin α)·(2cos α-4,2sin α)=-3,化简得cos α=18,所以ABu u u r·ADu u u r=12cos α=32.6.23⎛⎤⎥⎝⎦,【解析】如图,设α=ABu u u r,β=ACu u u r,则β-α=BCu u u r,∠ABC=60°,设α与β的夹角为θ,则0°<θ<120°,由正弦定理可得°||sin(120-)θα=°||sin60β,所以|α|=233sin(120°-θ).因为0°<θ<120°,所以0°<120°-θ<120°,所以0<sin(120°-θ)≤1,所以0<|α|≤23.(第6题)7. 4 【解析】b a +ab =6cos C ⇒6ab cos C=a 2+b 2⇒3(a 2+b 2-c 2)=a 2+b 2⇒a 2+b 2=232c ,所以tan tan C A +tan tan CB =sin cosC C ·cos sin sin cos sin sin B A B A A B +=sin cos C C ·sin()sin sin A B A B +=1cos C ·2sin sin sin C A B =2222-aba b c +·2c ab =22223-2c c c=2222c c =4.8. 58 【解析】如图,在△ABC 中,AD 为∠BAC 的平分线,CE 为AB 边上的中线,且AD ∩CE=O.在△AEO 中,由正弦定理得sin AE AOE ∠=sin EOEAO ∠.在△ACO 中,由正弦定理得sin AC AOC ∠=sin COCAO ∠,两式相除得AE AC =EO OC .因为AE=12AB=1,AC=3,所以EO OC =13,所以CO u u u r =3OE u u u r ,即AO u u u r -AC u u u r =3(AE u u u r -AO u u ur ),即4AO u u u r =3AE u u u r+AC u u u r ,所以4AO u u u r =32AB u u ur +AC u u u r ,从而AO u u u r =38AB u u u r +14AC u u u r .因为AO u u u r =x AB u u u r+y ACu u u r ,所以x=38,y=14,所以x+y=58.(第8题)二、 解答题9. (1) 方法一:在锐角三角形ABC 中,由sin A=35,得cos A=21-sin A =45,所以tan A=sin cos A A =34.由tan(A-B )=tan -tan 1tan ?tan A B A B +=-12,得tan B=2.方法二:在锐角三角形ABC 中,由sin A=35,得cos A=21-sin A =45,所以tanA=sin cos A A =34.又因为tan(A-B )=-12,所以tan B=tan[A-(A-B )]=tan -tan(-)1tan tan(-)A A B A A B +=31--42311-42⎛⎫ ⎪⎝⎭⎛⎫+⨯ ⎪⎝⎭=2. (2) 由(1)知tan B=2,得sin B=255,cos B=55, 所以sin C=sin(A+B )=sin A cos B+cos A sin B=11525,由正弦定理sin bB =sin cC ,得c=sin sin b C B =112.10. (1) 因为tan ∠ADC=-2,且∠ADC ∈(0,π),所以sin ∠ADC=255,cos ∠ADC=-55. 所以sin ∠ACD=sinππ--4ADC ∠⎛⎫ ⎪⎝⎭ =sin ∠ADC+π4=sin ∠ADC ·cos π4+cos ∠ADC ·sin π4=,在△ADC 中,由正弦定理得CD=·sin sin AD DACACD ∠∠=.(2) 因为AD ∥BC ,所以cos ∠BCD=-cos ∠ADC=,sin ∠BCD=sin ∠ADC=.在△BDC 中,由余弦定理得BD 2=BC 2+CD 2-2BC ·CD ·cos ∠BCD , 即BC 2-2BC-35=0,解得BC=7,所以S △BCD =12BC ·CD ·sin ∠BCD=12×7=7.11. (1) 因为m ·n =3b cos B ,所以a cos C+c cos A=3b cos B. 由正弦定理得sin A cos C+sin C cos A=3sin B cos B , 所以sin(A+C )=3sin B cos B , 所以sin B=3sin B cos B.因为B 是△ABC 的内角,所以sin B ≠0,所以cos B=13.(2) 因为a ,b ,c 成等比数列,所以b 2=ac. 由正弦定理得sin 2B=sin A ·sin C.因为cos B=13,B 是△ABC 的内角,所以sinB=,又1tan A +1tan C =cos sin A A +cos sin C C =cos ?sin sin ?cos sin sin A C A CA C +⋅ =sin()sin sin A C A C +⋅=sin sin sin B A C=2sin sin B B =1sin B=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021年高考数学二轮复习重难点突破解答题处理方法一.必备知识 1.正弦定理及其变形sin A sin B sin C变式:〔1〕 a = 2R sin A,b = 2R sin c = 27?sin C 〔边化角公式〕〔2〕 s in A = —,sin B = —,sin C =—〔角化边公式〕2R 2R 2R 〔3〕 a : b: c = sin A: sin B: sin C〔4〕 “_sinA a _ sin A b _ sin Bb sin 3c sinC c sinC2. 正弦定理适用情况: 〔1〕两角及任一边;〔2〕两边和一边的对角〔需要判断三角形解的情况〕.3. 余弦定理及其推论 a 2 =b 2 +c 2 -2〃ccos A b 2 = a 2 + c 2 一 2accos B c 2 =a 2 +b 2 -lab cosC4. 余弦定理适用情况:〔1〕两边及夹角;〔2〕三边.注.解三角形或判定三角形形状时,可利用正余弦定理实现边角转化〔这也是正 余弦定理的作用〕,统一成边的形式或角的形式. 5. 常用的三角形面积公式〔2〕 S=^absinC = ^6/csin B = ^bcsinA = 〔两边夹一角〕; 6.三角形中常用结论〔1〕 d+Z?>c,b+c>a,d+c 〉方〔即两边之和大于第三边,两边之差小于第三边〕〔2〕在A>BOd>/?U>sinA>sinB 〔即大边对大角,大角对大边〕解三角形类的=2R 〔/?为三角形外接圆半径〕ZABC= —(1)假设=求梯形ABCD 的面积;(3 )在 AABC 中,A + B + C = 7t ,所以 ① sin(A + B) = sinC : cos (A + B) = - cos C;即cos A+cosB+cosC 的取值范用是点睛:此类问题关键是运用正余弦定理进行边角互化。
2•多三角形问题(2021年佛山一模18题)如图,在梯形ABCD 中,ABIICD, AB = 2, CD = 5,® tan(A + B) = -tanC; 二、典型试题 1•条件为边角混合等式④sin C = cos — 2,⑤ cos = sin£ (2021-浙江卷)在锐角ZVIBC 中,角儿B, C 的对边分别为⑦b, c,且2hsinA = \/3a •(/)求角(//)求 cosA+cosB+cosC 的取值范围.【详解】⑴ 由2bsinA = ^a 结合正弦定理可得: 2sin Bsin A = "sin A,:, sin B =△ABC 为锐角三角形,故3 =彳.(〃)结合(1)的结论有:cos A + cos B + cos C = cos A + —+ cos2(2TTIT" =cos A- — cos A + —2 2llM7TsinA + 1 =—sinA + lcosA + 1 =sin| A +壬 +-2 2 I 6丿 2c 2 ▲龙Ov 齐-作 可得:0< A < —2龙,龙 2龙 —<A+—<——, 3 6 3那么sin7sine(2)假设4C 丄 BD,求 tanZABD.【解析】〔1〕设阮詁 在ZVIBC 中,由余弦定理得28 = X 2+4-2XXX 2X 〔--〕, 即 X 2+2X -24 = 0 ,解 得 x=4 或 x=-6 (舍),所以 BC =4 那么S^c 亠2x4禺 =2乜,因为仞=竺,所以Swc= 冷竺=5馆那么梯形 2 2 ABCD 的面积S = S“BC + S MX = 7希(2)设那么ZBDC=a, ZBAC=--a, ZDBC = — ^a,23ZBCA = a~-,在AABC 中,由正弦定理得一-—=―弘一6・, 兀、 ・/兀、在△ BDC 中,由正弦定理得一磐——=—两式相除得 ・“小 sina即 5V3tan 2a-7tana-2V3=0,解得 tana = ^ 或-Q,因为 a e卑L 即 tanZABD=^点睛:此类问题在多边形中找到需要的三角形进行过渡,本质还是正余弦定 理已经联立解方程的思路。
3.条件为面积、周长等要素〔2021*全国 2 卷〕A AB C 中,sin :A-sin :B-sin 2C=sinBsinC. 〔1〕 求 A ;〔2〕假设BC=3,求“13〔7周长的最大值.【详解】〔1〕由正弦定理可得:BC 2-AC 2-AB 2=AC AB ,sin(a - —) sin(y - a)sin(——一a)所以 5 Visin' a 一 7 sin a cos a - 2X /3COS 26Z = 0,人 AC 2+AB 2^BC 21 …人山八..2/r.・ cos A = --------------------- =——,・ Aw 〔°9 兀〕,・・A ----2ACAB 2 3〔2〕由余弓玄定理得:BC? = AC 2 + AB 2-2AC • AB cos A = AC 2 + AB 2 + AC AB =9, 即〔AC + AB 〕2-ACAB = 9-ACAB<^ AC \ 〔当且仅当 AC = AB 时取等号〕,:.^ =〔AC + ABy-AC-AB >{ AC+ AB\-\ AC ~A8 j =#〔AC + A3〕‘, 解得:AC +AB<2^3 〔当且仅当AC = AB 时取等号〕, :4ABC 周长厶=AC + A3 + BC S 3 + 2J5,ABC 周长的最大值为 3 + 2 •点睛:此类问题在正余弦定理的根底上熟记解三角的面积、周长公式,根本 不等式及变形也是经常用到的。
三、稳固练习 1.AABC 中,角 4、B 、C 的对边分别为 “、b 、c,且〔^/2a-c 〕cosB = bcosC.〔1〕求角B 的大小:2. 〔2021・江苏卷〕在△A3C 中,角久B, C 的对边分别为⑺ 伏c, d = 3,c = >/2.B = 45o . (1) 求sinC 的值;4(2) 在边BC 上取一点6使得cosZADC = --,求tan3. 〔广东省深圳、汕头、潮州、揭阳需校2021届髙三联考〕在锐角三角形ABC中,角A,B,C 所对的边分别是a,b,c,且c = 2/ , 2sin 〔2C--〕 = ^ .〔1〕假设a = 2、伍,求角A :(2)设向量m = (cos2A + l,cos4),n =,且m 丄n,求tan(—+ A)的值.4⑵求△ ABC面积的最大值.四、稳固练习答案1.【解析】试题分析:〔1〕血_c〕cosB = bcosC这个等式中既有边又有角,这种等式一般有两种考虑:要么只留边,要么只留角•在此题中这两种方法都行.思路一、由正弦泄理得:〔J,sinA—sinC〕cos3 = sinBcosC,然后用三角函数公式可求出COS 3・2 2 i 2 2 i 2 2思路二、由余弦泄理得:〔屈_c〕x" +「_ 7=bx“ + ?,化简得2ac 2aba2 +c2-b2 =迈ac.再由余弦泄理可得cos B = £.用正切和角公式可求出tan〔- + A〕.试题解析:(1)法一.•••(VTa-c)cosB = bcosC :. (>/2 sin A -sin C)cos B = sin B cos C :.y/2 sin A cos B = sin B cos C + sin C cos B = sin(B + C) = sin Asin A H 0 cos B = — /. ZB = — 6 分法二由余弦定理得:〔Q/ — c〕x"i「一广=b】m ,化简得:所以C osB = f/-~( -~/?- = —, B = -2ac 2 43tan A = —, tan(— + A)=4 42、【详解】(1)由余弦定理得h 2 =a 2+c 2-2accosB = 9 + 2-2x3xy/2x^- = 5,所以由正弦定理得盏二匕3心讐每,所以冷0日,所以c°sC = Rn 貝琴所以 sin ADAC = sin - ADAC) =sin(ZA£)C + ZC)由于SCE (O,勺,所以c5C 」sinSC=l^ 所以 3cos ZDAC 113.(1)由题意,得siii(2C — —) = ^-,C e (0,—),3 / 2即2C--e(--,—),所以2C-- = -,解得C = -. 3 3 3 3 33由正弦定理,得—,解得siiiA = ^.sinA sin 兰 -又avc,所以0 <AvC =冬,所以A =-・3 4(2)在Z\ABC 中,c = 2羽、C =—,贝IJ 由余弦定理,得 c 2= a 2+b 2-2abcos C,即 12 = a 2 +b 2-ab>ab所以Swc=丄"sinC<3ji (当且仅当-b 时,即△ABC 为等边三角形时,等号成立), 2 所以△4BC 的而积的最大值为3巧・4当 cos A =—时, 4(2)由于cosZADC = -- t ZADC e/ \恃打,所以S5C=4c°SC=|= sinZADC.cosC +cosZAPC.sinC = |x^ +>/5 2y/5x —=------- 525tan — + tan A 41 — tan — tan A。
