空心、实心的问题
判断空心实心的三种方法

判断空心实心的三种方法空心实心是指物体的形态、结构以及材质,是很多科学和工程实验中常用的概念。
对于物理学上的结构,一般情况下,空心物体指的是有内部空间的物体,而实心物体是没有内部空间的物体。
但是在实际的生活和工程实验中,要判断一个物体的空心实心、是不是比较困难的。
因为大家都知道,很多物体表面看起来很光滑,但实际上却有许多细小的小孔和缝隙,这使得判断比较复杂。
那么,如何判断一个物体是空心还是实心呢?下面就来介绍几种方法,以便以后在实际工作和生活中便捷有效地判断空心实心的物体。
第一种方法是重量测试法。
根据重量的大小可以很容易的判断物体是空心还是实心。
对于同样大小的物体来说,如果它重量比较轻,那么就是空心物体;如果它重量比较重,那么就是实心物体。
重量测试法最大的优势在于,不仅可以快速地判断物体的空心实心,还可以推测物体的大致结构和材质。
第二种方法是中心压力测试法。
这种方法可以判断一个物体表面看起来是空心的,但实际上可以有细小的小孔和缝隙。
在进行中心压力测试之前,可以先通过重量测试判断物体的空心实心,之后再施加中心压力,从而判断物体细节结构的组成。
第三种方法是声学测试法。
声学测试法是一种测试物体空心实心最简单、最实用的方法。
如果物体是空心的,那么把耳朵放在物体上,当外部环境产生噪声时,会有更明显的回声;如果物体是实心的,那么当外部环境产生的噪声通过物体时,会有更多的吸收效果,所以没有明显的回声。
以上就是判断一个物体是空心还是实心的三种方法。
它们的不同之处在于,重量测试法判断的快慢度、中心压力测试法的准确程度以及声学测试法的简单易行性。
当然,这三种方法也可以结合起来使用,以达到更准确的测试结果。
总之,准确判断一个物体的空心实心,不仅是很多物理学、工程学以及医学等科学实验中很常用的概念,也是很多日常生活中需要采用的方法。
只要我们准确认识这三种方法,就可以有效地判断物体的空心实心,从而更加有效地利用这些物体。
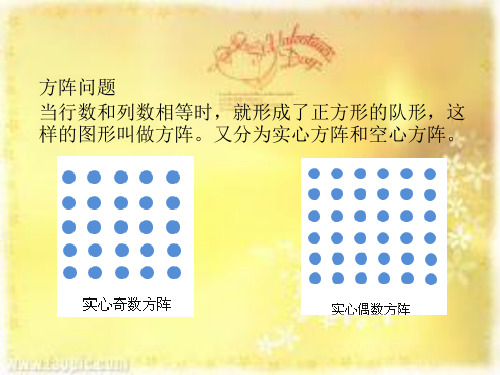
小学数学典型应用题16:方阵问题(含解析)

小学数学典型应用题16:方阵问题(含解析)方阵问题【含义】将若干人或物依一定条件排成正方形(简称方阵)。
根据已知条件求总人数或总物数,这类问题就叫做方阵问题。
【数量关系】(1)方阵每边人数与四周人数的关系:四周人数=(每边人数-1)×4每边人数=四周人数÷4+1(2)方阵总人数的求法:实心方阵:总人数=每边人数×每边人数空心方阵:总人数=外每边的人数平方-内每边的人数平方内每边人数=外每边人数-层数×2(3)若将空心方阵分成四个相等的矩形计算,则:总人数=(每边人数-层数)×层数×4解题思路和方法方阵问题有实心与空心两种。
实心方阵的求法是以每边的数自乘;空心方阵的变化较多,其解答方法应根据具体情况确定。
例1:佳一学校参加运动会团体操比赛的运动员排成了一个正方形队列。
如果要使这个正方形队列减少一行和一列,则要减少23人。
那么参加团体操表演的运动员一共有多少人?解:1、要知道参加表演的运动员共有多少人,只需要找到最外层每边有多少人即可。
2、一个正方形队列,减去一行和一列,就是去掉了两条边上的人数,其中顶点上的人数计算了两次,所以减少的人数=每边的人数×2-1。
所以开始每边有(23+1)÷2=12(人),参加表演的有12×12=144(人)。
例2:欢欢用围棋子围成一个三层空心方阵,最外一层每边有围棋子16枚,欢欢摆这个方阵共用了多少枚围棋子?解法1:1、本题考查的空心方阵,根据四周的枚数和每边上的枚数之间的关系,算出每一层的棋子数。
2、方阵每向里一层,每边的枚数就减少2枚。
知道最外一层每边放16枚,就可求出第二层及第三层每边枚数,知道各层每边的枚数,就可以求出各层的总数。
最外一层的棋子的枚数:(16-1)×4=60(枚),第二层棋子的枚数:(16-2-1)×4=52(枚),第三层棋子的枚数:(16-2-2-1×4=11×4=44(枚),摆这个方阵共用了60+52+44=156(枚)棋子。
小学数学应用题之方阵问题

小学数学应用题之方阵问题【含义】将若干人或物依一定条件排成正方形(简称方阵),根据已知条件求总人数或总物数,这类问题就叫做方阵问题。
【数量关系】(1)方阵每边人数与四周人数的关系:四周人数=(每边人数-1)×4每边人数=四周人数÷4+1(2)方阵总人数的求法:实心方阵:总人数=每边人数×每边人数空心方阵:总人数=外每边的人数平方-内每边的人数平方内每边人数=外每边人数-层数×2(3)若将空心方阵分成四个相等的矩形计算,则:总人数=(每边人数-层数)×层数×4【解题思路和方法】方阵问题有实心与空心两种。
实心方阵的求法是以每边的数自乘;空心方阵的变化较多,其解答方法应根据具体情况确定。
例1:佳一学校参加运动会团体操比赛的运动员排成了一个正方形队列。
如果要使这个正方形队列减少一行和一列,则要减少23人。
那么参加团体操表演的运动员一共有多少人?解:1、要知道参加表演的运动员共有多少人,只需要找到最外层每边有多少人即可。
2、一个正方形队列,减去一行和一列,就是去掉了两条边上的人数,其中顶点上的人数计算了两次,所以减少的人数=每边的人数×2-1。
所以开始每边有(23+1)÷2=12(人),参加表演的有12×12=144(人)。
例2:欢欢用围棋子围成一个三层空心方阵,最外一层每边有围棋子16枚,欢欢摆这个方阵共用了多少枚围棋子?解法1:1、本题考查的空心方阵,根据四周的枚数和每边上的枚数之间的关系,算出每一层的棋子数。
2、方阵每向里一层,每边的枚数就减少2枚。
知道最外一层每边放16枚,就可求出第二层及第三层每边枚数,知道各层每边的枚数,就可以求出各层的总数。
最外一层的棋子的枚数:(16-1)×4=60(枚),第二层棋子的枚数:(16-2-1)×4=52(枚),第三层棋子的枚数:(16-2-2-1)×4=11×4=44(枚),摆这个方阵共用了60+52+44=156(枚)棋子。
物体是否空心的判别方法

物体是否空心的判别方法普定县鸡场中学李树平在初中物理中,有一类关于判别物体是否空心的问题。
许多学生总是容易出错,在此我以一个例子来谈谈这类问题的解决办法,希望对学生在解决这类问题时有所帮助。
例:一个质量是178g,体积为30cm3的铜球,请判断它是空心还是实心的?(ρ铜=8.9×103kg/m3)分析:解决这类问题,我们可以从三个方面入手:一是比较密度;二是比较质量;三是比较体积。
通过计算出的密度、质量、体积与已知密度、质量、体积的比较来判断此铜球是空心还是实心。
解法一:比较密度计算出质量为178g,体积为30 cm3的铜球的密度与铜的密度ρ铜=8.9×103kg/m3作比较,若计算出的密度等于铜的密度ρ铜=8.9×103kg/m3,此铜球为实心的;若小于铜的密度ρ铜=8.9×103kg/m3为空心的。
ρ/铜=vm=30178=5.93g/cm3=5.93×103kg/m3ρ/铜<ρ铜即 5.93×103kg/m3<8.9×103kg/m3所以此铜球为空心的。
解法二:比较质量计算出体积为30 cm3的铜球的质量与题目告诉的178g作比较,若等于178g为实心,若大于178g为空心的。
m铜=ρ铜v=8.9×103×30×106=0.267kg=267g267g>178g所以此铜球为空心的。
解法三:比较体积计算出质量178g 的铜球的体积,与题目告诉的铜球体积30 cm 3作比 较,若等于30 cm 3为实心,若小于30 cm 3为空心的。
(ρ铜=8.9×103kg/m 3=8.9g/cm 3)v 铜= m =9.8178=20cm 320cm 3<30cm 3所以此铜球是空心的。
在实际的问题处理中,你是采用比较密度、体积还是质量,你可根据具体情况来选择,它们最后的结果都是相同的。
一空心

一、空心、实心问题例1:一质量为395g,体积为100cm3的铁球,问它是空心的还是实心的?若是空心的,空心部分的体积多大?(ρ铁=7.9g/cm3)反馈练习:1、有质量相等的两个球,它们的体积比是V1:V2=1:5,材料的密度比是ρ1: ρ2=4:1,其中有一个是空心的,已知实心球的体积是V,则空心球空心部分的体积是()A、VB、2VC、1/5VD、1/4V2、用同种材料制成的三个正方体,它们的边长分别为1cm、2cm、3cm,质量分别为3g、24g、54g,已知其中一个是空心的,请用两种不同方法鉴别出来。
3、体积和质量相等的铝球、铁球和铅球,密度分别是ρA1=2.7g/cm3,ρFe=7.9g/cm3,ρPb=11.3g/cm3,下列说法正确的是()A、若铝球是实心的,则铁球和铅球一定是空心的。
B、若铁球是实心的,则铝球和铅球一定是空心的。
C、若铅球是实心的,则铝球和铁球一定是空心的。
D、三个球都可能是空心的。
4、两个铜球质量相等,但体积不等,则它们()A、一定是空心球B、都是实心球C、至少有一个实心球D、至少有一个是空心球5、一个空心铜球,其空心部分是球体,它的质量与同外径的实心铁球质量相等,空心部分体积与铜球外观体积之比是多少?(ρ铁=7.9g/cm3 ρ铜=8.9g/cm3)6、体积是30cm3的空心铜球质量是89g,将它的中空部分注满某种液态物质后,总质量是361g,已知ρ铜=8.9g/cm3,那么注入的液态物质的密度是多少千克/米3?7、有甲、乙两个铁球,甲球是实心的,质量为7.8kg,体积为1dm3,乙球是空心的,乙的质量是甲球的4倍,体积为甲球的4.5倍,求乙球空心部分的体积是多少?(ρ铁=7.8g/cm3)8、体积为30cm3,质量是178g的铜球,问它是空心的还是实心的?若是空心的,在其中空部分铸满铝,求铝的质量是多少?(ρ铝=2.7g/cm3,ρ铜=8.9g/cm3)二、利用空瓶求密度例2:一空瓶质量是200g,装满水后称出瓶和水的总质量是700g,将瓶中水倒出,先在空瓶内装一些金属颗粒,称出瓶和金属颗粒总质量是1090g,然后将瓶内装满水,称出瓶、水和金属颗粒的总质量是1490g,求瓶内金属颗粒的密度是多少?它可能是什么金属?反馈练习:1、瓶中装满水时,称其总质量是88g,若装入10g的砂粒,水益出后把瓶的外部擦干,称其质量是94g,求砂粒的密度。
有关密度的几种常见计算题

有关密度的几种常见计算题一、根据公式计算密度、质量、体积。
1、一钢块的质量为35.8千克,切掉1/4后,求它的质量、体积和密度分别是多少?(ρ钢=7.9×10³kg/m³)2、小明在学校运动会上获得一块奖牌,他想知道这块奖牌是否由什么制成,于是他用天平和量杯分别测出该奖牌的质量和体积为14g和2cm3,并算出他的密度为多少kg/m3?小明通过查密度表知道,该奖牌是由_____制成的。
3、一个铁球的质量是3.9kg,铁的密度是7.9×10³kg/m³,求该铁球的体积是多少dm3?4、一块巨石的体积是1.5m3,已知巨石的密度是2.4g/cm3,求该巨石的质量是多少t?二、关于冰、水的问题。
1、体积为1 m³的冰化成水的体积多大?(ρ冰=0.9×10³kg/m³)2、体积为9 m³的水化成冰的体积多大?三、关于同体积的问题。
1、一个空杯子装满水,水的总质量为500克;用它装满酒精,能装多少克?(ρ酒=0.8×10³kg/m³)2、一个空杯子装满水,水的总质量为1千克;用它装另一种液体能装1.2千克,求这种液体的密度是多少?3、一零件的木模质量为200克,利用翻砂铸模技术,制作钢制此零件30个,需要多少千克钢材?(ρ木=0.6×10³kg/m³)4、质量是200g的瓶子,盛满水后的质量是1.2kg,若用这个瓶子盛满某种液体,液体和瓶子的总质量是13.8kg。
求这种液体的密度,并确定它是何种液体。
5、有1个空瓶装满水后总质量为64g,将水倒出,装满酒精后总质量为56g,求空瓶的质量。
(酒精的密度=800kg/立方米,水的密度=1000kg/立方米)四、有关取样法的问题1、有一个大型石碑,长2m,宽1m,高5m。
找到一块跟石碑材质一样的碎石,测得碎石的质量是50g,体积为20cm3。
方阵问题
例一:100人排成一个实心方阵,这个方阵每边有 多少人?
练习:1,121人排成一个实心方阵,这个方阵每边 有多少人?
2,每边站13人,可以排成一个共有多少人的实心 方阵?
例二:甲用棋子摆成了一个实心方阵,后来又用 了7个棋子添上去,使得原方阵增加一行一列, 成为一个大一点的实心方阵。求原来的实心方阵 有多少棋子?
2,用108人站成一个三层空心方阵,这 个方阵外层每边有多少人?
练习:正方形花坛,原来放了一些花,组成一个 实心方阵,后来运来21盆花添上去,使每行,每 列各增加一排,成一个大一点的将16人围成一个一层空心方阵,问每边站几 人?
练习,1,给一个方形建筑物插彩旗,每边插7面彩 旗,共插了多少面彩旗?
2,一个正方形棋盘,四边各放5枚棋子(四个角上 都放一枚)问一共有多少枚棋子?
例五:用棋子排成一个三层空心方阵,这 个方阵外层每边放了13颗棋子,问共用了 多少颗棋子?
例四:用棋子摆成一个两层的空心方阵,外 层每边有6个棋子,求这个二层空心方阵的 棋子总数?
练习:用棋子摆成一个两层的空心方阵,里 层每边有6个棋子,求这个二层空心方阵的 棋子总数?
练习:1,用棋子排成一个三层空心方阵, 这个方阵中间一层每边放了9颗棋子,问 共用了多少颗棋子?
初二物理专题五、空心实心的计算含解析

专题五、密度的计算一、知识网络二、考点梳理考点一、质量物体所含物质的多少叫质量。
要点诠释:1、单位:国际单位:kg ,常用单位:t、g、mg对质量的感性认识:一枚大头针约80mg一个苹果约150g一头大象约6t一只鸡约2kg2、质量的理解:物体的质量不随物体的形状、状态、位置、温度的改变而改变,所以质量是物体本身的一种属性。
3、测量:考点二、密度某种物质组成的物体的质量与它的体积之比叫做这种物质的密度。
要点诠释:1、公式:变形:2、单位:国际单位:kg/m3,常用单位g/cm3。
单位换算关系:1g/cm3=103kg/m31kg/m3=10-3g/cm3。
水的密度为1.0×103kg/m3,其物理意义为1立方米的水的质量为1.0×103千克。
3、理解密度公式:⑴同种材料,同种物质,不变,m与V成正比;物体的密度与物体的质量、体积、形状无关,但与质量和体积的比值有关;密度随温度、压强、状态等改变而改变,不同物质密度一般不同,所以密度是物质的一种特性。
⑵质量相同的不同物质,体积与密度成反比;体积相同的不同物质质量与密度成正比。
4、图象:如图所示:甲>乙5、测体积——量筒(量杯)⑴用途:测量液体体积(间接地可测固体体积)。
⑵使用方法:“看”:单位:毫升(ml)、量程、分度值。
“放”:放在水平台上。
“读”:量筒里的水面是凹形的,读数时,视线要和凹面的底部相平。
考点三、密度的测量及应用1、测固体的密度:说明:在测不规则固体体积时,采用排液法测量,这里采用了一种科学方法--等效代替法。
2、测液体密度:⑴原理:ρ=m/V⑵方法:①用天平测液体和烧杯的总质量m1;②把烧杯中的液体倒入量筒中一部分,读出量筒内液体的体积V;③称出烧杯和杯中剩余液体的质量m2 ;④得出液体的密度ρ=(m1-m2)/V。
3、密度的应用:⑴鉴别物质:密度是物质的特性之一,不同物质密度一般不同,可用密度鉴别物质。
⑵求质量:由于条件限制,有些物体体积容易测量但不便测量质量,用公式m=ρV可以算出它的质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m实 m球
铜球为空心.
练习
体积是30cm3的铝球,他的质量为 54g,问这个铅球是空心还是实心。 若是空心,空心部分体积为多少? 3 3 (铝=2.7x10 Kg/m )
用密度判断:
根据 ρ=m/v=54g/30cm3=1.8g/cm3 <2.7g/cm3 密度比铝的密度 小,所以该球为空心的!
解法一:比较密度法.
m球 3kg 3 3 球 6 . 0 10 kg / m V球 5 104 m3
6.0 10 kg / m 7.8 10 kg / m ,
3 3 3 3
即 球 铁 ,故此球是空心的.
解法二:比较体积法. 设质量是3kg的球是实心的
如何判别物体是实心还是空心
方法一、用物体的质量除以物体 的体积,得这个物体的密度。如 果物体的密度小于组成这个物体 的物质的密度,物体就是空心的! 称为:比较密度法 (简单)
方法二 • 用物质的质量除以物质的密度, 得实心部分的体积,如果实心 部分的体积小于物体的体积, 物体是空心的。 • 称为:相同质量比较体积法
m球 361g V球 40cm
3
铜 8.9g/cm3
判断球是空心还是实心 .
解法一、密度比较法
m球 316g 3 3 球 7 . 9 g/cm 8 . 9 g/cm V球 40cm3
球 铜
球为空心.
解法二、质量比较法
m实 铜V球 8.9g/cm 40cm 356g 316g
Hale Waihona Puke m 根据 VV实 m球
得:
铁
3kg 3 4 3 0 . 385 dm , 3.85 10 m 3 3 7.8 10 kg / m
3 3
而 0.385dm 0.5dm , 即 所以此球是空心的.
V实 V球 ,
解法三:比较质量法. m 3 0 . 5 dm 根据 的球是实心 V 得m=ρ V,设体积为 的,则其质量为 m实 铁V球 7.8 103 kg / m 3 5 104 m 3
用质量判断
根据 3 3 m=ρv=2.7g/cm x30cm =81g>54g 质量少了,所以该球是空心的!
用体积判断
根据 V=m/ρ=54g/2.7g/cm3=20cm3<30cm3 体积比告诉的小,说明是空心的! 且空心的体积为: V空=30cm3-20cm3=10cm3
(实用)
方法三
把物体看成是实心的,用组成这 种物体的物质的密度乘以这个物 体的体积,得实心物体的质量, 如果实心物体的质量大于物体本 身的质量,物体是空心的。 称为:相同体积 比较质量法
一只铁球质量是3kg,体积是 0.5dm 3 , 试判断此铁 球是空心的还是实心的.(已知铁的密度 是 7.8 10 3 kg / m 3)
3.9kg,
3.9kg>3kg,即 m实 m球 , 故此球是空心的. 解题心得归纳:
这三种方法用其中任何一种都可以判断出球是实心的还是 空心的.但如果题目还要求求出空心部分的体积,则用第 二种方法更简便些.
有一个体积是40cm3的铜球,它的质量是316g,这个 铜球是空心的还是实心的? 铜 8.9g/cm3 已知: 求:
