难点探究专题:平面直角坐标系中的新定义与规律题
专题03 平面直角坐标系(专题详解)(解析版)

专题03 平面直角坐标系专题03 平面直角坐标系 (1)7.1 平面直角坐标系 (2)知识框架 (2)一、基础知识点 (2)知识点1 有序数对 (2)知识点2 平面直角坐标系 (2)知识点3 点的坐标特点 (3)二、典型题型 (6)题型1 有序数对 (6)题型2 平面直角坐标系的概念 (6)题型3 点的坐标的特征 (6)一、点的位置与坐标 (7)二、点的坐标与距离 (8)三、点的坐标与平行于坐标轴的直线(数形结合思想) (8)四、点的坐标与图形的面积 (9)(1)知坐标,求面积 (9)(2)知面积,求坐标(方程思想) (10)(3)分类讨论 (12)三、难点题型 (14)题型1 确定点所在的象限 (14)题型2 点到坐标轴的距离 (14)题型3 探究平面直角坐标系坐标的变化规律 (15)7.2 坐标系的简单运用 (17)知识框架 (17)一、基础知识点 (17)知识点1 用坐标表示地理位置 (17)知识点2 用坐标表示平移 (18)二、典型题型 (20)题型1 用坐标表示地理位置 (20)题型2 用坐标表示平移 (21)一、点的平移 (21)(1)已知点和平移方式,求对应点 (21)(2)已知点和对应点,求平移方式 (21)二、图形的平移 (22)三、难点题型 (23)题型1 动点问题 (23)7.1 平面直角坐标系知识框架{基础知识点{有序数对平面直角坐标系点的坐标的特点典型题型{ 有序数对平面直角坐标系的概念点的坐标的特征{ 点的位置与坐标点的坐标与距离点的坐标与平行于坐标轴的直线(数形结合思想)点的坐标与图形的面积{知坐标,求面积知面积,求坐标(方程思想)分类讨论难点题型{确定点所在的象限点到坐标轴的距离探究平面直角坐标系坐标的变化规律 一、基础知识点知识点1 有序数对1)我们把有顺序的两个数a 与b 组成的数对,用于表示平面中某一确定位置的,叫作有序数对,记作(a ,b )注:①(a ,b )与(b ,a )表达的含义不同,注意有序数对的顺序②在表达有序数对时,一般行在前,列在后。
6.难点探究专题:平面直角坐标系中的变化规律.docx
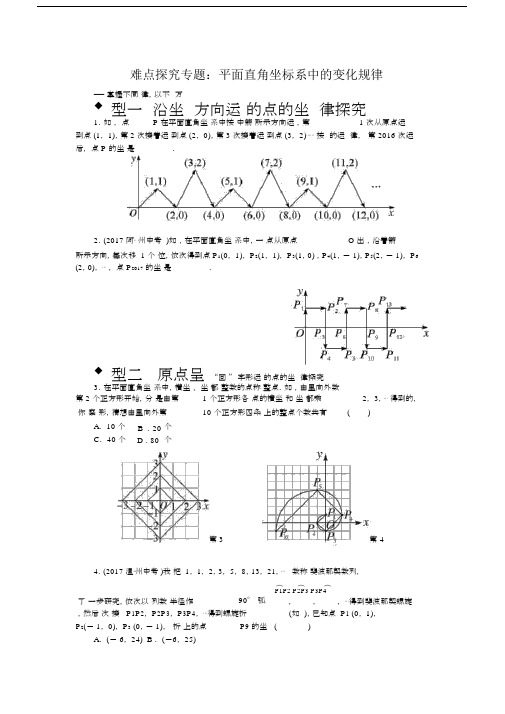
难点探究专题:平面直角坐标系中的变化规律—— 掌握不同 律,以不 万◆型一 沿坐 方向运 的点的坐 律探究1.如 , 点 P 在平面直角坐 系中按 中箭 所示方向运 ,第1 次从原点运到点 (1, 1),第 2 次接着运 到点 (2, 0),第 3 次接着运 到点 (3, 2)⋯⋯ 按 的运 律, 第 2016 次运 后, 点 P 的坐 是 ________.2.(2017 阿· 州中考 )如 ,在平面直角坐 系中,一 点从原点O 出 ,沿着箭所示方向,每次移 1 个 位,依次得到点 P 1(0, 1), P 2(1, 1), P 3(1,0) ,P 4(1,- 1),P 5(2,- 1), P 6(2,0), ⋯ , 点 P 2017 的坐 是 ________.◆型二 原点呈 “回 ” 字形运 的点的坐 律探究3.在平面直角坐 系中,横坐 、 坐 都 整数的点称 整点.如 ,由里向外数第 2 个正方形开始,分 是由第 1 个正方形各 点的横坐 和 坐 都乘 2, 3,⋯ 得到的, 你 察 形,猜想由里向外第10 个正方形四条 上的整点个数共有()A . 10 个 C . 40 个B .20 D .80个个第 3 第 44.(2017 温·州中考 )我 把 1, 1, 2,3, 5, 8,13, 21,⋯ 数称 斐波那契数列,︵ ︵ ︵了 一步研究,依次以 列数 半径作 P1P2 P2P3 P3P4, ⋯得到斐波那契螺旋90° 弧 ,,,然后 次 接 P 1P 2, P 2P 3, P 3P 4, ⋯得到螺旋折 (如 ),已知点 P 1 (0, 1),P 2(- 1, 0), P 3 (0,- 1), 折 上的点P 9 的坐 ()A . (- 6, 24)B . (-6, 25)C. (- 5, 24) D . (- 5, 25)◆ 型三形化中的点的坐探究5.(2017 河·南模 )如,点A(2, 0), B(0, 2),将扇形AOB 沿 x 正方向做无滑的,在程中点O 的点依次点O1,点 O2,点 O3⋯, O10的坐是 ()A. (16+ 4π, 0)B. (14+ 4π, 2)C. (14+ 3π,2)D. (12+ 3π, 0)6.如,在直角坐系中,第一次将三角形OAB 成三角形OA1B1,第二次将三角形 OA1B1成三角形 OA2B2,第三次将三角形OA2B2成三角形OA3B3.已知 A(1, 3),A1 (2, 3),A2(4, 3), A3(8, 3), B(2, 0), B1(4, 0), B2(8 ,0), B3(16, 0).(1)察每次后的三角形有何化,找出律,按此律再将三角形OA3B3成三角形 OA4B4, A4的坐是 __________, B4的坐是 __________ ;(2)若按 (1) 中找到的律将三角形 OAB 行了 n 次,得到三角形OA n B n,比每次中三角形点坐有何化,找出律,推点A n的坐是 __________,点 B n的坐是 __________.参考答案与解析1.(2016 , 0)解析:合象可知,当运次数偶数次,横坐与运次数相等.∵2016 偶数,∴运2016 次后,点P 点运到x 上,且P 的坐是 (2016, 0).2.(672, 1)解析:由已知得P7(2, 1), P13(4, 1),所以2017 ÷6= 336⋯⋯ 1,所以 P2017(336 ×2, 1),即 P2017(672, 1).P6n+1(2n, 1).因3.C解析:每个正方形四个点一定整点,由里向外第n 个正方形每条上除点外的整点个数如下表所示:由里向外第n 个正方形每条上除点外的整点个数1234⋯0123⋯可,第 n 个正方形每条上除点外有(n- 1)个整点,四条上除点外有4(n- 1)个整点,加上 4 个点,共有 4(n- 1)+4= 4n(个 )整点.当 n= 10 ,4n= 4×10= 40,即由里向外第 10 个正方形的四条上共有40 个整点.故 C.4.B 解析:由意, P5在 P2的正上方,推出P9在 P6的正上方,且到 P6的距离21+ 5=26,所以 P9的坐 (- 6,25),故 B.5.C6.(1)(16 , 3) (32, 0) (2)(2n,3)(2n+1, 0)解析: (1)∵ A1(2, 3), A2 (4,3) ,A3(8, 3),∴ A4的横坐 24= 16,坐 3.故点A4的坐 (16, 3).又∵ B1(4, 0),B2(8, 0), B3(16, 0),∴ B4的横坐 25=32,坐0.故点 B4的坐 (32, 0). (2)由 A123(2, 3), A (4,3) ,A (8, 3),可以它各点坐的关系横坐是2n,坐都是 3.故点 A n的坐 (2n, 0).由 B1 (4,0) ,B2(8, 0),B3(16, 0),可以它各点坐的关系横坐是2n+1,坐都是 0.故点 B n的坐(2n+1, 0).。
部编数学七年级下册专题11平面直角坐标系中利用点的坐标变化规律探究问题(解析版)含答案

专题11 平面直角坐标系中利用点的坐标变化规律探究问题(解析版)第一部分典例精析类型一点的运动规律探究(1)沿坐标轴运动的点的坐标规律探究1.(2022•丛台区开学)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,﹣1)…,根据这个规律探索可得,第10个点的坐标为 ,第55个点的坐标为 .思路引领:从图中可以看出横坐标为1的有一个点,横坐标为2的有2个点,横坐标为3的有3个点,…依此类推横坐标为n的有n个点.题目要求写出第10个点和第55个点的坐标,我们可以通过加法计算算出第10个点和第50个点分别位于第几列第几行,然后对应得出坐标规律,将行列数代入规律式.解:在横坐标上,第一列有一个点,第二列有2个点…第n列有n个点,并且奇数列点数对称而偶数列点数y轴上方比下方多一个,∵1+2+3+4=10,1+2+3+…+10=55,∴第10个点在第4列自下而上第4行,所以奇数列的坐标为(n,n−12)(n,n−12−1)…(n,1−n2);偶数列的坐标为(n,n2)(n,n2−1)…(n,1−n2),由加法推算可得到第55个点位于第10列自下而上第10行.代入上式得第10个点的坐标为(4,2),第55个点的坐标为(10,5),故答案为:(4,2),(10,5).总结提升:本题是对点的变化规律的考查,观察得到横坐标相等的点的个数与横坐标相同是解题的关键,还要注意横坐标为奇数和偶数时的排列顺序不同.2.(2022•麻城市校级模拟)如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒π2个单位长度,则第2022秒时,点P的坐标是 .思路引领:计算P点运动过程中走一个半圆所用的时间,根据规律即可求得第2022秒P点位置.解:由题意可知,点P运动一个半圆所用的时间为:π÷π2=2(秒),∵2022=1011×2,∴2022秒时,P在第1011个半圆的最末尾处,∴点P的坐标为(2022,0).故答案为:(2022,0).总结提升:本题主要考查的是坐标系中的规律探究问题,找出运动规律的同时也要考虑坐标系位置是解题的关键.3.(2021春•洛龙区期中)在平面直角坐标系中,一只蚂蚁从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点A2,…,第n次移动到点A n,则点A2021的坐标是( )A.(1010,0)B.(1010,1)C.(1009,0)D.(1009,1)思路引领:观察图形可知,A4,A8,…都在x轴上,求出OA4,OA8,…OA4n的长度,然后写出坐标即可;根据以上规律写出点A4n的坐标即可求出点A2020的坐标,则A2021点的坐标即可求出.解:由图可知,A4,A8,…都在x轴上,蚂蚁每次移动1个单位,∴OA4=2,OA8=4,…OA4n=2n,∴点A4n的坐标为(2n,0),∴点A2020的坐标为(1010,0),∴A2021(1010,1),故选:B.总结提升:本题主要考查了点的变化规律,仔细观察图形,确定出点A 4n 都在x 轴上是解题的关键.(2)绕定点呈“回”字形运动的点的坐标变化规律4.如图是一回形图,其回形通道的宽和OB 的长均为1, 回形线与射线OA 交于A 1,A 2,A 3,….若从O点到A 1点的回形线为第1圈(长为7),从A 1点到A 2点的回形线为第2圈,…,依此类推.则第10圈的长为 .思路引领:如图,以点O 为原心,建立平面直角坐标系,则A 1,A 2,A 3,…的坐标分别为(-1,0),(-2,0),(-3,0),…,A 10的坐标为(-10,0),然后大致描出第10圈的形状,很轻松求出第10圈的长.解:观察图形发现:第一圈的长是2(1+2)+1=7;第二圈的长是2(3+4)+1=15;第三圈的长是2(5+6)+1=23;则第n 圈的长是2(2n-1+2n )+1=8n-1.当n=10时,原式=80-1=79.故答案为79.题眼直击:坐标表示图形,规律探究.总结提升:依次计算第一圈长,第二圈长,……,探究这几个数的一般规律性,然后应用规律求出第10圈.5.(2022•金凤区校级二模)如图,在平面直角坐标系中,从点P 1(﹣1,0),P 2(﹣1,﹣1),P 3(1,﹣1),P 4(1,1),P 5(﹣2,1),P 6(﹣2,﹣2),…依次扩展下去,则P 2022的坐标为 .思路引领:根据题意可得到规律,P4n(n,n),P4n+1(﹣n﹣1,n),P4n+2(﹣n﹣1,﹣n﹣1),P4n+3(n+1,﹣n﹣1),再根据规律求解即可.解:根据题意可得到规律,P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),P7(2,﹣2),P8(2,2),P12(3,3),P16(4,4),...,P4n(n,n),P4n+1(﹣n﹣1,n),P4n+2(﹣n﹣1,﹣n﹣1),P4n+3(n+1,﹣n﹣1),∵2022=4×505+2,∴P2022(﹣506,﹣506),故答案为:(﹣506,﹣506).总结提升:本题主要考查规律型:点的坐标,读懂题意,找出点的坐标规律是解答此题的关键.类型二图形变换的点的坐标规律探究6.(2018春•兴城市期末)如图,在平面直角坐标系中,第一次将三角形OAB变换成三角形OA1B1,第二次将三角形OA1B1换成三角形OA2B2,第三次将三角形OA2B2换成三角形OA3B3,……,若A(﹣3,1),A1(﹣3,2),A2(﹣3,4),A3(﹣3,8),点B(0,2),B1(0,4),B2(0,6),B3(0,8),按这样的规律,将三角形OAB进行2018次变换,得到三角形OA2018B2018,则A2018的坐标是 .思路引领:探究规律后利用规律即可解决问题;解:∵A 1(﹣3,2),A 2 (﹣3,4),A 3(﹣3,8);∴A 点横坐标为﹣3,纵坐标依次为:2,22,23,…得出:A n (﹣3,2n ),∴n =2018时,A 2018(﹣3,22018),故答案为(﹣3,22018)总结提升:此题主要考查了规律型:点的坐标,根据题意得出A ,B 点横纵坐标变化规律是解题关键.7.12.如图,在直角坐标系中,第一次将三角形OAB 变换成三角形OA 1B 1第二次将OA 1B 1变换成三角形OA 2B 2,第三次将三角形OA 2B 2变换成三角形OA 3B 3,已知A(1,3),A 1(2,3),A 2(4,3),A 3(8,3),B(2,0),B 1(4,0),B 2(8,0),B 3(16,0).(1)求三角形OAB 的面积;(2)写出三角形OA 4B 4的各个顶点的坐标;(3)按此图形变化规律,你能写出三角形OA n B n 的面积与三角形OAB 的面积的大小关系吗?解:(1)S 三角形OAB =12×2×3=3;(2)根据图示知O 的坐标是(0,0);已知A(1,3),A 1(2,3),A 2(4,3),A 3(8,3),对于A 1,A 2…A n 坐标找规律比较从而发现A n 的横坐标为2n ,而纵坐标都是3;同理B 1,B 2…B n 也一样找规律,规律为B n 的横坐标为2n +1,纵坐标为0.由上规律可知:A 4的坐标是(16,3),B 4的坐标是(32,0);综上所述,O(0,0),A 4(16,3),B 4(32,0);(3)根据规律,后一个三角形的底边是前一个三角形底边的2倍,高相等都是4,所以OB n =2n +1,S 三角形OA n B n =12×2n +1×3=3×2n =2n S 三角形OAB ,即S 三角形A n B n =2n S 三角形OAB 。
平面直角坐标系找规律100题

平面直角坐标系找规律100题摘要:一、平面直角坐标系的基本概念1.有序数对和点2.平行于坐标轴的直线上的点的坐标特点3.各象限的角平分线上的点的坐标特点二、平面直角坐标系中的规律1.6 个1 循环2.点P4n 在直线yx 上(第三象限)3.相邻4 项之和都是04.x 轴正半轴上的点坐标三、平面直角坐标系中的应用1.用坐标表示地理位置2.用坐标表示平移正文:一、平面直角坐标系的基本概念平面直角坐标系是一种数学工具,它由两条互相垂直的数轴组成,通常用来表示平面上的点。
在平面直角坐标系中,每个点都可以用一个有序数对(a,b) 来表示,其中a 表示点在x 轴上的位置,b 表示点在y 轴上的位置。
在平面直角坐标系中,有一些特殊的直线和点具有特定的坐标特点。
例如,平行于x 轴的直线上的点的纵坐标相同,平行于y 轴的直线上的点的横坐标相同。
此外,各象限的角平分线上的点的坐标也有特定的规律,如第一、三象限角平分线上的点的横纵坐标相同,第二、四象限角平分线上的点的横纵坐标相反。
二、平面直角坐标系中的规律在平面直角坐标系中,有一些规律可以帮助我们更好地理解和描述点的运动和变化。
例如,"6 个1 循环"是指在x 轴上,每隔6 个点就会出现一个1,如同循环一样。
另外,点P4n 在直线yx 上(第三象限),这意味着点P 的横纵坐标都是负数。
此外,还有一个有趣的规律是,相邻4 项之和都是0。
这个规律在很多题目中都会出现,比如(x1, x2, x3, x4) = (1, 1, -1, -1),(x5, x6, x7, x8) = (1, -1, 1, -1) 等等。
三、平面直角坐标系中的应用在实际应用中,平面直角坐标系可以帮助我们解决很多实际问题。
例如,我们可以用坐标表示地理位置,从而更好地描述和导航。
同时,平面直角坐标系也可以帮助我们描述平移,这对于理解和解决很多物理和数学问题都非常有用。
此外,平面直角坐标系也是许多数学题目的基础,如初一数学题中的"关于平面直角坐标系和找规律",就需要我们熟练掌握平面直角坐标系的基本概念和规律。
平面直角坐标系规律题[技巧]
![平面直角坐标系规律题[技巧]](https://img.taocdn.com/s3/m/9a61090afd4ffe4733687e21af45b307e871f971.png)
0000000一个多边形,除了一个内角外,其余各角的和为2750°,则这一内角为()度分析:n边形的内角和是(n-2)•180°,因而内角和一定是180度的倍数.而多边形的内角一定大于0,并且小于180度,因而内角和除去一个内角的值,这个值除以180度,所得数值比边数要大,大的值小于1.则用内角的和除以180所得值,加上2,比这个数大的最小的整数就是多边形的边数.0000000因而多边形的边数是18,则这一内角为(18-2)×180-2750=130度.故答案为:130.0000000点评:正确理解多边形的内角和是180度的整数倍,以及多边形的角的范围,是解题的关键.00000001、(2007•遂宁)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)…根据这个规律探究可得,第88个点的坐标为2、如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,-1)…根据这个规律探索可得,第100个点的坐标为(14,2)00000000000000.0000000分析:从图中可以看出横坐标为1的有一个点,横坐标为2的有2个点,横坐标为3的有3个点,…依此类推横坐标为n的有n个点.题目要求写出第100个点的坐标,我们可以通过加法计算算出第100个点位于第几列第几行,然后对应得出坐标规律,将行列数代入规律式.故答案为(14,2).0000000点评:此题的考点在于对坐平面直角坐标系的熟练运用能力,学生也可从其它方面入手寻找规律.00000003、在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列(1,0)(2,0)(2,1)(1,1)(1,2)(2,2)(2,2)的后面为(3,2)(3,1)(3,0)(4,0)(4,1)(4,2)(4,3)(3,3)(2,3)(1,3)(1,4)(2,4)(3,4)(4,4)(5,4)(5,3)(5,2)(5,1)(5,0)(6,0)(6,1)…根据这个规律,第2012个点的横坐标为?如图,思路如下:当n为一个奇数平方时,设m²=n,则第n个点坐标为(m,0),第n-1个为(m,1) ,第n-2个为(m,2) 。
平面直角坐标系中的规律探索(含答案)

平面直角坐标系中的规律探索1、如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是()A、(13,13)B、(﹣13,﹣13)C、(14,14)D、(﹣14,﹣14)∵55=4×13+3,∴A55与A3在同一象限,即都在第一象限,根据题中图形中的规律可得:3=4×0+3,A3的坐标为(0+1,0+1),即A3(1,1),7=4×1+3,A7的坐标为(1+1,1+1),A7(2,2),11=4×2+3,A11的坐标为(2+1,2+1),A11(3,3);…55=4×13+3,A55(14,14),A55的坐标为(13+1,13+1);故选C.第1题第2题第3题2.如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2012的坐标为。
解:每四个点一个循环,A1 A5 A9……在x正半轴上A2 A6 A10……在第四象限A3 A7 A11……在x负半轴上A4 A8 A12……在第一象限有规律的所以A2012在第一象限∵2012÷4=503,∴点A2012在第一象限,横坐标是2,纵坐标是2012÷2=1006,∴A2012的坐标为(2,1006).3、如图,一个粒子在第一象限运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒运动一个单位长度,那么2010秒时,这个粒子所处位置为()A、(14,44)B、(15,44)C、(44,14)D、(44,15)设粒子运动到A1,A2,…,An时所用的间分别为a1,a2,…,an,则a1=2,a2=6,a3=12,a4=20∴a n=n(n+1).44×45=1980,故运动了1980秒时它到点A44(44,44);又由运动规律知:A1,A2,…,A n中,奇数点处向下运动,偶数点处向左运动.故达到A44(44,44)时向左运动30秒到达点(14,44),即运动了2010秒.所求点应为(14,44)4、如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)(4,0)根据这个规律探索可得,第100个点的坐标为.第4题第5题第6题到第n列有(1+2+3+4+……+n)个点,既n(n+1)/2个点.则可求当n=13时,有91个点.所以排到横坐标为13的点是第91个点,横坐标为13的点最后一个是(13,0),所以(13,0)是第91个点,所以可数得第100个点是(14,8)5、如图,已知A l(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1),….则点A2007的坐标为.易得4的整数倍的各点如A4,A8,A12等点在第三象限,∵2008÷4=502;∴A2008的坐标在第三象限,横坐标为-2008÷4=-502;纵坐标为-502,∴点A2008的坐标是(-502,-502).A2007的坐标在第二象限,故答案为:(-502,502).6、如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是()A.(2,0)B.(-1,1)C.(-2,1)D.(-1,-1)矩形的边长为4和2,周长为12,由题意知:第一次在BC边相遇;第二次在DE边相遇;第三次在A点相遇;此时甲、乙回到原出发点,则每相遇三次,两点回到出发点,∵2012÷3=670…2,故两个物体运动后的第2012次相遇地点的是:第二次相遇地点,在DE边相遇;此时相遇点的坐标为:(-1,-1),故选:D.7、如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是.点P第2009次跳动至点P2009的坐标是.第7题第8题经过观察可得:以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为100÷2=50;其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在y轴右侧.P1横坐标为1,P4横坐标为2,P8横坐标为3,依此类推可得到:Pn的横坐标为n÷4+1(n 是4的倍数).故点P100的横坐标为:100÷4+1=26,纵坐标为:100÷2=50,点P第100次跳动至点P100的坐标是(26,50).故答案填(26,50).(503,1005)8、如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…,则点A2010的坐标是.。
(完整版)平面直角坐标系规律题(带答案)

1.2.3.平面直角坐标系规律题如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中方向排列,如(1, 0), (2 , 0), ( 2, 1) , (1 , 1), (1 , 2), (2 ,2) ••…根据这个规律,第2016个点的坐标为什么?如图,一个质点在第一象限及x轴、y轴上运动,一秒钟后,它从原点运动到(0,1),然后接着按图中箭头所示方向运动[即(0,0)T( 0,1) T( 1,1) T( 1,0)T…],且每秒运动一个单位长度,那么第2016秒后质点所在位置的坐标是(如图,在平面直角坐标系上有点 A (1, 0),点A第一次跳动至点A1( -1 ,1),第四次向右跳动5个单位至点A4( 3,2 ),•••, 依此规律跳动下去,点A第100次跳动至点A100的坐标是.第2016次呢?)65%5 -4 -3-2 -1 ° 1 2 3 4 5'玄如图,在平面直角坐标系上有个点P ( 1 , 0),点P第1次向上跳动1个单位至点P1 (1, 1),紧接着第2次向左跳动2个单位至点P2 (-1 , 1 ),第3次向上跳动1个单位,第4次向JA -----------------------------右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第100次跳动至点P100的坐标是()。
电-------------第2016个点的坐标是( ) 4 --------------4.5、如图,在平面直角坐标系中,一动点从原点0出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0, 1),A2(1, 1),A3(1, 0),A4(2, 0),…,那么点A4n +1(n是自然数)的坐标为_________答案:1.解:根据图形,以最外边的正方形边长上的点为准,点的总个数等于例如:右下角的点的横坐标为 1,: 共有1 个, 1=12,右下角的点的横坐标为 2时, 共有 4 个, 4=22,右下角的点的横坐标为 3时, 共有 9 个, 9=32,右下角的点的横坐标为 4时, 共有 16个, 16=42,右下角的点的横坐标为 n时, 共有 n 2 个,T 452=2025,45 是奇数,/•第 2025 个点是(45, 0), 第2016个点是(45, 9),第4次跳动至点的坐标是(3,2), 第6次跳动至点的坐标是(4,3), 第8次跳动至点的坐标是(5,4), 第2n 次跳动至点的坐标是(n +1, n ),•••第100次跳动至点的坐标是(51,50).故答案为:(51,50). 经过观察可得:以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为 100十2=50 其中4的倍数的跳动都在 y 轴的右侧,那么第100次跳动得到的横坐标也在 y 轴右侧.P 1横坐标为1,P 4横坐 标为2, P 8横坐标为3,依此类推可得到:P n 的横坐标为n *4+1 (n 是4的倍数). 故点P 100的横坐标为:100* 4+仁26,纵坐标为:100* 2=50,点P 第100次跳动至点P 100的坐标是(26,50). 2. 3. (8 , 44)观察发现,第2次跳动至点的坐标是(2,1),x 轴上右下角的点的横坐标的平方,4.。
5.难点探究专题:平面直角坐标系中的新定义与规律题

难点探究专题:平面直角坐标系中的新定义与规律题——掌握不同规律,以不变应万变 ◆类型一 新定义1.在平面直角坐标系xOy 中,对于点P (a ,b )和点Q (a ,b ′),给出下列定义:若b ′=⎩⎪⎨⎪⎧b (a ≥1),-b (a <1),则称点Q 为点P 的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2, -5).如果一个点的限变点的坐标是(3,-1),那么这个点的坐标是( )A .(-1,3)B .(-3,-1)C .(3,-1)D .(3,1) 2.(2016·黔南州中考)在平面直角坐标系中,对于平面内任一点(a ,b ),若规定以下三种变换:①△(a ,b )=(-a ,b );②○(a ,b )=(-a ,-b );③Ω(a ,b )=(a ,-b ),按照以上变换,例如△(○(1,2))=(1,-2),则○(Ω(3,4))=________.3.(2016·常德中考)平面直角坐标系中有两点M (a ,b ),N (c ,d ),规定(a ,b )⊕(c ,d )=(a +c ,b +d ),则称点Q (a +c ,b +d )为点M ,N 的“和点”.若以坐标原点O 与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A (2,5),B (-1,3),若以O ,A ,B ,C 四点为顶点的四边形是“和点四边形”,则点C 的坐标是________.◆类型二 规律探究 4.一个质点P 在第一象限及坐标轴上运动,在第1秒钟,从原点运动到(0,1),然后按箭头的方向运动[即:(0,0)→(0,1)→(1,1)→(1,0)→…],每秒移动一个单位,则点P 运动到(7,7)位置时共运动了________秒.5.如图,正方形A 1A 2A 3A 4,A 5A 6A 7A 8,A 9A 10A 11A 12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A 1,A 2,A 3,A 4;A 5,A 6,A 7,A 8;A 9,A 10,A 11,A 12;…)的中心均在坐标原点O 上,各边均与x 轴或y 轴平行,若它们的边长依次是2,4,6,…,则顶点A 20的坐标为__________.6.如图,在平面直角坐标系中,将△ABO 绕点A 顺时针旋转到△AB 1C 1的位置,点B ,O 分别落在点B 1,C 1处,点B 1在x 轴上,再将△AB 1C 1绕点B 1顺时针旋转到△A 1B 1C 2的位置,点C 2在x 轴上,将△A 1B 1C 2绕点C 2顺时针旋转到△A 2B 2C 2的位置,点A 2在x 轴上,依次进行下去….若点A ⎝⎛⎭⎫32,0,点B (0,2),则点B 2的坐标为________;点B 2016的坐标为________.7.如图所示,在直角坐标系中,第一次将△OAB 变换成△OA 1B 1,第二次将△OA 1B 1变换成△OA 2B 2,第三次将△OA 2B 2变换成△OA 3B 3,已知A (1,3),A 1(2,3),A 2(4,3),A 3(8,3),B (2,0),B 1(4,0),B 2(8,0),B 3(16,0).(1)求△OAB 的面积;(2)写出△OA 4B 4的各个顶点的坐标;(3)按此图形变化规律,你能写出△OA n B n的面积与△OAB的面积的大小关系吗?参考答案与解析1.C2.(-3,4) 解析:○(Ω(3,4))=○(3,-4)=(-3,4).3.(1,8)或(-3,-2)或(3,2) 解析:∵以O ,A ,B ,C 四点为顶点的四边形是“和点四边形”,①当C 为A ,B 的“和点”时,C 点的坐标为(2-1,5+3),即C (1,8);②当B 为A ,C 的“和点”时,设C 点的坐标为(x 1,y 1),则⎩⎪⎨⎪⎧-1=2+x 1,3=5+y 1,解得C (-3,-2);③当A 为B ,C 的“和点”时,设C 点的坐标为(x 2,y 2),则⎩⎪⎨⎪⎧2=-1+x 2,5=3+y 2,解得C (3,2);∴点C 的坐标为(1,8)或(-3,-2)或(3,2).4.56 解析:质点P 每秒移动一个单位,(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒,2秒,3秒,到(1,1)用2秒,到(2,2)用6秒,到(3,3)用12秒,到(4,4)用20秒,依此类推,点P 运动到(7,7)位置时共运动了2+4+6+8+10+12+14=56(秒).5.(5,-5) 解析:∵204=5,∴A 20在第四象限.∵A 4所在正方形的边长为2,∴A 4的坐标为(1,-1),同理可得A 8的坐标为(2,-2),A 12的坐标为(3,-3),∴A 20的坐标为(5,-5).6.(6,2) (6048,2) 解析:∵A ⎝⎛⎭⎫32,0,B (0,2),∴Rt △AOB 中,AB =52,∴OC 2=OA +AB 1+B 1C 2=32+52+2=6,∴点B 2的横坐标为6,且B 2C 2=2,即点B 2的坐标是(6,2),∴点B 4的横坐标为2×6=12,∴点B 2016的横坐标为2016÷2×6=6048,点B 2016的纵坐标为2,即点B 2016的坐标是(6048,2).7.解:(1)S △OAB =12OB ·y A =12×2×3=3;(2)根据图示知O 的坐标是(0,0);已知A (1,3),A 1(2,3),A 2(4,3),A 3(8,3),对于A 1,A 2,…,A n 的坐标,找规律比较发现A n 的横坐标为2n ,而纵坐标都是3;同理B 1,B 2,…,B n 也一样找规律,规律为B n的横坐标为2n +1,纵坐标为0.由以上规律可知:A 4的坐标是(16,3),B 4的坐标是(32,0).综上所述,O (0,0),A 4(16,3),B 4(32,0);(3)根据规律,后一个三角形的底边是前一个三角形底边的2倍,高相等都是3,∴OB n =2n+1,S △OA n B n =12×2n +1×3=3×2n =2n S △OAB ,即S △OA n B n =2n S △OAB .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
难点探究专题:平面直角坐标系中的新定义与规律题
——掌握不同规律,以不变应万变
6.如图,在平面直角坐标系中,将△
绕点A顺时针旋转到△
O分别落在点B1,C
再将△AB1C1绕点B1
的位置,点C2在x轴上,将△
(2)写出△OA4B4的各个顶点的坐标;
(3)按此图形变化规律,你能写出△OA n B n的面积与△OAB的面积的大小关系吗?
参考答案与解析
1.C
2.(-3,4) 解析:○(Ω(3,4))=○(3,-4)=(-3,4).
3.(1,8)或(-3,-2)或(3,2) 解析:∵以O ,A ,B ,C 四点为顶点的四边形是“和点四边形”,①当C 为A ,B 的“和点”时,C 点的坐标为(2-1,5+3),即C (1,8);②当B 为A ,C 的“和点”时,设C 点的坐标
为(x 1,y 1),则⎩⎪⎨⎪
⎧-1=2+x 1,3=5+y 1,
解得C (-3,-
2);③当A 为B ,C 的“和点”时,设C 点
的坐标为(x 2,y 2),则⎩
⎪⎨⎪⎧2=-1+x 2,
5=3+y 2,解得C (3,
2);∴点C 的坐标为(1,8)或(-3,-2)或(3,2).
4.56 解析:质点P 每秒移动一个单位,(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒,2秒,3秒,到(1,1)用2秒,到(2,2)用6秒,到(3,3)用12秒,到(4,4)用20秒,依此类推,点P 运动到(7,7)位置时共运动了2+4+6+8+10+12+14=56(秒).
5.(5,-5) 解析:∵
20
4
=5,∴A 20在第四象限.∵A 4所在正方形的边长为2,∴A 4的坐标为(1,-1),同理可得A 8的坐标为(2,-2),A 12的坐标为(3,-3),∴A 20的坐标为(5,-5).
6.(6,2) (6048,2) 解析:∵A ⎝⎛⎭⎫
32,0,B (0,2),∴Rt △AOB 中,AB =5
2,∴OC 2=
OA +AB 1+B 1C 2=32+5
2+2=6,∴点B 2的横
坐标为6,且B 2C 2=2,即点B 2的坐标是(6,2),∴点B 4的横坐标为2×6=12,∴点B 2016的横坐标为2016÷2×6=6048,点B 2016的纵坐标为2,即点B 2016的坐标是(6048,2).
7.解:(1)S △OAB =12OB ·y A =1
2×2×3=3;
(2)根据图示知O 的坐标是(0,0);已知
A (1,3),A 1(2,3),A 2(4,3),A 3(8,3),对于A 1,A 2,…,A n 的坐标,找规律比较发现A n 的横坐标为2n ,而纵坐标都是3;同理
B 1,B 2,…,B n 也一样找规律,规律为B n
的横坐标为2n +
1,纵坐标为0.由以上规律可知:A 4的坐标是(16,3),B 4的坐标是(32,0).综上所述,O (0,0),A 4(16,3),B 4(32,0);
(3)根据规律,后一个三角形的底边是前一个三角形底边的2倍,高相等都是3,∴OB n =2n
+1
,S △OA n B n =12
×2n +
1×3=
3×2n =2n S △OAB ,即S △OA n B n =2n S △OAB .。
