材料力学第五章B
工程力学--材料力学(北京科大、东北大学版)第4版第五章习题答案
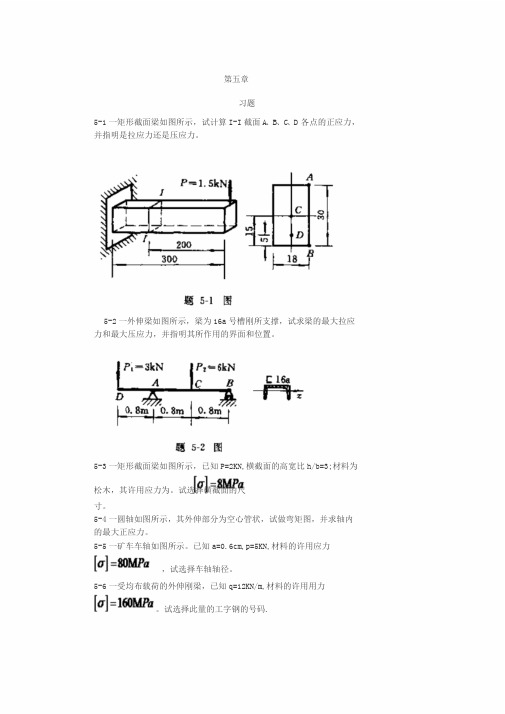
第五章习题5-1一矩形截面梁如图所示,试计算I-I截面A、B、C、D各点的正应力,并指明是拉应力还是压应力。
5-2一外伸梁如图所示,梁为16a号槽刚所支撑,试求梁的最大拉应力和最大压应力,并指明其所作用的界面和位置。
5-3一矩形截面梁如图所示,已知P=2KN,横截面的高宽比h/b=3;材料为松木,其许用应力为。
试选择横截面的尺寸。
5-4一圆轴如图所示,其外伸部分为空心管状,试做弯矩图,并求轴内的最大正应力。
5-5一矿车车轴如图所示。
已知a=0.6cm,p=5KN,材料的许用应力,试选择车轴轴径。
5-6一受均布载荷的外伸刚梁,已知q=12KN/m,材料的许用用力。
试选择此量的工字钢的号码.5-7图示的空气泵的操纵杆右端受力为8.5KN,截面I-I和II-II位矩形,其高宽比为h/b=3,材料的许用应力。
试求此二截面的尺寸。
5-8图示为以铸造用的钢水包。
试按其耳轴的正应力强度确定充满钢水所允许的总重量,已知材料的许用应力,d=200mm.5-9求以下各图形对形心轴的z的惯性矩。
5-10横梁受力如图所试。
已知P=97KN,许用应力。
校核其强度。
5-11铸铁抽承架尺寸如图所示,受力P=16KN。
材料的许用拉应力。
许用压应力。
校核截面A-A的强度,并化出其正应力分布图。
5-12铸铁T形截面如图所示。
设材料的许用应力与许用压应力之比为,试确定翼缘的合理跨度b.5-13试求题5-1中截面I-I上A、B、C、D各点处的切应力。
5-14制动装置的杠杆,在B处用直径d=30mm的销钉支承。
若杠杆的许用应力,销钉的,试求许可载荷和。
5-15有工字钢制成的外伸梁如图所示。
设材料的弯曲许用应力,许用且应力,试选择工字钢的型号。
5-16一单梁吊车由40a号工字钢制成,在梁中段的上下翼缘上各加焊一块的盖板,如图所示。
已知梁跨长=8m,=5.2m,材料的弯曲许用应力,许用且应力。
试按正应力强度条件确定梁的许可载荷,并校核梁的切应力。
材料力学性能 第五章 缺口试样的力学性能.
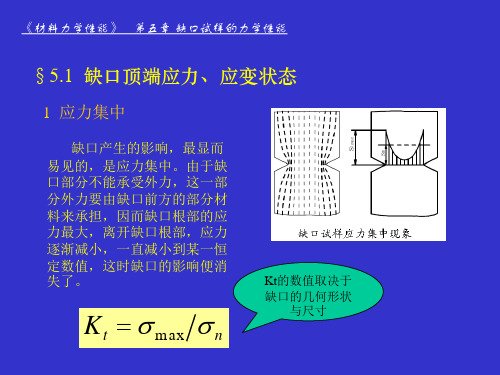
设想有一单位厚度的无限宽形板,对其施 加一拉应力后,与外界隔绝能源。在板内 制造一穿透裂纹,裂纹的扩张来自与系统 内部的弹性能释放。当裂纹扩张时,其表 面能增加了。
u uE us
系弹 统性 总应 能变
表 面 能
能
《材料力学性能》 第六章 断裂韧性基础
冷脆:材料因温度的降低 导致冲击韧性的急剧下降 并引起脆性破坏的现象
《材料力学性能》 第五章 缺口试样的力学性能
5.4.1 系列温度冲击试验
试验表明:随着温度降 低,冲击功由高阶能转 变为低阶能,材料由韧 性断裂过渡到脆性断裂, 断口形式也由纤维状断 口经过混合断口过渡为 结晶状断口,断裂性质 由微孔聚集型断裂过渡 为解理断裂。
定义: G u ( 2a2 ) 2a (2a) (2a) E E
G是弹性应变能的释放率或者裂纹扩展力。
《材料力学性能》 第六章 断裂韧性基础
恒位移条件: 裂纹扩展释 放出的弹性 能是三角形 OAC的面积。
恒载荷条件: 外力做的功一 半用于弹性能 的增加,一半 用于裂纹扩展 裂纹扩展释所 需的弹性能是 三角形OAC的 面积。
以 a 代替 2E a
1
1
2
2
1,
E
2
a
Griffith 公式
《材料力学性能》 第六章 断裂韧性基础
6.1.3 奥罗万(Orowan)的修正
Griffith研究的对象主要是玻璃这类很脆的材料,对于大多数金属材料, 虽然裂纹尖端由于应力集中作用,局部应力很高,但是一旦超过材料的屈 服强度,就会发生塑性变形。在裂纹尖端有一塑性区,材料的塑性越好强 度越低,产生的塑性区尺寸就越大。裂纹扩展必须首先通过塑性区,裂纹 扩展功主要耗费在塑性变形上,金属材料和陶瓷的断裂过程不同,主要区 别也在这里。由此,奥罗万修正了格里菲斯的断裂公式,得出:
材料力学习题解答[第五章]
![材料力学习题解答[第五章]](https://img.taocdn.com/s3/m/5c357285a0116c175f0e48fd.png)
5-1构件受力如图5-26所示。
试:(1)确定危险点的位置;(2)用单元体表示危险点的应力状态(即用纵横截面截取危险点的单元体,并画出应力)。
题5-1图解:a) 1) 危险点的位置:每点受力情况相同,均为危险点;2)用单元体表示的危险点的应力状态见下图。
b) 1) 危险点的位置:外力扭矩3T与2T作用面之间的轴段上表面各点;2)应力状态见下图。
c) 1) 危险点:A点,即杆件最左端截面上最上面或最下面的点;2)应力状态见下图。
d) 1)危险点:杆件表面上各点;2)应力状态见下图。
5-2试写出图5-27所示单元体主应力σ1、σ2和σ3的值,并指出属于哪一种应力状态(应力单位为MPa)。
10题5-2图解:a)1σ=50 MPa,2σ=3σ=0,属于单向应力状态AAT (a)(c)(d)364dFlπτ=a) b) c) d)a) b) c)b) 1σ=40 MPa, 2σ=0, 3σ=-30 MPa ,属于二向应力状态 c) 1σ=20 MPa, 2σ=10 MPa, 3σ=-30 MPa ,属于三向应力状态5-3已知一点的应力状态如图5-28所示(应力单位为MPa )。
试用解析法求指定斜截面上的正应力和切应力。
题5-3图解:a) 取水平轴为x 轴,则根据正负号规定可知: x σ=50MPa , y σ=30MPa , x τ=0, α=-30 带入式(5-3),(5-4)得 ατασσσσσα2sin 2cos 22x yx yx --++==45MPaατασστα2cos 2sin 2x yx +-== -8.66MPab) 取水平轴为x 轴,根据正负号规定:x σ= -40MPa , y σ=0 , x τ=20 MPa , α=120带入公式,得:240sin 20240cos 20402040---++-=ασ=7.32MPa x τ= 240cos 20240sin 2040+--=7.32MPac) 取水平轴为x 轴,则x σ= -10MPa , y σ=40MPa , x τ= -30MPa,α=30代入公式得:60sin )30(60cos 2401024010----++-=ασ=28.48MPa x τ= 60cos 3060sin 24010---=-36.65MPa5-4已知一点的应力状态如图5-29所示(应力状态为MPa )。
材料力学第五章 弯曲应力分析

B
D
1m
1m
1m
y2
20
120
FRA
F1=9kN FRB F2=4kN
A C
BD
1m
1m
1m
2.5 Fs
+
+
4 kN
-
6.5 2.5
M
kNm
-
+
4
解: FRA 2.5kN FRB 10.5kN
88
52
-
+
C 2.5
4 B 80
z
20
120
20
B截面
σ t max
M B y1 Iz
4 • 52 763
20
+
-
+
10
Fs
kN
10
20
30
30
25
25
M
kNm
max
M max W
[ ]
W Mmax 30 187.5cm3
[ ] 160
1)圆 W d 3 187.5
32
d 12.4cm
A d 2 121cm2
4
2)正方形
a3 W 187.5
6
3)矩形
a 10.4cm
A a2 108cm2
压,只受单向拉压. (c)同一层纤维的变形相同。 (d)不同层纤维的变形不相同。
推论:必有一层变形前后长度不变的纤维—中性层
中性轴
中性轴⊥横截面对称轴
中性层
横截面对称轴
二、变形几何关系
dx
dx
图(a)
O
O
zb
O yx b
y
图(b)
《材料力学》 第五章 弯曲内力与弯曲应力

第五章 弯曲内力与应力 §5—1 工程实例、基本概念一、实例工厂厂房的天车大梁,火车的轮轴,楼房的横梁,阳台的挑梁等。
二、弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线。
变形特点——杆轴线由直线变为一条平面的曲线。
三、梁的概念:主要产生弯曲变形的杆。
四、平面弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线,且都在梁的纵向对称平面内(通过或平行形心主轴且过弯曲中心)。
变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平面曲线。
五、弯曲的分类:1、按杆的形状分——直杆的弯曲;曲杆的弯曲。
2、按杆的长短分——细长杆的弯曲;短粗杆的弯曲。
3、按杆的横截面有无对称轴分——有对称轴的弯曲;无对称轴的弯曲。
4、按杆的变形分——平面弯曲;斜弯曲;弹性弯曲;塑性弯曲。
5、按杆的横截面上的应力分——纯弯曲;横力弯曲。
六、梁、荷载及支座的简化(一)、简化的原则:便于计算,且符合实际要求。
(二)、梁的简化:以梁的轴线代替梁本身。
(三)、荷载的简化:1、集中力——荷载作用的范围与整个杆的长度相比非常小时。
2、分布力——荷载作用的范围与整个杆的长度相比不很小时。
3、集中力偶(分布力偶)——作用于杆的纵向对称面内的力偶。
(四)、支座的简化:1、固定端——有三个约束反力。
2、固定铰支座——有二个约束反力。
3、可动铰支座——有一个约束反力。
(五)、梁的三种基本形式:1、悬臂梁:2、简支梁:3、外伸梁:(L 称为梁的跨长) (六)、静定梁与超静定梁静定梁:由静力学方程可求出支反力,如上述三种基本形式的静定梁。
超静定梁:由静力学方程不可求出支反力或不能求出全部支反力。
§5—2 弯曲内力与内力图一、内力的确定(截面法):[举例]已知:如图,F ,a ,l 。
求:距A 端x 处截面上内力。
解:①求外力la l F Y l FaF m F X AYBY A AX)(F, 0 , 00 , 0-=∴==∴==∴=∑∑∑ F AX =0 以后可省略不求 ②求内力xF M m l a l F F F Y AY C AY s ⋅=∴=-==∴=∑∑ , 0)( , 0∴ 弯曲构件内力:剪力和弯矩1. 弯矩:M ;构件受弯时,横截面上存在垂直于截面的内力偶矩。
材料力学课后习题答案5章

保留有限量,略去一阶和二阶微量后,得
足标 C 系指梁微段右端面的形心,对题图(b)亦同。 根据题图 b,由
∑F
略去微量 qdx 后,得
y
=0 ,FS左 + qdx − FS右 = 0
FS右 = FS左
仍据题图 b,由
(c)
∑M
C
=0 ,M 右 − M e − qdx(
dx ) − FS左 dx − M 左 = 0 2
11l 处有 FS2 = 0 , M 2 有极大值,其值为 24 121 2 M 2 max = M max = ql 1152
(d)解:1.建立剪力、弯矩方程
8
图 5-9d 坐标如图 5-9d(1)所示,由截面法易得剪力、弯矩方程分别为
q( x1 ) ⋅ x1 qx 2 =− 1 2 l ql FS2 = − + qx2 4 qx 3 M1 = − 1 3l q 2 ql l M 2 = x2 − ⋅ ( + x2 ) 2 4 6 FS1 = −
2 q0l q 0 x2 FS = − + 4 l q x3 ql M = 0 x2 − 0 2 4 3l
l (0 ≤ x2 ≤ ) 2 l (0 ≤ x2 ≤ ) 2
(e) (f)
3.画剪力、弯矩图 依据式(c)和(e)可绘剪力图,如图 5-9b(2)所示;依据式(d)和(f)可绘弯矩图,如图 5-9b(3) 所示。 (c)解:1.求支反力
=0 ,FS左 + F + qdx − FS右 = 0
保留有限量,略去微量 qdx 后,得
FS右 − FS左 = F
为了更一般地反映 F 作用处剪力的突变情况(把向下的 F 也包括在内) ,可将上式改写为
材料力学II材料力学孙训方

(f)
沿 x' 方向的线应变为
εa
3=
P ''' D?? OP
?
? xy d y cosa d y sina
?
g xy sina cosa
(g)
7
材料力学Ⅱ电子教案
第五章 应变分析 电阻应变计法基础
在ex ,ey ,gxy 同时存在时,沿x' 方向的线应变为
eα ? eα1 ? eα2 ? eα3
沿x' 方向的线应变为
εa
2=
P??D? OP
?
εy d y sina d y sina
?
εy sin 2 a
(d) (e)
6
材料力学Ⅱ电子教案
第五章 应变分析 电阻应变计法基础
3. 只有正值gxy(图d),BB??? PP???? g xy d y , OP 的伸长量为
P'''D'' ? PP???cos a ? g xy d y cosa
只需以为e横坐标,以 ? g / 2为纵坐标(向下为正),即可作出应
变圆。已知:ex?、e y?、g x?y,且ex ? e y。作出应变圆如图所示。
应变圆中,
1
1
D1(ex ,
g
2
xy )
,
D2 (e y ,?
2 g xy
),
OC
?
1 2
(e
x
? e y ),
半径为
CD1 ?
???e x ?
? 2
? ga
2
?
1 2
(e
x
?
e
y
)
sin
材料力学第五章

y
= ∫ y dA
2 A
1 1 π ⋅ d4 π ⋅ d4 I y = Iz = I ρ = ⋅ = z 2 2 32 64
1 π ⋅ (D4 − d 4 ) 对空心圆截面: 对空心圆截面: I = I = I = y z ρ 2 64
第五章 弯曲应力
§5-2 对称弯曲正应力 对称弯曲正应力
M⋅ y 二、弯曲正应力一般公式: 弯曲正应力一般公式: σ= Iz
Ip
弯曲 剪力Q 剪力
?
第五章 弯曲应力
§5-1 引言 y
梁段
M τ Q
z
σ
横截面上剪应力 横截面上正应力
横截面上内力
Q = ∫τdA
剪应力造成剪力
M = ∫σydA
正应力造成弯矩
剪应力和正应力的分布规律是什么? 剪应力和正应力的分布规律是什么?
超静定问题
第五章 弯曲应力
§5-1 引言
§5-2 对称弯曲正应力 对称弯曲正应力 §5-3 对称弯曲切应力 对称弯曲切应力 弯曲 §5-4 梁的强度条件与合理强度设计 梁的强度条件与合理强度设计 §5-5 双对称截面梁的非对称弯曲 双对称截面梁的非对称弯曲 §5-6 弯拉(压)组合 弯拉( 对称弯曲(平面弯曲): 对称弯曲(平面弯曲): 外力作用在纵向对称面内, 外力作用在纵向对称面内,梁轴线变形 后为一平面曲线,也在此纵向对称面内。 后为一平面曲线,也在此纵向对称面内。
(3)
Mz = ∫ σ ⋅ y ⋅ dA = M (5) A E 2 E 2 E (5) M z = ∫ ρ y dA = ∫ y dA = ρ I z = M
A
ρ
A
1 M = ρ EIz
第五章 弯曲应力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Problem 5.7
Please determine the probable locations of the shear centers of the following sections.
•
•
•
• •
Probons of shear flows and the probable distribution of shearing stresses of following sections.
If the origin of coordinates is at the centroid, y1 and z1 are called the centroidal principal axes.
If the origin of coordinates is at the centroid, Imax and Imin are called the centroidal principal moments of inertia.
z0 z
y0 y
Mz (Iy y0–Iyz z0)+My (Iz z0–Iyz y0) = 0
(Mz Iy-My Iyz)y0+(My Iz-Mz Iyz)z0= 0 —— the function of neutral axis.
z0
tan = y0 = -
Mz Iy-My Iyz My Iz-Mz Iyz
Read the Example 5.10 in page 129 and answer questions.
Problems of Chapter 12 :
5 . 25 5 . 42
Problem 5.6
An unsymmetrical thin-walled beam is subjected to the transverse loads, for only producing plane bending and not torsion the acting conditions of the loads are ( C ).
z1
O
z
y1 y
B
E
Cz
D
z1
dA
A
y y1
We get
Iy1z1 =
Iy – 2
Iz
sin2
+
Iyz cos2
(5.23)
Similarly
Iy1 = Iz1 =
Iy + 2
Iz
+
Iy + Iz 2
–
Iy
– 2
Iz
cos2
–
Iyz
sin2
Iy
– 2
Izcos2
+ Iyz sin2
(5.21) (5.22)
11 70
80 11
80 C
1z
z1
11 y y1
Iy = 2Iy1+Iy2= 2 (11593/12+5911352) +160 113/12 = 1.9810-6 m4 Iyz = 2Iyz1+Iyz2= 2 [ 59 11 (-74.5) 35 ] + 0 = – 3.3810-6 m4
2. Determine Imax and Imin
Example 5.4
Find: the centroidal principal moments of
inertia of the area as shown in the figure.
Solution:
1. Determine Iy , Iz and Iyz
Iz = 2Iz1+Iz2= 2 (59113/12+591174.52) + 111603/12 = 10.97106 mm4= 10.9710-6 m4
C. Through the shear center and parallel to the centroidal principal plane of inertia.
C is correct.
A is not complete; B is generally impossible to realize.
5.5 Principal moment of inertia
1. Product of inertia of the section
O
Iyz = A yz dA
A
Iyz may be positive, negative or zero.
z y
If y or z is symmetrical axis, Iyz must be zero.
(2)
Similarly, (only My )
=
My ( Iz z - Iyz y ) Iy Iz - Iyz2
(3)
Mz and My
=
Mz (Iyy Iy Iz -
-Iyzz) Iyz2
+
My (Izz Iy Iz -
-Iyzy) Iyz2
tan = Iy / Iyz (1) From = 0 and (4)
Imax Imin
=
Iy + Iz 2
+–
Iy
– 2
Iz
2
+
Iyz2
=
1.98+10.97
2
+–
1.98-10.97 2
2
+(-3.38)2
10-6
=
12.110-6 m4 0.8510-6 m4
3. Determine 1
tan21 = –2Iyz / (Iy–Iz)= 23.38/(1.98 –10.97)= – 0.752 1 = –18.5
3. Which method was used in order to enduce the formula of ?
The equilibrium method of infinitesimal element. 4. How can the shearing stresses of thin-walled beams be calculated ? According to (5.27), the key is to calculate Sz . 5. Whats the definition of the shear center ? The intersection of lines on which FSy and FSz act respectively.
z y dA
2. Parallel axis theorem
O
z
y
Iyz = A yz dA = A (a + yC) (b + zC) dA
-z z
= A yC zCdA + aA zCdA + bA yCdA + AabdA
y
= Iyczc+ a Syc+ b Szc+ abA = Iyczc+ abA
Chapter 12 Bending of Special Beams
Contents:
1. Normal stresses in unsymmetrical bending 2. Shearing stresses in open thin-walled members ;
Shear center
A. The plane the loads act on is parallel to or superposes on the centroidal principal plane of inertia;
B. Through the shear center and act in the principal plane of inertia;
z
2. Physical relation
= E =E
3. Statical relation
From (b) :
axaixsis
(b)
=
E
(
ysin
-
zcos
)
(f )
From (d),(f ) :
zz
O yy
z z ddAA
FN = A dA = 0 My = A z dA = 0 Mz = A y dA From (b), (c):A dA=
We can find: Iy1 + Iz1 = Iy + Iz = constant There must be the coordinate system, the moment of inertia about
its one axis is maximum and that about its another axis is minimum.
(c) (d) (e)
My = =
E
E
E
A
dA
=
0
yy
(sin AzydA-cos Az2dA)
( Iyz sin - Iy cos ) = 0 tan = Iy / Iyz
From (e),(f ) :
(1)
A dA = 0
Mz =
E
(sin
A y2dA-cos
A yzdA)
Neutral axis must be across centroid.
4. Principal moments of inertia
z1
From
d Iy1
d
=
0,
d Iz1
d
=
0,we
get:
Iy1z1=
0
And we obtained :
