《信号与系统》考研试题解答第一章信号与系统
信号与系统考研试题答案

信号与系统考研试题答案一、选择题1. 信号的傅里叶变换具有以下哪些性质?A. 线性B. 时移C. 频移D. 以上都有答案:D解析:傅里叶变换具有线性性质,即两个信号的傅里叶变换等于它们各自傅里叶变换的和;具有时移性质,即时域中的平移对应频域中的相乘以频率因子;具有频移性质,即频域中的平移对应时域中的相乘以复指数函数。
2. 下列哪个系统是线性时不变系统?A. 弹簧质量阻尼系统B. 电子滤波器C. 人体生理系统D. 经济系统答案:B解析:线性时不变系统是指系统对任何输入信号的响应可以分解为对每个单独输入分量的响应的线性组合,并且这种关系不随时间变化。
电子滤波器满足这一定义,而其他选项中的系统通常不具备这种性质。
3. 连续时间信号的拉普拉斯变换定义中,s表示什么?A. 复频域变量B. 时域变量C. 空间变量D. 频率变量答案:A解析:拉普拉斯变换是将连续时间信号从时域转换到复频域的数学工具,其中s代表复频域变量,它包含了频率和阻尼因子。
4. 在数字信号处理中,离散傅里叶变换(DFT)的主要应用是什么?A. 信号的去噪B. 信号的压缩C. 信号的频谱分析D. 信号的滤波答案:C解析:离散傅里叶变换(DFT)主要用于分析离散信号的频率成分,即信号的频谱分析。
而去噪、压缩和滤波通常是通过其他方法或变换来实现的。
二、填空题1. 一个连续时间信号若在整个时间轴上绝对可积,则其傅里叶变换存在的条件是________。
答案:该信号的傅里叶变换收敛解析:连续时间信号的傅里叶变换存在的必要条件是信号在整个时间轴上绝对可积,即其积分绝对值有限。
2. 在信号与系统中,单位脉冲函数通常用符号________表示。
答案:δ(t)解析:单位脉冲函数是一个理想化的信号,其在t=0处的值无限大,但在整个时间轴上的积分为1,通常用δ(t)表示。
三、简答题1. 简述线性系统和非线性系统的区别。
答案:线性系统满足叠加原理,即系统对多个输入信号的响应等于对每个单独输入信号响应的和。
陈后金《信号与系统》(第2版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】(上册)

图2-2
3.有一离散时间信号
(1)画出
(2)求序列 学]
使之满足
解:(1)
又 比较上述两式可得: 故如图2-3所示。
[电子科技大
图2-3
4.已知 如图2-4(a),画出
和
的波形。[北
京理工大学]
解:将 反转得 如图2-4(b)所示,将它们相加、减得 ,波形如图2-4(c)、(d)所示。
图2-4 5.已知f(t)的波形如图2-5所示,令r(t)=tu(t)。
大学]
图1-2 解:因为:
故:
y2(t)的波形如图1-3所示。
图1-3 3.将如图1-4(a)、(b)所示的连续信号展成如下形式:
给出信号
最简单的解析表达形式。[北京航空航天大学]
图1-4
解:(a)该信号可分为两段:
和
可化简为
故
,即:
(b)该信号可分为三段: 可化简为 故
,即
4.求
的值。[北京航空航天大学2006研]
,应该与齐次解有关,即系统的特征根为-1和-3,故特征方程应为 ,即a0=4,a1=3。
(2)设系统对激励 rzs(t),则
的零输入响应和零状态响应分别为rzi(t)和
由于
,则由线性时不变系统的微分特性可知
同时,设系统的单位冲激响应为h(t),则由线性时不变系统的叠加性 可知
由式(1)、式(2),并设
陈后金《信号与系统》(第2版)配 套模拟试题及详解
第一部分 名校考研真题 第1章 信号与系统分析导论 一、选择题
1.方程 天大学2007研] A.线性时不变 B.非线性时不变 C.线性时变 D.非线性时变 E.都不对 【答案】B
描述的系统是( )。[北京航空航
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
(NEW)吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解

目 录第1章 信号与系统1.1 复习笔记1.2 课后习题详解1.3 名校考研真题详解第2章 连续系统的时域分析2.1 复习笔记2.2 课后习题详解2.3 名校考研真题详解第3章 离散系统的时域分析3.1 复习笔记3.2 课后习题详解3.3 名校考研真题详解第4章 傅里叶变换和系统的频域分析4.1 复习笔记4.2 课后习题详解4.3 名校考研真题详解第5章 连续系统的s域分析5.1 复习笔记5.2 课后习题详解5.3 名校考研真题详解第6章 离散系统的z域分析6.1 复习笔记6.2 课后习题详解6.3 名校考研真题详解第7章 系统函数7.1 复习笔记7.2 课后习题详解7.3 名校考研真题详解第8章 系统的状态变量分析8.1 复习笔记8.2 课后习题详解8.3 名校考研真题详解第1章 信号与系统1.1 复习笔记一、信号的基本概念与分类信号是载有信息的随时间变化的物理量或物理现象,其图像为信号的波形。
根据信号的不同特性,可对信号进行不同的分类:确定信号与随机信号;周期信号与非周期信号;连续时间信号与离散时间信号;实信号与复信号;能量信号与功率信号等。
二、信号的基本运算1加法和乘法f1(t)±f2(t)或f1(t)×f2(t)两信号f1(·)和f2(·)的相加、减、乘指同一时刻两信号之值对应相加、减、乘。
2.反转和平移(1)反转f(-t)f(-t)波形为f(t)波形以t=0为轴反转。
图1-1(2)平移f(t+t0)t0>0,f(t+t0)为f(t)波形在t轴上左移t0;t0<0,f(t+t0)为f(t)波形在t轴上右移t0。
图1-2平移的应用:在雷达系统中,雷达接收到的目标回波信号比发射信号延迟了时间t0,利用该延迟时间t0可以计算出目标与雷达之间的距离。
这里雷达接收到的目标回波信号就是延时信号。
3.尺度变换f(at)若a>1,则f(at)波形为f(t)的波形在时间轴上压缩为原来的;若0<a<1,则f(at)波形为f(t)的波形在时间轴上扩展为原来的;若a<0,则f(at)波形为f(t)的波形反转并压缩或展宽至。
信号与系统(应自炉)习题答案第1章 习题解重点

(222222j t k j t j t j k f t k e
e
e
e
f t π
π
π
πππ+++++==⨯==
∴原函数是周期函数,令1k =,则基波周期为2π。
1-2.
求信号( 14sin( 110cos(2--+=t t t f的基波周期。
解:cos(101 t +的基波周期为15
π,s i n (4
1-8.
用阶跃函数写出题图1-8所示各波形的函数表达式。
t
t
t
(a (
bc
题图1-8
解:(a)((((((3[31]2[11]f t t u t u t u t u t =++-+++-- (((3[13]t u t u t +-+---
(((((
(3 3(1 1(1 1(3 3f
t t u t t u t t u t t u t =+++--++-+-+--(b)([( (1]2[(1 (2]4(2 f t u t u t u t u t u t =--+---+-
1 t -的基波周期为
1
2
π二者的最小公倍数为π,故( 14sin( 110cos(2--+=t t t f的基波周期为π。
1-3.
设(3, 0<=tt f ,对以下每个信号确定其值一定为零的t值区间。
(1)(t f -1(2)((t f t f -+-21(3)((t f t f --21(4)(t f 3(5)(f
《信号与系统》考研奥本海姆版2021考研名校考研真题

《信号与系统》考研奥本海姆版2021考研名校考研真题第一部分考研真题精选一、选择题1已知信号f(t)的频带宽度为Δω,则信号y(t)=f2(t)的不失真采样间隔(奈奎斯特间隔)T等于()。
[西南交通大学研]A.π/(Δω)B.π/(2Δω)C.2π/(Δω)D.4π/(Δω)【答案】B查看答案【解析】根据卷积定理可知,y(t)=f2(t)→[1/(2π)]F(jω)*F(j ω)。
若信号f(t)的频带宽度为Δω,则y(t)的频带宽度为2Δω。
则奈奎斯特采样频率为4Δω,所以不失真采样间隔(奈奎斯特间隔)T等于2π/(4Δω)=π/(2Δω)。
2已知f(t)↔F(jω),f(t)的频带宽度为ωm,则信号y(t)=f(t/2-7)的奈奎斯特采样间隔等于()。
[西南交通大学研]A.2π/ωmB.2π/(2ωm-7)C.4π/ωmD.π/ωm【答案】A查看答案【解析】根据时域和频域之间关系,可知若时域扩展,则频域压缩。
所以若f(t)的频带宽度为ωm,则信号y(t)=f(t/2-7)的频带宽度为ωm/2。
所以,其奈奎斯特采样频率为(ωm/2)×2=ωm,即奈奎斯特采样间隔等于2π/ωm。
3有限长序列x(n)的长度为4,欲使x(n)与x(n)的圆卷积和线卷积相同,则长度L的最小值为()。
[中国科学院研究生院2012研]A.5B.6C.7D.8【答案】C查看答案【解析】x(n)的长度为4,则其线卷积的长度为4+4-1=7。
当x(n)与x(n)的圆卷积L≥7时,x(n)与x(n)的圆卷积和线卷积相同,可知L的最小值为7。
4下面给出了几个FIR滤波器的单位函数响应。
其中满足线性相位特性的FIR滤波器是()。
[东南大学研]A.h(n)={1,2,3,4,5,6,7,8}B.h(n)={1,2,3,4,1,2,3,4}C.h(n)={1,2,3,4,4,3,2,1}D.h(n)={1,2,3,4,-1,-2,-3,-4}【答案】C查看答案【解析】线性相位FIR滤波器必满足某种对称性,即h(n)=h(N-1-n)或者h(n)=-h(N-1-n)。
(完整版)信号与系统第一章答案
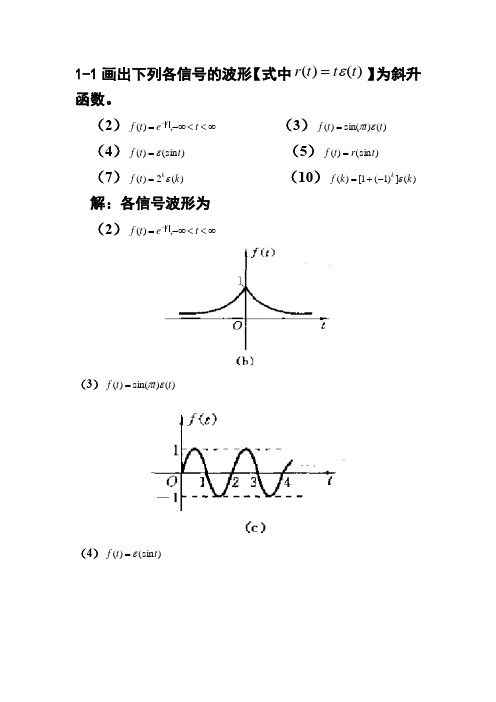
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t(7))t=(kf kε(2)(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f(5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(1-2章)【圣才出品】

第1章绪论
1.1复习笔记
本章作为《信号与系统》的开篇章节,是整个信号与系统学习的基础。
本章介绍了有关信号与系统的基本概念和术语,给出几种典型的信号和系统的表现形式,讲述了各信号与系统的特点以及信号之间的运算和转换。
通过本章学习,读者应掌握:如何判断信号类型、不同信号之间的运算、信号的分解以及系统类型的判断。
一、信号概述
1.信号的概念及分类(见表1-1-1)
表1-1-1信号的概念及分类
2.典型的连续信号(见表1-1-2)
表1-1-2典型的信号及表示形式
3.信号的运算(见表1-1-3)
表1-1-3信号的运算
4.阶跃函数和冲激函数
阶跃信号和冲激信号是信号与系统中最基础的两种信号,许多复杂信号皆可由二者或二者的线性组合表示。
具体见表1-1-4及表1-1-5。
(1)单位阶跃信号u(t)
表1-1-4单位阶跃信号u(t)
(2)单位冲激信号δ(t)
表1-1-5单位冲激信号δ(t)表示形式及性质
5.信号的分解
一个一般信号根据不同类型可分解为以下几种分量,具体见表1-1-6。
表1-1-6信号的分解
二、系统
1.系统概念及分类(见表1-1-7)
表1-1-7系统的概念及分类
系统模型如下:
输入信号经过不同系统可得到不同输出信号,具体见表1-1-8。
表1-1-8不同系统特性
1.2课后习题详解
1-1分别判断图1-2-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?
(a)
(b)
(c)
(d)
(e)
(f)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章信号与系统、单项选择题X1.1 (北京航空航天大学 2000年考研题) 试确疋下列信号的周期:(1) x(t) 3 cos 4t3;(A ) 2( B ) (C )-- (D)22(2)x(k) 2 cos —k sin —k 2cos —k —48 2 6(A ) 8 ( B )16 (C )2 (D )4X1.2 (东南大学2000 年考研题)下列信号•中属于功率信- 号的是 。
(A )cost (t)( B )e t(t)(C ) te t(t)ti(D ) e 11X1.3 (北京航空航天大学 2000年考研题) 设f (t )=0 , t<3,试确定下列信号为 0的t 值:(1)f (1-t)+ f(2-t);(A ) t >-2 或 t>-1(B )t=1 和 t=2(C ) t>-1(D ) t>-2(2)f (1-t) f(2-t))(A ) t >-2 或 t>-1 (B )t=1 和 t=2(C ) t>-1(D ) t>-2(3)t f3(A ) t >3 ( B )t=0 (C ) t<9 ( D )t=3X1.4 (浙江大学2002年考研题: )卜列表达式屮正确的是o(A ) (2t)(t)(B ) 1 (2t) 1 (t)(C ) (2t) 2 (t)(D ) 12⑴(2t)X1.5(哈尔滨工业大学2002年考研题) 某连续时间系统的输入f (t )和输出y (t )满足y(t) f(t) f(t 1),则该系统为 _______________(B )非因果、时不变、非线性 (D )因果、时不变、非线性(A )因果、时变、非线性 (C )非因果、时变、线性X1.6 (东南大学2001年考研题)微分方程y (t) 3y(t) 2y(t) f(t 10)所描述的系统为 __________ 。
(A )时不变因果系统 (B )时不变非因果系统 (C )时变因果系统(D )时变非因果系统X1.7 (浙江大学2003年考研题)y(k) f( k 1)所描述的系统不是 _______________________ 。
(A )稳定系统 (B )非因果系统 (C )非线性系统 (D )时不变系统X1.8 (西安电子科技大学2005年考研题)某连续系统的输入、输出关系为2t 1y(t) f( )d ,该系统是 ___________ ,、判断与填空题T1.1 (北京航空航天大学2001年考研题)判断下列说法是否正确,正确的打错误的打“X” 。
(1) 两个信号之和一定是周期信号。
[] (2)所有非周期信号都是能量信号。
[](3) 若f(k)是周期序列,则f(2k)也是周期序列。
[]T1.2判断下列叙述的正误,正确的在方括号中打,错误的在方括号中打“X(A ) 线性时变系统 (B )线性时不变系统 (C ) 非线性时变系统(D )非线性时不变系统 X1.9 (西安电子科技大学2001年考研题)若f(t)是已录制声音的磁带,则下列表述错误的是(A ) f(-1)表示将此磁带倒转播放产生的信号 (B ) f(21)表示将此磁带以二倍速度加快播放 (C ) f(21)表示原磁带放音速度降低一半播放 (D) 2f(t)表示将磁带的音量放大一倍播放X1.10 (北京交通大学2004年考研题)积分 55(t 3) ( 2t 4)dt(A ) -1(B ) -0.5(C ) 0(D) 0.5答案:X1.1(1)[C] ⑵[B], X1.2[A],X1.3(1)[C](2)[D](3)[C] ,X1.4[B],X1.5[D],X1.6[B],X1.7[D] ,X1.8[A] ,X1.9[C],X1.10[B]y(k) T [f(k)] kf(k),该系统为:无记忆系统[],线性系统[],因果系统[],时不变系统[],稳定系统[]。
(2)(华中科技大学 2004年考研题) f(t)cost sin , 2t ,该信号为周期信号[],周期为2[ ];f(k)sink cosk ,该信号为周期信号[],周期为12[]。
4 3(3)(华中科技大学 2003 年考研题) 信号 f (k)和y(k)为周期信号, 其和 f(k) + y(k)是周期的[]。
(4)(清华大学2000年考研题)由已知信号f(t)构造信号:F(t) f (t nT),n则F(t)是周期信号[](5)(清华大学2000年考研题)非线性系统的全响应必等于零状态响应与零输入响应之和[](6)(国防科技大学2002年考研题)冲激信号是一个高且窄的尖锋信号,它有有限的 面积和能量[]。
试判断上述哪些系统满足下列条件:(1)不是线性系统的是__ (3) 不是时不变系统的是T1.4 (北京航空航天大学 2001年考研题)已知以下四个系统:(1 )是线性系统的是 _______ ; (2)是时不变系统的是 _________ (3 )是因果系统的是 _______ ;( 4)是有记忆系统的是 _______ 。
2000年考研题)已知以下四个系统(B ) y(t) f(2t)(D ) y(t)tf(t)T1.3 (北京航空航天大学(A ) y(t) 2f(t) 3 (C ) y(t) f( t)(2)不是稳定系统的是 (4)不是因果系统的是(A )型 10y(t) f (t)dt(C )峻 y(t) f(t 10)dt 试判断上述哪些系统满足下列条件:(B )dy(t) dtt 2y(t) f(t)(D ) y(t) f(t 10) f 2(t)(1) f ,(t) _______________________ 2(t 2 2) (t 2)dt (2)f 2(t) ____________________ o (t 2 1) e t dt 。
(t cos n ) (t)(t) dt(1) (s in t) _______ ;(2) si nt (t) _________ 。
T1.8 (国防科技大学2001年考研题)计算积分:424t (t 1)dt____________ 。
T1.9 (北京交通大学2001年考研题)(1) 已知 f (t) t 2 4 (t),则 f (t) _______ ;(2)t 2 2t( t 1)dt_______ 。
t 2T1.10 (西安电子科技大学 2005年考研题)积分° 2 (2 )d 等于 ___________年考研题)已知f (k) { 3 ,4,5,6},则k 0g(k) f(2k 1) _______ 。
12tT1.12 (北京交通大学 2003年考研题)积分3e (t 2)dt 等于 ____________________ 。
3T1.13 (北京交通大学 2004年考研题)连续信号f (t) si nt 的周期T 0= ____________________ ,若对 f(t)以f s 1Hz 进行取样,所得离散序列 f(k)= ________________ ,该离散序列是否周期序列____________________________________________________ 。
T1.14 (北京交通大学2002年考研题)已知某系统的输入、输出关系为y(t) t 2 f (t)2x(0)(其中,x(0)为系统的初始状态,f(t)为外部激励),试判断系dt统是(线性、非线性) _____________ (时变时不变) ___________ 系统。
T1.5 (哈尔滨工程大学2002年考研题)计算下列信号的值:T1.6 (哈尔滨工业大学2002年考研题)计算积分:T1.7 (清华大学2001年考研题)计算下列各式: T1.11 (北京邮电大学 2003T1.15 (北京交通大学2002年考研题)(1)积分3 (2t23t) -t 2 dt 等于2(2)积分(2t 2) (4 2t)dt 等于_________ 。
答案:T1.1 (1) (2) (3)VT1.2 (1) v, v, £ 2 2(2) 2 2 v, 2, (3) V(4) 2 (5) 2 (6) 2T1.3 (1)A (2)D (3)BCD (4)BCT1.4 (1)ABC (2)ACD (3)AB (4)ABCDT1.5 (1)4 (2)0.5e-1T1.6 0T1.7 (1) (t n ) (2) (t)nT1.8 -2T1.9(1) 2 (t) 4 (t)T1.10 6 (t-2)T1.11 g(k) {0,4,6}T1.12 e-4T1.13 2 , sin k ,不是T1.14 线性、时变T1.15 (1)0 (2)1三、画图、证明与分析计算题J1.1 (电子科技大学2002年考研题)已知初始状态为零时的LTI系统,输入为f1(t)时对应的输出为y1(t),当输入为f2(t)时,求对应的输出为y2(t)[ f1(t)、y1(t)、f2(t)如图J1.1-1所示]。
解:由图J1.1-1可知,f2(t) f/t) f,t 1)f,t 2)图桃⑴-1 0 12 3 4图y1(t) T[x(0) 0, f1(t)]据LTI系统的线性、时不变性质,可得y2(t) T[x(O) 0, f 2(t)]T[x(0) 0, f i(t) f i(t 1) f i(t 2)]0, f i(t 1)] T[x(0) 0, f i(t 2)] y i(t) y i(t i) y i(t 2)由此,可得如图图Ji.i-2所示。
Ji.2 (北京邮电大学2004年考研题)已知f(-2t + i)波形如图Ji.2-i所示,试画出f(t)的波形。
解:方法一:将f(-2t+i)反转,可得f(2t+i),如图Ji.2-2(A )所示;对f(2t.+i))扩展一倍(横坐标乘以2),可得f(t+i),如图Ji.2-2(B)所示;对f(t+1)右移1个时间单位,可得f(t),如图Ji.2-2( C)所示。
方法二:f( 2t 1) f( 2(t 0.5))将f(-2t+1)左移0.5个时间单位,可得f(-2t),如图J1.2-3( A )所示;将f(-2t)反转,可得f(2t),如图J1.2-3( B)所示;对f(2t))扩展一倍(横坐标乘以2),可得f(t),如图J1.2-3( C)所示。
T[x(0) 0, f i(t)] T[x(0)I(B)图(C)J1.3(北京邮电大学2003年考研题)已知f(t)波形如图J1.3-1所示,试画出f 2波形。
解:将f(t)反转,可得f(-t),如图J1.3-2 (A )所示;J1.5 (上海交通大学2000年考研题)已知dt试画出f(t)的一种可能波形。
