空间群的推导总结
合集下载
第十一讲—空间群(3)资料讲解
+ ,- -, + +, - - ,+
+ ,- -, + +, - - ,+
+ ,- -, + +, - - ,+
俯视图(单胞)： (左)一般等效点位置 (右)对称元素分布
8 1 x,y,z; x,y,z; x,y,z; x,y,z;
x,y,z; x,y,z; x,y,z; x,y,z. 1 a mmm 0,0,0.
{R|} {R|t}、 {1|tn}、 {R|0} 、
点式空间群：由全部作用于同一个公共点
上的对称操作完全确定，或者说仅由点对称操 作和平移对称操作组合而产生。
۞ 螺旋轴或滑移面不是其基本操作。
۞ 点式空间群在单胞中一定至少有一个位置具有与
空间群点群相同的位置对称性
点对称条件
1(E)或1(i)
晶系
第十一讲—空间群(3)
第九讲 空间群(I)：点式空间群
晶体的宏观外形可视作一个连续整体的有限图形，而晶体 微观结构是不连续排列的原子在三维空间的无限展开。晶体 宏观对称性是晶体结构(原子排列对称性)即微观对称的反映。
点群中对称要素必须交于一点，只有方向的概念。微观对 称性中对称要素无须交于一点，要引入平移和位置的概念。
空间群：结晶学空间群就是能使三维周期物体(无
限大晶体)自身重复的所有几何对称操作的集合，
它构成数学意义上的群。
第十讲 空间群(II)：非点式对称操作
点对称操作：r’ = Rr r’=x’a + y’b +z’c r=xa + yb +zc 空间群操作：r’ = {R|t}r = Rr + t (赛兹算符)
第十一讲—空间群(3)1
的新对称操作，同样可由赛兹算符{RI}r=Rr+描述。晶体中有三
种不同的滑移面：轴滑移、对角n滑移、金刚石滑移。
轴向滑移：平移矢量平行于反映面，大小是单胞
轴长的一半。有a滑移、b滑移、c滑移；n滑移。
+
b
， +
a/2
+
+
b
+
b
b/2
_ ，
a/2
+
b/2
a/2
a/2
+
， +
b/2
b/2
a
a
a
n滑移 如 Pban
3
+ + + +
_ _ _ _
+ +
, ,
+ +
_ _
_ _
, ,
12 l
1
x,y,z; x,y,z; y,x,z; y,x,z;
y,x-y,z; y,x-y,z; x,y-x,z; x,y-x,z;
y-x,x,z; y-x,x,z; x-y,y,z; x-y,y,z.
x
, ,
Origin at 62m
Origin on 6
+
5/6+
1/3+ 1/2+ 2/3+ 1/6+ + 5/6+ 2/3+ 1/2+
1/3+ 1/6+ + 5/6+
Origin on 61
2/3+
P65 (C6, No. 170) P62 (C6, No. 171) P64 (C6, No. 172) P63 (C6, No. 173)
种不同的滑移面：轴滑移、对角n滑移、金刚石滑移。
轴向滑移：平移矢量平行于反映面，大小是单胞
轴长的一半。有a滑移、b滑移、c滑移；n滑移。
+
b
， +
a/2
+
+
b
+
b
b/2
_ ，
a/2
+
b/2
a/2
a/2
+
， +
b/2
b/2
a
a
a
n滑移 如 Pban
3
+ + + +
_ _ _ _
+ +
, ,
+ +
_ _
_ _
, ,
12 l
1
x,y,z; x,y,z; y,x,z; y,x,z;
y,x-y,z; y,x-y,z; x,y-x,z; x,y-x,z;
y-x,x,z; y-x,x,z; x-y,y,z; x-y,y,z.
x
, ,
Origin at 62m
Origin on 6
+
5/6+
1/3+ 1/2+ 2/3+ 1/6+ + 5/6+ 2/3+ 1/2+
1/3+ 1/6+ + 5/6+
Origin on 61
2/3+
P65 (C6, No. 170) P62 (C6, No. 171) P64 (C6, No. 172) P63 (C6, No. 173)
空间群的确定
c/2
c hh.‐2h.l
c/2
c ‐2h.hhl
c/2
c h.‐2h.hl
c/2
c, n hhl,h‐hl
(a ± b ± c)/4 d hhl,h‐hl
a/2
a, n hkk,hk‐k
(±a + b± c)/4 d hkk,hk‐k
b/2
b, n hkh,‐hkh
(±a ± b+ c)/4 d hkh,‐hkh
表 3 螺旋轴与衍射条件的关系
方向 平移距离 符号
[100] a/2 [100] a/2 [100] a/4 [010] b/2 [010] b/2 [010] b/4 [001] c/2 [001] c/2 [001] c/4 [001] c/2 [001] c/3 [001] c/6
21 42 41, 43 21 42 41, 43 21 42 41,43 63 31, 32, 62, 64 61, 65
hkl 衍射条件 无限制
h + k + l = 2n k + l = 2n, h + l = 2n, h + k = 2n k + l = 2n h + l = 2n h + k = 2n ‐h + k + l = 3n (正定向) h ‐ k + l = 3n (负定向)
表 2 滑移面与衍射条件的关系
Left-hand page: (1) Headline (2) Diagrams for the symmetry elements and the general
position (for graphical symbols of symmetry elements see Chapter 1.4) (3) Origin (4) Asymmetric unit (5) Symmetry operations
2.4 空间群的推导
c c m ⋅ c⊥ = m ⋅ m'⋅ = 2 ⋅ = 21 2 2
3. 空间群的推导：以点群C2v为例 空间群的推导：以点群C
3 3. 空间群 C2 v − Pcc 2
c c c ⋅ c⊥ = m ⋅ m⊥ ⋅ ⋅ = m ⋅ m⊥ = 2 2 2
4 C2 v − Pma 2 4. 空间群
m⊥a ⋅ a⊥b
3. 空间群的推导：以点群C2v为例 空间群的推导：以点群C
在与点群C 在与点群C2v同形的空间群推导中，我们可 以只考虑滑移面组合的情况，因为2 以只考虑滑移面组合的情况，因为2次轴可 右滑移面组合产生。这里的滑移面包括反映 面，2次轴包括2次旋转轴。在晶体32个点群 面，2次轴包括2次旋转轴。在晶体32个点群 中， C2v属于正交晶系，有P、I、C、F四种 属于正交晶系，有P 布拉维格子。C 点群中有2 布拉维格子。C2v点群中有2个正交的反映面， 对应与微观上就表现为两个正交的滑移面， 滑移面有m 滑移面有m，n，a，b，c，d，6种。考虑2 种。考虑2 个正交滑移面的组合，如n 个正交滑移面的组合，如n和a的组合，根据 对称元素组合原理：
C2 v − Pna 21 9. 空间群
3. 空间群的推导：以点群C2v为例 空间群的推导：以点群C 9
b+c a c a+b n ⋅ a = m⊥a ⋅ ⋅ m⊥b ⋅ = 2 ⋅ ⋅ 2 2 2 2 a+b = 21 ⋅ = 2 a +b 1 2 4
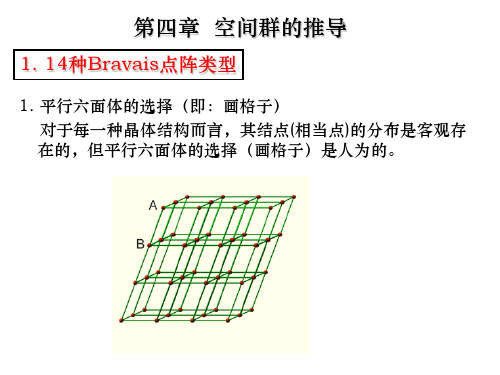
1. 14种Bravais点阵类型 14种Bravais点阵类型
例1：四方底心格子 ＝ 四方原始格子 所以，在14种布拉维格子中，四方底心格子不需要保留。
1. 14种Bravais点阵类型 14种Bravais点阵类型
晶体点群、空间群简要归纳
晶体点群、空间群简要归纳本⽂只是很简要的归纳，具体内容还请见李新征⽼师群论书和其在蔻享的群论课。
另外推荐肖瑞春⽼师科学⽹博客的这篇博⽂，介绍了群论及后续的学习：若研究中涉及群论和物理性质相关，其中陈纲的《晶体物理学基础》书特别好，易懂，将主动变换和被动变换等分析得特别清晰，不过此书太厚，注意⽤到什么学什么，⽤minimized的知识来科研，否则被导师批评...1.对称操作、对称元素对称操作：保持系统不变的操作。
对称元素：它是⼀个⼏何实体，对称操作可以依据对称元素施⾏对称操作。
对称元素可以是点、直线、⾯等。
2.点群：1）定义：三维实正交群O(3)群的有限⼦群物理理解：实际上点群是实际的物理系统在三维空间的⼀些对称操作的集合。
这些对称操作会保持⼀个点不动。
2）点群分类第⼀类点群：只包含纯转动元素的点群。
第⼆类点群：点群中，除了纯转动元素，还包含转动反演元素的点群。
因为点群是O(3)群的⼦群，⽽O(3)群中有固有转动和⾮固有转动。
3）点群的性质{()}性质1：点群这个集合可以写成C k(2π/n)、IC k′2π/n′的形式，其中n,→k′,n′取有限个⽅向和值；C k(2π/n)是绕→k轴转2π/n⾓的操作。
性质2：设G是点群，K是G的纯转动部分，由于纯转动部分的乘积以及逆元必属于这个纯转动部分,所以K也是G的纯转动⼦群,即K=G∩SO(3)∘.点群G与其有限⼦群K的关系有以下三种可能的情况：1.G=K, 即点群只包含纯转动操作；称为第⼀类点群。
2.若点群G中除了纯转动操作，还包含纯空间反演操作I, 则可以通过G=K∪IK得到这种情况对应的第⼆类点群。
3.若点群G中除了纯转动操作，且G中不包含纯反演操作I时 , 此第⼆类点群G⼀定与⼀个第⼀类G+同构,其中，G+=K∪K+, ⽽K+定义为:K+={Ig∣g∈G,但g∉K}根据这⾥的第3点，可以知道构造这种情况对应的第⼆类点群的⽅法：根据⼀个已知的第⼀类点群K∪K+，即可以构造⼀个第⼆类点群K∪I K+.还可以证明K必须是K∪K+的不变⼦群，其阶数是K∪K+的⼀半。
第十一讲—空间群(3)资料讲解
Origin on 6
1/3+
1/2+
1/6+
+
2/3+ 5/6+
1/3+
1/2+
1/6+
+
2/3+ 5/6+
Origin on 61
P65 (C63, No. 170) P62 (C64, No. 171) P64 (C65, No. 172) P63 (C66, No. 173)
2/3+
1/2+
沿??bac滑移面的abn轴滑移如pban对称轴符号符号号对称轴图示符号沿轴向的右手螺旋平移特征一次旋转轴1一个反演轴二次旋转轴二次螺旋轴三次旋转轴三次螺旋轴三次反演轴2213313231无无无无无无平行于纸面无无平行于纸面无无无无c2a2或b2c32c3符号号对称轴图示符号沿轴向的右手螺旋平移特征四次旋转轴4四次反演轴四次螺旋轴六次旋转轴六次螺旋轴六次反演轴43661654无无无无6无无c4c65c641422c43c4626364无无2c63c64c6对称面符号符号对称面反映面镜面轴滑移面mabcnd对角滑移面网金刚石滑移面图示符号滑移特征垂直于投影面平行于投影面有没有如果平面在z14的的高度就在符号边标注14无无沿沿100滑移a2或沿010滑移b2或沿lt
43
3c/4
4 四次反演轴
无
+ +
+ +
1/2+ 3/4+
1/4+
+
4
41
+
1/2+
1/2+
+
1/2+
1/4+
1/3+
1/2+
1/6+
+
2/3+ 5/6+
1/3+
1/2+
1/6+
+
2/3+ 5/6+
Origin on 61
P65 (C63, No. 170) P62 (C64, No. 171) P64 (C65, No. 172) P63 (C66, No. 173)
2/3+
1/2+
沿??bac滑移面的abn轴滑移如pban对称轴符号符号号对称轴图示符号沿轴向的右手螺旋平移特征一次旋转轴1一个反演轴二次旋转轴二次螺旋轴三次旋转轴三次螺旋轴三次反演轴2213313231无无无无无无平行于纸面无无平行于纸面无无无无c2a2或b2c32c3符号号对称轴图示符号沿轴向的右手螺旋平移特征四次旋转轴4四次反演轴四次螺旋轴六次旋转轴六次螺旋轴六次反演轴43661654无无无无6无无c4c65c641422c43c4626364无无2c63c64c6对称面符号符号对称面反映面镜面轴滑移面mabcnd对角滑移面网金刚石滑移面图示符号滑移特征垂直于投影面平行于投影面有没有如果平面在z14的的高度就在符号边标注14无无沿沿100滑移a2或沿010滑移b2或沿lt
43
3c/4
4 四次反演轴
无
+ +
+ +
1/2+ 3/4+
1/4+
+
4
41
+
1/2+
1/2+
+
1/2+
1/4+
空间群
m[001]
|
1 2
,
1 2
,
0
r
金刚石滑移
空间群推导
点群
点阵 点阵对称性和点群的协调性
点式空间群 能否替换
用对应的非点式操作替换点式操作 非点式空间群
非点操作的位置
5种平面点阵
矩形 (a≠b, 90°)
平面群：
pm, pg, p2mg, p2mm 和 p2gg
• 立方结构的晶体，其原子一般位于高对称 的位置上，如Au，Al等金属单质
平面群（自学）
• 10种平面点群，13种点式平面群 • 有滑移面非点式对称操作，17种平面群
国际表
提供的信息的是： 1. 空间群的国际符号 2. Schoenflies符号 3. 晶系 4. 晶类 5。一般等效点图： 单胞的投影，包含所有等效点位置。
一般等效位置 确定单胞内的原子数及位置
商群中h个基本操作作用后产生h个一般等效点 系
点阵类型加一般等效点系描述空间群
等效位置确定商群的对称性及所属的晶系 由点阵类型便知道平移群的对称性
国际表中对称操作的表示
对称操作的分类及几何符号
由对称操作的矩阵求对应的几何符号
1，查表确定对应点对称操作 2，确定对称元素的取向和位置 a，反映 b，纯旋转 c，旋转倒反
• 空间群： 国际符号： 空间群符号的意义： 空间群的熊夫利推导方法：
符号的意义：第一个字符表示布拉菲点阵， 后面的表示对称性，符号的顺序与轴的选 取有关
空间群的两个重要内容：一般等效位置的坐 标，相对特定原点的全部对称元素
空间群与点群的关系：
• 俯视图 • 矩阵
空间群的描述
• 一般等效位置及对称元素
第十一讲—空间群(3)
点式操作t = = 0
۞ 螺旋轴：11种，21；31、32；41、42、43； 61、62、63、64、65 ۞ 滑移面：a、b、c；n；d
空间群操作：r’ = {R|t}r = Rr + t (赛兹算符)
对非点式操作 t = ，是单胞的分数平移 对于点式操作t = = 0 {R|t}、 {1|tn}、 {R|0} 、
Origin on 6
+
5/6+
1/3+ 1/2+ 2/3+ 1/6+ + 5/6+ 2/3+ 1/2+
1/3+ 1/6+ + 5/6+
Origin on 61
2/3+
P65 (C6, No. 170) P62 (C6, No. 171) P64 (C6, No. 172) P63 (C6, No. 173)
空间群： 结晶学空间群 就是能使三维周期物体(无
限大晶体)自身重复的 所有 几何对称操作 的 集合 ，
它构成数学意义上的群。
第十讲
空间群(II)：非点式对称操作
r’=x’a + y’b +z’c r=xa + yb +zc
Байду номын сангаас
点对称操作：r’ = Rr
空间群操作：r’ = {R|t}r = Rr + t (赛兹算符) 对非点式操作 t = ，是单胞的分数平移，而对于
Conditions limiting possible reflections
General: hkl: No conditions 0kl: k + l = 2n hkl: l = 2n Special: hkl: h + k = 2n; l = 2n hkl: h + k + l = 2n
۞ 螺旋轴：11种，21；31、32；41、42、43； 61、62、63、64、65 ۞ 滑移面：a、b、c；n；d
空间群操作：r’ = {R|t}r = Rr + t (赛兹算符)
对非点式操作 t = ，是单胞的分数平移 对于点式操作t = = 0 {R|t}、 {1|tn}、 {R|0} 、
Origin on 6
+
5/6+
1/3+ 1/2+ 2/3+ 1/6+ + 5/6+ 2/3+ 1/2+
1/3+ 1/6+ + 5/6+
Origin on 61
2/3+
P65 (C6, No. 170) P62 (C6, No. 171) P64 (C6, No. 172) P63 (C6, No. 173)
空间群： 结晶学空间群 就是能使三维周期物体(无
限大晶体)自身重复的 所有 几何对称操作 的 集合 ，
它构成数学意义上的群。
第十讲
空间群(II)：非点式对称操作
r’=x’a + y’b +z’c r=xa + yb +zc
Байду номын сангаас
点对称操作：r’ = Rr
空间群操作：r’ = {R|t}r = Rr + t (赛兹算符) 对非点式操作 t = ，是单胞的分数平移，而对于
Conditions limiting possible reflections
General: hkl: No conditions 0kl: k + l = 2n hkl: l = 2n Special: hkl: h + k = 2n; l = 2n hkl: h + k + l = 2n
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二、与简单点群同态的空间群 可以由(Wi, 0)换成(Wi, wi)方法推导出来非点式空间群
三、空间群同形不变引伸原理简介 点群H
用点群P={Wi}中 的操作Wi引伸
点群Gp=H∧P
①查与Gp相协调的平移群T ②G=T∧Gp ③非点式替换
与点群Gp同态 的空间群G 与点群H同态 的空间群GH
用(Wi, wi)不变引伸
例三：与Pmm2同态的空间群的推导 利用商群 G/T与点群P同构（乘法表相同） G/T={T, T(W2,w2), T(W3, w3), …, T(Wh, wh)} P={1, W2, W3, …,Wh} P={mm2}={1, m[100], m[010], 2[001]} 乘法表有：(m[100])(m[010])=2[001] 与mm2同态的空间群有四个陪集： T, T(m[100], w2), T(m[010], w3), T(2[001], w4) 由乘法表：[T(m[100], w2)][T(m[010], w3)]=T(2[001], w4)] 由乘法公式： [T(m[100], w2)][T(m[010], w3)]=T(2[001], (m[100])w3+w2) 则有：(m[100])w3+w2=w4 (以tj为模） 即：w2，w3，w4是相互关联的 w2=k2a+(0,1)b/2+(0,1)c/2 （镜面在k2/2处） w3=k3b+(0,1)a/2+(0,1)c/2 （镜面在k3/2处） w4=(0, c/2) （坐标原点在轴上）
●空间群 (1) 点式空间群 当选择适当坐标，G可以按其点阵平称群T展开得到 的陪集为 G=T+T(W2,0)+…+T(Wh,0) 其陪集的代表操作(I,0), (W2,0),..全是点操作. -----对点式空间群G，它的点群P的对称操作也是G 本身的操作. -----点式空间群也可能有螺旋或滑移操作 (2) 非点式空间群 若无论如何选择坐标原点，无论选择陪集中的哪个 操作作为它的代表操作(Wi,wi)，其中总有些wi不等于0.
(m[100])w3+w2=w4
四、11对相互对映的空间群 每对空间群中的一个是另一个的镜象（左右手关系）。 不含镜面或倒反，含有非中性螺旋轴。 相应晶体有旋光性（使偏振面旋转）。
§6-4 由与简单点群同态的空间群推导较复 杂的空间群
一、简单点群 即为32个点群中只含有一个对称元素的8个点群。 方法：通过往简单点群(H)上添加对称元素而得到其他点 群(Gp) Gp=H∧P
§6-2 点式空间群的推导
点式空间群G可表示为 G=T+T(W2,0)+T(W3,0)+…+T(Wh,0) 已知平移群T为G的不变子群，P为与G相对应的点群 则G是T与P的半直积群：G=T∧P T有14种，P有32种，但G并不是14X32个群元。 因为只能选取在P中的点群操作Wi的作用下，用平移群T 描述的晶体点阵不变。即平移群体T具有点群P所 描述的对称性。 ●与Bravais点阵相协调的点群之间相乘，如： 正交晶系的四种点阵P，C，I，F与三种点群222， mm2，mmm相乘，---12种空间群
方法：把点式空间群中的点操作(Wi,0)依次换成(Wi,wi), 2→21, 4 →41, 42, 43, m→a, b, c, n, d 抛弃其中不可能的组合，归并其中相同的， →230种空间群 例一：与点群4（C4）同态的空间群的推导 同态的点式空间群：P4，I4 →P41，P42，P43，I41，I42，I43
~ = (W,w ) x = Wx + w x
证明所有(W,w) 操作构成一个群. 封闭性；单位元；逆元；结合律。---------成群 实仿射群有一个由纯平移(I,t)组成的子群，为不变子群
(W,w )(I,t )(W,w )
−1
= ( I,Wt )
仍为一纯平移
二、空间群及其与点阵平移群和晶体学点群的关系 1、空间群 （1）定义：晶体学空间群就是使某个三维周期性的客体 （晶体）变换成它自己（复原）的几何对称操作（平 移，点对称操作及两者组合操作）的集合。 （2）空间群(G)是实仿射群的子群 ●晶体的平移周期性决定了空间群的对称操作(W,w) 中的不能是任意量的旋转操作，只能是1,2,3,4,6轴的 旋转或旋转倒反操作 ●(W,w)中的平移量w也不能是任意的. w=wl+wg 内 禀平移分量wg则与坐标原点选取无关，只能取一定的 值。
《晶体学中的对称群》 Crystallographic Symmetry Group
中国科学院金属研究所 隋曼龄
2007.3.1-4.6
主要内容
第一章 第二章 第三章 第四章 第五章 第六章 第七章 第八章 对称操作 二维晶体学 群论初步 晶体学点群 点阵、晶系与晶体学中的坐标系 空间群的推导 空间群图表的认识与使用 空间群与晶体结构及相变
¼ a
c
●只要某空间群的点群是11个中心对称的点群之一，则 必有一个陪集 T( 1 , w ) 是的形式。 ●1与w+tj平移组合后，仍为倒反操作，但倒反中心移 至(w+tj)/2。tj为该空间群的任意一个点阵平移矢 量，可见该空间群有许多对称中心。 ●中心对称的空间群共有90种 ●对于中心对称的空间群，习惯把坐标原点放在对称中 心处。 对称中心位于：x/2, ¼+y/2, -¼+z/2 则有：x=0, y=-1/2, z=1/2 （以tj=uja+vjb+wjc为模） 即：21[010]位于：uj/2, 0, wj/2+1/4 c[010]位于：0, vj/2+1/4, 0
引伸时要求m,a,b,n,d能把与点群4同态的空间群分别变 换成它们自己，即只能将上述空间群中的对称元素配置所具备 的m, a, b, n, d对称性组合进去。 (1) 只含中性轴的空间群P4,P42,I4可与m,n组合，但不能与a,b 组合。且有I4/m=I4/n。 (2) 含有非中性轴的空间群I41不能与m,n组合(41→43)，但可与 a,b组合(41→43)。I41/a=I41/b。
2、点阵平移群 定义： 规定结合规则为矢量加法，规定零矢量为全同操作， 则平移操作的集合构成一个无限群---点阵平移群(T)
T = {( I , t j )}
t j = u j a + v jb + w j c
性质： （1）平移群是交换群（由于矢量加法遵从交换律） （2）平移群是空间群的一个子群，而且是不变子群 证明：空间群的点阵平移是该空间群G的一个不变子群 ---空间群中任一操作(W,w)变换(I, tj) ---仍是一个纯平移操作 ---由封闭性知，属于空间群的平移操作
P4
I4
P4
P41
P42 P43
I4
I41 I42=I4 I41=I43
例二：单斜晶系13种空间群的推导 单斜晶系：P，C b∥2，b⊥m 同态的点式空间群：P2, C2, Pm, Cm, P2/m, C2/m 2→21, m→a, c, n a P2 →P21 C2 →C21 = C2 Pm →Pc (Pa, Pn) C2 c Cm →Ca=Cm，Cc=Cn P2/m →P21/m，P2/c，P21/c C2/m →C21/m=C2/a=C21/a=C2/m C2/m →C2/c=C2/n=C21/c=C21/n a ¼ ¼ a ¼ a 1/4 1/4
●在证明P与G/T之间同构关系时，实际上也证明了： 旋轴的轴次与旋转轴的轴次是一样的。 ●空间群的点群就是让空间群对称操作中的所有平移 （包括点阵平移tj与小于初基平移的wi）都等于0 之后剩下的点对称操作的集合。 显然，空间群的点群必为32个晶体学点群之一。 ●空间群G与它的商群G/T同态，商群G/T与空间群的点 群P同构，则空间群G与它的点群P同态。 即每一个空间群总是与一个晶体学点群同态的。 ●空间群的点群P中的操作不一定是该空间群的对称操 作。如G中有41，但点群P中的4不一定是G中的 对称操作。
第六章 空间群的推导
§6-1 含有平移的操作构成的群 §6-2 点式空间群的推导 §6-3 由点式空间群推导非点式空间群 §6-4 由与简单点群同态的空间群推导较 复杂的空间群 §6-5 空间群的符号 §6-6 空间群的分类
§6-1 含有平移的操作构成的群
一、实仿射群：(Real affine group) 实仿射群是所有由点操作（包括纯旋转与非纯旋转） 与平移操作组成的复合操作 Seitz符号为 (W, w) 表示其中某一操作
§6-5 空间群的符号
一、Hermann-Manguin符号（国际晶体学表中采用） 由两部分组成： (1) 表示惯用晶胞有心类型的大写字母。 P，I，F，C或B或A，R，H → 14种Bravais点阵 (2) 表示空间群的对称元素的一组符号。 简略HM符号：尽可能略去对称轴。如：P bcn 完全HM符号：给出每一对称方向上的对称轴和对 21 2 21 称面两者。如： b c n ● 由简略HM符号的对称元素可以推导出完全HM符号中 那些多的对称元素。 ● 属于晶类 mmm, 4/mmm, 3m, 6/mmm, m3, m3m 的 空间群皆有简略HM符号。
⎛ a+b⎞ ⎜ I, ⎟ 2 ⎝ ⎠
2⊥有心面
⎛ b+c⎞ ⎟ ⎜ I, 2 ⎠ ⎝
2∥有心面
Cmm2与Amm2（或Bmm2）在物理上则是不同的空间群 此法可导出： 73个点式空间群，有*号的7个空间群是考虑到点群的对 称元素相对于晶胞的取向后得到的.
ห้องสมุดไป่ตู้
§6-3 由点式空间群推导非点式空间群
空间群G’
G=G’
不变引伸原则: 仅采用这样的(Wi,wi)，它们作用到GH中的任何 一个对称元素上变换而得的对称元素仍为GH中的对称元素。 x, y=axa-1, a→(Wi, wi)