八年级数学下等腰三角形和等边三角形培优练习题
八年级数学全等三角形(培优、数学竞赛)

北京四中八年级培优班数学全等三角形复习题1.如图1,已知在等边△ABC 中,BD =CE ,AD 与BE 相交于P ,则∠APE 的度数是 。
图1B 图2BA图32.如图2,点E 在AB 上,AC =AD ,BC =BD ,图中有 对全等三角形。
3.如图3,OA =OB ,OC =OD ,∠O =60°,∠C =25°,则∠BED 等于 度。
4.如图4所示的2×2方格中,连接AB 、AC ,则∠1+∠2= 度。
图4B图5AB图6CB5.如图5,下面四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确的命题。
( )①AE =AD ;②AB =AC ;③OB =OC ;④∠B =∠C 。
6.如图6,在△ABC 中,∠BAC =90°,延长BA 到点D ,使AD =21AB ,点E 、F 分别为边BC 、AC 的中点。
(1)求证:DF =BE ;(2)过点A 作AG ∥BC ,交DF 于点G ,求证:AG =DG 。
7.如图7,在四边形ABCD 中,对角线AC 平分∠BAD ,AB >AD ,下列结论正确的是( )A. AB -AD >CB -CDB. AB -AD =CB -CDC. AB -AD <CB -CDD. AB -AD 与CB -CD 的大小关系不确定图7BD图8CB8.In Fig. 8, Let △ABC be an equilateral triangle, D and E be points on edges AB and AC respectively, F be intersection of segments BE and CD, and ∠BFC=120°, then the magnitude relation between AD and CE is ( )A. AD>CEB. AD<CEC. AD=CED. indefinite(英汉小词典:equilateral 等边的;intersection 交点;indefinite 不确定的;magnitude 大小,量) 9.如图9,在△ABC 中,AC =BC =5,∠ACB =80°,O 为△ABC 中一点,∠OAB =10°,∠OBA =30°,则线段AO 的长是 。
八年级数学全等三角形(培优篇)(Word版含解析)

八年级数学全等三角形(培优篇)(Word版含解析)一、八年级数学轴对称三角形填空题(难)1.如图,在菱形ABCD中,ZABC=120° , AB=10cm,点P是这个菱形内部或边上的一点.若以P,B f C为顶点的三角形是等腰三角形,则P, A(P, A两点不重合)两点间的最短距离为____________ c m .【答案】1OJJ-1O【解析】解:连接3D,在菱形A3CD中,T Z ABC=120° , AB=BC=AD=CD=10 , :. Z A=Z C=60° ,二△ ABD , △ BCD都是等边三角形,分三种情况讨论:①若以边8C为底,则3C垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了"直线外一点与直线上所有点连线的线段中垂线段最短",即当点P与点D重合时,必最小,最小值^4=10 ;②若以边P3为底,ZPCB为顶角时,以点C为圆心,BC长为半径作圆,与AC相交于一点,则弧3D (除点8外)上的所有点都满足APBC是等腰三角形,当点P在AC上时,AP 最小,最小值为lOjJ-10 ;③若以边PC为底,ZPBC为顶角,以点3为圆心,BC为半径作圆,则弧AC上的点&与点D均满足APBC为等腰三角形,当点P与点A重合时,必最小,显然不满足题意,故此种情况不存在;综上所述,必的最小值为10>/3-10 (cm).故答案为:10x/I—10 .点睹:本题考查菱形的性质、等边三角形的性质,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.2.在等腰△遊中,肋丄肚交直线%于点以若妙丄万G则△磁的顶角的度数为【答案】30。
或150。
或90°【解析】试题分析:分两种情况:①3C为腰,②BC为底,根据直角三角形30。
角所对的直角边等于斜边的一半判断岀ZACD=3O°,然后分AD在^ABC内部和外部两种情况求解即可.解:①BC为腰,VAD丄 BC 于点D t AD= - BC f2:.ZACD二30。
《等腰三角形》培优专题

等腰三角形【分类解析】例1. 如图,已知在等边三角形ABC 中,D 是AC 的中点,E 为BC 延长线上一点,且CE =CD ,DM ⊥BC ,垂足为M 。
求证:M 是BE 的中点。
E例2. 如图,已知:AB C ∆中,AC AB =,D 是BC 上一点,且CA DC DB AD ==,,求BAC ∠的度数。
ABCD例3. 已知:如图,AB C ∆中,AB CD AC AB ⊥=,于D 。
求证:DCB 2B AC ∠=∠。
C4、中考题型:1.如图,△ABC 中,AB =AC ,∠A =36°,BD 、CE 分别为∠ABC 与∠ACB 的角平分线,且相交于点F ,则图中的等腰三角形有( )A. 6个B. 7个C. 8个D. 9个A 36° E DFBC 2.)已知:如图,在△ABC 中,AB =AC ,D 是BC 的中点,DE ⊥AB ,DF ⊥AC ,E 、F 分别是垂足。
求证:AE =AF 。
AE F BDC5、题形展示:例1. 如图,AB C ∆中, 100=∠=A AC AB ,,BD 平分ABC ∠。
求证:B C B D AD =+。
【实战模拟】1. 选择题:等腰三角形底边长为5cm ,一腰上的中线把其周长分为两部分的差为3cm ,则腰长为( ) A. 2cmB. 8cmC. 2cm 或8cmD. 以上都不对2. 如图,AB C ∆是等边三角形,BC BD 90CBD ==∠, ,则1∠的度数是________。
CA 1DB2 33. 求证:等腰三角形两腰中线的交点在底边的垂直平分线上.4. AB C ∆中, 120A AC AB =∠=,,AB 的中垂线交AB 于D ,交CA 延长线于E ,求证:BC 21DE =。
【试题答案】(实战模拟) 1. B2. 分析:结合三角形内角和定理,计算图形中角的度数是等边三角形性质的重要应用。
解:因为AB C ∆是等边三角形 所以 60ABC BC AB =∠=, 因为B C B D =,所以B D A B = 所以23∠=∠在AB D ∆中,因为 60ABC 90CBD =∠=∠, 所以 150ABD =∠,所以 152=∠ 所以 75ABC 21=∠+∠=∠3. 分析:首先将文字语言翻译成数学的符号语言和图形语言。
人教版 八年级数学 13.3 等腰三角形 培优训练(含答案)

人教版八年级数学13.3 等腰三角形培优训练一、选择题(本大题共10道小题)1. 如图,已知P A=PB,在证明∠A=∠B时,需要添加辅助线,下面有甲、乙两种辅助线的作法:甲:作底边AB的中线PC;乙:作PC平分∠APB交AB于点C.则()A.甲、乙两种作法都正确B.甲的作法正确,乙的作法不正确C.甲的作法不正确,乙的作法正确D.甲、乙两种作法都不正确2. 已知实数x、y满足|x-4|+y-8=0,则以x、y的值为两边长的等腰三角形的周长是()A. 20或16B. 20C. 16D. 以上答案均不对3. 如图,△ABC中,AB=AC,AD是∠BAC的平分线,已知AB=5,AD=3,则BC的长为()A. 5B. 6C. 8D. 104. 如图,∠AOB=50°,OM平分∠AOB,MA⊥OA于点A,MB⊥OB于点B,则∠MAB等于()A.50°B.40°C.25°5. 如图,下列条件不能推出△ABC是等腰三角形的是()A.∠B=∠C B.AD⊥BC,∠BAD=∠CADC.AD⊥BC,BD=CD D.AD⊥BC,∠BAD=∠ACD6. 如图所示,△ABC是等边三角形,D为AB的中点,DE⊥AC,垂足为E. 若AE=1,则△ABC的边长为()A. 2B. 4C. 6D. 87. 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠BCD的度数为()A.150°B.160°C.130°D.60°8. 如图,在△ABC中,∠BAC=72°,∠C=36°,∠BAC的平分线AD交BC于点D,则图中有等腰三角形()A.0个B.1个C.2个D.3个9. 如图所示的正方形网格中,网格线的交点称为格点. 已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形.....,那么符合题意的点C的个数是()A. 6B. 7C. 8D. 910. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在点O相连并可绕点O转动,点C固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是()A.60°B.65°C.75°D.80°二、填空题(本大题共6道小题)11. 如图,在等边三角形ABC中,点D在边AB上,点E在边AC上,将△ADE 折叠,使点A落在BC边上的点F处,则∠BDF+∠CEF=________°.12. 如图,在△ABC中,AB=AC,D是AC上一点,且BC=BD.若∠CBD=46°,则∠A=________°.13. 在△ABC中,若∠A=100°,∠B=40°,AC=5,则AB=________.14. 如图,BO平分∠CBA,CO平分∠ACB,MN过点O且MN∥BC,设AB=12,AC=18,则△AMN的周长为________.15. 如图,在△ABC中,若AB=AC=8,∠A=30°,则S△ABC=________.16. 一个等腰三角形的一边长是2,一个外角是120°,则它的周长是________.三、解答题(本大题共4道小题)17. 如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC 于点F.求证:DE=DF.18. 如图,在等边三角形ABC中,D为AC上一点,E为AB延长线上一点,DE ⊥AC交BC于点F,且DF=EF.(1)求证:CD=BE;(2)若AB=12,求BF的长.19. 如图,将一张长方形的纸条ABCD沿EF折叠,若折叠后∠AGC′=48°,AD交EC′于点G.(1)求∠CEF的度数;(2)求证:△EFG是等腰三角形.20. 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.求证:DF=2DC.人教版八年级数学13.3 等腰三角形培优训练-答案一、选择题(本大题共10道小题)1. 【答案】A2. 【答案】B【解析】∵|x -4|+y -8=0,∴x -4=0,y -8=0,解得x =4,y =8.分两种情况讨论:①当4为腰时,根据三角形三边关系知4+4=8,∴这样的等腰三角形不存在;②当8为腰时,则有4+8>8,这样能够组成等腰三角形,∴此三角形的周长是8+8+4=20.3. 【答案】C 【解析】∵AB =AC ,AD 平分∠BAC ,∴根据等腰三角形三线合一性质可知AD ⊥BC ,BD =CD ,在Rt △ABD 中,AB =5,AD =3,由勾股定理得BD =4,∴BC =2BD =8.4. 【答案】C[解析] ∵OM 平分∠AOB ,MA ⊥OA 于点A ,MB ⊥OB 于点B ,∴∠AOM =∠BOM =25°,MA =MB.∴∠OMA =∠OMB =65°.∴∠AMB =130°.∴∠MAB =12×(180°-130°)=25°.故选C.5. 【答案】D[解析] 选项A 由等角对等边可得△ABC 是等腰三角形;选项B 由所给条件可得△ADB ≌△ADC ,由全等三角形的性质可得AB =AC ;选项C 由垂直平分线的性质可得AB =AC ;选项D 不可以得到AB =AC. 6. 【答案】B7. 【答案】A[解析] ∵AB ∥ED ,∴∠E =180°-∠EAB =180°-120°=60°. 又∵AD =AE ,∴△ADE 是等边三角形.∴∠EAD =60°.∴∠BAD =∠EAB -∠EAD =120°-60°=60°.∵AB =AC =AD ,∴∠B =∠ACB ,∠ACD =∠ADC.在四边形ABCD 中,∠BCD =∠B +∠ADC =12(360°-∠BAD)=12×(360°-60°)=150°. 故选A.8. 【答案】D[解析] ∵∠BAC =72°,∠C =36°,∴∠ABC =72°.∴∠BAC =∠ABC. ∴CA =CB.∴△ABC 是等腰三角形.∵∠BAC 的平分线AD 交BC 于点D ,∴∠DAB=∠CAD=36°.∴∠CAD=∠C.∴CD=AD,∴△ACD是等腰三角形.∵∠ADB=∠CAD+∠C=72°,∴∠ADB=∠B.∴AD=AB.∴△ADB是等腰三角形.9. 【答案】C10. 【答案】D[解析] ∵OC=CD=DE,∴∠O=∠ODC,∠DCE=∠DEC.∴∠DCE=∠O+∠ODC=2∠ODC.∵∠O+∠OED=3∠ODC=∠BDE=75°,∴∠ODC=25°.∵∠CDE+∠ODC=180°-∠BDE=105°,∴∠CDE=105°-∠ODC=80°.二、填空题(本大题共6道小题)11. 【答案】120[解析] 由于△ABC是等边三角形,所以∠A=60°.所以∠ADE+∠AED=120°.因为将△ADE折叠,使点A落在BC边上的点F处,所以∠ADE=∠EDF,∠AED=∠DEF.所以∠ADF+∠AEF=2(∠ADE+∠AED)=240°.所以∠BDF+∠CEF=360°-(∠ADF+∠AEF)=120°.12. 【答案】46[解析] ∵BC=BD,∠CBD=46°,∴∠C=∠BDC=12(180°-46°)=67°.∵AB=AC,∴∠ABC=∠C=67°.∴∠A=46°.13. 【答案】514. 【答案】30[解析] ∵MN∥BC,∴∠MOB=∠OBC. ∵∠OBM=∠OBC,∴∠MOB=∠OBM.∴MO=MB.同理NO=NC.∴△AMN的周长=AM+MO+AN+NO=AM+MB+AN+NC=AB+AC=30.15. 【答案】16[解析] 如图,过点C作CD⊥AB,垂足为D,则△ADC是含30°角的直角三角形,那么DC=12AC=4,∴S△ABC=12AB·DC=12×8×4=16.16. 【答案】6[解析] 已知三角形的一外角为120°,则相邻内角度数为60°,那么含有60°角的等腰三角形是等边三角形.已知等边三角形的一边长为2,则其周长为6.三、解答题(本大题共4道小题)17. 【答案】证明:连接AD.∵AB=AC,D为BC的中点,∴AD平分∠BAC.又∵DE⊥AB,DF⊥AC,∴DE=DF.18. 【答案】解:(1)证明:如图,过点D作DM∥AB,交CF于点M,则∠MDF=∠E.∵△ABC是等边三角形,∴∠CAB=∠CBA=∠C=60°.∵DM∥AB,∴∠CDM=∠CAB=60°,∠CMD=∠CBA=60°.∴△CDM是等边三角形.∴CM=CD=DM.在△DMF 和△EBF 中,⎩⎨⎧∠MDF =∠E ,DF =EF ,∠DFM =∠EFB ,∴△DMF ≌△EBF(ASA).∴DM =BE. ∴CD =BE.(2)∵ED ⊥AC ,∠CAB =∠CBA =60°, ∴∠E =∠FDM =30°. ∴∠BFE =∠DFM =30°. ∴BE =BF ,DM =MF.∵△DMF ≌△EBF ,∴MF =BF. ∴CM =MF =BF.又∵BC =AB =12,∴BF =13BC =4.19. 【答案】解:(1)∵四边形ABCD 是长方形, ∴AD ∥BC.∴∠BEG =∠AGC′=48°. 由折叠的性质得∠CEF =∠C′EF , ∴∠CEF =12(180°-48°)=66°. (2)证明:∵四边形ABCD 是长方形, ∴AD ∥BC.∴∠GFE =∠CEF. 由折叠的性质得∠CEF =∠C′EF , ∴∠GFE =∠C′EF.∴GE =GF ,即△EFG 是等腰三角形.20. 【答案】证明:∵△ABC 是等边三角形, ∴∠A =∠B =∠ACB =60°. ∵DE ∥AB ,∴∠EDC =∠B =60°,∠DEC =∠A =60°. ∵EF ⊥DE ,∴∠DEF =90°. ∴∠F =90°-∠EDC =30°.∵∠ACB=∠EDC=∠DEC=60°,∴△EDC是等边三角形.∴DE=DC. ∵∠DEF=90°,∠F=30°,∴DF=2DE=2DC.。
八年级下证明二等腰三角形 - 培优

等腰三角形知识点等腰三角形⑴定义:有两条边相等的三角形叫做等腰三角形。
⑵性质:①等腰三角形的两个底角相等(简称“等边对等角”);②等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合(简称“三线合一”)。
③等腰三角形是轴对称图形。
⑶判定方法:①等腰三角形的定义;②如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称“等角对等边” )。
等边三角形(也叫正三角形)(1)定义:三条边都相等的三角形叫做等边三角形。
⑵性质:①等边三角形的各角相等,并且每一个角都等于60°;②等边三角形是轴对称图形。
⑶判定方法:①等边三角形的定义;②三个角都相等的三角形是等边三角形;③有一个角是60°的等腰三角形是等边三角形。
典型例题等腰三角形例1.等腰三角形的对称轴是()A.顶角的平分线B.底边上的高C.底边上的中线D.底边上的高所在的直线变式练习:性质“等腰三角形的三线合一”,其中所指的“线”之一是()A.等腰三角形底角的平分线B.等腰三角形腰上的高C.等腰三角形腰上的中线D.等腰三角形顶角的平分线变式练习.下列关于等腰三角形的性质叙述错误的是()A.等腰三角形两底角相等B.等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合C.等腰三角形是中心对称图形D.等腰三角形是轴对称图形例2.等腰三角形有两条边长为4cm和9cm,则该三角形的周长是()A.17cm B.22cm C.17cm或22cm D.18cm变式练习.等腰三角形的顶角是80°,则一腰上的高与底边的夹角是()A.40°B.50°C.60°D.30°变式练习.等腰三角形的一个外角是80°,则其底角是()A.100°B.100°或40°C.40°D.80°变式练习.如图所示,C 、E 和B 、D 、F 分别在∠GAH 的两边上,且AB=BC=CD=DE=EF ,∠A=18°,则∠GEF 的度数是( )A .80°B .90°C .100°D .108°ECA F G例3:如图,在等腰△ABC 中,AB=AC ,一腰上中线BD 将这个三角形的周长分为16和8的两部分,求这个等腰三角形的腰长与底边长.变式练习:如图,若P 为∠AOB 内一点,分别作出P 点关于OA 、OB 的对称点P1P 2,连接P 1P 2交OA 于M ,交OB 于N ,P 1P 2=15,则△PMN 的周长是变式练习:如图,在△ABC 中,AB=AC=10,ABC=∠ACB=15°,CD 是腰AB 上的高;求:△ABC 的面积.变式练习:如图,已知在△ABC 中,AB=AC ,∠BAC=120o ,AC 的垂直平分线EF 交AC 于点E ,交BC 于点F .求证:BF=2CF .例4:如图,在Rt △ABC 中,AB=AC ,∠BAC=90°,D 为 BC 的中点.(1)写出点D 到DABC 三个顶点 A 、B 、C 的距离的关系(不要求证明)(2)如果点M 、N 分别在线段AB 、AC 上移动,在移动中保持AN=BM ,请判断△DMN 的形状,并证明你的结论NMDBA C变式练习:在△ABC 中,AC=BC=2,∠C=90°,将一块等腰三角板的直角顶点放在斜边AB 的中点P 处,将三角板绕点P 旋转,三角板的两直角边分别交射线AC 、CB 于D 、E 两点.如图①、②、③是旋转三角板得到的图形中的3种情况,研究:(1)三角板绕点P 旋转,观察线段PD 与PE 之间有什么数量关系?并结合图②说明理由.(2)三角板绕点P 旋转,△PBE 是否能成为等腰三角形?若能,指出所有情况(即写出△PBE 为等腰三角形时CE 的长);若不能,请说明理由.培优例5:(1)等腰三角形的内角的度数之比为1:2,这个等腰三角形底角的度数为________(2)已知等腰三角形ABC 的三边长a,b,c 均为整数,且满足a+bc+b+ac=24,则这样的三角形共有__________个.例6.如图,若AB=AC ,BG=BH ,AK=KG ,则BAC ∠的度数是_______例7.如图,在△ABC 中,AC=BC ,90ACB ∠= ,D 是AC 上一点,AE BD ⊥交BD 的延长线于E ,且12AE BD =,求证:BD 是∠ABC 的角平分线例8.如图1,三角形ABC 的边BC 在直线l 上,AC BC ⊥,且AC=BC ,三角形EFP 的边FP 也在直线l 上,边EF 与边AC 重合,且EF=FP 。
初二数学等腰等边三角形培优题1(完整资料).doc

此文档下载后即可编辑等腰等边三角形培优题11.如图,将△ABC 绕直角顶点C 顺时针旋转90°,得到△DEC ,连接AD ,若∠BBB =25∘,则∠BBB =______.2.如图,P ,Q 是△ABC 的边BC 上的两点,且BP =PQ =QC =AP =AQ ,则∠ABC =_____.3.如图,在△BBBBBB 中,BB BB =BBBB ,CD 是∠BBBBBB 的平分线,BB BB //BBBB ,交AC 于点E .若∠BBBB =35∘,则∠BBB=.4.如图,等边△BBBBBB 中,AD 是中线,BBBB ⊥BBBB 于点E ,BBBB =3,则点D 到AB 的距离为:______.5.已知:在△ABC 中,AH ⊥BC ,垂足为点H ,若AB +BH =CH ,∠ABH =70∘,则∠BAC =______ ∘.6.如图,在△ABC 中,BI ,CI 分别平分∠ABC,∠ACB,过I 点作DE∥BC,交AB 于D ,交AC 于E ,给出下列结论:①△DBI 是等腰三角形;②△ACI 是(第1题) (第2题) (第3题)(第4题) (第6题) (第7题)等腰三角形;③AI 平分∠BAC;④△ADE 周长等于AB +AC .其中正确的是( )A . ①②③B . ②③④C . ①③④D . ①②④7.如图,已知AB =A 1B ,A 1B 1=A 1A 2,A 2B 2=A 2A 3,A 3B 3=A 3A 4,….若∠A=70°,则∠B n -1A n A n -1的度数为( )A . 702n ⎛⎫︒ ⎪⎝⎭B . 1702n +⎛⎫︒ ⎪⎝⎭C . 1702n -⎛⎫︒ ⎪⎝⎭D . 2702n +⎛⎫︒ ⎪⎝⎭8.如图,在等边△ABC 中,AD 是BC 边上的高,∠BDE=∠CDF=30°, 在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的有 (填序号) 9.如图所示,在Rt △ABC 中,∠A=30°,∠B=90°,AB=12,D 是斜边AC 的中点,P 是AB 上一动点,则PC+PD 的最小值为 .10.如图,已知△BBBBBB 是等边三角形,D 为BC 延长线上一点,CE 平分∠BBBBBB ,BBBB =BBBB ,BBBB =7, 则 AE 的长度是 . 11.如图,△ABC 中,BD 平分∠ABC ,BC 的垂直平分线交BC 于点E ,交BD于点F ,连接CF .若∠A =60°,∠ABD =24°,则∠ACF 的度数为 .12.如图,已知点C 是线段AB 的中点,点D 是线段BC 上的定点(不同于端点B 、C ),过点D 作直线l 垂直线段AB ,若点P 是直线l 上的任意一点,连接PA 、PB ,则能使△PAB 成为等腰三角形的点P 一共有_______ 个.(填写确切的数字)(第11题) (第9题) (第10题)(第8题)(第12题) (第13题)13.如图,AB=2,BC=5,AB⊥BC于点B,l⊥BC于点C,点P自点B开始沿射线BC移动,过点P作PQ⊥PA交直线l于点Q,当BP= 时,PA=PQ. 14.已知△ABC是等边三角形,E是AC边上一点,F是BC边延长线上一点,且CF=AE,连接BE,EF.(1)如图1,若E是AC边的中点,猜想BE与EF的数量关系为___________________.(2)如图2,若E是线段AC上的任意一点,其它条件不变,上述线段BE、EF 的数量关系是否发生变化,写出你的猜想并加以证明.(3)如图3,若E是线段AC延长线上的任意一点,其它条件不变,上述线段BE、EF的数量关系是否发生变化,写出你的猜想并加以证明。
等腰三角形和等边三角形培优精华

等腰三角形和等边三角形知识要点1、等腰三角形的定义:有两条边相等的三角形是等腰三角形。
等边三角形的定义:三条边都相等的三角形是等边三角形,又叫正三角形,等边三角形是特殊的等腰三角形。
2、等腰三角形的性质:(1)、等腰三角形的两个底角相等(简写成“等边对等角”)。
(2)、等腰三角形的顶角的平分线,底边上的中线,底边上的高重合(简写成“等腰三角形的三线合一”)。
(3)、等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)。
(4)、等腰三角形底边上的垂直平分线到两条腰的距离相等。
(5)、等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
(6)、等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。
(7)、等腰三角形是轴对称图形,只有一条对称轴,顶角平分线所在的直线是它的对称轴, 3、等腰三角形的判定:(1)、在同一三角形中,有两条边相等的三角形是等腰三角形(定义)。
(2)、在同一三角形中,有两个角相等的三角形是等腰三角形(简称:等角对等边)。
4、等边三角形的性质:⑴、等边三角形的三边都相等,内角都相等、且均为60度。
⑵、等边三角形每一条边上的中线、高线和每个角的角平分线互相重合。
⑶、等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线或所对角的平分线所在直线。
5、等边三角形的判定: ⑴三边相等的三角形是等边三角形(定义)。
⑵三个内角都相等的三角形是等边三角形(有两个角等于60度的三角形是等边三角形)。
⑶有一个角是60度的等腰三角形是等边三角形。
6、含30°角的直角三角形的重要结论:30°角所对的直角边是斜边的一半。
7、常做辅助线的方法:“遇到等腰常做高” 练习题1 2.7、3、5、22、如图,在等边△ABC 中,D 、E AD=CE ,则∠BCD+∠CBE= 度。
3、如图,点D 为等边三角形ABC 内的一点,BD=AD ,BE=AB , ∠DBE=∠DBC ,则∠BED 的度数是 度。
等边三角形培优专项练习试题与答案
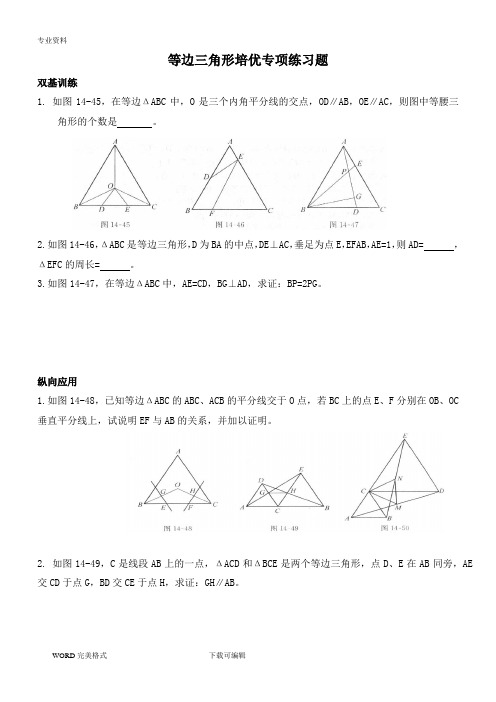
等边三角形培优专项练习题双基训练1. 如图14-45,在等边ΔABC中,O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中等腰三角形的个数是。
2.如图14-46,ΔABC是等边三角形,D为BA的中点,DE⊥AC,垂足为点E,EFAB,AE=1,则AD= ,ΔEFC的周长= 。
3.如图14-47,在等边ΔABC中,AE=CD,BG⊥AD,求证:BP=2PG。
纵向应用1.如图14-48,已知等边ΔABC的ABC、ACB的平分线交于O点,若BC上的点E、F分别在OB、OC垂直平分线上,试说明EF与AB的关系,并加以证明。
2. 如图14-49,C是线段AB上的一点,ΔACD和ΔBCE是两个等边三角形,点D、E在AB同旁,AE 交CD于点G,BD交CE于点H,求证:GH∥AB。
3.如图14-50,已知ABC是等边三角形,E是AC延长线上一点,选择一点D使得ΔCDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,求证:ΔCMN是等边三角形。
4.如图14-51,C是线段AB上一点,分别以BC、AC为边作等边ΔACD和ΔCBE,M为AE的中点,N为DB的中点,求证:ΔCMN为等边三角形。
5. 如图14-52,在四边形ABCD中,∠A+∠B=1200,AD=BC,以CD为边向形外作等边ΔCDE,连结AE,求证:ΔABE为等边三角形。
6. 如图14-53,已知ΔABC是等边三角形,D为AC上一点,∠1=∠2,BD=CE,求证:ΔADE是等边三角形。
7. 如图14-54,设在四边形ABCD中,∠A+∠B=1200,AD=BC,M、N、P分别是AC、BD、CD的中点。
求证:ΔMNP是等边三角形。
8. 如图14-55,在等腰梯形ABCD中,AB∥CD,AB>CD,AD=BC,对角线AC、BD交于点O,∠AOB=600,且E、F分别是OD、OA的中点,M是BC的中点,求证:ΔEFM是等边三角形。
9. 如图14-56,在ABCD中,ΔABE和ΔBCF都是等边三角形,求证:ΔDEF是等边三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学下等腰三角形和等边三角形培优练习题一、填空选择题:1.如下图1,等边△的边长为3,P 为上一点,且=1,D 为上一点,若∠=60°,则的长为( ) A .32B .23C .12D .342.如上图2,△中,D 、E 分别是、的中点,平分∠,交于点F ,若=6, 则的长是( )(A )2 (B )3 (C )25(D )4 3.如上图3,点A 的坐标是(2,2),若点P 在x 轴上,且△是等腰三角形,则点P 的坐标 不可能...是( )A .(4,0) B .(1.0) C .(-22,0) D .(2,0)4.如上图1,==,若∠A =40°,则∠的度数是( ) A .20oB .30oC .35oD .40o5.如上图2,△中,==6,=8,平分么交于点E ,点D 为的中点,连结,则△的周长是( ) A .7+5 B .10 C .4+25 D .126.如上图3,在△中,,∠36°,、分别是△、△的角平分线, 则图中的等腰三角形有 ( ) (A)5个 (B)4个 (C)3个 (D)2个7.在等腰ABC △中,AB AC ,一边上的中线BD 将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )A .7B .11C .7或11D .7或108.等腰三角形一腰上的高与另一腰的夹角为30º,腰长为4 ,则其腰上的高为 . 9.已知等腰ABC △的周长为10,若设腰长为x ,则x 的取值范围是 . 10.在△中,=,的垂直平分线与所在的直线相交所得到锐角为50°, 则∠B 等于_ 度.AD CPB60° ED CBA(第6题)BA DC1 2 3 4-1 12xy A11.如下图1,过边长为1的等边△的边上一点P ,作⊥于E ,Q 为延长线上一点,当=时,连交边于D ,则的长为( )A.13 B .12 C .23D .不能确定12.如下图2,等腰△ 中,,∠20°。
线段的垂直平分线交于D ,交于E ,连接,则∠等于( ) A 、80° B 、 70° C 、60° D 、50°ACDB13.如上图3,△内有一点D ,且,若∠20°,∠30°,则∠的大小 是( )A.100° B.80° C.70° D.50°14.已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是( )A .8B .7C . 4D .315.如下图1,在△中,D ,E 分别是边,的中点, 连接.若平分∠,则下列结论错误的是 ( )A .=2 B .∠A =∠ C .=2 D .⊥16.如上图2所示的正方形网格中,网格线的交点称为格点.已知A 、B 是两格点,如果C 也是图中的格点,且使得ABC 为等腰三角形.....,则点C 的个数是( ) A .6B .7C .8D .9BA第8题图AD BEC17、如上图3,把等腰直角△沿折叠,使点A 落在边上的点E 处.下面结论错误的 是( )A .= B .=C .=D .=18.已知:一等腰三角形的两边长x 、y 满足方程组2-3,328,x y x y =⎧⎨+=⎩则此等腰三角形的周长为( )A .5B .4C .3D .5或419.如图,点C 是线段上的一个动点,△和△是在同侧的两个等边三角形,,分别是△和△的高,点C 在线段上沿着从点A 向点B 的方向移动(不与点A ,B 重合),连接,得到四边形.这个四边形的面积变化情况为( )(A )逐渐增大 (B) 逐渐减小 (C) 始终不变 (D) 先增大后变小20.如图,吴伯伯家有一块等边三角形的空地,已知点E 、F 分别是边、的中点,量得=5米,他想把四边形用篱笆围成一圈放养小鸡,则需用篱笆的长是( )A 、15米B 、20米C 、25米D 、30米 21.如图1,△中,,∠80°。
则∠B 的度数是( ) A .40° B .35° C .25° D .20° 22.已知:△中,x ,6,则腰长x 的取值范围是( ) A .03x << B .3x > C .36x << D .6x >23.已知等腰三角形的一个内角为70°,则另外两个内角的度数是( )A .55°,55°B .70°,40°C .55°,55°或70°,40°D .以上都不对 24.如下图1,小红作出了边长为1的第1个正△A 1B 1C 1,算出了正△A 1B 1C 1的面积,然后分别取 △A 1B 1C 1三边的中点A 2,B 2,C 2,作出了第2个正△A 2B 2C 2,算出了正△A 2B 2C 2的面积,用同样的方法,作出了第3个正△A 3B 3C 3,算出了正△A 3B 3C 3的面积……,由此可得,第8个正△A 8B 8C 8的面积是( )A .731()2⨯B.831()2⨯C .731()4⨯ D .831()4⨯ (第20题图)FE CB A……图③图②图①25.如上图2所示,已知△和△均是等边三角形,点B、C、E在同一条直线上,与交于点O,与交于点G,与交于点F,连结、,则下列结论:①=②=③∥④∠=∠,其中正确结论的个数()A.1个B.2个C.3个D.4个26.如上图3,△中,垂直平分交于E,∠30°,∠80°,则∠.27.等腰三角形的两边长为4、9,则它的周长是 A.17 B.17或22 C.20 D.22 28.如下图3,将第一个图(图①)所示的正三角形连结各边中点进行分割,得到第二个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割,得到第三个图(图③);再将第三个图中最中间的小正三角形按同样的方式进行分割,……,则得到的第五个图中,共有个正三角形.29.如上图1,等边△的边长为6是边上的中线是上的动点是边上一点.若2的最小值为 . 30.如上图2,在△中,13,10,D是的中点,过点D作⊥于点E,则的长是。
31.如下图1,等腰三角形中,已知=,∠A=30°,的垂直平分线交于D,则∠的度数为 .32. 如上图2,在ABC△中,13AB AC==,10BC=,点D为BC的中点,DE DE AB⊥,垂足为点E,则DE等于() A.1013B.1513C.6013D.751333.如果一个等腰三角形的两边长分别是5和6,那么此三角形的周长是A.15 B.16 C.17 D.16或1734.边长为6的等边三角形中,其一边上高的长度为.35. 已知等边△中,如上图3,点分别在边上,把△沿直线翻折,使点B落在点Bˊ处,ˊˊ分别(第26题)EDCBA交边于点F ,G ,若∠80º ,则∠的度数为36. 在等腰△中,∠90°,=1,过点C 作直线l ∥,F 是l 上的一点,且=,则点F 到直线的距离为 .37. 如下图1,等边三角形中,D 、E 分别为、边上的两个动点,且总使,与交于点F ,⊥于点G ,则FGAF.38. 如上图2,在△中,,∠的角平分线交边于点D ,5,6,则.39. 等腰三角形的周长为14,其一边长为4,那么,它的底边为 . 二、解答题1. 如图,已知点D 为等腰直角△内一点,∠=∠=15°,E 为延长线上的一点,且=.(1)求证:平分∠;(2)若点M 在上,且,求证: .2.如图,在等腰三角形中,∠90°,D 为边上中点,过D 点作⊥,交于E ,交于F ,若4,3,求长.GFE CBA第37题D3.如图,等边△中,是∠的角平分线,D 为上一点,以为一边且在下方作等边△,连结. (1) 求证:△≌△;(2) 延长至Q, P 为上一点,连结、使==5, 若=8时,求的长.4. 已知:如图,锐角△的两条高、相交于点O ,且,(1)求证:△是等腰三角形;(2)判断点O 是否在∠的角平分线上,并说明理由。
5. 已知:在△中,,∠900,点D 是的中点,点E 是边上一点。
(1)直线垂直于于点F ,交于点G (如图①),求证:;(2)直线垂直于于,垂足为H ,交的延长线于点M (如图②),找出图中与相等的线段,并说明。
BAEDF C6.(1)如图,已知AB AC AD AE ==,.求证BD CE =.7.如图,点E ,F 在上,=,∠A =∠D ,∠B =∠C ,与交于点O . (1)求证:=;(2)试判断△的形状,并说明理由.8、如图,△和△都是等腰直角三角形,∠=∠=90°,交于F ,分别交,于点G 、H 。
试猜测线段和的位置和数量关系,并说明理由.ACED BADB EF CO9.如图,BCD∆和都是等腰直角三角形,∠∠90°,D为边上一点。
ACB∆(1)求证:△≌△;(2)若5,12,求的长。
10.如图1-28所示,D为△的边的延长线上一点,过D作⊥,垂足为F,交于E,且=,求证△是等腰三角形.11、如图1-29所示,在△中,∠=90°,⊥于点D,点E在上.=,过点E作的垂线,交的延长线于点F,求证=.12.如图,点E、C在上,,∠∠45°,∠∠90°.(1)求证:;(2)若交于M32,将线段绕点C顺时针旋转,使点E旋转到上的G处,求旋转角∠的度数.B13.如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点.(1)如果点P 在线段上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段上由C 点向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?14.如图, 已知等边三角形中,点D ,E ,F 分别为边,,的中点,M 为直线上一动点,△为等边三角形(点M 的位置改变时, △也随之整体移动) .(1)如图①,当点M 在点B 左侧时,请你判断与有怎样的数量关系?点F 是否在直线上?都请直...接.写出结论,不必证明或说明理由; (2)如图②,当点M 在上时,其它条件不变,(1)的结论中与的数量关系是否仍然成立?若成立,请利用图②证明;若不成立,请说明理由;(3)若点M 在点C 右侧时,请你在图③中画出相应的图形,并判断(1)的结论中与的数量关系是否仍然成立?若成立?请直接写出结论,不必证明或说明理由.15. 如图1,在等边△中,点D 是边的中点,点P 是线段上的动点(点P 与点C 不重合),连结. 将△绕点P 按顺时针方向旋转α角(0°<α<180°),得到△A 1B 1P ,连结1,射线1分别交射线、射线B 1B 于点E 、F .(1) 如图1,当0°<α<60°时,在α角变化过程中,△与△始终存在 关系(填“相似”或“全等”),并说明理由;(2)如图2,设∠β . 当60°<α<180°时,在α角变化过程中,是否存在△与△全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;(3)如图3,当α=60°时,点E 、F 与点B 重合. 已知4,设,△A 11的面 积为S ,求S 关于x 的函数关系图1图2图3111图① 图②图③A· BCD EF··N MFEDCB ANMFEDCBA·16、如图,△中,,∠36°,的垂直平分线交于E,D为垂足,连结.(1)求∠的度数;(2)若5,求长.。
