第7讲多元函数微分学及其应用II
多元函数微分法及其应用总结

多元函数微分法及其应用总结多元函数微分法及其应用是高等数学中一个重要的内容。
多元函数是指自变量有两个或者多个的函数,如z=f(x,y)。
而微分法是研究函数的变化率的一种方法。
本文将对多元函数微分法及其应用进行总结。
1. 多元函数微分法的基本概念多元函数的微分可以分为偏导数和全微分两种形式。
对于多元函数z=f(x,y),其偏导数表示函数在某一自变量上的变化率,可以记作∂z/∂x,∂z/∂y。
全微分表示函数在所有自变量上的变化率,可以记作dz。
多元函数的微分法有很多性质和定理,如链式法则、高阶偏导数、隐函数定理等。
2. 多元函数的极值与最值利用多元函数微分法,我们可以求多元函数的极值与最值。
对于多元函数z=f(x,y),其极值、最值的求解步骤大致如下:(1)求函数的偏导数,得到所有的偏导数;(2)令所有的偏导数等于零,求解出关于x和y的方程;(3)求解方程组,得到x和y的解;(4)将解代回原函数,求得z的值;(5)比较求得的z值,得到最大值或最小值。
3. 多元函数的泰勒展开多元函数的泰勒展开是利用多元函数在某一点附近进行近似求解的一种方法。
对于多元函数z=f(x,y),其泰勒展开公式为:f(x+Δx,y+Δy) = f(x,y) + (∂f/∂x)Δx + (∂f/∂y)Δy + 1/2(∂²f/∂x²)(Δx)² + 1/2(∂²f/∂y²)(Δy)² + (∂²f/∂x∂y)ΔxΔy + O(Δx²,Δy²)这里的O(Δx²,Δy²)表示高阶无穷小,Δx和Δy表示自变量的增量。
4. 多元函数微分法的应用多元函数微分法广泛应用于物理学、工程学和经济学等领域。
具体应用如下:(1)在物理学中,多元函数微分法可以用于描述粒子在空间中的运动轨迹,求解最优路径等问题。
(2)在工程学中,多元函数微分法可以用于建模和优化设计,如求解最优结构、最优控制等问题。
多元函数微分学的应用

多元函数微分学的应用一、极值问题多元函数微分学最重要的应用之一是求解极值问题。
通过求取函数的偏导数,我们可以找到函数的极值点。
这对于经济学家、物理学家和其他相关领域的研究者来说是非常重要的。
例如,在经济学中,我们可以使用多元函数微分学来确定产品的最优产量和价格,以使利润最大化。
在物理学中,我们可以使用多元函数微分学来优化力学系统的能量和动量。
二、方向导数与梯度方向导数是一个重要概念,它描述了函数在其中一点沿着一些方向的变化率。
梯度是一个向量,它指向函数值增加最快的方向,并且梯度的模表示函数在其中一点的最大变化率。
方向导数和梯度在工程技术中的应用非常广泛。
例如,在机器学习中,我们可以使用梯度下降算法来优化模型的参数,以最小化损失函数。
三、偏微分方程偏微分方程是描述自然现象的重要数学工具,包括热传导、扩散、波动等。
多元函数微分学为解偏微分方程提供了重要的数学基础。
通过偏微分方程的分析解或数值解,我们可以深入了解自然现象的行为和性质。
例如,在工程技术中,我们可以使用多元函数微分学来解决电磁场、弹性力学和流体力学等方面的问题。
四、约束优化约束优化是指在满足一定条件下找到使目标函数最大或最小的参数的问题。
多元函数微分学是解决约束优化问题的重要工具。
通过拉格朗日乘数法,我们可以将约束优化问题转化为无约束优化问题,并应用多元函数微分学的方法求解。
约束优化问题在经济学、运筹学和供应链管理等领域有着广泛的应用。
例如,在经济学中,我们可以使用约束优化来确定消费者的最优选择。
五、多元函数积分学多元函数微分学与多元函数积分学是紧密相关的。
多元函数微分学提供了计算多元函数导数的方法,而多元函数积分学则通过对函数的积分来研究函数的整体性质。
应用多元函数积分学,我们可以计算多元函数在其中一区域上的平均值、总值和概率密度等。
多元函数积分学在统计学、物理学和金融工程学等领域有广泛的应用。
例如,在统计学中,我们可以使用多元函数积分学来计算多维随机变量的期望和方差。
第七讲 多元函数微分学(基础班 专转本第七章)
类似地,当 x固定在 x 0,而 y 在 y 0处有改变量 y ,如 极 限 lim
y0
存在,则称此极限为函
z f ( x, y )在点( x 0 ,y 0 )处对 y 的偏导数,记为
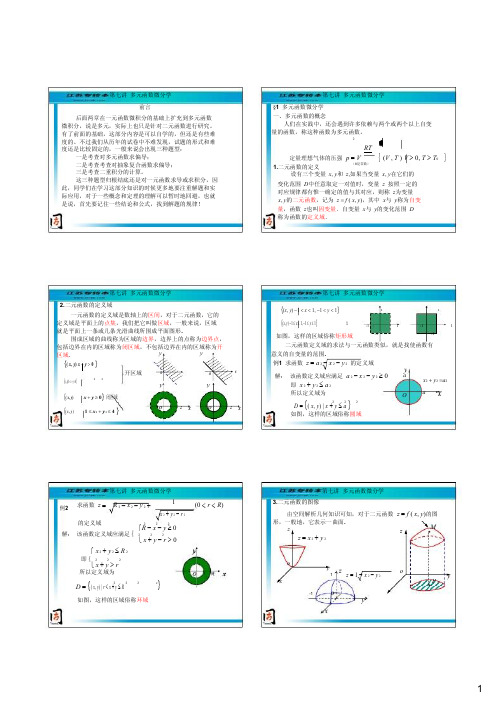
则称二元函数 z f ( x , y) 在点 P0 ( x 0 , y 0 )处连续.如果 f ( x , y) 在区域 D 内的每一点都连续, 则称 f ( x , y) 在区域 D 上连续. 注:类似的,我们也可以定义二元函数间断点的概念 二、偏导数与全微分 引例 一定量理想气体的压强 P,体积 V,热力学 度 T 三者之间的关系为 RT P (R 为常量 ).
第七讲 多元函数微分学 §1 多元函数微分学 一、多元函数的概念 人们在实践中,还会遇到许多依赖与两个或两个以上自变 量的函数,称这种函数为多元函数。
2
RT
定量理想气体的压强 p V (R是常数) 1.二元函数的定义 设有三个变量 x, y和 z,如果当变量 x, y在它们的
(V , T ) V 0, T T
x 0 0 y
xy 1 1
,
f y
x 0 0 y
,zy
x 0 y 0
或f y ( x 0 , y 0 )
.
lim
lim
xy 1 1
t 11
2
lim f ( x , y ) f ( x 0 , y0 )
dPT常数
第七讲 多元函数微分学
e x cos y
x 1 o y x 2 yo 2
求 极 限 例4 求极限 lim
xy
l i m
解: 这里 就不能直 接带入 x 0, y 0
多元函数微分法及应用

开区域连同它的边界一起称为闭区域.
例如,{( x, y ) | 1 x y 4}.
2 2
设 E 是平面上的一个非空点集, P 是 E 的一个点, 如果存在点 P 的一个去心邻域不含点集 E 的 点,则称 P 为 E 的孤立点.
多元函数的基本概念(52)
y
o
x
6
对于点集 E 如果存在正数 K ,使一切点 P E 与某一定点 A 间的距离 AP 不超过 K , 即 AP K 对一切 P E 成立,则称 E 为有界点集,否 则称为无界点集. 例如, y
{( x , y ) | 1 x 2 y 2 4}
有界闭区域;
o
x
{( x , y ) | x y 0}
无界开区域.
多元函数的基本概念(52)
7
聚点: 设 E 是平面上的一个点集,P 是平面上
的一个点,如果点 P 的任何一个邻域内总有无 限多个点属于点集 E,则称 P 为 E 的聚点.
特殊地当 n 1, 2, 3 时,便为数轴、平面、 空间两点间的距离; n维空间中邻域、区域等概念:
邻域: U ( P0 ) U ( P0 , ) P | | PP0 | , P R n
内点、边界点、区域、聚点等概念类似.
多元函数的基本概念(52) 11
二元函数:设 D 是平面上的一个点集,如果对于
如果非空点集 E 的点都是内点, 则称 E 为开集 .
例如,
2 2
P
E1 {( x , y ) 1 x y 4}
即为开集.
多元函数的基本概念(52)
E
4
如果点 P 的任一个邻域内既有属 于 E 的点, 也有不属于 E 的点(点 P 本身可以属于 E ,也 可以不属于 E ),则称 P 为 E 的边界点.
多元函数微分学及其应用归纳总结

多元函数微分学及其应用归纳总结一、多元函数的微分与偏导数1. 多元函数的微分定义为函数在其中一点上的线性逼近。
对于二元函数,微分为 dz=f_x*dx+f_y*dy,其中 f_x 和 f_y 分别为函数的偏导数。
对于一般的 n 元函数也可类似定义。
2.多元函数的偏导数表示函数沿着其中一个变量的变化率。
对于二元函数f(x,y),其偏导数f_x表示x方向上的变化率,f_y表示y方向上的变化率。
一般而言,当存在偏导数且连续时,函数在该点可微分。
3.偏导数的计算方法与一元函数相似,利用极限的定义求出偏导数表达式,对于高阶偏导数,可以反复求导。
4.混合偏导数表示函数在二个或二个以上变量上求偏导数后再对另外一个或另外几个变量求偏导数,其次序不影响结果。
二、多元函数的求导法则1. 多元函数的和、差、常数倍法则:设函数 f 和 g 在其中一点连续可导,则(f±g)'=f'±g',(kf)'=kf'。
2.多元函数的乘积法则:设函数f和g在其中一点连续可导,则(f·g)'=f'·g+g'·f。
3.多元函数的商法则:设函数f和g在其中一点连续可导且g不为零,则(f/g)'=(f'·g-g'·f)/g^24. 复合函数求导法则:设函数 y=f(u) 和 u=g(x) 在其中一点可导,则复合函数 y=f(g(x)) 的导数为dy/dx=f'(u)·g'(x),其中 x 和 u 为中间变量。
三、多元函数的极值与梯度1.多元函数的极值包括极大值和极小值。
在二元函数中,极值的必要条件为偏导数为零,充分条件为偏导数存在且满足一定条件。
2.多元函数的梯度是一个向量,其方向与函数在其中一点上变化最快的方向一致,大小表示变化率的大小。
梯度为零的点可能为极值点。
多元函数微分学的应用

多元函数微分学的应用一、多元函数微分学在物理学中的应用多元函数微分学在物理学中有重要的应用,可以用于描述和分析物体的运动和力学性质。
例如,当我们研究一个物体在空气中自由落体的过程时,可以通过建立物体的位置、速度和加速度之间的多元函数关系来描述物体的运动规律。
通过对这个多元函数进行微分,我们可以计算出物体的速度和加速度,并进一步研究物体的运动轨迹和运动的特性。
二、多元函数微分学在工程技术中的应用工程技术领域广泛应用多元函数微分学,其中一个重要的应用是工程优化。
通过建立多元函数模型,可以描述工程系统的性能与各种因素之间的关系,例如工程结构的刚度、强度和稳定性与材料、尺寸和几何形状等因素之间的关系。
通过对这些多元函数进行微分,可以找到使性能最优化的设计变量组合,从而优化工程系统的设计。
三、多元函数微分学在经济管理中的应用多元函数微分学在经济管理中也有广泛的应用,可以用于分析和优化经济系统的运行和决策问题。
例如,在经济学中,我们可以建立多元函数模型来描述生产函数、成本函数和效用函数等与经济生产和消费相关的关系。
通过对这些多元函数进行微分,可以分析生产效率、最小化成本和最大化效用的最优决策策略,从而实现经济系统的优化和管理。
四、多元函数微分学在生物学中的应用多元函数微分学也被广泛应用于生物学领域,可以用于描述和分析生物系统中的各种生物过程和生物现象。
例如,在生态学中,我们可以建立多元函数模型来描述种群数量与环境因素之间的关系。
通过对这些多元函数进行微分,可以研究种群的增长速率、极限状态和稳定性等生态学性质,从而深入理解和预测生态系统的动态演化。
总之,多元函数微分学具有广泛的应用领域,可以用于自然科学、工程技术和经济管理等各个领域中的建模、优化和解决实际问题。
通过对多元函数的微分,我们可以深入理解各种系统和过程的特性和规律,从而实现对这些系统和过程的优化和控制。
多元函数微分学的应用

多元函数微分学的应用在物理学中,多元函数微分学广泛应用于描述和分析物理问题。
例如,通过对位移、速度和加速度等量的求导,可以得到物体的运动学性质。
这种应用包括运动物体、弹性和流体力学等领域。
在力学中,多元函数微分学被用于描述复杂的力和能量系统。
例如,它可以帮助研究动力学系统的不稳定性和平衡性。
在经济学中,多元函数微分学也有重要的应用。
经济学中的许多问题可以用多元函数模型进行数学建模,如宏观经济模型、价格理论、产量与成本理论等。
例如,均衡理论用微分方程和最优化理论进行数学建模,研究市场供求关系和均衡价格。
在生物学中,多元函数微分学也有广泛应用。
生物学常常需要用复杂的数学模型来描述生态系统。
例如,生态系统中的食物网络和生物钟可以用微分方程进行数学建模和分析。
微分方程还可以用于描述细胞分化、神经反应和心脏功能等生物过程。
在金融学中,多元函数微分学同样具有重要的应用。
金融市场中的诸多因素可以建立数学模型来进行分析和预测。
例如,股票价格的变化可以用微分方程进行数学建模。
此外,数学模型也可以用于描述和分析各种金融衍生品的风险和收益。
在信息工程中,多元函数微分学同样有广泛应用。
例如,信号处理中的滤波器应用了傅里叶变换和微分方程等数学概念,可以进行自动控制和图像处理操作。
此外,微分方程还可以用于描述传感器网格、电路设计等信息科学领域的问题。
总之,多元函数微分学在各个领域都有广泛的应用。
它能够帮助我们理解和分析各种复杂的现象,解决实际问题,推动科学技术的进步。
因此,对多元函数微分学的深入学习和研究是今天各个领域中的重要任务之一。
多元函数微分学的应用

多元函数微分学的应用引言多元函数微分学是微积分的一个重要分支,通过研究多元函数的极限、连续性、可微性、偏导数、全微分以及二阶偏导数等概念和性质,为解决实际问题提供了强大的工具和方法。
本文将介绍多元函数微分学在实际应用中的一些案例和方法。
1. 函数的极限多元函数的极限是多元函数微分学的基础,它描述了函数在某一点处的趋近性。
在实际应用中,我们常常需要确定一个多元函数在某一点的极限,以便对问题进行分析和计算。
对于给定的多元函数f(x,y),如果当点(x,y)趋近于某一点(a,b)时,f(x,y)趋近于一个常数L,则称f(x,y)在点(a,b)处有极限,记为$\\lim_{(x, y) \\to (a, b)} f(x, y) = L$。
2. 函数的连续性函数的连续性是多元函数微分学的另一个重要概念。
一个多元函数f(x,y)在某一点(a,b)处连续,意味着在点(a,b)的任意一个邻域内,函数值和点(a,b)的距离趋近于零。
连续函数在实际应用中具有重要的意义,因为它们能够准确地描述函数的行为和性质。
3. 偏导数与全微分在实际问题中,我们常常需要计算多元函数的偏导数和全微分,以便分析函数的变化率和方向导数。
对于一个多元函数f(x,y),它的偏导数$\\frac{\\partialf}{\\partial x}$和$\\frac{\\partial f}{\\partial y}$分别表示函数在x方向和y方向上的变化率。
全微分df表示函数的微小变化量,它可以用偏导数表示为$df =\\frac{\\partial f}{\\partial x}dx + \\frac{\\partial f}{\\partial y}dy$。
4. 高阶偏导数在多元函数微分学中,我们还可以计算多元函数的高阶偏导数。
高阶偏导数描述了函数的高阶变化率和曲率性质。
例如,一个二阶偏导数$\\frac{\\partial^2 f}{\\partial x^2}$表示函数在x方向上的曲率,而一个二阶偏导数$\\frac{\\partial^2 f}{\\partial x \\partial y}$表示函数在x和y方向上的变化率的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四 应用1 几何应用例42(大连理工)求曲线32,,t z t y t x =-==上与平面42=++z y x 平行的切线方程。
解 曲线上任意一点切线的切向量为)3,2,1(2t t -,平面的法向量为)1,2,1(,由题设得0)1,2,1()3,2,1(2=⋅-t t ,解之得1=t ,或31=t 。
当1=t 时,切点为)1,1,1(-,切向量为)3,2,1(-,所以切线方程为112111-=-+=-z y x 。
当31=t 时,切点为)271,91,31(-,切向量为)31,32,1(-,所以切线方程为312713291131-=-+=-z y x ,即9127619313-=-+=-z y x 。
例43(北京科技大学2001)求曲线⎪⎩⎪⎨⎧=++=++,1,22222y xy x ze y x z在点)0,1,1(-P 处的切线与法平面方程。
解 记1),,(,2),,(2222-++=-++=y xy x z y x G ze y x z y x F z,则1022),(),(=++=∂∂Pzz Pyx ze e y z y G F ,同理可得0),(),(,1),(),(=∂∂=∂∂PPy x G F x z G F ,因此,曲线在点)0,1,1(-的切线方程和法平面方程分别为⎪⎩⎪⎨⎧=+=-,0,1111z y x 和0=+y x 。
思考题12(北京科技大学1999)求曲线⎩⎨⎧=++=++,0,6222z y x z y x 在点)1,2,1(-P 处的切线与法平面方程。
思考题13(四川大学2000)求曲面3=+-xy z e z在点)0,1,2(处的切平面方程。
例44(武汉水利电力学院)已知平面p nz my lx =++与椭球面1222222=++cz b y a x 相切,证明:2222222p n c m b l a =++。
证 设已知平面与椭球面的切点为),,(000z y x ,则过该点的切平面方程为0)()()(020020020=-+-+-z z cz y y b y x x a x , 即1202020=++z cz y b y x a x ,这样它与p nz my lx =++表示同一个平面,因此有0≠p ,且 p n cz p m b y p l a x ===202020,,, 又p nz my lx =++000,从而有2000000222222)(p n z m y l x p pn z pm y pl x n c m b l a =++=++=++。
例45(浙江理工大学,东北师范大学)证明:若函数),(v u F 有连续的偏导数,则曲面S :0),(=--mz ny lz nx F 上任一点的切平面都平行于直线L :nzm y l x ==。
证 曲面0),(=--mz ny lz nx F 上任一点的法向量为),,(),,(y x y u z y x mF lF nF nF F F F --=,直线L 的切向量为),,(n m l ,于是0)(),,(),,(=--++=⋅y x y x z y x mF lF n mnF nlF n m l F F F ,此说明曲面S 上任一点处的切平面都平行于直线L 。
例46(长沙铁道学院)求过直线⎩⎨⎧=-+=-+,0,272210z y x z y x 与曲面273222=-+z y x 相切的切平面方程。
解 过直线⎩⎨⎧=-+=-+,0,272210z y x z y x 的平面方程为0)(272210=-++--+z y x z y x λ,其法向量为)2,2,10(λλλ--++。
设曲面上的切点为),,(000z y x ,则该点的切平面法向量为),,3(000z y x -,于是有⎪⎪⎪⎩⎪⎪⎪⎨⎧=-+=+-++++=+=+,273,27)2()2()10(,22310202020000000z y x z y x z y x λλλλλλ 解之得1,1,1,3000-====λz y x ,或 19,17,17,3000-=-=-=-=λz y x ,故所求的切平面方程为279=-+z y x ,或 2717179-=-+z y x 。
2 函数的极值与最值多元函数最值问题较一元函数复杂,难点在于边界曲线上极值的计算。
例47(中国人民大学2000)证明:函数()()yyyex e y x f z -+==cos 1,有无穷多个极大值,但无极小值.证 ()()x e f yx sin 1-+=,()y y e y x f --=1cos ,令⎩⎨⎧==,0,0yx f f 得稳定点()()1cos ,,-=ππn n y x n n ,Z n ∈.()x e f y xx cos 1+-=,()y yy e y x f --=2cos ,x e f y xy sin -=,当n 为偶数时,022>=-=∆xy yy xx f f f ,02<-=xx f ,故f 在()0,2πk 上取极大值,当n 为奇数时()01222<+-=-=∆--e e f f f xy yy xx此处无极值,故f 为无穷多个极大值无极小值.例48(北京科技大学2001)求函数928222+--+=y x y x z 在D :1222≤+y x 上的最大值和最小值。
解 22,84-=-=y z x z y x ,令其为零得1,2==y x ,点D ∉)1,2(,故z 在D 上的最大最小值只能在D 的边界1222=+y x 上取到。
于是问题转化为:求1028+--=y x z 在条件1222=+y x 下的最大最小值。
构造Lagrange 乘法函数)12(102822-+-+--=y x y x L λ,求L 的所有偏导数,并令其等于零得⎪⎩⎪⎨⎧=-+=--=--,012,022,04822y x y x λλ 解之得,31,32==y x 或 31,32-=-=y x , 代入得4,16min max ==z z 。
思考题14(北京科技大学1998)求函数xy y x y x f 2),(22+-=在有界区域122≤+y x 上的最大值和最小值。
例49(华中师大2001)设),(y x f z =在有界闭区域D 上有二阶连续偏导数,且0,022222≠∂∂∂=∂∂+∂∂y x zyz x z 。
(1) 证明:),(y x f z =的最大值和最小值只能在D 的边界上取得。
证 由于),(y x f z =在有界闭区域D 上连续,故必存在最大最小值,因此只需证:D 内任意点不可能是极值点,由二元函数极值的充分条件知,只需证:在D 内恒有0)(2<-xy yy xx f f f 。
事实上,由已知条件(1)得0)()()(222<--=-xy xx xy yy xx f f f f f 。
思考题15(西北工业大学)在平面上求一点,使它与n 个定点的距离之平方和最小。
3 条件极值条件极值问题有时可转化为无条件极值来计算,但有时这种转化很繁,或不可能,因此必须使用Lagrange 乘数法。
此时的最大困难是方程组的求解和极值的判别。
当方程组的解唯一时,往往可根据实际意义去判断;有时这种判别是十分困难的,需要较高的技巧;当求最值时,而根据实际意义最值一定存在,这时可直接计算其值,然后比较大小即可。
例50(厦门大学)求函数()444,,z y x z y x f ++=在条件1=xyz 下的极值.该极值是极大值还是极小值?为什么?解 令()()1,,,444-+++=xyz z y x z y x L λλ,则043=+=yz x L x λ,043=+=xz y L y λ,043=+=xy z L z λ, .01=-=xyz L λ解之得四组解:()1,1,1,()1,1,1--,()1,1,1--,()1,1,1--.在这些点上,()3,,=z y x f .又在1=xyz 上,()3131,,344444444=⋅⋅≥++=yx y x y x y x z y x f ,且当 44441yx y x ==,即z y x ==时取等号,四组解均为极小值.例51(清华大学2000)求函数xz ky z y x f +=3),,(在条件0,1222≥=++z z y x 下的最大值和最小值。
解 Lagrange 乘法函数为)1(2223-++++=z y x xz ky L λ,求L 的偏导数,并令它们等于零得:⎪⎪⎩⎪⎪⎨⎧=-++==+==+==+=,01,02,023,022222z y x L z x L y ky L x z L z y xλλλλ由第一和第三个方程得0=x ,或21±=λ。
因此,当0=k 时,解为 ,0,22=±==y z x 或 ,0,22,22==±=y z x 或 1,0±===y z x 。
当0≠k 时,若31≥k ,则解为1,0±===y z x ,或 ,0,22=±==y z x或 ,0,22,22==±=y z x 或 ky k kz x 31,219312±=-=±=, 当31<k 时,解为 ,0,22=±==y z x 或 ,0,22,22==±=y z x 又f 为有界闭区域0,1222≥=++z z y x 上的连续函数,所以最大最小值一定存在,因此,当0=k 时,其边界上函数值为零,从而最大值为21,最小值为21-;当0≠k 时,其最大值与最小值仍然是21与21-,因此,所求的最大最小值21与21-。
例52(武汉大学2000)求函数222),,(z y x z y x f ++=在1=++cz by ax 下的最小值。
解 令)1(),,,(222-+++++=cz by ax z y x z y x L λλ,则1,2,2,2-++=+=+=+=cz by ax L c z L b y L a x L z y x λλλλ,令0====λL L L L z y x 得唯一解⎪⎪⎪⎩⎪⎪⎪⎨⎧++=++=++=,,,222222222c b a c z c b a b y c b a a x 显然f 有最小值,而稳定点唯一,故该点即为最小值点,因此最小值为222222222222222min 1)()()(cb ac b a c c b a b c b a a f ++=++++++++=。
例53(复旦大学1999)已知222cz by ax u ++=,其中0,0,0>>>c b a 。
