数学建模—警察与小偷
票贩子现象的原因和治理_基于警察与小偷博弈模型

中南财经政法大学研究生学报2008年第4期票贩子现象的原因和治理──基于警察与小偷博弈模型张凌翼(贵州大学管理学院,贵州贵阳550025)摘要:票贩子的出现让原本稀缺的火车票资源更为稀缺,这不仅损害了广大消费者的利益,也不利于社会的稳定,与建设和谐社会的宗旨相矛盾。
本文共分为三部分,第一部分提出了博弈论方法研究的理论基础;第二部分列出了警察与票贩子的博弈矩阵,分别用纯策略纳什均衡与混合策略纳什均衡的方法对票贩子与警察的博弈进行分析,得出了加大对警察的惩罚力度才能防范票贩子现象的结论;第三部分根据得出的结论提出了一些对策,指出对铁路客运进行改革才是治本的方法。
关键词:票贩子;博弈;纳什均衡每年的寒假对出门在外的人来说可谓喜忧参半,广大旅客在庆幸终于可以与家人团聚的同时,又在为如何回家的问题上担忧不已,回家过年的亲情之旅反倒成为令人难捱的苦旅。
虽然国家已采取了政策保证学生寒暑假可以买到坐票,但是某些车次的车票还是很紧俏,不预订很难买得到。
据国家发改委的数据显示,2006年春运的40天,全国的客流达到近21亿人次。
其中,铁路运输占的比重约1.5亿人次,公路则占18.55亿人次,其他的不到1亿人次是民航和水运来承担。
尽管铁路春运不到1.5亿人次,却成为社会关注的焦点。
[1](P22-27)在每年的这个时候,一个神秘的组织就会出现。
他们手里握有稀缺车次的车票,以高价卖给广大学生和其他过年要回家的人们,这样的人俗称“票贩子”,如果是有组织的票贩子,被称为“黄牛党”。
[2]这群人在进入12月份以后就变换手法地活动起来,是每年铁路和政府部门重点打击的对象。
一方面旅客一票难求,另一方面却出现“票贩子”兜售高价票的情形,为什么会出现这样的矛盾现象呢?为什么火车票票贩子屡禁不止?为什么列车运力总是短缺或过剩,不能达到均衡?下面本文以博弈论方法对这种现象进行分析。
一、博弈论方法研究的理论基础博弈论(Game Theory,又称对策论)是研究决策主体的行为在发生直接的相互作用时,人们如何进行决策以及这种决策的均衡问题。
第六章__纳什定理与零和游戏案例
零和游戏
“无毒不丈夫”也是零和博弈所致
著名经济学家茅于轼曾说:““在市场经济之前,人 类自利是妨碍别人的,是损人利己的。”他举例说,”过 去的帝王与将相就是这样一种博弈,他可以剥削你,抄你 的家;你可以造他的反,夺他的天下。一方得利,一方受 损,那是零和博弈。事实上也正是因为这种零和博弈反复 上演,才使中国历史的每一页都充满了阴谋与血腥,并且 使‘无毒不狠非丈夫’的文化观念深入到每一个中国人的 意识中。“
零和游戏
零和游戏——游戏者有输有赢,但整个游戏的 总成绩永远为零。
博弈的过程就是一个零和游戏:博弈当中的参
与者,其利益可能严格对立,一人所得永远等
于另一人所失。
零和游戏
[拉封丹寓言]狐狸与狼的零和博弈
一天晚上,狐狸踱步来到了水井旁,低头俯身看到井底 的月亮圆圆的,它认为这是块大奶酪。两只吊桶一上一下交 替打水上来,这只饿得发昏的狐狸顾不得那么多,它跨进一
两天两夜过去了,没有一只动物光顾水井,时间一分一秒地流 逝,银色的上弦月出现了。沮丧的狐狸正无计可施时,刚好一只口 渴的狼途经此地,狐狸不禁喜上眉梢,它对狼抬 起头打着招呼道: “喂,伙计,我免费招待你一顿美餐你看怎么样?你看到这个 了吗?”它指着井底的月亮对狼说,“这可是块十分好吃的干酪, 这是森林之神福纳用奶牛伊娥的奶做出来的,假如神王朱庇特病了, 只要尝到这美味可口的食物都会胃口顿开。我已吃掉了这奶酪的那 一半,剩下这半也够你吃一顿的了。就请委屈你钻到我特意为你准 备好的桶里下到井里来吧。” 狐狸尽量把故事编得天衣无缝,这只狼可是个笨蛋,居然中了 它的奸计。狼下到井里, 它的重量使狐狸升到了井口,这只被困 两天的狐狸终于得救了。
只水桶下到了井底,另一只水桶升到了井面。 下得井来,它才明白这圆月是吃不得的,自己已铸成大 错,处境十分地不利,长期下去就只有等死了。如果没有另 一个饥饿的替死鬼来打这月亮的主意,以同样的方式,落得 同样悲惨的下场把它从眼下窘迫的境地换出来,它怎能指望 活着回到地面上去呢?
小学C++趣味编程:逻辑判断与推理

思维过程
······
输出i,i存放的是数字,需要转换为对应字母
参考程序(完整)
举一反三
一天,校长到机器人教室 检查,看见一只仿生机器人— 猴子,做得十分可爱,便问是 谁做的,狐狸老师等人想和校 长开个玩笑,于是狐狸老师说: “是尼克做的。”尼克说: “不是我做的。”格莱尔说: “不是我做的。”如果他们中 有两个人说了假话,一人说了 真话,请你判断是谁做的。
小学生C++趣味编程第二版
第38课 警察抓小偷
——逻辑判断与推理
谁是小偷?
A、B、C、D 四人中有一个人是小偷,已知四个人中有 一个人说了假话,请根据四个人的供词来判断谁是小偷。
A:我不是小偷。 B:C 是小偷。 C:D 是小偷。 D:我不是小偷。
假设你是警察,请编个程序来判断一下, 谁是小偷。
Hale Waihona Puke 享新知A → 1 B → 2 C → 3 D → 4 i → 小偷
A:我不是小偷。B:C 是小偷。C:D 是小偷。D:我不是小偷。
(i != 1)+(i == 3)+(i == 4)+(i != 4)== 3
如果是真话,逻辑值为真,值为1;说了假话, 逻辑值为假,值为0。
一共4人,1个人说了假话,3人说真话。
举一反三
运行结果:
运行结果:
总结提炼
可以使用for循环的枚举和逻辑表达式 解决一些逻辑判断和逻辑推理问题,实现初 级的人工智能。
小偷与守卫博弈模型启示和在采购中的应用

小偷与守卫博弈模型启示和在采购中的应用小偷与守卫的博弈模型是博弈论里的一个很基本的一个模型,那下面就来简单介绍下这个博弈模型。
一个小偷欲偷窃,有一守卫看守仓库,如果小偷偷窃时看守在睡觉,则小偷就能得手,偷得价值为V 的赃物;如果小偷偷窃时守卫没有睡觉,则小偷就会被抓。
设小偷被抓住后要坐牢,负效用为-P ,守卫睡觉而未遭偷窃有S 的正效用,因睡觉被窃要被解雇,其负效用为-D 。
而如果小偷不偷,则它们既无得也无失,守卫不睡意味着出一份力挣一分钱,他也没有得失。
那么我们来写出此博弈的博弈矩阵,并分析加重对小偷和守卫的处罚能否对防止偷盗起到效果。
守卫睡觉 不睡觉偷小偷不偷那么我们来设守卫睡觉的概率为P 守卫显然守卫不 睡觉的概率为1-P 守卫,设小偷的概率为P 小偷,显然不偷的概率为1-P 小偷。
那么我们结下来分析他们各自的收益,在次假定P 小偷是个常数,那么E ξ小偷=V*P 小偷P 守卫-P*P 小偷(1- P 守卫)=(V+P) P 小偷P 守卫- P*P 小偷E ξ守卫=-D* P 小偷P 守卫+S*(1-P 小偷) P 守卫=S* P 守卫-(D+S) P 小偷P 守卫那么我们接下来以小偷的收益来作出他的函数,图形如下图所示:可以从图上可以看到,加大对小偷的惩罚力度,结果导致的是加大了守卫的睡觉的概率,这样一来不仅没有达到减少偷窃,反而是促进了偷窃的发生,这样一来就值得我们去反思了,在现在的社会,一般都是采取加大对小偷的惩罚,其实这种做法只可以在短时间内减少偷窃,但是时间一长反而是加大了守卫睡觉的概率,结果导致偷窃屡禁不止。
那么我们应该怎么去作呢?显然仅仅加大对小偷的惩罚力度是远远不行的,还要加大对守卫睡觉的负效用,即对守卫睡觉的惩罚,这样才可以大大减少偷窃的发生。
那么我们根据这个博弈模型可以知道,仅仅加大被管理者的惩罚是不够的,往往适当加大对管理者的惩罚才可以。
那么我们就把我们从这个博弈模型中说得到借鉴到采购管理中来,在很多公司的采购部门都是一个肥缺,采购员拿回扣已经是不成文的规定了,尽管公司出台一系列的政策但是都是屡禁不止,为什么呢?那么我们有什么办法可以减少呢?我们从上面的小偷与守卫的博弈模型可以知道,要想减少小偷的偷窃,不仅仅是要加大对小偷的惩罚力度,往往还要加大对守卫的管理和惩罚力度。
3.2.5警察与小偷的博弈:混合策略下的随机方式

警察与小偷的博弈:混合策略下的随机方式在美国西部的一个城镇,镇上只有一个警察负责全镇的治安状况。
现在我们假定,小镇的一头有一家超市,另一头有一家银行。
同时,我们再假定该地只有一个小偷。
因为只有一个人,所以警察一次只能在一个地方巡逻;同理,小偷一次也只能去一个地方,要么是超市,要么是银行。
如果警察恰好选择了小偷进行偷盗的地方巡逻,就能当场把这个小偷抓个正着;而如果这个小偷选择了没有经常巡逻的地方偷盗,那么他这一次就能够偷盗成功。
假设银行需要保护的财产价格为2万元,超市的财产价格为1万元。
那么警察怎么巡逻才能使效果最好?也可反过来说,小偷采取怎样的策略才能偷到最多的钱呢?一种最容易被警察采用且确实也更为常见的做法是,警察对银行进行巡逻。
这样的话,警察就可以保住2万元的财产不被偷窃。
但是假如小偷没有选择去银行,而是选择去了超市,那么小偷的偷窃一定就能成功,1万元就到手了。
思考一下,这种做法是警察的最好选择,策略吗?答案当然是否定的,现在我们完全可以通过博弈论的知识,对这种策略加以改进。
我们用抽签来决定警察去银行还是去超市。
因为银行的价值是超市的两倍,所以用两个签代表银行,如抽到1、2号签去银行,抽到3号签去超市。
这样警察便有2/3的机会去银行进行巡逻,1/3的机会去超市巡逻。
这种情况下,小偷的最优策略是:也以同样抽签的办法决定去银行还是去超市偷盗。
与警察相反,小偷如果抽到1、2号签就去超市偷盗,如果抽到3号签就去银行偷。
这样的话,小偷有1/3的机会去银行, 2/3的机会去超市。
结果似乎有些滑稽,警察的策略是使小偷最大得手率降至最低,而小偷谋求的是最小得手率的最大化,也就是说,警察的最优策略将把小偷的最差策略改良!这便是著名学家,“数学经济学”的奠基人冯·诺依曼提出的“最小最大定律”。
警察与小偷的博弈,提供了混合策略的思路。
所谓混合策略,就是指参与者采取的不是唯一的策略,而是其策略空间上的一种概率分布。
图论中的追捕问题——警察抓小偷

在确定的有限无向简单图上的游戏流程如下: 1.警察选择初始位置,位置可以重叠。 2.小偷选择初始位置,令 t=1。 3.第 t 回合开始,每个警察可以选择移动至邻居点或者停留。每个警察都只能移 动一步。 4.如果警察到达了小偷所在点则游戏结束,否则继续。 5.小偷可以选择移动至邻居点或者停留。小偷只能移动一步。 6.t = t+1,返回 3 注意我们定义的游戏是警察先选择初始位置,小偷后选择初始位置。每回合开始 也是警察先移动。后文中提到 “回合开始时”就是指轮到警察选择前的时刻。 游戏过程中,小偷和警察知道关于游戏的所有信息,包括:(1)图 G 的连接情况; (2)所有警察和小偷的。这种所有玩家拥有关于游戏的所有信息在博弈论中被称为 完全信息(complete information)。在[2]中,Isler 和 Karnad 较详细地研究了几种非完 全信息的情况。由于作者能力所限制,本文主要还是关注完全信息的警察抓小偷游戏。 我们将小偷所在位置令为 r,警察所在位置令为 c。如果警察不止一个时,我们把 警察所在位置集合令为 C。 在有些图上仅需要一个警察就能确保一定有能获胜的策略。我们将这类一个警察 可以抓住小偷的图称为 cop-win 图。与之相对的另一类图被称作 robber-win 图在一个 robber-win 图上小偷能有保证不被一个警察抓住的策略,这些最优的策略被称为制胜 策略(winning strategy)。我们假设警察和小偷在存在制胜策略时,一定使用制胜策 略。 定义 1.1:如果在图 G 上一个警察就能保证存在一定能抓住小偷的策略,那么称 G 为 cop-win 图。反正则称为 robber-win 图。
小偷博弈
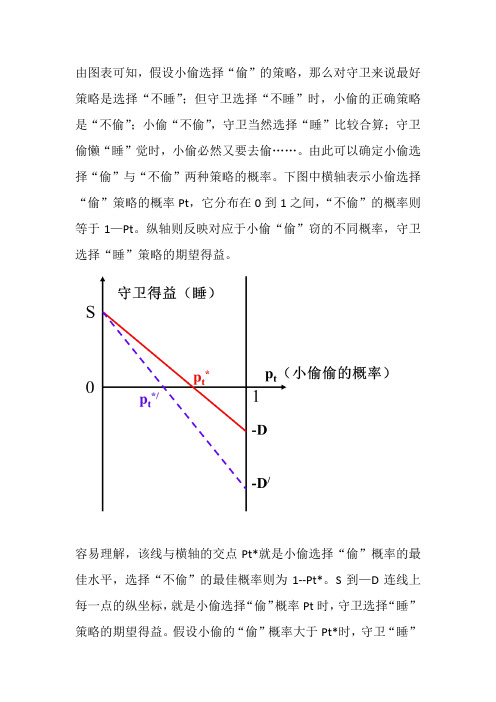
由图表可知,假设小偷选择“偷”的策略,那么对守卫来说最好策略是选择“不睡”;但守卫选择“不睡”时,小偷的正确策略是“不偷”;小偷“不偷”,守卫当然选择“睡”比较合算;守卫偷懒“睡”觉时,小偷必然又要去偷……。
由此可以确定小偷选择“偷”与“不偷”两种策略的概率。
下图中横轴表示小偷选择“偷”策略的概率Pt,它分布在0到1之间,“不偷”的概率则等于1—Pt。
纵轴则反映对应于小偷“偷”窃的不同概率,守卫选择“睡”策略的期望得益。
容易理解,该线与横轴的交点Pt*就是小偷选择“偷”概率的最佳水平,选择“不偷”的最佳概率则为1--Pt*。
S到—D连线上每一点的纵坐标,就是小偷选择“偷”概率Pt时,守卫选择“睡”策略的期望得益。
假设小偷的“偷”概率大于Pt*时,守卫“睡”的期望得益小于0,因此他肯定选择“不睡”。
从而小偷偷则被抓,对小偷来说不可取。
反之,如果小偷“偷”的概率小于Pt*,则守卫“睡”的期望得益大于0,天天睡大觉是合算的,即使小偷提高一些“偷”的概率,即作案频繁一些,只要不大于Pt*,守卫都会选择“睡”,从而小偷不用害怕被抓。
小偷在保证不被抓的前提下,“偷”概率越大收获就越大。
因此他会使“偷”的概率趋向于Pt*。
均衡点是小偷以概率Pt*和1—Pt*分别选择“偷”和“不睡”。
守卫采取“睡”与“不睡”的混合策略概率分布.也可以用同样的方法来确定,结论则为Pg*和1—Pg*是守卫的最佳概率选择。
现在再来考察当局为了抑制盗窃现象而加重对小偷惩罚时会出现的结果。
加重对小偷的惩罚会使P增大,在图二中,这相当于—P向下移动到—P’。
如果守卫混合策略中的概率分布不变,此时小偷“偷”的期望得益变为负值,小偷会停止“偷”。
但在长期中,小偷减少“偷”会使守卫更多地选择“睡”,最终守卫会将“睡”的概率提高到Pg*’,达到新的均衡,此时小偷的期望得益又恢复到0,他会重新选择新的策略。
由于小偷的策略概率分布是由图一决定,并不受P值影响,因此政府加重对小偷的惩罚,在长期中并不能抑制盗窃,最多只能抑制短期盗窃发生率,它的主要作用是使守卫可以更多地偷懒。
小学数学 数学神探 路遇抢劫犯

路遇抢劫犯
江东市抚河区公安局门前,亮着红色的警灯,告诉人们,这里可以报案,金色的盾牌可以为你撑腰壮胆,降妖除魔!
这天深夜11点,值勤的民警听到远处喊着"抓强盗"的急促呼救声。
值勤的民警叫于德华,是个虎彪彪的棒小伙子,他飞步赶到出事现场,只见一胖一瘦两个人正扭打在一起,见公安人员来了,都说自己的手表被对方抢了。
于德华问:"表是什么牌,何种表带?那两人异口同声地回道:"上海牌,黑色人造革表带。
"富有破案经验的于德华从地上捡起手表,只做了个简单的动作,便断定了二人中谁是拦路抢劫犯,并将他押回了公安局审问。
答案:
值班民警于德华将手表分别在两个人手上试戴,根据表带洞扣痕迹,他判断出了谁是那只上海表的主人,谁是抢劫犯。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模
——警察与小偷
问题:
某个小镇上只有一名警察,他要负责整个镇的治安。
现在我们假定,小镇的一头有一家酒馆,另一头有一家银行。
在假定该地有一个小偷,要实施偷窃。
因为分身乏术,警察只能在一个地方巡逻;而小偷也只能去一个地方。
假定银行需要保护的财产价格为2万美元,酒馆的财产价格为一万美元。
若警察在某地巡逻,而小偷也选择了去该地,就会被警察抓住;若警察没有巡逻的地方儿小偷去了,则小偷偷盗成功。
1、警察怎样巡逻才能使效果最好?小偷的最优选择是什么?警察与小偷之间谁赢得
机会更多一些?
2、除了一般的分析上述问题,你能否找到一种理论来指导问题的求解?怎样求解?
问题分析:
1、银行与酒馆所需要保护的财产价格的不同,必然会影响警察和小偷对自己行动方案的选择。
2、警察和小偷都是人,都有思维,都能站在对方的立场,揣测对方态度,得到自己的行动方案,所以警察和小偷所站立场也决定着偷盗能否发生
3、酒馆和银行营业时间不相同,酒馆营业时间一般在于下午和晚上,而银行则主要在白天,这也是影响着巡逻方案和偷盗方案
4、小偷作案需要时间
5、警察需要休息
6、银行防盗设备,力度较大
针对问题:
1、警察巡逻效果好坏,我认为有两个判断标准,即偷盗未成功和偷盗成功但是损失最少。
小偷的最优选择即小偷不被抓,而不是是否盗到最多的财产
而谁赢的机会更多,就要综合自己所给出的假论
2、运用统计学中的概率进行求解,假设条件,把场景理想化,再利用概率计算警察成功的概率和小偷成功的概率,进行求解
解:
1、考虑一:可用于偷窃的时间
银行营业时间一般为8:00到17:00,而酒馆的营业时间一般为10:00到23:00(所有数据均由网上查询)
银行小偷可用于盗窃的时间为18:00点到0:00
酒馆小偷可用于盗窃的时间为23:00到0:00(7:00到10:00为白天,
不易实行盗窃)
考虑二:财产价值
银行所要保护的财产价格为2万美元,而酒馆的财产价格为1万考虑三:
所占立场
所以,警察巡逻的最好方案
17:00--23:00 警察在银行。
(肯定不被盗,酒馆营业)
23:00--次日7:00 警察安排2/3*8h在银行,1/3*8h在酒馆(有被盗可能但银行资产为2万,而酒馆为一万,损失最小)
7:00--8:00 警察在酒馆(银行有被盗风险,但白天不易盗窃,
且银行有早到职员)
8:00--10:00 警察在酒馆(肯定不被盗银行在营业)
10:00--17:00 警察休息(肯定不被盗,都在营业)
小偷的最优选择
23:00--次日7:00 小偷去盗窃酒馆(虽然酒馆只有1万美元的财产,但小偷只要盗窃得手即为成功,且警察此时只有1/3的概率在酒馆巡逻,酒馆防盗系统较银行弱,成功机率较大)
综上,警察赢的机率比较大。
2、运用统计学中的概率来指导问题的求解
建立模型并求解
假设条件
(1)小偷作案时间和警察来往两地时间和吃饭时间忽略不计,一律记为全部在职。
(2)银行和酒馆防盗设备,强度相同。
(3)银行的营业时间为8:00--17:00,酒馆营业时间为10:00--23:00.
(4)设白天偷窃成功的概率为1/5,银行职员早去使得偷窃成功的概率也为1/5 由1警察最优的巡逻方案可知17:00--23:00,8:00--17:00肯定不被盗,可以只需分析23:00--次日7:00和7:00--8:00两个时间段
先分析23:00--次日7:00
警察的选择:
A、根据财产区别设警察去银行的概率为2/3,去酒馆的概率为1/3
B、警察若想到小偷的作案目的是钱并成功而不是为获得最大利益,且考虑财产
区别,决定两边巡逻的概率各位1/2
小偷的选择:
C、小偷去两边的概率都为1/2
D、小偷考虑了财产区别,且站在警察的立场上觉得警察有更大的概率去银行所
以决定去银行的概率为1/3,去酒馆的概率为2/3
方案一:A+C
小偷偷窃成功的概率P(1)=2/3*1/2+1/3*1/2=1/2
损失=1*2/6+2*1/6=2/3万方案二:A+D
小偷偷窃成功的概率P(2)=1/3*1/3+2/3*2/3=5/9
损失=2*1/9+1*4/9=2/3万方案三:B+C
小偷偷窃成功的概率P(3)=1/2*1/2+1/2*1/2=1/2
损失=2*1/4+1*1/4=3/4万方案四:B+D
小偷偷窃成功的概率P(4)=2/3*1/2+1/3*1/2=1/2
损失=1*1/3+2*1/6=2/3万再分析7:00--8:00
警察在银行
小偷偷窃成功的概率P(5)=1/5
损失=1*1/5=1/5万警察在酒馆
小偷偷窃成功的概率P(6)=1/5*1/5=1/25
损失=2*1/25=2/25万
综上:
23:00--7:00 虽然方案一和方案四巡逻效果完全相同,但方案四不可控制因素太多,所以选择方案一
7:00--8:00 比较而言警察在酒馆效果较好
由方案二得小偷的最优选择为A+D,即23:00--7:00 去酒馆行窃
但就总体而言,警察赢的机率会更多一些。
