几种特殊的图
集合以及集合的两种表示方法_列举法和描述法.ppt

2. 选择适当的定义条件来表达下一集合 “10的整数倍的集合”
解:A 10K K I
4
3. (1)给出集合A、B、C 的例子,使 A B, B C, 但 AC 。 (2)给出集合A、B、C 的例子,使 A B, B C,且 AC 。
解: (1)令 A a, B {a},b, C {{a},b}, d (2)令 A a, B {a},b, C {{a},b}, a
4. 证明集合(A B) (A (B C))的补集是 (A B) (A B) (A C)
证明: ((A B ') (A' (B C '))) '
(A B')'(A'(B C'))' (A'B) (A (B'C)) (A'B) (A B') (A C)
(4) 几种特殊的关系: 集合A上的恒等关系IA, 普遍关系UA,以及空关系。
总结
12
第二章 关系
3. 二元关系的表示方法 (1) 集合的表示方法:列举法和描述法均可用来表示关系。
(2) 关系矩阵表示法,用来表示由有限集A到有限集B的关系。
(3) 关系图表示法:常用来表示定义在有限集A上的关系。
4. 集合A上关系的性质
在 中,则必有(a,c)也出现在 中。
总结
13
第二章 关系
5. 关系的运算
(1)对集合A上给定的关系 ,求其逆关系 。
(2)对给定的由集A到集B的关系
求其复合关系 1 2 。
1
和由集B到集C的关系
2
,
特殊情形:对集合A上给定的关系 ,求复合关系 2 。
几个典型问题和几种特殊的图

欧拉( 欧拉( Euler )图问题
3
1736年欧拉把这个问题抽象成图论问题:用四个点v 1736年欧拉把这个问题抽象成图论问题:用四个点v1, 把这个问题抽象成图论问题 v2, v3, v4表示两岸及两个岛(称为顶点),用两点间的连 表示两岸及两个岛(称为顶点 顶点) 表示桥(称为边 问题转化为: 线e1, e2, e3, e4, e5, e6, e7表示桥(称为边),问题转化为: 从任何一个顶点出发,通过每一条边一次且仅一次,最 从任何一个顶点出发,通过每一条边一次且仅一次 每一条边一次且仅一次, 后回到该顶点,是否存在满足条件的走法? 后回到该顶点,是否存在满足条件的走法?
13
B
7
3:哈密顿周游世界问题
英国数学家哈密顿于1856年提出周游世界的问题 英国数学家哈密顿于1856年提出周游世界的问题: 年提出周游世界的问题: G=<V,E>是连通无向图 是连通无向图: 哈密顿图 设G=<V,E>是连通无向图: 且城与城之间只有一 – 若要周游世界上的二十个名城, 若要周游世界上的二十个名城, 如果G中存在一条路径,经过G ①如果G中存在一条路径,经过G中每个结点且只经过 条路,则能否把每一个城走且只走一次, 条路,则能否把每一个城走且只走一次,最后返回到 一次,则称该路径为哈密顿路径; 一次,则称该路径为哈密顿路径; 原地. 原地. 中存在一条回路,经过G 如果G ②如果G中存在一条回路,经过G中每个结点且只经过 一次,则称该路径为哈密顿回路。 20个顶点分别表示 一次,则称该路径为哈密顿回路。 用20个顶点分别表示 – 该问题可以抽象为图论问题: 该问题可以抽象为图论问题: 存在哈密顿回路的图称为哈密顿图。 存在哈密顿回路的图称为哈密顿图。 20个城市,两个顶点间的连线表示城市间的路,要求 20个城市 两个顶点间的连线表示城市间的路, 个城市, 找一条从某点出发,经过各个顶点一次且仅一次, 顶点一次且仅一次 找一条从某点出发,经过各个顶点一次且仅一次,最 后能否返回到出发点的路线? 后能否返回到出发点的路线? 哈密顿(Hamilton)圈 哈密顿(Hamilton)圈问题
脐诊彩色图(珍藏版)

脐诊彩⾊图(珍藏版)简介脐部粗看似乎每⼈没有什么区别,其实千变万化,千姿百态,⼏乎很少有⼈相同。
脐眼的⼤⼩、脐孔的深浅、脐蕊的⾼低、脐壁有⽆倾斜都不尽相同,观脐诊病就是看脐部的这些变化来诊断疾病。
肚脐诊断⼋卦⽅位太过与不及的肚脐脐孔朝脐缘外扩,属太过为实;脐孔朝脐缘内延,属不及为虚。
根据太过与不及来制定对疾病治疗的针法配伍。
根据疾病的情况采⽤“五⾏⽣克制化”来进⾏补泻。
⼋卦⽅位与五⾏对应震巽→⽊,⾉坤→⼟,乾兑→⾦,离→⽕,坎→⽔。
如乾位出现脐形的变化,可能是病⼈的⼤肠(内⼋卦)或头脑(外⼋卦)出现问题,同时也提⽰了病⼈出现的是“五⾏⾦病”,是⾦太过的病还是⾦不及的病,就要看具体的病⼈肚脐来进⾏补泻治疗。
(⼀)⼋卦⽅位的太过与不及1 乾位的问题乾位有包,肠寒、慢性肠炎。
乾位有痣,为肠癌。
乾位有硬结,像⽯头粒似的,乾位⿎起来为肠癌。
⼤便不好,肚⼦痛,⼀见风满⼝⽛痛。
乾位⽑细⾎管是青紫⾊的。
乾位⿎起来并发⽩,为晚期肠癌。
指肚下感觉起伏不定,为肠道长有息⾁,有⼏个起伏就有⼏个息⾁,⼤便细。
乾主⼤肠,肺与⼤肠相表⾥,⼤肠有病,肺也就不好。
乾(⼤肠)与巽(胆)相克。
上腹部上扬凸起的的⼈都是⼤便不好,⼤肠有问题,乾主⼤肠,乾位⼀摸有⼤的结节。
⼤便⼲燥,不成形。
先看巽位有没有沟纹,如果有沟纹为薄⾦克⽊叶,则先扎乾+巽,再沿着⼤肠经取⽳,⼤肠与坤位也有关系,就再扎脾经公孙⽳。
治疗:扎四隅位坤、⾉、巽、乾,配扎体针⾜三⾥、公孙。
2 兑位的问题兑位有条索为肺炎。
有条索但有顶⼿点为钙化点。
兑位有包为肺⽓肿、积液、阴虛、肺炎、热。
兑位有痣为肺癌,肺结核、脓肿。
像⽔袋,⼀摸⽔就下去为胸膜炎。
兑为肺、属⾦,从兑位起针,再去扎肺经上的⽳位调理肺病,⼟⽣⾦,⼟好⾦就好。
肺弱⽤⽣,肺过⽤克(⽕克⾦)。
3 离位的问题离位有包为头部疾病、脑垂体下垂、记忆⼒减退、⼼衰。
离位有痣为⼼梗、⼼死、⼼脏病、⼩肠燥热。
离属⼼与⼩肠。
突发性⼼脏病:坎+离,内关(双)、⼈中、百会、关元。
第九章 几类特殊图

(这里ai表示边i,i=0,1,2,…,15),对 应的16个二进制数字序列为 0000101001101111,将序列两端闭 合,便得到16个二进制数字的一个 圆形排列,可以验证正好符合我们 的要求。
哈密顿通路、哈密顿回路: 无向图或有向图G中经过 每个顶点一次且仅一次的通路,称为哈密顿通路; 经过每个顶点一次且仅一次的初级回路,称为哈密 顿回路。
推论 无向图G为欧拉图当且仅当,G是连通图且无奇 度顶点。
判断下面图是否为欧拉图。
定理9.2 有向图D有欧拉通路当且仅当,D是连通图, 并且所有顶点的入度等于出度,或者除两个顶点外, 其余顶点的入度等于出度,而这两个顶点,一个入度 比出度大1,另一个入度比出度小1。
推论 有向图D是欧拉图当且仅当,D是连通图且所有 顶点的入度等于出度。
K3,3
X
Y
x1 y1
x2 y2
x3 y3
x4
证明 必要性 设G=〈V1, V2,E〉为二部图,证明G中 无奇数长度的回路。若G中无回路,结论当然成立。
若G中有回路,设C=u0u1u2…ut-1u0为G中的一条回 路,其长度为t 。不妨设u0∈V1,则对于每个小于t的 正奇数i,ui∈V2,而对于每个小于t的正偶数j,uj∈ V1 。因为G中存在边(ut-1, u0),所以ut-1∈ V2 ,因而t -1必为奇数,即t
在判别一个二部图是否存在从V1到V2的匹配时,可 以先检查“t条件”是否满足,这是比较容易进行的。 如果“t条件”不满足,可再进一步用“相异性条件” 检查。
例 求图9.14(a)的最大匹配。 解 显然满足 “t条件”(t=2),所以存在从V1到V2的 匹配,也即最大匹配。
地质图的种类和基本内容

地质图的种类和基本内容⼀、地质图的种类和基本内容⽤规定的符号、线条、⾊彩来反映⼀个地区地质条件和地质历史发展的图件,叫地质图。
它是依据野外探明和收集的各种地质勘测资料,按⼀定⽐例投影在地形底图上编制⽽成的,是地质勘察⼯作的主要成果之⼀。
(⼀)地质图的种类1、普通地质图以⼀定⽐例尺的地形图为底图,反映⼀个地区的地形、地层岩性、地质构造、地壳运动及地质发展历史的基本图件,称为普通地质图,简称地质图。
在⼀张普通地质图上,除了地质平⾯图(主图)外,⼀般还有⼀个或两个地质剖⾯图和综合地层柱状图,普通地质图是编制其它专门性地质图的基本图件。
按⼯作的详细程度和⼯作阶段不同,地质图可分为⼤⽐例尺的(>1:25000)、中⽐例尺的〔1:5000~1:10万〕、⼩⽐例尺的(1:20万~1:100万)。
在⼯程建设中,⼀般是⼤⽐例尺的地质图。
2、地貌及第四纪地质图以⼀定⽐例尺地地形图为底图,主要反映⼀个地区的第四纪沉积层的成因类型、岩性及其形成时代、地貌单元的类型和形态特征的⼀种专门性地质图,称为地貌及第四纪地质图。
3、⽔⽂地质图以⼀定⽐例尺地地形图为底图,反映⼀个地区总的⽔⽂地质条件或某⼀个⽔⽂地质条件及地下⽔的形成、分布规律的地质图件,称为⽔⽂地质图。
4、⼯程地质图⼯程地质图是各种⼯程建筑物专⽤的地质图,如房屋建筑⼯程地质图、⽔库坝址⼯程地质图、铁路⼯程地质图等。
⼯程地质图⼀般是以普通地质图为基础,只是增添了各种与⼯程有关的⼯程地质内容。
如在地下洞室纵断⾯⼯程地质图上,要表⽰出围岩的类别、地下⽔量、影响地下洞室稳定性的各种地质因素等。
1、平⾯地质图平⾯地质图⼜称为主图,是地质图的主体部分,主要包括:地理概况:图区所在的地理位置(经纬度、坐标线)、主要居民点(城镇、乡村所在地)、地形、地貌特征等。
⼀般地质现象:地层、岩性、产状、断层等。
特殊地质现象:崩塌、滑坡,泥⽯流、喀斯特、泉及主要蚀变现象。
2、地质剖⾯图在平⾯图上,选择⼀条⾄数条有代表性的图切剖⾯,以表⽰岩性、褶皱、断层的空间展布形态及产状、地貌特征等。
几种特殊地貌的等高线(高三一轮复习可用)

300
400
H
400 河流
300
300 H
400
400 300
河流
峡谷:两山脊间的狭窄部分,是修建 水库的最好选址。
岱崮地貌:是 指以岱崮为代 表的山峰顶部 平展开阔如平 原,峰巅周围 峭壁如刀削, 峭壁以下是逐 渐平缓山坡的 地貌景观,崮 是山东独有的 一种特异地貌 景观
地上河
喀斯特地貌主要在石灰岩广布地区,因高温多 雨的气候条件,石灰岩受侵蚀和沉积而成。图 表示的是喀斯特峰林,其峰体多呈圆锥形,四 周陡峭,峰体中有山间洼地(溶盆)。
喀斯特峰林等高线地形图
在等高线地形图上山间洼地以数条圆弧形等 高线表示,在峰林顶部和斜坡等高线多以圆 形或椭圆形封闭。
黄土地貌等高线地形图
火山口湖等高线地形图及景观图
火山喷发物堆积形成为火山锥。火山口 它通常位于火山的顶端,是一个圆形洼 地,常积水成湖。
火山地貌
等高线为近似的圆形, 自里往外,数值先增大 后减小。示坡线画在等 高线内外两侧。
冲积扇是水力搬运碎屑物质堆积于山谷出口附近形成一般 呈扇形的地貌类型。其等高线呈圆弧形,高密低疏。 下图西南方等高线密集处为山地,山前为冲积扇。本图地 势西南高东北低,由西南向东北倾斜。
岱崮地貌等高线地形图及景观图
在等高线地形图中崮顶等高线稀疏,外 围为陡崖(等高线上标有示坡线),向 山麓过渡等高线由密集变稀疏。
地上河等高线地形图
在地上河等高线图中表现为河道整 体部分等高线向低海拔处凸出,而 河床处等高线则向高海拔处凸出。
地上河等高线地形图及景观图
(AB 河段位于平原上,水流平缓,是地 上河,河水补给地下水,无支流汇入。)
UML的九种模型图

UML的九种模型图本⽂转⾃,仅供学习交流!⼀、作为⼀种建模语⾔,UML的定义包括UML语义和UML表⽰法两个部分。
UML语义:描述基于UML的精确元模型定义。
UML表⽰法:定义UML符号的表⽰法,为开发者或开发⼯具使⽤这些图形符号和⽂本语法为系统建模提供了标准。
这些图形符号和⽂字所表达的是应⽤级的模型,在语义上它是UML元模型的实例。
⼆、标准建模语⾔UML可以由下列5类图来定义。
⽤例图:从⽤户⾓度描述系统功能,并指出各功能的操作者。
静态图:包括类图和对象图。
类图描述系统中类的静态结构,不仅定义系统中的类,表⽰类之间的联系,如关联、依赖、聚合等,也包括类的属性和操作,类图描述的是⼀种静态关系,在系统的整个⽣命周期都是有效的。
对象图是类图的实例,⼏乎使⽤与类图完全相同的标识。
⼀个对象图是类图的⼀个实例。
由于对象存在⽣命周期,因此对象图只能在系统某⼀时间段存在。
⾏为图:描述系统的动态模型和组成对象间的交互关系,包括状态图和活动图。
状态图描述类的对象所有可能的状态以及事件发⽣时状态的转移条件,状态图是对类图的补充,活动图描述满⾜⽤例要求所要进⾏的活动以及活动间的约束关系,有利于识别并进⾏活动。
交互图:描述对象间的交互关系,包括时序图和协作图。
时序图显⽰对象之间的动态合作关系,它强调对象之间消息发送的顺序,同时显⽰对象之间的交互;协作图描述对象间的协作关系,协作图跟时序图相似,显⽰对象间的动态合作关系。
除显⽰信息交换外,协作图还显⽰对象以及它们之间的关系。
如果强调时间和顺序,则使⽤时序图;如果强调上下级关系,则选择协作图。
实现图:包括组件图和部署图。
组件图描述代码部件的物理结构及各部件之间的依赖关系,组件图有助于分析和理解部件之间的相互影响程度;部署图定义系统中软硬件的物理体系结构。
采⽤UML来设计系统时,第⼀步是描述需求;第⼆步根据需求建⽴系统的静态模型,以构造系统的结构;第三步是描述系统的⾏为。
其中在第⼀步与第⼆步中所建⽴的模型都是静态的,包括⽤例图、类图、对象图、组件图和部署图等5种图形,是标准建模语⾔UML的静态建模机制。
想学好几何怎能不知道奇异四边形?一篇文章详解邻等对补四边形!
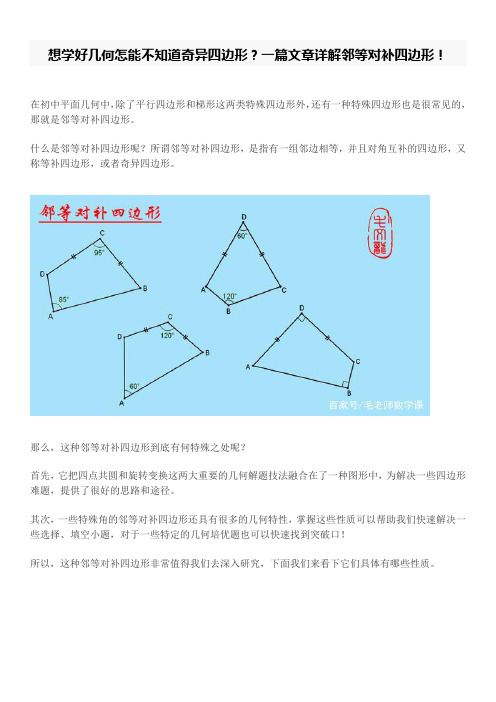
想学好几何怎能不知道奇异四边形?一篇文章详解邻等对补四边形!在初中平面几何中,除了平行四边形和梯形这两类特殊四边形外,还有一种特殊四边形也是很常见的,那就是邻等对补四边形。
什么是邻等对补四边形呢?所谓邻等对补四边形,是指有一组邻边相等,并且对角互补的四边形,又称等补四边形,或者奇异四边形。
那么,这种邻等对补四边形到底有何特殊之处呢?首先,它把四点共圆和旋转变换这两大重要的几何解题技法融合在了一种图形中,为解决一些四边形难题,提供了很好的思路和途径。
其次,一些特殊角的邻等对补四边形还具有很多的几何特性,掌握这些性质可以帮助我们快速解决一些选择、填空小题,对于一些特定的几何培优题也可以快速找到突破口!所以,这种邻等对补四边形非常值得我们去深入研究,下面我们来看下它们具体有哪些性质。
最特殊的邻等对补四边形莫过于这种60°+120°的结构了,它有哪些性质呢?首先,就是四个顶点共圆,其次,就是对角线BD平分∠ABC,这个结论放在圆中很好证明,等弦对等角即可。
最后我们通过旋转变换得到了一个等边三角形,从而得到AB+BC=BD这种线段的数量关系。
前两个结论是邻等对补四边形的通用结论,最后的线段关系,不同的图形有各自的结论。
第二种常见的邻等对补四边形就是这种双90°的结构,仍然是通过四点共圆和旋转变换可以证得以上3个结论。
可能出题者更青睐于此这种图形,导致它出现的频率较高,题目类型主要是计算题,一般是求对角线长度和四边形的面积。
掌握了上述思想方法和结论后,此类题便可迎刃而解。
最后一种特殊的邻等对补四边形就是这种120°+60°的结构了,具体结论和证明方法在此不再赘述。
下面我们结合几道具体的例题,来看下此类题的具体考法和邻等对补四边形的性质如何运用。
以上5道例题就是初中邻等对补四边形的常见考法,同学们可以先自己尝试着挑战一下,看看普通的方法这类题怎么处理?接下来再看我下面的解析,相信就可以感受到这些数学思维方法和几何性质结论的妙用了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) 平面图G V, E , V v, E e,若v 3,则e 3v 6
(2)和(3)仅为必要条件,只能判断一个图不是平面图
判定条件:一个图是平面图G的充分必要条件是 G不含与K3,3或K5在2度结点内同构的子图。
几种特殊的图
平面图
相关概念
面和面的边界 面的次数 有限面与无限面 同胚或同构
图的着色
结点着色、边着色、面着色 结点着色的方法:韦而奇.鲍威尔 面着色->边着色->结点着色 定理11:P205 对偶图
几种特殊的图
树
树的判别: G V , E , V n, E 图m,是树的 充分必要条件是:
G是无回路的连通图; 无回路,且m=n-1; 连通且m=n-1 无回路,若增加一条边,就得到一条仅一条回路 连通,若删去任一边,G则不连通; 每一对结点之间有一条且仅有一条通路。 证明略
点deg-(v)-deg+(v)=1。 (定理2)
几种特殊的图
哈密顿图
通过图G的每个结点一次,且仅一次的通路, 次的回路, 就是哈密顿回路。
存在哈密顿回路的图就是哈密顿图。
几种特殊的图
哈密顿图
哈密顿图的判定: (1) 在无向简单图G =<V,E>中,若 V 3
概念,会用哈夫曼算法求最优二叉树。
几种特殊的图
本章重点:
欧拉图和哈密顿图 平面图 树的基本概念。
几种特殊的图
欧拉图
包含图G的每一条边,且每条边仅出现一次
的通路,就是欧拉通路。
包含图G的每一条边,且每条边仅出现一次
的回路,就是欧拉回路。 存在欧拉回路的图,就是欧拉图。
几种特殊的图
欧拉图
欧拉图的判定:
(1) 无向连通图G是欧拉图 G不含奇数度的结点(即G 的
所有结点的度均为偶数(0视为偶数));(定理1)
(2) 非0平凡图G 是欧拉图 G 最多有两个奇数度的结点;
(定理1的推论)
(3) 有向图D是欧拉图 D是连通的,且D的所有结点的入
度等于出度。或除两个结点外,均出度等于入度,且这两
几种特殊的图
树
相关概念
树和森林 无向树与有向树 树叶与分支点 平凡树、生成树和最小生成树 树枝、弦和生成树的补 根数、树叶、分支点(树根、内点) 层数和树高 祖先、父亲、儿子和兄弟 m元树、m元完全树和m元正则完全数
几种特殊的图
树
任何非平凡树至少有两片树叶 求最小生成树的算法--Kruskal算法 定理17: (m-1)i = t - 1 哈夫曼树:最优二叉树
定理19:P215(证明略) 哈夫曼算法 前缀码 前缀码和二叉树
几种特殊的图
本章重点:
欧拉图 哈密顿图 平面图 树的基本概念。
u, v G, deg(u) deg(v) V
则G是哈密顿图;——充分条件 (2) 如果无向图<V,E>时哈密顿图,V1是V的任意非空子集,
则有P(G-V1)<|V1|,。其中P(G-V1)是从G中删除 V1后所得的图的连通支数。——必要条件
(3)有向完全图D=<V,E>, 若 V 3,则图D是哈密顿
图。
几种特殊的图
平面图
重要结论
r
(1) 平面图 G V , E , V v, E e,则 deg(ri ) 2e
(所有面的次数之和=边数的2倍)。
i 1
(2) 欧拉公式:平面图G V, E , V v, E e, 面数为r,
v e r 2则(结点数与面数之和=边数+2)。
几种特殊的图
教学要求
理解欧拉通路(回路)、欧拉图的概念,掌握欧拉图 的判别方法。
理解哈密顿通路(回路)、哈密顿图的概念 了解平面图的概念:平面图、面、边界、面的次数
和非平面图。掌握欧拉公式的应用。 了解无向树、树叶、分支点、平凡树、生成树和最
小生成树等概念。会求最小生成树。 了解有向树、根树、有序树、最优二元(叉)树等
