北航 线性系统第10讲
哈尔滨工程大学 自动控制原理 第1章 线性系统的状态空间描述PPT课件

箱”内部的某些部分),是对系统的一种不完全描述。
7
第1章 线性系统的状态空间描述
例如:
从输入—输出关系来看,它们具有相同的传递函数:
G(s) 1 s 1
但事实上这是两个内部结构完全不同的系统。这两个 系统是不等价的,一个是能控不能观,的一个是能观 不能控的。这表明系统的内部特性比起由传递函数表 达的外部特性要复杂得多,输入—输出描述没有包含 系统的全部信息,不能完整的描述一个系统。
Qu(t)u(t)
14
第1章 线性系统的状态空间描述
三. 系统状态空间描述的基本概念
1.状态和状态变量:系统在时间域中的行为或运动
信息的集合称为状态。确定系统状态的一组独立(数
目最少)的变量称为状态变量,是完全决定系统当前
行为的一个最小变量组,记为 x1(t), x2(t), , xn(t)。
几点说明:
3.状态空间:以n个线性无关的状态变量作为基底 所组成的 n 维空间称为状态空间Rn。
4.状态轨线:随着时间推移,系统状态x(t)在状态
空间所留下的轨迹称为状态轨线或状态轨迹。
17
第1章 线性系统的状态空间描述
5.状态方程(※):描述系统状态变量与输入变量之 间关系的一阶微分方程组(连续时间系统)或一阶差分方 程组(离散时间系统)称为系统的状态方程。状态方程表 征了系统由输入所引起的内部状态变化,其一般形式 为:
统行为所必需的系统变量的最少个数,减少变量数 将破坏表征的完全性,而增加变量数将是完全表征 系统行为所不需要的。
3)状态变量组选取上的不唯一性: 由于系统中变量的个数必大于n,而其中仅有n
个是线性无关的,因此决定了状态变量组在选取 上的不唯一性。 4)系统的任意选取的两个状态变量组之间为线性 非奇异变换的关系。
线性系统理论-郑大钟(第二版)PPT课件

0
0
0
1
0
a0 a1 a2 an1 1
xn1 xn
y (b0 bna0 ), (b1 bna1), , (bn1 bnan1) x bnu
确定性系统和不确定性系统
称一个系统为确定性系统,当且仅当不论是系统的特性和参数还是系统的 输入和扰动,都是随时间按确定的规律而变化的.
称一个动态系统为不确定性系统,或者系统的特性和参数中包含某种不确 定性,或者作用于系统的输入和扰动是随机变量
2.4 由系统输入输出描述导出状态空间描述
由输入输出描述导出状态空间描述
状态空间描述形式
离散时间线性时不变系统 x(k 1) Gx(k ) Hu(k ) y(k) Cx(k) Du(k)
n n阵G : 系统矩阵 n p阵H : 输入矩阵 q n阵C : 输出矩阵 q p阵D : 传输矩阵
离散时间线性时变系统 x(k 1) G(k) x(k) H (k)u(k) y(k) C(k) x(k) D(k)u(k)
选择状态变量
uR2
R2 R1 R2
R1R2 R1 R2
uc
iL
R2 R1 R2
e
2.2 线性系统的状态空间描述
uc
iL
(R1
1
R2 R1
)C
L(R1 R2 )
(
R1
R1 R2 R1R2
)C
uc
iL
(R1
1
R2 R2
)C
e
L(R1 R2 )
多变量频域方法
一是频域方法
二是多项式矩阵方法
第一部分: 线性系统时间域理论
线性系统时间域理论是以时间域数学模型为系统描述,直接在时间域内分析 和综合线性系统的运动和特性的一种理论和方法
北京航空航天大学 线性代数 课件 空间向量

刘敬伟 博士 jwliu_2005@
机动
目录
上页
下页
返回
结束
相 关 事 宜
学习辅导用书:
《高等代数方法指导》姚幕生编---复旦大学出版社 参考书: 1.《高等代数》第三版,北京大学数学系编—高教出版社 2.《线性代数》第三版,同济大学数学系编—高教出版社 作业规格:16开作业纸,注明姓名、学号 交作业时间:每周四上完《高代》课后 答疑时间:每周三、四、五 19:00---21:00
机动 目录 上页 下页 返回 结束
2. 向量的减法
规定: b a = b + ( a ) 特别地,当 b = a 时
b a = a a = a + ( a ) = 0
a
b b a b + ( a )
a
三角不等式:
ab a b
ab a b
机动 目录 上页 下页 返回 结束
机动 目录 上页 下页 返回 结束
推论2. 向量a, b, c 不共面的充分必要条件是: 由k1a + k2b + k3c = 0 可以推出 k1 = k2 = k3= 0 . 由于上述命题, 使得向量的线性运算可以用 来解决有关点的共线或共面问题以及线段的 定比分割问题. 例2. 设向量a, b, c , 证明 a + b, b + c, c a 共面. 证: 因为 1(a + b) + (1)(b + c) + 1(c a)=0, 且 1, 1, 1 不全为零, 由命题3可知, a + b, b + c, c a 共面.
c=a+b.
机动 目录 上页 下页 返回 结束
线性系统Linear Systems

頻域分析: 使用的
系統數學模型有: 轉移函數 頻率轉移函數 脈波轉移函數等
頻域分析中需要做
幅度響應、 相角響應、 波德圖、 頻譜分析等估算,及 頻率響應曲線之繪製
Lecture 1
信號與系統
在本章我們要介紹下列主題: 信號及系統概述 連續時間信號 離散時間信號 連續與離散時間信號之變換 抽樣定理
類比(Analog)與數位 與數位(Digital)信號 類比 與數位 信號
類比式信號: 類比式信號 CT signal (連續時間式信號) Physical meaning (具有確定單位) Measurable (可利用某種程序量測之) 數位式信號: 數位式信號 DT signal (離散式時間信號) Quantized (可以階化) Can be binary encoded/ decoded (可作二值編 碼或解碼)
CT/DT、 類比 數位信號 、 類比/數位信號
DSP (數位信號處理) 數位信號處理)
類比至數位變換 (A/D):
CT DT PAM/PTM binary code then stored into memory/ processed by PC
數位至類比變換 (D/A):
code
DSP
PWM
時域分析 (Time-domain analysis)
系統分析方法有兩類:時域分析及頻域分析 時域分析: 使用的
系統數學模型有: CT微分方程式、 DT差分方程式、 CT狀態方程式、 與DT差分狀態方程 式等 時域分析中,需做: 脈衝響應、 步階響應、 迴旋積分、 弦波穩態響應等輸出 之估算
自动控制原理(北航)电子教案扰动下对稳态误差及减小稳态误差的措施(第10讲)
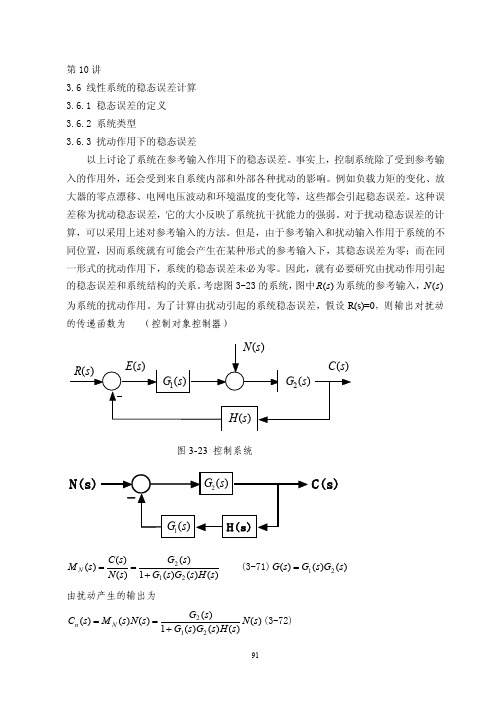
第10讲3.6 线性系统的稳态误差计算3.6.1 稳态误差的定义3.6.2 系统类型3.6.3 扰动作用下的稳态误差以上讨论了系统在参考输入作用下的稳态误差。
事实上,控制系统除了受到参考输入的作用外,还会受到来自系统内部和外部各种扰动的影响。
例如负载力矩的变化、放大器的零点漂移、电网电压波动和环境温度的变化等,这些都会引起稳态误差。
这种误差称为扰动稳态误差,它的大小反映了系统抗干扰能力的强弱。
对于扰动稳态误差的计算,可以采用上述对参考输入的方法。
但是,由于参考输入和扰动输入作用于系统的不同位置,因而系统就有可能会产生在某种形式的参考输入下,其稳态误差为零;而在同一形式的扰动作用下,系统的稳态误差未必为零。
因此,就有必要研究由扰动作用引起的稳态误差和系统结构的关系。
考虑图3-23的系统,图中)(s R 为系统的参考输入,)(s N 为系统的扰动作用。
为了计算由扰动引起的系统稳态误差,假设R(s)=0,则输出对扰动的传递函数为 (控制对象控制器)图3-23 控制系统N(s)C(s))()()(1)()()()(212s H s G s G s G s N s C s M N +== (3-71))()()(21s G s G s G = 由扰动产生的输出为)()()()(1)()()()(212s N s H s G s G s G s N s M s C N n +==(3-72)系统的理想输出为零,故该非单位反馈系统响应扰动的输出端误差信号为)()()()(1)()(0)(212s N s H s G s G s G s C s E n n +-=-=(3-73) 根据终值定理和式(3-73)求得在扰动作用下的稳态误差为)()()()(1)()(lim 2120s N s H s G s G s sG s sE e n s ssn +-==→ (3-74) 若令图3-23中的21)()(,)()(222111ννs s W K s G s s W K s G == (3-75)为讨论方便起见假设1)(=s H 则系统的开环传递函数为νs s W K s W K s G s G s G )()()()()(221121==(3-76)1)0()0(,2121==+=W W ννν。
北航线性系统2017第12讲

!
q ×1 向量
⎡#⎤ ni −1 N i (s ) = ⎢ ⎥ s + #⎦ ⎣ N
Ni ni −1
Ni ni − 2
⎡#⎤ ni −2 ⎡#⎤ 1 ⎡#⎤ + " + ⎢ ⎥s + ⎢ ⎥ ⎢#⎥ s #⎦ #⎦ ⎣ ⎦ ⎣ ⎣ N N N
1 ⎡1 s " s n −1 ⎤ co (s I − Ao ) = ⎦ det(s I − A o ) ⎣
−1
容易验证,c( sI − A ) −1 B=G ( s )。
2)实现中(A, c)与单变量时的可观测标准形是完全一样的。
3)注意到在严格正则、各元互质时,d (s )既是系统的 极点多项式,又是特征多项式,故由定理(3-8), 极点多项式 是特征多项式 故 定 (A, B, c)必是最小实现。
二、向量传递函数的实现
一个元素为多项式的矩阵,总可以写成矩阵 为系数的多项式,例如:
⎡2s3 + 5s2 + 3s s3 + 4s2 + 6s + 4⎤ ⎢ ⎥ 2 s +6 s +1 ⎢ ⎥ ⎣ ⎦ 2×2
⎡ 2 1 ⎤ 3 ⎡5 4 ⎤ 2 ⎡ 3 6 ⎤ ⎡0 4⎤ =⎢ s +⎢ s +⎢ s+⎢ ⎥ ⎥ ⎥ ⎥ 0 0 1 0 0 1 6 1 ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦
(3 37) (3-37)
- 7:若Δ( s )与Cadj ( sI − A )B无非常数的公因式, 定 定理3 无非常数的公因式 则系统( A, B, C)是可控和可观测的。
线性系统理论讲义
对于线性系统
X A(t)X B(t)u Y C(t)X D(t)u
1/2,12/50
时变系统和时不变系统
若向量f,g不显含时间变量t,即
f
g
f (x, u) g(x, u)
该系统称为时不变系统
若向量f,g显含时间变量t,即
f
g
f (x, u, t) g(x, u, t)
该系统称为时变系统
x t ,K , x t 为坐
1
n
标轴构成的 n 维空间。
(5)状态方程:描述系统状态与输入之间关系
的、一阶微分方程(组):x&(t) Ax(t) Bu(t)
(6) 输出方程:描述系统输出与状态、输入之间关
系的数学表达式: y(t) Cx(t) Du(t)
(7)状态空间表达式: (5)+ (6). 状态变量的特点: (1)独立性:状态变量之间线性独立. (2)多样性:状态变量的选取并不唯一,实
4/18,17/50
写成矩阵形式: x1
x2
0
0
xn1 xn
0
a0
1 0 0 1
0 0 a1 a2
0 0
x1 x2
0 0
1 an
1
xn1
xn
u 0 1
y b0 a0bn
b1 a1bn
bn2 an2bn
x1
x2
bn1 an1bn bnu
5/18,18/50
结论2 给定单输入,单输出线性时不变系统的输入输出描述,其对应的状态空
uc
R2C
duc dt
R1iL
R1C
duc dt
L diL dt
L diL dt
【线性系统课件】线性系统概论
四. 系统矩阵描述
• 一般形式
后者不但适用于描述线性定常系统,也适用于线性时变系统。 微分算子描述。
学习过程
• 郑大钟《线性系统理论》1-4章自学; • 重点讲述第五章及以后的频域理论。 • 参考书目
– Chi-Tsong Chen, Linear system theory and design
• 状态空间:
状态向量取值的空间是有限维的实向量空间(Rn,R),称 为状态空间.
• 动态方程:
----描述输入输出和状态之间唯一关系的方程组. ----动态方程都是因果的.
x (t ) f ( x , u , t ) y (t ) g ( x , u , t )
.
x (t 0 ) x 0
定义时不变性: 松驰系统是时不 变的,当且仅当 成立,否则称为时变的。
) u (t )
对任意的
HQ u Q H u
,u
均
松驰、线性、时不变系统
Q g ( , ) Q H ( t ) HQ ( t ) H ( t ( )) g ( , ) t
对动力学系统,若初始状态未知,或 t1 之前的输入未知,则
u [ t1 , ) y [ t1 , ) 不一一对应,
这样对研究系统的关键性质无用。 假定:系统是初始松驰的,输出只由此后的输入唯一地确定 工程上,常假定系统在负无穷时间是松驰的 在松驰性的假定下,有
y Hu
H 为某一算子或函数 称在负无穷时初始松驰的系统为松驰系统。 线性: 因果性 松驰性 时不变性
t0
综上,线性、因果、
t0
时 松 驰 的 系 统 , 其 I/O 描 述 为
线性系统课件
21
1 2 10 B1 , B2 , B3 3 9 27
则特解为:
1 2 2 10 rf ( t ) t t 3 9 27
可见,特解是由激励与系统方程共同决定的。 激励决定特解形式 系统方程决定系数
四、能控性和能观测性的概念
古典中:C(s)既是输出又是被控量
n 1
d r (t ) d r (t ) dr(t ) an n an 1 n1 a1 a0r (t ) dt dt dt m m 1 d e( t ) d e( t ) de(t ) bm m bm1 m1 b1 b0e(t ) dt dt dt
二、线性定常连续系统的能控性判据
二、线性系统判定方法
判断下述微分方程所对应的系统是否为线性系统?
d r (t ) 10r ( t ) 5 e( t ) ,t 0 dt
分析:根据线性系统的定义,证明此系统是否具有 齐次性和叠加性。可以证明:
系统不满足齐次性 系统不具有叠加性
此系统为非线性系统。 请看下面证明过程
证明齐次性
1.3 传递函数描述法的局限性
对于非零初始条件,这种描述不能应用。更为重要的是,输入输出描述不能揭示系统的内部行为。
例如:
从输入—输出关系来看,它们具有相同的传递函数:
1 G( s) s 1
但事实上这是两个不同的系统。这两个系统是不等价的 ,一个是能观不能控的,一个是能控不能观的。这表明 系统的内部特性比起由传递函数表达的外部特性要复杂 得多,输入—输出描述没有包含系统的全部信息,不能 完整的描述一个系统。
当e1 ( t ) e2 ( t ) 同时作用于系统时,若该系统为线性系统, 应有
《线性系统综合》PPT课件
状态反响与输出反响、 状态观测器,
带观测器的状态反响闭环系统。
2021/5/29
第6章 线性系统综合
概述
系统综合是系统分析的逆问题。 系统分析问题即为对系统构造和参数,以及确定好系统
的外部输入(系统鼓励)下,对系统运动进展定性分析 如能控性、能观性、稳定性等 和定量运动规律分析
如系统运动轨迹、系统的性能品质指标等。 的探讨。
– 以现代技术的观点,这些方法应方便地使用计算机 实现,其相应的数值计算方法具有较好的数值稳定 性,即在计算过程中可能出现的计算误差是否被不 断放大、传播,还是被抑制在一个小的范围,其影响 逐渐减弱。
2021/5/29
第6章 线性系统综合
• 在综合问题中,不仅存在可综合问题和算法求解问题,还存在 控制系统在工程实现上所涌现的一些理论问题。如:
• 这就需要基于状态观测理论,根据系统模型,利用直接测量到 的输入输出信息来构造或重构状态变量信息。
• 状态获取问题
• 对状态反响控制系统,要实现已求解的状态反响规律,需要获 取被控系统的状态信息,以构成反响。
• 但对许多实际系统,所考虑的状态变量是描述系统内部信息的 一组变量,可能并不完全能直接测量或以经济的方式测量。
• 这就需要基于状态观测理论,根据系统模型,利用直接测量到 的输入输出信息来构造或重构状态变量信息。
而系统综合问题为系统系统构造和参数,以及所期望的 系统运动形式或关于系统运动动态过程和目标的某 些特征,所需要确定的是那么需要施加于系统的外部 2021/5/29 输入的大第小6章或线性规系统律综合。
– 一般情况下,控制理论开展与控制系统设计的追求目标为解析的反 响控制作用规律(反响控制律)。
– 对复杂的动力学被控系统,在解析反响控制规律难于求解的情形下, 需要求系统的数值反响控制规律或外部输入函数的数值解序列(开 环控制输入)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十讲线性时不变系统的标准形1. 可控标准形定理3-1:设系统(3-1)可控,则可通过等价变换将其⎡变成如下所示的可控标准形(第二可控标准形):010*******⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥ ###%##x x u 000010⎢⎥⎢⎥⎢⎥⎢⎥−−−−⎦"1211211[]−−−⎢⎥⎢⎥⎣⎦⎣=+"n n n n n a a a a y x duββββ3求可控标准形的方法一:先求变换阵P11)[n −U=b Ab A b];"计算可控性矩阵12);U h −计算,并记其最后一行为h ⎡⎤hA ⎢⎥⎢⎥23)P hA ⎢⎥=⎢⎥#给出变换阵:;1hA −×⎢⎥⎢⎥⎣⎦n n n4为可逆阵只要证明对任意给定的P这样构造的是否可逆?:问题P为证明为可逆阵,只要证明对任意给定的αααα="h⎡⎤12[]n20hAPα⎢⎥⎢⎥hAα⎢⎥==⎢⎥#1hA−⎢⎥⎢⎥⎣⎦n112h hA hAααα−⇔+++="nn7⇒≡α即可。
为此,我们考虑右乘上式并考虑到1120(*)h hA hAααα−+++="n n b 1)用右乘上式,并考虑到21000−−(34)0,0,0,1hb hAb hAb hA b ====,(3-4)n n 有右乘(*)式,并考虑到(3-4)及0;n α=0Ab =2)用右乘(*)式,并考虑到(34)及之事实,有n α10α−=#n 依次类推,有8依次类推有0i αα=⇒≡0求可控标准形的方法二:先求变换阵P −11211−−⎡⎤⎢⎥"n n a a a 1). 令基底为:23110[]0−−−⎢⎥=⎢⎥⎢⎥⎥P b Ab A b ""##$#-1n n n a a 12:[]q q q ="n 110100⎢⎢⎥⎣⎦"a d t()−−1212det(n n n ns s a s a s a −=++++I A "注意到显然有q bn =1112q b Ab A bA n n n a a −−−−=+++"而221212()q q A b A b q Aq n n n n n n a a a −−−=+++=+"9211Aq q q n n a −=−⇒2223q b Ab Ab −−−=+++"n n n a a 32323()q A b A b q Aq −−−−=+++=+" n n n n n n a a a 依次有3q 322Aq q q n na −⇒=−121A 依次,有-1,1,2,,1,q =q +Aq i n i n i a i n +=−"i =−=−"最后由1n −+++11,2,,,1Aq q q i i n n i n a +−⇒最后,由−112q b Ab A b n n a a −−="考虑到凯莱哈密尔顿定理,有12−−−=++=−++Aq Ab A b A b A b "n n a a a a 102111q q n n n n讨论:P .由变换阵的唯一性可给1出)为:11211h −−−⎡⎤⎛⎞⎡⎤"n n a a a 231210[]00hA P b Ab A b hA −−−⎢⎥⎜⎟⎢⎥⎢⎥⎜⎟⎢⎥⎢⎥⎜⎟==⎢⎥$"#$$n n n a a 1110−⎢⎥⎜⎟⎢⎥⎢⎥⎜⎟⎢⎥⎜⎟#n a 1100P hA −⎢⎥⎢⎥⎣⎦⎝⎠⎣⎦13例题:设系统状态方程为2210−−⎡⎤⎡⎤⎢⎥⎢⎥=− 02011401x x u +⎢⎥⎢⎥−⎢⎥⎢⎥⎣⎦⎣⎦解先判断可控性再计算变换矩阵将状态方试将系统状态方程化为第二可控标准形。
:先判断可控性,再计算变换矩阵,将状态方程化为可控标准形。
3⎡2014124−⎤⎢⎥⎡⎤==−⎣⎦⎢⎥U b A b A b 1411det 0,−⎢⎥⎣⎦≠U 故系统可控。
16现构造变换矩阵P210⎡[]1522211Uh −⎤⎢⎥=−=−⎢⎥211−⎢⎥⎣⎦2TTT T=则变换矩阵为[()()]P h hA hA 1211210322121−−⎡⎤⎡⎤⎢⎥⎢⎥=−−=P P 即423201⎢⎥⎢⎥−−⎢⎥⎢⎥⎣⎦⎣⎦17求可观标准形的方法一:先求变换阵P−1⎡⎤c A1);⎢⎥⎢⎥⎢⎥cA V=#计算可观测性矩阵1n −⎢⎥⎣⎦cA 12);V h −计算,并记后一列其最为113)[]Ph Ah Ah n n n −−×="给出变换阵:;20求可观标准形的方法二:先求变换阵P1−−⎡⎤"a a a 1212310−−⎡⎤⎢⎥⎢⎥⎢⎥c cA "$n n n n a a 1100−⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥P ###a n 1cA 100⎢⎥⎣⎦⎢⎥⎣⎦"以上两种求P 阵的方法的分析均与可控标准形阵的方法类似求P 阵的方法类似。
21下面介绍变换的具体做法。
1).不失一般性,假设B =[b 1b 2,……b p ]列满秩;2).列出可控性矩阵:111n n n −−−A 1121212[]n p p p −=BA BA BU b b b A b A b A b b A b A b """"按上面的排列顺序,自左向右挑选出n 个线性无关向量再重新排列如下:量,再重新排列如下:12111111222μμμ−−−b Ab Ab b Ab Ab b Ab Ab """"P p p p12μμμ+++="n26显然有p11−=P 令3).12111111222[]P p p p μμμ−−−b Ab A b b Ab A b b Ab A b """"12pμμμ4).求出P 1,以h i 表示P 1阵的1121pi μμμμ+∑"、、及行,×⎡⎤⎢⎥×⎫⎪1h ⎢⎥⎢⎥⎢⎥#1⎪⎬⎪⎪⎭μ行1P ⎢⎥⎢⎥×=⎢⎥⎢⎥##1μ⎢⎥×⎢⎥×⎢⎥p μ⎫⎪⎪⎬27h p ⎢⎥⎢⎥⎢⎥⎣⎦#⎪⎪⎭1pi n μ∑=第行讨论:1)P 2的可逆性证明:200P =⇒≡只要证明:若有列向量,满足即可。
ααα⎡⎤11A ⎢⎥⎢⎥h h a )由111A μ−⎢⎥⎢⎥⎢⎥⎢⎥#h 2221PA μαα−⎢⎥==⎢⎥⎢⎥#h h 2⎢⎥⎢⎥⎢⎥#ph 1A μ−⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦#P p h 290,1,2,,;0,1(),,11h A ij i i i i p a j ⇔==−−=""αμ特别,有1h ⎡⎤2h ⎢⎥⎢⎥#0=αh ×⎢⎥⎢⎥⎣⎦p p n11[]h h P A b μ−"-11,,的零空间恰恰是由中除去易见,i T T T p ib)后的向量b −−−1222211(222)1Ab A b b Ab A b b Ab A b ×−""""μμμP n p p p p n α所张成的,因而必可表示为这些向量的线性组合。
302p =这是由于(以为例说明)×⎡⎤⎢⎥×⎢⎥⎢⎥#112111111222[]−−⎢⎥⎢⎥=h b Ab A b b Ab A b I "" μμ010⎡⎤⎢⎥⎢⎥⎢⎥=%""11−⎢⎥×⎢⎥×⎢⎥P 0001⎢⎥⎢⎥⎢⎥⎣⎦%"⎢⎥⎢⎥#21112111110,0,,0,000111h b h Ab h A b A h b −−−===="μμN 12⎣⎦P h 11212120,0,,0;2h b h Ab h A b ==="μ10,0,,0;1h b h Ab h Ab −==="μ2121212222222221,,;0,0,,10,22h b h Ab AAh h b b −−===="μμ311[]h h "这说明,,的零空间确实是由这些向量所张成的。
T T T p一般地,我们有11,1,2,,h Ab i i i i pμ−=="及0,21.h A b ji k k i k i a =≠=−−<或者c)将表示为这些向量的线性组合:α(),i j 若但μ12222p iii−−−=∑"μμμ1)左乘上式两边并注意到式式有11220A b A b A b i i pi pa a a +++∑∑α1(-1)(-2)h A 现用左乘上式两边,并注意到式、式,有a a 3210=h A α122221111112121−−−+++=+++∑∑∑ h Ab h Ab h Ab "p i i i i i pi pa a a μμμ01111121112100h A b a a −−−=⇒=⇒=;μμμ2h A 再左乘,有222122222200h Ab μμμ−−−=⇒=",,a a 330≡依次类推,我们可以证明。
α证完。
×⎡⎤2p =以为例:−⎢⎥×⎢⎥#10=h B 10=h AB 111[1]μ=×12b ]h A [b 12111μμ−−⎢⎥⎢⎥⎢⎥=h b Ab A b b Ab A b I ""1010⎡⎤⎢⎥⎢⎥⎢⎥=%""11111222[]−⎢⎥×⎢⎥×P 0001⎢⎥⎢⎥⎢⎥⎣⎦%"⎢⎥⎢⎥⎢⎥#11210μμ−−"由此推得:N12⎣⎦P h 1110,[01,;]h A B h A h B B ×===#22220,,0;h A h B B μ−=="3521122122h AB h A [b b ]μμ−−=?2112222120,,0;222h B h A B h A B h A[b b ]−−−==="为?讨论μμμ注意到基底的选取法则注意到基底的选取法则:222111121212b b Ab Ab Ab Ab Ab Ab μμμ−−−"""22110Ab h A b 1μμ−−=p p1222122h AB h A [b b ]=[01]μ−⇒=121出现在上述列中,必有)若;2112Ab μ−不出现在上述各列中,)若则必可表示为2222121212b b Ab Ab Ab A b Ab μμ−−""p 的线性组合,故仍有21210h Ab μ−=361222122h A B h A [b b ]=[01]μ−⇒=P.85 例题3-2设系统动态方程(A , B , C )为0001000⎡⎤⎡⎤⎢⎥⎢⎥100200001221140010010−⎡⎤⎢⎥⎢⎥===⎢⎥−−−⎢⎥⎢⎥⎣⎦A B C 2360613⎢⎥⎢⎥−−−⎣⎦⎣⎦2试求其可控标准形。
