人教版2020高中数学 专题01 空间几何体专题复习考点精准剖析与创新训练 新人教A版必修2
2020高考人教版文科数学总复习讲义:立体几何课时1含答案

空间几何体的结构及三视图、直观图■复习目标■1. 了解柱、锥、台、球的定义、性质及它们之间的关系.2 •掌握柱、锥、台、球的结构特征.3•能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等及其简易组合)的三视图, 能识别上述三视图所表示的立体模型,会用斜二测法画出它们的直观图.. ____________________________________________®知识梳理1.柱、锥、台、球的结构特征(1) 正视图是光线自物体的前面向后面正投影所得的投影图•俯视图是光线自物体的上面向下面正投影所得的投影图.侧视图是光线自物体的左面向右面正投影所得的投影图.(2) 三视图的排列规则:先画正视图,俯视图画在正视图的下方,长度与正视图相等,侧视图则安排在正视图的正右方,高度与正视图相同•3. 直观图空间几何体的直观图常用斜二测法来画,基本步骤是:(1) 画几何体的底面①在已知图形中取互相垂直的x轴和y轴,两轴交于点0,画直观图时,把它们画成对应的x'轴与y'轴,两轴相交于0 '点,且使/ x' O' y'= 45°或135° .②已知图形中平行于x轴或y轴的线段,在直观图中,分别画成平行于x'轴或y'轴的线段.③在已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y轴的线段,长度为原来的一半•(2) 画几何体的高在已知图形中过0点作z轴垂直于xOy平面,在直观图中对应的z'轴也垂直x' O' y' 平面,已知图形中平行于z轴的线段在直观图中仍平行于z'轴且长度相等•(3) 成图根据实际图形,顺次连接线段的端点,并整理(去掉辅助线,将被遮挡部分改为虚线),就得到了几何体的直观图.1 •根据三视图确定直观图的常用结论(1) 三视图为三个三角形,对应三棱锥;(2) 三视图为两个三角形,一个四边形,对应四棱锥;(3) 三视图为两个三角形,一个带圆心的圆,对应圆锥;(4) 三视图为一个三角形,两个四边形,对应三棱柱;⑸三视图为两个四边形,一个圆,对应圆柱.2 •用斜二测画法画出的水平放置的平面图形的直观图的面积是原图形面积的热身练习1. 下列四个命题:① 有两个面互相平行,其余各面都是四边形的几何体叫棱柱; ② 各个面都是三角形的几何体是三棱锥;③ 用一个平面去截棱锥,棱锥的底面与截面之间的部分是棱台;④ 两个面互相平行且相似,其余各面都是梯形的多面体是棱台. 其中正确的命题有(A )A . 0个B . 1个C . 2个D . 3个馆谅①假,如棱台有两个面互相平行,其余各面是四边形; 由图1至图3可知②、③、④都是错误的.2. 下列说法正确的是(C )A .以直角三角形的一边为轴旋转所得到的旋转体是圆锥B .以直角梯形的一腰为轴旋转所得的旋转体是圆台C .以半圆的直径为轴旋转一周所得到的旋转体是球D .圆锥的侧面展开图为扇形,这个扇形所在圆的半径等于圆锥底面圆的半径噩3 A 是错误的,以直角三角形的直角边..为轴旋转所得到的旋转体才是圆锥; B 是错误的.以直角梯形的垂直于底的腰 为轴旋转所得的旋转体是圆台;C 是正确;D 是错误的,C._2 "4.(D)圆锥的侧面展开图为扇形,这个扇形所在圆的半径等于圆锥的母线长.故选3.A .①②B .①③C .①④D .②④CD 圆锥和正四棱锥的正视图和侧视图都是等腰三角形.4. (2018全国卷川)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼.图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是(A )由题意可知带卯眼的木构件的直观图如图所示,. 咼频考点 ______________________________-:空间几何体的结构特征鈕11(经典真题)若空间中n 个不同的点两两距离都相等,则正整数n 的取值A .至多等于3B .至多等于4C .等于 5D .大于5殛 根据n 的取值构造相应的几何图形或几何体求解.n = 2时,可以;n = 3时,为正三角形,可以;n = 4时,为正四面体,可以; n = 5时,为四棱锥,侧面为正三角形,底面为菱形且对角线长与边长不可能相等.B本题考查了空间想象能力和推理论证能力,试题有较大的难度•根据题目特点善 于构造几何图形和空间几何体是解决这类问题的关键.变式採究1•在正方体上任意选择4个顶点,它们可能是如下各种几何形体的 4个顶点,这些几何体是 ①③④⑤•(写出所有正确结论的编号)由直观图可知其俯视图应选 A.5.如果一个水平放置的平面图形的斜二测直观图是一个底角为 的等腰梯形,那么这个平面图形的面积是(C )A. 1 + 于 B . 1+ .245 °腰和上底长均为1,所以其面积 S =-2^ X 2 = 2+2.C . 2 + ,2D £+¥① 矩形;② 不是矩形的平行四边形;③ 有三个面为等腰直角三角形,有一个面为等边三角形的四面体; ④ 每个面都是等边三角形的四面体; ⑤ 每个面都是直角三角形的四面体.A .①④③B .①②③C .⑤④③D .①④⑥薛3由四面体ABCD 四个顶点是长方体的四个顶点, 可得四面体ABCD 的正视图为①, 侧视图为②,俯视图为③•故四面体ABCD 的三视图分别为①②③.B❺® (1)解决三视图问题,要从以下几个方面加以把握:①搞清正视、侧视、俯视的方向,同一物体由于正视、侧视的方向不同或放置的位置不 同,所画的三视图可能不同.作出正方体ABCD — A ' B ' C ' D '.① 显然可能;②不可能; ③取一个顶点处的三条棱,连接各棱端点构成的四面体; ④取正方体中对面上的两条异面直线对角线的四个端点构成的四面体, —B ' BC 时各面均为直角三角形.如图,四面体 ABCD 的四个顶点是长方体的四个顶点女口 B ' — ACD ';⑤取 D(长方体是虚拟图形,起辅助 作用),则四面体 ABCD 的三视图分别是(①②③④⑤⑥代表图形)(空间几何体的三视图C② 遵循“长对正、高平齐、宽相等 ”的原则.③ 注意几何体中与投影面垂直或平行的线段在三视图中的特点. ④ 要注意实线、虚线的画法,可视轮廓线画成实线,不可视的画成虚线.(2)画三视图时,要注意所给几何体与熟知的几何体的联系,如将几何体放置在正方体(或长方体)中或补形成正方体等,有利用发现线、面与投影面的位置关系,从而准确作出相应 的三视图.变式採究2. (1)在如图所示的空间直角坐标系 O — xyz 中,一个四面体的顶点坐标分别是 (0,0,2),(2,2,0), (1,2,1), (2,2,2).给出编号为①、②、③、④的四个图,贝U幼该四面体的正视图和俯视图分别为(D)2'设A(0,0,2), B(2,2,0), C(1,2,1), D(2,2,2),贝U ABCD 即为满足条件的四面体,得出正视 图和俯视图分别为④和②•(2)由图可知其侧视图为三角形, 根据三视图的“高平齐”得侧视图的高为.3,又由“宽相等”可知侧视图的宽度和俯视图的宽度相等,得侧视图的底为1X sin 60 =~23.所以侧视图的面积为S = |x 訂 3=3.A .①和②B .③和①C .④和③ D .④和②(2)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为 (C)A 亞 A. 4 B. { 3 C.3D . 1堪3 (1)在空间直角坐标系中构建棱长为2的正方体,兰厂 由三视图得到空间几何体的直观图A . 3 .2B . 2 3 C. 2 ,2 D . 2如图所示,A . 10B . 12C . 14D . 16FT/0 X(2017北京卷)某四棱锥的三视图如图所示, 则该四棱锥的最长棱的长度为解析可知SD 为该四棱锥的最长棱. 由三视图可知正方体的棱长为 故SD =22+ 22 + 22= 2 3.B将三视图还原为直观图时, 菩案 2,若能将其放置到 “正方体”或“长方体”中去研究, 不仅能较易得到直观图,同时还能发现各元素之间的数量关系与位置关系, 便于问题的解 决.变式探究3. (2017全国卷I )某多面体的三视图如图所示,其中正视图和左视图都由正方形和等 2,俯视图为等腰直角三角形.该多面体的各个面中有 这些梯形的面积之和为 (B ) 腰直角三角形组成,正方形的边长为 若干个是梯形,正(主灌图 侧佐)视图cia将三视图还原为直观图,如图:可知该多面体是由直三棱柱和三棱锥组合而成的,且直三棱柱的底面是直角边长为2的等腰直角三角形,侧棱长为 2.三棱锥的底面是直角边长为2的等腰直角三角形,高为2.因此该多面体各个面中有2个梯形,且这两个梯形全等,梯形的上底长为2,下底长为4,高为2.1故这些梯形的面积之和为2 X 2 x (2 + 4)X 2 = 12.■I课时小结1 •与柱、锥、台、球有关的概念题,要结合其定义和结构特征,作出准确的判断,若说明命题是假命题,只需要举出一个反例即可.2 •画三视图要注意“长对正、高平齐、宽相等”.3•三视图和直观图是空间几何体的不同的表现形式,空间几何体的三视图可以使我们很好地把握空间几何体的性质. 由空间几何体可以画出它的三视图,同样由三视图可以想象出空间几何体的形状,两者之间可以相互转化.。
2020年高考数学专题提升: 空间几何体(含答案)
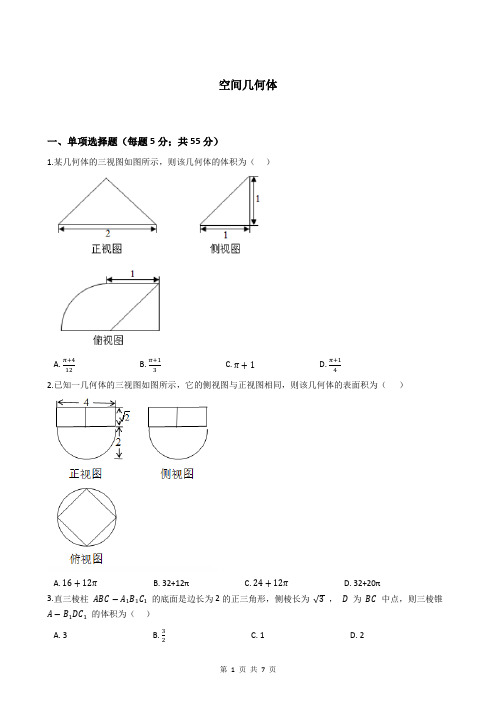
空间几何体一、单项选择题(每题5分;共55分)1.某几何体的三视图如图所示,则该几何体的体积为()A. π+412B. π+13C. π+1D. π+142.已知一几何体的三视图如图所示,它的侧视图与正视图相同,则该几何体的表面积为()A. 16+12πB. 32+12πC. 24+12πD. 32+20π3.直三棱柱ABC−A1B1C1的底面是边长为2的正三角形,侧棱长为√3,D为BC中点,则三棱锥A−B1DC1的体积为()A. 3B. 32C. 1D. 24.如图所示的三视图表示的几何体的体积为323,则该几何体的外接球的表面积为( )A. 12πB. 24πC. 36πD. 48π5.一个由两个圆柱组合而成的密闭容器内装有部分液体,小圆柱底面半径为r1,大圆柱底面半径为r2,如图1放置容器时,液面以上空余部分的高为ℎ1,如图2放置容器时,液面以上空余部分的高为ℎ2,则ℎ1ℎ2=()A. r2r1 B. (r2r1)2 C. (r2r1)3 D. √r2r16.如图,长方体ABCD−A1B1C1D1的体积是36,点E在棱CC1上,且CE=2EC1,则三棱锥E-BCD的体积是()A. 3B. 4C. 6D. 127.某几何体的正视图和侧视图如图1所示,它的俯视图的直观图是平行四边形A′B′C′D′,如图2所示.其中A′B′=2A′D′=4,则该几何体的表面积为( )A. 16+12πB. 16+8πC. 16+10πD. 8π8.某几何体的三视图如图所示,若该几何体的体积为10,则棱长为a的正方体的外接球的表面积为()3A. 12πB. 14πC. 4√3πD. 16π9.斗拱是中国古典建筑最富装饰性的构件之一,并为中国所特有.图一图二是斗拱实物图,图三是斗拱构件之一的“斗”的几何体.本图中的斗是由棱台与长方体形凹槽(长方体去掉一个小长方体)组成.若棱台两底面面积分别是400cm2,900cm2,高为9cm,长方体形凹橹的体积为4300cm3,那么这个斗的体积是()注:台体体积公式是V=1(S' +√S′S+S)h.3A. 5700cm3B. 8100cm3C. 10000cm3D. 9000cm310.在四棱锥P−ABCD中,PB=PD=2,AB=AD=1,PC=√3PA=3,∠BAD= 120°,AC平分∠BAD,则四棱锥P−ABCD的体积为()A. √62B. √6 C. √63D. √311.《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为()(注:1丈=10尺=100寸,π≈3.14,sin22.5∘≈513)A. 600立方寸B. 610立方寸C. 620立方寸D. 633立方寸二、填空题(每空4分;共44分)12.如图,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,正视图中的曲线为四分之一圆弧,则该几何体的表面积是________.13.已知某正四棱锥的底面边长和侧棱长均为2cm,则该棱锥的体积为________ cm3.14.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为________.15.祖暅是我国南北朝时代的伟大科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”,称为祖暅原理.意思是底面处于同一平面上的两个同高的几何体,若在等高处的截面面积始终相等,则它们的体积相等.利用这个原理求半球O的体积时,需要构造一个几何体,该几何体的三视图如图所示,则该几何体的体积为________,表面积为________.16.如图,长方体ABCD−A1B1C1D1的体积是120,E为CC1的中点,则三棱锥E-BCD的体积是________.17.学生到工厂劳动实践,利用3D打印技术制作模型,如图,该模型为长方体ABCD-A1B1C1D1,挖去四棱推O一EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H,分别为所在棱的中点,AB=BC=6cm,AA1=4cm,3D打印所用原料密度为0.9g/cm2,不考虑打印损耗,制作该模型所需原料的质量为________g.18.某三棱锥的三视图如图所示,则该三棱锥体积是________,四个面的面积中最大的是________.19.在《九章算术》中有称为“羡除”的五面体体积的求法.现有一个类似于“羡除”的有三条棱互相平行的五面体,其三视图如图所示,则该五面体的体积为________.20.如图,在棱长为2的正方体ABCD−A1B1C1D1中,E、F分别为棱A1D1、C1D1的中点,NBC1,若P、M分别为线段D1B、EF上的动点,则|PM|+是线段BC1上的点,且BN=14|PN|的最小值为________.参考答案一、单项选择题1.【答案】A2.【答案】A3.【答案】C4.【答案】C5.【答案】B6.【答案】B7.【答案】A8.【答案】A9.【答案】C10.【答案】A11.【答案】D二、填空题12.【答案】24√213.【答案】4314.【答案】1315.【答案】2π;(3 +√2)π316.【答案】1017.【答案】118.818.【答案】1;3√5219.【答案】2420.【答案】√6。
2020学年高中数学第1章空间几何体章末复习课学案新人教A版必修2(2021-2022学年)

第1章空间几何体正方体;③侧棱垂直于底面两条边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体。
其中真命题的个数是( )A.1 B.2 C.3 D.4(2)在四棱锥的四个侧面中,直角三角形最多可有()A.1个B.2个 C.3个 D.4个(1)A(2)D[(1)①若侧棱不垂直于底面,则底面是矩形的平行六面体不是长方体,错误;②若底面是菱形,则棱长都相等的直四棱柱不是正方体,错误;③若侧棱垂直于底面两条平行边,则侧棱不一定垂直于底面,故侧棱垂直于底面两条边的平行六面体不一定是直平行六面体,错误;④若平行六面体对角线相等,则对角面皆是矩形,于是可得侧棱垂直于底面,因此对角线相等的平行六面体是直平行六面体,正确.(2)如图所示,在长方体ABCDA1B1C1D1中,取四棱锥A1。
ABCD,则此四棱锥的四个侧面都是直角三角形.]ﻬ与空间几何体结构特征有关问题的解答技巧(1)紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本元素,然后再依据题意判定.(2)通过举反例对结构特征进行辨析,即要说明一个命题是错误的,只要举出一个反例即可.1.棱台上、下底面面积分别为16,81,有一平行于底面的截面,其面积为36,则截面截得两棱台高的比为( )A.1∶1B.1∶2 C.2∶3D.3∶4C[将棱台还原为棱锥,设顶端小棱锥的高为h,两棱台的高分别为x1,x2,则错误!未定义书签。
错误!未定义书签。
=错误!,解得x1=错误!,错误!错误!=错误!,解得x2=错误!未定义书签。
h. 故错误!未定义书签。
=错误!未定义书签。
]【例2】如图所示的三棱锥O.ABC为长方体的一角.其中OA,OB,OC两两垂直,三个侧面OA B,OAC,OBC的面积分别为1。
5cm2,1 cm2,3 cm2,求三棱锥O.ABC的体积.ﻬ[解]设OA,OB,OC的长依次为x cm,ycm,z cm,则由已知可得错误!未定义书签。
2020版高中数学第1章空间几何体本章方略总结课件新人教A版必修2

类型
表面积相关公式
棱柱 S 全=S 侧+2S 底,其中 S 侧=l 侧棱长·c 直截面周长
体积公式 V=S 底·h
圆柱 S 全=2πr2+2πrh(r:底面半径,h:高)
棱锥
S 全=S 侧+S 底
V=πr2h
V=13S 底·h 高
S 全=πr2+πrl(r:底面半径,l:母线
圆锥 长)
棱台
S 全=S 侧+S 上底+S 下底
(2)中心投影与平行投影的区别与联系: ①中心投影和平行投影都是画空间图形常用的方法.平行投影用于斜二测画法和三 视图.经中心投影后的图形与原图形相比虽然改变较多,但直观性强,看起来最像原来 的物体. ②画实际效果图时,一般用中心投影法,画立体几何图形时一般用平行投影法.
Hale Waihona Puke 三、空间几何体的表面积与体积
子
图例
(1)底面是多边形,各侧面均是三 棱锥 角形;(2)各侧面有一个公共顶点. 金字塔
圆锥
(1)底面是圆;(2)是以直角三角形
的一条直角边所在的直线为旋转 泥工用的重
轴,其余两边旋转形成的面所围 成的几何体.
心锤
(1)两底面相互平行;(2)是用一个 棱台 平行于 棱锥 底面 的平 面去 截棱
锥,底面和截面之间的部分.
A.12
B.18
C.24
图3 D.36
【解析】 如图 4,这个几何体是一个长方体(长、宽、高分别为 5,4,3)挖去一个 底面为等腰梯形(上底为 3,下底为 5,高为 3)的四棱柱后得到的,其中四棱柱的底面积 S =(3+52)×3=12,故这个几何体的体积为 5×4×3-12×3=60-36=24.故选 C.
A.158 C.182
2020新课标高考数学讲义:立体几何含解析

球
S=4πR2
V= πR3
2.空间线面位置关系的证明方法
(1)线线平行: ⇒a∥b、 ⇒a∥b、
⇒a∥b、 ⇒c∥b.
(2)线面平行: ⇒a∥α、 ⇒a∥α、 ⇒a∥α.
(3)面面平行: ⇒α∥β、 ⇒α∥β、
⇒α∥γ.
(4)线线垂直: ⇒a⊥b.
(5)线面垂直: ⇒l⊥α、 ⇒a⊥β、 ⇒a⊥β、 ⇒b⊥α.
(6)面面垂直: ⇒α⊥β、 ⇒α⊥β.
[提醒]要注意空间线面平行与垂直关系中的判定定理和性质定理中的条件.如由α⊥β、α∩β=l、m⊥l、易误得出m⊥β的结论、就是因为忽视面面垂直的性质定理中m⊂α的限制条件.
3.用空间向量证明平行垂直
设直线l的方向向量为a=(a1、b1、c1)、平面α、β的法向量分别为μ=(a2、b2、c2)、υ=(a3、b3、c3).则有:
若存在某个位置.使得AD⊥BC、又因为AD⊥AB、则AD⊥平面ABC、所以AD⊥AC、而斜边CD小于直角边AD、矛盾、故C错误.
6. 如图、在四棱锥PACBD中、底面ACBD为正方形、PD⊥平面ACBD、BC=AC=a、PA=PB= a、PC= a、则点C到平面PAB的距离为________.
解析:
解析:选B.若存在某个位置、使得AC⊥BD、作AE⊥BD于E、则BD⊥平面AEC、所以BD⊥EC、在△ABD中、AB2=BE·BD、BE= 、而在△BCD中、BC2=BE·BD、BE= 、两者矛盾.故A错误.
若存在某个位置、使得AB⊥CD、又因为AB⊥AD、则AB⊥平面ACD、所以AB⊥AC、故AC=1、故B正确、D错误.
4.用向量求空间角
(1)直线l1、l2的夹角θ有cosθ=|cos〈l1、l2〉|(其中l1、l2分别是直线l1、l2的方向向量).
新人教版高中数学必修第二册《空间几何体》课堂精点练习及答案

高一数学《空间几何体》课堂精点练习一、选择题1.已知球的表面积为36π,则该球的体积为()A.8π3B.16π3C.16πD.36π2.如图,'''A B C△是ABC△的直观图,其中''''A B A C,那么ABC△是()A.等腰三角形B.钝角三角形C.等腰直角三角形D.直角三角形3.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A.πB.3π4C.π2D.π44.某三棱锥的三视图如图所示,则该三棱锥的各个面中,最大的面积是()A.62B.22C.1 D.645.某四棱锥的三视图如图所示,则该四棱锥的外接球半径为()A.1 B 3C2D.126.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为()A .4B .43C .23D .37.将一个直角边长为1的等腰直角三角形绕其一条直角边旋转一周所形成几何体的侧面积为( ) A .4πB .2πC .22πD .2π8.某三棱锥的三视图如图所示,则该三棱锥的体积等于( )A .43B .2C .83D .69.一个几何体的三视图如图所示,该几何体外接球的表面积为( )A .28πB .32πC .36πD .112π310.在长方体1111ABCD A B C D -中,4AB =,3BC =,15AA =,M ,N 分别在线段1AA 和AC 上,2MN =,则三棱锥1C MND -体积的最小值为( ) A .4B .321C .432D .2411.如图是某几何体的三视图,则该几何体的体积为( )A .83B .43C .8D .412.已知正方体、等边圆柱(轴截面是正方形)、球的体积相等,它们的表面积分别为S 正,S 柱,S 球,则( ) A .S S S <<正球柱 B .S S S <<正柱球C .S S S <<正球柱D .S S S <<正球柱二、填空题13.各条棱长均为2的四面体的体积为____.14.已知正三棱柱111ABC A B C -的高为6,4AB =,点D 为棱1BB 的中点,则四棱锥1C A ABD -的表面积是________.15.某几何体的三视图如图所示,则此几何体的体积是__________, 表面积是____________.16.《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为直角三角形的四面体).在如图所示的堑堵111ABC A B C -中,15AA AC ==,3AB =,4BC =, 则阳马111C ABB A -的外接球的表面积是________.三、解答题17.如图,三棱柱111ABC A B C -内接于一个圆柱,且底面是正三角形,如果圆柱的体积是2π,底面直径与母线长相等. (1)求圆柱的侧面积;(2)求三棱柱111ABC A B C -的体积.【经典集训】18.如图所示,半径为R 的半圆内的阴影部分是以直径AB 所在直线为轴,旋转一周得到的一几何体,求该几何体的表面积和体积.(其中30BAC ∠=︒)19.一几何体按比例绘制的三视图如图所示:(1)试画出它的直观图;(2)求它的表面积和体积.参考答案一、选择题1.D 2.D 3.B 4.A 5.B 6.B 7.B 8.A 9.D 10.A 11.B 12.C 二、填空题 13.1314.2394336++ 15.90,138 16.50πS = 三、解答题17.解:(1)设底面圆的直径为2r ,由题可知2π22πV r r =⋅=圆柱, ∴1r =,∴圆柱的侧面积2π24πS r r =⋅=. (2)因为ABC △为正三角形,底面圆的半径为1, ∴可得边长3AB =,∴三棱柱111ABC A B C -的体积133332222V =⨯⨯⨯=. 18.解:过C 作1CO AB ⊥于点1O ,由已知得90BCA ∠=︒, ∵30BAC ∠=︒,2AB R =,∴3AC R =,BC R =,132CO R =. ∴24πS R =球,12333π22πAO S R R R ⨯⨯==圆锥侧, 1232π3π2BO S R R R =⨯⨯=圆锥侧, ∴112222331134ππππ222AO BO S S S S R R R R =++++=+=几何体表球圆锥侧圆锥侧.又∵34π3V R =球,12211111ππ34AO V AO CO R AO ⋅⋅⋅=⋅=圆锥,12211111ππ·34BO V BO CO R BO =⋅⋅⋅=圆锥,∴()1135π6AO BO V V V V R +==-几何体球圆锥圆锥.19.解:(1)直观图如图所示.(2)由三视图可知该几何体是长方体被截去一个三棱柱,且该几何体的体积是以1A A ,11A D ,11A B 为棱的长方体的体积的34,在直角梯形11AA B B 中,作11BE A B ⊥于E ,则四边形1AA EB 是正方形,11AA BE ==,在1BEB Rt △中,1BE =,11EB =,所以12BB =所以几何体的表面积11111111112ABCD AA D D A B C D BB C C AA B B S S S S S S +++=+正方形正方形矩形矩形梯形 ()(11212121121722=+⨯+⨯⨯+⨯+=.几何体的体积3312142V =⨯⨯⨯=.所以该几何体的表面积为7232.。
立体几何初步空间几何与点线面二轮复习专题练习(一)含答案人教版高中数学新高考指导

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.如图,正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,点P 在球面上,如果163P ABCD V -=,则球O 的表面积是(A )4π (B )8π (C )12π (D )16π(2020年高考四川文) 2.设三棱柱ABC-A 1B 1C 1的体积是V ,P.Q 分别是侧棱AA 1上的点,且PA=QC 1,则四棱锥B-A PQC 的体积为( )A.V 61 B.V 41 C.V 31 D.V 21 (2020全国3理) 3.对于平面α和共面的直线m 、,n 下列命题中真命题是(A )若,,m m n α⊥⊥则n α∥ (B )若m αα∥,n ∥,则m ∥n(C )若,m n αα⊂∥,则m ∥n (D )若m 、n 与α所成的角相等,则m ∥n (2020福建理) 4.到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是( )A. 直线B. 椭圆C. 抛物线D. 双曲线(2020重庆理数)(10)5.正方体ABCD-1111A B C D 中,B 1B 与平面AC 1D 所成角的余弦值为 A .23B .33C .23D .63(2020全国I )文 6.如果直线l 、m 与平面α、β、γ满足:l =β∩γ,l ∥α,m ⊂α和m ⊥γ,那么必有( )A .α⊥γ且l ⊥mB .α⊥γ且m ∥βC .m ∥β且l ⊥mD .α∥β且α⊥γ(2020全国文7理5)7.不在同一直线上的五个点,能确定平面的最多个数是---------------------------------------( )(A) 8个 (B) 9个 (C) 10个 (D) 12 8.线a 、b 和平面α,下面推论错误的是 A.b a ⊥⇒⎭⎬⎫⊆⊥ααb a B αα⊥⇒⎭⎬⎫⊥b b // a aC ααα⊆⇒⎭⎬⎫⊥⊥a //a b b a 或D b //a b //a ⇒⎭⎬⎫⊆αα9.正方体的两条对角线相交所成角的正弦值等于------( ) (A)22 (B)13(C)223 (D)101010.如图,已知正方体1111ABCD A B C D -中,点E F 、分别在11AB BC 、上(不与线段的端点重合),且AE BF =。
高中数学 第一章 空间几何体复习 新人教版必修2

综合应用
例1、(P36 A10) 直角三角形的三边长分别为3cm、 4cm、5cm,绕三边旋转一周分别形成三个几何体.说明 它们的结构特征,画出其直观图和三视图,并求出它们 的表面积和体积.
35 4
S1 36 V1 16
正视图
侧视图
俯视图
45 3
S2 24 V2 12
正视图
侧视图
俯视图
1、如图所示,甲、乙、丙是三个立体图形的三视图,
A 甲、乙、丙对应的标号正确的是( )
甲
乙
丙
①长方体 ②圆锥 ③三棱锥 ④圆柱
A.④③②
B.②①③
C.①②③
D 2、正方体的内切球和外接球的半径之比为(
D.③②④ )
A. 3 :1
B. 3 : 2
C. 2 : 3
D. 3 : 3
两个共底的正四棱锥
D
A C
B
Q
P
D A
C B
Q
S1800 3cm2
正视图
V9000 2cm3 俯视图
侧视图
正四面体:各面都是等边三角形的三棱锥
S1
S
正(主)视图
A1
C
B1
O
A
D
B
侧(左)视图
S
S1
俯视图呢?
C
C1
3
a
正(主)视图
长a
侧(左)视图
宽
俯视图
注意:不含虚线
例 2、圆锥底面半径为 1cm,高为 2cm ,其中
有一个内接正方体,求这个内接正方体的棱长.
解析:过圆锥的顶点 S 和正方体底面的一条对角线 CD
作圆锥的截面,得圆锥的轴截面 SEF,正方体对角面 CDD1C1 , 如图所示.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题01 空间几何体专题本重点包括柱、锥、台、球的概念、性质、表面积与体积,直观图与三视图,这些是立体几何的基础,也是研究空间问题的基本载体,所以是高考考查的热点。
知识框架1、空间几何体的结构2、空间几何体的三视图和直观图3、空间几何体的表面积和体积一、考查形式与特点1、本章内容多以客观题出现,考查基本知识,对空间几何体的特征与性质的理解,三视图和直观图,几何体表面积与体积的计算等。
三视图考查特点:一是给出空间图形,选择其三视图;二是已知其中两种三视图,画出另外一种视图;三是三视图与面积体积计算结合在一起考查。
2、球体在近几年的高考中出现频率较高,特别是棱柱、棱锥中球的内切、外接问题,在复习时更要注意多练习相关的题目。
对球中的体积、表面积、球面距离等问题也要进行重点掌握。
3、培养与发展考生的空间想象能力、推理证明能力、运用图形语言进行交流的能力。
考查空间想象能力及空间模型的构造能力。
二、方法策略1、“化整为零”是本章的基本思想。
将一个复杂的几何体分割成若干个常见的熟悉的几何体,或者把几个简单的几何体组合成一个新的几何体,目的在于化繁为简,寻求解题的捷径。
立体几何和平面几何有着密切的联系,空间图形的局部性往往可以透过平面图形的性质去研究,利用截面可以把锥体中的元素关系转化为三角形中的元素关系。
2、“以直代曲”的思想方法即通过空间图形的展开将立体几何问题转化为平面几何问题,曲面问题转化为平面问题,如在推导圆柱、圆锥、圆台的侧面积公式时,就是将其侧面展开,转化为长方形、扇形、圆环来解决。
3、三视图之间的投影规律为:正、俯视图――长对正;正、侧视图――高平齐;俯、侧视图――宽相等。
三视图是新增内容,是高考考查重点,它能极大培养学生的空间想象能力与感知能力,熟悉常见简单几何体三视图在数量上的关系,善于将三视图中的数量关系与原几何体的数量关系联系起来,进行相关的计算。
4、球的表面积与体积的计算的关键是求出球的半径,然后再利用表面积公式及体积公式求解.球的表面积与体积问题常置于多面体的组合体中,解答时要充分利用切、接点正确作出过球心截面,从而使空间问题转化为平面问题,再利用球的半径与多面体的元素的关系求解.特别要注意的题型是球与长方体、正方体的组合体.5、解决问题的重要手段:截、展、拆、拼(1)“截”是指截面,平行于柱、锥、台底面的截面,旋转体的轴截面是帮助我们解题的有力“工具”。
(2)“展”指的是侧面或某些面的展开图。
(3)“拆”指的是将一个几何体拆成几个几何体,比如,探求三棱锥的体积公式还有一种方法是将一个三棱柱拆成三个等体积的三棱锥。
(4)“拼”指的是将小几何体嵌入一个大几何体中去,比如,求三棱锥体积公式,既可用上面“拆”的方法,也可用“拼”的方法。
三.复习指导1、在正棱锥、台体中,要利用直角三角形(高、斜高及底面边心距组成一个直角三角形、高、侧棱于底面外接圆的半径组成一个直角三角形,底面的边心距、外接圆半径及底边一半组成一个直角三角形,侧棱、斜高与底面一半组成一个直角三角形),进行有关计算。
2、解与直观图有关的问题时,应熟练掌握斜二侧画法的规则,关键是确定直观图的顶点或其他关键点,因此,尽量把定点或其他关键点放在轴上或与轴平行的直线上。
3、求柱、锥、台的体积时,根据体积公式,需要具备已知底面积和高两个重要条件,底面积一般可由底面边长或半径求出,但当高不知道时,求高比较困难,一般要转化为平面几何知识求出高。
4、在复习中应注意对简单组合体的概念、性质以及面积、体积公式的理解和运用,在面积与体积的计算中,应以棱锥和不规则几何体的表面积、体积计算为主,注意分割与补体等思想方法的灵活运用,5、加强数学思想方法的训练。
转化、化归思想贯穿立体几何始终,是处理立体几何问题的基本数学思想,在复习中考生应注意培养化归、转化意识,掌握常见的化归、转化方法。
如:等积转化,立体几何问题向平面问题转化等,复习本章时还要注意加强阅读能力、理解能力的训练。
另外还要注意识图、理解图、应用图的能力的长期培养,做题时多画、多看、多想,在训练中,还应变换图形的位置角度,克服“标准图”带来的思维定势,真正树立空间观念。
典例剖析1.三视图与直观图例1、已知某线段的正视图、俯视图、侧视图对应线段长度分别为2,4,4,试求此线段的长度。
【分析】能正确画出对应线段的三视图是解决此题的关键。
【点评】能够把三视图的投影面移到对应的空间几何体上是画三视图的一种有效方法。
例2.如图是一个几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是()Aπ334 B π63 Cπ21D π33 【答案】B【点评】本题考查了三视图的知识,解决本题的关键是由三视图明确是怎样的一个几何体,同时要熟记圆锥的体积公式。
2.几何体表面积、体积的计算例3三棱柱111C B A ABC -中,若E 、F 分别为AB 、AC 的中点,平面11C EB 将三棱柱分成体积为21,V V 的两部分,那么21:V V =________.【答案】7:5【解析】设三棱柱的高为h ,上下底的面积为S ,体积为V , 则Sh V V V =+=21,因为E 、F 分别为AB 、AC 的中点, 所以Sh S S S S h V S S AEF 127)4141(31,411=⋅++=∆=,Sh V Sh V 12512=-=,所以21:V V =7:5. 【点评】解题的关键是棱柱、棱台间的转化关系,建立起求解体积的几何元素之间的对应关系,最后用统一的量建立比值得到结论即可.例4.如图(1)所示,一只装了水的密封瓶子,其内部可以看成是由半径为1cm 和半径为3cm 的两个圆柱组成的简单几何体.当这个几何体如图(2)水平放置时,液面高度为20cm ,当这个几何体如图(3)水平放置时,液面高度为28cm ,则这个简单几何体的总高度为( ) ( ) A .29cm B .30cm C .32cm D .48cm【分析】求解本题抓住解题关键:无论如何放置,水的体积是不变的。
根据这点结合体积公式就可以求解。
【答案】A3.考查空间几何体与线、面关系得交汇例5:两个相同的正四棱锥底面重合组成一个八面体,可放于棱长为1的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上,把满足上述条件的八面体称为正方体的“正子体”. (1)若正子体的六个顶点分别是正方体各面的中心,求异面直线DE 与CF 所成的角;(2)问此正子体的体积V 是否为定值?若是,求出该定值;若不是,求出体积大小的取值范围.【解题思路】求异面直线所成角一般通过平移转化为平面角解决,或利用向量法也是求解这类问题的重要方法,可以使问题转化为代数运算解决。
第二问通过设出边长,可以列出关于体积的目标函数,最终转化为二次函数来解决。
21)21(2)1(2222+-=-+=x x x AD 故]1,21[2∈=AD S ABCD]31,61[3122131231∈=⋅⋅⋅=⋅⋅⋅=ABCD ABCD ABCD S S h S V【点评】本题考查了组合问题,这类问题一般涉及两类几何体组合在一起,由于组合体能考查学生更多的几何体知识,能够更好考查空间想象能力,符合大纲能力要求的“空间考查能力”,组合体已成为近几年高考命题的新热点。
需要抓住组合体之间的联系,把空间问题转化为平面问题解决是处理空间几何问题常见的方法。
【创新题求解方法】一.公式法例1(2018•新课标Ⅰ)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A.122πB.12π C.82πD.10π【分析】利用圆柱的截面是面积为8的正方形,求出圆柱的底面直径与高,然后求解圆柱的表面积.【答案】B【点评】本题考查圆柱的表面积的求法,考查圆柱的结构特征,截面的性质,解决本题的关键是求得圆柱的底面半径和高。
再利用公式求得表面积。
二.等体积法等积变换法:①相同的几何体的体积相等:同一个几何体可以用不同的面做底(注意:三棱锥的任一个面可作为三棱锥的底面);液状物体的形状改变体积不变(比如:水在容器中形状可以多变),②等底面积等高的两个同类几何体的体积相等,体积相等的两个几何体叫做等积体。
例2(2018•南京建邺区一模)如图,直三棱柱ABC﹣A1B1C1的各条棱长均为2,D为棱B1C1上任意一点,则三棱锥D﹣A1BC的体积是.【分析】由已知可得三棱柱ABC ﹣A 1B 1C 1为正三棱柱,分别求出三角形BCD 的面积及A 1 到平面BCC 1B 1的距离,再由等积法得答案.【答案】233【解析】如图,由题意可知,三棱柱ABC ﹣A 1B 1C 1为正三棱柱. 如图,D 为棱B 1C 1上任意一点,则1222,2BCD S =⨯⨯=V . A 1 到平面BCC 1B 1 的距离d=3.∴11123233D A BC A BCD V V --==⨯⨯=. 故答案为:23. 【点评】本题考查棱柱的结构特征,考查利用等积法求多面体的体积,本题就是根据变换底面和高来证明相关的等量关系的.在三棱锥中,用换底面(同时也换高)的方法,常常能把复杂问题简单化、直观化. 三割补法例3(2018•安徽模拟)如图1所示是一种生活中常见的容器,其结构如图2,其中ABCD 是矩形,ABFE 和CDEF 都是等腰梯形,且AD ⊥平面CDEF ,现测得AB=20cm ,AD=15cm ,EF=30cm ,AB 与EF 间的距离为25cm ,则几何体EF ﹣ABCD 的体积为 cm 3.【分析】所求几何体是非规则几何体,把几何体的体积分解为三棱锥A ﹣DCE ,A ﹣EFC 与B ﹣AFC 的体积,然后利用等积法求解.【答案】3500∴几何体EF﹣ABCD的体积为V EF﹣ABCD=V A﹣DCE+V A﹣EFC+V B﹣AFC=1000+1500+1000=3500cm3.故答案为:3500.【点评】本题考查利用等积法求多面体的体积,考查割补法在求解不规则几何体中的巧妙运用。
四构造法例4如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC 向上折起,使A、B重合于点P,则P﹣DCE三棱锥的外接球的体积为()A.327B6C6D6【答案】C【点评】通过构造长方体或正方体,使得分散问题集中在一个特殊的空间几何体中,使得所求问题直观化、简单化。
【创新测试题】 一.选择题1.将边长是2的正方形以其一边所在直线为旋转轴绕转一周,所得几何体的侧面积( ). A. 2π B. 8π C. 4π D. 6π 【答案】B【解析】边长是2的正方形,绕其一边旋转一周得到的几何体是圆柱,则所得几何体的侧面积是2228.ππ⨯⨯=2.一个球的表面积是16π,那么这个球的体积为( ) A.316π B. 332πC. π16D. π24 【答案】B【解析】一个球的表面积是16π,所以球的半径为:2;那么这个球的体积为:=⨯3234π332π。
