七年级数学上有理数有理数教案华东师大版
七年级上册第第2章有理数精典教学案华东师大版初中数学

七年级上册教案
教师:
班级:
2013.9
第一节认识负数预设课时:3 实际完成课时:
第二节有理数的分类预设课时:3 实际完成课时:
第三节数轴预设课时:3 实际完成课时:
下列图形中不是数轴的是()
下面正确的是()
第四节相反数预设课时:3 实际完成课时:
第五节绝对值预设课时:3 实际完成课时:
第六节有理数大小的比较预设课时:3 实际完成课时:
第七节有理数的加法1
预设课时:3 实际完成课时:
3)如果小丽第一秒向西走5米,第二秒原地不动,两秒后这个人从起点向东运动了
第七节有理数的加法2 预设课时:3 实际完成课时:
第八节有理数的减法预设课时:3 实际完成课时:
第九节有理数的加减混合运算预设课时:3 实际完成课时:
第十节有理数的乘法预设课时:3 实际完成课时:
第十一节有理数的除法预设课时:3 实际完成课时:
第十二节有理数的乘方预设课时:3 实际完成课时:
第十三节科学记数法、近似数和有效数字预设课时:3 实际完成课时:
千米,用科学记数法表示(保留
C
由四舍五入取得的近似数,它精确到(
C D、十亿位
第十四节有理数的混合运算预设课时:3 实际完成课时:。
初中数学华师大版七年级上册《2.1.2有理数》教案
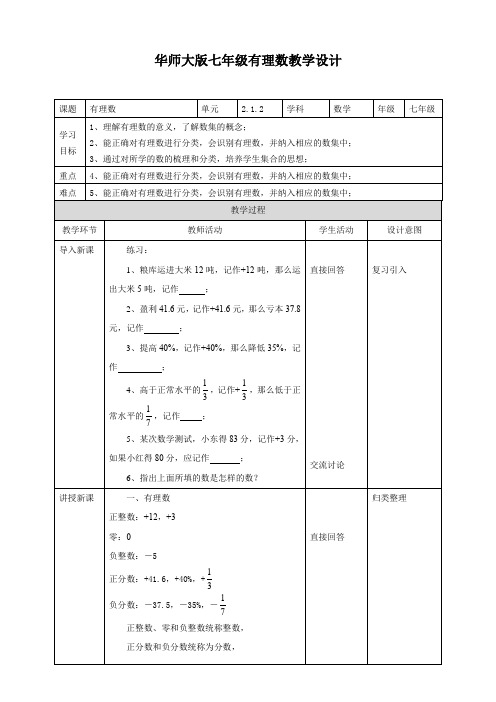
华师大版七年级有理数教学设计(5)自然数集:所有正整数与零组成的数集叫做非负数集,即自然数集。
(6)非正数集,非零数集,非负数集。
四、例题例1、把下列各数填入表示所在的数集的圈里:-18,227,3.1416,0,2012,-35,-0.142857,95%.分析:1、正数集中有哪些数?2、负数集中有哪些数?3、整数集中有哪些数?4、有理数集中有哪些数?解:例2、下面两个圈分别表示负数集和分数集,请找出9个数填入这两个圈中,使其中每个圈中正好有6个数,你能说出这两个圈重叠部分表示什么数的集合吗?分析:1、负数集里有哪些数?2、分数集中有哪些数?3、重叠部分表示什么数?解:例3、分别观察下面各题中依次排列的一些数,猜测它们的排列各有什么规律?请按你猜测的规律,接着写出后面的3个数。
你能分别说出各题排列的数中第2018个数是什么吗?第2019个数呢?(1)-1,2,-3,4,-5,6,,,,(2)12342345--,,,,,,,…分析:1、正负数的排列规律是什么?2、数字的排列规律是什么?解:(1)-7,8,-9第2018个数是2018,第2019个数是-2019.(2)567 678-,,第2018个数是20182019-,第2019个数是20192020;五、练习:1、下列各数:5%,-0.75,123-,0,-25%,18,-67,1113,3.14,负数有:;分数有:;非负数有:;负分数有:;正整数有:;2、下面两个圈分别表示负数集和整数集,请找出9个数填入这两个圈中,使其中每个圈中正好有6个数,你能说出这两个圈重叠部分表示什么数的集合吗?3、观察下面一列数:-1,2,-3,4,…,将这列数排列成下列形式:-12 -3 4-5 6 -7 8 -910 -11 12 -13 14 -15 16…按照上述规律排下去,第5行从左边起第4个数是;第6行从右边起第4个数是;第10行从左边起第9个数是;-51排在第行从左边起第个数。
华东师大版七年级数学上册《有理数》教案(精品教学设计)

a《有理数》教案目标预设一.知识与能力:1.能把给出的有理数按要求分类.2.了解数0在有理数分类中的应用.二.过程与方法:经历从实际中抽出数学模型,从数形结合两个侧面理解问题,并能选择处理数学信息,做出大胆猜测.三.情感态度与价值观:体会数学知识,以现实世界的联系,体现数学充满着探索性.重点和难点有理数的分类方法.教学准备温度计.预习导学1.观察下面依次排列的一列数,它的排列有什么规律?请接着写出后面的3个数,你能写出第2002个数是什么吗?①﹣1,1,﹣1,1,﹣1,1,﹣1,,,,…②2,﹣4,﹣6,8,10,﹣12,﹣14,16, , , ,…2.甲乙两人同时从A 地出发,如果甲向南走48m 记作+48m ,则乙向北走32m 记作 ;这时甲、乙两人相距 m .教学过程一.创设情景,谈话导入.1.教师问:你所知道的数可以分成哪些种类?你是按照什么划分的?2.0.1、﹣0.5、5.32、﹣150.25等为什么被划为分数?我们学过的小数都是分数吗?二.精讲点拨,质疑问难.1.给出新的整数,分数的概念:引进负数后,数的范围扩大了.整数包括:正整数,负整数和零.同样分数包括:正分数,负分数.即:整数——⎪⎩⎪⎨⎧负整数 零 正整数 分数——⎩⎨⎧负分数 正分数 2.给出有理数概念:整数与分数统称为有理数.即有理数⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数也可分为有理数⎪⎩⎪⎨⎧负有理数零正有理数 3.正数和零统称为非负数 和 统称为非正数.4.有理数都可表示成b a的形式.三.课堂活动,强化训练.1.下列各数是正数还是负数,整数还是分数? ﹣5,8,8.4,﹣81,02.将下列各数填入表示集合的在括号里.﹣5,0.3,43,﹣21,8848,﹣392,0,﹣231,213.4 正整数集合:{ }. 负数集合:{ }. 整数集合:{ }. 分数集合:{ }.3.学生练习.把有理数6.4,﹣9,32,+10,﹣43,﹣0.021,﹣1,731,﹣8.5,25,﹣10按两种标准分类.。
七年级数学上册 第2章 有理数2.6 有理数的加法(有理数加法的运算律)教案 (新版)华东师大版-(

【基本目标】【知识与能力】经历探索有理数加法运算律过程,理解有理数加法运算律,能熟练运用运算律简化运算,提倡算法的多样化.【过程与方法】在具体情境中探索运算律,并提倡算法的多样化,对复杂问题能探索解决问题的有效方法,并试图寻找其它途径,并解释其合理性.【情感、态度、价值观】重视过程对中学生的归纳,概括,描述,交流等能力的考察.【教学重点】合理运用运算律简化运算.【教学难点】理解运算律在实际问题中的应用.一、情境导入,激发兴趣1.有理数加法的法则是什么?在进行有理数加法运算时要注意什么?2.小学我们学过哪些加法的运算律?那么,引入负数后,这些运算律在有理数X围内还成立吗?【教学说明】让学生回顾加法运算法则,为后面的学习奠定基础.通过提问,引起学生的思考,引入本节课的学习内容.二、合作探究,探索新知1.请在下列图案内任意填入一个有理数,要求相同的图案内填相同的数(至少有一个是负数).算出各算式的结果,比较左、右两边算式的结果是否相同.(1)△+□和□+△(2)(△+□)+○和△+(□+○)【教学说明】让学生自主探究,激发学生探究的兴趣,提醒学生注意观察运算的结果,思考其中的规律.2.请同学们说说自己的结果,你发现了什么?【教学说明】让学生自由发言,学生通过探究,很容易就能得出结论:加法运算律在有理数X围内仍然是成立的.3.归纳总结:有理数的加法仍满足加法交换律和结合律.(1)加法交换律:两个数相加,交换加数的位置,______不变,表示为:a+b=______.(2)加法结合律:三个数相加,先把______相加,或者先把______相加,和不变.表示为:(a+b)+c=a+______.【教学说明】教师根据学生的回答及时进行归纳,形成知识点,加深学生的印象. 三、示例讲解,掌握新知例1 计算:(1) (+26)+(-18)+5+(-16);(2)(-1.75)+1.5+(+7.3)+(-2.25)+(-8.5).例2 10筐苹果,以每筐30kg为准,超过的千克数记作正数,不足的千克数记作负数,记录如下:问这10筐苹果总共重多少千克?【教学说明】先让学生进行观察,确定计算的顺序,比较不同方法的难易性,及时进行总结.四、练习反馈,巩固提高1.在横线上填写运算律名称.(-193)+(-215)+(+193)=(-193)+(+193)+(-215)__________________=[(-193)+(+193)]+(-215)__________________=0+(-215)=-2152.算一算:(1)16+(-25)+24+(-35);(2)(-3.48)+5.33+(-9.52)+(-5.33)+(-3.05);(3) (-325)+(-134)+(-235)+(+234)+(-113).【教学说明】让学生先独立思考,然后可以小组内互相交流,比较哪一种方法最简单,及时进行总结,教师及时点拨和强调.解题策略:(1)把正数和负数分别结合在一起相加;(2)把互为相反数的结合,能凑整的结合.【答案】1.加法交换律,加法结合律2.(1)-20(2)-16.05(3)-5 7 6五、师生互动,课堂小结1.加法的运算律有哪些?2.怎样运用加法的运算律进行简便运算?(1)互为相反数的两个数可以先相加;(2)几个数相加得整数的可以先相加;(3)同分母的分数可以先相加;(4)符号相同的数可以先相加.【教学说明】让学生先在小组内进行交流,形成统一意见,然后再全班进行交流得出结论,教师及时进行归纳和总结.完成本课时对应的练习.本节课主要是运用加法的运算律进行简便运算.在教学中要引导学生先进行观察,确定运算的思路,比较运算的难易性,及时进行总结,形成一定的计算方法.。
七年级数学上册第2章有理数学案(15份)华东师大版8(优秀教案)

华东师大版本七年级数学上册导教案设计:设计时间:审查:履行时间:班次:小组名称:姓名:课型:综合课课题:绝对值学习目标:. 认识绝对值的代数意义和几何意义及绝对值的性质.. 会求一个已知数的绝对值. 会在已知一个数的绝对值条件下求这个数.. 在利用数轴解决有关问题的过程中,学会用数形联合思想解决问题,领会分类进行议论的数学思想,感觉数学的神秘.要点难点:绝对值的代数意义和几何意义一、抽测反应:1、相反数等于它自己的数是,相反数大于它自己的数是,相反数小于它自己的数是。
2、正数的相反数是,负数的相反数是,零的相反数是。
、在数轴上画出表示数与与的点.二、自主学习阅读教材第页的内容,并研究以下问题:1. 计算汽车行驶所耗的汽油时考虑汽车行驶的行程吗?考虑汽车的方向吗?2. 依据你阅读中获得的信息和对绝对值的理解,用自己的语言说出什么叫绝对值.三、沟通展现:正数的绝对值是什么的绝对位是什么?负数的绝对值是什么?说出你的依照互为相反数的两个数的绝对值之间有何关系?. 假如字母表示有理数,则数的绝对值如何表示?. 先填空,你能从中考证什么规律?1()︱︱︱︱︱︱5()︱︱(3)︱︱︱︱︱︱规律:5.化简:()︱(1 )︱21()︱1︱3. 把以下各式的绝对值符号去掉() ︱一 ( ≥);()︱一︱(>).. 已知︱一︱十︱十︱,你能算出十的值吗?8.若︱︱。
则9.绝对值小于 . 的整数有 .绝对值不大于的非负整数有。
四、梳理小结:、绝对值的意义()几何意义:在数轴上表示数的点与原点的距离。
()代数意义(性质):一个正数的绝对值绝对值是它自己; 一个负数的绝对值是它的相反数;a a0零的绝对值是零。
即| a |0 a0a a0、绝对值的一个重要性质:非负性。
即一个数的绝对值不行能是负数。
五、检测达标:. 以下说法,正确的选项是( ). π的相反数是 ..任何有理数的绝对值必是正数是负数.的相反数的绝对值是.. 若︱︱,则是( ),负数正数.负数或.计算:() ︱一︱︱一︱() ︱一︱︱︱ .六、课后反省、这节课我学到了什么?、这节课我的表现().很满意的。
华师大七年级数学有理数教案

华师大七年级数学有理数教案理解有理数的概念,懂得有理数的两种分类方法:会判别一个有理数是整数还是分数,是正数、负数还是零。
一起看看华师大七年级数学有理数教案!欢送查阅!华师大七年级数学有理数教案1一、知识与才能理解有理数的概念,懂得有理数的两种分类方法:会判别一个有理数是整数还是分数,是正数、负数还是零。
二、过程与方法经历对有理数进展分类的探究过程,初步感受分类讨论的思想。
三、情感态度与价值观通过对有理数的学习,体会到数学与现实世界的严密联络。
教学重难点及打破在引入了负数后,本课对所学过的数按照一定的标准进展分类,提出了有理数的概念。
分类是数学中解决问题的常用手段,通过本节课的学习,使学生理解分类的思想并进展简单的分类是数学才能的表达,老师在教学中应引起足够的重视。
关于分类标准与分类结果的关系,分类标准确实定可向学生作适当的浸透,集合的概念比拟抽象,学生真正承受需要很长的过程,本课不宜过多展开。
教学准备用电脑制作动画表达有理数的分类过程。
教学过程四、课堂引入1、我们把小学里学过的数归纳为整数与分数,引进了负数以后,我们学过的数有哪些?将如何归类?2.举例说明现实中具有相反意义的量。
3.假如由A地向南走3千米用3千米表示,那么-5千米表示什么意义?4.举两个例子说明+5与-5的区别。
华师大七年级数学有理数教案2教学目的1.理解代数和的概念,理解有理数加减法可以互相转化,会进展加减混合运算;2. 通过学习一切加减法运算,都可以统一成加法运算,继续浸透数学的转化思想;3.通过加法运算练习,培养学生的运算才能。
教学建议(一)重点、难点分析^p本节课的重点是根据运算法那么和运算律准确迅速地进展,难点是省略加号与括号的代数和的计算.由于减法运算可以转化为加法运算,所以加减混合运算实际上就是有理数的加法运算。
理解运算符号和性质符号之间的关系,把任何一个含有有理数加、减混合运算的算式都看成和式,这是因为有理数加、减混合算式都看成和式,就可灵敏运用加法运算律,简化计算.(二)知识构造(三)教法建议1.通过习题,复习、稳固有理数的加、减运算以及加减混合运算的法那么与技能,讲课前老师要认真总结、分析^p 学生在进展有理数加、减混合运算时常犯的错误,以便在这节课分析^p 习题时,有意识地帮助学生改正.2.关于“去括号法那么”,只要学生理解,并不要求追究所以然.3.任意含加法、减法的算式,都可把运算符号理解为数的性质符号,看成省略加号的和式。
七年级数学第2章有理数2.15用计算器进行计算教案华东师大版

2。
15用计算器进行计算【基本目标】1。
进一步熟练掌握有理数的运算;2。
培养学生运用计算器的能力及正确、熟练地运用计算器解决问题.【教学重点】培养学生的运用计算器的能力及正确、熟练地运用计算器解决问题.【教学难点】培养学生运用计算器的能力及正确、熟练地运用计算器计算有理数的混合运算。
一、情境导入,激发兴趣问题:已知一个圆柱的底面半径长2.32 cm,高为7.06cm,求这个圆柱的体积.我们知道,圆柱的体积=底面积×高.因此,计算这个圆柱的体积就要作一个较复杂的运算:π×2。
322×7.06.这种计算,我们可以利用电子计算器(简称计算器)来完成。
计算器是一种常用的计算工具,利用计算器可以进行许多种复杂的运算.【教学说明】通过一个具体的实际应用的例子引入本节课,让学生自主使用计算器进行计算,提高学生探究的兴趣。
二、示例讲解,掌握新知例1 (1)用计算器求345+21.3。
用计算器进行四则运算,只要按算式的书写顺序按键,输入算式,再按等号键,显示器上就显示出计算结果.解:用计算器求345+21。
3的过程为:键入,显示器显示运算式子345+21.3,再按=,在第二行显示运算结果366。
3,∴345+21。
3=366.3。
(2)用计算器求105。
3—243.【教学说明】这个计算很简单,可以让学生先叙述按键的顺序,再按照顺序计算试一试。
例2 (1)用计算器求31。
2÷(-0。
4)。
解:用计算器求31.2÷(-0.4)的按键顺序是:.显示结果为―78,∴31。
2÷(-0.4)=—78。
注意:①31.2÷(-0.4)不能按成31。
2 ÷-0。
4=,那样计算器会按31.2-0。
4进行计算的.②输入0.4时可以省去小数点前的0,按成。
4。
(2)用计算器求8.2×(—4.3) ÷2。
5.【教学说明】让学生先观察式子的特点,叙述按键的顺序,再按照顺序进行计算,尤其要注意加括号。
华东师大版七年级数学上册2.7有理数的减法优秀教学案例

1.情境导入:通过生活实例,引出有理数减法的问题,激发学生的学习兴趣。
2.讲解示范:运用直观的教学手段,讲解有理数减法的运算方法,让学生清晰地理解减法运算。
3.实践练习:设计丰富的练习题,让学生在实践中掌握有理数减法的运算技巧。
4.总结提升:引导学生总结有理数减法的运算规律,提高他们的数学思维能力。
2.培养学生克服困难的勇气和信心,面对运算问题不轻易放弃。
3.培养学生严谨治学的态度,注意运算过程中的细节,避免错误。
4.通过对有理数减法的学习,使学生认识到数学在生活中的重要性,提高他们的数学应用能力。
三、教学重难点
1.教学重点:理解有理数减法的概念,掌握有理数减法的基本运算方法。
2.教学难点:减去一个负数和加上一个正数的运算理解,以及有理数减法在实际问题中的应用。
3.减法运算的法则:教师讲解减法运算的法则,如借位、退位等,并引导学生总结出减法运算的规律。
(三)学生小组讨论
1.小组合作:教师将学生分成小组,让学生共同讨论有理数减法的运算方法,以及遇到的问题和解决办法。
2.交流分享:各小组派代表分享自己的讨论成果,其他小组成员进行评价和补充。
(四)总结归纳
1.教师引导学生总结有理数减法的运算规律,帮助学生巩固所学知识。
2.提醒注意事项:教师提醒学生在进行有理数减法运算时,要注意运算符号和数据的准确性。
(五)作业小结
1.布置作业:教师布置一些有关有理数减法的练习题,让学生在课后进行巩固练习。
2.作业反馈:教师对学生的作业进行批改,及时给予反馈,帮助学生提高。
五、案例亮点
1.情境导入的生动性:本案例通过生活实例和媒体素材的引入,使学生能够直观地感受到有理数减法在现实生活中的应用,激发了学生的学习兴趣,提高了他们的学习积极性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1.2 有理数
教学目标:
知识与技能:理解有理数的意义;能把给出的有理数按要求分类;了解数0在有理数分类中的作用。
过程与方法:通过本节的学习,培养学生树立分类讨论的观点和能正确地进行分类的能力。
情感态度与价值观:通过联系与发展、对立与统一的思考方法对学生进行辩证唯物主义教育。
教学重点:有理数的分类
教学难点:掌握有理数的两种分类
教材分析:正确进行有理数的分类,可为今后绝对值的学习,有理数大小比较及有理数的运算打下基础。
同时可培养学生对事物进行分类讨论的思想,因此成为本节课的重点。
两种分类是按不同标准划分的,学生很容易混淆,因此成为本节课的难点,本节课是继负数引入后的一节课,它把以前所学的数作了梳理和归纳,使得知识系统化,能培养学生分类讨论的思想。
本节课旨在通过学生观察、思考、探索、总结知识,培养学生的讨论、交流、总结、归纳能力和合作探究意识,树立分类讨论思想。
教学方法:情境教学法、生生互动法
课时安排:一课时
教具:投影仪(电脑)
附板书设计:
2.1.2 有理数
1、 有理数的两种分类:
(1) (2)
教学反思:
本节课通过情境教学导入新课,并且在教学过程中,教师扮演的是组织者、引导者、合作者的角色,学生成为了学习的主人,主动去观察、讨论、交流、总结、归纳,体现了新课程理念,但在整个的教学过程中还缺乏与实际生活的联系,
教师在此方面还须努力挖掘这
方面的素材,让学生真正体会到数学知识来源于生活,又反作用于生活。
整数
正整数 负整数
负分数
有理数 0 有理数
正有理数
负有理数
正整数
正分数
负整数 负分数
零
正分数 分数。
