法向量经典练习题
高三数学利用直线方向向量与平面法向量解决计算问题试题答案及解析

高三数学利用直线方向向量与平面法向量解决计算问题试题答案及解析1.如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2,AB=BC=1,动点P,Q分别在线段C1D,AC上,则线段PQ长度的最小值是().A.B.C.D.【答案】C【解析】建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),C1(0,1,2),设点P的坐标为(0,λ,2λ),λ∈[0,1],点Q的坐标为(1-μ,μ,0),μ∈[0,1],∴PQ==,当且仅当λ=,μ=时,线段PQ的长度取得最小值.2.如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是________.【答案】【解析】以C为坐标原点,CA,CB,CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,A1(1,0,2),B(0,1,0),A(1,0,0),C(0,0,0),则=(-1,1,-2),=(-1,0,0),cos〈,〉===.3.已知正四棱锥P-ABCD的侧棱与底面所成角为60°,M为PA中点,连接DM,则DM与平面PAC所成角的大小是________.【答案】45°【解析】设底面正方形的边长为a,由已知可得正四棱锥的高为a,建立如图所示空间直角坐标系,则平面PAC的法向量为n=(1,0,0),D,A0,-a,0,P,M,=,所以cos 〈,n〉==,所以DM与平面PAC所成角为45°.4.如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点.那么异面直线OE和FD1所成的角的余弦值等于 ().A.B.C.D.【答案】D【解析】建立如图所示的空间直角坐标系,则O(1,1,0),E(0,2,1),D1(0,0,2),F(1,0,0),=(-1,1,1),=(-1,0,2),∴·=3,||=,||=,∴cos〈,〉==.即OE与FD1所成的角的余弦值为.5.在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为________.【答案】【解析】如图,建立空间直角坐标系Dxyz,则D1(0,0,1),C1(0,2,1),A1(1,0,1),B(1,2,0),∴=(0,2,0),设平面A1BC1的一个法向量为n=(x,y,z),由得,令y=1,得n=(2,1,2),设D1C1与平面A1BC1所成角为θ,则sin θ=|cos〈,n〉|===.6.平行四边形中,且以为折线,把折起,使平面平面,连接(1)求证:;(2)求二面角的余弦值.【答案】(1)参考解析;(2)【解析】(1)直线与直线垂直的证明通过转化为证明直线与平面垂直,由于通过翻折为两个垂直的平面所以只需证明直线AB垂直与两个平面的交线BD即可,通过已知条件利用余弦定理即可得到直角.(2)求二面角的问题通常就是建立空间直角坐标系,根据BD与DC垂直来建立.通过写出相应点的坐标,以及相应的平面内的向量,确定两平面的法向量,并求出法向量的夹角,再判断法向量的夹角与二面角的大小是相等还是互补,即可得到结论.试题解析:(1)在中,所以所以,因为平面平面,所以平面,所以;…3分(2)在四面体ABCD中,以D为原点,DB为轴,DC为轴,过D垂直于平面BDC的射线为轴,建立如图的空间直角坐标系.则D(0,0,0),B(,0,0),C(0,1,0),A(,0,1)设平面ABC的法向量为,而由得:取再设平面DAC的法向量为而由得:取所以即二面角B-AC-D的余弦值是【考点】1.线线垂直的判定.2.面面垂直性质.3.二面角的求法.4.空间坐标系的应用.5.法向量的求法.7.如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA和CD所成角等于60°.(1)求证:面PCD⊥面PBD;(2)求直线PC和平面PAD所成角的正弦值的大小;(3)在棱PA上是否存在一点E,使得二面角A-BE-D的余弦值为?若存在,指出点E在棱PA上的位置,若不存在,说明理由.【答案】(1)见解析(2)存在【解析】(1)证明:PB⊥底面ABCD,∴PD⊥CD,又∵CD⊥PD,PD∩PB=P,PD,PB⊂平面PBD.∴CD⊥平面PBD,又CD⊂平面PCD,∴平面PCD⊥平面PBD.(2)如图,以B为原点,BA,BC,BP所在直线分别为x,y,z轴,建立空间直角坐标系,设BC=a,BP=b,则B(0,0,0),A(2,0,0),C(0,a,0),D(2,2,0),P(0,0,b).∵=(2,2,-b),=(2,2-a,0),CD⊥PD,∴·=0,∴4+4-2a=0,a=4,又=(2,0,-b),=(2,-2,0),异面直线PA和CD所成角等于60°,∴=,即=,解得b=2,=(0,4,-2),=(0,2,0),=(2,0,-2).设平面PAD的一个法向量为n1=(x1,y1,z1),则由得取n1=(1,0,1),∵sin θ===,∴直线PC和平面PAD所成角的正弦值为.(3)解假设存在,设=λ,且E(x,y,z),则(x,y,z-2)=λ(2,0,-2),E(2λ,0,2-2λ),设平面DEB的一个法向量为n2=(x2,y2,z2),则由得取n2=(λ-1,1-λ,λ),又平面ABE的法向量n3=(0,1,0),由cos θ==,得=,解得λ=或λ=2(不合题意).∴存在这样的E点,E为棱PA上的靠近A的三等分点.8.如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,O为AC与BD的交点,E为PB上任意一点.(1)证明:平面EAC⊥平面PBD;(2)若PD∥平面EAC,并且二面角B-AE-C的大小为45°,求PD∶AD的值.【答案】(1)见解析(2)∶2【解析】(1)证明因为PD⊥平面ABCD,∴PD⊥AC,又ABCD是菱形,∴BD⊥AC,又BD∩PD=D,故AC⊥平面PBD,又AC⊂平面EAC.所以平面EAC⊥平面PBD.(2)解连接OE,因为PD∥平面EAC,所以PD∥OE,所以OE⊥平面ABCD,又O是BD的中点,故此时E为PB的中点,以点O为坐标原点,射线OA,OB,OE所在直线分别为x,y,z轴,建立空间直角坐标系O-xyz.设OB=m,OE=h,则OA=m,A,B(0,m,0),E(0,0,h),=(-m,m,0),=(0,-m,h),向量n1=(0,1,0)为平面AEC的一个法向量,设平面ABE的一个法向量n2=(x,y,z)则n2·=0,且n2·=0,即-mx+my=0且-my+hz=0.取x=1,则y=,z=,则n2=,∴cos 45°=|cos〈n1,n2〉|===,解得=,故PD∶AD=2h∶2m=h∶m=∶2.9.如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=PD.(1)求证:平面PQC⊥平面DCQ;(2)若二面角Q-BP-C的余弦值为-,求的值.【答案】(1)见解析(2)1【解析】(1)证明:设AD=1,则DQ=,DP=2,又∵PD∥QA,∴∠PDQ=∠AQD=45°,在△DPQ中,由余弦定理可得PQ=.∴DQ2+PQ2=DP2,∴PQ⊥DQ,又∵PD⊥平面ABCD,∴PD⊥DC,∵CD⊥DA,DA∩PD=D,∴CD⊥平面ADPQ.∵PQ⊂平面ADPQ,∴CD⊥PQ,又∵CD∩DQ=D,∴PQ⊥平面DCQ.又PQ⊂平面PQC,所以平面PQC⊥平面DCQ.(2)解如图,以D为坐标原点,DA,DP,DC所在直线为x轴,y轴,z轴,建立空间直角坐标系D-xyz.设AD=1,AB=m(m>0).依题意有D(0,0,0),C(0,0,m),P(0,2,0),Q(1,1,0),B(1,0,m),则=(1,0,0),=(-1,2,-m),=(1,-1,0),设n1=(x1,y1,z1)是平面PBC的法向量,则即因此可取n1=(0,m,2).设n2=(x2,y2,z2)是平面PBQ的法向量,则即可取n2=(m,m,1).又∵二面角Q-BP-C的余弦值为-,∴|cos 〈n1,n2〉|=|-|.∴=,整理得m4+7m2-8=0.又∵m>0,解得m=1.因此,所求的值为110.在等腰梯形ABCD中,AD∥BC,AD=BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).(1)求证:AC⊥平面ABC′;(2)求证:C′N∥平面ADD′;(3)求二面角A-C′N-C的余弦值.【答案】(1)见解析(2)见解析(3)-【解析】(1)证明∵AD=BC,N是BC的中点,∴AD=NC,又AD∥BC,∴四边形ANCD 是平行四边形,∴AN=DC,又∠ABC=60°,∴AB=BN=AD,∴四边形ANCD是菱形,∴∠ACB=∠DCB=30°,∴∠BAC=90°,即AC⊥AB,又平面C′BA⊥平面ABC,平面C′BA∩平面ABC=AB,∴AC⊥平面ABC′.(2)证明:∵AD∥BC,AD′∥BC′,AD∩AD′=A,BC∩BC′=B,∴平面ADD′∥平面BCC′,又C′N⊂平面BCC′,∴C′N∥平面ADD′.(3)解:∵AC⊥平面ABC′,AC′⊥平面ABC.如图建立空间直角坐标系,设AB=1,则B(1,0,0),C(0,,0),C′(0,0,),N,∴′=(-1,0,),′=(0,-,),设平面C′NC的法向量为n=(x,y,z),则即取z=1,则x=,y=1,∴n=(,1,1).∵AC′⊥平面ABC,∴平面C′AN⊥平面ABC,又BD⊥AN,平面C′AN∩平面ABC=AN,∴BD⊥平面C′AN,BD与AN交于点O,O则为AN的中点,O,∴平面C′AN的法向量=.∴cos〈n,〉==,由图形可知二面角A-C′N-C为钝角,所以二面角A-C′N-C的余弦值为-11.如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F且EF=,则下列结论中错误的是 ().A.AC⊥BEB.EF∥平面ABCDC.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值【答案】D【解析】∵AC⊥平面BB1D1D,又BE⊂平面BB1,D1D.∴AC⊥BE,故A正确.∵B1D1∥平面ABCD,又E、F在直线D1B1上运动,∴EF∥平面ABCD,故B正确.C中由于点B到直线B1D1的距离不变,故△BEF的面积为定值,又点A到平面BEF的距离为,故VA-BEF为定值.当点E在D1处,点F为D1B1的中点时,建立空间直角坐标系,如图所示,可得A(1,1,0),B(0,1,0),E(1,0,1),F,∴=(0,-1,1),=,∴·=.又||=,||=,∴cos〈,〉==. ∴此时异面直线AE与BF成30°角.②当点E为D1B1的中点,点F在B1处时,此时E,F(0,1,1),∴=,=(0,0,1),∴·=1,||=,∴cos〈,〉===≠,故选D.12.已知正方体的棱长为,,点N为的中点,则()A.B.C.D.【答案】A【解析】以为原点,分别以所在直线为x轴,y轴,z轴建立空间直角坐标系,则A(0,0,a),N(a,0,),(a,a,0),设M(x,y,z),因为,所以(x-0,y-0,z-a)=(a-x,a-y,0-z)即,解得,即M(,,),所以=,故选A.【考点】空间向量的坐标运算和向量的模.13.如图所示,四棱锥S ABCD的底面是正方形,每条侧棱的长都是底面边长的倍,P为侧棱SD上的点.(1)求证:AC⊥SD;(2)若SD⊥平面PAC,求二面角P AC D的大小;(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.【答案】(1)证明详见解析;(2)30°;(3)存在 SE∶EC=2∶1【解析】(1)设AC交BD于O,以、、分别为S,D,C,x轴、y轴、z轴的正方向,建立空间直角坐标系,则S,D,C,求出,的坐标,并计算得到·=0,从而AC⊥SD.(2)为平面PAC的一个法向量,为平面DAC的一个法向量,向量与的夹角等于二面角P AC D的平面角,根据向量的夹角公式计算出与的夹角即可.(3)假设存在一点E使BE∥平面PAC,设=t(0≤t≤1),则= +=+t,因为·=0,可建立关于t的等式,解之即可.试题解析:(1)证明:连接BD,设AC交BD于O,由题意知SO⊥平面ABCD,以O为坐标原点,、、分别为x轴、y轴、z轴的正方向,建立空间直角坐标系.设底面边长为a,,则高SO= a.于是S,D,C,=,=,·=0,故OC⊥SD,从而AC⊥SD. 4分(2)解:由题设知,平面PAC的一个法向量为=,平面DAC的一个法向量为=,则cos<,>==,故所求二面角的大小为30°. 8分(3)解:在棱SC上存在一点E使BE∥平面PAC.,由(2)知是平面PAC的一个法向量,且=,=, 设=t(0≤t≤1),=+=+t=,而·=0t=,即当SE∶EC=2∶1时,BE∥平面PAC. 12分【考点】1.空间两向量垂直的充要条件;2.二面角;3.直线与平面平行判定.14.如图在四棱锥中,底面是边长为的正方形,侧面底面,且.(1)求证:面平面;(2)求二面角的余弦值.【答案】(1)证明过程详见解析;(2).【解析】本题主要以四棱锥为几何背景考查线面垂直、面面垂直的判定以及二面角的求法,可以运用传统几何法,也可以用空间向量法求解,突出考查空间想象能力和计算能力.第一问,法一,先利用面面垂直的性质判断出,从而平面,所以垂直于面内的任意的线,由,判断是等腰直角三角形,所以且,所以面,利用面面垂直的判定定理得面面垂直,法二,利用空间向量法,通过证明,其它过程与法一相同;第二问,由第一问得到平面的法向量为,而平面的法向量需要计算求出,,所以,最后用夹角公式求夹角余弦值.试题解析:(1)解法一:因为面面平面面为正方形,,平面所以平面∴ 2分又,所以是等腰直角三角形,且,即,,且、面,面又面,∴面面. 6分解法二:如图,取的中点, 连结,.∵, ∴.∵侧面底面,平面平面,∴平面,而分别为的中点,∴,又是正方形,故.∵,∴,.以为原点,向量为轴建立空间直线坐标系,则有,,,,,.∵为的中点, ∴ 2分(1)∵,,∴,∴,从而,又,,∴平面,而平面,∴平面平面. 6分(2)由(1)知平面的法向量为,设平面的法向量为,∵,∴由,,可得取,则故.∴,即二面角的余弦值为, 12分【考点】1.线面垂直;2.空间向量法;3.面面垂直;4.夹角公式.15.斜三棱柱,其中向量,三个向量之间的夹角均为,点分别在上且,=4,如图(Ⅰ)把向量用向量表示出来,并求;(Ⅱ)把向量用表示;(Ⅲ)求与所成角的余弦值.【答案】(Ⅰ),;(Ⅱ);(Ⅲ)与所成的角的余弦值.【解析】(Ⅰ)把向量用向量表示出来,像这一类题,先找以A为始点,以M为终点的封闭图形,因为向量是用向量表示出来,而,可在平面找,然后转化为与共线的向量,可求得,求,求向量的模,往往转化为模的平方来解,由,故,利用数量积展开,由,之间的夹角均为,可求得的值;(Ⅱ)把向量用表示,和(Ⅰ)解题思想一样,只是他在空间中找;(Ⅲ)求与所成角的余弦值,利用,分别求出,即可.试题解析:(Ⅰ),所以,因为,所以(Ⅱ),(Ⅲ),,,COS=即为与所成的角的余弦值.【考点】向量加法与减法的几何意义,向量的夹角.16.已知:四棱锥P—ABCD的底面为直角梯形,且AB∥CD,∠DAB=90o,DC=2AD=2AB,侧面PAD与底面垂直,PA=PD,点M为侧棱PC上一点.(1)若PA=AD,求PB与平面PAD的所成角大小;(2)问多大时,AM⊥平面PDB可能成立?【答案】(1)(2)AM⊥平面PDB不可能成立.【解析】解:(1)以AD中点O为坐标原点,建立如图所示空间直角坐标系,设AB=2则 2分平面PAD的法向量就是4分设所求夹角为,则 5分(2)设, 7分若AM⊥平面PDB,则 8分得不可能同时成立,AM⊥平面PDB不可能成立. 10分【考点】空间中垂直问题以及线面角点评:主要是考查了线面角的求解,以及线面垂直的证明,属于中档题。
求法向量的练习题

求法向量的作业化考试-----2014-11-28 一、选择题(每小题6分,共24分)1、m ={8,3,a },n ={2b ,6,5},若m ∥n ,则a +b 的值为( ) A.0B.25C.221 D.82、已知()()()2,5,1,2,2,4,1,4,1A B C ---,则向量AB AC u u u r u u u r与的夹角为( )A. 030 B.045 C.060 D.0903、已知a =(2,-1,3),b =(-1,4,-2),c =(7,5,λ),若a ,b ,c 共面,则实数λ等于( )A.627B.637C.607D.6574.如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为( )A.6 B.552 C.15 D.10二、解答题(每小题15分,共计75分) 1.如图,已知正四棱柱ABCD -A 1B 1C 1D 1的棱长AA 1=2,AB=1,按图中所建立的坐标系,求平面BDC 1,平面A 1BC 1,平面ABC 1D 1的法向量。
2如图,在长方体1111ABCD A B C D -中,E 、F 分别是棱BC ,1CC 上的点,2CF AB CE ==,1::1:2:4AB AD AA =(1) 求异面直线EF 与1A D 所成角的余弦值; (2) 求平面1A ED 、1A ED F --的法向量。
3.如图,已知棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 是A 1B 1的中点,求平面ABC 1D 1的法向量。
4.已知棱长为1的正方体ABCD -A 1B 1C 1D 1,求平面A 1BC 1、 平面ABCD 的法向量。
A 1B 1C 1D 1 AB C Dx y zy xD 1A 1D B 1C 1C BA FED 1C 1B 1A 1DCBAozyE z D 1 yA C 1B 1A 1BD C。
空间的法向量测试题

空间的法向量测试题1. 已知平面α,β的法向量分别为a ⃗ =(2,3,λ),b ⃗ =(4,μ,−2)(其中λ,μ∈R),若α//β,则λ+μ的值为( )A. −52B. −5C. 52D. 52. 平面α的法向量u ⃗ =(2,−2,2),平面β的法向量v ⃗ =(1,2,1),则下列命题正确的是( )A. α,β平行B. α,β垂直C. α,β重合D. α,β不垂直3. 若两个向量AB ⃗⃗⃗⃗⃗ =(1,2,3),AC⃗⃗⃗⃗⃗ =(3,2,1),则平面ABC 的一个法向量为( ) A. (−1,2,−1) B. (1,2,1) C. (1,2,−1) D. (−1,2,1)4. 若直线l 的方向向量a ⃗ =(1,2,−1),平面α的一个法向量m ⃗⃗⃗ =(−2,−4,k),若l ⊥α,则实数k =( )A. 2B. −10C. −2D. 10 5. 若直线l 的方向向量为(2,1,m),平面α的法向量为(1,12,2),且l ⊥α,则m =( )A. 2B. 3C. 4D. 5 6. 已知v 1⃗⃗⃗⃗ ,v 2⃗⃗⃗⃗ 分别为直线l 1,l 2的方向向量(l 1,l 2不重合),n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ 分别为平面α,β的法向量(α,β不重合),则下列说法中,正确的是( )A. v 1⃗⃗⃗⃗ //v 2⃗⃗⃗⃗ ⇔l 1//l 2 B. v 1⃗⃗⃗⃗ ⊥v 2⃗⃗⃗⃗ ⇔l 1⊥l 2 C. n 1⃗⃗⃗⃗ //n 2⃗⃗⃗⃗ ⇔α//βD. n 1⃗⃗⃗⃗ ⊥n 2⃗⃗⃗⃗ ⇔α⊥β7. 以下命题正确的是( )A. 直线l 的方向向量为a⃗ =(1,−1,2),直线m 的方向向量b ⃗ =(2,1,−12),则l 与m 垂直;B. 直线l 的方向向量a⃗ =(0,1,−1),平面α的法向量n ⃗ =(1,−1,−1),则l ⊥α; C. 平面α,β的法向量分别为n 1⃗⃗⃗⃗ =(0,1,3),n 2⃗⃗⃗⃗ =(1,0,2),则α//β;D. 平面α经过三点A (1,0,−1),B (0,1,0),C (−1,2,0),向量n⃗ =(1,u,t)是平面α的法向量,则u +t =1.8. 已知直线l 的一个方向向量d⃗ =(2,3,5),平面α的一个法向量u ⃗ =(−4,m,n),若l ⊥α,则m +n =______.9. 设u⃗ =(−2,2,t),v ⃗ =(6,−4,5)分别是平面α,β的法向量,若α⊥β,则实数t 的值是______.10. 设μ⃗ =(−1,2,t),v ⃗ =(1,−4,3)分别是平面α,β的法向量,若α⊥β,则实数t 的值为 .答案和解析1. 解:∵平面α,β的法向量分别为a ⃗ =(2,3,λ),b ⃗ =(4,μ,−2)(其中λ,μ∈R),α//β, ∴a ⃗ //b ⃗ ,即有24=3μ=λ−2,解得μ=6,λ=−1,∴λ+μ=−1+6=5.故选:D .2.解:平面α的法向量u ⃗ =(2,−2,2),平面β的法向量v ⃗ =(1,2,1),因为u ⃗ ⋅v ⃗ =2−4+2=0,所以两个平面垂直.故选:B .3.解:两个向量AB⃗⃗⃗⃗⃗ =(1,2,3),AC ⃗⃗⃗⃗⃗ =(3,2,1),设平面ABC 的一个法向量n ⃗ =(x,y ,z), 则{n ⃗ ⋅AB ⃗⃗⃗⃗⃗ =x +2y +3z =0n⃗ ⋅AC ⃗⃗⃗⃗⃗ =3x +2y +z =0,取x =−1,得平面ABC 的一个法向量为(−1,2,−1). 故选:A .4.解:∵直线l 的方向向量a⃗ =(1,2,−1),平面α的一个法向量m ⃗⃗⃗ =(−2,−4,k),l ⊥α, ∴α⃗ //m ⃗⃗⃗ ,∴1−2=2−4=−1k ,解得k =2.故选A .5.解:因为直线l 的方向向量为(2,1,m),平面α的法向量为(1,12,2),且l ⊥α,所以存在实数λ,使得(2,1,m)=λ(1,12,2),所以{2=λ1=12λm =2λ,解得λ=2,m =4.故选C .6.解:∵v 1⃗⃗⃗⃗ ,v 2⃗⃗⃗⃗ 分别为直线l 1,l 2的方向向量(l 1,l 2不重合),∴v 1⃗⃗⃗⃗ //v 2⃗⃗⃗⃗ ⇔l 1//l 2,v 1⃗⃗⃗⃗ ⊥v 2⃗⃗⃗⃗ ⇔l 1⊥l 2;∵n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ 分别为平面α,β的法向量(α,β不重合),∴n 1⃗⃗⃗⃗ //n 2⃗⃗⃗⃗ ⇔α//β,n 1⃗⃗⃗⃗ ⊥n 2⃗⃗⃗⃗ ⇔α⊥β,故答案为ABCD .7.解:选项A ∵a⃗ =(1,−1,2),b ⃗ =(2,1,−12),∴a ⃗ ·b ⃗ =1×2−1×1+2×(−12)=0, ∴a ⃗ ⊥b ⃗ ,∴直线l 与m 垂直,A 正确;选项B :a⃗ =(0,1,−1),n ⃗ =(1,−1,−1),∴a ⃗ ·n ⃗ =0×1+1×(−1)+(−1)×(−1)=0, ∴a ⃗ ⊥n ⃗ ,∴l//α或l ⊂α,B 错误;选项C :∵n 1⃗⃗⃗⃗ =(0,1,3),n 2⃗⃗⃗⃗ =(1,0,2),∴n 1⃗⃗⃗⃗ ·n 2⃗⃗⃗⃗ =0×1+1×0+3×2=6≠0, ∴α⊥β不成立,C 错误;选项D :∵点A(1,0,−1),B(0,1,0),C(−1,2,0),∴AB ⃗⃗⃗⃗⃗ =(−1,1,1),BC ⃗⃗⃗⃗⃗ =(−1,1,0),向量n⃗ =(1,u,t)是平面α的法向量, ∴{n ⃗ ·AB ⃗⃗⃗⃗⃗ =0n ⃗ ·BC ⃗⃗⃗⃗⃗ =0,即{−1+μ+t =0−1+μ=0,则μ+t =1,D 正确.故选AD . 8.解:因为直线l 的一个方向向量d⃗ =(2,3,5),平面α的一个法向量u ⃗ =(−4,m,n),l ⊥α,则有d ⃗ =(2,3,5)和u ⃗ =(−4,m,n)平行,故有−42=m 3=n 5,解之得m =−6,n =−10,则m +n =−16.故答案为−16.9.解:∵u⃗=(−2,2,t),v⃗=(6,−4,5)分别是平面α,β的法向量,α⊥β,∴μ⃗⋅v⃗=−12−8+5t=0,解得t=4.故答案为:4.10.解:因为μ⃗=(−1,2,t),v⃗=(1,−4,3)分别是平面α,β的法向量,α⊥β,所以μ⃗⊥v⃗,所以μ⃗·ν⃗=0,得:(−1)×1+2×(−4)+t×3=0,解得t=3.故答案为3.。
法向量的题目

1、已知平面α内有一个三角形ABC,其顶点A, B, C的坐标分别为(1,2,0), (2,3,1), (3,4,3),求平面α的一个法向量n可以是:A. (1,1,-1)B. (1,-1,1)C. (-1,1,1)D. (1,1,1)(答案:C)2、设平面π通过三点A(1,0,-1), B(0,1,0), C(-1,2,0),则平面π的一个法向量是:A. (1,1,1)B. (1,-1,-1)C. (-1,1,-1)D. (1,-2,1)(答案:A)3、给定平面方程2x - y + 3z = 6,则该平面的一个法向量为:A. (2,-1,3)B. (2,1,-3)C. (-2,1,3)D. (2,1,3)(答案:D)4、若直线l的方向向量为(1,2,-3),且直线l在平面α内,平面α内另有一点P(1,-1,2),则平面α内不可能与直线l垂直的向量是:A. (-6,3,2)B. (3,-6,-2)C. (2,-1,1)D. (-1,2,3)(答案:C)5、已知平面β由点A(1,2,3), B(4,5,6), C(7,8,9)确定,则下列向量中,不可能是平面β的法向量的是:A. (-1,-1,-1)B. (1,1,1)C. (1,-2,1)D. (-1,1,-1)(答案:C)6、设平面γ通过原点及两点M(1,2,3), N(4,5,6),则平面γ的一个法向量可以是:A. (1,1,1)B. (1,-1,1)C. (-1,1,1)D. (1,1,-1)(答案:A)7、已知平面δ的法向量为n=(a,b,c),且向量m=(1,2,3)在平面δ上,若n与m的点积为4,则下列哪组(a,b,c)可能是n的坐标?A. (1,1,1)B. (-1,-1,-1)C. (1,-1,1)D. (-1,2,-1)(答案:D)8、给定三个点A(1,2,3), B(4,5,6), C(7,8,10),若平面ε经过这三点,则下列向量中哪一个不可能是平面ε的法向量?A. (1,-2,1)B. (-1,1,-1)C. (1,1,-1)D. (3,-3,3)(答案:A)。
高三数学利用直线方向向量与平面法向量解决证明问题试题

高三数学利用直线方向向量与平面法向量解决证明问题试题1.已知直线的法向量为,则该直线的倾斜角为.(用反三角函数值表示)【答案】【解析】直线法向量为,则其斜率为,倾斜角为.【考点】直线的法向量与斜率.2.如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.(1)求证:A1B∥平面ADC1;(2)若AB=BB1=2,求A1D与平面AC1D所成角的正弦值.【答案】(1)见解析(2)【解析】(1)证明:因为三棱柱ABC-A1B1C1是直三棱柱,所以四边形A1ACC1是矩形.连接A1C交AC1于O,则O是A1C的中点,又D是BC的中点,所以在△ADC1中,OD∥A1B,因为A1B⊄平面ADC1,OD⊂平面ADC1,所以A1B∥平面ADC1.(2)解:因为△ABC是等边三角形,D是BC的中点,所以AD⊥BC.以D为原点,建立如图所示空间坐标系D-xyz.由已知AB=BB1=2,得D(0,0,0),A(,0,0),A1(,0,2),C1(0,-1,2).则=(,0,0),=(0,-1,2),设平面AC1D的法向量为n=(x,y,z),由得取z=1,则x=0,y=2,∴n=(0,2,1),又=(,0,2),∴cos〈,n〉==,设A1D与平面ADC1所成角为θ,则sin θ=|cos〈,n〉|=,故A1D与平面ADC1所成角的正弦值为.3.已知等差数列的前n项和为,且,则过点和的直线的一个方向向量的坐标可以是()A.B.(2,4)C.D.(-1,-1)【答案】A【解析】直线的斜率.又,所以它的一个方向向量可以为,与它共线,故选A.【考点】1、等差数列;2、直线的方向向量.4.如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC 上,PC⊥平面BDE.(1) 证明:BD⊥平面PAC;(2) 若PA=1,AD=2,求二面角B-PC-A的正切值.【答案】(1)见解析;(2).【解析】(1)先利用直线与平面垂直的性质定理,得到和,因为,所以利用直线与平面垂直的判定定理可知,;(2)首先分别以射线,,为轴,轴,轴的正半轴建立空间直角坐标系,由直线与平面垂直的性质定理得到,那么矩形为正方形,由此可知此正方形的边的长度,根据坐标系表示四棱锥出各个顶点的坐标,分别求出平面和平面的法向量的坐标,根据二面角与其法向量夹角的关系,求得二面角的余弦值,再由同角三角函数的基本关系得到所求二面角的正切值.试题解析:(1)证明∵,,∴.2分同理由,可证得.又,∴. 4分(2)如图,分别以射线,,为轴,轴,轴的正半轴建立空间直角坐标系.由(1)知,又,∴.故矩形为正方形,∴. 6分∴.∴.设平面的一个法向量为,则,即,∴,取,得.∵,∴为平面的一个法向量.10分所以. 11分设二面角的平面角为,由图知,,所以.∴所以,即二面角的正切值为. 12分【考点】1.直线与平面垂直的判定定理;2.直线与平面垂直的性质定理;3.平面和平面所成的角(二面角);4.勾股定理;5.同角三角函数的基本关系;6.平面的法向量5.在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥面ABC,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且.(Ⅰ)求证:EF∥平面BDC1;(Ⅱ)求二面角E-BC1-D的余弦值.【答案】(1)要证明线面平行,则先证明EF∥A1O,然后利用下面平行的判定定理来得到。
12级高二数学法向量的应用练习题
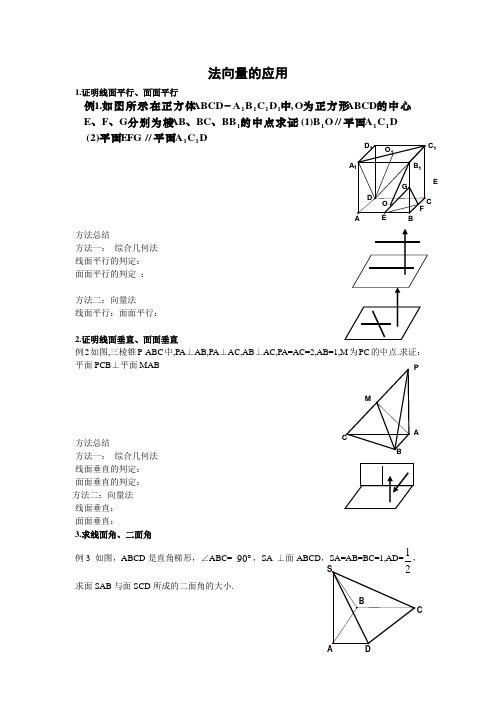
法向量的应用1.证明线面平行、面面平行方法总结方法一: 综合几何法 线面平行的判定: 面面平行的判定 :方法二:向量法线面平行:面面平行:2.证明线面垂直、面面垂直例2如图,三棱锥P-ABC 中,PA ⊥AB,PA ⊥AC,AB ⊥AC,PA=AC=2,AB=1,M 为PC 的中点.求证:平面PCB ⊥平面MAB方法总结方法一: 综合几何法 线面垂直的判定: 面面垂直的判定: 方法二:向量法 线面垂直: 面面垂直:3.求线面角、二面角例3 如图,ABCD 是直角梯形,∠ABC= ︒90,SA ⊥面ABCD ,SA=AB=BC=1,AD=1,求面SAB 与面SCD 所成的二面角的大小.D C A //EFG )2( D C A //O B )1(:BB BC AB G FE ,ABCD O ,D C B A ABCD ,.11111111111平面平面平面的中点求证、、分别为棱、、的中心为正方形中在正方体如图所示例-E A C 1AP方法总结方法一: 综合几何法方法二:向量法4.求点到面的距离例4.已知正四棱柱1111D C B A ABCD -中,AB=1,1AA =2,E 为1CC 中点. 求点1D 到平面BDE 的距离.方法总结方法一: 综合几何法方法二:向量法5.综合应用(备选)三、巩固练习 1、 在棱长AB=AD=2,1AA =3的长方体中,点E 是平面11B BCC 上的动点,点F 是CD 的中点。
(1)确定E 的位置,使F AB E D 11平面⊥(2)求二面角B AF B --1的大小。
2、 在三棱锥S-ABC 中,△ABC 是边长为4的正三角形。
平面SAC ⊥平面ABC ,SA=SC=32,M 、N 分别为AB 、SB 的中点。
(1)证明:AC ⊥SB (2)求二面角N-CM-B 的大小(3)求点B 到平面CMN 的距离。
EA C 1.Q MN P )2()3(PA 33PBA PC )2(PAD PMN )1(:.Q PD MQ BC AD N M .ABC D PA 2ABC D P .5的余弦值的条件下求二面角在的长;,求所成角的正弦值为与平面直线;平面平面求证于的中点,、分别为、底面的正方形,侧棱,底面是边长为如图四棱锥例--⊥⊥⊥-。
高中数学322平面的法向量与平面的向量表示同步练习选修21
3.2.2平面的法向量与平面的向量表示一、选择题1.下列命题中正确的是( )A .如果一条直线与平面的一条斜线在这个平面内的射影垂直,则它也和这条斜线垂直B .如果一条直线与平面的一条斜线垂直,则它与斜线在平面上的射影垂直C .如果一向量和斜线在平面内的射影垂直,则它垂直于这条斜线D .如果一非零向量和一平面平行,且和一条斜线垂直,则它垂直于斜线在平面内的射影[答案] D[解析] 由三垂线定理知D 成立.2.在正方体ABCD —A 1B 1C 1D 1中,平面ACB 1的一个法向量为( ) A.BD 1→B.DB →C.BA 1→D.BB 1→[答案] A3.点A (a,0,0),B (0,b,0),C (0,0,c ),则平面ABC 的一个法向量为( ) A .(bc ,ac ,ab ) B .(ac ,ab ,bc ) C .(bc ,ab ,ac )D .(ab ,ac ,bc )[答案] A[解析] 设法向量为n =(x ,y ,z ),则AB ·n =0,AC →·n =0,则⎩⎨⎧-ax +by =0-ax +cz =0∴n =(bc ,ac ,ab ).故选A.4.在正方体ABCD -A 1B 1C 1D 1中,若E 为A 1C 1的中点,则直线CE 垂直于( ) A .AC B .BD C .A 1DD .A 1A[答案] B[解析] 直线CE 在平面AC 内的射影为AC , 又AC ⊥BD ,∴BD ⊥CE ,故选B.5.正方体AC 1中,E ,F 分别是AB ,CD 的中点,则下列直线中不互相垂直的是( ) A .B 1C 与C 1D 1B .D 1B 与B 1CC.D1B与EF D.A1B与B1C1 [答案] C[解析] D1B与EF所成角等于∠D1BC,其余弦值为33,故选C.6.若平面α、β的法向量分别为u=(-2,3,-5),v=(3,-1,4),则( ) A.α∥βB.α⊥βC.α、β相交但不垂直D.以上均不正确[答案] C[解析] ∵u=(-2,3,-5),v=(3,-1,4),∴u与v不平行且u与v不垂直,故选C.7.平面α的一个法向量为v1=(1,2,1),平面β的一个法向量v2=-(2,4,2),则平面α与平面β( )A.平行B.垂直C.相交D.不能确定[答案] A[解析] 由v1∥v2故可判定α∥β.8.设平面α的法向量为(1,2,-2),平面β的法向量(-2,-4,k),若α∥β,则k=( )A.2 B.-4C.4 D.-2[答案] C[解析] ∵α∥β,∴1-2=2-4=-2k,∴k=4,故选C.9.若直线l的方向向量为a=(-1,0,-2),平面α的法向量为u=(4,0,8),则( )A.l∥αB.l⊥αC.l⊂αD.l与α斜交[答案] B[解析] ∵u=-4a,∴u∥a,∴a⊥α,∴l⊥α.故选B.10.在正方体ABCD—A1B1C1D1中,E、F分别是BB1、CD的中点,则( )A .面AED ∥面A 1FD 1B .面AED ⊥面A 1FD 1C .面AED 与面A 1FD 相交但不垂直 D .以上都不对 [答案] B[解析] 以D 为原点,DA →、DC →,DD 1→分别为x ,y ,z 建立空间直角坐标系求面AED 的法向量n 1与面A 1FD 1的法向量n 2.∵n 1·n 2=0,∴n 1⊥n 2, ∴平面AED ⊥平面A 1FD 1. 二、填空题11.若直线l 与β的法向量分别是a =(1,0,-2),b =(-1,0,2),则直线l 与β的位置关系是________.[答案] l ⊥β[解析] ∵a ∥b ,∴l ⊥β.12.已知l ∥α,且l 的方向向量为(2,m,1),平面α的法向量为⎝ ⎛⎭⎪⎫1,12,2,则m=________.[答案] -8[解析] 设a =(2,m,1),b =(1,12,2).∵l ∥α,∴a⊥b ,∴2+12m +2=0,∴m =-8.13.已知正四棱锥(如图所示),在向量PA →-PB →+PC →-PD →,PA →+PC →,PB →+PD →,PA →+PB →+PC →+PD →中,不能作为底面ABCD 的法向量的向量是________.[答案] PA →-PB →+PC →-PD →[解析] ∵PA →-PB →+PC →-PD →=BA →+DC →=0,不能作为这个平面的法向量,对其它三个化简后可知均与PO →共线.而PO ⊥平面ABCD ,它们可作为这个平面的法向量.14.如图所示,已知矩形ABCD ,AB =1,BC =a ,PA ⊥平面ABCD ,若在BC 上只有一个点Q 满足PQ ⊥QD ,则a 的值等于________.[答案] 2[解析] 以A 为原点,建立如图所示坐标系,则A (0,0,0),B (1,0,0),D (0,a,0),C (1,a,0),设Q (1,x,0),P (0,0,z ),PQ →=(1,x ,-z ),QD →=(-1,a -x,0).由PQ →·QD →=0,得-1+x (a -x )=0, 即x 2-ax +1=0.当Δ=a 2-4=0,即a =2时,Q 只有一个. 三、解答题15.已知△ABC 的三个顶点坐标分别为A (0,0,2),B (4,2,0),C (2,4,0),求平面ABC 的单位法向量.[解析] AB →=(4,2,-2),AC →=(2,4,-2) 设n =(x ,y ,z )是平面ABC 的单位法向量,则有⎩⎪⎨⎪⎧|n |2=1,n ·AB →=0,n ·AC →=0,⇒⎩⎨⎧x 2+y 2+z 2=1,2x +y -z =0,x +2y -z =0.取z >0,得x =y =111,z =311. ∴n =111(1,1,3).16.如图所示,M 、N 、P 分别是正方体ABCD —A 1B 1C 1D 1中的棱CC 1、BC 、CD 的中点.求证:A 1P ⊥平面DMN .[证明] 建立如图所示的空间直角坐标系,设正方体棱长为2,则D (0,0,0),A 1(2,0,2),P (0,1,0),M (0,2,1),N (1,2,0). ∴向量A 1P →=(0,1,0)-(2,0,2)=(-2,1,-2), DM →=(0,2,1)-(0,0,0)=(0,2,1),DN →=(1,2,0).∴A 1P →·DM →=(-2,1,-2)·(0,2,1) =(-2)×0+1×2+(-2)×1=0.A 1P →·DN →=(-2,1,-2)·(1,2,0)=(-2)×1+1×2+(-2)×0=0. ∴A 1P →⊥DM →,A 1P →⊥DN →,即A 1P ⊥DM ,A 1P ⊥DN ,又DM ∩DN =D , ∴A 1P ⊥平面DMN .17.棱长为a 的正方体ABCD —A 1B 1C 1D 1中,在棱DD 1上是否存在点P 使B 1D ⊥面PAC?[解析] 以D 为原点建立如图所示的坐标系,设存在点P (0,0,z ),AP →=(-a,0,z ),AC →=(-a ,a,0),DB 1→=(a ,a ,a ),∴B 1D ⊥面PAC ,∴DB 1→·AP →=0,DB 1→·AC →=0.∴-a 2+az =0.∴z =a ,即点P 与D 1重合. ∴点P 与D 1重合时,DB 1⊥面PAC .18.如图所示,ABCD 为矩形,PA ⊥平面ABCD ,PA =AD ,M 、N 、Q 分别是PC 、AB 、CD 的中点,(1)求证:MN ∥PAD ;(2)求证:平面QMN ∥平面PAD ; (3)求证:MN ⊥平面PCD .[解析] (1)如图以A 为原点,以AB ,AD ,AP 所在直线为坐标轴建立空间直角坐标系,设B (b,0,0),D (0,d,0),P (0,0,d ),则C (b ,d,0) ∵M ,N ,Q 分别是PC ,AB ,CD 的中点, ∴M ⎝ ⎛⎭⎪⎫b 2,d 2,d 2,N ⎝ ⎛⎭⎪⎫b2,0,0,Q ⎝ ⎛⎭⎪⎫b2,d ,0∴MN →=⎝⎛⎭⎪⎫0,-d 2,-d 2,∵面PAD 的一个法向量为m =(1,0,0) ∴MN →·m =0,即MN →⊥m , ∴MN 不在面PAD 内, ∴MN ∥面PAD ,(2)QN →=(0,-d,0),QN →⊥m , 又QN 不在面PAD 内, 又QN ∥面PAD . 又∵MN ∩QN =N , ∴面MNQ ∥平面PAD .(3)PD →=(0,d ,-d ),DC →=(b,0,0),∴MN →·PD →=⎝ ⎛⎭⎪⎫-d 2d +⎝ ⎛⎭⎪⎫-d 2(-d )=0,MN →·DC →=0,∴MN →⊥PD →,MN →⊥DC ,又PD ∩DC =D , ∴MN →⊥平面PCD .。
高三数学平面法向量的求法试题
高三数学平面法向量的求法试题1.已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.(1)证明:⊥平面(2)求平面与平面所成角的余弦值;【答案】(1)通过建系证明,.得到,.故⊥平面.(2)二面角C-NB1-C1的余弦值为.【解析】(1)证明:∵该几何体的正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形,∴两两垂直.以分别为轴建立空间直角坐标系如图.则.∴,.∴,.又与相交于,∴⊥平面. ………6分(2)∵⊥平面,∴是平面的一个法向量,设为平面的一个法向量,则,所以可取.则.∴所求二面角C-NB1-C1的余弦值为. 12分【考点】本题主要考查立体几何中的垂直关系,角的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离的计算。
证明过程中,往往需要将立体几何问题转化成平面几何问题加以解答。
本题解答,通过建立适当的空间直角坐标系,利用向量的坐标运算,简化了繁琐的证明过程,实现了“以算代证”,对计算能力要求较高。
2.如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC BD,垂足为H,PH是四棱锥的高,E为AD中点;(Ⅰ)证明:PE BC;(Ⅱ)若APB=ADB=60°,求直线PA与平面PEH所成角的正弦值。
【答案】(1)略(2)【解析】求解和证明立体几何问题一方面可以直接利用几何方法,通过证明或找到线面之间的关系,依据判定定理或性质进行证明求解.以为原点,分别为轴,线段的长为单位长,建立空间直角坐标系如图,则(Ⅰ)设则可得因为所以……………………5分(Ⅱ)由已知条件可得设为平面的法向量则即因此可以取,由,可得所以直线与平面所成角的正弦值为…………………12分3.如图,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB上一点(I) 当点E为AB的中点时,求证;BD1//平面A1DE(II)求点A1到平面BDD1的距离;(III) 当时,求二面角D1-EC-D的大小.【答案】(1)略(2)A1到面BDD1的距离为(3)D1-EC-D的大小为【解析】(I) 要证BD1//平面A1DE,只要证明BD1平行该面内的一条直线,取中点,由中位线可证得;(II)等积法求高;(III)可以用传统法找出平面角也可以向量法求。
法向量解立体几何专题训练
法向量解立体几何专题训练一、运用法向量求空间角1、向量法求空间两条异面直线a, b 所成角θ,只要在两条异面直线a, b 上各任取一个向量''AA BB 和,则角<','AA BB >=θ或π-θ,因为θ是锐角,所以cos θ=''''AA BB AA BB ⋅⋅, 不需要用法向量;2、设平面α的法向量为n =x, y, 1,则直线AB 和平面α所成的角θ的正弦值为sin θ=cos2π-θ = |cos<AB , n >| = AB AB n n•• 3、 设二面角的两个面的法向量为12,n n ,则<12,n n >或π-<12,n n >是所求角;这时要借助图形来判断所求角为锐角还是钝角,来决定<12,n n >是所求,还是π-<12,n n >是所求角; 二、运用法向量求空间距离 1、求两条异面直线间的距离设异面直线a 、b 的公共法向量为(,,)n x y z =,在a 、b 上任取一点 A 、B,则异面直线a 、b 的距离d =AB ·cos ∠BAA '=||||AB n n • 2、求点到面的距离求A 点到平面α的距离,设平面α的法向量法为(,,1)n x y =,在α内任取一点B,则A 点到平面α的距离为d =||||AB n n •,n 的坐标由n 与平面α内的两个不共线向量的垂直关系,得到方程组类似于前面所述, 若方程组无解,则法向量与XOY 平面平行,此时可改设(1,,0)n y =三、证明线面、面面的平行、垂直关系设平面外的直线a 和平面α、β,两个面α、β的法向量为12,n n ,则1a//a n α⇔⊥ 1a a//n α⊥⇔12////n n αβ⇔ 12n n αβ⊥⇔⊥四、应用举例:例1:如右下图,在长方体ABCD —A 1B 1C 1D 1中,已知AB= 4, AD =3, AA 1= 2. E 、F 分别是线段AB 、BC 上的点,且EB= FB=1. 1 求二面角C —DE —C 1的正切值; 2 求直线EC 1与FD 1所成的余弦值.解:I 以A 为原点,1,,AB AD AA 分别为x 轴,y 轴,z 轴的正向建立空间直角坐标系,则D0,3,0、D 10,3,2、E3,0,0、F4,1,0、C 14,3,2 于是,11(3,3,0),(1,3,2),(4,2,2)DE EC FD =-==- 设法向量(,,2)n x y =与平面C 1DE 垂直,则有13301320n DE x y x y x y z n EC ⊥-=⇒⇒==-++=⊥⎫⎫⎪⎬⎬⎭⎪⎭11111(1,1,2),(0,0,2),cos 3||||1tan 2n AA CDE n AA C DE C n AAn AA θθθ∴=--=∴--•-===⨯∴=向量与平面垂直与所成的角为二面角的平面角 II 设EC 1与FD 1所成角为β,则1111cos 14||||1EC FD EC FD β•===⨯例2:高考辽宁卷17如图,已知四棱锥P-ABCD,底面ABCD 是菱形,∠DAB=600,PD⊥平面ABCD,PD=AD,点E 为AB 中点,点F 为PD 中点;1证明平面PED ⊥平面PAB ; 2求二面角P-AB-F 的平面角的余弦值 证明:1∵面ABCD 是菱形,∠DAB=600,∴△ABD 是等边三角形,又E 是AB 中点,连结BD ∴∠EDB=300,∠BDC=600,∴∠EDC=900, 如图建立坐标系D-ECP,设AD=AB=1,则PF=FD=12∴P0,0,1,E2,0,0,B2,12,0∴PB=32,12,-1,PE=2,0,-1,平面PED的一个法向量为DC=0,1,0 ,设平面PAB的法向量为n=x, y, 1由11(,,1),1)01022(,,1)1)010x y x y xn PBn PE yx y x⎧⎧•-=--=⎪⎧=⊥⎪⎪⎪⇒⇒⇒⎨⎨⎨⊥⎪⎪⎪⎩=•-=-=⎩⎪⎩∴n∵DC·n=0 即DC⊥n∴平面PED⊥平面PAB2解:由1知:平面PAB的法向量为n0, 1, 设平面FAB的法向量为n1=x, y, -1, 由1知:F0,0,12,FB,12,-12,FE,0,-12,由111111(,,1)(,)00222222110(,,1))0022x y x y xn FBn FE yx y x⎧⎧-•-=-+=⎪⎧=⊥⎪⎪⎪⎪⇒⇒⇒⎨⎨⎨⊥⎪⎪⎪⎩=-•-=+=⎩⎪⎩∴n1∴二面角P-AB-F的平面角的余弦值cosθ= |cos<n, n1>| =11n5714nnn•=•例3:在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=4CP.Ⅰ求直线AP与平面BCC1B1所成的角的大小结果用反三角函数值表示;Ⅱ设O点在平面D1AP上的射影是H,求证:D1H⊥AP;Ⅲ求点P到平面ABD1的距离.解: Ⅰ如图建立坐标系D-ACD1, ∵棱长为4 ∴A4,0,0,B4,4,0,P0,4,1∴AP = -4, 4, 1 , 显然DC=0,4,0为平面BCC1B1的一个法向量,∴直线AP与平面BCC1B1所成的角θ的正弦值sinθ= |cos<AP,DC >|=22216433334414=++• ∵θ为锐角,∴直线AP 与平面BCC 1B 1所成的角θ为arcsin 43333Ⅲ 设平面ABD 1的法向量为n =x, y, 1,∵AB =0,4,0,1AD =-4,0,4由n ⊥AB ,n ⊥1AD 得0440y x =⎧⎨-+=⎩ ∴ n =1, 0,1,∴点P 到平面ABD 1的距离 d =322AP n n•=例4:在长、宽、高分别为2,2,3的长方体ABCD-A 1B 1C 1D 1中,O 是底面中心,求A 1O 与B 1C 的距离;解:如图,建立坐标系D-ACD 1,则O1,1,0,A 12,2,3,C0,2,0∴1(1,1,3)AO =-- 1(2,0,3)B C =-- 11(0,2,0)A B = 设A 1O 与B 1C 的公共法向量为(,,1)n x y =,则113(,,1)(1,1,3)0302(,,1)(2,0,3)023032x n AO x y x y x y x n B C y ⎧=-⎧⎪⊥•--=-+-=⎧⎧⎪⎪⇒⇒⇒⎨⎨⎨⎨•--=--=⊥⎩⎩⎪⎪⎩=⎪⎩ ∴ 33(,,1)22n =-∴ A 1O 与B 1C 的距离为d =()1122330,2,0,,122||332211||11331222A B n n ⎛⎫•-⎪•⎝⎭===⎛⎫⎛⎫-++ ⎪ ⎪⎝⎭⎝⎭例5:在棱长为1的正方体ABCD-A 1B 1C 1D 1中,E 、F 分别是B 1C 1、C 1D 1的中点,求A 1到面BDFEABCDA 1B 1D 1C 1O的距离;解:如图,建立坐标系D-ACD 1,则B1,1,0,A 11,0,1,E12,1,1 ∴(1,1,0)BD =-- 1(,0,1)2BE =- 1(0,1,1)A B =-设面BDFE 的法向量为(,,1)n x y =,则(,,1)(1,1,0)002112(,,1)(,0,1)01022x y x y n BD x y x y x n BE •--=--=⎧⎧⎧⊥=⎧⎪⎪⎪⇒⇒⇒⎨⎨⎨⎨=-•-=-+=⊥⎩⎪⎪⎪⎩⎩⎩ ∴ (2,2,1)n =-∴ A 1到面BDFE 的距离为d =()()()1220,1,12,2,1|||3|13||221A B n n -•-•-===+-+新课标高二数学空间向量与立体几何测试题1一、选择题1.在正三棱柱ABC —A 1B 1C 1中,若AB =2BB 1,则AB 1与C 1B 所成的角的大小为A .60°B .90°C .105°D .75°2.如图,ABCD —A 1B 1C 1D 1是正方体,B 1E 1=D 1F 1=411B A ,则BE 1与DF 1所成角的余弦值是A .1715 B .21 C .178 D .23 3.如图,A 1B 1C 1—ABC 是直三棱柱,∠BCA=90°,点D 1、F 1分别是A 1B 1、A 1C 1的中点,若BC=CA=CC 1,则BD 1与AF 1所成角的余弦值是A .1030 B .21 C .1530 D .1015 4.正四棱锥S ABCD -的高2SO =,底边长2AB =,则异面直线BD 和SC 之间的距离图图FEA BCDA 1B 1D 1C 1AA 1DCB B 1C 1图A .515 B .55 C .552 D .105 5.已知111ABC A B C -是各条棱长均等于a 的正三棱柱,D 是侧棱1CC 的中点.点1C 到平面1AB D 的距离A .a 42B .a 82C .a 423D .a 226.在棱长为1的正方体1111ABCD A B C D -中,则平面1AB C 与平面11A C D 间的距离A .63 B .33 C .332 D .23 7.在三棱锥P -ABC 中,AB ⊥BC,AB =BC =21PA,点O 、D 分别是AC 、PC 的中点,OP ⊥底面ABC,则直线OD 与平面PBC 所成角的正弦值A .621B .338 C .60210D .302108.在直三棱柱111C B A ABC -中,底面是等腰直角三角形, 90=∠ACB ,侧棱21=AA ,D,E分别是1CC 与B A 1的中点,点E 在平面ABD 上的射影是ABD ∆的重心G .则B A 1与平面ABD 所成角的余弦值A .32 B .37C .23 D .73 9.正三棱柱111C B A ABC -的底面边长为3,侧棱3231=AA ,D 是CB 延长线上一点,且BC BD =,则二面角B AD B --1的大小A .3π B .6πC .65πD .32π10.正四棱柱1111D C B A ABCD -中,底面边长为22,侧棱长为4,E,F 分别为棱AB,CD 的中点,G BD EF =⋂.则三棱锥11EFD B -的体积VA .66B .3316 C .316D .16二、填空题11.在正方体1111ABCD A B C D -中,E 为11A B 的中点,则异面直线1D E 和1BC 间的距离 . 12. 在棱长为1的正方体1111ABCD A B C D -中,E 、F 分别是11A B 、CD 的中点,求点B 到截面1AEC F 的距离 .13.已知棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 、F 分别是B 1C 1和C 1D 1的中点,点A 1到平面DBEF 的距离 .14.已知棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 是A 1B 1的中点,求直线AE 与平面ABC 1D 1所成角的正弦值 . 三、解答题 15.已知棱长为1的正方体ABCD -A 1B 1C 1D 1,求平面A 1BC 1与平面ABCD 所成的二面角的大小16.已知棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 、F 、M 分别是A 1C 1、A 1D 和B 1A 上任一点,求证:平面A 1EF ∥平面B 1MC .17.在四棱锥P —ABCD 中,底面ABCD 是一直角梯形,∠BAD=90°,AD ∥BC,AB=BC=a,AD=2a,且PA ⊥底面ABCD,PD 与底面成30°角. 1若AE ⊥PD,E 为垂足,求证:BE ⊥PD ; 2求异面直线AE 与CD 所成角的余弦值.18.已知棱长为1的正方体AC 1,E 、F 分别是B 1C 1、C 1D 的中点. 1求证:E 、F 、D 、B 共面;2求点A 1到平面的BDEF 的距离; 3求直线A 1D 与平面BDEF 所成的角.19.已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点,求:ⅠD1E与平面BC1D所成角的大小;Ⅱ二面角D-BC1-C的大小;Ⅲ异面直线B1D1与BC1之间的距离.高二数学空间向量与立体几何专题训练2一、选择题1.向量a=2x,1,3,b=1,-2y,9,若a与b共线,则A.x=1,y=1 B.x=错误!,y=-错误!C.x=错误!,y=-错误! D.x=-错误!,y=错误! 2.已知a=-3,2,5,b=1,x,-1,且a·b=2,则x的值是A.6 B.5 C.4 D.33.设l1的方向向量为a=1,2,-2,l2的方向向量为b=-2,3,m,若l1⊥l2,则实数m的值为A.3 B.2 C.14.若a,b均为非零向量,则a·b=|a||b|是a与b共线的A.必要不充分条件 B.充分不必要条件C.充分必要条件 D.既不充分也不必要条件5.在△ABC中,错误!=c,错误!=b.若点D满足错误!=2错误!,则错误!=b+错误!c 错误!c-错误!b 错误!b-错误!c 错误!b+错误!c6.已知a,b,c是空间的一个基底,设p=a+b,q=a-b,则下列向量中可以与p,q一起构成空间的另一个基底的是A.a B.b C.c D.以上都不对7.已知△ABC的三个顶点A3,3,2,B4,-3,7,C0,5,1,则BC边上的中线长为A.2 B.3 C.错误!错误!8.与向量a=2,3,6共线的单位向量是A.错误!,错误!,错误! B.-错误!,-错误!,-错误!C.错误!,-错误!,-错误!和-错误!,错误!,错误! D.错误!,错误!,错误!和-错误!,-错误!,-错误!9.已知向量a=2,4,x,b=2,y,2,若|a|=6且a⊥b,则x+y为A.-3或1 B.3或-1 C.-3 D.110.已知a=x,2,0,b=3,2-x,x2,且a与b的夹角为钝角,则实数x的取值范围是A.x>4 B.x<-4 C.0<x<4 D.-4<x<0.11.已知空间四个点A1,1,1,B-4,0,2,C-3,-1,0,D-1,0,4,则直线AD与平面ABC所成的角为A.30° B.45° C.60° D.90°12.已知二面角α-l-β的大小为50°,P为空间中任意一点,则过点P且与平面α和平面β所成的角都是25°的直线的条数为A.2 B.3 C.4 D.5二、填空题13.已知{i,j,k}为单位正交基底,且a=-i+j+3k,b=2i-3j-2k,则向量a+b与向量a-2b的坐标分别是________;________.14.在△ABC中,已知错误!=2,4,0,错误!=-1,3,0,则∠ABC=________.15.正方体ABCD-A1B1C1D1中,面ABD1与面B1BD1所夹角的大小为________.16.在下列命题中:①若a,b共线,则a,b所在的直线平行;②若a,b所在的直线是异面直线,则a,b一定不共面;③若a,b,c三向量两两共面,则a,b,c三向量一定也共面;④已知三向量a,b,c,则空间任意一个向量p总可以唯一表示为p=xa+yb+zc,其中不正确的命题为________.三、解答题17.如图所示,PD垂直于正方形ABCD所在的平面,AB=2,PC与平面ABCD所成角是45°,F 是AD的中点,M是PC的中点.求证:DM∥平面PFB.18.如图,正四棱柱ABCD—A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.1证明A1C⊥平面BED;2求二面角A1-DE-B的余弦值.19.正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点.1证明:平面AED⊥平面A1FD1;2在AE上求一点M,使得A1M⊥平面DAE.高考真题能力提升1.如图,平面PAC⊥平面ABC,ABC∆是以AC为斜边的等腰直角三角形,,,E F O分别为PA,PB,AC的中点,16AC=,10PA PC==.I设G是OC的中点,证明://FG平面BOE;II证明:在ABO∆内存在一点M,使FM⊥平面BOE,并求点M到OA,OB的距离.2.如图,在三棱锥P ABC -中,PA ⊥底面,,60,90ABC PA AB ABC BCA ︒︒=∠=∠=, 点D ,E 分别在棱,PB PC 上,且//DE BCⅠ求证:BC ⊥平面PAC ;Ⅱ当D 为PB 的中点时,求AD 与平面PAC 所成的角的大小; Ⅲ是否存在点E 使得二面角A DE P --为直二面角 并说明理由.3.如图,四棱锥P ABCD -的底面是正方形,PD ABCD ⊥底面,点E 在棱PB 上.Ⅰ求证:平面AEC PDB ⊥平面;Ⅱ当2PD AB =且E 为PB 的中点时,求AE 与平面PDB 所成的角的大小.4.在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,4PA AD ==,2AB =. 以AC 的中点O 为球心、AC 为直径的球面交PD 于点M ,交PC 于点N . 1求证:平面ABM ⊥平面PCD ; 2求直线CD 与平面ACM 所成的角的大小; 3求点N 到平面ACM 的距离.yz DMCB PA NONMA BDCO5. 如图,在四棱锥O ABCD -中,底面ABCD 四边长为1的菱形,4ABC π∠=,OA ABCD ⊥底面, 2OA =,M 为OA 的中点,N 为BC 的中点Ⅰ证明:直线MN OCD 平面‖;Ⅱ求异面直线AB 与MD 所成角的大小; Ⅲ求点B 到平面OCD 的距离;6. 如图,正三棱柱ABC -A 1B 1C 1的所有棱长都为2,D 为CC 1中点; Ⅰ求证:AB 1⊥面A 1BD ;Ⅱ求二面角A -A 1D -B 的大小; Ⅲ求点C 到平面A 1BD 的距离;7.如图所示,AF 、DE 分别是⊙O 、⊙O 1的直径.AD 与两圆所在的平面均垂直,AD =8,BC 是⊙O 的直径,AB =AC =6,OE Ⅰ求二面角B —AD —F 的大小;Ⅱ求直线BD 与EF 所成的角.8.如图,在长方体ABCD —A 1B 1C 1D 1中,AD=AA 1=1,AB=2,点E 在棱AB 上移动.1证明:D 1E ⊥A 1D ;2当E 为AB 的中点时,求点E 到面ACD 1的距离;3AE 等于何值时,二面角D 1—EC —D 的大小为4π.9. 如图,边长为2的等边△PCD 所在的平面垂直于矩形ABCD 所在的平面,BC =22, M 为BC 的中点Ⅰ证明:AM ⊥PM ;Ⅱ求二面角P -AM -D 的大小; Ⅲ求点D 到平面AMP 的距离;10.如图,已知AB ⊥平面ACD ,DE ⊥平面ACD ,△ACD 为等边三角形,2AD DE AB ==,F 为CD 的中点. 1 求证://AF 平面BCE ; 2 求证:平面BCE ⊥平面CDE ; 3 求直线BF 和平面BCE 所成角的正弦值.1A C M PD C B A A BCD EF11. 如图,已知等腰直角三角形RBC ,其中∠RBC =90º,2==BC RB .点A 、D 分别是RB 、RC 的中点,现将△RAD 沿着边AD 折起到△PAD 位置,使PA ⊥AB ,连结PB 、PC . 1求证:BC ⊥PB ;2求二面角P CD A --的平面角的余弦值.12. 如图,正三棱柱ABC -111C B A 的底面边长是2,D 是侧棱C 1C 的中点,直线AD 与侧面C C BB 11所成的角为45°.1 求二面角A-BD-C 的大小; 2求点C 到平面ABD 的距离.13. 如图,P 、O 分别是正四棱柱1111ABCD A B C D -上、下底面的中心,E 是AB 的中点,1AB kAA =. Ⅰ求证:1A E ∥平面PBC ;Ⅱ当k =,求直线PA 与平面PBC 所成角的大小;Ⅲ 当k 取何值时,O 在平面PBC 内的射影恰好为PBC ∆ABCD1A 1B 1C A 1C14. 如图,在正四棱锥P ABCD -中,PA AB a ==,点E 在棱PC 上.Ⅰ问点E 在何处时,//PA EBD 平面,并加以证明; Ⅱ当//PA EBD 平面时,求点A 到平面EBD 的距离; Ⅲ求二面角C PA B --的大小.15.如图所示,在长方体1111ABCD A B C D -中,AB=AD=1,AA 1=2,M 是棱CC 1的中点 Ⅰ求异面直线A 1M 和C 1D 1所成的角的正切值; Ⅱ证明:平面ABM ⊥平面A 1B 1M 116.已知三棱锥P -ABC 中,PA ⊥ABC,AB ⊥AC,PA=AC=½AB,N 为AB 上一点,AB=4AN,M,S 分别为PB,BC 的中点. Ⅰ证明:CM ⊥SN ;Ⅱ求SN 与平面CMN 所成角的大小.EPDCBA17.如图,四棱锥S-ABCD 中,SD ⊥底面ABCD,AB ⊥⊥Ⅰ证明:SE=2EB ; Ⅱ求二面角A-DE-C 的大小 .18.如图,在多面体ABCDEF 中,四边形ABCD 是正方形,EF ∥AB ,EF FB ⊥,2AB EF =,90BFC ∠=︒,BF FC =,H 为BC 的中点;ABCDEFHⅠ求证:FH ∥平面EDB ;Ⅱ求证:AC ⊥平面EDB ; Ⅲ求二面角B DE C --的大小;19.如图,在直三棱柱111ABC A B C -中,13,4,5,4AC BC AB AA ==== 1求证1;AC BC ⊥2在AB 上是否存在点D 使得1?AC CD ⊥ 3在AB 上是否存在点D 使得11//A C CDB 平面A1C BCD1A 1B20、如图,在四棱锥P —ABCD 中,PD ⊥底面ABCD,底面ABCD 为正方形,PD=DC,E 、F 分别是AB 、PB 的中点. Ⅰ求证:EF ⊥CD ;Ⅱ在平面PAD 内求一点G,使GF ⊥平面PCB,并证明你的结论; Ⅲ求DB 与平面DEF 所成角的大小.21、如图, 在直三棱柱ABC -A 1B 1C 1中,∠ACB=90°,CB=1,CA=3, AA 1=6,M 为侧棱CC 1上一点, 1AM BA ⊥. 1求证: AM ⊥平面1A BC ; 2求二面角B -AM -C 的大小; 3求点C 到平面ABM 的距离.ABCABCM22、如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=BC=CC1=2.I证明:AB1⊥BC1;II求点B到平面AB1C1的距离.III求二面角C1—AB1—A1的大小。
向量法解二面角例题与练习题
§向量法求二面角例1(2010江西卷20)如图,BCD ∆与MCD ∆都是边长为2的正三角形,平面MCD ⊥平面BCD ,AB ⊥平面BCD ,23AB =.(1)求直线AM 与平面BCD 所成的角的大小; (2)求平面ACM 与平面BCD 所成的二面角的正弦值.练习:1..若二面角的两个半平面的法向量分别为(4,2,0)和(3,-6,5),则这个二面角的余弦值是( ) A.0 B.32 C.12D. 22 2.(2011年全国新课标)如图,四棱锥P-ABCD 中,底面ABCD 为平行四边形,∠DAB=60°,AB=2AD,PD ⊥底面ABCD.(Ⅰ)证明:PA ⊥BD ; (Ⅱ)若PD=AD ,求二面角A-PB-C 的余弦值。
课后作业:1. .如图,四棱锥P —ABCD 中,P A ⊥底面ABCD .底面ABCD 为边长是1的正方形,P A =1,求平面PCD 与平面P AB 夹角的大小为____________.2. 如图,正方体的棱长为1,O BC C B 11 ,求:(1)AO 与11C A 所成的角; (2)AO 与平面AC 所成角的正切值; (3)平面AOB 与平面AOC 所成的角.4. (2011·辽宁)如图,四边形ABCD 为正方形,PD ⊥平面ABCD ,PD ∥QA ,QA =AB =12PD .(1)证明:平面PQC ⊥平面DCQ ; (2)求二面角Q -BP -C 的余弦值.5. (2012·天津改编)如图,在四棱锥P-ABCD 中,PA ⊥平面ABCD ,AC ⊥AD ,AB ⊥BC ,∠BAC =45°,PA =AD =2,AC =1.(1)证明:PC ⊥AD ; (2)求二面角A-PC-D 的正弦值.6.1111111111112(1)(2)(3)ABCD A B C D AD CD a AA AB aAC B C AC BCC C AB A -∠∠====--O 1为直四棱柱,底面ABCD 是直角梯形,DAB=ADC=90,,求异面直线和所成角;求和底面B 所成角;求二面角的大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【山东省淄博市第一中学2012届高三第一学期期中理】
1、(满分12分):
如图所示的几何体是由以等边三角形ABC为底面的棱
FA平面ABC,
柱被平面D E F所截而得,已知⊥
CE
=BD
AF
AB O为BC的中点
=
,2
,1
=
,3
,2=
(1)求证:AO∥平面DEF
(2)求证:平面DEF⊥平面BCED
(3)求平面DEF与平面ABC相交所成锐角二面角
的余弦值
【山东省枣庄市2012届高三上学期期末理】2.(本题满分12分)
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
(1)证明:面PBD⊥面PAC;
(2)求锐二面角A—PC—B的余弦值.
【山东省临清三中2012届高三12月模拟理】3.(本小题满分12分)
如图,在四棱锥P-ABCD中,P A⊥平面ABCD,底面ABCD是
菱形,AB=2,∠BAD=60°.
(Ⅰ)求证:BD⊥平面P AC;
(Ⅱ)若P A=AB,求PB与AC所成角的余弦值;
(Ⅲ)当平面PBC与平面PDC垂直时,求P A的长.
4.在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF。
(Ⅰ)求证:BD⊥平面AED;
(Ⅱ)求二面角F-BD-C的余弦值。
【答案】1、 证明:⑴取DE 中点G,建系如图,则A(0,3,0)、B(-1,0, 0)、C(1,0,0)、 D(-1,0,1),E(1,0,3)、F(0,3,2)、G(0,0,2),
DE →=(2,0,2),DF →=(1,3,1).
设平面DEF 的一法向量m →=(x,y,z),
则⎩⎪⎨⎪⎧m →∙DE →=0m →∙DF →=0
即⎩⎨⎧x+z=0x+ 3y+z=0 ,不妨取x=1,则y=0,z=-1, ∴m →=(1,0,-1),平面ABC 的一法向量n →=(0,0,1),OA →=(0,3,0). OA →∙n →=0,∴OA →⊥n →.又OA ⊄平面DEF,∴OA //平面DEF.
⑵显然,平面BCED 的一法向量为v →=(0,1,0),v →∙n →
=0,∴平面DEF ⊥平面BCED
⑶由⑴知平面DEF 的一法向量m →=(1,0,-1),平面ABC 的一法向量n →=(0,0,1),
cos<m →,n →>=m →∙n →|m →|∙|n →| =- 22 ∴求平面DEF 与平面ABC 相交所成锐角二面角的余弦值为22 .
【答案】2.(1)因为四边形ABCD 是菱形,
所以AC .BD ⊥
因为PA ⊥平面ABCD ,
所有PA ⊥BD.…………………………2分
又因为PA ⋂AC=A ,
所以BD ⊥面 PAC.……………………3分
而BD ⊂面PBD ,
所以面PBD ⊥面PAC.…………………5分
(2)如图,设AC ⋂BD=O.取PC 的中点Q ,连接OQ.
在△APC 中,AO=OC ,CQ=QP ,OQ 为△APC 的中位线,所以OQ//PA.
因为PA ⊥平面ABCD ,
所以OQ ⊥平面ABCD ,……………………………………………………6分 以OA 、OB 、OQ 所在直线分别为x 轴、z 轴,建立空间直角坐标系O .xyz - 则()()(),0,0,3,0,1,0,0,0,3-C B A
()
.2,0,3P ………………………………………………………………………7分 因为BO ⊥面PAC , 所以平面PAC 的一个法向量为().0,1,0=OB …………………………………8分 设平面PBC 的一个法向量为(),,,z y x n =
而()()
,2,1,3,0,1,3--=--= 由⎪⎩⎪⎨⎧⊥⊥,,BC n 得⎪
⎩⎪⎨⎧=-+-=--.023,03x y x y x 令,1=x 则.3,3-=-=z y
所以()
3,3,1--=为平面PBC 的一个法向量.……………………………10分 c o s <,
>.7213
3113-=++⨯-==……………………12分
【答案】3.(I )证明:因为四边形ABCD 是菱形, 所以AC ⊥BD .
又因为P A ⊥平面ABCD , 所以P A ⊥BD ,所以BD ⊥平面P AC . ……………4分 (Ⅱ)设AC ∩BD =O . 因为∠BAD =60°,P A =AB =2, 所以BO =1,AO =CO =3. 如图,以O 为坐标原点,OB 、OC 所在直线及过点O 且与P A 平行的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系O -xyz ,则
P (0,-3,2),A (0,-3,0),B (1,0,0),C (0,3,0).
所以PB =(1,3,-2),AC =(0,23,0). 设PB 与AC 所成角为θ,则
cos θ==622×23=64
. ………………8分 (Ⅲ)由(Ⅱ)知BC =(-1,3,0).
设P (0,-3,t ) (t >0),则 BP =(-1,-3,t ).
设平面PBC 的法向量m =(x ,y ,z ), 则BC ·m =0,BP ·m =0.
所以⎩⎨⎧ -x +3y =0,-x -3y +tz =0,
令y =3,则x =3,z =6t , 所以m =⎝⎛⎭⎫3,3,6t . 同理,可求得平面PDC 的法向量n =⎝
⎛⎭⎫-3,3,6t . 因为平面PBC ⊥平面PDC , 所以m·n =0,即-6+36t 2=0. 解得t =6. 所以当平面PBC 与平面PDC 垂直时,PA =6. ……………………12分。
