(遵义专用)201X届中考数学复习 第17课时 三角形及其性质 3 典型例题剖析(课后作业)课件(1
中考数学复习 第17课时 三角形基本性质测试-人教版初中九年级全册数学试题

第四单元三角形第十七课时三角形基本性质基础达标训练1. (2017某某)若一个三角形的两边长分别为5和8,则第三边长可能是( )A. 14B. 10C. 3D. 22. (2017某某四市)如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )A. 100°B. 80°C. 60°D. 40°第2题图第3题图3. (2017某某省卷)将一把直尺与一块三角板如图放置,若∠1=45°,则∠2为( )A. 115°B. 120°C. 135°D. 145°4. (2017某某)如图,AB∥CD,∠A=70°,∠C=40°,则∠E等于( )A. 30°B. 40°C. 60°D. 70°第4题图第5题图5. (2017某某建设兵团)如图,AB∥CD,∠A=50°,∠C=30°,则∠AEC等于( )A. 20°B. 50°C. 80°D. 100°6. (2017德阳)如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC =60°,∠ABE=25°,则∠DAC的大小是( )A. 15°B. 20°C. 25°D. 30°第6题图第7题图7. (人教八上P83第10题改编)如图,△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O,与AB、AC相交于点M、N,且MN∥BC,AB=2,AC=3,则△AMN的周长为( )A. 4B. 5C. 6D. 78. (2017某某)在△ABC中,∠A∶∠B∶∠C=2∶3∶4,则∠A的度数为________.第9题图9. (2017某某)将一副三角板如图叠放,则图中∠α的度数为________.能力提升训练1. (2017某某省卷)已知a,b,c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )A. 2a+2b-2cB. 2a+2bC. 2cD. 02. 如图,在Rt△ABC中,∠ACB=60°,DE是斜边AC的中垂线,分别交AB、AC于D、E 两点,若BD=2,则AC的长是( )A. 4B. 4 3C. 8D. 8 3第2题图第3题图3. (2017某某)如图,直角△ABC 中,∠B =30°.点O 是△ABC 的重心,连接CO 并延长交AB 于点E ,过点E 作EF ⊥AB 交BC 于点F ,连接AF 交CE 于点M ,则MO MF的值为( ) A. 12 B. 54 C. 23 D. 33第4题图4. 如图,已知△ABC 的周长为27 cm ,AC =9 cm ,BC 边上中线AD =6 cm ,△ABD 的周长为19 cm ,AB =________.5. (2017某某)在△ABC 中,已知BD 和CE 分别是边AC ,AB 上的中线,且BD ⊥CE ,垂足为O ,若OD =2 cm ,OE =4 cm ,则线段AO 的长度为________cm.拓展培优训练1. 如图,在Rt △ABC 中,∠C =90°,∠A =30°,∠C 的平分线与∠B 的外角的平分线交于E 点,则∠AEB 是( )第1题图A. 50°B. 45°C. 40°D. 35°2. 已知直线AM 是△ABC 中BC 边上的中线,点P 是△ABC 的重心,过点P 作EF (EF ∥BC ),分别交AB 、AC 于点E 、点F ,则BE AE +CF AF=________. 答案1. B2. B3. C4. A5. C6. B7. B8. 40°9. 15°10. 16 【解析】∵DE 是AB 边的垂直平分线,∴AE =BE ,∵在Rt △ABC 中,∠BAC =90°,AB =8,AC =6,∴BC =AB 2+AC 2=10,∴△ACE 的周长为AC +AE +CE =AC +BE +CE =AC +BC =6+10=16.能力提升训练1. D 【解析】由三角形中任意两边之和大于第三边,可知a +b >c ,∴c -a -b =c -(a +b )<0,∴|c -(a +b )|=a +b -c ,|a +b -c |=a +b -c ,∴|a +b -c |-|c -a -b |=0.2. B 【解析】∵在Rt △ABC 中,∠ACB =60°,∴∠A =30°,∵DE 垂直平分斜边AC ,∴AD =CD ,∴∠A =∠ACD =30°,∴∠DCB =60°-30°=30°,∵BD =2,∴CD =AD =4,∴AB =2+4=6,在△BCD 中,由勾股定理得C B =23,在△ABC 中,由勾股定理得AC =AB 2+BC 2=43.3. D 【解析】∵O 是△ABC 的重心,∴CO =23CE ,∵△ABC 是直角三角形,∴CE =BE =AE ,∵∠B =30°,∴∠FAE =∠B =30°,∠BAC =60°,∴∠FAE =∠CAF =30°,△ACE 是等边三角形,∴CM =12CE ,∴OM =23CE -12CE =16CE ,即OM =16AE ,∵BE =AE ,∴EF =33AE ,∵EF ⊥AB ,∴∠AFE =60°,∴∠FEM =30°,∴MF =12EF ,∴MF =36AE ,∴MO MF =16AE 36AE=33. 4. 8 cm 【解析】设AB =xcm ,BD =ycm ,∵AD 是BC 边的中线,∴BC =2BD =2y cm ,由题意得⎩⎪⎨⎪⎧x +9+2y =27x +6+y =19,解得⎩⎪⎨⎪⎧x =8y =5,∴AB =8 cm .第5题解图5. 4 5 【解析】连接AO 并延长,交BC 于H ,由勾股定理得,DE =OE 2+OD 2=25,∵BD 和CE 分别是边AC 、AB 上的中线,∴BC =2DE =45,O 是△ABC 的重心,∴AH 是边BC的中线,又∵BD ⊥CE ,∴OH =12BC =25,∵点O 是△ABC 的重心,∴AO =2OH =4 5. 拓展培优训练1. B 【解析】在Rt △ABC 中,∠C =90°,∠A =30°,则∠ABC =60°,∵EB 是∠B 的外角的平分线,∴∠ABE =60°,∵E 点是∠C 的平分线与∠B 的外角平分线的交点,∴E 点到CB 的距离等于E 点到AB 的距离,也等于E 点到CA 的距离,∴AE 是∠A 的外角的平分线,∴∠BAE =150°2=75°,∴∠AEB =180°-60°-75°=45°.第2题解图2. 1 【解析】如解图,分别过B 、C 两点作BG 、CK 平行于AM 交直线EF 于G 、K ,则有BE AE=BG AP ,CF AF =CK AP ,两式相加得BE AE +CF AF =BG +CK AP ,又∵在平行四边形BCKG 中,PM =12(BG +CK ),由P 为重心,得AP =2PM ,故BE AE +CF AF =2PM 2PM=1.。
中考数学复习第四单元三角形第17课时三角形

识
巩
固
高
频
考
向
探
究
考点四 命题(mìng tí)与定理
在日常生活中,为了交流方便,我们就要对名称和术语的含
定义
义加以描述,作出明确的规定,也就是给它们下定义
定义
命
题
分类
组成
基本事实
判断一件事情的语句,叫做命题
题设成立时,结论一定成立的命题叫做⑰ 真命题(mìng tí)
题设成立时,结论不一定成立的命题叫做⑱
定理
一个命题的题设和结论分别为另一个命题的结论和题设,这样的两个命
互逆命题 题,称为互逆命题,如果我们把其中一个命题称为原命题,那么另一个命题
就是它的㉑
互逆定理
逆命题
如果一个定理的逆命题经过证明是正确的,那么这个逆命题也可以称为
原定理的㉒
逆定理 ,一个定理和它的逆定理是互逆定理
第七页,共三十三页。
基
第十一页,共三十三页。
②
基
础
知
识
巩
固
高
频
考
向
探
究
考向一 命题(mìng tí)与定理
例1
1
1
[2019·北京]用三个不等式 a>b,ab>0, < 中的两个不等式作为题设,余下的
一个不等式作为结论组成一个命题,组成真命题的个数为 (
A.0
B.1
C.2
第十二页,共三十三页。
D.3
)
基
础
知
识
巩
固
பைடு நூலகம்
高
频
考
向
探
究
[答案(dáàn)] D
2019届中考数学(遵义专用)专项训练课件:第17课 全等三角形

考点二 全等三角形的判定及其相关计算 【例2】[2018· 安顺]如图,点D,E分别在线段AB,AC上,CD与BE 相交于点O,已知AB=AC,现添加以下的哪个条件仍不能判定 △ABE≌△ACD
D
B.AD=AE D.BE=CD
A.∠B=∠C C.BD=CE
【解析】 已知 AB=AC, ∠A 为公共角, A.如添加∠B=∠C, 利用 ASA 即 可 证 明 △ABE≌△ACD ; B. 如 添 AD = AE , 利 用 SAS 即 可 证 明 △ABE≌△ACD;C.如添 BD=CE,由等量关系可得 AD=AE,利用 SAS 即 可 证 明 △ABE≌△ACD ; D. 如 添 BE = CD , 因 为 SSA 不 能 证 明 △ABE≌△ACD,所以此选项不能作为添加的条件.故选 D.
对应边 相 1.能够__________ 完全重合 的两个图形叫做全等图形.全等三角形_______
等,________ 对应角 相等. 2.全等三角形中的对应线段(角平分线、中线、高、中位线)______ 相等 ,
相等 . 相等 ,对应面积______ 对应周长______
3.三角形全等的判定定理 (1)_________ 边边边 ”或 三条边 对应相等的两个三角形全等(简写成“________ “SSS”). (2)两边和它们的_____ 边角边 ” 夹角 对应相等的两个三角形全等(简写成“_______ 或“SAS”).
【变式练习】 如图是5×5的正方形网格,以格点D,E为两个顶点作位置不同的格 点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多 可以作出
B
网络画板: /singleFile.html?id=72988#posts/72988
【北师大版】中考数学总复习课件:第17课时三角形

考点聚焦
归类探究
回归教材
第17课时┃ 三角形
探究三 三角形中重要线段的应用
命题角度: 1.三角形的中线、角平分线、高线; 2.三角形的中位线.
考点聚焦
归类探究
回归教材
第17课时┃ 三角形
例 3 [2014·枣庄] 如图 17-2,△ABC 中,AB=4,AC=3,
AD,AE 分别是其角平分线和中线,过点 C 作 CG⊥AD 于点 F,
3.直角三角形的两个锐角__互__余____
4.三角形的外角和为___3_6_0_°__
在任意一个三角形中,最多有三个锐角,最少有两个 拓展
锐角;最多有一个钝角,最多有一个直角
考点聚焦
归类探究
回归教材
第17课时┃ 三角形
归类探究
探究一 三角形三边的关系 命题角度: 1. 利用三角形的三边关系判断三条线段能否组成三角形; 2. 利用三角形的三边关系求字母的取值范围; 3. 三角形的稳定性.
第17课时 三角形
第17课时┃ 三角形
考点聚焦
考点1 三角形的分类
直角三角形 1.按角分:三角形斜三角形锐 钝角 角三 三角 角形 形 2.按边分:
不等边三角形 三角形等腰三角形底 等边 边和三腰角不形相等的等腰三角形
考点聚焦
归类探究
回归教材
第17课时┃ 三角形
考点2 三角形中的重要线段
重要线段
中考预测
1.三角形两边长分别为3和5,则周长l的范围是
A.6<l<15
B.6<l<16
C.11<l<13
D.10<l<16
(D)
解 析 关键在于第三边的取值范围.
考点聚焦
归类探究
回归教材
专题17 三角形及其性质-2年中考1年模拟备战2018年中考数学精品系列(原卷版)
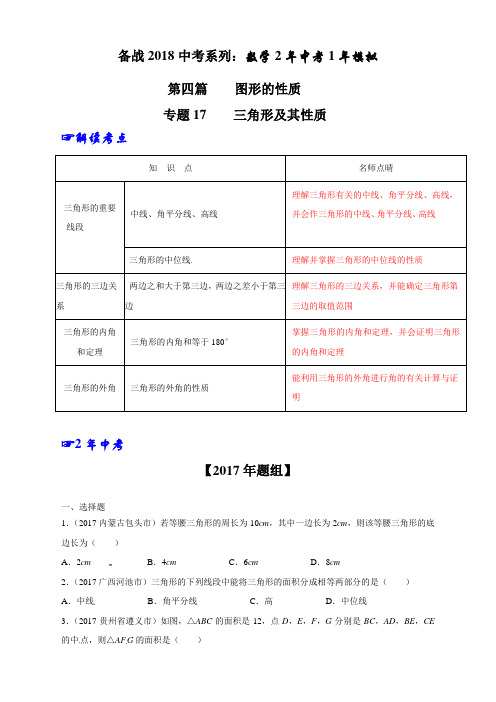
备战2018中考系列:数学2年中考1年模拟第四篇图形的性质专题17三角形及其性质☞解读考点知识点名师点晴三角形的重要线段来源学科网][来源学科网Z,X,X,K][来源:Z#xx#k.][来源:Zxxk.]中线、角平分线、高线来源:Z_xx_k.][来源:ZXXK][来源学+科+网理解三角形有关的中线、角平分线、高线,并会作三角形的中线、角平分线、高线来源:Zxxk.][来源:][来源:ZXXK][来源学#科#网Z#X#X#K][来源:]三角形的中位线理解并掌握三角形的中位线的性质三角形的三边关系两边之和大于第三边,两边之差小于第三边理解三角形的三边关系,并能确定三角形第三边的取值范围三角形的内角和定理三角形的内角和等于180°掌握三角形的内角和定理,并会证明三角形的内角和定理三角形的外角三角形的外角的性质能利用三角形的外角进行角的有关计算与证明☞2年中考【2017年题组】一、选择题1.(2017内蒙古包头市)若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为()A.2cm B.4cm C.6cm D.8cm2.(2017广西河池市)三角形的下列线段中能将三角形的面积分成相等两部分的是()A.中线B.角平分线C.高D.中位线3.(2017贵州省遵义市)如图,△ABC的面积是12,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AF G的面积是()A .4.5B .5C .5.5D .64.(2017南宁)如图,△ABC 中,∠A =60°,∠B =40°,则∠C 等于( )A .100°B .80°C .60°D .40°5.(2017南宁)如图,△ABC 中,AB >AC ,∠CAD 为△ABC 的外角,观察图中尺规作图的痕迹,则下列结论错误的是( )A .∠DAE =∠B B .∠EAC =∠C C .AE ∥BCD .∠DAE =∠EAC6.(2017广西贵港市)从长为3,5,7,10的四条线段中任意选取三条作为边,能构成三角形的概率是( )A .14B .12C .34D .1 7.(2017江苏省扬州市)若一个三角形的两边长分别为2和4,则该三角形的周长可能是( )A .6B .7C .11D .128.(2017四川省雅安市)一个等腰三角形的边长是6,腰长是一元二次方程27120x x -+=的一根,则此三角形的周长是 ( )A .12B .13C .14D .12或149.(2017四川省巴中市)若一个三角形三个内角的度数之比为1:2:3,则这个三角形是( )A .锐角三角形B .等边三角形C .钝角三角形D .直角三角形10.(2017德州)观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为()A.121B.362C.364D.729二、填空题11.(2017四川省广安市)如图,Rt△ABC中,∠C=90°,BC=6,AC=8,D、E分别为AC、AB的中点,连接DE,则△ADE的面积是.12.(2017宁夏)在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=13DM.当AM⊥BM时,则BC的长为.13.(2017贵州省黔南州)如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是.14.(2017黑龙江省绥化市)如图,顺次连接腰长为2的等腰直角三角形各边中点得到第1个小三角形,再顺次连接所得的小三角形各边中点得到第2个小三角形,如此操作下去,则第n个小三角形的面积为.15.(2017四川省成都市)在△ABC 中,∠A :∠B :∠C =2:3:4,则∠A 的度数为 .16.(2017四川省达州市)△ABC 中,AB =5,AC =3,AD 是△ABC 的中线,设AD 长为m ,则m 的取值范围是 .17.(2017贵州省黔西南州)已知一个等腰三角形的两边长分别为3和6,则该等腰三角形的周长是 .18.(2017四川省巴中市)若a 、b 、c 为三角形的三边,且a 、b 满足29(2)0a b -+-= ,第三边c 为奇数,则c = .19.(2017四川省泸州市)在△ABC 中,已知BD 和CE 分别是边AC 、AB 上的中线,且BD ⊥CE ,垂足为O .若OD =2cm ,OE =4cm ,则线段AO 的长度为 cm .20.(2017山东省淄博市)设△ABC 的面积为1.如图1,分别将AC ,BC 边2等分,D 1,E 1是其分点,连接AE 1,BD 1交于点F 1,得到四边形CD 1F 1E 1,其面积S 1=13. 如图2,分别将AC ,BC 边3等分,D 1,D 2,E 1,E 2是其分点,连接AE 2,BD 2交于点F 2,得到四边形CD 2F 2E 2,其面积S 2=16; 如图3,分别将AC ,BC 边4等分,D 1,D 2,D 3,E 1,E 2,E 3是其分点,连接AE 3,BD 3交于点F 3,得到四边形CD 3F 3E 3,其面积S 3=110; …按照这个规律进行下去,若分别将AC ,BC 边(n +1)等分,…,得到四边形CD n E n F n ,其面积S = .三、解答题21.(2017内蒙古呼和浩特市)如图,等腰三角形ABC 中,BD ,CE 分别是两腰上的中线.(1)求证:B D =CE ;(2)设BD 与CE 相交于点O ,点M ,N 分别为线段BO 和CO 的中点,当△ABC 的重心到顶点A 的距离与底边长相等时,判断四边形DEMN 的形状,无需说明理由.【2016年题组】一、选择题1.(2016贵州省铜仁市)如图,已知∠AOB =30°,P 是∠AOB 平分线上一点,CP ∥OB ,交OA 于点C ,PD ⊥OB ,垂足为点D ,且PC =4,则PD 等于( )A . 1B . 2C . 4D . 82.(2016贵州省毕节市)到三角形三个顶点的距离都相等的点是这个三角形的( )A .三条高的交点B .三条角平分线的交点C .三条中线的交点D .三条边的垂直平分线的交点3.(2016广西河池市)下列长度的三条线段不能组成三角形的是( )A .5,5,10B .4,5,6C .4,4,4D .3,4,54.(2016广西百色市)三角形的内角和等于( )A .90°B .180°C .300°D .360°5.(2016广西贵港市)在△ABC 中,若∠A =95°,∠B =40°,则∠C 的度数为( )A .35°B .40°C .45°D .50°6.(2016江苏省盐城市)若a 、b 、c 为△ABC 的三边长,且满足420a b -+-=,则c 的值可以为( )A .5B .6C .7D .87.(2016湖南省岳阳市)下列长度的三根小木棒能构成三角形的是( )A .2cm ,3cm ,5cmB .7cm ,4cm ,2cmC .3cm ,4cm ,8cmD .3cm ,3cm ,4cm8.(2016贵州省安顺市)已知实数x ,y 满足480x y -+-=,则以x ,y 的值为两边长的等腰三角形的周长是( )A .20或16B .20C .16D .以上答案均不对9.(2016湖北省荆门市)已知3是关于x 的方程2(1)20x m x m -++=的一个实数根,并且这个方程的两个实数根恰好是等腰△ABC 的两条边的边长,则△ABC 的周长为( )A .7B .10C .11D .10或1110.(2016湖北省襄阳市)如图,AD 是∠EAC 的平分线,AD ∥BC ,∠B =30°,则∠C 的度数为( )A .50°B .40°C .30°D .20°11.(2016湖北省鄂州市)如图所示,AB ∥CD ,EF ⊥BD ,垂足为E ,∠1=50°,则∠2的度数为( )A .50°B .40°C .45°D .25°12.(2016湖北省黄石市)如图所示,线段AC 的垂直平分线交线段AB 于点D ,∠A =50°,则∠BDC =( )A .50°B .100°C .120°D .130°13.(2016湖南省湘西州)一个等腰三角形一边长为4cm ,另一边长为5cm ,那么这个等腰三角形的周长是( )A .13cmB .14cmC .13cm 或14cmD .以上都不对14.(2016青海省)已知等腰三角形的腰和底的长分别是一元二次方程2680x x -+=的根,则该三角形的周长为( )A .8B .10C .8或10D .1215.(2016宁夏)菱形ABCD 的对角线AC ,BD 相交于点O ,E ,F 分别是AD ,CD 边上的中点,连接EF .若EF =2,BD =2,则菱形ABCD 的面积为( )A .22B .2C .62D .8216.(2016广东省广州市)如图,已知△ABC 中,AB =10,AC =8,BC =6,DE 是AC 的垂直平分线,DE 交AB 于点D ,连接CD ,则CD =( )A .3B .4C .4.8D .517.(2016新疆)如图,在△ABC 中,D 、E 分别是AB 、AC 的中点,下列说法中不正确的是( )A .DE =12BCB .AD AE AB AC = C .△ADE ∽△ABCD .S △ADE :S △ABC =1:2 18.(2016广西梧州市)在△ABC 中,AB =3,BC =4,AC =2,D 、E 、F 分别为AB 、BC 、AC 中点,连接DF 、FE ,则四边形DBEF 的周长是( )A.5B.7C.9D.1119.(2016陕西省)如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC 的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为()A.7B.8C.9D.1020.(2016江苏省苏州市)如图,在四边形ABCD中,∠ABC=90°,AB=BC =22,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为()A.2B .C .D.321.(2016湖北省咸宁市)如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①12DEBC=;②ΔDOEΔCOB12SS=;③AD OEAB OB=;④ΔODEΔADC13SS=其中正确的个数有()A.1个B.2个C.3个D.4个22.(2016湖南省永州市)对下列生活现象的解释其数学原理运用错误的是()A.把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理B.木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理C.将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理D.将车轮设计为圆形是运用了“圆的旋转对称性”的原理23.(2016内蒙古包头市)如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为()A.3B.33C.32D.2224.(2016江苏省淮安市)如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于12MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是()A.15B.30C.45D.6025.(2016福建省厦门市)如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,则下列结论正确的是()A.EF=CF B.EF=DE C.CF<BD D.EF>DE 26.(2016辽宁省葫芦岛市)如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为()A.4B.8C.23D.43二、填空题27.(2016上海市)在△ABC中,点D、E分别是边AB、AC的中点,那么△ADE的面积与△ABC 的面积的比是.28.(2016山东省青岛市)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为.29.(2016江苏省南京市)如图,AB、CD相交于点O,OC=2,OD=3,AC∥BD,EF是△ODB的中位线,且EF=2,则AC的长为.30.(2016湖北省随州市)如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=13BD,连接DM、DN、MN.若AB=6,则DN= .31.(2016辽宁省沈阳市)如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,M E,DN与ME 相交于点O.若△OMN是直角三角形,则DO的长是.32.(2016青海省西宁市)如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是.33.(2016黑龙江省大庆市)如图,①是一个三角形,分别连接这个三角形三边中点得到图②,再连接图②中间小三角形三边的中点得到图③,按这样的方法进行下去,第n个图形中共有三角形的个数为.34.(2016江苏省淮安市)已知一个等腰三角形的两边长分别为2和4,则该等腰三角形的周长是.35.(2016河北省)如图,已知∠AOB=7°,一条光线从点A出发后射向OB边.若光线与OB边垂直,则光线沿原路返回到点A,此时∠A=90°-7°=83°.当∠A<83°时,光线射到OB边上的点A1后,经OB反射到线段AO上的点A2,易知∠1=∠2.若A1A2⊥AO,光线又会沿A2→A1→A原路返回到点A,此时∠A=__ ___°.……若光线从点A发出后,经若干次反射能沿原路返回到点A,则锐角∠A的最小值=___ ____°.[来源:学36.(2016江苏省连云港市)如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2= .37.(2016湖北省随州市)已知等腰三角形的一边长为9,另一边长为方程28150x x -+=的根,则该等腰三角形的周长为 .38.(2016青海省)如图,已知∠CAE 是△ABC 的外角,AD ∥BC ,且AD 是∠EAC 的平分线,若∠B =71°,则∠BAC = .39.(2016湖南省常德市)如图,OP 为∠AOB 的平分线,PC ⊥OB 于点C ,且PC =3,点P 到OA 的距离为 .40.(2016四川省广安市)如图,三个正方形的边长分别为2,6,8;则图中阴影部分的面积为 .41.(2016浙江省宁波市)如图,点A 为函数9y x =(x >0)图象上一点,连结OA ,交函数1y x =(x >0)的图象于点B ,点C 是x 轴上一点,且AO =AC ,则△ABC 的面积为 .42.(2016浙江省金华市)由6根钢管首尾顺次铰接而成六边形钢架AB CDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=F A=2米.(铰接点长度忽略不计)(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是米.(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是米.三、解答题43.(2016福建省厦门市)如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n﹣m,n)是四边形ABCD内的一点,且△P AD与△PBC的面积相等,求n﹣m的值.44.(2016山东省滨州市)如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC 于点E,F,G,连接ED,DG.(1)请判断四边形EBGD的形状,并说明理由;(2)若∠ABC=30°,∠C=45°,ED=210,点H是BD上的一个动点,求HG+HC的最小值.45.(2016湖北省咸宁市)证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.已知:如图,∠AOC=∠BOC,点P在OC上,求证:.请你补全已知和求证,并写出证明过程.46.(2016福建省厦门市)如图,在平面直角坐标系中xOy中,已知点A(1,m+1),B(a,m+1),C(3,m+3),D(1,m+a),m>0,1<a<3,点P(n﹣m,n)是四边形ABCD内的一点,且△P AD与△PBC的面积相等,求n﹣m的值.47.(2016浙江省绍兴市)如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.(1)若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,如图,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.(2)若固定一根木条AB不动,AB=2cm,量得木条CD=5cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A、C、D能构成周长为30cm的三角形,求出木条AD,BC的长度.48.(2016山东省淄博市)如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.(1)求证:A E=AF;(2)求证:B E=12(AB+AC).49.(2016广东省)如图,已知△ABC中,D为AB的中点.(1)请用尺规作图法作边AC的中点E,并连结DE(保留作图痕迹,不要求写作法);(2)在(1)的条件下,若DE=4,求B C的长.50.(2016广西钦州市)如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF (1)求证:B F=DC;(2)求证:四边形ABFD是平行四边形.51.(2016北京市)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.(1)求证:B M=MN;(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.☞考点归纳归纳1:三角形的有关线段基础知识归纳:中线:连接一个顶点与它对边中点的线段,三角形的三条中线的交点叫做三角形的重心高线:从三角形一个顶点到它对边所在直线的垂线段.角平分线:一个内角的平分线与这个角的对边相交,顶点与交点之间的线段中位线:连接三角形两边中点的线段基本方法归纳:三角形的中位线平行线于第三边,且等于第三边的一半注意问题归纳:三角形的中线将三角形分成面积相等的两部分【例1】(2017江苏省镇江市)如图,Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,过AC的中点E作EF∥CD交AB于点F,则EF= .归纳2:三角形的三边关系基础知识归纳:三角形两边的和大于第三边,两边的差小于第三边.基本方法归纳:三角形的三边关系是判断三条线段能否构成三角形的依据,并且还可以利用三边关系列出不等式求某些量的取值范围.注意问题归纳:三角形的三边关系是中考的热点问题之一,是解决三角形的边的有关问题的重要依据.【例2】(2017贵州省黔西南州)已知一个等腰三角形的两边长分别为3和6,则该等腰三角形的周长是.归纳3:内角和定理基础知识归纳:三角形三个内角的和等于180°.基本方法归纳:在同一个三角形中,大边对大角,小边对小角.注意问题归纳:三角形的内角和定理是求三角形一个角的度数或证明角相等的重要工具.【例3】(2017湖南省郴州市)小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于()A.180°B.210°C.360°D.270°归纳4:三角形的外角基础知识归纳:(1)三角形的外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于任何一个和它不相邻的内角.基本方法归纳:三角形的外角等于与它不相邻的两个内角的和.注意问题归纳:三角形的外角是解决角的计算与角的大小比较的重要工具.【例4】(2017浙江省绍兴市)已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.(1)如图,若点D在线段BC上,点E在线段AC上.①如果∠ABC=60°,∠ADE=70°,那么α=_______,β=_______.②求α、β之间的关系式.(2)是否存在不同于以上②中的α、β之间的关系式?若存在,求出这个关系式,若不存在,请说明理由.☞1年模拟一、选择题1.三角形的重心是()A.三角形三条边上中线的交点B.三角形三条边上高线的交点C.三角形三条边垂直平分线的交点D.三角形三条内角平行线的交点2.如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB 所在直线的距离等于()A.1B.2C.32D.23.如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为()A.54°B.62°C.64°D.74°4.如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的()A.B.C.D.5.长度分别为2,7,x的三条线段能组成一个三角形,x的值可以是()A.4B.5C.6D.96.在探索“尺规三等分角”这个数学名题的过程中,曾利用了下图,该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠F AE=∠FEA.若∠ACB=21°,则∠ECD的度数是()A.7°B.21°C.23°D.24°7.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于()A.30°B.40°C.60°D.70°8.如图,在△ABC中,∠BAC=x°,∠B=2x°,∠C=3x°,则∠BAD=()A.145°B.150°C.155°D.160°9.小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于()A.180°B.210°C.360°D.270°10.已知a,b,c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为()A.2a+2b﹣2c B.2a+2b C.2c D.011.如图,∠ACD=120°,∠B=20°,则∠A的度数是()A.120°B.90°C.100°D.30°12.如图,在ΔABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE =25°,则∠DAC的大小是()A.15°B.20°C.25°D.30°A.15°B.20°C.25°D.30°13.如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=13 CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为()A.6B.4C.7D.1214.如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是()A.∠ECD=112.5°B.DE平分∠FDC C.∠DEC=30°D.AB=2CD二、填空题15.如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为m.16.在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1= °.三、解答题17.已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.(1)如图,若点D在线段BC上,点E在线段AC上.①如果∠ABC=60°,∠ADE=70°,那么α=_______,β=_______.②求α、β之间的关系式.(2)是否存在不同于以上②中的α、β之间的关系式?若存在,求出这个关系式,若不存在,请说明理由.。
中考数学 专题17 三角形及其性质(解析版)

第四篇图形的性质专题17三角形及其性质知 识 点名师点晴中线、角平分线、高线理解三角形有关的中线、角平分线、高线,并会作三角形的中线、角平分线、高线三角形的重要线段三角形的中位线理解并掌握三角形的中位线的性质三角形的三边关系两边之和大于第三边,两边之差小于第三边理解三角形的三边关系,并能确定三角形第三边的取值范围三角形的内角和定理三角形的内角和等于180°掌握三角形的内角和定理,并会证明三角形的内角和定理三角形的外角三角形的外角的性质能利用三角形的外角进行角的有关计算与证明归纳1:三角形的有关线段基础知识归纳:中线:连接一个顶点与它对边中点的线段,三角形的三条中线的交点叫做三角形的重心高线:从三角形一个顶点到它对边所在直线的垂线段.角平分线:一个内角的平分线与这个角的对边相交,顶点与交点之间的线段中位线:连接三角形两边中点的线段基本方法归纳:三角形的中位线平行线于第三边,且等于第三边的一半注意问题归纳:三角形的中线将三角形分成面积相等的两部分【例1】(2019湖北省恩施州,第6题,3分)如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,已知∠ADE=65°,则∠CFE的度数为( )A.60° B.65° C.70° D.75°【答案】B.【分析】根据三角形的中位线定理得到DE∥BC,EF∥AB,由平行线的性质得出∠ADE=∠B,∠B=∠EFC,即可得出答案.【详解】∵点D、E、F分别是AB、AC、BC的中点,∴DE∥BC,EF∥AB,∴∠ADE=∠B,∠B=∠EFC,∴∠ADE=∠EFC=65°.故选B.【点睛】本题考查了三角形的中位线定理,平行线的性质的应用,注意:两直线平行,同位角相等.考点:三角形中位线定理.归纳2:三角形的三边关系基础知识归纳:三角形两边的和大于第三边,两边的差小于第三边.基本方法归纳:三角形的三边关系是判断三条线段能否构成三角形的依据,并且还可以利用三边关系列出不等式求某些量的取值范围.注意问题归纳:三角形的三边关系是中考的热点问题之一,是解决三角形的边的有关问题的重要依据.【例2】(2019四川省内江市,第9题,3分)一个等腰三角形的底边长是6,腰长是一元二次方程x 2﹣8x +15=0的一根,则此三角形的周长是( )A .16B .12C .14D .12或16【答案】A .【分析】先利用因式分解法解方程求出x 的值,再根据三角形三边关系得出三角形的三边长度,继而相加即可得.【详解】解方程x 2﹣8x +15=0,得:x =3或x =5,若腰长为3,则三角形的三边为3、3、6,显然不能构成三角形;若腰长为5,则三角形三边长为5、5、6,此时三角形的周长为16.故选A .【点睛】本题考查了解一元二次方程和等腰三角形的性质,三角形的三边关系定理等知识点,能求出符合的所有情况是解答此题的关键.考点:1.解一元二次方程﹣因式分解法;2.三角形三边关系;3.等腰三角形的性质.归纳 3:内角和定理基础知识归纳:三角形三个内角的和等于180°.基本方法归纳:在同一个三角形中,大边对大角,小边对小角.注意问题归纳:三角形的内角和定理是求三角形一个角的度数或证明角相等的重要工具.【例3】(2019青岛,第7题,3分)如图,BD 是△ABC 的角平分线,AE ⊥BD ,垂足为F .若∠ABC =35°,∠C =50°,则∠CDE 的度数为( )A .35°B .40°C .45°D .50°【答案】C .【分析】根据角平分线的定义和垂直的定义得到∠ABD =∠EBD ∠ABC ,∠AFB =∠EFB =90°,12=352︒=推出AB =BE ,根据等腰三角形的性质得到AF =EF ,求得AD =ED ,得到∠DAF =∠DEF ,根据三角形的外角的性质即可得到结论.【详解】∵BD 是△ABC 的角平分线,AE ⊥BD ,∴∠ABD =∠EBD ∠ABC ,∠AFB =∠EFB =9012=352︒=°,∴∠BAF =∠BEF =90°﹣17.5°,∴AB =BE ,∴AF =EF ,∴AD =ED ,∴∠DAF =∠DEF .∵∠BAC =180°﹣∠ABC ﹣∠C =95°,∴∠BED =∠BAD =95°,∴∠CDE =95°﹣50°=45°.故选C .【点睛】本题考查了三角形的内角和,全等三角形的判定和性质,三角形的外角的性质,熟练掌握全等三角形的判定和性质是解题的关键.考点:三角形内角和定理.归纳 4:三角形的外角基础知识归纳:(1)三角形的外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于任何一个和它不相邻的内角.基本方法归纳:三角形的外角等于与它不相邻的两个内角的和.注意问题归纳:三角形的外角是解决角的计算与角的大小比较的重要工具.【例4】(2019黑龙江省哈尔滨市,第18题,3分)在△ABC 中,∠A =50°,∠B =30°,点D 在AB 边上,连接CD ,若△ACD 为直角三角形,则∠BCD 的度数为 度.【答案】60或10.【分析】当△ACD 为直角三角形时,存在两种情况:∠ADC =90°或∠ACD =90°,根据三角形的内角和定理可得结论.【详解】分两种情况:①如图1,当∠ADC =90°时.∵∠B=30°,∴∠BCD=90°﹣30°=60°;②如图2,当∠ACD=90°时.∵∠A=50°,∠B=30°,∴∠ACB=180°﹣30°﹣50°=100°,∴∠BCD=100°﹣90°=10°.综上,则∠BCD的度数为60°或10°.故答案为:60或10.【点睛】本题考查了三角形的内角和定理和三角形外角的性质,分情况讨论是本题的关键.考点:1.三角形内角和定理;2.三角形的外角性质;3.分类讨论.【2019年题组】一、选择题1.(2019内蒙古包头市,第10题,3分)已知等腰三角形的三边长分别为a、b、4,且a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,则m的值是( )A.34 B.30 C.30或34 D.30或36【答案】A.【分析】分三种情况讨论,①当a=4时,②当b=4时,③当a=b时;结合韦达定理即可求解.【详解】当a=4时,b<8.∵a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,∴4+b=12,∴b=8不符合;当b=4时,a<8.∵a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,∴4+a=12,∴a=8不符合;当a=b时.∵a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,∴12=2a=2b,∴a=b=6,∴m+2=36,∴m=34.故选A.【点睛】本题考查了一元二次方程根与系数的关系;根据等腰三角形的性质进行分类讨论,结合韦达定理和三角形三边关系进行解题是关键.考点:1.一元二次方程的解;2.根的判别式;3.三角形三边关系;4.等腰三角形的性质;5.分类讨论.2.(2019内蒙古赤峰市,第13题,3分)如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )A.65° B.70° C.75° D.85°【答案】B.【分析】根据三角形外角与内角的关系及三角形内角和定理解答.【详解】∵DE⊥AB,∠A=35°,∴∠AFE=∠CFD=55°,∴∠ACB=∠D+∠CFD=15°+55°=70°.故选B.【点睛】本题考查了三角形外角与内角的关系:三角形的一个外角等于和它不相邻的两个内角的和.三角形内角和定理:三角形的三个内角和为180°.考点:三角形内角和定理.3.(2019四川省内江市,第4题,3分)下列事件为必然事件的是( )A.袋中有4个蓝球,2个绿球,共6个球,随机摸出一个球是红球B.三角形的内角和为180°C.打开电视机,任选一个频道,屏幕上正在播放广告D.抛掷一枚硬币两次,第一次正面向上,第二次反面向上【答案】B.【分析】一定会发生的事情称为必然事件.依据定义即可解答.【详解】A.袋中有4个蓝球,2个绿球,共6个球,随机摸出一个球是红球是不可能事件;B.三角形的内角和为180°是必然事件;C.打开电视机,任选一个频道,屏幕上正在播放广告是随机事件;D.抛掷一枚硬币两次,第一次正面向上,第二次反面向上是随机事件.故选B.【点睛】本题考查了随机事件,关键是理解必然事件为一定会发生的事件;解决此类问题,要学会关注身边的事物,并用数学的思想和方法去分析、看待、解决问题,提高自身的数学素养.考点:1.三角形内角和定理;2.随机事件.4.(2019四川省眉山市,第5题,3分)如图,在△ABC中,AD平分∠BAC交BC于点D,∠B=30°,∠ADC=70°,则∠C的度数是( )A.50° B.60° C.70° D.80°【答案】C.【分析】由∠B=30°,∠ADC=70°,利用外角的性质求出∠BAD,再利用AD平分∠BAC,求出∠BAC,再利用三角形的内角和,即可求出∠C的度数.【详解】∵∠B=30°,∠ADC=70°,∴∠BAD=∠ADC﹣∠B=70°﹣30°=40°.∵AD平分∠BAC,∴∠BAC=2∠BAD=80°,∴∠C=180°﹣∠B﹣∠BAC=180°﹣30°﹣80°=70°.故选C.【点睛】本题考查了三角形的外角性质定理,角平分线的定义以及三角形的内角和定理,本题较为综合,但难度不大.考点:1.三角形内角和定理;2.三角形的外角性质.5.(2019自贡,第6题,4分)已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为( )A.7 B.8 C.9 D.10【答案】C.【分析】根据三角形的三边关系“第三边大于两边之差,而小于两边之和”,求得第三边的取值范围;再根据第三边是整数,从而求得周长.【详解】设第三边为x,根据三角形的三边关系,得:4﹣1<x<4+1,即3<x<5.∵x为整数,∴x的值为4.三角形的周长为1+4+4=9.故选C.【点睛】本题考查了三角形的三边关系.关键是正确确定第三边的取值范围.考点:三角形三边关系.6.(2019枣庄,第3题,3分)将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )A.45° B.60° C.75° D.85°【答案】C.【分析】先根据三角形的内角和得出∠CGF=∠DGB=45°,再利用∠α=∠D+∠DGB可得答案.【详解】如图,∵∠ACD=90°、∠F=45°,∴∠CGF=∠DGB=45°,则∠α=∠D+∠DGB=30°+45°=75°.故选C.【点睛】本题考查了三角形的外角的性质,解题的关键是掌握三角形的内角和定理和三角形外角的性质.考点:三角形的外角性质.7.(2019滨州,第10题,3分)满足下列条件时,△ABC不是直角三角形的为( )A.AB BC=4,AC=5 B.AB:B C:A C=3:4:5C .∠A :∠B :∠C =3:4:5D .|cosA |+(tanB 2=012-【答案】C .【分析】依据勾股定理的逆定理,三角形内角和定理以及直角三角形的性质,即可得到结论.【详解】A .∵,∴△ABC 是直角三角形,错误;22254251641+=+==B .∵(3x )2+(4x )2=9x 2+16x 2=25x 2=(5x )2,∴△ABC 是直角三角形,错误;C .∵∠A :∠B :∠C =3:4:5,∴∠C ,∴△ABC 不是直角三角形,正51807590345=⨯︒=︒≠︒++确;D .∵|cosA |+(tanB 2=0,∴,∴∠A =60°,∠B =30°,∴∠C =9012-12cosA tanB ==,°,∴△ABC 是直角三角形,错误.故选C .【点睛】本题考查了直角三角形的判定及勾股定理的逆定理,掌握直角三角形的判定及勾股定理的逆定理是解题的关键.考点:1.非负数的性质:绝对值;2.非负数的性质:偶次方;3.三角形内角和定理;4.勾股定理的逆定理;5.特殊角的三角函数值.8.(2019广西,第3题,3分)下列事件为必然事件的是( )A .打开电视机,正在播放新闻B .任意画一个三角形,其内角和是180°C .买一张电影票,座位号是奇数号D .掷一枚质地均匀的硬币,正面朝上【答案】B .【分析】必然事件就是一定发生的事件,即发生的概率是1的事件.【详解】∵A ,C ,D 选项为不确定事件,即随机事件,故不符合题意,∴一定发生的事件只有B ,任意画一个三角形,其内角和是180°,是必然事件,符合题意.故选B .【点睛】本题考查了对必然事件的概念的理解.解决此类问题,要学会关注身边的事物,并用数学的思想和方法去分析、看待、解决问题,提高自身的数学素养.用到的知识点为:必然事件指在一定条件下一定发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.考点:1.三角形内角和定理;2.随机事件.9.(2019广西,第5题,3分)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )A.60° B.65° C.75° D.85°【答案】C.【分析】利用三角形外角性质(三角形的一个外角等于不相邻的两个内角和)解题或利用三角形内角和解题皆可.【详解】如图:∵∠BCA=60°,∠DCE=45°,∴∠2=180°﹣60°﹣45°=75°.∵HF∥BC,∴∠1=∠2=75°.故选C.【点睛】主要考查了一副三角板所对应的角度是60°,45°,30°,90°和三角形外角的性质.本题容易,解法很灵活.考点:1.平行线的性质;2.三角形的外角性质.10.(2019广西百色市,第1题,3分)三角形的内角和等于( )A.90° B.180° C.270° D.360°【答案】B.【分析】根据三角形的内角和定理进行解答便可.【详解】因为三角形的内角和等于180度.故选B.【点睛】本题考查了三角形的内角和定理,熟记“三角形的内角和等于180度“是解题的关键.考点:三角形内角和定理.11.(2019江苏省徐州市,第3题,3分)下列长度的三条线段,能组成三角形的是( )A .2,2,4B .5,6,12C .5,7,2D .6,8,10【答案】D .【分析】根据三角形两边之和大于第三边可以判断各个选项中的三天线段是否能组成三角形,本题得以解决.【详解】∵2+2=4,∴2,2,4不能组成三角形,故选项A 错误.∵5+6<12,∴5,6,12不能组成三角形,故选项B 错误.∵5+2=7,∴5,7,2不能组成三角形,故选项C 错误.∵6+8>10,∴6,8,10能组成三角形,故选项D 正确.故选D .【点睛】本题考查了三角形三边关系,解答本题的关键是明确三角形两边之和大于第三边.考点:三角形三边关系.12.(2019江苏省扬州市,第7题,3分)已知n 是正整数,若一个三角形的3边长分别是n +2、n +8、3n ,则满足条件的n 的值有( )A .4个B .5个C .6个D .7个【答案】D .【分析】分两种情况讨论:①若n +2<n +8≤3n ,②若n +2<3n ≤n +8,分别依据三角形三边关系进行求解即可.【详解】①若n +2<n +8≤3n ,则:,解得:,即4≤n <10,∴正整数n 有628383n n n n n +++⎧⎨+≤⎩>104n n ⎧⎨≥⎩<个:4,5,6,7,8,9;②若n +2<3n ≤n +8,则:,解得:,即2<n ≤4,∴正整数n 有2个:3和4;23838n n n n n +++⎧⎨≤+⎩>24n n ⎧⎨≤⎩>综上所述:满足条件的n 的值有7个.故选D .【点睛】本题考查了三角形三边关系的运用,在运用三角形三边关系判定三条线段能否构成三角形时,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.考点:1.三角形三边关系;2.分类讨论.13.(2019江苏省淮安市,第5题,3分)下列长度的3根小木棒不能搭成三角形的是( )A .2cm ,3cm ,4cm B .1cm ,2cm ,3cmC.3cm,4cm,5cm D.4cm,5cm,6cm【答案】B.【分析】看哪个选项中两条较小的边的和大于最大的边即可.【详解】A.2+3>4,能构成三角形,不合题意;B.1+2=3,不能构成三角形,符合题意;C.4+3>5,能构成三角形,不合题意;D.4+5>6,能构成三角形,不合题意.故选B.【点睛】本题考查了三角形三边关系,看能否组成三角形的简便方法:看较小的两个数的和能否大于第三个数.考点:三角形三边关系.14.(2019浙江省台州市,第4题,4分)下列长度的三条线段,能组成三角形的是( )A.3,4,8 B.5,6,10 C.5,5,11 D.5,6,11【答案】B.【分析】根据三角形的三边关系即可求【详解】A选项,3+4=7<8,两边之和小于第三边,故不能组成三角形B选项,5+6=11>10,10﹣5<6,两边之各大于第三边,两边之差小于第三边,故能组成三角形C选项,5+5=10<11,两边之和小于第三边,故不能组成三角形D选项,5+6=11,两边之和不大于第三边,故不能组成三角形故选B.【点睛】本题考查了三角形的三边关系,要掌握并熟记三角形的三边关系:在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边.考点:三角形三边关系.15.(2019浙江省杭州市,第7题,3分)在△ABC中,若一个内角等于另外两个内角的差,则( )A.必有一个内角等于30° B.必有一个内角等于45°C.必有一个内角等于60° D.必有一个内角等于90°【答案】D.【分析】根据三角形内角和定理得出∠A+∠B+∠C=180°,把∠C=∠A+∠B代入求出∠C即可.【详解】∵∠A+∠B+∠C=180°,∠A=∠C﹣∠B,∴2∠C=180°,∴∠C=90°,∴△ABC是直角三角形.故选D.【点睛】本题考查了三角形内角和定理的应用,能求出三角形最大角的度数是解答此题的关键,注意:三角形的内角和等于180°.考点:三角形内角和定理.16.(2019浙江省绍兴市,第5题,4分)如图,墙上钉着三根木条a,b,C,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角是( )A.5° B.10° C.30° D.70°【答案】B.【分析】根据对顶角相等求出∠3,根据三角形内角和定理计算,得到答案.【详解】∠3=∠2=100°,∴木条a,b所在直线所夹的锐角=180°﹣100°﹣70°=10°.故选B.【点睛】本题考查了三角形内角和定理、对顶角的性质,掌握三角形内角和等于180°是解题的关键.考点:1.对顶角、邻补角;2.三角形内角和定理.17.(2019金华,第3题,3分)若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A.1 B.2 C.3 D.8【答案】C.【分析】根据三角形三边关系定理得出5﹣3<a<5+3,求出即可.【详解】由三角形三边关系定理得:5﹣3<a<5+3,即2<a<8,即符合的只有3.故选C.【点睛】本题考查了三角形三边关系定理,能根据定理得出5﹣3<a<5+3是解答此题的关键,注意:三角形的两边之和大于第三边,三角形的两边之差小于第三边.考点:三角形三边关系.18.(2019湖北省荆门市,第4题,3分)将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则∠1的度数是( )A.95° B.100° C.105° D.110°【答案】C.【分析】根据题意求出∠2、∠4,根据对顶角的性质、三角形的外角性质计算即可.【详解】由题意得:∠2=45°,∠4=90°﹣30°=60°,∴∠3=∠2=45°,由三角形的外角性质可知,∠1=∠3+∠4=105°.故选C.【点睛】本题考查了三角形的外角性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.考点:1.三角形内角和定理;2.三角形的外角性质;3.多边形内角与外角.19.(2019湖南省长沙市,第4题,3分)下列事件中,是必然事件的是( )A.购买一张彩票,中奖B.射击运动员射击一次,命中靶心C.经过有交通信号灯的路口,遇到红灯D.任意画一个三角形,其内角和是180°【答案】D.【分析】先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,必然事件和不可能事件都是确定的.【详解】A.购买一张彩票中奖,属于随机事件,不合题意;B.射击运动员射击一次,命中靶心,属于随机事件,不合题意;C.经过有交通信号灯的路口,遇到红灯,属于随机事件,不合题意;D.任意画一个三角形,其内角和是180°,属于必然事件,符合题意.故选D.【点睛】本题考查了必然事件,事先能肯定它一定会发生的事件称为必然事件.考点:1.三角形内角和定理;2.随机事件.20.(2019贵州省毕节市,第12题,3分)在下列长度的三条线段中,不能组成三角形的是( )A.2cm,3cm,4cm B.3cm,6cm,6cmC.2cm,2cm,6cm D.5cm,6cm,7cm【答案】C.【分析】根据三角形任意两边的和大于第三边,进行分析判断.【详解】A.2+3>4,能组成三角形;B.3+6>6,能组成三角形;C.2+2<6,不能组成三角形;D.5+6>7,能够组成三角形.故选C.【点睛】本题考查了能够组成三角形三边的条件.注意:用两条较短的线段相加,如果大于最长那条就能够组成三角形.考点:三角形三边关系.21.(2019贵州省黔东南州,第7题,4分)在下列长度的三条线段中,不能组成三角形的是( )A.2cm,3cm,4cm B.3cm,6cm,6cmC.2cm,2cm,6cm D.5cm,6cm,7cm【分析】根据三角形任意两边的和大于第三边,进行分析判断.【详解】A.2+3>4,能组成三角形;B.3+6>6,能组成三角形;C.2+2<6,不能组成三角形;D.5+6>7,能够组成三角形.故选C.【点睛】本题考查了能够组成三角形三边的条件.注意:用两条较短的线段相加,如果大于最长那条就能够组成三角形.考点:三角形三边关系.22.(2019辽宁省丹东市,第7题,3分)等腰三角形一边长为2,它的另外两条边的长度是关于x的一元二次方程x2﹣6x+k=0的两个实数根,则k的值是( )A.8 B.9 C.8或9 D.12【答案】B.【分析】根据一元二次方程的解法以及等腰三角形的性质即可求出答案.【详解】当等腰三角形的底边为2时,此时关于x的一元二次方程x2﹣6x+k=0的有两个相等实数根,∴△=36﹣4k=0,∴k=9,此时两腰长为3.∵2+3>3,∴k=9满足题意,当等腰三角形的腰长为2时,此时x=2是方程x2﹣6x+k=0的其中一根,∴4﹣12+k=0,∴k=8,此时另外一根为:x=4.∵2+2=4,∴不能组成三角形.综上所述:k=9.故选B.【点睛】本题考查了一元二次方程,解题的关键是熟练运用一元二次方程的解法以及等腰三角形的性质,本题属于中等题型.考点:1.一元二次方程的解;2.根的判别式;3.三角形三边关系;4.等腰三角形的性质;5.分类讨论.23.(2019辽宁省抚顺市,第7题,3分)若一个等腰三角形的两边长分别为2,4,则第三边的长为( )A.2 B.3 C.4 D.2或4【分析】分4是腰长与底边两种情况,再根据三角形任意两边之和大于第三边讨论求解即可.【详解】①4是腰长时,三角形的三边分别为4、4、2,能组成三角形,所以,第三边为4;②4是底边时,三角形的三边分别为2、2、4.∵2+2=4,∴不能组成三角形.综上所述:第三边为4.故选C.【点睛】本题考查了等腰三角形的性质,三角形的三边关系,难点在于要分情况讨论.考点:1.三角形三边关系;2.等腰三角形的性质;3.分类讨论.24.(2019辽宁省营口市,第4题,3分)如图,AD是△ABC的外角∠EAC的平分线,AD∥BC,∠B=32°,则∠C的度数是( )A.64° B.32° C.30° D.40°【答案】B.【分析】根据平行线的性质求出∠EAD,根据角平分线的定义得到∠EAC=2∠EAD=64°,根据三角形的外角性质计算即可.【详解】∵AD∥BC,∴∠EAD=∠B=32°.∵AD是△ABC的外角∠EAC的平分线,∴∠EAC=2∠EAD=64°.∵∠EAC是△ABC的外角,∴∠C=∠EAC﹣∠B=64°﹣32°=32°.故选B.【点睛】本题考查了平行线的性质、三角形的外角性质、角平分线的定义,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.考点:1.平行线的性质;2.三角形内角和定理;3.三角形的外角性质.25.(2019辽宁省铁岭市,第7题,3分)如图,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )A .45°B .50°C .55°D .80°【答案】B .【分析】连接AC 并延长交EF 于点M .由平行线的性质得∠3=∠1,∠2=∠4,再由等量代换得∠BAD =∠3+∠4=∠1+∠2=∠FCE ,先求出∠FCE 即可求出∠A .【详解】连接AC 并延长交EF 于点M .∵AB ∥CF ,∴∠3=∠1.∵AD ∥CE ,∴∠2=∠4,∴∠BAD =∠3+∠4=∠1+∠2=∠FCE .∵∠FCE =180°﹣∠E ﹣∠F =180°﹣80°﹣50°=50°,∴∠BAD =∠FCE =50°.故选B .【点睛】本题考查了平行线的性质以及三角形的内角和定理,属于基础题型.考点:1.平行线的性质;2.三角形内角和定理.26.(2019黑龙江省大庆市,第8题,3分)如图,在△ABC 中,BE 是∠ABC 的平分线,CE 是外角∠ACM 的平分线,BE 与CE 相交于点E ,若∠A =60°,则∠BEC 是( )A .15°B .30°C .45°D .60°【答案】B .【分析】根据角平分线的定义得到∠EBM ∠ABC 、∠ECM ∠ACM ,根据三角形的外角性质计算即12=12=可.【详解】∵BE 是∠ABC 的平分线,∴∠EBM ∠ABC .12=∵CE 是外角∠ACM 的平分线,∴∠ECM ∠ACM ,则∠BEC =∠ECM ﹣∠EBM (∠ACM ﹣∠12=12=⨯ABC )∠A =30°.12=故选B .【点睛】本题考查了三角形的外角性质、角平分线的定义,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.考点:三角形的外角性质.27.(2019内蒙古赤峰市,第8题,3分)如图,菱形ABCD 周长为20,对角线AC 、BD 相交于点O ,E 是CD 的中点,则OE 的长是( )A .2.5B .3C .4D .5【答案】A .【分析】由菱形的性质可先求得菱形的边长,再由三角形中位线定理可求得OE 的长.【详解】∵四边形ABCD 为菱形,∴CD =BC 5,且O 为BD 的中点.204==∵E 为CD 的中点,∴OE 为△BCD 的中位线,∴OE CB =2.5.12=故选A .【点睛】本题考查了菱形的性质,掌握菱形的四条边都相等、对角线互相垂直平分是解题的关键.考点:1.直角三角形斜边上的中线;2.三角形中位线定理;3.菱形的性质.28.(2019广西河池市,第7题,3分)如图,在△ABC 中,D ,E 分别是AB ,BC 的中点,点F 在DE 延长线上,添加一个条件使四边形ADFC 为平行四边形,则这个条件是( )A .∠B =∠F B .∠B =∠BCFC .AC =CFD .AD =CF【答案】B .【分析】利用三角形中位线定理得到DE ∥AC ,DE =AC ,结合平行四边形的判定定理进行选择.12【详解】∵在△ABC 中,D ,E 分别是AB ,BC 的中点,∴DE 是△ABC 的中位线,∴DE ∥AC ,DE =12AC .A .根据∠B =∠F 不能判定AC ∥DF ,即不能判定四边形ADFC 为平行四边形,故本选项错误.B .根据∠B =∠BCF 可以判定CF ∥AB ,即CF ∥AD ,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC 为平行四边形,故本选项正确.C .根据AC =CF 不能判定AC ∥DF ,即不能判定四边形ADFC 为平行四边形,故本选项错误.D .根据AD =CF ,FD ∥AC 不能判定四边形ADFC 为平行四边形,故本选项错误.故选B .【点睛】本题三角形的中位线的性质和平行四边形的判定.三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.考点:1.三角形中位线定理;2.平行四边形的判定.29.(2019江苏省盐城市,第4题,3分)如图,点D 、E 分别是△ABC 边BA 、BC 的中点,AC =3,则DE 的长为( )A .2B .C .3D .4332【答案】D .【分析】直接利用中位线的定义得出DE 是△ABC 的中位线,进而利用中位线的性质得出答案.【详解】∵点D 、E 分别是△ABC 的边BA 、BC 的中点,∴DE 是△ABC 的中位线,∴DE AC =1.5.12故选D .【点睛】本题考查了三角形中位线定理,正确得出DE 是△ABC 的中位线是解题的关键.考点:三角形中位线定理.30.(2019湖北省襄阳市,第10题,3分)如图,AD 是⊙O 的直径,BC 是弦,四边形OBCD 是平行四边形,AC 与OB 相交于点P ,下列结论错误的是( )A .AP =2OPB .CD =2OPC .OB ⊥ACD .AC 平分OB【答案】A .【分析】利用圆周角定理得到∠ACD =90°,再根据平行四边形的性质得到CD ∥OB ,CD =OB ,则可求出∠A =30°.在Rt △AOP 中利用含30度的直角三角形三边的关系可对A 选项进行判断;利用OP ∥CD ,CD ⊥AC 可对C 选项进行判断;利用垂径可判断OP 为△ACD 的中位线,则CD =2OP ,原式可对B 选项进行判断;同时得到OB =2OP ,则可对D 选项进行判断.【详解】∵AD 为直径,∴∠ACD =90°.∵四边形OBCD 为平行四边形,∴CD ∥OB ,CD =OB .在Rt △ACD 中,sinA ,∴∠A =3012CD AD ==°.在Rt △AOP 中,AP ,所以A 选项的结论错误;=∵OP ∥CD ,CD ⊥AC ,∴OP ⊥AC ,所以C 选项的结论正确;∴AP =CP ,∴OP 为△ACD 的中位线,∴CD =2OP ,所以B 选项的结论正确;∴OB =2OP ,∴AC 平分OB ,所以D 选项的结论正确.故选A .【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理和平行四边形的性质.考点:1.三角形中位线定理;2.平行四边形的性质;3.垂径定理;4.圆周角定理.31.(2019西藏,第6题,3分)如图,在△ABC 中,D ,E 分别为AB 、AC 边上的中点,则△ADE 与△ABC 的面积之比是( )A .1:4B .1:3C .1:2D .2:1【答案】A .【分析】根据相似三角形的性质即可求出答案.。
中考数学复习第四单元三角形第17课时三角形
⑥ BC
高线
⑩ 锐角(ruìjiǎo)
三角形的三条高的交点在三角形
AD⊥⑧
,即
BC
的内部; ⑪
三角形的三条高的交点是直
直角(zhíjiǎo)
∠ADB=⑨________
∠ADC
角顶点; ⑫
三角形的三条高所在直线的
钝角
=90°
交点在三角形的外部,这个点称为垂心
内
部,中线将三角形分成两个面积相等的三角形
[解析]∵|a-7|+(b-1)2=0,
c=
.
∴a-7=0,b-1=0,即a=7,b=1,
由三角形两边之和大于第三(dì sān)边,两
高
频
考
向
探
究
边之差小于第三边得到7-1<c<7+1,
即6<c<8.
∵c为奇数,∴c=7.故填7.
第十九页,共三十三页。
基
础
知
识
巩
固
高
频
考
向
探
究
考向三
三角形内角与外角(wài jiǎo)的应用
有两个(liǎnɡ ɡè)锐角”是
.(填“真命题”或
[答案]真命题
[解析]如果三角形有两个直角或钝角,那
么内角和就大于180°,所以三角形中最多
“假命题”)
只能(zhī nénɡ)有一个钝角或直角,至少有两个
高
频
考
向
探
究
锐角,故原命题为真命题.
第十五页,共三十三页。
基
础
知
识
巩
固
3. [2019·安徽]命题(mìng tí)“如果a+b=0,那么a,b互为相反数”的逆命题为
