铰链和辊轴的受力分析-完整版
辊间轴向力分析

四辊可逆轧机轧辊轴向力分析由于工作辊是主动辊, 它带动支承辊转动。
因此若把工作辊表面的线速度沿支承辊的轴线和与轴线垂直的方向分解, 则所得的分量v b1必定等于支承辊表面的线速度v b, (假设两辊在沿着支承辊圆周的切线方向无滑动) 即:v b= v w cosa= v b1同时也得到了v w沿支承辊轴线的分量v wc 为v wc= v w sina。
上式表明, 两辊轴线的不平行使工作辊沿支承辊的轴线产生了相对滑动。
不难看出, 只要两辊的轴线不平行, 即a 角不为零, 相对滑动速度v wc就始终不为零。
尽管a 角很小,工作辊表面各质点与支承辊表面各质点沿轴向的相对滑动速度v wc仍不可忽视, 而这一滑动必将产生轴向滑动摩擦力, 换言之, 只要两辊的轴线不平行, 两辊间就有滑动摩擦力存在。
工作中, 辊系将受到轧制力P 的作用, 两辊的接触面是一条窄带,图1下辊系支撑辊和工作辊接触面速度分析在这条窄带上, 两辊沿支承辊的轴线有一个相对滑动速度v wc , 根据摩擦理论可知: 支承辊必定要给工作辊一个与v wc方向相反的滑动摩擦力的作用, 而它本身同时受到一个与v wc方向相同的滑动摩擦力的作用,两摩擦力在接触窄带上是以剪应力流的形式存在的。
当两辊轴线夹角不变而转动方向相反时则摩擦力反向,即随着轧件的往复轧制工作辊将做往复窜动,这种现象是与实际情况相符的。
轴向力及窜动距离大小计算。
假设轧制力为P,两辊夹角α,辊间压力为F,轧件长度l,锻钢与铸铁间摩擦系数f,工作辊轴向受力为X1,工作辊窜动距离为A。
F≈1.04P,X1=Ffcosα=1.04Pfcosα[设f=0.1,P=3000吨,夹角为0.1度,则F=1.04×3000×0.1×cos(0.1×3.14159÷180)=312吨] A=lsinαcosα[设l=25000mm,α=0.1度,则A=25000×sin(0.1×3.14159÷180)×cos(0.1×3.14159÷180)=43.6mm]从以上各式可知,轧件越长则窜动距离越远,轧制力越大窜动力越大,这是与实际情况相符的。
平面构件的受力分析

的垂直距离d有关,用它们的乘积来度量,
称为力矩。
二、基本公理
公理1 二力平衡公理
作用于刚体上的两个力,使刚体平衡的必要与充分条件是: 这两个力大小相等 | F1 | = | F2 | , 方向相反 F1 = –F2 , 作用在同一直线上。
公理2 加减平衡力系原理
在已知力系上加上或减去任意一个平衡力系,并不改变原 力系对刚体的作用。
5、受力图上只画外力,不画内力。 一个力,属于外力还是内力,因研究对象的不同,有 可能不同。当物体系统拆开来分析时,原系统的部分 内力,就成为新研究对象的外力。
6 、同一系统各研究对象的受力图必须整体与局部一致,相 互协调,不能相互矛盾。 对于某一处的约束反力的方向一旦设定,在整体、局 部或单个物体的受力图上要与之保持一致。
FA
千牛顿(kN)
2. 力系:是指作用在物体上的一群力。 (1)平衡力系 (2)等效力系 (3)合力 (4)分力
F2 F3
A
F
3.刚体
就是在力的作用下,大小和形状都不 变的物体。
4.力矩
若某物体具有一固定支点O,受力F作用,
当力F的作用线不通过固定支点O时,则物
d
体将产生转动效应。
OLeabharlann F其转动效应与力F的大小和点O到力F作用线
P P
N
N
NB NA
3.光滑圆柱铰链约束
概念:物体经圆柱铰链联接所形成的约束,圆柱铰链是由两个 端部带圆孔的构件,用一个销轴连接而成的。
YA
A
A
XA
A
②固定铰支座
固定铰支座
滑槽与销钉 (双面约束)
二力杆
活动铰支座(辊轴支座)
正八工作辊的轴向力原因以及计算比较

工作辊轴承轴向力的原因分析以及计算比较一.轴向力产生的原因:1.跑偏当钢带跑偏时由于钢带与工作辊摩擦,导致工作辊往跑偏方向偏移,同时两侧水平受力不均,轧辊产生一定的水平方向交叉产生轴向力。
2. 轧机牌坊倾斜这其中包括机架牌坊相对中心线的不对称、下支承辊楔铁的不水平都会导致工作辊产生倾斜产生轴向力。
3.机架的震动由于轧机在工作时产生震动,导致轧辊在各个方向窜动。
4.弯辊力不均弯辊力是作用在轴承座上,操作侧与传动侧的弯辊力产生差值时,轧辊两侧受力不同产生倾斜,观察对比发现,轧机在工作时1、2、3架的弯辊力两侧差值一般小于5KN,4、5架差值差值一般在20KN左右,有的甚至达到80KN 以上。
5. 轧辊的弧度和轧辊的应力变形以及轧辊轴向的硬度不均轧辊有一定的弧度,在轧制过程中轧辊也可能会向两边产生一定的倾斜产生轴向力,当轴向的硬度不均时,轧辊在轧制过程中产生的变形量不同,轧辊也会出现倾斜。
6.轧制中两边的张力不均在轧制过程中机架与机架之间存在张力,当操作侧与传动侧的张力产生偏差时由于摩擦会使工作辊在水平方向产生一定的交叉产生轴向力。
观察发现在轧制时1、2、3架之间的张力差值几乎为0,而4、5架之间的张力差达到30KN。
7.轧制过程中的边浪、镰刀弯当轧制过程中产生边浪时,说明轧辊两侧的间隙量产生了差值,这就说明轧辊有了一定的倾斜,这也会产生轴向力。
8. 轧制力的偏差轧制过程中轧制出现偏差时由于轧辊受力不均也会产生倾斜,实际观察发现4、5架的轧制力偏差可以达到2t。
9.轧辊扁头与接轴器扁头配合间隙大导致轧机在运转时甩动量大产生的轴向力。
10.轧辊与接轴架的中心不同轴中间辊产生偏心转动,产生轴向力。
11.十字万向传动轴的十字头轴承间隙过大在轧制过程中使万向轴跳动过大产生轴向力。
对于以上轴向力产生的原因,其中轧辊交叉产生的轴向力最大,同时又会导致轴承座中的轴承内外圈产生不同轴,导致轴承产生局部磨损严重,游隙增大,滚动体局部受力,大大降低了推力轴承的寿命。
开炼机辊筒受力分析

开炼机辊筒受力分析开炼机的辊筒工作时受有较大的横压力、摩擦力、温度应力、大小驱动齿轮和速比齿轮的作用力。
由于胶料横压力的作用,辊筒要承受弯曲应力,由于胶料的摩擦力和轴承的摩擦力作用,辊筒要承受扭转应力,可见辊筒实际上是受有弯曲和扭转的复合应力。
此外,辊筒的自重作用都必须给予考虑。
由于辊筒内外温度差而引起的温度应力和冷硬铸造产生的内应力都对辊筒强度有影响,在精确计算时都应考虑。
担内应力因计算困难,一般可在安全系数中考虑即可。
辊筒在工作状态下的负荷如图2-33所示。
1.胶料对辊筒的横压力P p=p·L公斤P px=P p·cosβ公斤P py=P p sinβ公斤式中P p——总横压力,公斤;P——单位横压力,公斤/厘米;P px,P py——横压力的水平分力,垂直分力,公斤。
2.驱动齿轮的作用力大小驱动齿轮在传动过程中,齿轮间便产生相互作用的力(如图2-33所示):圆周作用力P的方向与节圆相切;径向作用力T的方向与齿轮的半径方向一致。
大驱动齿轮圆周作用力:P =12d M k 公斤 式中M k ——作用在大驱动齿轮上的扭矩,公斤∙厘米;d 1——大驱动齿轮的节圆直径,厘米。
这里应指出:经电动机、减速器、大驱动齿轮传来的扭矩,是供前后辊加工胶料的需要,故由前后辊筒共同承担。
即 M k =M k1+M k2公斤∙厘米M k1=9740011n N 公斤∙厘米 M k2=9740022n N 公斤∙厘米式中 M k ---大驱动齿轮的扭矩,公斤∙厘米;M k1、M k2——前、后辊扭矩,公斤∙厘米;N 1、N 2——后、前辊消耗功率,千瓦;n 1、n 2——后、前辊转数,转/分。
在炼胶时可粗略地认为M k1=M k2圆周作用力的水平分力和垂直分力分别为:P x =P ·cos α'公斤P y =P ·sin α'公斤式中 α'——大小驱动齿轮轴线与垂直线偏移角(一般α'=15~200)。
铰链承重实验报告总结

铰链承重实验报告总结
本实验旨在研究铰链的承重能力。
实验结果表明,铰链能够承受较大的重量,但其承重能力受到多个因素的影响。
首先,我们发现铰链的材质对其承重能力有着决定性的影响。
在实验中,我们使用了不同材质的铰链进行测试,包括钢铁、铝合金和塑料等。
结果显示,钢铁铰链的承重能力最高,而塑料铰链的承重能力最低。
其次,铰链的设计也会影响其承重能力。
在实验中,我们比较了不同设计的铰链,包括单铰链和双铰链。
结果表明,双铰链相对于单铰链来说,承重能力更强。
这是因为双铰链能够分担重量,减小了每个铰链所承受的力的大小。
此外,我们还发现铰链的润滑状况对其承重能力有着影响。
通过在实验中调整润滑剂的使用量,我们发现适量的润滑剂可以减小摩擦力,提高铰链的承重能力。
总而言之,铰链的承重能力受到材质、设计和润滑状况等多个因素的影响。
为了确保铰链正常工作,我们需要选择合适的材质和设计,并对其进行适当的润滑。
此外,在实际应用中,我们还需要根据具体情况对铰链进行加固,以增加其承重能力。
轿车行李箱盖铰链受力分析及在设计中的应用

轿车行李箱盖铰链受力分析及在设计中的应用行李箱平衡铰链,是指使用弹性元件,可以在行李箱盖开启和关闭时平衡盖重力的铰链结构,因为平衡铰链结构简单、有足够强度和可靠耐久等优点,大部分车型特别是中低档车型,基本上采用这种结构的铰链,其弹性元件采用扭杆。
在行李箱盖使用过程中,一般要求启动开启装置后,能自动弹开一定高度,介在半开(一定的打开角度)状态下要保持静止不动以防落下伤人,同时在最在打开位置时有足够的保持力,以防风力作用下自行落下关闭。
一、轿车行李箱盖平衡铰链的受力分析1、铰链情况介绍:行李箱盖平衡铰链简图如图1所示,图2为左侧铰链的侧视图。
图1 行李箱铰链简图(只装一边扭杆)图2 左侧铰链的左侧视图从图2可以看出,扭杆的运动受铰链支架和联杆的约束,只能绕安装口旋转。
因此,支架、铰链、联杆、扭杆构成了四连杆机构,其中铰链支架为固定杆,其它均可以活动。
图2只为铰链的侧视图,实际零件并不在一个平面内。
但是,把各零件投影到同一个平面内,并不影响受力分析,所以可以把铰链的四连机构看作一个平面四连杆机构来分析。
此平面四连杆机构的受力如图3所示:图3:铰链平面四连杆机构的受力图(数据为设定的)图3中,AD表示铰链支架,AB为扭杆,BC为联杆,CD为铰链,其长度如图所示,而四连杆的之间角度φ1、φ2、φ3和φ4的初始值(即行李箱盖铰链全关时的角度)也已经在图3中表示。
另外,把扭杆的扭矩记为M T,而铰链所受的重力(包含行李箱盖和铰链本身)记为G,但是在分析中,把G换为重力对D点的力矩可能更为方便,因此铰链CD就受到重力矩M G的作用。
显然,M T和M G都为变量,随行李箱铰链的开启角度变化而改变。
2、杆的受力分析:存在摩擦力作用时,BC杆不能视作为一根二力杆,在行李盖向上运动时,BC杆的受力如图4所示。
其中摩擦力作用的效果是一个摩擦力隅。
另外,如果把图4中的摩擦力隅M B和M C定义为正负值,则图4可以用于行李箱盖打开和关闭时的受力。
工程力学(静力学答案)
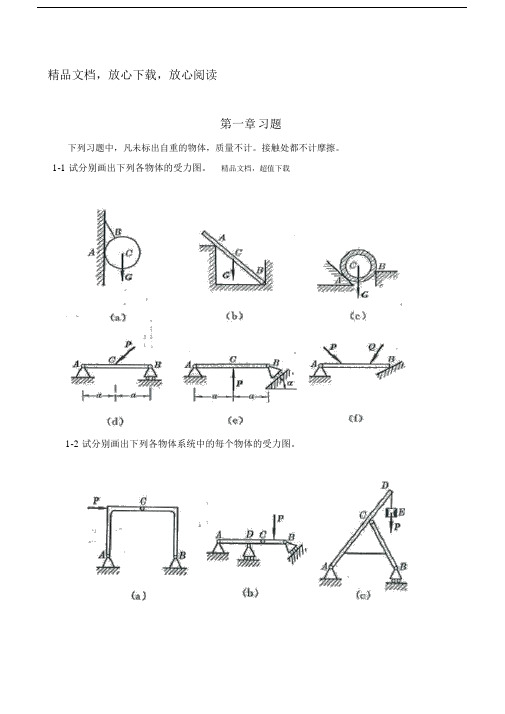
精品文档,放心下载,放心阅读第一章习题下列习题中,凡未标出自重的物体,质量不计。
接触处都不计摩擦。
1-1 试分别画出下列各物体的受力图。
精品文档,超值下载1-2 试分别画出下列各物体系统中的每个物体的受力图。
1-3 试分别画出整个系统以及杆BD ,AD ,AB(带滑轮 C,重物 E 和一段绳索)的受力图。
1-4 构架如图所示,试分别画出杆HED ,杆 BDC 及杆 AEC 的受力图。
1-5 构架如图所示,试分别画出杆BDH ,杆 AB ,销钉 A 及整个系统的受力图。
1-6 构架如图所示,试分别画出杆AEB ,销钉 A 及整个系统的受力图。
1-7 构架如图所示,试分别画出杆AEB ,销钉 C,销钉 A 及整个系统的受力图。
1-8 结构如图所示,力 P 作用在销钉 C 上,试分别画出 AC ,BCE 及 DEH 部分的受力图。
参考答案1-1 解:1-2 解:1-3 解:1-4 解:1-5 解:1-6 解:1-7 解:1-8 解:第二章 习题参考答案2-1 解:由解析法, F RX X P 2 cos P 3 80NF RYY P 1 P 2 sin 140NF R F 2 F 2 161.2N故: RX RY(F R , P 1) arccos F RY 29 44F R2-2 解:即求此力系的合力,沿OB建立 x 坐标,由解析法,有F RX X P1 cos45 P2P3 cos453KNF RY Y P1 sin45 P3 sin 450故:F R F RX2F RY23KN 方向沿OB。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a)由平衡方程有:X 0 F AC sin 30F AB0Y 0 F AC cos30W0联立上二式,解得:F AB0.577W (拉力)FAC 1.155W(压力)(b)由平衡方程有:X 0 F AC F AB cos700Y 0 F AB sin 70W0联立上二式,解得:FAB 1.064W(拉力)F AC0.364W (压力)(c)由平衡方程有:X 0 F AC cos60F AB cos300Y 0 F AB sin 30F AC sin 60 W0联立上二式,解得:FAB 0.5W(拉力)FAC 0.866W(压力)(d)由平衡方程有:X 0 F AB sin 30F AC sin 300Y 0 F AB cos30F AC cos30 W0联立上二式,解得:FAB 0.577W(拉力)FAC 0.577W(拉力)2-4 解:( a)受力分析如图所示:x 0 F RA4P cos 45 0 42由22F RA15.8 KNF RA2F RB P sin 45 042由Y 022F RB7.1KN(b)解:受力分析如图所示:由x 0 F RA 3F RB cos45 P cos45 0 10FRA 1F RB sin 45 P sin 45 0Y 010联立上二式,得:F RA22.4KNF RB10KN2-5 解:几何法:系统受力如图所示三力汇交于点 D,其封闭的力三角形如图示所以:FRA5KN(压力)F RB 5KN(与X轴正向夹150度)2-6 解:受力如图所示:已知, F R G1,F AC G2x 0F r 0由F AC coscos G1 G2由Y 0 F AC sinF N W 0F N W G2 sin W G22G122-7 解:受力分析如图所示,取左半部分为研究对象x 0由P F RA cos 45 F CB cos45 0 Y 0 F CB sin 45F RA sin 450联立后,解得:FRA0.707 PF RB0.707 P由二力平衡定理FRBFCBFCB0.707 P2-8 解:杆 AB,AC均为二力杆,取 A 点平衡x 0由F AC cos 60 F AB cos30 W 0Y 0 F AB sin 30F AC sin 60 W0联立上二式,解得:F AB7.32KN (受压)FAC 27.3KN(受压)2-9 解:各处全为柔索约束,故反力全为拉力,以D, B 点分别列平衡方程(1)取 D 点,列平衡方程x 0T DB sinW cos0由T DB Wctg0(2)取 B 点列平衡方程由Y 0 T sinT BD cos0T T BD ctg Wctg 230KN 2-10 解:取 B 为研究对象:FBC由Y 0 F BC sinP 0Psin取 C 为研究对象:x 0F DC sin F CE sin0由F BC cos由Y 0F BC sin F DC cos F CE cos0联立上二式,且有FBCFBC解得:P cos1 FCEsin2cos2取 E 为研究对象:由 Y 0 F NH F CE cos0F CE F CE 故有:F NH P cos 1 P2 sin 2 cos cos22sin 2-11 解:取 A 点平衡:x 0F AB sin 75 F AD sin 75 0Y 0 F AB cos75 F AD cos75 P 0PF AD F AB联立后可得: 2cos 75取 D 点平衡,取如图坐标系:x 0F AD cos5 F ND cos80 0cos5F ND F ADcos80由对称性及F AD F ADF N2F ND2 cos5FAD2 cos5P166.2KNcos80cos802cos 75 2-12 解:整体受力交于O点,列 O点平衡x 0由F RA cosF DC P cos30 0Y 0 F RA sin P sin 300联立上二式得:F RA 2.92 KNFDC 1.33KN(压力)列 C点平衡4x0FDC FAC53Y0FBCFAC5联立上二式得:FAC1.67KN(拉力)F BC 1.0KN (压力)2-13 解:(1)取 DEH部分,对 H点列平衡x 0 F RD 2F RE 0 5Y0FRD1Q 05联立方程后解得:FRD5QF RE2Q(2)取 ABCE部分,对 C 点列平衡x0F RE F RA cos 450Y 0 F RB F RA sin 45 P0且F RE F RE联立上面各式得:FRA2 2QF RB 2Q P(3)取 BCE 部分。
工程力学静力学(北京科技大东北大学)所有课后习题答案详解供参习

第二章 习题参考答案2-1解:由解析法,23cos 80RX F X P P N θ==+=∑故: 161.2R F N ==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有故: 3R F KN ==方向沿OB 。
2-3解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:联立上二式,解得:0.577AB F W =(拉力)1.155AC F W =(压力)(b ) 由平衡方程有:联立上二式,解得:1.064AB F W =(拉力)0.364AC F W =(压力)(c ) 由平衡方程有:联立上二式,解得:0.5AB F W =(拉力)0.866AC F W =(压力)(d ) 由平衡方程有:联立上二式,解得:0.577AB F W =(拉力)0.577AC F W =(拉力)2-4解:(a )受力分析如图所示:由0x =∑ cos 450RA F P =由0Y =∑ sin 450RA RB F F P +-=(b)解:受力分析如图所示:由联立上二式,得:2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN =(压力)5RB F KN =(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由0x =∑ cos 0AC r F F α-=由0Y =∑ sin 0AC N F F W α+-=2-7解:受力分析如图所示,取左半部分为研究对象由0x =∑ cos45cos450RA CB P F F --=联立后,解得: 0.707RA F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由0x =∑ cos60cos300AC AB F F W ⋅--=联立上二式,解得: 7.32AB F KN =-(受压)27.3AC F KN =(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由0x =∑ sin cos 0DB T W αα-=(2)取B 点列平衡方程由0Y =∑ sin cos 0BD T T αα'-=2-10解:取B 为研究对象:由0Y =∑ sin 0BC F P α-=取C 为研究对象:由0x =∑ cos sin sin 0BC DC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BC BC F F '= 解得:取E 为研究对象:由0Y =∑ cos 0NH CE F F α'-=CE CE F F '=故有:2-11解:取A 点平衡:联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:由对称性及 AD AD F F '=2-12解:整体受力交于O 点,列O 点平衡由 0x =∑cos cos300RA DC F F P α+-=联立上二式得: 2.92RA F KN =1.33DC F KN =(压力)列C 点平衡联立上二式得: 1.67AC F KN =(拉力)1.0BC F KN =-(压力)2-13解:(1)取DEH 部分,对H 点列平衡联立方程后解得: RD F(2)取ABCE 部分,对C 点列平衡且 RE RE F F '=联立上面各式得: RA F =(3)取BCE 部分。
