2019.6.26哈尔滨市中考数学试题
2019年黑龙江省哈尔滨市中考数学试题(含分析解答)
A.
B.
C.பைடு நூலகம்
D.
4.(3 分)(2018•哈尔滨)六个大小相同的正方体搭成的几何体如图所示,其俯视图
是( )
A.
B.
C.
D.
5.(3 分)(2018•哈尔滨)如图,点 P 为⊙O 外一点,PA 为⊙O 的切线,A 为切点,PO 交
⊙O 于点 B,∠P=30°,OB=3,则线段 BP 的长为( )
A.3 B.3 C.6 D.9 6.(3 分)(2018•哈尔滨)将抛物线 y=﹣5x2+1 向左平移 1 个单位长度,再向下平移 2 个单位长度,所得到的抛物线为( ) A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1 C.y=﹣5(x+1)2+3 D.y=﹣5(x﹣1)2+3
23.(8 分)(2018•哈尔滨)为使中华传统文化教育更具有实效性,军宁中学开展以 “我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书
第 3 页(共 45 页)
法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范 围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完 整的统计图,请你根据图中提供的信息回答下列问题: (1)本次调查共抽取了多少名学生? (2)通过计算补全条形统计图; (3)若军宁中学共有 960 名学生,请你估计该中学最喜爱国画的学生有多少名?
二、填空题(每小题 3 分,共计 30 分) 11.(3 分)(2018•哈尔滨)将数 920000000 科学记数法表示为 12.(3 分)(2018•哈尔滨)函数 y= 中,自变量 x 的取值范围是
. .
13.(3 分)(2018•哈尔滨)把多项式 x3﹣25x 分解因式的结果是
2019年黑龙江省哈尔滨市中考数学试卷附分析答案
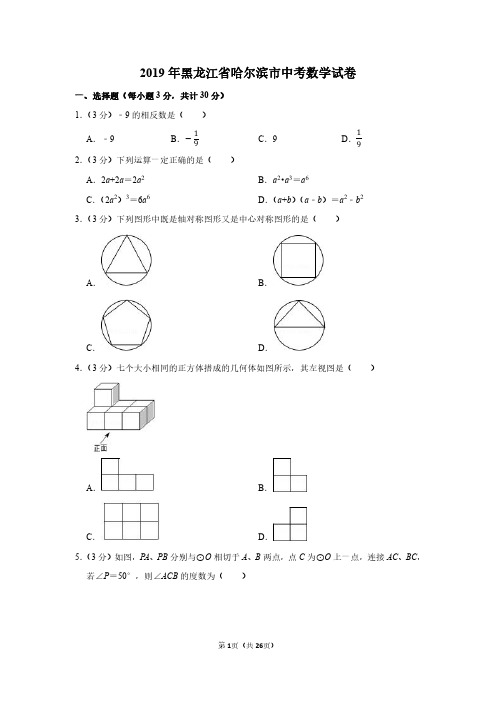
=a(a2﹣6ab+9b2)
=a(a﹣3b)2.
故答案为:a(a﹣3b)2.
t 14.(3 分)不等式组
的解集是 x≥3 .
t
t
【解答】解:解不等式
0,得:x≥3,
解不等式 3x+2≥1,得:x ,
∴不等式组的解集为 x≥3,
故答案为:x≥3. 15.(3 分)二次函数 y=﹣(x﹣6)2+8 的最大值是 8 .
故答案为:6.26×106.
12.(3 分)在函数 y
t t
中,自变量 x 的取值范围是
x
.
【解答】解:函数 y
t t
中分母 2x﹣3≠0,
∴x ;
第 10页(共 26页)
故答案为 x ;
13.(3 分)把多项式 a3﹣6a2b+9ab2 分解因式的结果是 a(a﹣3b)2 .
【解答】解:a3﹣6a2b+9ab2
第 7页(共 26页)
A.
B.
C.
D.
【解答】解:这个立体图形的左视图有 2 列,从左到右分别是 2,1 个正方形,
故选:B.
5.(3 分)如图,PA、PB 分别与⊙O 相切于 A、B 两点,点 C 为⊙O 上一点,连接 AC、BC,
若∠P=50°,则∠ACB 的度数为( )
A.60°
B.75°
C.70°
=2,则 A′B 的长为
.
17.(3 分)一个扇形的弧长是 11πcm,半径是 18cm,则此扇形的圆心角是
度.
18.(3 分)在△ABC 中,∠A=50°,∠B=30°,点 D 在 AB 边上,连接 CD,若△ACD
为直角三角形,则∠BCD 的度数为
2019年哈尔滨市中考数学试题及答案

2019年哈尔滨中考数学试卷一.选择题(共10小题)1.﹣9的相反数是()A.﹣9 B.﹣C.9 D.2.下列运算一定正确的是()A.2a+2a=2a2B.a2•a3=a6C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b23.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.4.七个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.5.如图,PA、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为()A.60°B.75°C.70°D.65°6.将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为()A.y=2(x+2)2+3 B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3 D.y=2(x+2)2﹣37.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为()A.20% B.40% C.18% D.36%8.方程=的解为()A.x=B.x=C.x=D.x=9.点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是()A.(4,﹣1)B.(﹣,1)C.(﹣4,﹣1)D.(,2)10.如图,在▱ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD 于点N,则下列式子一定正确的是()A.=B.=C.=D.=二.填空题(共10小题)11.将数6260000用科学记数法表示为.12.在函数y=中,自变量x的取值范围是.13.把多项式a3﹣6a2b+9ab2分解因式的结果是.14.不等式组的解集是.15.二次函数y=﹣(x﹣6)2+8的最大值是.16.如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC =2,则A′B的长为.17.一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是度.18.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为度.19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为.20.如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,则BC的长为.三.解答题(共7小题)21.先化简再求值:(﹣)÷,其中x=4tan45°+2cos30°.22.图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.(1)在图1中画出以AC为底边的等腰直角三角形ABC,点B在小正方形顶点上;(2)在图2中画出以AC为腰的等腰三角形ACD,点D在小正方形的顶点上,且△ACD的面积为8.23.建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名.24.已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.(1)如图1,求证:AE=CF;(2)如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的.25.寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?26.已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是⊙O的两条弦,AB⊥OE于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P.(1)如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN 交于点R,连接RG,若HK:ME=2:3,BC=,求RG的长.27.如图,在平面直角坐标系中,点O为坐标原点,直线y=x+4与x轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为﹣,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF 的延长线与y轴的负半轴交于点M,连接QM、MR,若tan∠QMR=,求直线PM 的解析式.答案:1.C.2.D.3.B.4.B.5.D.6.B.7.A.8.C.9.A.10.D.11.6.26×106.12.x≠.13.a(a﹣3b)2.14.x≥3.15.8.16..17.110.8.60°或10.19..20.2.21.解:原式=[﹣]÷=(﹣)•=•=,当x=4tan45°+2cos30°=4×1+2×=4+时,原式===.22.解:23.解:(1)根据题意得:18÷30%=60(名),答:在这次调查中,一共抽取了60名学生;(2)60﹣(18+9+12+6)=15(名),则本次调查中,选取国防类书籍的学生有15名,补全条形统计图,如图所示:(3)根据题意得:1500×=225(名),答:该校最想读科技类书籍的学生有225名.24.解:(1)∵四边形ABCD为矩形∴AB∥CD且AB=CD∴∠ABE=∠CDF∵AE⊥BD ∴∠AEB=90°∵CE⊥BD∴∠CFD=90°∴△ABE≌△CDF(AAS)∴AE=CF.(2)△AFD,△ABE,△BEC,△FDC.25.解:(1)设每副围棋x元,每副中国象棋y元,根据题意得:,∴,答:每副围棋16元,每副中国象棋10元;(2)设购买围棋z副,则购买象棋(40﹣z)副,根据题意得:16z+10(40﹣z)≤550,∴z≤25,答:最多可以购买25副围棋;26.解:(1)如图1,∵AB⊥OE于点D,CH⊥MN于点K∴∠ODB=∠OKC=90°∵∠ODB+∠DFK+∠OKC+∠EON=360°∴∠DFK+∠EON=180°∵∠DFK+∠HFB=180°∴∠HFB=∠EON∵∠EON=2∠EHN∴∠HFB=2∠EHN(2)如图2,连接OB,∵OA⊥ME,∴∠AOM=∠AOE∵AB⊥OE∴∠AOE=∠BOE∴∠AOM+∠AOE=∠AOE+∠BOE,即:∠MOE=∠AOB∴ME=AB∵∠EON=4∠CHN,∠EON=2∠EHN ∴∠EHN=2∠CHN∴∠EHC=∠CHN∵CH⊥MN∴∠HPN=∠HNM∵∠HPN=∠EPM,∠HNM=HEM∴∠EPM=∠HEM∴MP=ME∴MP=AB(3)如图3,连接BC,过点A作AF⊥BC于F,过点A作AL⊥MN于L,连接AM,AC,由(2)知:∠EHC=∠CHN,∠AOM=∠AOE∴∠EOC=∠CON∵∠EOC+∠CON+∠AOM+∠AOE=180°∴∠AOE+∠EOC=90°,∠AOM+∠CON=90°∵OA⊥ME,CH⊥MN∴∠OQM=∠OKC=90°,CK=HK,ME=2MQ,∴∠AOM+∠OMQ=90°∴∠CON=∠OMQ∵OC=OA∴△OCK≌△MOQ(AAS)∴CK=OQ=HK∵HK:ME=2:3,即:OQ:2MQ=2:3∴OQ:MQ=4:3∴设OQ=4k,MQ=3k,则OM===5k,AB=ME=6k在Rt△OAC中,AC===5k∵四边形ABCH内接于⊙O,∠AHC=∠AOC=×90°=45°,∴∠ABC=180°﹣∠AHC=180°﹣45°=135°,∴∠ABF=180°﹣∠ABC=180°﹣135°=45°∴AF=BF=AB•cos∠ABF=6k•cos45°=3k在Rt△ACF中,AF2+CF2=AC2即:,解得:k1=1,(不符合题意,舍去)∴OQ=HK=4,MQ=OK=3,OM=ON=5∴KN=KP=2,OP=ON﹣KN﹣KP=5﹣2﹣2=1,在△HKR中,∠HKR=90°,∠RHK=45°,∴=tan∠RHK=tan45°=1∴RK=HK=4∴OR=RN﹣ON=4+2﹣5=1∵∠CON=∠OMQ∴OC∥ME∴∠PGO=∠HEM∵∠EPM=∠HEM∴∠PGO=∠EPM∴OG=OP=OR=1∴∠PGR=90°在Rt△HPK中,PH===2∵∠POG=∠PHN,∠OPG=∠HPN∴△POG∽△PHN∴,即,PG=∴RG===.27.解:(1)∵y=x+4,∴A(﹣3,0)B(0,4),∵点C与点A关于y轴对称,∴C(3,0),设直线BC的解析式为y=kx+b,将B(0,4),C(3,0)代入,,解得k=,b=4,∴直线BC的解析式;(2)如图1,过点A作AD⊥BC于点点D,过点P作PN⊥BC于N,PG⊥OB于点G.∵OA=OC=3,OB=4,∴AC=6,AB=BC=5,∴sin∠ACD=,即,∴AD=,∵点P为直线y=x+4上,∴设P(t,t+4),∴PG=﹣t,cos∠BPG=cos∠BAO,即,∴,∵sin∠ABC=,∴PN==,∵AP=BQ,∴BQ=5+,∴S=,即S=;(3)如图,延长BE至T使ET=EP,连接AT、PT、AM、PT交OA于点S.∵∠APE=∠EBC,∠BAC=∠BCA,∴180°﹣∠APE﹣∠BAC=180°﹣∠EBC﹣∠ACB,∴∠PEA=∠BEC=∠AET,∴PT⊥AE,PS=ST,∴AP=AT,∠TAE=∠PAE=∠ACB,AT∥BC,∴∠TAE=∠FQB,∵∠AFT=∠BFQ,AT=AP=BQ,∴△ATF≌△QBF,∴AF=QF,TF=BF,∵∠PSA=∠BOA=90°,∴PT∥BM,∴∠TBM=∠PTB,∵∠BFM=∠PFT,∴△MBF≌△PTF,∴MF=PF,BM=PT,∴四边形AMPQ为平行四边形,∴AP∥MQ,MQ=AP=BQ,∴∠MQR=∠ABC,过点R作RH⊥MQ于点H,∵sin∠ABC=sin∠MQR=,设QR=25a,HR=24a,则QH=7a,∵tan∠QMR=,∴MH=23a,BQ=MQ=23a+7a=30a,BR=BQ+QR=55a,过点R作RK⊥x轴于点K.∵点R的纵坐标为﹣,∴RK=,∵sin∠BCO=,∴CR=,BR=,∴,a=,∴BQ=30a=3,∴5+=3,t=,∴P(),∴,∵BM=PT=2PS=,BO=4,∴OM=,∴M(0,),设直线PM的解析式为y=mx+n,∴,解得,∴直线PM 的解析式为y =.选择填空解析:一、选择题(每小题3分,共计30分) 1、-9的相反数是( )。
2019年中考数学试题-2019年黑龙江省哈尔滨市中考试题带答案详解

黑龙江省哈尔滨市2019年中考试卷试卷
第I 卷选择题(共
30分)一、选择题(每小题
3分,共计30分)1.-9的相反数是(
)(A )-9
(B )-91(C )9 (D )91【答案】C
【解析】﹣9的相反数是9,故选:C .
2.下列运算一定正确的是(
). (A )2222a a a
(B )632a a a (C )6326)
2(a a (D )2
2))((b a b a b a 【答案】D 【解析】2a+2a =4a ,A 错误;a 2?a 3=a 5,B 错误;(2a 2)3=8a 6
,C 错误;故选:D .
3.下列图形中既是轴对称图形又是中心对称图形的是(). 【答案】B
【解析】A.是轴对称图形,但不是中心对称图形,故此选项错误;
B.是中心对称图形,也是轴对称图形,故此选项正确;
C.是轴对称图形,不是中心对称图形,故此选项错误;
D.是轴对称图形,不是中心对称图形,故此选项错误.故选:
B .4.七个大小相同的正方体搭成的几何体如图所示,其左视图是().
【答案】B
【解析】这个立体图形的左视图有
2列,从左到右分别是2,1个正方形,故选:B .
5.如图,P A,PB 分别与⊙O 相切于A,B 两点,点C 为⊙O 上一点,连接AC,BC,若∠P=50°,则。
2019哈尔滨中考数学试卷及答案(word版)

2019哈尔滨中考数学试卷及答案(word版)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2019哈尔滨中考数学试卷及答案(word版)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2019哈尔滨中考数学试卷及答案(word版)(word版可编辑修改)的全部内容。
哈尔滨市2019年初中升学考试数学试卷一、选择题(每小题3分,共计30分)1、-9的相反数是( )A.—9B.C.9D. -19 192、下列运算正确的是( )A. B.2a +2a =2a 2a 2∙a 3=a 6C. D 。
(2a 2)3=6a 6(a +b)(a ‒b)=a 2‒b 23、下列图形中,既是轴对称图形又是中心对称图形的是( )A B C D4、七个大小相同的正方体搭成的几何体如图所示,其左视图是( )5、如图,PA 、PB 分别与⊙O 相切于A 、B 两点,点C 为⊙O 上一点,连接AC 、BC ,若∠P =50º,则∠ACB 的度数为( )A 。
60ºB 。
75ºC.70ºD.65º6、抛物线向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为y =2x 2( )A B.y =2(x +2)2+3 y =2(x ‒2)2+3C. D 。
y =2(x ‒2)2‒3 y =2(x +2)2‒37、某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( )A 。
20%B 。
40% C. 18% D 。
2019年哈尔滨中考数学试题(解析版)

{题目}12.(2019年哈尔滨T12)函数 y= 3x 中,自变量 x 的取值范围是 . 2x-3
{答案} x 3 2
{解析}本题考查了函数自变量的取值范围;熟练掌握函数中自变量的取值范围的求法是解题的关
键,函数 y= 3x 中分母 2x-3 0 ,∴ x 3 ,因此本题答案为 x 3 .
{题目}18.(2019年哈尔滨T18)在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接 CD,若△ACD为直角三角形,则∠BCD的度数为 度.
{答案}10或60 {解析}本题考查了三角形的内角和定理和三角形外角的性质,分情况讨论是本题的关键,当△ACD
为直角三角形时,存在两种情况:∠ADC=90°或∠ACD=90°,根据三角形的内角和定
所得到的抛物线为( )
A. y=2x+22+3
B. y=2x-22+3
C. y=2x-22-3
D. y=2x+22-3
{答案}B
{解析}本题考查了二次函数的图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减,
将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,得到的抛物线的解析式
{答案} 13 {解析}本题考查了旋转的性质,勾股定理,熟练掌握旋转的性质是本题的关键,∵将△ABC绕点C
逆时针旋转得到△A'B'C,∴AC=A'C=3,∠ACB=∠ACA'=45°,∴∠A'CB=90°∴
A'B= BC 2+A,C2 = 13 ,因此本题答案为 13 . {分值}3
{章节:[1-23-1]图形的旋转} {考点:旋转的性质} {考点:勾股定理的应用} {类别:常考题} {类别:易错题} {难度:3-中等难度}
2019年黑龙江省哈尔滨市中考数学试卷及答案解析
2019年黑龙江省哈尔滨市中考数学试卷一、选择题(每小题3分,共计30分)1.﹣9的相反数是()A.﹣9B.−19C.9D.192.下列运算一定正确的是()A.2a+2a=2a2B.a2•a3=a6C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b23.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.4.七个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.5.如图,P A、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为()A .60°B .75°C .70°D .65°6.将抛物线y =2x 2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( )A .y =2(x +2)2+3B .y =2(x ﹣2)2+3C .y =2(x ﹣2)2﹣3D .y =2(x +2)2﹣37.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( ) A .20% B .40%C .18%D .36%8.方程23x−1=3x的解为( )A .x =311 B .x =113C .x =37D .x =739.点(﹣1,4)在反比例函数y =k x 的图象上,则下列各点在此函数图象上的是( ) A .(4,﹣1)B .(−14,1)C .(﹣4,﹣1)D .(14,2)10.如图,在▱ABCD 中,点E 在对角线BD 上,EM ∥AD ,交AB 于点M ,EN ∥AB ,交AD 于点N ,则下列式子一定正确的是( )A .AM BM=NE DEB .AM AB=AN ADC .BCME=BE BDD .BD BE=BC EM二、填空题(每小题3分,共计30分) 11.将数6260000用科学记数法表示为 . 12.在函数y =3x2x−3中,自变量x 的取值范围是 . 13.把多项式a 3﹣6a 2b +9ab 2分解因式的结果是 .14.不等式组{3−x2≤03x +2≥1的解集是 .15.二次函数y =﹣(x ﹣6)2+8的最大值是 .16.如图,将△ABC 绕点C 逆时针旋转得到△A ′B ′C ,其中点A ′与A 是对应点,点B ′与B 是对应点,点B ′落在边AC 上,连接A ′B ,若∠ACB =45°,AC =3,BC =2,则A ′B 的长为 .17.一个扇形的弧长是11πcm ,半径是18cm ,则此扇形的圆心角是 度.18.在△ABC 中,∠A =50°,∠B =30°,点D 在AB 边上,连接CD ,若△ACD 为直角三角形,则∠BCD 的度数为 度.19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为 .20.如图,在四边形ABCD 中,AB =AD ,BC =DC ,∠A =60°,点E 为AD 边上一点,连接BD 、CE ,CE 与BD 交于点F ,且CE ∥AB ,若AB =8,CE =6,则BC 的长为 .三、解答题(其中21~22题各7分,23-24题各8分,25~27题各10分,共计60分) 21.(7分)先化简再求值:(x+2x−2−x 2−2x x 2−4x+4)÷x−4x−2,其中x =4tan45°+2cos30°.22.(7分)图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.(1)在图1中画出以AC为底边的等腰直角三角形ABC,点B在小正方形顶点上;(2)在图2中画出以AC为腰的等腰三角形ACD,点D在小正方形的顶点上,且△ACD 的面积为8.23.(8分)建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名.24.(8分)已知:在矩形ABCD 中,BD 是对角线,AE ⊥BD 于点E ,CF ⊥BD 于点F . (1)如图1,求证:AE =CF ;(2)如图2,当∠ADB =30°时,连接AF 、CE ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD 面积的18.25.(10分)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?26.(10分)已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是⊙O的两条弦,AB ⊥OE于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P.(1)如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN 交于点R,连接RG,若HK:ME=2:3,BC=√2,求RG的长.27.(10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=43x+4与x轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为−25,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF的延长线与y轴的负半轴交于点M,连接QM、MR,若tan∠QMR=2423,求直线PM的解析式.2019年黑龙江省哈尔滨市中考数学试卷参考答案与试题解析一、选择题(每小题3分,共计30分)1.﹣9的相反数是()A.﹣9B.−19C.9D.19【解答】解:﹣9的相反数是9,故选:C.2.下列运算一定正确的是()A.2a+2a=2a2B.a2•a3=a6C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b2【解答】解:2a+2a=4a,A错误;a2•a3=a5,B错误;(2a2)3=8a6,C错误;故选:D.3.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.【解答】解:A、是轴对称图形,但不是中心对称图形,故此选项错误;B、是中心对称图形,也是轴对称图形,故此选项正确;C、是轴对称图形,不是中心对称图形,故此选项错误;D、是轴对称图形,不是中心对称图形,故此选项错误.故选:B.4.七个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.【解答】解:这个立体图形的左视图有2列,从左到右分别是2,1个正方形,故选:B.5.如图,P A、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为()A.60°B.75°C.70°D.65°【解答】解:连接OA、OB,∵P A、PB分别与⊙O相切于A、B两点,∴OA⊥P A,OB⊥PB,∴∠OAP=∠OBP=90°,∴∠AOB=180°﹣∠P=180°﹣50°=130°,∴∠ACB=12∠AOB=12×130°=65°.故选:D.6.将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为()A.y=2(x+2)2+3B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3D.y=2(x+2)2﹣3【解答】解:将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,得到的抛物线的解析式为y=2(x﹣2)2+3,故选:B.7.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为()A.20%B.40%C.18%D.36%【解答】解:设降价的百分率为x根据题意可列方程为25(1﹣x)2=16解方程得x1=15,x2=95(舍)∴每次降价得百分率为20%故选:A.8.方程23x−1=3x的解为()A.x=311B.x=113C.x=37D.x=73【解答】解:去分母得:2x=9x﹣3,解得:x=3 7,经检验x=37是分式方程的解,故选:C.9.点(﹣1,4)在反比例函数y=kx的图象上,则下列各点在此函数图象上的是()A.(4,﹣1)B.(−14,1)C.(﹣4,﹣1)D.(14,2)【解答】解:将点(﹣1,4)代入y=k x,∴k=﹣4,∴y=−4 x,∴点(4,﹣1)在函数图象上,故选:A.10.如图,在▱ABCD 中,点E 在对角线BD 上,EM ∥AD ,交AB 于点M ,EN ∥AB ,交AD 于点N ,则下列式子一定正确的是( )A .AM BM=NE DEB .AM AB=AN ADC .BCME=BE BDD .BD BE=BC EM【解答】解:∵在▱ABCD 中,EM ∥AD ∴易证四边形AMEN 为平行四边形 ∴易证△BEM ∽△BAD ∽△END ∴AM BM=NE BM=DE BE,A 项错误AM AB =ND AD ,B 项错误 BC ME =ADME =BD BE ,C 项错误 BD BE=AD ME=BC ME,D 项正确故选:D .二、填空题(每小题3分,共计30分)11.将数6260000用科学记数法表示为 6.26×106 . 【解答】解:6260000用科学记数法可表示为6.26×106, 故答案为:6.26×106.12.在函数y =3x 2x−3中,自变量x 的取值范围是 x ≠32 . 【解答】解:函数y =3x2x−3中分母2x ﹣3≠0, ∴x ≠32; 故答案为x ≠32;13.把多项式a 3﹣6a 2b +9ab 2分解因式的结果是 a (a ﹣3b )2 . 【解答】解:a 3﹣6a 2b +9ab 2 =a (a 2﹣6ab +9b 2)=a (a ﹣3b )2. 故答案为:a (a ﹣3b )2.14.不等式组{3−x2≤03x +2≥1的解集是 x ≥3 .【解答】解:解不等式3−x 2≤0,得:x ≥3,解不等式3x +2≥1,得:x ≥−13, ∴不等式组的解集为x ≥3, 故答案为:x ≥3.15.二次函数y =﹣(x ﹣6)2+8的最大值是 8 . 【解答】解:∵a =﹣1<0, ∴y 有最大值,当x =6时,y 有最大值8. 故答案为8.16.如图,将△ABC 绕点C 逆时针旋转得到△A ′B ′C ,其中点A ′与A 是对应点,点B ′与B 是对应点,点B ′落在边AC 上,连接A ′B ,若∠ACB =45°,AC =3,BC =2,则A ′B 的长为 √13 .【解答】解:∵将△ABC 绕点C 逆时针旋转得到△A ′B ′C , ∴AC =A 'C =3,∠ACB =∠ACA '=45° ∴∠A 'CB =90° ∴A 'B =√BC 2+A′C2=√13故答案为√1317.一个扇形的弧长是11πcm ,半径是18cm ,则此扇形的圆心角是 110 度. 【解答】解:根据l =nπr 180=nπ⋅18180=11π, 解得:n =110, 故答案为:110.18.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为60°或10度.【解答】解:分两种情况:①如图1,当∠ADC=90°时,∵∠B=30°,∴∠BCD=90°﹣30°=60°;②如图2,当∠ACD=90°时,∵∠A=50°,∠B=30°,∴∠ACB=180°﹣30°﹣50°=100°,∴∠BCD=100°﹣90°=10°,综上,则∠BCD的度数为60°或10°;故答案为:60°或10;19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为16.【解答】解:列表得:(1,6)(2,6)(3,6)(4,6)(5,6)(6,6)(1,5)(2,5)(3,5)(4,5)(5,5)(6,5)(1,4)(2,4)(3,4)(4,4)(5,4)(6,4)(1,3)(2,3)(3,3)(4,3)(5,3)(6,3)(1,2) (2,2) (3,2) (4,2) (5,2) (6,2) (1,1)(2,1)(3,1)(4,1)(5,1)(6,1)由表可知一共有36种情况,两枚骰子点数相同的有6种, 所以两枚骰子点数相同的概率为636=16,故答案为:16.20.如图,在四边形ABCD 中,AB =AD ,BC =DC ,∠A =60°,点E 为AD 边上一点,连接BD 、CE ,CE 与BD 交于点F ,且CE ∥AB ,若AB =8,CE =6,则BC 的长为 2√7 .【解答】解:如图,连接AC 交BD 于点O∵AB =AD ,BC =DC ,∠A =60°, ∴AC 垂直平分BD ,△ABD 是等边三角形 ∴∠BAO =∠DAO =30°,AB =AD =BD =8, BO =OD =4 ∵CE ∥AB∴∠BAO =∠ACE =30°,∠CED =∠BAD =60° ∴∠DAO =∠ACE =30°∴AE =CE =6 ∴DE =AD ﹣AE =2 ∵∠CED =∠ADB =60° ∴△EDF 是等边三角形 ∴DE =EF =DF =2∴CF =CE ﹣EF =4,OF =OD ﹣DF =2 ∴OC =√CF 2−OF 2=2√3 ∴BC =2+OC2=2√7三、解答题(其中21~22题各7分,23-24题各8分,25~27题各10分,共计60分) 21.(7分)先化简再求值:(x+2x−2−x 2−2xx 2−4x+4)÷x−4x−2,其中x =4tan45°+2cos30°. 【解答】解:原式=[x+2x−2−x(x−2)(x−2)2]÷x−4x−2=(x+2x−2−x x−2)•x−2x−4=2x−2•x−2x−4 =2x−4, 当x =4tan45°+2cos30°=4×1+2×√32=4+√3时,原式=4+3−4=3 =2√33. 22.(7分)图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC 的两个端点均在小正方形的顶点上.(1)在图1中画出以AC 为底边的等腰直角三角形ABC ,点B 在小正方形顶点上; (2)在图2中画出以AC 为腰的等腰三角形ACD ,点D 在小正方形的顶点上,且△ACD 的面积为8.【解答】解;(1)作AC的垂直平分线,作以AC为直径的圆,垂直平分线与圆的交点即为点B;(2)以C为圆心,AC为半径作圆,格点即为点D;23.(8分)建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名.【解答】解:(1)根据题意得:18÷30%=60(名), 答:在这次调查中,一共抽取了60名学生; (2)60﹣(18+9+12+6)=15(名),则本次调查中,选取国防类书籍的学生有15名, 补全条形统计图,如图所示:(3)根据题意得:1500×960=225(名), 答:该校最想读科技类书籍的学生有225名.24.(8分)已知:在矩形ABCD 中,BD 是对角线,AE ⊥BD 于点E ,CF ⊥BD 于点F . (1)如图1,求证:AE =CF ;(2)如图2,当∠ADB =30°时,连接AF 、CE ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD 面积的18.【解答】(1)证明:∵四边形ABCD 是矩形, ∴AB =CD ,AB ∥CD ,AD ∥BC , ∴∠ABE =∠CDF ,∵AE ⊥BD 于点E ,CF ⊥BD 于点F , ∴∠AEB =∠CFD =90°,在△ABE 和△CDF 中,{∠ABE =∠CDF ∠AEB =∠CFDAB =CD ,∴△ABE ≌△CDF (AAS ), ∴AE =CF ;(2)解:△ABE 的面积=△CDF 的面积=△BCE 的面积=△ADF 的面积=矩形ABCD 面积的18.理由如下:∵AD ∥BC ,∴∠CBD =∠ADB =30°, ∵∠ABC =90°, ∴∠ABE =60°, ∵AE ⊥BD , ∴∠BAE =30°, ∴BE =12AB ,AE =12AD ,∴△ABE 的面积=12BE ×AE =12×12AB ×12AD =18AB ×AD =18矩形ABCD 的面积, ∵△ABE ≌△CDF ,∴△CDF 的面积═18矩形ABCD 的面积;作EG ⊥BC 于G ,如图所示: ∵∠CBD =30°,∴EG =12BE =12×12AB =14AB , ∴△BCE 的面积=12BC ×EG =12BC ×14AB =18BC ×AB =18矩形ABCD 的面积,同理:△ADF 的面积=18矩形ABCD 的面积.25.(10分)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?【解答】解:(1)设每副围棋x 元,每副中国象棋y 元,根据题意得:{3x +5y =988x +3y =158, ∴{x =16y =10, ∴每副围棋16元,每副中国象棋10元;(2)设购买围棋z 副,则购买象棋(40﹣z )副,根据题意得:16z +10(40﹣z )≤550,∴z ≤25,∴最多可以购买25副围棋;26.(10分)已知:MN 为⊙O 的直径,OE 为⊙O 的半径,AB 、CH 是⊙O 的两条弦,AB⊥OE 于点D ,CH ⊥MN 于点K ,连接HN 、HE ,HE 与MN 交于点P .(1)如图1,若AB 与CH 交于点F ,求证:∠HFB =2∠EHN ;(2)如图2,连接ME 、OA ,OA 与ME 交于点Q ,若OA ⊥ME ,∠EON =4∠CHN ,求证:MP =AB ;(3)如图3,在(2)的条件下,连接OC 、BC 、AH ,OC 与EH 交于点G ,AH 与MN交于点R,连接RG,若HK:ME=2:3,BC=√2,求RG的长.【解答】解:(1)如图1,∵AB⊥OE于点D,CH⊥MN于点K∴∠ODB=∠OKC=90°∵∠ODB+∠DFK+∠OKC+∠EON=360°∴∠DFK+∠EON=180°∵∠DFK+∠HFB=180°∴∠HFB=∠EON∵∠EON=2∠EHN∴∠HFB=2∠EHN(2)如图2,连接OB,∵OA⊥ME,∴∠AOM=∠AOE∵AB⊥OE∴∠AOE=∠BOE∴∠AOM+∠AOE=∠AOE+∠BOE,即:∠MOE=∠AOB∴ME=AB∵∠EON=4∠CHN,∠EON=2∠EHN∴∠EHN=2∠CHN∴∠EHC=∠CHN∵CH⊥MN∴∠HPN=∠HNM∵∠HPN=∠EPM,∠HNM=HEM∴∠EPM=∠HEM∴MP=ME∴MP=AB(3)如图3,连接BC,过点A作AF⊥BC于F,过点A作AL⊥MN于L,连接AM,AC,由(2)知:∠EHC=∠CHN,∠AOM=∠AOE∴∠EOC=∠CON∵∠EOC+∠CON+∠AOM+∠AOE=180°∴∠AOE+∠EOC=90°,∠AOM+∠CON=90°∵OA⊥ME,CH⊥MN∴∠OQM=∠OKC=90°,CK=HK,ME=2MQ,∴∠AOM+∠OMQ=90°∴∠CON=∠OMQ∵OC=OA∴△OCK≌△MOQ(AAS)∴CK=OQ=HK∵HK:ME=2:3,即:OQ:2MQ=2:3∴OQ:MQ=4:3∴设OQ=4k,MQ=3k,则OM=√OQ2+MQ2=√(4k)2+(3k)2=5k,AB=ME=6k在Rt△OAC中,AC=√OA2+OC2=√(5k)2+(5k)2=5√2k∵四边形ABCH内接于⊙O,∠AHC=12∠AOC=12×90°=45°,∴∠ABC=180°﹣∠AHC=180°﹣45°=135°,∴∠ABF=180°﹣∠ABC=180°﹣135°=45°∴AF=BF=AB•cos∠ABF=6k•cos45°=3√2k在Rt△ACF中,AF2+CF2=AC2即:(3√2k)2+(3√2k+√2)2=(5√2k)2,解得:k1=1,k2=−17(不符合题意,舍去)∴OQ=HK=4,MQ=OK=3,OM=ON=5∴KN=KP=2,OP=ON﹣KN﹣KP=5﹣2﹣2=1,在△HKR中,∠HKR=90°,∠RHK=45°,∴RKHK=tan∠RHK=tan45°=1∴RK=HK=4∴OR=RN﹣ON=4+2﹣5=1∵∠CON=∠OMQ∴OC∥ME∴∠PGO=∠HEM∵∠EPM=∠HEM∴∠PGO=∠EPM∴OG=OP=OR=1∴∠PGR=90°在Rt△HPK中,PH=2+PK2=√42+22=2√5∵∠POG=∠PHN,∠OPG=∠HPN∴△POG∽△PHN∴PGPO =PNPH,即PG1=2√5,PG=2√55∴RG=√RP2−PG2=22−(255)2=4√55.27.(10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=43x+4与x轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为−25,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF的延长线与y轴的负半轴交于点M,连接QM、MR,若tan∠QMR=2423,求直线PM的解析式.【解答】解:(1)∵y=43x+4,∴A(﹣3,0),B(0,4),∵点C与点A关于y轴对称,∴C(3,0),设直线BC 的解析式为y =kx +b ,将B (0,4),C (3,0)代入,{3k +b =0b =4, 解得k =−43,b =4,∴直线BC 的解析式y =−43x +4;(2)如图1,过点A 作AD ⊥BC 于点D ,过点P 作PN ⊥BC 于N ,PG ⊥OB 于点G .∵OA =OC =3,OB =4,∴AC =6,AB =BC =5,∴sin ∠ACD =AD AC =OB BC , 即AD 6=45, ∴AD =245,∵点P 为直线y =43x +4上,∴设P (t ,43t +4), ∴PG =﹣t ,cos ∠BPG =cos ∠BAO ,即PG PB =OA AB=35, ∴PB =−53t ,∵sin ∠ABC =PN PB =AD AB =2455=2425, ∴PN =2425PB =2425×(−53t)=−85t ,∵AP=BQ,∴BQ=5+53 t,∴S=12BQ⋅PN=12(5+53t)⋅(−85t),即S=−43t2−4t;(3)如图,延长BE至T使ET=EP,连接AT、PT、AM,PT交OA于点S.∵∠APE=∠EBC,∠BAC=∠BCA,∴180°﹣∠APE﹣∠BAC=180°﹣∠EBC﹣∠ACB,∴∠PEA=∠BEC=∠AET,∴PT⊥AE,PS=ST,∴AP=AT,∠TAE=∠P AE=∠ACB,AT∥BC,∴∠TAF=∠FQB,∵∠AFT=∠BFQ,AT=AP=BQ,∴△ATF≌△QBF,∴AF=QF,TF=BF,∵∠PSA=∠BOA=90°,∴PT∥BM,∴∠TBM=∠PTB,∵∠BFM=∠PFT,∴△MBF≌△PTF,∴MF=PF,BM=PT,∴四边形AMQP为平行四边形,∴AP∥MQ,MQ=AP=BQ,∴∠MQR=∠ABC,过点R作RH⊥MQ于点H,∵sin∠ABC=sin∠MQR=RHRQ=2425,设QR=25a,HR=24a,则QH=7a,∵tan∠QMR=24 23,∴MH=23a,BQ=MQ=23a+7a=30a,BR=BQ+QR=55a,过点R作RK⊥x轴于点K.∵点R的纵坐标为−2 5,∴RK=2 5,∵sin∠BCO=BOBC=sin∠KCR=KRCR=45,∴CR=12,BR=112,∴55a=112,a=110,∴BQ=30a=3,∴5+53t=3,t=−65,∴P(−65,125),∴PS=12 5,∵BM=PT=2PS=245,BO=4,∴OM=4 5,∴M(0,−4 5),设直线PM的解析式为y=mx+n,∴{−65m+n=125n=−45,解得{m =−83n =−45, ∴直线PM 的解析式为y =−83x −45.。
2019年黑龙江省哈尔滨市中考数学试卷(精品推荐)
2019年黑龙江省哈尔滨市中考数学试卷一、选择题(每小题3分,共计30分)1.(3分)﹣9的相反数是()A.﹣9 B.﹣C.9 D.2.(3分)下列运算一定正确的是()A.2a+2a=2a2B.a2•a3=a6C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b23.(3分)下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.4.(3分)七个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.5.(3分)如图,PA、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为()A.60°B.75°C.70°D.65°6.(3分)将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为()A.y=2(x+2)2+3 B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3 D.y=2(x+2)2﹣37.(3分)某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为()A.20% B.40% C.18% D.36%8.(3分)方程=的解为()A.x=B.x=C.x=D.x=9.(3分)点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是()A.(4,﹣1)B.(﹣,1)C.(﹣4,﹣1)D.(,2)10.(3分)如图,在▱ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是()A.=B.=C.=D.=二、填空题(每小题3分,共计30分)11.(3分)将数6260000用科学记数法表示为.12.(3分)在函数y=中,自变量x的取值范围是.13.(3分)把多项式a3﹣6a2b+9ab2分解因式的结果是.14.(3分)不等式组的解集是.15.(3分)二次函数y=﹣(x﹣6)2+8的最大值是.16.(3分)如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B的长为.17.(3分)一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是度.18.(3分)在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为度.19.(3分)同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为.20.(3分)如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,则BC的长为.三、解答题(其中21~22题各7分,23-24题各8分,25~27题各10分,共计60分)21.(7分)先化简再求值:(﹣)÷,其中x=4tan45°+2cos30°.22.(7分)图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.(1)在图1中画出以AC为底边的等腰直角三角形ABC,点B在小正方形顶点上;(2)在图2中画出以AC为腰的等腰三角形ACD,点D在小正方形的顶点上,且△ACD的面积为8.23.(8分)建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名.24.(8分)已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.(1)如图1,求证:AE=CF;(2)如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的.25.(10分)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?26.(10分)已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是⊙O的两条弦,AB⊥OE 于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P.(1)如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN交于点R,连接RG,若HK:ME=2:3,BC=,求RG的长.27.(10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=x+4与x轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为﹣,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF的延长线与y 轴的负半轴交于点M,连接QM、MR,若tan∠QMR=,求直线PM的解析式.2019年黑龙江省哈尔滨市中考数学试卷参考答案一、选择题(每小题3分,共计30分)1.C; 2.D; 3.B; 4.B; 5.D; 6.B; 7.A; 8.C; 9.A; 10.D;二、填空题(每小题3分,共计30分)11.6.26×106; 12.x≠; 13.a(a﹣3b)2; 14.x≥3; 15.8; 16.; 17.110;18.60°或10; 19.; 20.2;三、解答题(其中21~22题各7分,23-24题各8分,25~27题各10分,共计60分)21.; 22.; 23.; 24.; 25.; 26.; 27.;。
黑龙江省哈尔滨市2019年中考数学试题
绝密★启用前黑龙江省哈尔滨市2019年中考数学试题试卷副标题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 一、单选题1.-9的相反数是( ). A .-9; B .19-; C .9; D .19【答案】C 【解析】 【分析】根据只有符号不同的两个数互为相反数(或和为零的两个数互为相反数)判断即可. 【详解】解:-9的相反数是9, 故选:C . 【点睛】本题主要考查了相反数,掌握相反数的定义是解题的关键. 2.下列运算一定正确的是( ). A .2222a a a +=; B .236a a a ⋅=; C .()32626a a =;D .22()()a b a b a b +-=-【答案】D 【解析】 【分析】根据同类项的合并、幂的运算法则、平方差公式判断.试卷第2页,总20页……………………※答※※题※……………………【详解】解:224a a a +=,A 错误;235a a a ⋅=,B 错误;()32628a a =,C 错误;故选:D . 【点睛】本题主要考查了整式的运算法则及乘法公式,熟练运用整式的法则和公式是解题的关键.3.下列图形中既是轴对称图形又是中心对称图形的是( ). A .B .C .D .【答案】B 【解析】 【分析】根据轴对称图形(在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形)和中心对称图形(在平面内,把一个图形绕着某个点旋转180°,旋转后的图形能与原来的图形重合)的概念综合判断即可. 【详解】解:A.是轴对称图形,但不是中心对称图形,故此选项错误; B.是中心对称图形,也是轴对称图形,故此选项正确; C.是轴对称图形,不是中心对称图形,故此选项错误; D.是轴对称图形,不是中心对称图形,故此选项错误. 故选:B . 【点睛】本题考查了轴对称图形和中心对称图形的概念,熟练掌握两者的判别方法是解题的关键.4.七个大小相同的正方体搭成的几何体如图所示,其左视图是( ).○……………○……__班级:__________○……………○……A . B . C . D .【答案】B 【解析】 【分析】左视图是从左面观察几何体,据此即可判断. 【详解】解:这个立体图形的左视图有2列,从左到右分别是2,1个正方形, 故选:B . 【点睛】本题主要考查几何题的三视图,准确理解三视图是的含义是解题的关键.5.如图,PA .PB 分别与O e 相切于A .B 两点,点C 为O e 上一点,连接AC .BC ,若50P ∠=︒,则ACB ∠的度数为( ).A .60︒;B .75︒;C .70︒;D .65︒.【答案】D 【解析】 【分析】连接OA .OB ,由切线的性质可知90OAP OBP ∠=∠=︒,由四边形内角和可求出AOB ∠的度数,根据圆周角定理(一条弧所对的圆周角等于它所对的圆心角的一半)可知ACB ∠的度数. 【详解】解:连接OA .OB ,∵PA .PB 分别与O e 相切于A .B 两点, ∴OA PA ⊥,OB PB ⊥, ∴90OAP OBP ∠=∠=︒,∴180********AOB P ∠=︒-∠=︒-︒=︒, ∴111306522ACB AOB ︒︒∠=∠=⨯=. 故选:D .试卷第4页,总20页…………○………………○……【点睛】本题主要考查了圆的切线性质及圆周角定理,灵活应用切线性质及圆周角定理是解题的关键.6.将抛物线22y x =向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ). A .22(2)3y x =++; B .22(2)3y x =-+; C .22(2)3y x =--; D .22(2)3y x =+-.【答案】B 【解析】 【分析】根据抛物线图像的平移规律“左加右减,上加下减”即可确定平移后的抛物线解析式. 【详解】解:将抛物线22y x =向上平移3个单位长度,再向右平移2个单位长度,得到的抛物线的解析式为()2223y x =-+, 故选:B . 【点睛】本题考查了二次函数的平移规律,熟练掌握其平移规律是解题的关键.7.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( ). A .20%; B .40%;C .18%;D .36%.【答案】A 【解析】 【分析】可设降价的百分率为x ,第一次降价后的价格为()251x -,第一次降价后的价格为()2251x -,根据题意列方程求解即可.【详解】解:设降价的百分率为x根据题意可列方程为()225116x -= 解方程得115x =,295x =(舍) ∴每次降价得百分率为20% 故选:A . 【点睛】本题考查了一元二次方程的在销售问题中的应用,正确理解题意,找出题中等量关系是解题的关键. 8.方程2331x x =-的解为( ). A .311x =; B .113x =; C .37x =; D .73x =. 【答案】C 【解析】 【详解】 解:2331x x=- 23(31)(31)(31)x x x x x x -=--,∴293x x =-,∴37x =; 将检验37x =是方程的根,∴方程的解为37x =;故选:C . 【点睛】本题主要考查了分式方程及其解法,解分式方程的步骤为:去分母,化为整式方程;移项、合并同类项;系数化为1;检验;结论,熟练掌握分式方程的解法是解题的关键. 9.点()1,4-在反比例函数ky x=的图象上,则下列各点在此函数图象上的是( ). A .()41-, B .1,14⎛⎫-⎪⎝⎭C .()4,1--D .1,24⎛⎫⎪⎝⎭【答案】A试卷第6页,总20页…装………不※※要※※在※※…装………【解析】 【分析】用待定系数法确定反比例函数的解析式,再验证选项中的点是否满足解析式即可,若满足函数解析式,则在函数图像上. 【详解】解:将点()1,4-代入k y x=, ∴4k =-, ∴4y x-=, ∴点()41-,在函数图象上, 故选:A . 【点睛】本题考查了反比例函数解析式的求法及根据解析式确定点在函数图形上,会求反比例函数的解析式是解题的关键.10.如图,在平行四边形ABCD 中,点E 在对角线BD 上,EM AD P ,交AB 于点M ,EN AB P ,交AD 于点N ,则下列式子一定正确的是( ).A .AM NEBM DE= B .AM ANAB AD= C .BC BEME BD= D .BD BCBE EM= 【答案】D 【解析】 【分析】由题意可证四边形AMEN 为平行四边形,BEM BAD END △△△∽∽,根据相似三角形对应线段成比例及平形四边形对边相等的性质判断即可. 【详解】解:∵在ABCD Y 中,EM AD P ∴易证四边形AMEN 为平行四边形 ∴易证BEM BAD END △△△∽∽∴AM NE DEBM BM BE==,A项错误AM NDAB AD=,B项错误BC AD BDME ME BE==,C项错误BD AC BCBE ME ME==,D项正确故选:D.【点睛】本题主要考查了相似三角形的性质、平行四边形的判定与性质,熟练运用两者性质确定线段比例关系是解题的关键.试卷第8页,总20页第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题11.将数6 260 000科学记数法表示为__________. 【答案】66.2610⨯ 【解析】 【分析】科学计数法是把一个数写成10n a ⨯的形式,其中110,a n ≤<为整数,据此即可表示. 【详解】解:6260000用科学记数法可表示为66.2610⨯, 故答案为:66.2610⨯. 【点睛】本题主要考查了科学计数法,准确掌握科学计数法的表示方法是解题的关键. 12.在函数323xy x =-中,自变量x 的取值范围是__________. 【答案】32x ≠ 【解析】 【分析】根据分式的分母不为零即可确定自变量x 的取值范围. 【详解】 解:函数323xy x =-中分母230x -≠, ∴32x ≠; 故答案为32x ≠; 【点睛】本题主要考查了函数及分式的概念,明确分式的分母不为零这一条件是解题的关键. 13.分解因式:32269a a b ab -+=__________. 【答案】()23a a b - 【解析】【分析】因式分解时有公因式先提公因式,然后再考虑用公式法.继续分解. 【详解】解:32269a a b ab -+()22 69a a ab b =-+ ()23a a b =-.故答案为:()23a a b =-. 【点睛】本题主要考查了因式分解,熟练掌握提公因式法和公式法是解题的关键.14.不等式组302321xx -⎧≤⎪⎨⎪+≥⎩的解集是__________.【答案】3x ≥. 【解析】 【分析】先求出两个不等式的解集,取两个解集的公共部分即为不等式组的解集. 【详解】解:解不等式302x-≤,得:3x ≥, 解不等式321x +≥,得:13x ≥-,∴不等式组的解集为3x ≥, 故答案为:3x ≥. 【点睛】本题考查了一元一次不等式组的解法,确定两个不等式解集的公共部分是解题的关键. 15.二次函数2(6)8y x =--+的最大值是__________. 【答案】8 【解析】 【分析】二次函数的顶点式2()y a x h b =-+在x=h 时有最值,a>0时有最小值,a<0时有最大值,题中函数 10a =-<,故其在6x =时有最大值. 【详解】试卷第10页,总20页……订………线※※内※※答※※题……订………解:∵10a =-<, ∴y 有最大值,当6x =时,y 有最大值8. 故答案为8. 【点睛】本题考查了二次函数顶点式求最值,熟练掌握二次函数的表达式及最值的确定方法是解题的关键.16.如图将ABC △绕点C 逆时针旋转得到A B C ''△,其中点A '与A 是对应点,点B ′与B 是对应点,点B ′落在边AC 上,连接A B ',若45ACB ∠=︒,3AC =,2BC =,则A B '的长为__________.【解析】 【分析】由旋转的性质可知3AC AC ='=,45ACB ACA ∠=∠'=︒,故90ACB ∠'=︒,根据勾股定理即可求解. 【详解】解:∵将ABC △绕点C 逆时针旋转得到A B C ''△, ∴3AC AC ='=,45ACB ACA ∠=∠'=︒ ∴90ACB ∠'=︒ ∴A B '==【点睛】本题主要考查了旋转的性质,对应角相等,对应线段相等,旋转角相等,以及勾股定理,灵活运用旋转的性质是解题的关键.17.一个扇形的弧长是11cm π,半径是18cm ,则此扇形的圆心角是________度. 【答案】110 【解析】外…………○…学校:__内…………○…【分析】将扇形弧长和半径的值代入弧长的计算公式180n rl π=(r 为圆的半径,n ︒为扇形的圆心角度数,l 为扇形的弧长)即可求解.【详解】 解:根据1811180180n r n l πππ⋅===, 解得:110n =, 故答案为:110. 【点睛】本题考查了弧长的计算公式,熟练掌握公式,正确理解公式中每个字母所表示的含义是解题的关键.18.在ABC △中,50A ∠=︒,30B ∠=︒,点D 在AB 边上,连接CD ,若ACD V 为直角三角形,则BCD ∠的度数为_______________度. 【答案】60︒或10︒ 【解析】 【分析】当ACD ∆为直角三角形时,有两种情况90ADC ∠=︒或90ACD ∠=︒,依据三角形内角和定理,结合具体图形分类讨论求解即可. 【详解】解:分两种情况:①如图1,当90ADC ∠=︒时,∵30B ∠=︒,∴903060BCD ∠=︒-︒=︒; ②如图2,当90ACD ∠=︒时,试卷第12页,总20页…………○………………○……∵50A ∠=︒,30B ∠=︒,∴1803050100ACB ∠=︒-︒-︒=︒, ∴1009010BCD ∠=︒-︒=︒, 综上,则BCD ∠的度数为60︒或10︒; 故答案为:60︒或10︒; 【点睛】本题主要考查了三角形内角和定理以及数学的分类讨论思想,能够正确进行分类是解题的关键.19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为_______________. 【答案】16【解析】 【分析】用列表法将所有可能结果列举出来,确定所有情况及点数相同的情况,求比值即可. 【详解】 解:列表得:…………外…………○…………订…………学:___________考号:_______…………内…………○…………订…………由表可知一共有36种情况,两枚骰子点数相同的有6种, 所以两枚骰子点数相同的概率为61366=, 故答案为:16. 【点睛】本题考查了用列表法求概率,能够准确列举出所有结果是解题的关键.20.如图,在四边形ABCD 中,AB AD =,BC DC =,60A ∠=︒,点E 为AD 边上一点,连接BD .CE ,CE 与BD 交于点F ,且CE AB ∥,若8AB =,6CE =,则BC 的长为_______________.【答案】 【解析】 【分析】由AB AD =,BC DC =知点A,C 都在BD 的垂直平分线上,因此,可连接AC 交BD 于点O ,易证ABD △是等边三角形,EDF V 是等边三角形,根据等边三角形的性质对三角形中的线段进行等量转换即可求出OB,OC 的长度,应用勾股定理可求解. 【详解】解:如图,连接AC 交BD 于点O∵AB AD =,BC DC =,60A ∠=︒, ∴AC 垂直平分BD ,ABD △是等边三角形试卷第14页,总20页∴30BAO DAO ∠=∠=︒,8AB AD BD ===,4BO OD == ∵CE AB ∥∴30BAO ACE ∠=∠=︒,60CED BAD ∠=∠=︒ ∴30DAO ACE ∠=∠=︒∴6AE CE == ∴2DE AD AE =-= ∵60CED ADB ∠=∠=︒ ∴EDF V 是等边三角形 ∴2DE EF DF ===∴4CF CE EF =-=,2OF OD DF =-= ∴OC == ∴BC ==【点睛】本题主要考查了等边三角形的判定与性质、勾股定理,综合运用等边三角形的判定与性质进行线段间等量关系的转换是解题的关键. 三、解答题21.先化简再求值:22224()2442x x x x x x x x +---÷--+-其中4tan452cos30x =︒+︒. 【答案】3【解析】 【分析】先将多项式进行因式分解,根据分式的加减乘除混合运算法则,先对括号里的进行通分,再将除法转化为乘法,约分化简即可. 【详解】解:原式()()2224222x x x x x x x ⎡⎤-+-=-÷⎢⎥---⎢⎥⎣⎦22224x x x x x x +-⎛⎫=-⋅ ⎪---⎝⎭装............○...姓名:___________班级装............○ (22)24x x x -=⋅-- 24x =-, 当4tan452cos304124x ︒︒=+=⨯+=+ 原式===【点睛】本题主要考查了分式的加减乘除混合运算,熟练应用分式的基本性质进行约分和通分是解题的关键.22.图1.2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC 的两个端点均在小正方形的顶点上;(1)在图1中画出以AC 为底边的等腰直角ABC △,点B 在小正方形顶点上;(2)在图2中画出以AC 为腰的等腰ACD V ,点D 在小正方形的顶点上,且ACD V 的面积为8.【答案】(1)详见解析;(2)详见解析; 【解析】 【分析】(1)由题可知,点B 满足,90BA BC ABC ︒=∠=这两个条件,BA BC =说明点B 在AC 的垂直平分线上,90ABC ︒∠=说明点B 在以AC 为直径的圆上,故可作AC 的垂直平分线及以AC 为直径的圆,其交点即为所求;(2)由题可知,点D 满足CA=CD ,故可以C 为圆心,AC 为半径作圆,交于一格点D ,经计算ACD V 的面积为8,故点D 即为所求. 【详解】试卷第16页,总20页……装…………○…………线…………※※不※※要※※在※※装※……装…………○…………线…………解;(1)作AC 的垂直平分线,作以AC 为直径的圆,垂直平分线与圆的交点即为点B ; (2)以C 为圆心,AC 为半径作圆,格点即为点D ;【点睛】本题主要考查了利用线段垂直平分线的性质及圆的性质作图,正确理解题意并知晓作图依据是解题的关键.23.建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动,为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育.科技.国防.农业.工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图,请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生? (2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名?【答案】(1)在这次调查中,一共抽取了60名学生;(2)详见解析;(3)该校最想读科技类书籍的学生有225名. 【解析】 【分析】(1)由图可知想读教育书籍的人数为18人,所占的百分比为30%,想读教育书籍的人数 其所占百分比=一共抽取的学生人数;(2)想读国防书籍的人数等于抽取的学生总数减去想读其它书籍的人数,根据所求值补全条形统计图即可;(3)先求出抽取学生外…………○……………订…………○……学校:级:___________考号:___________内…………○……………订…………○……中想读科技类书籍的人数所占百分比,再用海庆中学共有的学生总数乘以百分比即可. 【详解】解:(1)根据题意得:1830%60÷= (名), 答:在这次调查中,一共抽取了60名学生; (2)()6018912615-+++=(名), 则本次调查中,选取国防类书籍的学生有15名, 补全条形统计图,如图所示:(3)根据题意得:9150022560⨯=(名), 答:该校最想读科技类书籍的学生有225名. 【点睛】本题主要考查了用样本估计总体、条形与扇形统计图的综合,条形统计图表示的是每组的具体数据,扇形统计图表示的是部分在总体中所占的百分比,理解条形与扇形统计图各自的特征,灵活应用两个图中的数据是解题的关键.24..已知:在矩形ABCD 中,BD 是对角线,AE BD ⊥于点E ,CF BD ⊥于点F ;(1)如图1,求证:AE CF =;(2)如图2,当30ADB ∠=︒时,连接AF .CE ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD 面积的18. 【答案】(1)详见解析;(2)ABE △的面积CDF =△的面积BCE =△的面积ADF=△试卷第18页,总20页的面积=矩形ABCD 面积的18. 【解析】 【分析】(1)结合矩形的性质和已知条件可证ABE CDF △≌△,根据全等三角形对应边相等即知AE CF =,此题得证;(2)可利用直角三角形中30°角所对的直角边等于斜边的一半确定三角形的面积与矩形的面积之间的等量关系.. 【详解】(1)证明:∵四边形ABCD 是矩形, ∴AB CD =,AB CD ∥ ,AD BC ∥, ∴ABE CDF ∠=∠,∵AE BD ⊥于点E ,CF BD ⊥于点F , ∴90AEB CFD ∠=∠=︒,在ABE △和CDF V 中,ABE CDFAEB CFD AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()ABE CDF AAS △≌△, ∴AE CF =;(2)解:ABE △的面积CDF =△的面积BCE =△的面积ADF =△的面积=矩形ABCD 面积的18.理由如下: ∵AD BC ∥,∴30CBD ADB ∠=∠=︒, ∵90ABC ∠=︒, ∴60ABE ∠=︒, ∵AE BD ⊥, ∴30BAE ∠=︒,∴12BE AB =,12AE AD =, ∴ABE △的面积111111222288BE AE AB AD AB AD =⨯=⨯⨯=⨯=矩形ABCD 的面积,∵ABE CDF △≌△,订…………○……__考号:___________订…………○……∴CDF V 的面积18=矩形ABCD 的面积; 作EG BC ⊥于G ,如图所示: ∵30CBD ∠=︒,∴11112224EG BE AB AB ==⨯=, ∴BCE V 的面积1111122488BC EG BC AB BC AB =⨯=⨯=⨯=矩形ABCD 的面积,同理:ADF V 的面积18=矩形ABCD 的面积.【点睛】本题主要考查了矩形的性质、全等三角形的判定与性质、直角三角形中30°角所对的直角边等于斜边的一半,灵活应用矩形的性质证全等,熟练掌握直角三角形30°角的性质是解题的关键.25.寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用,若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋? 【答案】(1)每副围棋16元,每副中国象棋10元;(2)最多可以购买25副围棋; 【解析】 【分析】(1)可设每副围棋x 元,每副中国象棋y 元,根据“若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元”可列出关于x,y 的二元一次方程组,用消元法解之即可.(2)由(1)可知一副围棋和象棋的价格,可设购买围棋z 副,“购买围棋和中国象棋共40副”,知购买象棋()40z -副,根据“总费用不超过550元”可列出关于z 的一元一次不等式组,求出z 的解集,取最大值即可. 【详解】解:(1)设每副围棋x 元,每副中国象棋y 元,试卷第20页,总20页根据题意得:359883158x y x y +=⎧⎨+=⎩,∴1610x y =⎧⎨=⎩, ∴每副围棋16元,每副中国象棋10元; (2)设购买围棋z 副,则购买象棋()40z -副, 根据题意得:()161040550z z +-≤, ∴25z ≤,∴最多可以购买25副围棋; 【点睛】本题考查了二元一次方程组及一元一次不等式的实际应用,理解题意,找准题中等量关系是解题的关键.。
2019年黑龙江省哈尔滨市中考数学试题及标准答案
@def+&/fg‘/bc,
’% hi/j#kl #( mn>?*ohi/j#kl $%) pqrstuvwtn<="tx
yz&nu{|,
)% }~BDz"& &"Mkl?&C&f,
.%- /0123 &" 452675
!"#$%&’() & *+,- &$ *.
;%& .#4<=8>)5/%.?=@"
%
%
#$$ >! $ 2ABC %& 9D6.EFGHI
H% %’&"= ’ >)5/%.?=@%
#!$ >! ! 2ABC %& 9F.EFIH% %&(" = ( >)5/%.?=@"J!%&( .KL9 )" !*+ !"# " $%
& !$
+ï !! b!$
*!+,$"%&$ ! ’#-) !" ’$
//! *0%*"/1*! /%! 2! ! ! /!! 3"34!5#%! %
/(! 2"!!
/)! -!
/*! #/! ! /+! //"! /-6 /" ! *"!
/.6
/ *
!
%"6 %# + 6
.!/0$"12 #$%&& $3 ’ ’#&!%&( $4 ) ’#&*%&’ $4 $+ ’#-) ," ’$
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019.6.26哈市中考数学试题
1、-9的相反数是( )。
A 、-9; B 、-9
1
; C 、9; D 、9
1。
2、下列运算一定正确的是( )。
A 、2222a a a =+;
B 、632a a a =∙;
C 、6326)2(a a =;
D 、22))((b a b a b a -=-+。
3、下列图形中既是轴对称图形又是中心对称图形的是( )。
4、七个大小相同的正方体搭成的几何体如图所示,其左视图是( )。
5、如图,PA 、PB 分别与⊙0相切于A 、B 两点,点C 为⊙O 上一点,连接AC 、BC,若∠P=50°,则∠ACB 的度数为( )。
A 、60°; B 、75°; C 、70°; D 、65°。
6、将抛物线22x y =向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( )。
A 、3)2(22++=x y ;B 、3)2(22+-=x y ;C 、3)2(22--=x y ;D 、3)2(22-+=x y 。
7、某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( )。
A 、20%; B 、40%; C 、18%; D 、36%。
8、方程
x x 3132=-的解为( )。
A 、x=113; B 、x=311; C 、x=73; D 、x=3
7。
9、点(-1,4)在反比例函数x k
y =的图象上,则下列各点在此函数图象上的是( )。
A 、(4,-1);
B 、(-41,1);
C 、(-4,-1);
D 、(4
1
,2)。
10、如图,在平行四边形ABCD 中,点E 在对角线BD 上,EM ∥AD,交AB 于点M,EN ∥AB,交AD 于点N,则下列式子一定正确的是( )。
A 、
DE NE BM AM =; B 、AD AN AB AM =; C 、BD BE ME BC =; D 、EM
BC
BE BD =。
11、将数6 260 000科学记数法表示为_______________。
12、在函数3
23-=
x x
y 中,自变量x 的取值范围是_______________。
13、分解因式:22396ab b a a +-=_______________。
14、不等式组⎪⎩⎪⎨⎧≥+≤-1
230
2
3x x
的解集是________________。
15、二次函数8)6(2+--=x y 的最大值是_______________。
16、如图将△ABC 绕点C 逆时针旋转得到△A ′B ′C,其中点A ′与A 是对应点,点B ′与B 是对应点,点B ′落在边AC 上,连接A ′B,若∠ACB=45°,AC=3,BC=2,则A ′B 的长为____。
17、一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是_____________度。
18、在△ABC 中,∠A=50°,∠B=30°,点D 在AB 边上,连接CD,若△ACD 为直角三角形,则∠BCD 的度数为_______________度。
19、同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为_______________。
20、如图,在四边形ABCD 中,AB=AD,BC=DC,∠A=60°,点E 为AD 边上一点,连接BD 、CE,CE 与BD 交于点F,且CE ∥AB,若AB=8,CE=6,则BC 的长为_______________。
21、先化简再求值:2
4
)44422(2--÷
+----+x x x x x x x ,其中x=4tan45°+2cos30°。
22、图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形
的边长均为1,线段AC 的两个端点均在小正方形的顶点上;(1)在图1中画出以AC 为底边的等腰直角△ABC,点B 在小正方形顶点上;(2)在图2中画出以AC 为腰的等腰△ACD,点D 在小正方形的顶点上,且△ACD 的面积为8。
23、建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动,为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图,请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过
计算补全条形统计图;(3)如果海庆中学
共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名
24、已知:在矩形ABCD 中,BD 是对角线,AE ⊥BD 于点E,CF ⊥BD 于点F ;(1)如图1,求证:AE=CF ;(2)如图2,当∠ADB=30°时,连接AF 、CE,在不添加任何辅助线的情况下,请直
接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD 面积的8
1。
25、寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用,若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?
26、已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是⊙O的两条弦,AB⊥OE于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P;(1)如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;
(3)如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN交于点R,连接RG,若HK:ME=2:3,BC=2,求RG的长。
4x+4与x轴交于点A,与y轴交27、如图,在平面直角坐标系中,点0为坐标原点,直线y=
3
于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;
(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t的取值范围);
2, (3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为-
5
连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF的延长线与y轴的负半轴交
24,求直线PM的解析式。
于点M,连接QM、MR,若tan∠QMR=
23。
