浙教版九年级下册考点专题训练-【学案】建立二次函数模型解决商品经济问题
九年级下册数学二次函数实践与探索(2)导学案及练习

九年级下册数学二次函数实践与探索(2)导学案及练习[本课知识重点]让学生进一步体验把实际问题转化为有关二次函数知识的过程.[创新思维]二次函数的有关知识在经济生活中的应用更为广阔,我们来看这样一个生活中常见的问题:某广告公司设计一幅周长为12米的矩形广告牌,广告设计费为每平方米1000元,设矩形一边长为x 米,面积为S 平方米.请你设计一个方案,使获得的设计费最多,并求出这个费用.你能解决它吗?类似的问题,我们都可以通过建立二次函数的数学模型来解决.[实践与探索]例1.某化工材料经销公司购进了一种化工原料共7000千克,购进价格为每千克30元。
物价部门规定其销售单价不得高于每千克70元,也不得低于30元。
市场调查发现:单价定为70元时,日均销售60千克;单价每降低1元,日均多售出2千克。
在销售过程中,每天还要支出其他费用500元(天数不足一天时,按整天计算)。
设销售单价为x 元,日均获利为y 元。
(1)求y 关于x 的二次函数关系式,并注明x 的取值范围;(2)将(1)中所求出的二次函数配方成ab ac a b x a y 44)2(22-++=的形式,写出顶点坐标;在直角坐标系画出草图;观察图象,指出单价定为多少元时日均获利最多,是多少? 分析 若销售单价为x 元,则每千克降低(70-x )元,日均多售出2(70-x )千克,日均销售量为[60+2(70-x )]千克,每千克获利为(x-30)元,从而可列出函数关系式。
解 (1)根据题意,得500)]70(260)[30(--+-=x x y650026022-+-=x x (30≤x ≤70)。
(2)y 650026022-+-=x x 1950)65(22+--=x 。
顶点坐标为(65,1950)。
二次函数草图略。
经观察可知,当单价定为65元时,日均获利最多,是1950元。
例2。
某公司生产的某种产品,它的成本是2元,售价是3元,年销售量为100万件.为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费是x (十它们的关系如下表:(2)如果把利润看作是销售总额减去成本费和广告费,试写出年利润S (十万元)与广告费x (十万元)的函数关系式;(3)如果投入的年广告费为10~30万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增大?解 (1)设二次函数关系式为c bx ax y ++=2。
二次函数综合(5种题型)-2023年新九年级数学核心知识点与常见题型通关讲解练(浙教版)(解析版)

重难点专项突破:二次函数综合(5种题型)【题型细目表】 题型一:线段周长问题题型二:面积问题题型三:角度问题题型四:特殊三角形问题题型五:特殊四边形问题【考点剖析】题型一:线段周长问题一、解答题【答案】(1)()1,0B b +;(2)b =【分析】(1)根据A 、B 两点关于二次函数的对称轴对称,求得点B 的坐标;(2)根据A 的坐标,求出,b c 的关系式,根据平移求出B '的坐标,代入二次函数,求得b 值.【详解】解(1)∵2y x bx c =−++∴对称轴:直线22b b x a =−= ∴2122b AB b ⎛⎫=⨯+=+ ⎪⎝⎭∵A 点横坐标为-1∴()1,0B b +(2)把()1,0A −代入2y x bx c =−++ 得:10b c −−+=,即1c b =+∵平移线段CB ,使C 与D 重合点∴B 平移后得点31,12b B b ⎛⎫+−− ⎪⎝⎭ ∵点B 在抛物线上 ∴233111122b b b b b ⎛⎫⎛⎫−+++++=−− ⎪ ⎪⎝⎭⎝⎭,解得b = ∵0b >∴b =【点睛】涉及到了点的平移变换和一元二次方程,熟练掌握二次函数的有关性质和点的平移规则是解题的关键. 2.(2023·浙江·九年级专题练习)如图,在平面直角坐标系中,抛物线23y ax bx =+−经过点A (-1,0),B (5,0).(1)求抛物线的表达式.(2)过点C (0,m )作直线l x ∥轴交抛物线于点P ,Q (点P 在点Q 的左侧),若3QC PC =,求m 的值.【答案】(1)2312355y x x =−− (2)215. 【分析】(1)把点A (-1,0),B (5,0)代入抛物线表达式进行计算即可解答;(2)根据已知QC=3PC ,可设点P (-n ,m ),点Q (3n ,m ),然后代入(1)中二次函数表达式即可解答.【详解】(1)把点A (-1,0),B (5,0)代入抛物线y=ax2+bx-3中可得:3025530a b a b −−⎧⎨+−⎩==,解得:35125a b ⎧=⎪⎪⎨⎪=−⎪⎩, ∴抛物线的表达式为:2312355y x x =−−;(2)∵PQ ∥x 轴,QC=3PC ,∴设点P (-n ,m ),点Q (3n ,m ),把点P (-n ,m ),点Q (3n ,m )代入2312355y x x =−−中可得:223123552736355n n m n n m ⎧+−=⎪⎪⎨⎪−−=⎪⎩,解得:2215n m =⎧⎪⎨=⎪⎩, ∴m 的值为215.【点睛】本题考查了待定系数法求二次函数解析式,二次函数图象上点的坐标特征,准确熟练地进行计算是解题的关键.(1)求抛物线1P 的对称轴和点(2)求线段AB 和CD 的长度.【答案】(1)对称轴=1x −;点A 的横坐标是-3(2)7AB =;7CD =【分析】(1)根据对称轴公式直接求抛物线P1的对称轴,以及A ,E 关于对称轴x=-1对称和点E 的横坐标直接求出点A 的横坐标;(2)求出P2的对称轴,再求出点B 的坐标,从而求得AB 的长,把1x =分别代入两个函数表达式,求得7m n −=−,从而求得CD 的长.【详解】(1)抛物线1P 的对称轴12b x a =−=−∵点A 与点E 关于直线=1x −对称,且点E 的横坐标是1∴点A 的横坐标是3−(2)抛物线2P 的对称轴522b x a =−= ∵点B 与点E 关于直线52x =对称,且点E 的横坐标是1 ∴点B 的横坐标是4∴()437AB =−−=把1x =分别代入两个函数表达式,得1215m n ++=−+即7m n −=−由题意,当0x =时,D y n =,C y m =.∴7CD n m =−=【点睛】本题考查二次函数的性质,关键是判断点A 与点E 关于对称轴x=-1对称,点B 与点E 关于对称轴52x =对称. 4.(2023·浙江·九年级专题练习)已知二次函数l 1:y =x 2+6x +5k 和l 2:y =kx 2+6kx +5k ,其中k ≠0且k ≠1.(1)分别直接写出关于二次函数l 1和l 2的对称轴及与y 轴的交点坐标;(2)若两条抛物线l 1和l 2相交于点E ,F ,当k 的值发生变化时,判断线段EF 的长度是否发生变化,并说明理由;(3)在(2)中,若二次函数l 1的顶点为M ,二次函数l 2的顶点为N ;①当k 为何值时,点M 与点N 关于直线EF 对称?②是否存在实数k ,使得MN =2EF ?若存在,求出实数k 的值,若不存在,请说明理由.【答案】(1)l1的对称轴为x =﹣3,和y 轴的交点坐标为(0,5k);l2的对称轴为x =﹣3,与y 轴的交点坐标(0,5k)(2)不发生变化,见解析(3)①k 为﹣1;②73或﹣13【分析】(1)二次函数l1的对称轴为x =﹣2ba =﹣621⨯=﹣3,令x =0,则y =5k ,故该抛物线和y 轴的交点坐标为(0,5k );同理可得l2的对称轴为x =﹣3,与y 轴的交点坐标(0,5k );(2)可令y1=y2,求出点E 、F 的横坐标,从而得到点E 、F 的坐标,进行得到EF 的长,就可解决问题;(3)易得点M 、N 的坐标及直线EF 的关系式,然后根据条件建立关于k 的方程,就可解决问题.(1)解:二次函数l1的对称轴为x =﹣2ba =﹣621⨯=﹣3,令x =0,则y =5k ,故该抛物线和y 轴的交点坐标为(0,5k );同理可得:l2的对称轴为x =﹣3,与y 轴的交点坐标(0,5k );(2)解:线段EF 的长度不发生变化,理由:当y1=y2时,x2+6x+5k =kx2+6kx+5k ,整理得:(k ﹣1)(x2+6x )=0.∵k≠1,∴x2+6x =0,解得:x1=0,x2=﹣6.不妨设点E 在点F 的左边,则点E 的坐标为(﹣6,5k ),点F 的坐标为(0,5k ),∴EF =|0﹣(﹣6)|=6,∴线段EF 的长度不发生变化;(3)解:①由y1=x2+6x+5k =(x+3)2+5k ﹣9得M (﹣3,5k ﹣9),由y2=kx2+6kx+5k =k (x+3)2﹣4k 得N (﹣3,﹣4k ).∵直线EF 的关系式为y =5k ,且点M 与N 关于直线EF 对称,∴﹣4k ﹣5k =5k ﹣(5k ﹣9),解得:k =﹣1,∴当k 为﹣1时,点M 与N 关于直线EF 对称;②∵MN =|(5k ﹣9)﹣(﹣4k )|=|9k ﹣9|,MN =2EF =12,∴|9k ﹣9|=12,解得k1=73,k2=﹣13,∴实数k 为73或﹣13.【点睛】本题主要考查了二次函数的性质、解一元二次方程、轴对称的性质、解绝对值方程等知识,需要注意的是当两点横坐标相同时,两点之间的距离应为这两点纵坐标差的绝对值. (1)求抛物线的解析式及顶点(2)判断ABC 的形状,证明你的结论;(3)点M 是抛物线对称轴上的一个动点,当(4)在该抛物线位于第四象限内的部分上是否存在点【答案】(1)抛物线的解析式为:213222y x x =−−;325,28D ⎛⎫− ⎪⎝⎭ (2)ACB △是直角三角形(3)35,24M ⎛⎫− ⎪⎝⎭,ACM △的最小周长为:(4)存在,()2,3P −【分析】(1)根据点()1,0A −在抛物线2122y x bx =+−上,解出b ,得到抛物线的解析式,根据顶点坐标公式,即可求出点D 的坐标;(2)根据(1)得抛物线的解析式,求出点B 的坐标,根据勾股定理的逆定理即可;(3)当点M 在BC 与对称轴的交点上,根据点A ,点B 是对称点,连接AM ,则AM BM =且A ,C ,M 三点在一条直线上,距离最短,设BC 的解析式为:()0y kx b k =+≠,求出BC 的解析式,则得到点M 的坐标,即可;(4)以BC 为底,则12CPB S BC h =,当点P 到BC 的距离最远时,CPB △的面积最大如图所示,作直线l BC ∥,当直线l 与抛物线132222y x x =−−仅有一个交点时,h 最大,交点即为点P .【详解】(1)∵点()1,0A −在抛物线2122y x bx =+−上, ∴1022b =−−, ∴32b =−, ∴抛物线的解析式为:213222y x x =−−; ∵顶点坐标公式为:42,24bac b a a −⎛⎫− ⎪⎝⎭, ∴点325,28D ⎛⎫− ⎪⎝⎭.∴抛物线的解析式为:2122y x =−;325,28D⎛⎫− ⎪⎝⎭.(2)∵抛物线213222y x x =−−与y 轴交于点C ,∴0x =,=2y −,∴2OC =, ∵抛物线213222y x x =−−与x 轴交于点A ,点B , ∴2130222x x =−−,∴=1x −,4x =,∴点()4,0B ,∴1OA =,4OB =,5AB =,∵2225AC OA OC =+=;222222420BC OC OB =+=+=;225AB =,∴222AC BC AB +=,∴ABC 是直角三角形.(3)∵点A ,点B 是对称点,点M 在BC 与对称轴的交点上,∴AM BM =此时A ,C ,M 三点在一条直线上,距离最短,ACM C AC BC =+=设BC 的解析式为:()0y kx b k =+≠,∴042k b b =+⎧⎨−=⎩,解得:122k b ⎧=⎪⎨⎪=−⎩, ∴122y x =− 当32x =时,1352224y =⨯−=−, ∴点35,24M ⎛⎫− ⎪⎝⎭;∴点M 的坐标为35,24M ⎛⎫− ⎪⎝⎭,ACM △的最小周长为:(4)存在,理由如下:∵以BC 为底, ∴12CPB S BC h =⨯,当点P 到BC 的距离最远时,CPB △的面积最大,作直线l BC ∥,且与213222y x x =−−仅有一个交点,设直线l 的解析式为y kx b =+,∵l BC ∥,∴12k =,即12y x b =+,∵直线l 与213222y x x =−−仅有一个交点, ∴21312222x x x b −−=+仅有一个实数根, ∴()144202b −⨯⨯−−=,解得4b =−,∴直线l 的解析式为:1y x 42=−, 由214213222y x y x x ⎧=−⎪⎪⎨⎪=−−⎪⎩,解得23x y =⎧⎨=−⎩, ∴点()2,3P −.【点睛】本题考查二次函数与几何的综合,解题的关键是掌握待定系数法求解析式,勾股定理的逆定理,线段的距离.【答案】(1)证明见详解;(2)交点坐标为(0,a-1)或(-1,-1);(3)证明见详解【分析】(1)先确定出抛物线的顶点坐标,即可得出结论;(2)联立二次函数的解析式与一次函数的解析式,求出方程组的解即可;(3)表示出MN 的长度再利用函数最值求出范围即可得出结论【详解】解:(1)证明:二次函数2221(1)1y ax ax a a x =++−=+−, 顶点坐标为()1,1−−,把()1,1−−代入,1y ax a =+−中左边=-1,右边=-1∴左边=右边,∴二次函数图象的顶点必在一次函数1y ax a =+−的图象上;(2)联立解析式得:2211y ax ax a y ax a ⎧=++−⎨=+−⎩,解得x=0 或x=-1当x=0时,y=a-1 坐标为(0,a-1)当x=-1时,y=-1坐标为(-1,-1)∴交点坐标为(0,a-1)或(-1,-1)(3)证明:由题意可知2(,21)M m am am a ++−,(,1)N m am a +−由(2)可知,当a >0时,-1<x <0有221ax ax a ++−<1ax a +−∴221(21)MN am a am am a am am =+−−++−−−= =21()24a a m −++ 当10m −≤≤时,04a MN ≤≤∵02a <≤ ∴102MN ≤≤ 【点睛】二次函数综合题,主要考查了抛物线的顶点坐标的确定,抛物线与一次函数交点确定,极值的确定,用分类讨论的思想解决问题是解本题的关键. 7.(2023·浙江·九年级专题练习)如图,已知抛物线2:L y x bx c =++经过点(0,5),(5,0)A B −.(1)求,b c 的值;(2)连结AB ,交抛物线L 的对称轴于点M .①求点M 的坐标;②将抛物线L 向左平移(0)m m >个单位得到抛物线1L .过点M 作//MNy 轴,交抛物线1L 于点N .P 是抛物线1L 上一点,横坐标为1−,过点P 作//PE x 轴,交抛物线L 于点E ,点E 在抛物线L 对称轴的右侧.若10PE MN +=,求m 的值.【答案】(1)4,5−−;(2)①(2,3)−;②1或.【分析】(1)直接运用待定系数法求解即可;(2)①求出直线AB 的解析式,抛物线的对称轴方程,代入求解即可;②根据抛物线的平移方式求出抛物线1L 的表达式,再分三种情况进行求解即可.【详解】解:(1)把点(0,5),(5,0)A B −的坐标分别代入2y x bx c =++,得5,2550.c b c =−⎧⎨++=⎩.解得4,5.b c =−⎧⎨=−⎩,b c ∴的值分别为4,5−−.(2)①设AB 所在直线的函数表达式为()0y kx n k =+≠,把(0,5),(5,0)A B −的坐标分别代入表达式,得5,50.n k n =−⎧⎨+=⎩,解得1,5.k n =⎧⎨=−⎩AB ∴所在直线的函数表达式为5y x =−.由(1)得,抛物线L 的对称轴是直线2x =,当2x =时,53y x =−=−.∴点M 的坐标是(2,3)−.②设抛物线1L 的表达式是2(2)9y x m =−+−, //MN y 轴,∴点N 的坐标是()22,9m −.∵点P 的横坐标为1,−∴点P 的坐标是()21,6m m −−,设PE 交抛物线1L 于另一点Q ,∵抛物线1L 的对称轴是直线2,//x m PE x =−轴,∴根据抛物线的轴对称性,点Q 的坐标是()252,6m m m −−.(i )如图1,当点N 在点M 下方,即0m <≤52(1)62PQ m m =−−−=−,()22396MN m m =−−−=−,由平移性质得,QE m =,∴626PE m m m =−+=−10PE MN +=Q ,∴26610m m −+−=,解得12m =−(舍去),21m =.(ii )图2,当点N 在点M 上方,点Q 在点P 右侧,3m ≤时,26,6PE m MN m =−=−,10PE MN +=Q ,26610m m ∴−+−=,解得1m =(舍去),2m =(舍去).(ⅲ)如图3,当点N 在点M 上方,点Q 在点P 左侧,即3m >时,2,6PE m MN m ==−,10PE MN +=Q ,2610m m ∴+−=,解得1m =(舍去),2m =.综上所述,m 的值是1或.【点睛】本题属于二次函数综合题,考查了待定系数法求函数的解析式、抛物线的平移规律和一元二次方程等知识点,数形结合、熟练掌握相关性质是解题的关键. 8.(2023·浙江·九年级专题练习)如图,抛物线2y x bx c =−++经过()()1,0,3,0A B −两点,且与y 轴交于点C .(1)求该抛物线的函数表达式;(2)抛物线上是否存在点P ,使得BCP 是以BC 为直角边的直角三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,说明理由;(3)点M 为OC 的中点,若有一动点P 自点M 处出发,沿直线运动至x 轴上的某点(设为点E ),再沿直线运动至该抛物线对称轴上的某点(设为点F ),最后又沿直线运动至点C ,则点P 运动的总路程最短为______.(请直接写出答案)【答案】(1)223y x x =−++;(2)存在,点P 的坐标为(1,4)或(-2,-5);(3) 【分析】(1)利用待定系数法求解;(2)分两种情况:①当C 为直角顶点时,过点C 作CP ⊥BC ,交抛物线于点P ,过点P 作PH ⊥y 轴于H ,得到PH=CH ,设P (2,23a a a −++),则2233a a a =−++−,求出a 即可;②当B 为直角顶点时,过点B 作BP ⊥BC ,交抛物线于点P ,交y 轴于R ,过点P 作PG ⊥y 轴于G ,求出OB=OR=3,PG=RG ,设P (2,23a a a −++),则2233a a a −=−−−,求出a 即可;(3)做M 点关于x 轴的对称点M ',做C 点关于对称轴的对称点C ',连接M 'C 交x 轴于E 点,交对称轴于F ,此时点P 运动的总路程最短,由勾股定理求出M C ''=即可求出点P 运动的路径得到答案.【详解】解:(1)将()()1,0,3,0A B −代入2y x bx c =−++,得10930b c b c −−+=⎧⎨−++=⎩,解得23b c =⎧⎨=⎩,∴该抛物线的函数表达式是223y x x =−++;(2)存在.①当C 为直角顶点时,过点C 作CP ⊥BC ,交抛物线于点P ,过点P 作PH ⊥y 轴于H ,∵OB=OC ,∠BOC=90°,∴△BOC 为等腰直角三角形,∠BCO=45°,∴∠PCH=45°,∴△PHC 为等腰直角三角形,即PH=CH ,设P (2,23a a a −++),则2233a a a =−++−,解得121,0a a ==(舍去),此时2234a a −++=,∴P (1,4);②当B 为直角顶点时,过点B 作BP ⊥BC ,交抛物线于点P ,交y 轴于R ,过点P 作PG ⊥y 轴于G , ∵∠CBO=45°,∴∠GPR=∠OBR=45°,∴△PRG 为等腰直角三角形,∴OB=OR=3,PG=RG ,设P (2,23a a a −++),则2233a a a −=−−−,解得122,3a a =−=(舍去),此时2235a a −++=−,∴P (-2,-5);综上,点P 的坐标为(1,4)或(-2,-5);(3)如图3,做M 点关于x 轴的对称点M ',做C 点关于对称轴的对称点C ',连接M 'C 交x 轴于E 点,交对称轴于F∴,ME M E CF C F ='='∵ME EF CF M EF C F M C ++='E++'=''此时点P 运动的总路程最短∵点M 为OC 的中点,C (0,3)∴3(0,)2M ∴3(0,)2M '− ∵2223(1)4y x x x =−++=−−+,∴抛物线的对称轴为直线x=1,∵C (0,3)∴(2,3)C '9 22MC CC ='=∴∴M C ''===, ∴点P运动的路径,故答案为:.【点睛】此题考查了二次函数的综合知识,待定系数法求函数解析式,抛物线的对称轴,直角三角形的性质,勾股定理,等腰直角三角形的性质,最短路径问题,综合掌握各知识点是解题的关键.题型二:面积问题一、解答题1.(2023·浙江衢州·校考一模)如图,抛物线22y ax bx =++经过点()()1040,,,A B −,与y 轴交于点C .【答案】(1)2222y x x =−++(2)存在,点D 的坐标为:(1,3)或(2,3)或(5,-3)(3)【分析】(1)用待定系数法解答;(2)设D (x ,y ),根据题意及利用三角形面积列出方程,求出y 的值后代入抛物线的解析式即可解答(3)由勾股定理解得AC 的长,再根据勾股定理逆定理证明ABC 为直角三角形,设直线AC 与直线BE 交于点F ,过点F 作FM ⊥x 轴于点M ,由平行线分线段成比例解得FM 的长,求得点F 的坐标,最后根据两点间的距离公式解答.【详解】(1)解:把点()()1040,,,A B −代入抛物线22y ax bx =++得2016420a b a b −+=⎧⎨++=⎩,1232a b ⎧=−⎪⎪∴⎨⎪=⎪⎩ ∴213222y x x =−++(2)由题意可知(0,2),(1,0),(4,0)C A B −5,2AB OC ∴==1152522ABC S AB OC ∴=⋅=⨯⨯=23ABC ABD S S =△△ 315522ABD S ∴=⨯= 设D (x ,y ),11155222AB y y ∴⋅=⨯=3y ∴=当y=3时,由2132322x x −++=,解得:1x =或2x =此时点D 的坐标为(1,3)或(2,3);当y=-3时,由2132322x x −++=−,解得:5x =或2x =−(舍去) 此时点D 的坐标为(5,-3);综上所述,点D 的坐标为:(1,3)或(2,3)或(5,-3);(3)1,2,4,5AO OC OB AB ====AC BC ∴===222AC BC AB ∴+=ABC ∴为直角三角形,即BC AC ⊥如图,设直线AC 与直线BE 交于点F ,过点F 作FM ⊥x 轴于点M ,由题意得:45FBC ∠=︒CF BC ∴==OC FMAO AC OM CF ∴=1OM2OC AC OM FM AF ∴==2FM ∴6FM ∴=(2,6),(4,0)F B ∴BF ∴==【点睛】本题考查二次函数的图象上点的特征、待定系数法求二次函数解析式、勾股定理、平行线分线段成比例、两点间的距离公式等,关键是利用面积关系求出点D 的坐标. (1)求抛物线的解析式;(2)当0<x <3时,直接写出y (3)点P 为抛物线上一点,若【答案】(1)2y x 2x 3=−++(2)04y <≤(3)(4,5)−P 或(2,5)P −−【分析】(1)将A 与B 的坐标代入抛物线的解析式即可求出b 与c 的值,(2)根据图象即可求出y 的取值范围,(3)设P (x ,y ),△PAB 的高为|y|,AB=4,由S △PAB=10列出方程即可求出y 的值,从而可求出P 的坐标.【详解】(1)解:将点A (﹣1,0),B (3,0)两点代入y =2x −+bx+c ∴0=1+0=9+3+b c b c −−−⎧⎨⎩,解得=2=3b c ⎧⎨⎩,∴抛物线的解析式为:2y x 2x 3=−++,2y x 2x 3=−++;(2)==−++−−+22y (x 1x 3)x 24,物线的对称轴为=1x ,开口向下,y 的最大值为4,如图,∴0<x <3时,04y <≤;(3)设P (x ,y ),∴△PAB 的高为|y|,A (﹣1,0),B (3,0),4AB ∴=,14102ABP S y ∴=⨯⨯=△,解得5y =±,当=5y 时,2523x x =−++,此时方程无解,当5y =−时,−2523x x =−++,解得124,2x x ==−,(4,5)P ∴−或(2,5)P −−.【点睛】本题考查了二次函数的综合问题,待定系数法求解析式,二次函数图象的性质,掌握二次函数的性质是解题的关键. 3.(2023秋·浙江衢州·九年级校考阶段练习)已知拋物线2()30y ax bx a =++≠与x 轴交于(1,0)A −,(3,0)B 两点,与y 轴交于点C .(1)求抛物线的表达式.(2)连接AC ,BC ,求ABC S .(3)拋物线上是否存在一点E ,使得由.【答案】(1)223y x x =−++(2)6(3)()12,()1,()12−或()12−【分析】(1)把()1,0A −,()3,0B 两点坐标代入解析式即可求解;(2)先求出C 点坐标,即可得到ABC S , (3)根据23ABE ABC S S =△△求出2E y =,代入解析式即可求解.【详解】(1)解:把()1,0A −,()3,0B 两点代入()230y ax bx a =++≠中,得030933a b a b =−+⎧⎨=++⎩,解得12a b =−⎧⎨=⎩,∴抛物线的表达式为223y x x =−++;(2)解:当0x =时,3y =,即()0,3C , ∴3OC =,∵()1,0A −,()3,0B ,∴1OA =,3OB =,∴4AB =,∴1143622ABC S AB OC =⋅⋅=⨯⨯=△,即所求面积为6;(3)解:∵6ABC S =, ∴226433ABE ABC S S ==⨯=△△, ∵142ABE E S AB y =⋅⋅=△, ∴2E y =,把2y =代入抛物线表达式得:2223x x =−++,解得1x =把=2y −代入抛物线表达式得:2223x x −=−++,解得1x =综述所述,点E 的坐标为()12或()1或()12−或()12−.【点睛】此题主要考查二次函数的图象与性质,解题的关键是熟知待定系数法及三角形的面积公式的应用. ,求POA 的面积.【答案】(1)m=3,24y x x =−+ (2)0x <或3x >(3)3【分析】(1)由点A 在一次函数y x =上,可将点A 的坐标代入y x =即可求出m ,然后将求出的点A 坐标代入2y x bx =−+即可求出b 值;(2)观察图象找出二次函数图像在一次函数图像下方部分的自变量取值范围即可;(3)求出点P 的坐标及抛物线与x 轴的另一个交点坐标,先计算由点A 、点P 、点O ,及抛物线与x 轴的另一个交点所构成的四边形面积,然后减去由点A 、点O ,及抛物线与x 轴的另一个交点所构成的三角形面积即可.【详解】(1)解:因为点A 在一次函数y x =上,所以()3m ,满足y x =,即3x =时y m =,可得:3m =;将点A ()33,代入2y x bx =−+得:2333b =−+,解得4b =,故二次函数的表达式为:24y x x =−+, 综上所得,故答案为:m=3,24y x x =−+. (2)解:由图象可知,一次函数与二次函数交于()()0,03,3,两点,观察图象可以看出在0x <或3x >时,2y x bx =−+的图象在y x =图象的下方,所以当0x <或3x >时,2x bx x −+<,故答案为:0x <或3x >.(3)解:方法一:如图1所示,因为点P 为抛物线顶点,所以点P 坐标为:()24,,抛物线与x 轴的另一个交点为点()40B ,,点()33A ,, 则四边形APOB 的面积()11124431139222=⨯⨯+⨯+⨯+⨯⨯=, ABO 的面积14362=⨯⨯=,∴POA 的面积=四边形APOB 的面积−ABO 的面积96=−3=,∴POA 的面积为3,故答案为:3.方法二:如图2所示,过点P 作PC x ⊥轴,垂足为C ,交OA 于点D ,过点A 作AE PC ⊥,垂足为E , 224(2)4y x x x =−+=−−+,∴顶点(2,4)P ,把2x =代入直线方程y x =中得:2y =,2()2D ∴,,422PD ∴=−=, POA 的面积OPD =的面积APD +的面积,111()222PD OC PD AE PD OC AE =⋅+⋅=+ 1232=⨯⨯3=.【点睛】本题考查了二次函数的图像及性质,结合图像求几何图形的面积及解对应的一元二次不等式,关键是解题过程要始终运用数形结合的思想方法.【答案】(1)1a =,3b =,4c =;(2)点E 的坐标为(1,6)时,面积最大;(3)d 最小值为5,此时F 点的坐标为(1,2).【分析】(1)将A 、C 两个点的坐标代入二次函数解析式,即可得出b 、c 的值,将点A (-1,0)代入一次函数中,即可求得a 的值;(2)设点E 的横坐标为m ,则点E 的纵坐标为234m m −++,过点E 作x 轴的垂线l ,交x 轴于点G ,交AD于点H ,则点H 的坐标为(),1m m +.过点D 作l 的垂线,垂足为T ,联立直线方程和二次函数方程,即可得出D 的坐标,再根据ΔΔΔAED AEH HED S S S =+,得出含m 的函数,根据函数图象,可知,当1m =时,面积取得最大值,从而可得出E 的坐标;(3)过A 作y 轴的平行线AS ,过作FG ⊥y 轴交AS 于点M ,过F 作FN ⊥x 轴于N ,根据角平分线的性质可得:FM FN = ,即有11d FE FM FE FN =+−=+−,可知当N 、F 、E 所在直线与x 轴垂直时,d 取得最小值,即可得出点F 的坐标.【详解】解:(1)∵点C (0,4),A (-1,0)在函数的图象上,∴410c b c =⎧⎨−−+=⎩,解得:34b c =⎧⎨=⎩,二次函数解析式为:234y x x =−++, ∵点A (-1,0)在一次一次函数y x a =+上,∴01a =−+,∴1a =,一次函数解析式为:1y x =+;所以1a =,3b =,4c =;(2)设点E 的横坐标为m ,则点E 的纵坐标为234m m −++,过点E 作x 轴的垂线l ,交x 轴于点G ,交AD于点H ,则点H 的坐标为(),1m m +.过点D 作l 的垂线,垂足为T ,将1y x =+与2y 34x x =−++联立组成方程组,解得点D 的坐标为(3,4), 所以ΔΔΔ1122AED AEH HED S S S EH AG EH DT =+=⨯+⨯ ()12EH AG DT =+ ()2134142m m m =−++−−⨯ ()2218m =−−+∵函数图象开口向下,存在最大值,∴AED S ∆有最大值,当1m =时,最大值为8,此时点E 的坐标为(1,6);(3)过A 作y 轴的平行线AS ,过F 作FG ⊥y 轴交AS 于点M ,过F 作FN ⊥x 轴于N ,如图所示:∵点D 的坐标为(3,4),点A 坐标为(-1,0)∴45DAB ∠=︒,∴AD 平分SAB ∠,∴FM FN = ,∴11d FE FM FE FN =+−=+−显然,当N 、F 、E 所在直线与x 轴垂直时,1d FE FN =+−最小,最小值为615d =−=,此时点F 的横坐标为1,代入1y x =+得:F 点的坐标为(1,2).【点睛】题目主要考查二次函数与一次函数的综合问题,二次函数、一次函数解析式的确定,组成面积的最值,角平分线的性质等,理解题意,作出相应辅助线,结合函数的基本性质是解题关键. 6.(2023·浙江·九年级专题练习)如图,已知二次函数y =2x 2﹣8x +6的图象与x 轴交于点A 和点B ,与y 轴交于点C ,顶点为D .求四边形ADBC 的面积.【答案】四边形ADBC 的面积为8.【分析】先把抛物线解析式化成顶点式,求出C 、D 的坐标,然后求出A 、B 的坐标,最后根据=ABC ABD ADBC S S S +△△四边形进行求解即可.【详解】解:∵抛物线解析式为()()22228624446222y x x x x x =−+=−+−+=−−,∴点C 的坐标为(0,6),点D 的坐标为(2,-2),令0y =,则22860x x −+=,∴2430x x −+=,解得1x =或3x =,∴点A 的坐标为(1,0),点B 的坐标为(3,0),∴AB=2,∴=ABC ABD ADBC S S S +△△四边形()11=22C D AB y AB y ⋅+⋅−()11262222=⨯⨯+⨯⨯−8=.【点睛】本题主要考查了求二次函数与坐标轴的交点,二次函数的顶点坐标,四边形面积,解题的关键在于能够熟练掌握二次函数的相关知识.把AOB 的面积分成相等的两部分.个单位,使其顶点落在AOB 的内部(不包括边界)【答案】(1)23b c =⎧⎨=⎩;(2)①3y x =;m <<. 【分析】(1)将(2,3),(1,0)A B −代入2y x bx c =−++中,列方程组求解即可.(2)直线OP 把AOB 的面积分成相等的两部分.则此直线必过AB 中点,求出中点坐标求解即可.(3)因为平移,所以过点D的直线必然与OP 平行,顶点要在三角形内部,画图分析即可.【详解】(1)将(2,3),(1,0)A B −代入2y x bx c =−++,得42310b c b c −++=⎧⎨−−+=⎩,解得:23b c =⎧⎨=⎩.(2)①取AB 的中点C ,∵(2,3),(1,0)A B − ∴13,22C ⎛⎫ ⎪⎝⎭又∵P 是第一象限内抛物线上一点,且直线OP 把AOB 的面积分成相等的两部分.∴直线OP 必过AB 的中点C∴直线OP 的表达式为:3y x =②由(1)可得抛物线的一般式为:223y x x =−++,将一般式转化为顶点式如下:2223(1)4y x x x =−++=−−+∴顶点坐标为()1,4D设过抛物线的顶点(1,4),且与直线OP 平行的直线解析式为:3'y x b =+将顶点()1,4D 代入3'y x b =+,得3'4b +=,解得'1b =∴31y x =+设AB y mx n =+,将(2,3)A ,(1,0)B −代入,得230m n m n +=⎧⎨−+=⎩, 解得11m n =⎧⎨=⎩∴1AB y x =+联立:311y x y x =+⎧⎨=+⎩ ,得:{01x y ==, 设直线31y x =+与直线AB 的交点坐标为点M ,与x 轴的交点坐标为N ,则()0,1M 1,03N ⎛⎫− ⎪⎝⎭ , 抛物线顶点落在AOB 的内部,即顶点在点M ,点N 之间,如图:∴DM ==DN ==m <<【点睛】本题考查的是二次函数的综合,二次函数的解析式求法,两点之间的距离公式,中点坐标公式等相关知识点,根据题意数形结合是解题的关键.【答案】(1)223y x x =+−;(2)存在,638;(3)点M 的坐标为⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭【分析】(1)利用待定系数法求解即可; (2)先求出C 、D 的坐标,设点()2,23(31)H a a a a +−−<<−,即可得到OBH OCHOBHC S S S =+△△四边形21123||22OB a a OC a =⨯+−+⨯,由此求解即可;(3)先求出E 点坐标,利用待定系数法求出直线BD 的解析式,利用PC PE =求出P 点坐标,设设(,0)M d ,则()2,23G d d d +−,()22,23N d d −+−,利用FM MG =建立方程求解即可.【详解】解:(1)∵抛物线2y x bx c =++的图象经过点(1,0)A ,(3,0)B − ∴10930b c b c ++=⎧⎨−+=⎩,∴23b c =⎧⎨=−⎩,∴抛物线的解析式为223y x x =+−;(2)当=1x −时,4y =−,所以点(1,4)D −−,当0x =时3y =−,,所以点(0,3)C − 设点()2,23(31)H a a a a +−−<<−所以OBH OCHOBHC S S S =+△△四边形21123||22OB a a OC a =⨯+−+⨯()2333222a a a =−−−2399222a a =−−+当322b a a =−=−时,638OBHC S =四边形. (3)由(1)知,抛物线的解析式为223y x x =+−;∴(0,3)C −,抛物线的顶点(1,4)D −−,∴(1,0)E −,设直线BD 的解析式为y mx n =+,∴304m n m n −+=⎧⎨−+=−⎩,∴26m n =−⎧⎨=−⎩∴直线BD 的解析式为26y x =−−,设点(,26)P m m −−, ∵(0,3)C −,(1,0)E −,根据勾股定理得,222(1)(26)PE m m =++−−,222(263)PC m m =+−−+,∵PC PE =,∴2222(1)(26)(263)m m m m ++−−=+−−+,∴2m =−,∴2(2)62y =−⨯−−=−,∴(2,2)P −−, 如图,作PF x ⊥轴于F ,∵(2,0)F −,设(,0)M d ,则()2,23G d d d +−,()22,23N d d −+−∴以点F ,N ,G ,M 四点为顶点的四边形为正方形,必有FM MG =,∴2|2|23d d d +=+−∴d =或d =,∴点M的坐标为⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭,⎫⎪⎪⎝⎭.【点睛】本题主要考查了二次函数的综合,待定系数法求函数解析式,正方形的性质,两点距离公式等等,【答案】(1)(0,2),(4,0),抛物线的解析式是211242y x x =−++;(2)四边形ABCM 面积最大值为8,此时点M 的坐标为(2,2);(3)34m −≤≤−或32m −≤≤【分析】(1)对直线122y x =−+,分别令x=0,y=0求出相应的y ,x 的值即得点A 、C 的坐标,根据待定系数法即可求出抛物线的解析式,利用抛物线的对称性即可求出点B 的坐标;(2)过点M 作ME ⊥x 轴于点E ,交直线AC 于点F ,如图1所示.设点M 的横坐标为m ,则MF 的长可用含m 的代数式表示,然后根据S 四边形ABCM=S △ABC+S △AMC 即可得出S 四边形ABCM 关于m 的函数关系式,再利用二次函数的性质即可求出四边形ABCM 面积的最大值及点M 的坐标;(3)当m >0时,分旋转后点A '与点O '落在抛物线上时,分别画出图形如图2、图3,分别用m 的代数式表示出点A '与点O '的坐标,然后代入抛物线的解析式即可求出m 的值,进而可得m 的范围;当m <0时,用同样的方法可再求出m 的一个范围,从而可得结果.【详解】解:(1)对直线122y x =−+,当x=0时,y=2,当y=0时,x=4,∴点A 的坐标是(0,2),点C 的坐标是(4,0),把点A 、C 两点的坐标代入抛物线的解析式,得:2214404c b c =⎧⎪⎨−⨯++=⎪⎩,解得:122b c ⎧=⎪⎨⎪=⎩,∴抛物线的解析式为211242y x x =−++, ∵抛物线的对称轴是直线1x =,C (4,0), ∴点B 的坐标为(﹣2,0);故答案为:A (0,2),C (4,0),抛物线的解析式是211242y x x =−++; (2)过点M 作ME ⊥x 轴于点E ,交直线AC 于点F ,如图1所示.设M (m ,211m m 242−++),则F (m ,122m −+),∴221112424122m m m mMF m ⎛⎫⎛⎫=−−+=−++− ⎪ ⎪⎝⎭⎭+⎝,∴S 四边形ABCM=S △ABC+S △AMC =1122BC AO MF OC⋅+⋅2111624224m m ⎛⎫=⨯⨯+⨯−+⨯ ⎪⎝⎭21262m m =−++ ()21282m =−−+,∵0<m <4,∴当m=2时,四边形ABCM 面积最大,最大值为8,此时点M 的坐标为(2,2);(3)若m >0,当旋转后点A '落在抛物线上时,如图2,线段O A ''与抛物线只有一个公共点, ∵点A '的坐标是(m+2,m ),∴()()21122242m m m−++++=,解得:3m =−3m =−;当旋转后点O '落在抛物线上时,如图3,线段O A ''与抛物线只有一个公共点, ∵点O '的坐标是(m ,m ),∴211242m m m−++=,解得:m=2或m=﹣4(舍去);∴当m >0时,若线段O A ''与抛物线只有一个公共点,m 的取值范围是:32m −≤≤;若m <0,当旋转后点O '落在抛物线上时,如图4,线段O A ''与抛物线只有一个公共点, ∵点O '的坐标是(m ,m ),∴211242m m m−++=,解得:m=﹣4或m=2(舍去);当旋转后点A '落在抛物线上时,如图5,线段O A ''与抛物线只有一个公共点, ∵点A '的坐标是(m+2,m ),∴()()21122242m m m−++++=,解得: 3m =−3m =−;∴当m <0时,若线段O A ''与抛物线只有一个公共点,m 的取值范围是:34m −≤≤−;综上,若线段O A ''与抛物线只有一个公共点,m 的取值范围是:34m −≤≤−或32m −≤≤. 【点睛】本题是二次函数的综合题,主要考查了待定系数法求二次函数的解析式、旋转的性质、一元二次方程的解法、二次函数的图象与性质以及抛物线上点的坐标特点等知识,具有较强的综合性,属于中考压轴题,熟练掌握二次函数的图象与性质、灵活应用数形结合的思想是解题的关键.【答案】(1)224y x x =−−+;(2)点M 的坐标为(2,-4);(3)n 的值为9.【分析】(1)直接把点B (-3,1)代入抛物线解析式进行求解即可; (2)由抛物线解析式为()2222y x kx k x x k=−+−=−+−,则当2x =时,4y =−,函数值与k 的取值无关,由此即可得到答案; (3)设直线BM 的解析式为1y k x b=+,直线BM 于y 轴的交点为E ,可求得直线BM 的解析式为2y x =−−,得到E 点坐标为(0,-2),从而求出15ABM S =V ;如图所示,在直线AB 上方作直线1l ∥AB ,且直线1l与抛物线只有一个交点1P ,对应的在直线AB 下方作直线2l ∥AB ,其中直线1l 与直线AB 的距离等于直线2l与直线AB 的距离,则123==ABP ABP ABP S S S △△△(等底等高),根据除去1P ,2P ,3P 这三个位置外,符合21=S nS 的P 点的个数为4个或2个;推出12ABP S nS =△,由此先求出直线AB 的解析式为4y x =+,则可设直线1l的解析式为2y x b =+,联立2224y x b y x x =+⎧⎨=−−+⎩得22340x x b +−+=,求得2254b =,从而求出点1P 的坐标为(32−,194),过点1P作x 轴的垂线交AB 于H ,根据111ABP P BH P AHS S S =+V V V ,求出1ABP S V 即可得到答案.【详解】解:(1)∵抛物线22y x kx k =−+−经过点B (-3,1),∴()21332k k=−−−−,∴2k =−,∴抛物线解析式为224y x x =−−+; (2)∵抛物线解析式为()2222y x kx k x x k=−+−=−+−,当2x =时,4y =−,函数值与k 的取值无关, ∴点M 的坐标为(2,-4);(3)∵抛物线224y x x =−−+与y 轴交于点A ,∴点A 的坐标为(0,4), 设直线BM 的解析式为1y k x b=+,直线BM 于y 轴的交点为E ,∴113124k b k b −+=⎧⎨+=−⎩,∴112k b =−⎧⎨=−⎩,∴直线BM 的解析式为2y x =−−, ∴E 点坐标为(0,-2), ∴()111522ABM ABE AME M B S S S AE x AE x =+=⋅+⋅−=V V V ;如图所示,在直线AB 上方作直线1l ∥AB ,且直线1l 与抛物线只有一个交点1P,对应的在直线AB 下方作直线2l ∥AB ,其中直线1l与直线AB 的距离等于直线2l 与直线AB 的距离, ∴123==ABP ABP ABP S S S △△△(等底等高),∵除去1P ,2P ,3P 这三个位置外,符合21=S nS 的P 点的个数为4个或2个;∴12ABP S nS =△,设直线AB 的解析式为21y k x b =+,∴211314k b b −+=⎧⎨=⎩,∴2114k b =⎧⎨=⎩,∴直线AB 的解析式为4y x =+, ∴可设直线1l 的解析式为2y x b =+,联立2224y x b y x x =+⎧⎨=−−+⎩得22340x x b +−+=, ∴()22344b ∆=+−=0 ,∴2254b =,∴29304x x ++=,解得32x =−,∴点1P 的坐标为(32−,194),过点1P作x 轴的垂线交AB 于H , ∴点H 的横坐标为32−,∴点H 的纵坐标为52,∴194PH =,∴111ABP P BH P AHS S S =+V V V ()()111122H B A H PH x x PH x x =⋅−+⋅−()112A B PH x x =⋅−278=,∴27158n =,∴409n =.【点睛】本题主要考查了二次函数与一次函数综合,平行线间距问题,待定系数法求函数解析式等等,解题的关键在于能够利用数形结合的思想进行求解.【答案】(1)A 点坐标为(2,0),抛物线对称轴为直线x=1;(2)4;(3)(4,﹣8).【分析】(1)在y =﹣x2+2x 中,令y=0,求得x 的值,从而确定A 点坐标,利用对称轴公式2bx a =−求得抛物线对称轴;(2)分别求得B 点和C 点坐标,求得直线OD 的解析式,然后通过求解△OBD 的面积求得平行四边形的面积;(3)结合平行四边形的性质及平移的思想分析点B ,点D 及点C 的坐标,然后仿照(2)中的解题思路分析求解.【详解】解:(1)在y =﹣x2+2x 中,令y=0,可得:﹣x2+2x=0,解得:x1=0,x2=2, ∵抛物线y =﹣x2+2x 与x 轴正半轴交于点A , ∴A 点坐标为(2,0),抛物线y =﹣x2+2x 的对称轴为直线()221x =−⨯−=1,即A 点坐标为(2,0),抛物线对称轴为直线x=1; (2)设OD 与抛物线对称轴交于点E ,连接BD ,∵点B B 的纵坐标是﹣3, ∴B 点坐标为(1,-3),∵点D 在抛物线上,且点D 的横坐标是52,∴点D 的纵坐标为255222⎛⎫−+⨯ ⎪⎝⎭=54−, ∴D 点坐标为55,24⎛⎫− ⎪⎝⎭,设直线OD 的解析式为OD y kx=,将D 点坐标为55,24⎛⎫− ⎪⎝⎭代入,可得5524k =−,解得:12k =−, ∴直线OD 的解析式为12OD y x=−,当x=1时,12y =−,∴E 点坐标为11,2⎛⎫− ⎪⎝⎭, ∴1522BOD S BE =⨯△=()51342⎡⎤⨯−−−⎢⎥⎣⎦=258, ∴S ▱OBCD =2524BOD S =△, 故答案为:254;(3)设OD 与抛物线对称轴交于点E ,连接BD ,设B 点坐标为(1,-b ),D a ,﹣a2+2a ),∵点D 在抛物线上,且在对称轴右侧,且点C 在抛物线上,四边形OBCD 为平行四边形,∴OB=CD ,OB ∥CD ,∵将点O 向右平移1个单位长度,再向下平移b 个单位长度后得到点B ,∴将点D 向右平移1个单位长度,再向下平移b 个单位长度后可得到点C ,∴C 点坐标为(a+1,﹣a2+2a-b ),将C 点坐标代入到y =﹣x2+2x 中,可得:﹣(a+1)2+2(a+1)=﹣a2+2a-b ,整理,可得:b=2a-1,设直线OD 的解析式为1OD y k x =,将D 点坐标(a ,﹣a2+2a ),代入,可得22ka a a =−+,解得:2k a =−+,∴直线OD 的解析式为()2OD y a x =−+,当x=1时,2y a =−+,。
浙教版九年级下册考点专题训练-【说课稿】二次函数

浙教版九年级下册考点专题训练二次函数一、说课内容:华师版九年级下册第二十六章第一节二次函数二、教材分析:1、教材的地位和作用这节课是在学生已经学习了一次函数、正比例函数、反比例函数的基础上,来学习二次函数的概念。
二次函数是初中阶段研究的最后一个具体的函数,也是最重要的,在历年来的中考题中占有较大比例。
同时,二次函数和以前学过的一元二次方程、一元二次不等式有着密切的。
进一步学习二次函数将为它们的解法提供新的方法和途径,并使学生更为深刻的理解“数形结合”的重要思想。
而本节课的二次函数的概念是学习二次函数的基础,是为后来学习二次函数的图象做铺垫。
所以这节课在整个教材中具有承上启下的重要作用。
2、教学目标和要求:(1)知识与技能:使学生理解二次函数的概念,掌握根据实际问题列出二次函数关系式的方法,并了解如何根据实际问题确定自变量的取值范围。
(2)过程与方法:复习旧知,通过实际问题的引入,经历二次函数概念的探索过程,提高学生解决问题的能力.(3)情感、态度与价值观:通过观察、操作、交流归纳等数学活动加深对二次函数概念的理解,发展学生的数学思维,增强学好数学的愿望与信心.3、教学重点:对二次函数概念的理解。
4、教学难点:由实际问题确定函数解析式和确定自变量的取值范围。
三、教法学法设计:1、从创设情境入手,通过知识再现,孕伏教学过程2、从学生活动出发,通过以旧引新,顺势教学过程3、利用探索、研究手段,通过思维深入,领悟教学过程四、教学过程:(一)复习提问1.什么叫函数?我们之前学过了那些函数?2.它们的形式是怎样的?3.一次函数(y=kx+b)的自变量是什么?函数是什么?常量是什么?为什么要有k≠0的条件? k值对函数性质有什么影响?【设计意图】复习这些问题是为了帮助学生弄清自变量、函数、常量等概念,加深对函数定义的理解.强调k≠0的条件,以备与二次函数中的a进行比较.(二)引入新课函数是研究两个变量在某变化过程中的相互关系,我们已学过正比例函数,反比例函数和一次函数。
九年级数学下学期-建立二次函数模型解决商品经济问题

建立二次函数模型解决商品经济问题一、明确学习目标1、能运用二次函数分析和解决简单的实际问题,培养分析问题和解决问题的能力和应用数学的意识.2、经历探索实际问题与二次函数的关系的过程,深刻理解二次函数是刻画现实世界的一个有效的数学模型.3、通过学习和合作交流,了解数学带给人们的价值及美感.二、自主预习1、求下列函数的最大值或最小值.(1)5322--=x x y(2)432+--=x x y2、某商品现在的售价为每件60元,每星期可卖出300件,已知商品的进价为每件40元,那么一周的利润是多少?学生展示,师生互评.商场的服装,经常出现涨价、降价,这其中有何奥妙呢?商家的利润是否随涨价而增大,随降价而减小?三、合作探究活动1 1、阅读教材第49页问题及探究1和探究2并思考:(1)涨价的情况;(2)如何确定函数关系式?(3)变量x 有范围要求吗?2、教师分层引导:(1)销售额为多少?(2)进货额为多少?(3)利润y 与每件涨价x 元的函数关系式是什么?(4)变量x 的范围如何确定?(5)如何求最值?3、解决问题:活动2 例某建筑的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料长为15m(图中所有线条长度之和),当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?教师点拨:此题较复杂,特别要注意:中间线段用x的代数式来表示时,要充分利用几何关系;要注意顶点的横坐标是否在自变量x的取值范围内.四、当堂检测1、如图所示,从一张矩形纸较短的边上找一点E,过E点剪下两个正方形,它们的边长分别是AE、DE,要使剪下的两个正方形的面积和最小,点E应选在何处?为什么?2、如图所示,有一块空地,空地外有一面长10m的围墙,为了美化生活环境,准备靠墙修建一个矩形花圃,用32m长的不锈钢作为花圃的围栏,为了浇花和赏花的方便,准备在花圃的中间再围出一条宽为1m的通道及在左右花圃各放一个1m宽的门,花圃的宽AD究竟应为多少米才能使花圃的面积最大?五、拓展提升某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.。
浙教版九年级全册初三数学(基础版)(全册知识点考点梳理、重点题型分类巩固练习)(家教、补习、复习用)

浙教版九年级全册初中数学全册知识点梳理及重点题型巩固练习二次函数y=ax 2(a ≠0)与y=ax 2+c(a ≠0)的图象与性质—知识讲解(基础)【学习目标】1.理解二次函数的概念,能用待定系数法确定二次函数的解析式;2.会用描点法画出二次函数y=ax 2(a≠0) 与()20y ax c a =+≠的图象,并结合图象理解抛物线、对称轴、顶点、开口方向等概念;3. 掌握二次函数y=ax 2(a≠0) 与()20y ax c a =+≠的图象的性质,掌握二次函数()20y axa =≠与()20y ax c a =+≠之间的关系;(上加下减).【要点梳理】要点一、二次函数的概念 1.二次函数的概念一般地,形如y=ax 2+bx+c (a≠0,a, b, c 为常数)的函数是二次函数. 若b=0,则y=ax 2+c ; 若c=0,则y=ax 2+bx ; 若b=c=0,则y=ax 2.以上三种形式都是二次函数的特殊形式,而y=ax 2+bx+c (a ≠0)是二次函数的一般式. 二次函数由特殊到一般,可分为以下几种形式: ①(a≠0);②(a≠0);③(a≠0);④(a≠0),其中;⑤(a≠0).要点诠释:如果y=ax 2+bx+c(a,b,c 是常数,a≠0),那么y 叫做x 的二次函数.这里,当a=0时就不是二次函数了,但b 、c 可分别为零,也可以同时都为零.a 的绝对值越大,抛物线的开口越小.2.二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标)(或称交点式).要点诠释:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.要点二、二次函数y=ax 2(a ≠0)的图象及性质 1.二次函数y=ax 2(a ≠0)的图象用描点法画出二次函数y=ax 2(a≠0)的图象,如图,它是一条关于y 轴对称的曲线,这样的曲线叫做抛物线.因为抛物线y=x 2关于y 轴对称,所以y 轴是这条抛物线的对称轴,对称轴与抛物线的交点是抛物线的顶点,从图上看,抛物线y=x 2的顶点是图象的最低点。
浙教版九年级下册考点专题训练-【教案】求二次函数的表达式
浙教版九年级下册考点专题训练教学内容求二次函数的表达式学情分析教学目标知识与能力:1、掌握二次函数表达式的表达方式。
2、会用待定系数法求二次函数的表达式。
3、学会利用二次函数解决实际问题。
过程与方法:能根据二次函数的图像及性质解决生活中的实际问题情感态度与价值观:通过数学活动,体会实际生活与数学的密切,感受数学带给人们的作用,激发学习热情,培养学习兴趣。
教学重难点重点:会用待定系数法求二次函数的表达式难点:会选用适当函数表达式求二次函数的表达式媒体运用班班通教学过程:(一)知识回顾:在我们学习二次函数之前,我们学习过哪些函数?(学生回答)这些函数的表达式是?(学生回答)我们在前面刚刚学习了二次函数,二次函数的表达式有哪些?(一般式、顶点式、交点式)还记得我们是怎样求一次函数和正比例函数的表达式吗?(用待定系数法求解)如:一直线经过(2,3)和(-4,5)两点,求这个函数的表达式?(学生做,教师检查)(二)课题引入:今天,我们类比一次函数和正比例函数表达式的求法,同样采用待定系数法求二次函数表达式。
(书写课题)1、通过例题讲解让学生熟悉二次函数表达式的求法。
例1、已知一个二次函数的图象过点1101427(-,)、(,)、(,)三点,求这个函数的表达式?二次手工备课例2、已知抛物线的顶点为13(,-)求抛物线的表(-,-),与轴交点为05达式?例3、已知抛物线与x轴交于1010(-,),(,)并经过点01A BM(,),求抛物线的表达式?学生活动:讨论交流,归纳总结求二次函数的表达式易犯的错误2、通过做题组二使学生能够灵活的选择二次函数的表达式来求表达式。
根据下列已知条件,选择合适的方法求二次函数的表达式:1、已知抛物线的顶点经过原点,且过点(2,8)2、已知抛物线的顶点是(-1,-2)并且过点(1,10)3、已知抛物线过三点(0,-2)(1,0)(2,3)学生活动:(交流合作得出正确答案并归纳总结方法)3、在掌握了各类求二次函数表达式的方法和技巧的基础上,通过本题组的练习进一步提升学生利用二次函数的图像及性质解决生活中的实际问题的能力。
九年级下第五章《二次函数》解答题专题训练(2)含答案
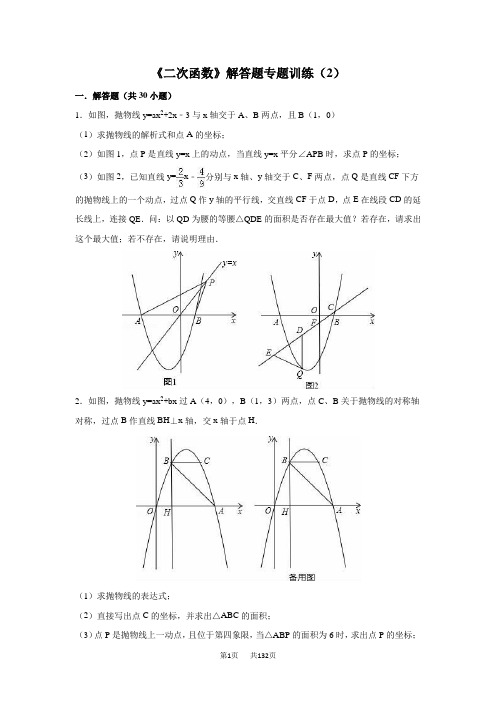
《二次函数》解答题专题训练(2)一.解答题(共30小题)1.如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)(1)求抛物线的解析式和点A的坐标;(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;(3)如图2,已知直线y=x﹣分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.2.如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的表达式;(2)直接写出点C的坐标,并求出△ABC的面积;(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.3.如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y=x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x 轴相交于点B,与CD交于点K.(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.①点B的坐标为(、),BK的长是,CK的长是;②求点F的坐标;③请直接写出抛物线的函数表达式;(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H 运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1•S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.4.如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y 轴交于点C(0,3),已知对称轴x=1.(1)求抛物线L的解析式;(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.5.如图,抛物线y=x 2+bx +c 与x 轴交于点A 和点B (3,0),与y 轴交于点C (0,3). (1)求抛物线的解析式;(2)若点M 是抛物线在x 轴下方上的动点,过点M 作MN ∥y 轴交直线BC 于点N ,求线段MN 的最大值;(3)在(2)的条件下,当MN 取得最大值时,在抛物线的对称轴l 上是否存在点P ,使△PBN 是等腰三角形?若存在,请直接写出所有点P 的坐标;若不存在,请说明理由.6.已知抛物线C :y=x 2﹣3x +m ,直线l :y=kx (k >0),当k=1时,抛物线C 与直线l 只有一个公共点.(1)求m 的值;(2)若直线l 与抛物线C 交于不同的两点A ,B ,直线l 与直线l 1:y=﹣3x +b 交于点P ,且,求b 的值;(3)在(2)的条件下,设直线l 1与y 轴交于点Q ,问:是否在实数k 使S △APQ =S △BPQ ?若存在,求k 的值,若不存在,说明理由.7.如图,已知抛物线y=x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.8.如图,抛物线y=x2+bx+c与直线y=x﹣3交于A、B两点,其中点A在y轴上,点B 坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.(1)求抛物线的解析式;(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标.9.如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.(1)写出点D的坐标.(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c (a≠0)的图象过点A.①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)、y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.10.如图,在平面直角坐标系中,已知抛物线C1:y=的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.(1)结合图象,直接写出不等式x2+6x+2<kx+b的解集;(2)若抛物线C2的顶点与点M关于原点对称,求p的值及抛物线C2的解析式;(3)若直线l沿y轴向下平移q个单位长度后,与(2)中的抛物线C2存在公共点,求3﹣4q的最大值.11.如图,直线l:y=﹣x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.(1)求△AOB的周长;(2)设AQ=t>0,试用含t的代数式表示点P的坐标;(3)当动点P,Q在直线l上运动到使得△AOQ与△BPO的周长相等时,记tan∠AOQ=m,若过点A的二次函数y=ax2+bx+c同时满足以下两个条件:①6a+3b+2c=0;②当m≤x≤m+2时,函数y的最大值等于,求二次项系数a的值.12.已知抛物线与x轴交于A(6,0)、B(﹣,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.(1)求此抛物线的解析式;(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.①当点F为M′O′的中点时,求t的值;②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.13.如图,已知二次函数y=﹣x2+bx+c的图象交x轴于点A(﹣4,0)和点B,交y轴于点C(0,4).(1)求这个二次函数的表达式;(2)若点P在第二象限内的抛物线上,求四边形AOCP面积的最大值和此时点P的坐标;(2)在平面直角坐标系内,是否存在点Q,使A,B,C,Q四点构成平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.14.如图所示,抛物线y=ax2﹣x+c经过原点O与点A(6,0)两点,过点A作AC⊥x 轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.(1)求抛物线的解析式,并求出点C和点D的坐标;(2)求点A关于直线y=2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;(3)点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.15.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(﹣1,4).(1)求此抛物线的解析式;(2)设点D为已知抛物线对称轴上的任意一点,当△ACD与△ACB面积相等时,求点D 的坐标;(3)点P在线段AM上,当PC与y轴垂直时,过点P作x轴的垂线,垂足为E,将△PCE 沿直线CE翻折,使点P的对应点P′与P、E、C处在同一平面内,请求出点P′坐标,并判断点P′是否在该抛物线上.16.综合与探究如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(﹣2,0),(6,﹣8).(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;(2)试探究抛物线上是否存在点F,使△FOE≌△FCE?若存在,请直接写出点F的坐标;若不存在,请说明理由;(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,试探究:当m为何值时,△OPQ是等腰三角形.17.如图,在平面直角坐标系xOy中,抛物线y=a(x+1)2﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,﹣),顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P,Q两点,点Q在y轴的右侧.(1)求a的值及点A,B的坐标;(2)当直线l将四边形ABCD分为面积比为3:7的两部分时,求直线l的函数表达式;(3)当点P位于第二象限时,设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否为菱形?若能,求出点N的坐标;若不能,请说明理由.18.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx经过两点A(﹣1,1),B(2,2).过点B作BC∥x轴,交抛物线于点C,交y轴于点D.(1)求此抛物线对应的函数表达式及点C的坐标;(2)若抛物线上存在点M,使得△BCM的面积为,求出点M的坐标;(3)连接OA、OB、OC、AC,在坐标平面内,求使得△AOC与△OBN相似(边OA与边OB对应)的点N的坐标.19.如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.(1)求该二次函数的解析式;(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.20.阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线经过B、C两点,顶点D在正方形内部.(1)直接写出点D(m,n)所有的特征线;(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?21.如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.(1)求二次函数y=ax2+bx+c的表达式;(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行与y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.22.如图,抛物线y=ax2+bx﹣经过点A(1,0)和点B(5,0),与y轴交于点C.(1)求抛物线的解析式;(2)以点A为圆心,作与直线BC相切的⊙A,请判断⊙A与y轴有怎样的位置关系,并说明理由;(3)在直线BC上方的抛物线上任取一点P,连接PB、PC,请问:△PBC的面积是否存在最大值?若存在,求出这个值和此时点P的坐标;若不存在,请说明理由.23.如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线l:y=﹣x+7上时,记为点E,F,当点C的对应点落在边OA 上时,记为点G.(1)求点E,F的坐标;(2)求经过E,F,G三点的抛物线的解析式;(3)当点C的对应点落在直线l上时,求CD的长;(4)在(2)中的抛物线上是否存在点P,使以E,F,P为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.24.在直角坐标系xOy中,A(0,2)、B(﹣1,0),将△ABO经过旋转、平移变化后得到如图1所示的△BCD.(1)求经过A、B、C三点的抛物线的解析式;(2)连结AC,点P是位于线段BC上方的抛物线上一动点,若直线PC将△ABC的面积分成1:3两部分,求此时点P的坐标;(3)现将△ABO、△BCD分别向下、向左以1:2的速度同时平移,求出在此运动过程中△ABO与△BCD重叠部分面积的最大值.25.已知抛物线y=x2+(2m+1)x+m(m﹣3)(m为常数,﹣1≤m≤4).A(﹣m﹣1,y1),B(,y2),C(﹣m,y3)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O 逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.(1)用含m的代数式表示抛物线的顶点坐标;(2)若无论m取何值,抛物线与直线y=x﹣km(k为常数)有且仅有一个公共点,求k的值;(3)当1<PH≤6时,试比较y1,y2,y3之间的大小.26.如图1(注:与图2完全相同),二次函数y=x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.(1)求该二次函数的解析式;(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).27.如图,直线y=﹣x+3与x轴、y轴分别相交于点B、C,经过B、C两点的抛物线y=ax2+bx+c 与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.(1)求该抛物线的解析式;(2)连接PB、PC,求△PBC的面积;(3)连接AC,在x轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.28.如图,在直角坐标系中,抛物线y=a(x﹣)2+与⊙M交于A,B,C,D四点,点A,B在x轴上,点C坐标为(0,﹣2).(1)求a值及A,B两点坐标;(2)点P(m,n)是抛物线上的动点,当∠CPD为锐角是,请求出m的取值范围;(3)点e是抛物线的顶点,⊙M沿cd所在直线平移,点C,D的对应点分别为点C′,D′,顺次连接A,C′,D′,E四点,四边形AC′D′E(只要考虑凸四边形)的周长是否存在最小值?若存在,请求出此时圆心M′的坐标;若不存在,请说明理由.29.如图1,已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,抛物线y=﹣x2+bx+c 过A、B两点,且与x轴交于另一点C.(1)求b、c的值;(2)如图1,点D为AC的中点,点E在线段BD上,且BE=2ED,连接CE并延长交抛物线于点M,求点M的坐标;(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,如图2,P为△ACG内以点,连接PA、PC、PG,分别以AP、AG为边,在他们的左侧作等边△APR,等边△AGQ,连接QR①求证:PG=RQ;②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.30.如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.(1)求此抛物线的解析式;(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标;(3)当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时,是否存在使△BDE为直角三角形的情况,若存在,请直接写出符合要求的E点的坐标;若不存在,请说明理由.31.如图,已知抛物线y=ax2+2x+6(a≠0)交x轴与A,B两点(点A在点B左侧),将直尺WXYZ与x轴负方向成45°放置,边WZ经过抛物线上的点C(4,m),与抛物线的另一交点为点D,直尺被x轴截得的线段EF=2,且△CEF的面积为6.(1)求该抛物线的解析式;(2)探究:在直线AC上方的抛物线上是否存在一点P,使得△ACP的面积最大?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由.(3)将直尺以每秒2个单位的速度沿x轴向左平移,设平移的时间为t秒,平移后的直尺为W′X′Y′Z′,其中边X′Y′所在的直线与x轴交于点M,与抛物线的其中一个交点为点N,请直接写出当t为何值时,可使得以C、D、M、N为顶点的四边形是平行四边形.32.如图,在平面直角坐标系中,四边形ABCD是以AB为直径的⊙M的内接四边形,点A,B在x轴上,△MBC是边长为2的等边三角形,过点M作直线l与x轴垂直,交⊙M于点E,垂足为点M,且点D平分.(1)求过A,B,E三点的抛物线的解析式;(2)求证:四边形AMCD是菱形;(3)请问在抛物线上是否存在一点P,使得△ABP的面积等于定值5?若存在,请求出所有的点P的坐标;若不存在,请说明理由.33.如图,在平面直角坐标系中,有抛物线y=a(x﹣h)2.抛物线y=a(x﹣3)2+4经过原点,与x轴正半轴交于点A,与其对称轴交于点B,P是抛物线y=a(x﹣3)2+4上一点,且在x轴上方,过点P作x轴的垂线交抛物线y=a(x﹣h)2于点Q,过点Q作PQ的垂线交抛物线y=a(x﹣h)2于点Q′(不与点Q重合),连结PQ′,设点P的横坐标为m.(1)求a的值;(2)当抛物线y=a(x﹣h)2经过原点时,设△PQQ′与△OAB重叠部分图形的周长为l.①求的值;②求l与m之间的函数关系式;(3)当h为何值时,存在点P,使以点O,A,Q,Q′为顶点的四边形是轴对称图形?直接写出h的值.34.已知,抛物线y=ax2(a≠0)经过点A(4,4),(1)求抛物线的解析式;(2)如图1,抛物线上存在点B,使得△AOB是以AO为直角边的直角三角形,请直接写出所有符合条件的点B的坐标:.(3)如图2,直线l经过点C(0,﹣1),且平行与x轴,若点D为抛物线上任意一点(原点O除外),直线DO交l于点E,过点E作EF⊥l,交抛物线于点F,求证:直线DF一定经过点G(0,1).35.如图,顶点为A(,1)的抛物线经过坐标原点O,与x轴交于点B.(1)求抛物线对应的二次函数的表达式;(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.36.如图,抛物线L:y=﹣(x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=(k>0,x>0)于点P,且OA•MP=12,(1)求k值;(2)当t=1时,求AB的长,并求直线MP与L对称轴之间的距离;(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;(4)设L与双曲线有个交点的横坐标为x0,且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.37.如图,抛物线C1:y=﹣x2+2x的顶点为A,与x轴的正半轴交于点B.(1)将抛物线C1上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式;(2)将抛物线C1上的点(x,y)变为(kx,ky)(|k|>1),变换后得到的抛物线记作C2,抛物线C2的顶点为C,点P在抛物线C2上,满足S△PAC =S△ABC,且∠APC=90°.①当k>1时,求k的值;②当k<﹣1时,请直接写出k的值,不必说明理由.38.如图,在平面直角坐标系xOy中,将二次函数y=x2﹣1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.(1)求N的函数表达式;(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求PA2+PB2的最大值;(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.39.如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.(1)求该二次函数的解析式及点M的坐标;(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).40.如图,已知抛物线y=﹣x2﹣x+2与x轴交于A、B两点,与y轴交于点C(1)求点A,B,C的坐标;(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.参考答案与解析1.(2016•深圳)如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)(1)求抛物线的解析式和点A的坐标;(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;(3)如图2,已知直线y=x﹣分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.【分析】(1)把B点坐标代入抛物线解析式可求得a的值,可求得抛物线解析式,再令y=0,可解得相应方程的根,可求得A点坐标;(2)当点P在x轴上方时,连接AP交y轴于点B′,可证△OBP≌△OB′P,可求得B′坐标,利用待定系数法可求得直线AP的解析式,联立直线y=x,可求得P点坐标;当点P在x轴下方时,同理可求得∠BPO=∠B′PO,又∠B′PO在∠APO的内部,可知此时没有满足条件的点P;(3)过Q作QH⊥DE于点H,由直线CF的解析式可求得点C、F的坐标,结合条件可求得tan∠QDH,可分别用DQ表示出QH和DH的长,分DQ=DE和DQ=QE两种情况,分别用DQ的长表示出△QDE的面积,再设出点Q的坐标,利用二次函数的性质可求得△QDE 的面积的最大值.【解答】解:(1)把B(1,0)代入y=ax2+2x﹣3,可得a+2﹣3=0,解得a=1,∴抛物线解析式为y=x2+2x﹣3,令y=0,可得x2+2x﹣3=0,解得x=1或x=﹣3,∴A点坐标为(﹣3,0);(2)若y=x平分∠APB,则∠APO=∠BPO,如图1,若P点在x轴上方,PA与y轴交于点B′,由于点P在直线y=x上,可知∠POB=∠POB′=45°,在△BPO和△B′PO中,∴△BPO≌△B′PO(ASA),∴BO=B′O=1,设直线AP解析式为y=kx+b,把A、B′两点坐标代入可得,解得,∴直线AP解析式为y=x+1,联立,解得,∴P点坐标为(,);若P点在x轴下方时,同理可得△BOP≌△B′OP,∴∠BPO=∠B′PO,又∠B′PO在∠APO的内部,∴∠APO≠∠BPO,即此时没有满足条件的P点,综上可知P点坐标为(,);(3)如图2,作QH⊥CF,交CF于点H,∵CF为y=x﹣,∴可求得C(,0),F(0,﹣),∴tan∠OFC==,∵DQ∥y轴,∴∠QDH=∠MFD=∠OFC,∴tan∠HDQ=,不妨设DQ=t,DH=t,HQ=t,∵△QDE是以DQ为腰的等腰三角形,=DE•HQ=×t×t=t2,∴若DQ=DE,则S△DEQ=DE•HQ=×2DH•HQ=×t×t=t2,若DQ=QE,则S△DEQ∵t2<t2,∴当DQ=QE时△DEQ的面积比DQ=DE时大.设Q点坐标为(x,x2+2x﹣3),则D(x,x﹣),∵Q点在直线CF的下方,∴DQ=t=x﹣﹣(x2+2x﹣3)=﹣x2﹣x+,当x=﹣时,t max=3,)max=t2=,∴(S△DEQ即以QD为腰的等腰三角形的面积最大值为.【点评】本题主要考查二次函数的综合应用,涉及知识点有待定系数法、角平分线的定义、全等三角形的判定和性质、三角形的面积、等腰三角形的性质、二次函数的性质及分类讨论等.在(2)中确定出直线AP的解析式是解题的关键,在(3)中利用DQ表示出△QDE的面积是解题的关键.本题考查知识点较多,综合性较强,计算量大,难度较大.2.(2016•丹东)如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的表达式;(2)直接写出点C的坐标,并求出△ABC的面积;(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.【分析】(1)利用待定系数法求二次函数的表达式;(2)根据二次函数的对称轴x=2写出点C的坐标为(3,3),根据面积公式求△ABC的面积;(3)因为点P是抛物线上一动点,且位于第四象限,设出点P的坐标(m,﹣m2+4m),利用差表示△ABP的面积,列式计算求出m的值,写出点P的坐标;(4)分别以点C 、M 、N 为直角顶点分三类进行讨论,利用全等三角形和勾股定理求CM 或CN 的长,利用面积公式进行计算.【解答】解:(1)把点A (4,0),B (1,3)代入抛物线y=ax 2+bx 中,得 解得:,∴抛物线表达式为:y=﹣x 2+4x ;(2)点C 的坐标为(3,3),又∵点B 的坐标为(1,3),∴BC=2,∴S △ABC =×2×3=3;(3)过P 点作PD ⊥BH 交BH 于点D ,设点P (m ,﹣m 2+4m ),根据题意,得:BH=AH=3,HD=m 2﹣4m ,PD=m ﹣1,∴S △ABP =S △ABH +S 四边形HAPD ﹣S △BPD ,6=×3×3+(3+m ﹣1)(m 2﹣4m )﹣(m ﹣1)(3+m 2﹣4m ),∴3m 2﹣15m=0,m 1=0(舍去),m 2=5,∴点P 坐标为(5,﹣5).(4)以点C 、M 、N 为顶点的三角形为等腰直角三角形时,分三类情况讨论:①以点M 为直角顶点且M 在x 轴上方时,如图2,CM=MN ,∠CMN=90°,则△CBM ≌△MHN ,∴BC=MH=2,BM=HN=3﹣2=1,∴M (1,2),N (2,0),由勾股定理得:MC==,∴S △CMN =××=; ②以点M 为直角顶点且M 在x 轴下方时,如图3,作辅助线,构建如图所示的两直角三角形:Rt △NEM 和Rt △MDC ,得Rt △NEM ≌Rt △MDC ,∴EM=CD=5,MD=ME=2,由勾股定理得:CM==,∴S△CMN=××=;③以点N为直角顶点且N在y轴左侧时,如图4,CN=MN,∠MNC=90°,作辅助线,同理得:CN==,∴S△CMN=××=17;④以点N为直角顶点且N在y轴右侧时,作辅助线,如图5,同理得:CN==,∴S△CMN=××=5;⑤以C为直角顶点时,不能构成满足条件的等腰直角三角形;综上所述:△CMN的面积为:或或17或5.【点评】本题是二次函数的综合题,考查了利用待定系数法求二次函数的表达式,考查了等腰直角三角形和全等三角形的判定和性质;本题的一般思路为:①根据函数的表达式设出点的坐标,利用面积公式直接表示或求和或求差列式,求出该点的坐标;②利用等腰直角三角形的两直角边相等,构建两直角三角形全等,再利用全等性质与点的坐标结合解决问题.3.(2016•沈阳)如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y=x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.①点B的坐标为(10、0),BK的长是8,CK的长是10;②求点F的坐标;③请直接写出抛物线的函数表达式;(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H 运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1•S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.【分析】(1)①根据四边形OCKB是矩形以及对称轴公式即可解决问题.②在RT△BKF中利用勾股定理即可解决问题.③设OA=AF=x,在RT△ACF中,AC=8﹣x,AF=x,CF=4,利用勾股定理即可解决问题.(2)不变.S1•S2=289.由△GHN∽△MHG,得=,得到GH2=HN•HM,求出GH2,根据S1•S2=•OG•HN••OG•HM即可解决问题.【解答】解:(1)如图1中,①∵抛物线y=x2﹣3x+m的对称轴x=﹣=10,∴点B坐标(10,0),∵四边形OBKC是矩形,∴CK=OB=10,KB=OC=8,故答案分别为10,0,8,10.②在RT△FBK中,∵∠FKB=90°,BF=OB=10,BK=OC=8,∴FK==6,∴CF=CK﹣FK=4,。
数学九年级下册第2章二次函数 教学+习题课件(付,525)

海浪为劈风斩浪的航船饯行,为随波逐 流的轻舟送葬.
第2章 二 次 函 数 2.1 建立二次函数模型
1.理解二次函数及其相关概念.(重点) 2.会辨别哪些函数是二次函数.(重点) 3.会用二次函数表示简单变量之间的关系.(重点、难点)
请完成以下各题: 1.正方形的面积y与边长x之间的关系是y=__. 2积.为三y角,则形的y关一于边x是的这关边系式上为高的y=_2_倍__,_设.三角形x2这条边的长为x,面 3.在半径为4cm的圆中,挖去一个边长为xcm的正方形,剩下部分 的面积为ycm2,则y关于x的关系式1 x为2 y=_______.
(1)y=3(x-1)²+1. 是二次函数,a=3,b=-6,c=4
(2) y x 1 . x
(3)s=3-2t².
不是二次函数 是二次函数,a=-2,b=0,c=3
(4) y
1 x2
. x
不是二次函数
(5)y=(x+3)²-x². 不是二次函数
(6)v=10πr². 是二次函数,a=10π,b=0,c=0
y=(4+x)(3+2x)=2x2+11x+12
1.(莆田·中考)某同学利用描点法画二次函数 y=ax2+bx+c(a≠0)
的图象时,列出的部分数据如下表:
x
0
1
2
3
4
y
3
0 -2 0
3
经检查,发现表格中恰好有一组数据计算错误,请你根据
上述信息写出该二次函数的解析式: y x2 4x 3 .
解:因为该函数为二次函数,
则
m2 -m=2 m2 -1 0
① ②
解①得:m=2或m=-1,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙教版九年级下册考点专题训练
建立二次函数模型解决商品经济问题
一、明确学习目标
1、能运用二次函数分析和解决简单的实际问题,培养分析问题和解决问题的能力和应用数学的意识.
2、经历探索实际问题与二次函数的关系的过程,深刻理解二次函数是刻画现实世界的一个有效的数学模型.
3、通过学习和合作交流,了解数学带给人们的价值及美感.
二、自主预习
1、求下列函数的最大值或最小值.
(1)5322--=x x y
(2)432+--=x x y
2、某商品现在的售价为每件60元,每星期可卖出300件,已知商品的进价为每件40元,那么一周的利润是多少?
学生展示,师生互评.
商场的服装,经常出现涨价、降价,这其中有何奥妙呢?商家的利润是否随涨价而增大,随降价而减小?
三、合作探究
活动1 1、阅读教材第49页问题及探究1和探究2并思考:
(1)涨价的情况;
(2)如何确定函数关系式?
(3)变量x 有范围要求吗?
2、教师分层引导:
(1)销售额为多少?
(2)进货额为多少?
(3)利润y 与每件涨价x 元的函数关系式是什么?
(4)变量x 的范围如何确定?
(5)如何求最值?
3、解决问题:
活动2 例某建筑的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料长为15m(图中所有线条长度之和),当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?
教师点拨:此题较复杂,特别要注意:中间线段用x的代数式来表示时,要充分利用几何关系;要注意顶点的横坐标是否在自变量x的取值范围内.
四、当堂检测
1、如图所示,从一张矩形纸较短的边上找一点E,过E点剪下两个正方形,它们的边长分别是AE、DE,要使剪下的两个正方形的面积和最小,点E应选在何处?为什么?
2、如图所示,有一块空地,空地外有一面长10m的围墙,为了美化生活环境,准备靠墙修建一个矩形花圃,用32m长的不锈钢作为花圃的围栏,为了浇花和赏花的方便,准备在花圃的中间再围出一条宽为1m的通道及在左右花圃各放一个1m宽的门,花圃的宽AD究竟应为多少米才能使花圃的面积最大?。
