浙教版九年级上专题《相似三角形的基本模型》
三角形相似的判定课件浙教版数学九年级上册(完整版)
E
D
F
作业布置
选做题：
3.如图，AB∥EF∥DC，AD∥BC，EF与AC交于点G，则相似三角形共
有( C )。 A．3对 B．5对 C．6对 D．8对
作业布置
选做题： 4.如图所示，△ABC中，BD⊥AC于点D，CE⊥AB于点E，BD与CE相 交于点F，连结DE. 求证：△BEF∽△CDF；
证明：∵BD⊥AC，CE⊥AB， ∴∠BEF＝∠CDF＝90°， 又∵∠EFB＝∠DFC， ∴△BEF∽△CDF.
F
∴△ADE∽△ABC.
新知讲解
判定三角形相似的预备定理：
平行于三角形一边的直线和其他两边相交，所构成的三角形与原三 角形相似.
根据上述预备定理，我们可以得到以下三角形相似的判定定理：
有两个角对应相等的两个三角形相似.
新知讲解
已知：如图，在△ABC与△A'B'C'中，∠A=∠A'，∠B=∠B'. 求证：△ABC∽△A'B'C'.
作业布置
【综合实践类作业】 5.如图，在△ABC中，∠ACB＝90°，CD是AB边上的高，BE平分 ∠ABC，BE分别与AC，CD相交于点E，F. 求证：△AEB∽△CFB.
证明：∵∠ACB＝90°，∴∠ACD＋∠BCD＝90°. ∵CD为AB边上的高， ∴∠ADC＝90°，∴∠A＋∠ACD＝90°， ∴∠A＝∠BCD.∵BE平分∠ABC， ∴∠ABE＝∠CBE，∴△AEB∽△CFB.
F
AD AE，BF AE，DE AE， AB AC BC AC BC AC
AD BF DE
AB BC BC
新知讲解
【合作学习】
如图，在△ABC中，D，E分别是AB，AC上的点，DE∥BC.
相似三角形的常见模型
初中数学 ︵ 九年级 ︶培优篇初中数学 ︵ 九年级 ︶培优篇【基本模型】①如图，在ABC 中，点D 在AB 上，点E 在AC 上，//DEBC ，则ADE ABC △△∽，AD AE DEAB AC BC．②模型拓展1：斜交A 字型条件：C ADE ，图2结论：~ADE ACB ；③模型拓展2： 如图，∠ACD ＝∠B ⇔△ADC ∽△ACB ⇔AD AC CDAC AB BC．初中数学 ︵ 九年级︶培优篇【例1】如图，王华晚上由路灯A 下的B 处走到C 处时，测得影子CD 的长为1米，继续往前走2米到达B 处时，测得影子EF 的长为2米，已知王华的身高是1.5米，那么路灯A 的高度等于_________．【变式1-1】有一块直角三角形木板，∠B ＝90°，AB ＝1.5m ，BC ＝2m ，要把它加工成一个面积尽可能大的正方形桌面．甲、乙两位同学的加工方法分别如图1、图2所示．请你用学过的知识说明哪位同学的加工方法更好（加工损耗忽略不计）．初中数学 ︵ 九年级 ︶培优篇 【变式1-2】（2022•衢州二模）已知菱形ABCD ，E 是BC 边上一点，连接AE 交BD 于点F （1）如图1，当E 是BC 中点时，求证：AF ＝2EF ；（2）如图2，连接CF ，若AB ＝5，BD ＝8，当△CEF 为直角三角形时，求BE 的长； （3）如图3，当∠ABC ＝90°时，过点C 作CG ⊥AE 交AE 的延长线于点G ，连接DG ，若BE ＝BF ，求tan ∠BDG 的值．初中数学 ︵九年级 ︶培优篇 ③模型拓展：如图，∠A ＝∠C ⇔△AJB∽△CJD ⇔A B JA C D JC【例2】如图，在平行四边形ABCD 中，E 为边AD 的中点，连接AC 、BE 交于点F ．若△AEF 的面积为2，则△ABC 的面积为（ ） A ．8B ．10C ．12D ．14初中数学 ︵ 九年级 ︶培优篇 【变式2-1】如图，在△ABC 中，BC ＝6，AEA F EBFC，动点P 在射线EF 上，BP 交CE 于点D ，∠CBP 的平分线交CE 于点Q ，当CQ ＝14CE 时，EP ＋BP 的值为（ ）A ．9B ．12C ．18D ．24【变式2-2】如图，在Rt △ACB 中，∠ACB =90°，AC =4，BC =3，点D 为AC 上一点，连接BD ，E 为AB 上一点，CE ⊥BD 于点F ，当AD =CD 时，求CE 的长．【变式2-3】如图，已知D 是BC 的中点，M 是AD的中点．求AN:NC的值．初中数学 ︵ 九年级︶培优篇【例3】如图，在平行四边形ABCD 中，∠ABC 的平分线交AC 于点E ，交AD 于点F ，交CD 的延长线于点G ，若AF ＝2FD ，则BEEG的值为（ ） A ．12B ．13C ．23D ．34【变式3-1】（2020•杭州）如图，在正方形ABCD 中，点E 在BC 边上，连接AE ，∠DAE 的平分线AG 与CD 边交于点G ，与BC 的延长线交于点F ．设＝λ（λ＞0）．（1）若AB ＝2，λ＝1，求线段CF 的长． （2）连接EG ，若EG ⊥AF ， ①求证：点G 为CD 边的中点． ②求λ的值．初中数学 ︵ 九年级 ︶培优篇【例4】如图，在△ABC 中，45ABC ，AB A D A E ，D A E 90 ，C E，则CD 的长为______．初中数学 ︵ 九年级 ︶培优篇 【变式4-1】矩形ABCD 中，AD ＝9，AB ＝12，点E 在对角线BD 上（不与B 、D 重合），EF ⊥AE 交CD 于F 点，连接AF 交BD 于G 点． （1）如图1，当G 为DE 中点时． ①求证：FD ＝FE ； ②求BE 的长．（2）如图2，若E 为BD 上任意点，求证：AG 2＝BG •GE ．初中数学 ︵ 九年级 ︶培优篇 【变式4-2】如图，ABC 中，,,AB AC AB AC 点D E 、分别是BC AC 、的中点，AF BE ⊥与点F ．（1）求证：2AE FE BE ；（2）求A F C 的大小；（3）若DF=1，求△ABF 的面积．初中数学 ︵ 九年级 ︶培优篇结论：AH ⊥GF ，△AGF ∽△ABC ，GF AHBC AM【例5】如图1，在△ABC 中，AB =AC =5，BC =6，正方形DEFG 的顶点D 、G 分别在AB 、AC 上，EF 在BC 上． （1）求正方形DEFG 的边长；（2）如图2，在BC 边上放两个小正方形DEFG 、FGMN ，则DE= ．初中数学 ︵ 九年级 ︶培优篇 【变式5-1】有一块锐角三角形卡纸余料ABC ，它的边BC ＝120cm ，高AD ＝80cm ，为使卡纸余料得到充分利用，现把它裁剪成一个邻边之比为2：5的矩形纸片EFGH 和正方形纸片PMNQ ，裁剪时，矩形纸片的较长边在BC 上，正方形纸片一边在矩形纸片的较长边EH 上，其余顶点均分别在AB ，AC 上，具体裁剪方式如图所示． （1）求矩形纸片较长边EH 的长；（2）裁剪正方形纸片时，小聪同学是按以下方法进行裁剪的：先沿着剩余料△AEH 中与边EH 平行的中位线剪一刀，再沿过该中位线两端点向边EH 所作的垂线剪两刀，请你通过计算，判断小聪的剪法是否正确．初中数学 ︵ 九年级︶培优篇 ②拓展：（1）在正方形、长方形中经常会出现射影定理模型，如图，在有射影定理模型．（2）如图，在圆中也会出现射影定理模型．【例6】如图，四边形ABCD 中，AD ∥BC ，∠B ＝90°，E 为AB 上一点，分别以ED 、EC 为折痕将两个角(∠A 、∠B )向内折起，点A 、B 恰好落在CD 边的点F 处，若AD ＝3，BC ＝5，则EF 的长是（ ） A.15B ．215C ．17D ．217初中数学 ︵ 九年级 ︶培优篇 【变式6-1】如图所示，在△ABC 中，∠ABC ＝90°，BD ⊥AC ，DE ⊥BC ，垂足分别为D 、E 两点，则图中与△ABC 相似的三角形有（ ） A ．4个B ．3个C ．2个D ．1个【变式6-2】如图，在R t △ABC 中，∠ACB ＝90°，点D 在AB 上，且AD AC ＝ACAB． （1）求证 △ACD ∽△ABC ；（2）若AD ＝3，BD ＝2，求CD 的长．【变式6-3】ABC 中，90ABC ，BD AC ，点E 为B D 的中点，连接A E 并延长交B C 于点F ，且有AF CF ，过F 点作FH AC 于点H ． （1）求证：AD E CD B ∽； （2）求证：=2A E EF ； （3）若FHB C 的长．初中数学 ︵ 九年级 ︶培优篇②如图所示，BDE 和ABC 则ABD CBE ∽△△，且相似比为总结：旋转相似型中由公共旋转顶点、一点及其旋转后的对应点组成的三角形与由公共旋转顶点、另一点及其旋转后的对应点组成的三角形相似．初中数学 ︵ 九年级 ︶培优篇【例7】如图，在△ABC 与△ADE 中，∠ACB ＝∠AED ＝90°，∠ABC ＝∠ADE ，连接BD 、CE ，若AC ：BC ＝3：4，则BD ：CE 为（ ） A ．5：3B ．4：3C ．√5：2D ．2：√3【变式7-1】如图，点E 是菱形ABCD 对角线CA 的延长线上任意一点，以线段AE 为边作一个菱形AEFG ，且菱形AEFG ∽菱形ABCD ，相似比是：2，连接EB ，GD ．（1）求证：EB ＝GD ；（2）若∠DAB ＝60°，AB ＝2，求GD 的长．初中数学 ︵ 九年级 ︶培优篇 【变式7-2】如图，正方形ABCD ，对角线AC ，BD 相交于O ，Q 为线段DB 上的一点，90MQN ，点M 、N 分别在直线BC 、DC 上．（1）如图1，当Q 为线段OD 的中点时，求证：1132DN BM BC ；（2）如图2，当Q 为线段OB 的中点，点N 在CD 的延长线上时，则线段DN 、BM 、BC 的数量关系为 ；（3）在（2）的条件下，连接MN ，交AD 、BD 于点E 、F ，若:3:1M B M C ，N Q ，求EF 的长．初中数学 ︵ 九年级 ︶培优篇 补充：其他常见的一线三等角图形【例8】【感知】如图①，在四边形ABCD 中，点P 在边AB 上（点P 不与点A 、B 重合），90A B DPC ．易证DAP PBC △△∽．（不需要证明） 【探究】如图②，在四边形ABCD 中，点P 在边AB 上（点P 不与点A 、B 重合），A B D PC ．若4PD ，8P C ，6BC ，求AP 的长．【拓展】如图③，在ABC 中，8AC BC ，12A B ，点P 在边AB 上（点P 不与点A 、B 重合），连结CP ，作CPE A ，PE 与边BC 交于点E ，当CPE △是等腰三角形时，直接写出AP 的长．初中数学 ︵ 九年级 ︶培优篇 【变式8-1】如图，在矩形ABCD 中，CD ＝4，E 是BC 的中点，连接AE ，tan ∠AEB 43，P 是AD 边上一动点，沿过点P 的直线将矩形折叠，使点D 落在AE 上的点D ¢处，当A P D △是直角三角形时，PD 的值为（ ）A ．23或67B ．83或247C ．83或307D ．103或187初中数学 ︵ 九年级 ︶培优篇 【变式8-2】（2022秋•温州校级月考） 【推理】如图1，在正方形ABCD 中，点E 是CD 上一动点，将正方形沿着BE 折叠，点C 落在点F 处，连结BE ，CF ，延长CF 交AD 于点G ． （1）求证：BCE CDG △△≌． 【运用】（2）如图2，在【推理】条件下，延长BF 交AD 于点H ．若45HD HF ，9C E ，求线段DE 的长．【拓展】（3）将正方形改成矩形，同样沿着BE 折叠，连结CF ，延长CF ，BF 交直线AD 于G ，两点，若AB k BC ，45HD HF ，求DEEC的值（用含k 的代数式表示）．。
4.5 相似三角形的性质及其应用第2课时 相似三角形的性质(2)浙教版数学九年级上册课件
三角形相似的 性质（2）
周长比 =相似比 面积比 =相似比的平方
1.填空： （1）如果三角形的边长扩大到原来的100倍，那么三角 形的周长扩大到原来的____1_0_0倍；面积扩大到原来的 ___1_0_0_0倍0 . （2）如果三角形的周长扩大到原来的100倍，那么三角 形的边长扩大到原来的____1_0_0倍. （3）如果三角形的面积扩大到原来的100倍，那么三角 形的边长扩大到原来的_____1_0倍.
3
5
4
10 6
8
相似比
3
5
4
10 6
8
相似三角形的周长和面积有以下性质：
相似三角形的周长之比等于相似比； 相似三角形的面积之比等于相似比的平方.
A
B
C
A′
B′
C′
A
如图，分别作△ABC，△A′B′C′的BC，
B
B′C′边上的高线AD，A′D′.
∵△ABC∽△A，在等边三角形ABC中，点D，E分别在边AB，AC上， DE∥BC. 如果BC=8 cm，AD:DB=1:3，则△ADE的周长等 于___6___cm，△ADE的面积等于______cm2.
感谢观看！
∵AD，A′D′分别是BC， B′C′边上的高线，
∴∠ADB=∠A′D′B′=90°，
B′
DC A′
C′ D′
A B DC
A′
B′
C′
D′
解：（1）在△ABC和△ADE中， ∵∠CAB=∠EAD（公共角）， ∠B=∠ADE（已知）， ∴△ABC∽△ADE.
如图，D，E分别是AC，AB上的点，∠ADE=∠B， AG⊥BC于点G，AF⊥DE于点F. 若AD=3，AB=5，求： （2）△ADE与△ABC的周长之比. （3）△ADE与△ABC的面积之比.
新浙教版数学九年级上册4.5相似三角形的性质及其应用精品PPT课件
新浙教版九（上）§第四章
旧知尝试
1.相似三角形对应边的比叫做 相似比 2.相似三角形的性质：相似三角形的对应角 相等 , 对应边成比例 相似比 . 相似比 相似比 3. 相似三角形对应角平分线之比等于 ，对应边上的中线 3:5 之比等于 , 对应边上的高线之比等于 2:5 . 4.如图：△ABC中AE:EC=2：3，则 AE:AC= ,CE:AC= 若△ADE与四边形BCED的面积之比是 4:25 4：21 A 则 △ADE与△ABC的面积之比是
D
E C
Байду номын сангаас
B
探究新知
A
在8×8的正方形网格中，△ABC∽△A/B/C/，探究下面 的问题：
1、两个相似三角形的相似比是多少？
A B B C A C = = =2 BC AC AB
新知尝试
2、两个相似三角形的周长比是多少？
C 6+2 5+4 2 2(3 + 5 + 2 2) ΔA B C = = C 3+ 5 +2 2 3+ 5+2 2 / / / ΔA B C
探究新知
A
相似三角形的周长比等于相似比; 相似三角形的面积比等于相似比的平方
已知:Δ ABC∽Δ A/B/C/，相似比为k, SΔ A B C CΔ ABC 2 = k = k 求证: C SΔ A / B / C / Δ A B C
/ / /
证明：∵△ABC∽△A/B/C/且相似比为k
B
A/
C
A B B C A C / / = / / = / / =k AB BC AC
AD AB ∴ / / = / / =k AD AB
C/
浙教版九年级数学上册第四章：相似三角形基本模型练习题(含答案)
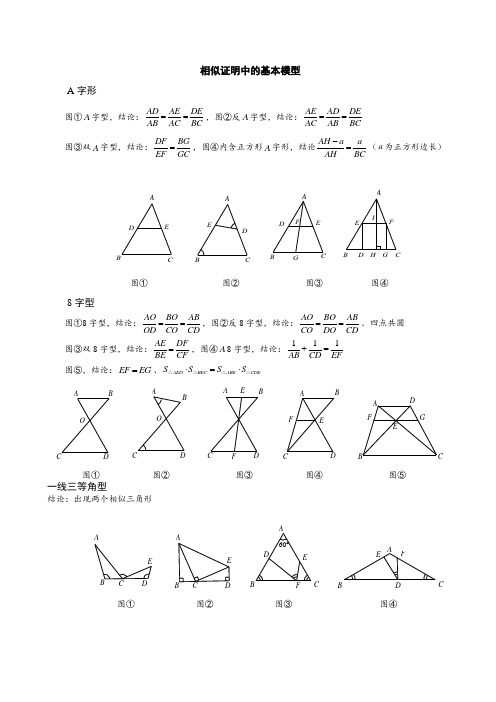
相似证明中的基本模型A 字形图①A 字型，结论：AD AE DE AB AC BC ==，图②反A 字型，结论：AE AD DEAC AB BC== 图③双A 字型，结论：DF BG EF GC =，图④内含正方形A 字形，结论AH a aAH BC-=（a 为正方形边长）IH G FED CB AGFEDC BAEDCB A ED C BA图① 图② 图③ 图④8字型图①8字型，结论：AO BO AB OD CO CD ==，图②反8字型，结论：AO BO AB CO DO CD==、四点共圆 图③双8字型，结论：AE DF BE CF=，图④A 8字型，结论：111AB CD EF += 图⑤，结论：EF EG =、AED BEC ABE CDE S S S S ⋅=⋅△△△△EFD C BA F ED C BAOD C BAODC BAGFED CB A图① 图② 图③ 图④ 图⑤一线三等角型结论：出现两个相似三角形HE DC B AE DC BAEDCBAC60°F E DCB AFED CB A图① 图② 图③ 图④角分线定理与射影定理图①内角分线型，结论：AB BD AC DC =，图②外角分线型，结论：AB BDAC CD= 图③斜射影定理型，结论：2AB BD BC =⋅，图④射影定理型，结论：1、2AC AD AB =⋅，2、2CD AD BD =⋅，3、2BC BD BA =⋅D C BD BCAEDB AD B A梅涅劳斯型常用辅助线G FEDCBAGFEDCBA G E DC B ADEFCBA四、相似证明中的面积法面积法主要是将面积的比，和线段的比进行相互转化来解决问题． 常用的面积法基本模型如下：如图：1212ABC ACDBC AHS BCS CD CD AH ⋅⋅==⋅⋅△△． 图1：“山字”型H DC B A如图：1212ABC BCDBC AHS AH AO S DG OD BC DG ⋅⋅===⋅⋅△△． 图2：“田字”型G HODCBA如图：ABD ABD AED ACE AED ACE S S S AB AD AB ADS S S AE AC AE AC⋅=⋅=⋅=⋅△△△△△△．图3：“燕尾”型CDEB A考点一：相似三角形【例1】 如图，D 、E 是ABC ∆的边AC 、AB 上的点，且AD AC ⋅=AE AB ⋅，求证：ADE B ∠=∠.EDCBA【答案】∵AD AC AE AB ⋅=⋅ ∴AD ABAE AC=∵DAE BAC ∠=∠∴DAE ∆∽BAC ∆∴ADE B ∠=∠ 【例2】 如图，在ABC ∆中，AD BC ⊥于D ，CE AB ⊥于E ，ABC ∆的面积是BDE ∆面积的4倍，6AC =，求DE 的长.ED CB A【答案】∵AD BC ⊥，CE AB ⊥，ABD CBE ∠=∠ ∴ABD ∆∽CBE ∆∴BE BCBD AB=∵EBD CBA ∠=∠ ∴BED ∆∽BCA ∆∴11322DEDE AC AC===⇒== 【例3】 如图，ABC △中，60ABC ∠=︒，点P 是ABC △内一点，使得APB BPC CPA ∠=∠=∠，86PA PC ==，，则PB =________．PCBA【解析】120APB BPC ∠=∠=︒，60BAP ABP ABC ABP CBP ∠=︒-∠=∠-∠=∠，故ABP BCP △∽△，2PB PA PC =⋅．【例4】 如图，已知三个边长相等的正方形相邻并排，求EBF EBG ∠+∠．HGFED CB A【答案】45︒ 【解析】连接DF 、CG ，则45EDF EBF DFB ∠=∠+∠=︒，若DFB EBG ∠=∠，则EBF EBG ∠+∠可求，问题的关键是证明BCG FDB △∽△．考点二：相似三角形与边的比例☞考点说明：可运用相似三角形模型，常用A 字形与8字形【例5】 在ABC ∆中，BD CE =，DE 的延长线交BC 的延长线于P ， 求证：AD BP AE CP ⋅=⋅.PE D CBA MPED C BA【答案】过C 作CM AB ∥交DP 于M ，∵CM AB ∥，∴PCM PBD ∆∆∽， ∴CM PC BD PB =， ∵CM AB ∥，∴CEM AED ∆∆∽， ∴CM AD CE AE =， ∵BD CE =， ∴CM CM CE BD =， ∴PC AD PB AE=， ∴AD BP AE CP ⋅=⋅【例6】 如图，在ABC ∆的边AB 上取一点D ，在AC 取一点E ，使AD AE =，直线DE 和BC 的延长线相交于P ，求证：BP BDCP CE= PEDCBA4321MPE D CBA【答案】过C 作CM AB ∥交DP 于M ，∵CM AB ∥，∴PCM PBD ∆∆∽， ∴BP BD CP CM =， ∵CM AB ∥， ∴14∠=∠， 又∵AD AE =，∴12∠=∠，∴24∠=∠， ∵23∠=∠， ∴34∠=∠， ∴CM CE = ∴BP BD CP CE= 【例7】 如图，M 、N 为ABC △边BC 上的两点，且满足BM MN NC ==，一条平行于AC 的直线分别交AB 、AM 和AN 的延长线于点D 、E 和F .求证：3EF DE =.F NMED CBAK HF N MG ED CBA【答案】过M ，N 分别作AC 的平行线交AB 于H ，G 两点，NH 交AM 于K ，∵BM MN NC ==， ∴BG GH HA ==，易知12HK GM =，12GM HN =，∴14HK HN =，即13HK KN =，又∵DF HN ∥， ∴13DE HK EF KN ==，即3EF DE =. 考点三：相似三角形与内接矩形☞考点说明：内接矩形问题是相似三角形中比较典型的问题，考查了相似三角形对应高的比等于相似比【例1】 一块直角三角形木板的一条直角边AB 长为1.5米，面积为1.5平方米，工人师傅要把它加工成一个面积最大的正方形桌面，请甲、乙两位同学进行设计加工方案。
相似三角形的性质及其应用课件浙教版九年级数学上册(完整版)
三角形的重心分每一条中线成1：2的两条线段.
课堂练习
【知识技能类作业】 必做题：
1.（1）两个相似三角形的相似比为1:2, 则对应高的比为__1_：__2____， 则对应中线的比为__1__：__2___. （2）两个相似三角形对应中线的比为1:4 ，则对应高的比为_1_：__4__ .
A'
D'
C'
新知讲解
解：∵△ABC∽△A'B'C'，∴∠B=∠B'， AB BC . A'B' B'C'
∵ AD，A'D'分别是△ABC与△A'B'C'的中线，
∴BD= 1 BC，B'D'= 1 B'C'，
2
2
BD
BC
AB .
A
B'D' B'C' A'B'
∴△ABD∽△A'B'D'，
AD A'D'
1 2
.
证明：如图，连结DE.
∵BD，CE是△ABC的两条中线，∴
DE
∥=
1 2
BC.
∴∠EDB=∠DBC，∠DEC=∠ECB，
∴△DEP∽△BCP.
DB PP
EP CP
DE BC
1 2
.
新知讲解
例2中，如果再作BC边上的中线，这条中线与AC边上的中线BD的交 点也必定分BD成1：2的两条线段，也就是点P. 这就证明了三角形的三条中线相交于一点.
作业布置
选做题： 3.如图，在△ABC中，BC＝120，高AD＝60，正方形EFGH的一边在 BC上，点E，F分别在AB，AC上，AD交EF于点N，则AN的长为( B). A．15 B．20 C．25 D．30
浙教版数学九上42《相似三角形》课件
浙教版数学九上42《相似三角形》课件一、教学内容本节课选自浙教版数学九年级上册第42讲《相似三角形》。
教学内容主要包括教材第5章第3节的相似三角形的判定和性质。
详细内容包括：相似三角形的定义、判定方法（AA、SAS、SSS）、相似三角形的性质（对应角相等、对应边成比例、周长比和面积比相等），以及相似三角形在实际问题中的应用。
二、教学目标1. 让学生掌握相似三角形的定义、判定方法及其性质。
2. 培养学生运用相似三角形知识解决实际问题的能力。
3. 提高学生的逻辑思维能力和空间想象能力。
三、教学难点与重点教学难点：相似三角形的判定方法、性质的应用。
教学重点：相似三角形的定义、判定方法、性质。
四、教具与学具准备教具：多媒体课件、黑板、粉笔。
学具：直尺、圆规、三角板。
五、教学过程1. 实践情景引入通过展示生活中的相似图形（如相似的建筑、家具等），引导学生发现相似图形的美和实用价值。
2. 例题讲解（1）已知三角形ABC与三角形DEF相似，求证：对应角相等、对应边成比例。
（2）已知三角形ABC中，AB=6cm，BC=8cm，AC=10cm。
三角形DEF 中，DE=4cm，EF=5cm，DF=6.4cm。
判断两个三角形是否相似，并说明理由。
3. 随堂练习（1）已知三角形ABC与三角形DEF相似，已知对应边的比值为2:1，求证：对应角相等。
4. 讲解相似三角形的判定方法、性质和应用。
5. 课堂小结六、板书设计1. 相似三角形的定义2. 相似三角形的判定方法（AA、SAS、SSS）3. 相似三角形的性质（1）对应角相等（2）对应边成比例（3）周长比和面积比相等4. 实际应用七、作业设计1. 作业题目：（1）已知三角形ABC与三角形DEF相似，对应边的比值为3:2，求证：对应角相等。
（2）已知三角形ABC中，AB=4cm，BC=6cm，AC=8cm。
三角形DEF 中，DE=3cm，EF=4.8cm，DF=6cm。
判断两个三角形是否相似，并说明理由。
新浙教版九年级上册初中数学 第1课时 相似三角形的性质 教学课件
A
A'
对应中线 对应角平分线
B
D
C
A
B' D' C' A'
BD
C
B' D' C'
新课讲解
相似三角形对应线段的比 由此我们可以得到： 相似三角形对应高的比、对应中线与对应角平分线的比都等于相似比。 一般地，我们有： 相似三角形对应线段的比等于相似比。
新课讲解
典例分析
例 已知 △ABC∽△DEF，BG、EH 分别是 △ABC和 △DEF 的角平分线，
DQ 是中线，若 AP＝2，则 DQ的值为( C )
A．2 B．4 C．1
D. 1
2
拓展与延伸
如图，这是圆桌正上方的灯泡 (点A) 发出的光线照 射桌面形成阴影的示意图，
已知桌面的直径为 1.2 米，桌面距离地面为 1 米，若灯泡距离地面 3 米，则地
面上阴影部分的面积约为多少 (结果保留两位小数)？
以高为例 A
解：如图，分别作出 △ABC 和 △A' B' C' 的
高 AD 和 A' D'
则∠ADB =∠A' D' B'=90° ∵△ABC ∽△A′B′C′
BD
C
∴∠B＝∠B'
A'
∴△ABD ∽△A' B' D'
∴ AD AB k A'D' A'B'
B' D'
C'
新课讲解
如图，△ABC ∽△A′B′C′，相似比为 k，它们对应高、对应中线、对应
BC = 6 cm，EF = 4cm，BG= 4.8 cm. 求 EH 的长。
浙教版数学九年级上册 第4章 相似三角形 知识点汇总 及例题讲解
⎧⎧⎪⎪⎨⎪⎪⎪⎩⎪⎪⎧⎪⎪⎨⎨⎪⎪⎩⎪⎪⎪⎪⎪⎩比例的性质平行线分线段成比例成比例线段平行线分线段成比例定理相似三角形定义相似三角形的基本判定相似三角形判定相似三角形性质位似一、比例的性质1．a cad bc b d=⇔=，这一性质称为比例的基本性质,由它可推出许多比例形式； 2．a c b db d ac =⇔=(反比定理)； 3．a c a bb dcd =⇔=(或d c b a =)(更比定理)；4．a c a b c db d b d ++=⇔=(合比定理)； 5．ac a b cd b d b d --=⇔=(分比定理)； 6．a c a b c d b d a b c d++=⇔=--(合分比定理)； 7．(0)a c m a c m a b d n b d n b d n b++⋅⋅⋅+==⋅⋅⋅=++⋅⋅⋅+≠⇔=++⋅⋅⋅+(等比定理).二、 黄金分割如图，若线段AB 上一点C 把线段AB 分成两条线段AC 和BC （AC BC >），且使AC 是AB 和BC 的比例中项（即2AC AB BC =⋅）则称线段AB 被点C 黄金分割，点C 叫线段AB 的黄金分割点，其中510.6182AC AB AB -=≈，相似三角形知识精讲知识网络图0.382BC AB AB =≈，AC 与AB 的比叫做黄金比．三、平行线分线段成比例定理1．定理：三条平行直线截两条直线，截得的对应线段成比例．2．推论：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．3．推论的逆定理：如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边． 4．三角形一边的平行线性质平行于三角形的一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例． 如图，AB CD EF ∥∥，则AC BD CE DF AC BD CE DFCE DF AC BD AE BF AE BF====，，，．若将AC 称为上，CE 称为下，AE 称为全，上述比例式可以形象地表示为====上上下下上上下下，，，下下上上全全全全．当三条平行线退化成两条的情形时，就成了“A ”字型，“X ”字型．则有 AE AF AE AF EFBC EF EB FC AB AC BC⇔===∥，．四、相似三角形的定义1．相似三角形：形状相同的两个三角形叫做相似三角形．如图，ABC △与A B C '''△相似，记作ABC A B C '''△∽△，符号∽读作“相似于”．AAB C D E FFEDC B A A BE F F ECBA2．相似三角形的相似比：相似三角形对应边的比叫做相似比；全等三角形的相似比是1，“全等三角形”一定是“相似形”，“相似形”不一定是“全等形”。
浙教版数学九上42《相似三角形》课件
浙教版数学九上42《相似三角形》课件一、教学内容本节课的教学内容来自于浙教版数学九年级上册第42章《相似三角形》。
本章节主要内容包括：相似三角形的定义、性质及判定。
具体的教学内容有：1. 相似三角形的定义：如果两个三角形的对应角相等，对应边成比例，那么这两个三角形相似。
2. 相似三角形的性质：相似三角形的对应边成比例，对应角相等。
3. 相似三角形的判定：如果两个三角形的对应角相等，对应边成比例，那么这两个三角形相似。
二、教学目标1. 理解相似三角形的定义，掌握相似三角形的性质和判定方法。
2. 能够运用相似三角形的知识解决实际问题，提高学生的数学应用能力。
3. 培养学生的逻辑思维能力，提高学生的数学素养。
三、教学难点与重点重点：相似三角形的定义、性质和判定。
难点：相似三角形的判定方法的灵活运用。
四、教具与学具准备教具：黑板、粉笔、多媒体课件。
学具：笔记本、尺子、三角板。
五、教学过程1. 实践情景引入：2. 知识讲解：教师运用多媒体课件，详细讲解相似三角形的性质和判定方法。
同时，教师结合例题，让学生跟随步骤，体会相似三角形的判定方法。
3. 随堂练习：教师给出几组三角形，让学生判断它们是否相似。
学生通过自主练习，巩固所学知识。
4. 课堂讲解：教师针对学生在练习中遇到的问题，进行讲解和解答。
5. 板书设计：教师在黑板上板书相似三角形的定义、性质和判定方法，方便学生复习和记忆。
6. 作业设计：（1）判断下列三角形是否相似，并说明理由：题目：如图，在△ABC和△DEF中，AB=DE，BC=EF，AC=DF。
答案：△ABC～△DEF（对应角相等，对应边成比例）。
（2）已知：在△ABC中，AB=5cm，BC=8cm，AC=10cm。
求△ABC的周长。
答案：△ABC的周长=5+8+10=23cm。
六、课后反思及拓展延伸1. 课后反思：本节课通过实践情景引入，让学生直观地理解相似三角形的定义。
在知识讲解环节，运用多媒体课件，详细讲解相似三角形的性质和判定方法，并结合例题，让学生跟随步骤，体会相似三角形的判定方法。
秋九年级数学上册 第4章 相似三角形 专题训练 相似三角形的五种基本模型 (新版)浙教版-(新版)浙
相似三角形的五种基本模型► 模型一 “A ”字型1．如图9－ZT －1，在△ABC 中，点D ，E 分别在边AB ，AC 上，DE ∥BC ，DE ＝3，BC ＝9.(1)求AD AB的值；(2)若BD ＝10，求EDAD的值．图9－ZT －12．如图9－ZT －2，在Rt △ACB 中，∠C ＝90°，AC ＝4 cm ，BC ＝3 cm ，点P 由点B 出发沿BA 方向向点A 匀速运动，速度为1 cm/s ；点Q 由点A 出发沿AC 方向向点C 匀速运动，速度为2 cm/s.连结PQ ，设运动时间为t s(0＜t ＜2)，当t 为何值时，以A ，P ，Q 为顶点的三角形与△ABC 相似？图9－ZT －2►模型二“X”字型3．如图9－ZT－3，已知AB，CD，EF都与BD垂直，垂足分别是B，D，F，且AB＝1，CD＝3，那么EF的长是( )A.13B.23C.34D.459－ZT－39－ZT－44．如图9－ZT－4，在Rt△ABC中，∠A＝90°，AB＝AC，BC＝20，DE是△ABC的中位线，M是边BC上一点，BM＝3，N是线段MC上的一个动点，连结DN，ME，DN与ME相交于点O.若△OMN是直角三角形，则DO的长是________．5．2017·株洲如图9－ZT－5所示，正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上，EF与BC相交于点G，连结CF.求证：(1)△ADE≌△CDF；(2)△ABG∽△CFG.图9－ZT －5► 模型三 旋转型6．如图9－ZT －6，已知AB AD ＝BC DE ＝ACAE，求证：△ABD ∽△ACE .图9－ZT －67．如图9－ZT －7，在△ABC 和△AED 中，AB ·AD ＝AC ·AE ，∠CAE ＝∠BAD ，S △ADE ＝4S △ABC.求证：DE ＝2CB .图9－ZT－7►模型四垂直型图9－ZT－88．如图9－ZT－8，在矩形ABCD中，AB＝3，BC＝4，点P从点A出发，按A→B→C的方向在AB和BC上移动，记PA＝x，点D到直线PA的距离为y，则y关于x的函数图象大致是( )图9－ZT－9►模型五一线三等角型图9－ZT－109．如图9－ZT －10，△AOB 是直角三角形，∠AOB ＝90°，OB ＝2OA ，点A 在反比例函数y ＝1x 的图象上．若点B 在反比例函数y ＝kx的图象上，则k 的值为( ) A ．－4 B ．4 C ．－2 D ．210．(1)尝试：如图9－ZT －11①，已知A ，E ，B 三点在同一条直线上，且∠A ＝∠B ＝∠DEC ＝90°.求证：△ADE ∽△BEC ；(2)一位同学在尝试了上题后还发现：如图9－ZT －11②③，只要A ，E ，B 三点在同一条直线上，且∠A ＝∠B ＝∠DEC ，则(1)中结论总成立．你同意吗？请选择其中之一说明理由．图9－ZT －1111．如图9－ZT －12，等边三角形ABC 的边长为6，D 是BC 边上的动点，∠EDF ＝60°. (1)求证：△BDE ∽△CFD ；(2)当BD ＝1，FC ＝3时，求BE 的长．图9－ZT －12详解详析1．解：(1)∵DE ∥BC ，∴△AED ∽△ACB ，∴AD AB ＝DE BC ＝13.(2)∵AD AB ＝13，BD ＝10，∴AD AD ＋10＝13，∴AD ＝5，∴ED AD ＝35.2．解：在Rt △ABC 中，AB ＝BC 2＋AC 2＝5(cm)，由题意知AP ＝(5－t )cm ，AQ ＝2t cm.当PQ ∥BC 时，△AQP ∽△ACB ，∴AQ AC ＝AP AB ，∴2t 4＝5－t 5，解得t ＝107，107＜2，符合题意； 当PQ ⊥AB 时，△APQ ∽△ACB ，∴AQ AB ＝AP AC ，∴2t 5＝5－t 4，解得t ＝2513，2513＜2，符合题意． 综上所述，当t ＝107 或2513 时，以A ，P ，Q 为顶点的三角形与△ABC 相似．3．C [解析]∵AB ，CD ，EF 都与BD 垂直，∴AB ∥EF ∥CD ，∴△ABE ∽△DCE ，∴BE CE ＝AB CD＝13，同理△BEF ∽△BCD ，∴EF CD ＝BE BC ＝BE BE ＋CE ＝14.∴EF ＝14CD ＝34.故选C. 4.256或5013[解析] 如图，作EF ⊥BC 于点F ，DN ′⊥BC 于点N ′且交EM 于点O ′，此时∠MN ′O ′＝90°.∵DE 是△ABC 的中位线， ∴DE ∥BC ，DE ＝12BC ＝10.∵DN ′∥EF ，∴四边形DEFN ′是平行四边形．∵∠EFN ′＝90°，∴四边形DEFN ′是矩形，∴EF ＝DN ′，DE ＝FN ′＝10.∵AB ＝AC ，∠A ＝90°，∴∠B ＝∠C ＝45°， ∴BN ′＝DN ′＝EF ＝FC ＝5，MN ′＝5－3＝2，而DE MN ′＝DO ′O ′N ′，∴102＝DO ′5－DO ′，∴DO ′＝256； 当∠MON ＝90°时，则△DOE ∽△EFM ，∴DO EF ＝DE EM.∵EM ＝EF 2＋MF 2＝13，∴DO ＝5013.故答案为256或5013.5．证明：(1)由正方形ABCD 和等腰直角三角形DEF ，得∠ADC ＝∠EDF ＝90°，AD ＝CD ，DE ＝DF ，∴∠ADE ＋∠ADF ＝∠ADF ＋∠CDF ， ∴∠ADE ＝∠CDF .在△ADE 和△CDF 中，⎩⎪⎨⎪⎧DE ＝DF ，∠ADE ＝∠CDF ，AD ＝CD ，∴△ADE ≌△CDF .(2)如图，延长BA 到点M ，交DE 于点M ， ∵△ADE ≌△CDF ， ∴∠EAD ＝∠FCD ，即∠EAM ＋∠MAD ＝∠BCD ＋∠BCF . ∵∠MAD ＝∠BCD ＝90°， ∴∠EAM ＝∠BCF . ∵∠EAM ＝∠BAG ， ∴∠BAG ＝∠BCF . 又∵∠AGB ＝∠CGF ， ∴△ABG ∽△CFG .6．证明：∵AB AD ＝BC DE ＝AC AE，∴△ABC ∽△ADE ， ∴∠BAC ＝∠DAE ，∴∠BAC －∠DAF ＝∠DAE －∠DAF ，即∠BAD ＝∠CAE .∵AB AD ＝AC AE ，∴AB AC ＝ADAE，∴△ABD ∽△ACE .7．证明：∵AB ·AD ＝AC ·AE ，∴AB AE ＝AC AD.又∵∠CAE ＝∠BAD ，∴∠CAE ＋∠DAC ＝∠BAD ＋∠DAC ， 即∠DAE ＝∠CAB ， ∴△ADE ∽△ACB . 又∵S △ADE ＝4S △ABC ，∴S △ADES △ABC＝4， ∴⎝ ⎛⎭⎪⎫DE CB 2＝S △ADE S △ABC＝4，∴DE CB ＝2， ∴DE ＝2CB .8．D [解析] 整个运动过程分成两段：①当点P 在AB 上运动时，即0≤x ≤3，随着x 的增加y 值不变，y ＝4；②如图，当点P 在BC 上运动时，3＜x ≤5， ∵∠BAP ＋∠DAP ＝90°， ∠BAP ＋∠APB ＝90°， ∴∠DAP ＝∠APB .又∵∠AED ＝∠ABP ＝90°，∴△ADE ∽△PAB ，∴AD AP ＝DE AB， 即4x ＝y 3， ∴y ＝12x.故选D.9．A [解析] 如图，过点A ，B 分别作AC ⊥x 轴，BD ⊥x 轴，垂足分别为C ，D .设点A 的坐标是(m ，n )，则AC ＝n ，OC ＝m . ∵∠AOB ＝90°， ∴∠AOC ＋∠BOD ＝90°. ∵∠DBO ＋∠BOD ＝90°， ∴∠DBO ＝∠AOC .又∵∠BDO ＝∠ACO ＝90°， ∴△BDO ∽△OCA ，∴BD OC ＝OD AC ＝OBOA.∵OB ＝2OA ，∴BD ＝2m ，OD ＝2n .∵点A 在反比例函数y ＝1x的图象上， ∴mn ＝1.∵点B 在反比例函数y ＝k x的图象上，点B 的坐标是(－2n ，2m )， ∴k ＝－2n ·2m ＝－4mn ＝－4.故选A.10．解：(1)证明：∵∠A ＝∠B ＝∠DEC ＝90°，∴∠DEA ＋∠CEB ＝90°. ∵∠DEA ＋∠D ＝90°，∴∠D ＝∠CEB ，∴△ADE ∽△BEC .(2)同意，以题图②为例说明：∵∠A ＝∠DEC ，∠A ＋∠D ＝∠DEC ＋∠CEB ，∴∠D ＝∠CEB .又∵∠A ＝∠B ，∴△ADE ∽△BEC .11．解：(1)证明：∵△ABC 是等边三角形，∴∠B ＝∠C ＝60°，∴∠EDB ＋∠BED ＝120°.∵∠EDF ＝60°，∴∠CDF＋∠EDB＝120°，∴∠BED＝∠CDF，∴△BDE∽△CFD.(2)∵△BDE∽△CFD，∴BDCF＝BECD，即13＝BE5，解得BE＝53.。
浙教版数学九年级上册4 相似三角形课件
2 相似三角形的性质
A
相似三角形的对应角相
等,对应边成比例.
相似三角形对应边的比,叫 B
做两个相似三角形的相似比
(或相似系数)
注意:两个三角B′
如图， A′B′ = 1
AB
2
形的前后C顺序.
1 则△A′B′C′与△ABC的相似比为 2
A′ C′
1.下列命题中，正确的是（ C ）
A.所有的等腰三角形都相似 B.所有的直角三角形都相似 C.所有的等边三角形都相似 D.所有的矩形都相似
2.若△ABC∽△ A′B′C′，且AB：A′B′=1:2.
则△ABC与△ A′B′C′相似比是
，
1
△ A′B′C′与△ABC的相似比是 2 ．
3．已知△ADE∽△ABC，点A、D、E分别与点
A、B、C对应，且相似比为 2 ，若DE= 4cm，
求BC的长.
5
DE 2， BC 5
BC 5 DE 5 4 10(cm).
►为你理想的人，否则，爱的只是你在他身上找到的你的影子。 ►有时候，我们愿意原谅一个人，并不是我们真的愿意原谅他，而是我们 不愿意失去他。不想失去他，惟有假装原谅他。不管你爱过多少人，不管 你爱得多么痛苦或快乐。最后，你不是学会了怎样恋爱，而是学会了，怎 样去爱自己。
►在有欢声笑语的校园里，满地都是雪，像一块大地毯。房檐上挂满了冰 凌，一根儿一根儿像水晶一样，真美啊！我们一个一个小脚印踩在大地毯 上，像画上了美丽的图画，踩一步，吱吱声就出来了，原来是雪在告我们： 和你们一起玩儿我感到真开心，是你们把我们这一片寂静变得热闹起来。 对了，还有树。树上挂满了树挂，有的树枝被压弯了腰，真是忽如一夜春 风来，千树万树梨花开。真好看呀！ ►冬天，一层薄薄的白雪，像巨大的轻软的羊毛毯子，覆盖摘在这广漠的 荒原上，闪着寒冷的银光。
4.3 相似三角形 课件(共25张PPT)2023-2024学年浙教版九年级上册数学
(1)求∠ACB，∠ACD的度数.
(2)写出△ABC与△ACD的对应边成比例的比例式，并说出
相似比.
A
D
C
B
如图，D是AB上的一点，△ABC∽△ACD，且
AD∶AC=2∶3，∠ADC=65°，∠B=37°.
A
(1)求∠ACB，∠ACD的度数.
D
解：∵△ABC∽△ACD，
A
D
B
E
C
证明：∵D，E分别是AB，AC的中点，
∴DE∥BC，DE= BC.
A
∴∠ADE=∠B，∠AED=∠C.
D
在△ADE和△ABC中，
∠ADE=∠B，∠AED=∠C，∠A=∠A
ቋ
=
=
=
⇒△ADE∽△ABC(相似三角形的定义).
B
E
C
例2 如图，D，E分别是△ABC的AB，AC边上的点，
B
例3 如果两个三角形都与第三个三角形相似，那么这两个三角
形相似吗？为什么？
解：相似. 理由如下：
设△ABC∽△A1B1C1，△A1B1C1∽△A2B2C2.
由△ABC∽△A1B1C1，得∠A=∠A1，∠B=∠B1，
∠C=∠C1，
=
=
.
由△A1B1C1∽△A2B2C2，得∠A1=∠A2，
边是对应边；
④相似三角形对应边所对的角是对应角，两条对应边所夹的
角是对应角.
两个全等三角形是不是相似三角形？如果是，那么它
们的相似比是多少？