传热学第五章_对流换热原理-6
合集下载
传热学-5 对流传热原理
电场与温度场：微分方程相同，内容不同。 强制对流换热与自然对流换热：微分方程的形式和内容都 有差异。 外掠平板和外掠圆管：控制方程相同，单值性条件不同。
5-4 相似原理简介
1）几何相似 对应的长度量成固定比例，对应的角度相等。
若（1）（2）相似
a' a ''
b' b ''
c' c ''
h' h ''
' ''
P' P ''
CF
5-4 相似原理简介
4）初始条件和边界条件相似 保证定解条件一致。
几何相似是运动相似和动力相似的前提； 动力相似是决定流动相似的主要因素（保证）； 运动相似是几何相似和动力相似的表现。
y
u
u
tw x
5-1 对流传热概述
特点： （1）导热与热对流同时存在的复杂热传递过程； （2）必须有流体和壁面的直接接触和宏观运动， 也必须有温差； （3）由于流体的黏性和受壁面摩擦阻力的影响，紧 贴壁面处会形成速度梯度很大的流动边界层； （4）紧贴壁面处同时形成温度梯度很大的热边界层。
5-1 对流传热概述
偏微分方程+定解条件
速度场和温度场
表面传热系数h
2 实验法
相似原理指导下通过实验获得表面传热系数的 计算式（是目前工程计算的主要依据）。
对流传热问题的研究方法
3 比拟法
通过研究热量传递与动量传递的共性或类似特性, 建立起表面传热系数 h 与阻力系数 cf 间的相互联系, 通过较易测定的阻力系数来获得相应的表面传热系数 值。
主流区：速度梯度为0， 0 可视为无粘性理想流
5-4 相似原理简介
1）几何相似 对应的长度量成固定比例，对应的角度相等。
若（1）（2）相似
a' a ''
b' b ''
c' c ''
h' h ''
' ''
P' P ''
CF
5-4 相似原理简介
4）初始条件和边界条件相似 保证定解条件一致。
几何相似是运动相似和动力相似的前提； 动力相似是决定流动相似的主要因素（保证）； 运动相似是几何相似和动力相似的表现。
y
u
u
tw x
5-1 对流传热概述
特点： （1）导热与热对流同时存在的复杂热传递过程； （2）必须有流体和壁面的直接接触和宏观运动， 也必须有温差； （3）由于流体的黏性和受壁面摩擦阻力的影响，紧 贴壁面处会形成速度梯度很大的流动边界层； （4）紧贴壁面处同时形成温度梯度很大的热边界层。
5-1 对流传热概述
偏微分方程+定解条件
速度场和温度场
表面传热系数h
2 实验法
相似原理指导下通过实验获得表面传热系数的 计算式（是目前工程计算的主要依据）。
对流传热问题的研究方法
3 比拟法
通过研究热量传递与动量传递的共性或类似特性, 建立起表面传热系数 h 与阻力系数 cf 间的相互联系, 通过较易测定的阻力系数来获得相应的表面传热系数 值。
主流区：速度梯度为0， 0 可视为无粘性理想流
传热学第五章对流换热
1.流动边界层（Velocity boundary layer ）
如果流体为没有粘性流体，流体流过平板时，流速在截 面上一直保持不变。 如果流体为粘性流体，情况会如何呢？我们用一测速仪 来测量壁面附近的速度分布。测量发现在法向方向上， 即y方向上，壁面上速度为零，随着y方向的增加，流速 急剧增加，到达一薄层后，流速接近或等于来流速度， 德国科学家普朗特L.Prandtl研究了这一现象，并且在 1904年第一次提出了边界层的、分类 三、对流换热的机理 四、影响因素 五、研究方法 六、h的物理意义
一.定义
流体流过与其温度不同的固体表面时所发生的热量交换称为 对流换热。 对流换热与热对流不同， 既有热对流，也有导热； 不是基本传热方式。 对流换热遵循牛顿冷却定律：
qw tw
x
y
t∞
u∞
图5-1 对流换热过程示意
圆管内强制对流换热 其它形式截面管道内的对流换热 外掠平板的对流换热 外掠单根圆管的对流换热 外掠圆管管束的对流换热 外掠其它截面形状柱体的对流换热 射流冲击换热
外部流动
对 流 换 热
有相变
自然对流(Free convection) 混合对流 沸腾换热 凝结换热
大空间自然对流 有限空间自然对流
大容器沸腾 管内沸腾 管外凝结 管内凝结
λ ∂t 换热微分方程（描写h的本质，hx = − ∆t ( ∂y ) y =0 dA） 连续性方程（描写流体流动状态，即质量守恒） 动量微分方程（描写流动状态，即动量守恒） 能量微分方程（描写流体中温度场分布）
对流换热微分方程组 先作假设： （1）仅考虑二维问题； （2）流体为不可压缩的牛顿流体，稳定流动； （3）常物性，无内热源； （4）忽略由粘性摩擦而产生的耗散热。 以二维坐标系中的微元体为分析对象，根据热力学第一定 律，对于这样一个开口系统，有：
传热学 第5章6
9
9 /16
4/9
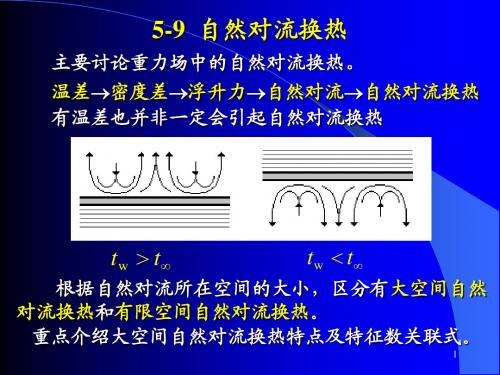
适用范围： 适用范围： Ra ≤ 10 对于常热流边界条件下竖壁的自然对流换热， 对于常热流边界条件下竖壁的自然对流换热 ， 壁 面温度未知， 并且沿壁面分布不均匀， 面温度未知 ， 并且沿壁面分布不均匀 ， 往往需要确定 局部壁面温度。引进一个修正的局部格拉晓夫数 局部壁面温度。 引进一个修正的局部格拉晓夫数
8
3. 大空间自然对流换热特征数关联式
特征数关联式： 特征数关联式： Nu = C (GrPr ) = cRa 自模化 定性温度： 定性温度：tm = ( tw + t∞ ) 2
n n
9
(1)竖平壁或竖圆柱 对于竖圆柱， 对于竖圆柱，如果满足下式
d 35 ≥ 1/ 4 H Gr 可以按垂直壁面处理。 可以按垂直壁面处理。 丘吉尔（ Churchill）和朱（ Chu） 丘吉尔（S. W. Churchill）和朱（H. H. S. Chu）提 出了对等壁温和常热流边界条件 对等壁温和常热流边界条件、 出了 对等壁温和常热流边界条件 、 对层流和湍流都适 用的竖壁面自然对流换热计算公式： 用的竖壁面自然对流换热计算公式：
空气在水平圆柱表面的自然对流换热关联式 空气在水平圆柱表面的自然对流换热关联式 定性温度： 定性温度：tm = ( t w + t∞ ) 2
Nu = 0.36 + 0.363Gr
1/ 6
+ 0.0914Gr
1/ 3
适用范围： 适用范围： Gr = 106 ~ 1.3 × 1013 （4） 球体表面的自然对流换热 丘吉尔推荐了球体外部自然对流换热关联式 丘吉尔推荐了球体外部自然对流换热关联式
ρ∞ ρ ≈ αρ ( t t∞ ) = αρθ
9 /16
4/9
适用范围： 适用范围： Ra ≤ 10 对于常热流边界条件下竖壁的自然对流换热， 对于常热流边界条件下竖壁的自然对流换热 ， 壁 面温度未知， 并且沿壁面分布不均匀， 面温度未知 ， 并且沿壁面分布不均匀 ， 往往需要确定 局部壁面温度。引进一个修正的局部格拉晓夫数 局部壁面温度。 引进一个修正的局部格拉晓夫数
8
3. 大空间自然对流换热特征数关联式
特征数关联式： 特征数关联式： Nu = C (GrPr ) = cRa 自模化 定性温度： 定性温度：tm = ( tw + t∞ ) 2
n n
9
(1)竖平壁或竖圆柱 对于竖圆柱， 对于竖圆柱，如果满足下式
d 35 ≥ 1/ 4 H Gr 可以按垂直壁面处理。 可以按垂直壁面处理。 丘吉尔（ Churchill）和朱（ Chu） 丘吉尔（S. W. Churchill）和朱（H. H. S. Chu）提 出了对等壁温和常热流边界条件 对等壁温和常热流边界条件、 出了 对等壁温和常热流边界条件 、 对层流和湍流都适 用的竖壁面自然对流换热计算公式： 用的竖壁面自然对流换热计算公式：
空气在水平圆柱表面的自然对流换热关联式 空气在水平圆柱表面的自然对流换热关联式 定性温度： 定性温度：tm = ( t w + t∞ ) 2
Nu = 0.36 + 0.363Gr
1/ 6
+ 0.0914Gr
1/ 3
适用范围： 适用范围： Gr = 106 ~ 1.3 × 1013 （4） 球体表面的自然对流换热 丘吉尔推荐了球体外部自然对流换热关联式 丘吉尔推荐了球体外部自然对流换热关联式
ρ∞ ρ ≈ αρ ( t t∞ ) = αρθ
传热学第五章对流换热
第五章
§5-1 §5-2 §5-3 §5-4 §5-5 §5-6 §5-7 §5-8
对流换热
Convective heat transfer
对流换热概说 对流换热的数学描写 对流换热边界层微分方程组 对流换热边界层积分方程组 相似理论与量纲分析 管内受迫流动 横向外掠圆管的对流换热 自然对流换热及实验关联式
λ ∂t 换热微分方程（描写h的本质，hx = − ∆t ( ∂y ) y =0 dA） 连续性方程（描写流体流动状态，即质量守恒） 动量微分方程（描写流动状态，即动量守恒） 能量微分方程（描写流体中温度场分布）
对流换热微分方程组 先作假设： （1）仅考虑二维问题； （2）流体为不可压缩的牛顿流体，稳定流动； （3）常物性，无内热源； （4）忽略由粘性摩擦而产生的耗散热。 以二维坐标系中的微元体为分析对象，根据热力学第一定 律，对于这样一个开口系统，有：
同理：（） dτ qm hout − qm hin ≈ ρcp (
y
H y + dy − H y =
∂t ∂v ⋅ v + ⋅ t )dxdydτ ∂y ∂y
（qm h)out − (qm h)in ∴ ∂t ∂t ∂u ∂v = ρ c p (u + v )dxdy + ρ c p t ( + )dxdy ∂x ∂y ∂x ∂y ∂t ∂t = ρ c p (u + v )dxdy (d ) ∂x ∂y
1.流动边界层（Velocity boundary layer ）
如果流体为没有粘性流体，流体流过平板时，流速在截 面上一直保持不变。 如果流体为粘性流体，情况会如何呢？我们用一测速仪 来测量壁面附近的速度分布。测量发现在法向方向上， 即y方向上，壁面上速度为零，随着y方向的增加，流速 急剧增加，到达一薄层后，流速接近或等于来流速度， 德国科学家普朗特L.Prandtl研究了这一现象，并且在 1904年第一次提出了边界层的概念。
§5-1 §5-2 §5-3 §5-4 §5-5 §5-6 §5-7 §5-8
对流换热
Convective heat transfer
对流换热概说 对流换热的数学描写 对流换热边界层微分方程组 对流换热边界层积分方程组 相似理论与量纲分析 管内受迫流动 横向外掠圆管的对流换热 自然对流换热及实验关联式
λ ∂t 换热微分方程（描写h的本质，hx = − ∆t ( ∂y ) y =0 dA） 连续性方程（描写流体流动状态，即质量守恒） 动量微分方程（描写流动状态，即动量守恒） 能量微分方程（描写流体中温度场分布）
对流换热微分方程组 先作假设： （1）仅考虑二维问题； （2）流体为不可压缩的牛顿流体，稳定流动； （3）常物性，无内热源； （4）忽略由粘性摩擦而产生的耗散热。 以二维坐标系中的微元体为分析对象，根据热力学第一定 律，对于这样一个开口系统，有：
同理：（） dτ qm hout − qm hin ≈ ρcp (
y
H y + dy − H y =
∂t ∂v ⋅ v + ⋅ t )dxdydτ ∂y ∂y
（qm h)out − (qm h)in ∴ ∂t ∂t ∂u ∂v = ρ c p (u + v )dxdy + ρ c p t ( + )dxdy ∂x ∂y ∂x ∂y ∂t ∂t = ρ c p (u + v )dxdy (d ) ∂x ∂y
1.流动边界层（Velocity boundary layer ）
如果流体为没有粘性流体，流体流过平板时，流速在截 面上一直保持不变。 如果流体为粘性流体，情况会如何呢？我们用一测速仪 来测量壁面附近的速度分布。测量发现在法向方向上， 即y方向上，壁面上速度为零，随着y方向的增加，流速 急剧增加，到达一薄层后，流速接近或等于来流速度， 德国科学家普朗特L.Prandtl研究了这一现象，并且在 1904年第一次提出了边界层的概念。
传热学对流传热原理
+v
t y
=
cp
2t x2
+
2t y2
4个方程，4个未知量 —— 可求得速度场(u,v)和温度场(t) 以及压力场(p), 既适用于层流，也适用于湍流（瞬时值）
➢ 边界层型对流传热问题的数学描写
动量方程中的惯性力项和能量方程中的对流 项均为非线性项，难以直接求解
边界层理论
简化
流动
普朗特 速度边界层
2t y2
→固体中的热传导过程是介质中传热过程的一个特例。
稳态对流换热微分方程组:
(常物性、无内热源、二维、不可压缩牛顿流体)
u v 0 x y
（u
u x
v
u y
)
Fx
p x
(
2u x 2
2u y 2
)
（u
v x
v
v y
)
Fy
p y
(
2v x 2
2v y 2
)
hx
t
t
y
w
,x
u
t x
5.4 相似原理与量纲分析
1、目的—— 简化实验 • 减少自变量的个数
1
1
hx x
0.332
u x
2
3
v a
Nu x
0.332
Re
1 x
2
Pr
1
3
• 缩小实验模型的尺寸 • 反映同一类现象的规律性
建立基于相似理论的实验关联式
（1）相似分析法；（2）量纲分析法
控制方程的无量纲化
二维、稳态、常物性、不可压缩、不计重力、无内热源、 无粘性耗散、牛顿流体的外掠平板强迫对流换热。
• y=0：u = 0, v = 0, t = tw
第五章-传热学
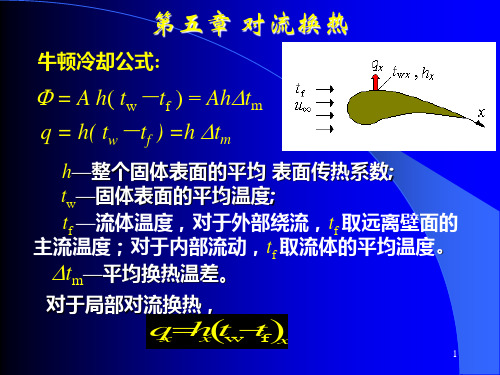
h
' h,x
' h,y
cpuxtvytdxdy
8
单位时间内微元体热力学能的增加为
dU
d
cp
t
dxdy
于是根据微元体的能量守恒
h
dU
d
可得
2t x2
2t y2
dxdy
cpuxtvytdxdy
cp
t
dxdy
cptux tvy ttu xv y
2t x2
2t y2
2
20
cp
uxt
v t y
＝
2t x2
2t y2
1
11 1
1
2
1 1
1
2
对流换热微分方程组简化为
h t tw tf y w
u v 0 x y
简化方程组只有4个方
程，但仍含有h、u、v、 p、t 等5个未知量，方
程组不封闭。如何求解？
uuxvuy1ddpxy2u2
u t x
v t y
26
第六节 相似理论基础
相似原理指导下的实验研究仍然是解决复杂对流换 热问题的可靠方法。
相似原理回答三个问题： （1）如何安排实验？ （2）如何整理实验数据？ （3）如何推广应用实验研究结果？
一、 相似原理的主要内容
1.物理现象相似的定义 2.物理现象相似的性质 3.相似特征数之间的关系 4.物理现象相似的条件
三、解的函数形式——特征数关联式
特征数是由一些物理量组成的无量纲数，例如毕 渥数Bi和付里叶数Fo。对流换热的解也可以表示成 特征数函数的形式，称为特征数关联式。
通过对流换热微分方程的无量纲化可以导出与对 流换热有关的特征数。
传热学第五章
h Atw t
以后除非特殊声明外,我们所说的对流换热系数皆指平均对流换
热系数,以 h 表示.
h(x)规律说明
Laminar region
x (x) h (x) 导热
Transition region
扰动
h(x)
Turbulent region
湍流部分的热阻很小,热阻主要集中在
粘性底层中.
2.按有无相变分
单相介质传热:对流换热时只有一种流体.
相变换热:传热过程中有相变发生.
物质有三态,固态,液态,气态或称三相.
相变换热有分为:
沸腾换热:(boiling heat transfer)物质由液态变为气态时发生 的换热.
凝结换热:(condensation heat transfer)物质由气态变为 液态时发生的换热. 熔化换热(melting heat transfer) 凝固换热(solidification heat transfer) 升华换热(sublimation heat transfer) 凝华换热（sublimation heat transfer ）
由上述分析可见,边界层控制着传热过程,故一些研究人员试图通过
破坏粘性底层来达到强化传热的目的,并取得了一些成果.
二、边界层微分方程组.
牛顿流体(Newtonian fluid),常物性,无内热源,耗散不计,稳态,
二维,略去重力.
完性分析已知：u，t，l 的量级为0(1) ， t 的量级为0(）
以此五个量为分析基础。
2.动量方程(momentum equation)
u v 0 x y
u
u
u x
v
u y
Fx
p x
传热学第五章 对流换热计算
R 2 e3 1 00 0 ， P 0 1 r0 .5 0 5， 0 Pf0 r0 .0 5 20 P wr
2019/11/19
23
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
例1 空气以2m/s的速度在内径为10 mm的管内流动， 入口处空气的温度为20℃，管壁温度为120℃，试确 定将空气加热至60℃所需管子的长度。
2019/11/19
20
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
③短管 当管子的长径比l/d<60时，属于短管内流动换 热，进口段的影响不能忽视。此时亦应在按 照长管计算出结果的基础上乘以相应的修正
系数Cl。 cl 1dl0.7
充分发展区：边界层汇合于管子中心线以后的 区域，即进入定型流动的区域。
2019/11/19
3
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
充分发展段为层流流动
为什么平均换热系数比局部换热系数高？
入口段的边界层厚度较薄，传热阻力小，表面传热系数 大（即，对流换热强）
为什么气体和液体的修正方式不一样？
2019/11/19
18
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
② 螺旋管或弯管 弯曲的管道中流动的流体，在弯曲处由于离 心力的作用会形成垂直于流动方向的二次流 动，从而加强流体的扰动，带来换热的增强。
2019/11/19
23
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
例1 空气以2m/s的速度在内径为10 mm的管内流动， 入口处空气的温度为20℃，管壁温度为120℃，试确 定将空气加热至60℃所需管子的长度。
2019/11/19
20
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
③短管 当管子的长径比l/d<60时，属于短管内流动换 热，进口段的影响不能忽视。此时亦应在按 照长管计算出结果的基础上乘以相应的修正
系数Cl。 cl 1dl0.7
充分发展区：边界层汇合于管子中心线以后的 区域，即进入定型流动的区域。
2019/11/19
3
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
充分发展段为层流流动
为什么平均换热系数比局部换热系数高？
入口段的边界层厚度较薄，传热阻力小，表面传热系数 大（即，对流换热强）
为什么气体和液体的修正方式不一样？
2019/11/19
18
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
② 螺旋管或弯管 弯曲的管道中流动的流体，在弯曲处由于离 心力的作用会形成垂直于流动方向的二次流 动，从而加强流体的扰动，带来换热的增强。
传热学-对流换热PPT课件
传热学-对流换热
对流换热：工程上流体流过一物体表面时的热量传递过程。 自然界中的种种对流现象 电子器件冷却 强制对流与自然对流
沸腾换热原理 空调蒸发器、冷凝器 动物的身体散热
➢ 热对流（Convection）
流体中（气体或液体）温度不同的各部分之间，由于 发生相对的宏观运动而把热量由一处传递到另一处的现象。
ρ↑、c ↑(单位体积流体能携带更多能量）→h↑ 4、动力粘度 µ [N.s/m2]、运动粘度 ν=µ/ ρ [m2/s]
µ ↑（有碍流体流动，不利于热对流）→h↓ 5、体膨胀系数 α [1/k]
α ↑（自然对流换热增强）→h↑
四、换热壁面的几何尺寸、形状及位置
影响到流体沿壁面的流动状态、速度分布和温度， 从而影响对流换热系数。
内部流动对流换热： 管内或槽内
外部流动对流换热： 外掠平板、圆管、 管束
五、 流体有无相变（流体相变）：
单相换热 Single phase heat transfer： 相变换热 Phase change：
凝结、沸腾、升华、凝固、融化等
流体相变时吸收或放出汽化潜热比比热容大得多， 且破坏了层流底层强化了传热。
5、层流底层（贴壁流体层）
流体在做湍流运动时，在管壁附近形成一层 流速很低的极薄的层流，称为层流底层。
层流底层的厚度随着流速的增加（即Re增加） 而减薄。
湍流核心
层流底层
二、边界层
（一）速度(流动)边界层
1、速度边界层的形成原因 粘性流体流过固体壁面时，
由于流体与壁面之间摩擦阻力 的影响，壁面附近的流体速度 会减小，即从来流速度减小到 壁面的零速度。 2、速度边界层图，见右图。
W/(m2 C)
——当流体与壁面温度相差 1°C时、单位壁面面积 上、单位时间内所传递的热量。
对流换热：工程上流体流过一物体表面时的热量传递过程。 自然界中的种种对流现象 电子器件冷却 强制对流与自然对流
沸腾换热原理 空调蒸发器、冷凝器 动物的身体散热
➢ 热对流（Convection）
流体中（气体或液体）温度不同的各部分之间，由于 发生相对的宏观运动而把热量由一处传递到另一处的现象。
ρ↑、c ↑(单位体积流体能携带更多能量）→h↑ 4、动力粘度 µ [N.s/m2]、运动粘度 ν=µ/ ρ [m2/s]
µ ↑（有碍流体流动，不利于热对流）→h↓ 5、体膨胀系数 α [1/k]
α ↑（自然对流换热增强）→h↑
四、换热壁面的几何尺寸、形状及位置
影响到流体沿壁面的流动状态、速度分布和温度， 从而影响对流换热系数。
内部流动对流换热： 管内或槽内
外部流动对流换热： 外掠平板、圆管、 管束
五、 流体有无相变（流体相变）：
单相换热 Single phase heat transfer： 相变换热 Phase change：
凝结、沸腾、升华、凝固、融化等
流体相变时吸收或放出汽化潜热比比热容大得多， 且破坏了层流底层强化了传热。
5、层流底层（贴壁流体层）
流体在做湍流运动时，在管壁附近形成一层 流速很低的极薄的层流，称为层流底层。
层流底层的厚度随着流速的增加（即Re增加） 而减薄。
湍流核心
层流底层
二、边界层
（一）速度(流动)边界层
1、速度边界层的形成原因 粘性流体流过固体壁面时，
由于流体与壁面之间摩擦阻力 的影响，壁面附近的流体速度 会减小，即从来流速度减小到 壁面的零速度。 2、速度边界层图，见右图。
W/(m2 C)
——当流体与壁面温度相差 1°C时、单位壁面面积 上、单位时间内所传递的热量。
传热学第五章对流传热的理论基础
30
实验数据如何整理（整理成什么样函数关系） 强制对流：Nu f (Re,Pr)； Nux f ( x' , Re,Pr)
自然对流换热：Nu f (Gr, Pr) 混合对流换热：Nu f (Re, Gr, Pr)
Nu — 待定特征数 （含有待求的 h）
Re，Pr，Gr — 已定特征数
特征关联式的具体函数形式、定性温度、特征长度等的确 定需要通过理论分析，同时又具有一定的经验性。
2
流体流过固体表面时，。。。
普朗特边界层理论：粘性流体流过固体表面时，粘滞性 起作用的区域仅仅局限在靠近壁面的薄层内。
3
2. 对流传热系数
u∞ ; t ∞
tw
由傅里叶定律：
q t y w
W m2
对流传热的定义式： q ht h tw t [W/m2 ]
在边界层不脱落的前提下：
q ht = t y w
x为当前点与板前缘的距离。 Pr=
a
1
1
hx x
0.332
u x
2
a
3
Nux 0.332Re1x 2 Pr1 3
上述理论解与实验值吻合。
注意：层流
18
2. 对于外掠平板层流分析解的几个讨论
（1）局部对流传热系数，平均对流传热系数
局部对流传热系数
Nux
hx x
11
0.332Rex 2 Pr 3
第五章 对流传热的理论基础
1
5.1 对流传热概述
1. 对流传热的定义、研究对象
流体流过固体表面时，流体与固体之间的热量传递。
工程上约定的计算习惯：
若tw t，Φ hA(tw t ) W 若tw t，Φ hA(t tw ) W
实验数据如何整理（整理成什么样函数关系） 强制对流：Nu f (Re,Pr)； Nux f ( x' , Re,Pr)
自然对流换热：Nu f (Gr, Pr) 混合对流换热：Nu f (Re, Gr, Pr)
Nu — 待定特征数 （含有待求的 h）
Re，Pr，Gr — 已定特征数
特征关联式的具体函数形式、定性温度、特征长度等的确 定需要通过理论分析，同时又具有一定的经验性。
2
流体流过固体表面时，。。。
普朗特边界层理论：粘性流体流过固体表面时，粘滞性 起作用的区域仅仅局限在靠近壁面的薄层内。
3
2. 对流传热系数
u∞ ; t ∞
tw
由傅里叶定律：
q t y w
W m2
对流传热的定义式： q ht h tw t [W/m2 ]
在边界层不脱落的前提下：
q ht = t y w
x为当前点与板前缘的距离。 Pr=
a
1
1
hx x
0.332
u x
2
a
3
Nux 0.332Re1x 2 Pr1 3
上述理论解与实验值吻合。
注意：层流
18
2. 对于外掠平板层流分析解的几个讨论
（1）局部对流传热系数，平均对流传热系数
局部对流传热系数
Nux
hx x
11
0.332Rex 2 Pr 3
第五章 对流传热的理论基础
1
5.1 对流传热概述
1. 对流传热的定义、研究对象
流体流过固体表面时，流体与固体之间的热量传递。
工程上约定的计算习惯：
若tw t，Φ hA(tw t ) W 若tw t，Φ hA(t tw ) W
第五章 对 流 换 热
第五章 对 流 换 热本章内容要求：1 、重点内容： 对流换热及其影响因素；牛顿冷却公式；用分析方法求解对流换热问题的实质边界层概念及其应用相似原理无相变换热的表面传热系数及换热量的计算2 、掌握内容：对流换热及其影响因素；用分析方法求解对流换热问题的实质3 、讲述基本的内容：对流换热概述； 对流换热的数学描写； 对流换热的边界层微分方程组； 边界层积分方程组的求解及比拟理论； 相似原理及量纲分析； 相似原理的应用； 内部流动强制对流换热实验关联式； 外部流动强制对流换热实验关联式； 自然对流换热实验关联式在绪论中已经指出， 对流换热是发生在流体和与之接触的固体壁面之间的热量传递过程， 是发生在流体中的热量传递过程的特例。
由于流体系统中流体的运动，热量将主要以热传导和热对流的方式进行，这必然使热量传递过程比单纯的导热过程要复杂得多。
本章将在对换热过程进行一般性讨论的基础上，将质量守恒、动量守恒和能量守恒的基本定律应用于流体系统，导出支配流体速度场和温度场的场方程－对流换热微分方程组。
由于该方程组的复杂性，除少数简单的对流换热问题可以通过分析求解微分方程而得出相应的速度分布和温度分布之外，大多数对流换热问题的分析求解是十分困难的。
因此，在对流换热的研究中常常采用实验研究的方法来解决复杂的对流换热问题。
在这一章，我们将 通过方程的无量纲化和实验研究方法的介绍而得到常用的准则及准则关系式。
讨论的重点放在工程上常用的管内流动、平行流过平板以及绕流圆管的受迫对流换热，大空间和受限空间的自然对流换热，以及蒸汽凝结与液体沸腾换热。
§5-1 对流换热概述本节要求：1。
对流换热的概念：流体−−→−温差固体壁面； 2．对流换热中，导热核对流通式汽作用；3．对流换热的影响因素：)(f w t t hA -=Φ，h ——过程量；4．对流换热系数如何确定：0=∂∂∆-=y y tt h λ1 对流换热过程对流换热是发生在流体和与之接触的固体壁面之间的热量传递过程 ，（ 直接接触是与辐射换热的区别），是宏观的热对流与微观的热传导的综合传热过程。
传热学-第五章-对流原理.
三个准则数分别称为努谢尔特准则，雷诺 准则和普朗特准则，相应地用符号Nu、Re 和Pr表示，代入式(d)中，得
N uARcePer
写成一般形式的无量纲关系式，则为
u＝f〔Re,Pr)
上两式称之为准则方程式，式中的系 数和指数，或方程的具体形式由试验确
定。
至于自然对流换热，无论是理论分析还 是试验分析，都觉察正是由于壁面和流 体之间存在的温度差，使流体密度不均 匀所产生的浮升力，导致了自然对流运 动的发生和进展。自然对流换热系数α 与其影响因素的一般关系式为
如下图，流体接触管道后，便从两侧流过， 并在管壁上形成边界层。正对着来流方向 的圆管最前点，即φ＝０处，流速为零， 边界层厚度为零。此后，在圆管壁上形成 层流边界层，并随着φ角的增大而增厚。 当厚度增加到肯定程度时，便过渡到紊流 边界层。在圆管壁φ＝8０°四周处，流体 脱离壁面并在圆管的后半部形成旋涡。
明显，流体温度的分布与流体的流淌有关， 深受速度边界层的影响。流体呈层流状态时， 流体微团沿相互平行的流线进展，没有横向 流淌，不发生物质交换，壁面法线方向上的 热量传递，根本上靠分子的导热进展，层内 温度变化较大，温度分布呈抛物线型。对于 紊流边界层，其中层流底层的热量传递也是 靠导热，而在紊流核心层的热交换，除靠分 子的导热外，主要靠流体涡流扰动的对流混 合，从而使得层流底层的温度梯度最大，而 在紊流核心层温度变化平缓比较均匀全都。
二、
从上节可以知道，在大多数状况下， 影响无相变对流换热过程的换热系数 α的物理因素可归结为流体流态、物 性、换热壁面状况和几何条件、流淌 缘由四个方面。争论说明，对于管内 受迫流淌，假设假定物性是常数，不 随温度而变，争论的是平均对流换热 系数。影响换热系数α的因素有流速V， 管径D，流体密度ρ，动力粘度μ，比 热cp和导热系数λ。
《传热学》第5-6章-对流换热
dxdy
λ
∂ 2t ∂x2
+
∂ 2t ∂y 2
dxdy
−
ρc
p
∂
(ut
∂x
)
+
∂
(vt
∂y
)dxdy
=
ρc p
∂t ∂τ
dxdy
ρc
p
∂t ∂τ
+ u ∂t ∂x
+ v ∂t ∂y
+
t
∂u ∂x
+
∂v ∂y
=
λ
∂ 2t ∂x 2
+
似，已很少再用
5-2对流换热的数学描述
1) 对流换热微分方程
取边长为∆x, ∆y, ∆z=1的微元体为研究对象
当粘性流体在壁面上流动时，由于 粘性的作用，流体的流速在靠近壁 面处随离壁面的距离的缩短而逐渐 降低；在贴壁处被滞止，处于无滑 移状态（即：y=0, u=0）
在这极薄的贴壁流体层中， 热量只能以导热方式传递
∂ρ ∂T
p
λ ↑⇒ h ↑ (流体内部和流体与壁面间导热热阻小)
ρ、c ↑⇒ h ↑ (单位体积流体能携带更多能量)
µ ↑⇒ h ↓ (有碍流体流动、不利于热对流)
α ↑⇒ 自然对流换热增强
5) 换热表面的几何因素
对流换热分类
1
对流换热的主要研究方法
v (1) 分析法——解析解 v (2) 数值法——近年发展的方法 v (3) 实验法——主要方法（拟合公式） v (4) 比拟法——热量传递与动量传递 的相
在层流边界层与层流底层内，垂直于壁面方向上的热量传递 主要靠导热。紊流边界层的主要热阻在层流底层。
第五章对流传热理论基础
动量方程中的惯性力项和能量方程中的对流项均为非线性项，难以直接求解
简化
流动
普朗特 速度边界层
类比
对流换热
波尔豪森 热边界层
38
传热学
一、流动边界层
1、流动边界层及其厚度 定义：当流体流过固体壁面时,由于流 体粘性的作用,使得在固体壁面附近存 在速度发生剧烈变化的薄层称为流动 边界层或速度边界层。
实际流动 ≈ 边界层区粘性流动+主流区无粘性理想流动
大空间自然对流 有限空间自然对流
沸腾换热 有相变
凝结换热
大容器沸腾 管内沸腾
管外凝结 管内凝结
14
传热学
六、研究对流传热的方法（确定h的方法）
四种：1）分析法；2）实验法；3）比拟法；4）数值法
适当介绍
重点介绍 一定介绍
不作介绍
1）分析法
解析：二维、楔形流、平板 边界层积分方程（近似解析）
2）实验法
u∞
y δ
0x xc
粘性底层
掠过平板时边界层的形成与发展
湍流核心 缓冲层
41
传热学
层流： 流体做有秩序的分层流动，各层互不干扰，只有分子扩散，
无大微团掺混
湍流： 流体微团掺混，紊乱的不规则脉动
粘性底层 :速度梯度较大、分子扩散—导热
湍流边界层
缓冲层 :导热+对流 湍流核心 :质点脉动强化动量传递，速度变化
换热表面的形状、大小、换热表面与流体运动方向的 相对位置及换热表面的状态（光滑或粗糙）
内部流动对流传热：管内或槽内 外部流动对流传热：外掠平板、圆管、管束
10
传热学
11
传热学
(5) 流体的热物理性质：
热导率 [W (m C)] 比热容 c [J (kg C)]
简化
流动
普朗特 速度边界层
类比
对流换热
波尔豪森 热边界层
38
传热学
一、流动边界层
1、流动边界层及其厚度 定义：当流体流过固体壁面时,由于流 体粘性的作用,使得在固体壁面附近存 在速度发生剧烈变化的薄层称为流动 边界层或速度边界层。
实际流动 ≈ 边界层区粘性流动+主流区无粘性理想流动
大空间自然对流 有限空间自然对流
沸腾换热 有相变
凝结换热
大容器沸腾 管内沸腾
管外凝结 管内凝结
14
传热学
六、研究对流传热的方法（确定h的方法）
四种：1）分析法；2）实验法；3）比拟法；4）数值法
适当介绍
重点介绍 一定介绍
不作介绍
1）分析法
解析：二维、楔形流、平板 边界层积分方程（近似解析）
2）实验法
u∞
y δ
0x xc
粘性底层
掠过平板时边界层的形成与发展
湍流核心 缓冲层
41
传热学
层流： 流体做有秩序的分层流动，各层互不干扰，只有分子扩散，
无大微团掺混
湍流： 流体微团掺混，紊乱的不规则脉动
粘性底层 :速度梯度较大、分子扩散—导热
湍流边界层
缓冲层 :导热+对流 湍流核心 :质点脉动强化动量传递，速度变化
换热表面的形状、大小、换热表面与流体运动方向的 相对位置及换热表面的状态（光滑或粗糙）
内部流动对流传热：管内或槽内 外部流动对流传热：外掠平板、圆管、管束
10
传热学
11
传热学
(5) 流体的热物理性质：
热导率 [W (m C)] 比热容 c [J (kg C)]
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2－2）管内流体平均温度
t f
c p tudf
f
c pudf
2 R 2um
R
turdr
0
f
其中，tf为根据焓值计算的截断面平均温度。
由热平衡方程
dQ hx (tw t f )x * 2R * dx cpumR2dt f
和
dQ q * 2R * dx
可得
dt f 2q 2hx (tw t f ) x
t
( tw t r tw t f
)rR
( r )rR tw t f
const
而同时又有
q
(
t r
)
r
R
h(t w
tf
)
于是，得
(
t r
)
r
R
h
const
tw t f
上式又表明，常物性流体在热充分发展段的一个特点是 换热系数保持不变。
另外，如果边界层在管 中心处汇合时流体流动 仍然保持层流，那么进 入充分发展区后也就继 续保持层流流动状态， 从而构成流体管内层流 流动过程。
若 Pr<1, 则意味着流动进口段长于热进口段； 1－3）管内流动充分发展段的流态判断
Re 2300 2300 Re 10 4 Re 10 4
层流 过渡流 旺盛湍流
2）管内流体平均速度与平均温度
2－1）管内流体运动平均速度
um
f udf 0f
2
R 2
R rudr V
0
f
其中，V－体积流量；f－管的截断面积；u－局部流速
dx c pum R
c pum R
积分上式可得全管长流体的平均温度。
由于热边界存在有均匀壁温和均匀热流两种典型情
况。对于均匀热流边界情况(q=const)，在常物性
条件下，有
dt f 2q const
dx cpumR
这意味着，流体断面温度呈线性变化，即有
tf
1 2 (t f
't f
'')
其中， tf’为进口断面的平均温度； tf’’为出口断面的平均温度。
恒定温度的情况
管内流动温度对速度分布的影响示意图
大温差情况下计算换热时准则式右边要乘以物性修
正项 。 对于液体，乘以
f w n
如液体被加热，n=0.11；如液体被冷却，n=0.25；
对于气体，则乘以:
T f Tw n
如气体被加热，n=0.55；如气体被冷却，n=0。另外，
温度取绝对温标数值。
tm t f t w
tf
(t
' f
t
"
)
/
2
2 管内强制对流换热的准则关系式 ①管内紊流换热准则关系式
当管内流动的雷诺数Re≥104时，管内流体处于旺盛 的紊流状态。当流体与壁面的温差较小时，此时的 换热计算可采用迪图斯-贝尔特（Dittus-Boelter） 准则关系式
Nu 0.023Re 0.8 Pr n
入口段热边界层较薄，局部表面传热系数比充分 发展段高，且沿主流方向逐渐降低。
流动进口段长度：
层流：L 0.06 Re; 紊流 : L 50
d
d
热进口段长度：
层流：LTtw 0.055 Re Pr; d
紊流 : L 50 d
Lqw t
0.07 Re Pr
d
由于
Pr
a
若 Pr>1, 则意味着流动进口段短于热进口段；
'')
t't' ' ln t'
t' '
t
tw
t=C
tf
t tw = C
tf
入口段
充分发展段 x
恒热流时
恒壁温时
x
其中，tf’, tf”分别为出口、进口截面上的平均温
度。
当进口与出口截面上的温差比(tw - tf'')/(tw - tf')
在0.5 2之间时，可按如下算术平均温差计算，结 果的差别在4%以内。
50℃；对于水≤2030℃ ，对于油类流体≤10℃。
当流体与管壁之间的温差较大时，因管截面上流体 温度变化比较大，流体的物性受温度的影响会发生 改变，尤其是流体黏性随温度的变化导致管截面上 流体速度的分布也发生改变，进而影响流体与管壁 之间的热量传递和交换，如下图。
液体被加热或气体被冷却
液体被冷却或气体被加热
b）进口段:自管口至流体流速和流态分布定型的距离。
一般地，自进口到充分发展段之间地区域称为入口段。
1－2）性质与特点
a）充分发展段流动的特点 u 0
x
( tw t ) 0 x tw t f
v 0 其中，t=t(x,r)
上式表明，充分发展段流动的一个特点是无量纲温度
随管长保持不变。
另外，由于
特流征体尺的寸平为均d温(内度径)，特t f 征 t流f 速tf为 2um；，流定体性被温加度热为
(即tw>tf)n=0.4,流体被冷却(即tw<tf) n=0.3。
使用范围：Ref = 104 1.2×105, Prf = 0.7 120,
l/d 60 ； 所 谓 温 差 （ tw-tf ） 较小 ， 指 对 于 气 体 ≤
§5-7 内部流动强制对流换热实验关联式
1、管(槽)内强制对流流动和换热换热的特征
流体在管内流动属于内部流动过程，其主要特征是， 流动存在着两个明显的区段，即流动进口区段和流 动充分发展区段
1）进口段和充分发展段
1－1）定义
a）充分发展段:流体流速分布及流态定型，流动边界
层及热边界层汇合于管子中心线，称流动或换热已充 分发展。
在热充分发展段，由于h=const ，q= h* (tf-tw),
得
dt f dtw
dx dx
这说明，管壁温度tw也是沿管长呈线性变化，且 变化速率与流体断面温度变化速率相同。
对于均匀壁温情况（tw=const），在常物性条件下，
dt由f 2q 2hx (tw t f ) x
dx c pum R
c pum R
得
d (tw t f ) x 2hx dx
(t w t f ) x
c pum R
积分后可得
t' exp( 2h * x )
t ' '
c pum R
这表明，流体温度将沿管长按对数曲线规律变化。于
是，全管长流体平均温度为 t f t w t m
其中，
t m
(t w
t f ' ) (t w t f ln( t w t f ' ) tw t f ''
如果边界层在管中心处 汇合时流体已经从层流 流动完全转变为紊流流 动，那么进入充分发展 区后就会维持紊流流动 状态，从而构成流体管 内紊流流动过程。
b）入口段流动的特点
当流体温度和管璧温度不同时，在管子的进口区域 同时也有热边界层在发展，随着流体向管内深入， 热边界层最后也会在管中心汇合，从而进入热充分 发展的流动换热区域，在热边界层汇合之前也就必 然存在热进口区段。