1.4角的平分线的性质导学案(1)
湘教版数学八年级下册1.4《角平分线的性质》教学设计

湘教版数学八年级下册1.4《角平分线的性质》教学设计一. 教材分析湘教版数学八年级下册1.4《角平分线的性质》是初中数学的重要内容,主要介绍了角平分线的性质。
本节课的内容是学生学习几何知识的基础,也是学生进一步学习圆的知识的前提。
通过本节课的学习,学生可以掌握角平分线的性质,并能够运用角平分线的性质解决一些实际问题。
二. 学情分析学生在学习本节课之前,已经学习了角的概念、线的概念等基础知识,对几何图形有一定的认识。
但是,学生对角平分线的性质还没有接触过,对于如何运用角平分线的性质解决实际问题还需要引导。
三. 教学目标1.知识与技能:学生能够理解角平分线的性质,并能够运用角平分线的性质解决一些实际问题。
2.过程与方法:通过学生自主探究、合作交流的方式,培养学生的几何思维能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识。
四. 教学重难点1.角平分线的性质的推导过程。
2.如何运用角平分线的性质解决实际问题。
五. 教学方法采用问题驱动法、学生自主探究法、合作交流法等教学方法。
通过引导学生提出问题、自主探究、合作交流的方式,激发学生的学习兴趣,培养学生的几何思维能力。
六. 教学准备教师准备PPT、黑板、粉笔等教学工具。
学生准备课本、笔记本等学习工具。
七. 教学过程1.导入(5分钟)教师通过一个实际问题引导学生思考:“如何找到一个角的平分线?”学生可以自由发言,教师引导学生提出问题,引出本节课的主题——角平分线的性质。
2.呈现(10分钟)教师通过PPT展示角平分线的性质,让学生初步了解角平分线的性质。
然后,教师引导学生自主探究,让学生通过观察、思考、推理等过程,推导出角平分线的性质。
3.操练(10分钟)教师通过PPT展示一些练习题,让学生运用角平分线的性质解决问题。
学生在纸上完成练习题,教师选取部分学生的作业进行讲解和评价。
4.巩固(10分钟)教师通过PPT展示一些巩固题,让学生再次运用角平分线的性质解决问题。
1.4 角平分线(1)性质定理与逆定理

老师期望: 老师期望:
驶向胜利 的彼岸
独立作业
2
习题1.8
如图,求作一点P, PC=PD,并且点 P,使 并且点P 2. 如图,求作一点P,使PC=PD,并且点P到∠AOB 的两边的距离相等. 的两边的距离相等.
B
D● C● O A
驶向胜利 的彼岸
老师期望: 老师期望: 养成用数学解释生活的习惯. 养成用数学解释生活的习惯.
A D 1 2 E B P C
定理 角平分线上的点到这个角的两边 距离相等. 距离相等. 的平分线,P ,P是 ∵OC是∠AOB的平分线,P是OC上任意一 ,PD⊥OA,PE⊥OB,垂足分别是D,E(已 垂足分别是D,E( 点,PD⊥OA,PE⊥OB,垂足分别是D,E(已 知) ∴PD=PE(角平分线上的点到这个角的两边 ∴PD=PE(角平分线上的点到这个角的两边 距离相等). 距离相等). 在一个角的内部, 逆定理 在一个角的内部,且到角的两O 边距离相等的点,在这个角的平分线上. 边距离相等的点,在这个角的平分线上. PD⊥OA,PE⊥ B,垂足分别 A,PE⊥OB, ∵PA=PB, PD⊥ A,PE⊥ B,垂足分别 D,E(已知 已知), 是D,E(已知), AOB的平分线上.(在一个角 的平分线上.( ∴点P在∠AOB的平分线上.(在一个角 的内部,且到角的两边距离相等的点, 的内部,且到角的两边距离相等的点, 在这个角的平分线上). 在这个角的平分线上). 用尺规作角的平分线. 用尺规作角的平分线. 邻补角的角平分线之间的关系. 邻补角的角平分线之间的关系.
D
B
3.作射线O 3.作射线OC. 作射线 则射线O 就是∠ 的平分线. 则射线OC就是∠AOB的平分线. 请你说明O 为什么是∠ 的平分线,并与同伴进行交流. 请你说明OC为什么是∠AOB的平分线,并与同伴进行交流.
角的平分线的性质(1)

11.3.1角的平分线的性质执笔人:王金梅审核人:董介文孙秀云【学习内容】教材P19-20【学习目标】1.掌握作已知角的平分线的方法,并掌握角平分线的性质。
2.在探究作已知角的平分线的方法和角平分线的性质的过程中,发展几何直觉。
3.提高综合运用三角形全等的有关知识解决问题的能力。
4.初步了解角的平分线的性质在生活、生产中的应用。
5.在探讨作角的平分线的方法及角的平分线的性质的过程中,培养学生探究问题的兴趣,增强解决问题的信心,获得解决问题的成功体验,逐步培养学生的理性精神。
【学习重点】利用尺规作已知角的平分线,角的平分线的性质的证明及运用。
【学习难点】角的平分线性质的探究;运用角平分线的性质解决相关的实际问题。
【教学准备】平分角的仪器(自制)、三角尺、圆规、多媒体课件。
【学习过程】[知识回顾]1、全等三角形的性质:若△ABC≌△DEF,则有。
2、三角形全等的判定方法有:。
3、如图,AB=AD,BC=DC,求证AC是∠DAB的平分线[自主探究]【活动1】问题:在纸上任意画一个角,用剪刀剪下,用折纸的方法,如何确定角的平分线?学生实验:通过折纸的方法作角的平分线。
教师展示课件,并展示学生作品。
[设计意图]回忆角的平分线的定义,掌握角的平分线的简易作法。
让学生体验成功。
【活动2】 ( 体会平分角的仪器道理)议一议:如何将一个角平分是一个有趣的实验课题,有一个简易平分角的仪器,如图,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?(教师演示,并介绍“平分角的仪器”的特点。
学生将实物图抽象出数学图形,思考后组内交流.)本次活动中,教师重点关注:(1)学生是否能从简易角平分仪器中抽象出两个三角形;(2)学生能否运用三角形全等的条件证明两个三角形全等,从而说明线段AE 是∠BAD 的平分线。
(师生共同分析讨论,探究问题的解答.)分析:要说明AC 是∠DAC 的平分线,其实就是证明∠CAD=∠CAB 。
角平分线 优秀教案

学习环节 学习目标 学习评价
学习活动
设计意图
目标 1:
通过 自主学习 能够用数
1. 学 生 的 合
探究活动二:
作探究是否
真 正 合 作 是 1. 已经证明角平分线的性质定让学
否充分交流.
生自己说出这个定理的逆命题大
致有两种情况,然后引导学生分析
1.本探究活动 是对上一探究 活动的进一巩 固和练习,老
分钟完成!显示 活动要求具体明 确,组织有序.
5. 关 注 学 生 在定理证明 后用来解决 实际问题时 能否记住不
思路.
4.出示活动要求:同桌合作3分钟完成! 完成后学生以组为单位,代表发言, 最后出示整理的证明过程以供同学们
4.写出角平分 线性质定理的 几何语言让学 生感知数学语 言简洁明了的
再写出定理 证明环节而 直接利用这 个现成的结 论进行推理 和计算.
决实际问题。
五、教法、学法:
本节课充分运用多媒体和几何画板直观生动的优势,引导学生操作、观察、思考、归纳。 适时启发诱导,让学生展开讨论,充分发挥学生的主体参与意识,激发学习兴趣,调动学习 的积极性。体现新课程标准的要求,让学生成为学习的主体,而教师是学习的组织者、引导 者与合作者。学生始终处于积极、主动、有趣的学习状态中,从而实现教与学的最优化,最 终达成本节课的学习目标。
角的平分线上
空间,进一体
(2) 如果一个点到角的两边的距离相 等 ,那么它就在这个角的平分线上.
现学生的主体 地位和老师的 主导作用.
3.经过上一个
探究活动让学
生在老师的参
与和引导下获
取一定的经验
用于本次活动
中,让学生学
2.展示第二个探索活动的要求和完成 任务内容,引导、组织学生以小组为 单位进行探索、合作、交流.
湘教版八下数学1.4.1《角平分线的性质》教学设计

湘教版八下数学1.4.1《角平分线的性质》教学设计一. 教材分析《角平分线的性质》是湘教版八年级下册数学第1.4.1节的内容。
本节主要让学生了解角平分线的性质,学会用角平分线判定角的相等和边的垂直平分关系。
教材通过生活实例引入角平分线的概念,接着引导学生探究角平分线的性质,最后通过角平分线的应用,使学生感受数学与生活的紧密联系。
二. 学情分析八年级的学生已具备一定的几何知识,对图形的性质有一定的了解。
但在探究角平分线的性质过程中,需要学生具备较强的观察能力、分析能力和推理能力。
此外,学生可能对角平分线与边的关系理解不够深入,因此在教学过程中需要引导学生反复探究、总结。
三. 教学目标1.理解角平分线的性质,并能运用角平分线判断角的相等和边的垂直平分关系。
2.培养学生的观察能力、分析能力和推理能力。
3.激发学生学习数学的兴趣,感受数学与生活的紧密联系。
四. 教学重难点1.角平分线的性质2.运用角平分线判断角的相等和边的垂直平分关系五. 教学方法1.采用问题驱动法,引导学生主动探究角平分线的性质。
2.运用几何画板软件,动态展示角平分线的性质,增强学生的直观感受。
3.采用合作交流法,让学生在小组内讨论、分享解题心得,提高学生的合作能力。
4.运用实例分析法,让学生感受数学与生活的紧密联系。
六. 教学准备1.准备相关课件,展示角平分线的性质。
2.准备几何画板软件,用于动态展示角平分线的性质。
3.准备生活实例,使学生感受数学与生活的联系。
4.准备练习题,巩固所学知识。
七. 教学过程1.导入(5分钟)利用生活实例引入角平分线的概念,引导学生思考:如何判断一个角是否为另一个角的平分线?2.呈现(10分钟)展示几何画板软件,动态展示角平分线的性质。
引导学生观察、分析,总结角平分线的性质。
3.操练(10分钟)学生分组讨论,尝试运用角平分线判断角的相等和边的垂直平分关系。
教师巡回指导,解答学生疑问。
4.巩固(10分钟)出示练习题,让学生独立完成。
湘教版八下数学1.4角平分线的性质第1课时角平分线的性质和判定教学设计

湘教版八下数学1.4角平分线的性质第1课时角平分线的性质和判定教学设计一. 教材分析湘教版八下数学第1.4节角平分线的性质,主要讲述了角平分线的性质和判定。
本节课的内容是学生学习几何知识的重要组成部分,也是学生进一步学习圆的性质和线段平分线性质的基础。
通过本节课的学习,学生可以掌握角平分线的性质和判定方法,为以后的学习打下坚实的基础。
二. 学情分析学生在学习本节课之前,已经掌握了角的定义、角的计算等基本知识,同时也学习了线段的性质和判定。
但是,对于角平分线的性质和判定,学生可能还比较陌生。
因此,在教学过程中,教师需要引导学生通过观察、思考、操作等活动,自主探索角平分线的性质和判定方法,从而达到理解掌握的目的。
三. 教学目标1.知识与技能:学生能够理解角平分线的性质,掌握角平分线的判定方法。
2.过程与方法:学生通过观察、操作、思考等活动,培养自己的逻辑思维能力和空间想象力。
3.情感态度与价值观:学生通过对角平分线性质的学习,增强对数学的兴趣和好奇心,培养自己的探索精神。
四. 教学重难点1.重点:角平分线的性质。
2.难点:角平分线的判定方法。
五. 教学方法采用问题驱动法、引导发现法、合作交流法等教学方法,引导学生通过观察、操作、思考等活动,自主探索角平分线的性质和判定方法。
六. 教学准备教师准备多媒体教学课件、角平分线的模型、练习题等教学资源。
七. 教学过程1.导入(5分钟)教师通过提问方式引导学生回顾已学过的角和线段的知识,为新课的学习做好铺垫。
2.呈现(10分钟)教师通过多媒体课件呈现角平分线的性质和判定方法,引导学生观察、思考,引导学生发现角平分线的性质和判定方法。
3.操练(10分钟)教师学生进行小组合作交流,让学生通过实际操作,进一步理解和掌握角平分线的性质和判定方法。
4.巩固(10分钟)教师通过出示一些练习题,让学生独立完成,巩固所学知识。
5.拓展(10分钟)教师出示一些拓展题,引导学生思考,进一步深化对角平分线性质和判定方法的理解。
角平分线的性质导学案
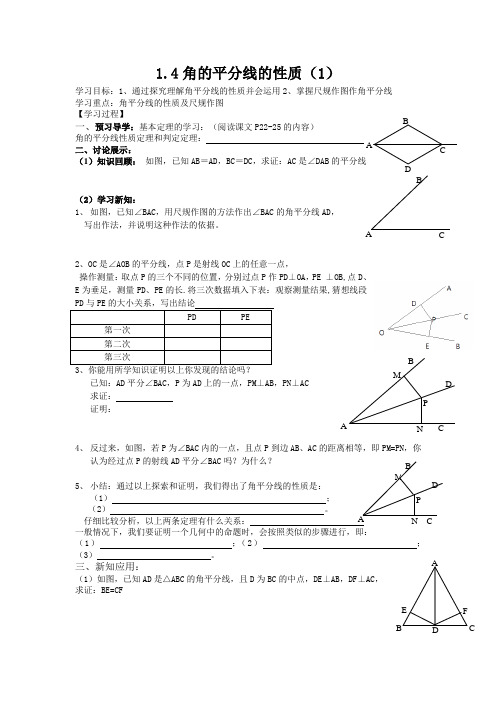
1.4角的平分线的性质(1)学习目标:1、通过探究理解角平分线的性质并会运用2、掌握尺规作图作角平分线 学习重点:角平分线的性质及尺规作图【学习过程】 一、预习导学:基本定理的学习:(阅读课文P22-25的内容)角的平分线性质定理和判定定理: 二、讨论展示:(1)知识回顾: 如图,已知AB =AD ,BC =DC ,求证:AC 是∠DAB 的平分线(2)学习新知:1、 如图,已知∠BAC ,用尺规作图的方法作出∠BAC 的角平分线AD ,写出作法,并说明这种作法的依据。
2、OC 是∠AOB 的平分线,点P 是射线OC 上的任意一点,操作测量:取点P 的三个不同的位置,分别过点P 作PD ⊥OA ,PE ⊥OB,点D 、E 为垂足,测量PD 、PE 的长.将三次数据填入下表:观察测量结果,猜想线段3、你能用所学知识证明以上你发现的结论吗? 已知:AD 平分∠BAC ,P 为AD 上的一点,PM ⊥AB ,PN ⊥AC 求证: 证明:4、 反过来,如图,若P 为∠BAC 内的一点,且点P 到边AB 、AC 的距离相等,即PM=PN ,你认为经过点P 的射线AD 平分∠BAC 吗?为什么?5、 小结:通过以上探索和证明,我们得出了角平分线的性质是:(1) ; (2) 。
仔细比较分析,以上两条定理有什么关系:一般情况下,我们要证明一个几何中的命题时,会按照类似的步骤进行,即:(1) ;(2) ;(3) 。
三、新知应用:(1)如图,已知AD 是△ABC 的角平分线,且D 为BC 的中点,DE ⊥AB ,DF ⊥AC , 求证:BE=CFA B D C A B C C A B CN M P D A B C N M P D。
北师大版数学八年级下册1.4《角平分线》教案

北师大版数学八年级下册1.4《角平分线》教案一. 教材分析《角平分线》是北师大版数学八年级下册第1章“几何变换”中的一个重要内容。
本节课主要介绍了角平分线的性质及其在几何图形中的应用。
学生通过学习角平分线,可以进一步理解几何图形的性质,提高解决问题的能力。
二. 学情分析学生在学习本节课之前,已经掌握了线段的中垂线、垂直平分线的性质,对几何图形的变换有一定的了解。
但部分学生对角平分线的概念和性质理解不够深入,运用角平分线解决实际问题的能力较弱。
三. 教学目标1.理解角平分线的定义及其性质;2.学会运用角平分线解决简单几何问题;3.培养学生的空间想象能力和解决问题的能力。
四. 教学重难点1.角平分线的定义及其性质;2.运用角平分线解决实际问题。
五. 教学方法采用讲授法、示范法、讨论法、实践法等多种教学方法,引导学生通过观察、思考、操作、交流等活动,掌握角平分线的性质和应用。
六. 教学准备1.准备相关课件和教学素材;2.准备角平分线的模型或实物;3.准备练习题和拓展题。
七. 教学过程1.导入(5分钟)利用课件或实物展示,引导学生回顾线段的中垂线、垂直平分线的性质。
提问:线段的垂直平分线和中垂线有什么关系?它们在几何图形中有什么作用?2.呈现(10分钟)展示角平分线的模型或实物,引导学生观察并思考:角平分线是什么?它有什么特点?通过示范和讲解,阐述角平分线的定义及其性质。
3.操练(10分钟)学生分组讨论,尝试运用角平分线解决简单几何问题。
教师巡回指导,解答学生疑问。
4.巩固(10分钟)出示练习题,让学生独立完成。
教师选取部分学生的作业进行点评,指出错误并讲解原因。
5.拓展(10分钟)出示拓展题,引导学生运用所学知识解决实际问题。
学生分组讨论,教师巡回指导。
6.小结(5分钟)总结本节课所学内容,强调角平分线的性质及其在几何图形中的应用。
7.家庭作业(5分钟)布置适量的作业,让学生巩固所学知识。
8.板书(5分钟)设计简洁明了的板书,突出角平分线的性质和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(6)1.4角的平分线的性质导学案(1)
学习目标:
1、掌握角平分线的性质
2、会用尺规作一个已知角的平分线. 教学重点:角平分线的性质
教学难点:探索作角平分线的过程 一、知识链接
1、角平分线是以一个角的顶点为端点的一条 ,它把这个角分成两个 的角。
2、你能用尺规作图的方法做出一个角的角平分线么?
二、自主学习
已知:如上图,OC 平分∠AOB ,点P 在OC 上,PD ⊥OA 于D ,PE ⊥OB 于E. 求证:PD=PE
归纳:
归纳角平分线的性质: 用几何语言表述:
PE
PD OB PE OA PD AOB OC AOB P =∴⊥⊥∠∠,)(平分或的平分线上在点 进一步思考,若PD ⊥OA 于D ,PE ⊥OB 于E. PD=PE ,那么点P 在∠AOB 的角平分线上么?
归纳角平分线的逆定理:
三、合作探究
1、已知:如图,AD 是△ABC 的中线,AB=AC ,DE ⊥AB 于E ,DF ⊥AC 于 F. 求证:DE=DF.
O
B
A
C
P
D
E
D
C
B A E
F
2
1O
B
A
C
P
D
E
D
C
A
E
B
2..如图,在△ABC 中,∠C=90°,AD 是∠BAC 的平分线,DE ⊥AB 于E ,F 在
AC 上,BD=DF ;求证:CF=EB.
四、课堂检测
1、已知:如图,BM ,ABC 的角平分线 P ,CN 相交于点
求证:点P 到三边AB ,BC ,CA 的距离相等。
2、如图,△ABC 中,∠C =90°,AC =BC ,AD 平分∠CAB 交BC 于D ,DE ⊥AB 于E ,且AB =6㎝,则△DEB 的周长为?
3、已知:如图,CD ⊥AB 于D ,BE ⊥AC 于E ,∠1=∠2. 求证:OB=OC
2.如图,四边形ABCD 中AB=AD ,CB=CD ,点P 是对角线AC 上一点,PE ⊥BC 于E ,PF ⊥CD 于F ,求证:PE=PF
D
A
C
E O
65
4
321
B
P A
B C M
N
.。
