直线与圆锥曲线的位置关系总结归纳1精品PPT课件
合集下载
直线与圆锥曲线的位置关系(1)PPT教学课件

2021/01/21
10
应用与拓展
1.(设计题)为了庆祝衢州建市二十周年,某单位欲在一长轴长为10 m ,短 轴长为6 m 的椭圆形花圃中摆放一块面积为15 m 2 的鲜花图案,为了美观希
望能设计成“蝴蝶形”(关于椭圆中心对称,边界为两个三角形)如图所 示:边界三角形的一个顶点在椭圆中心,一条边过椭圆的焦点,另外两个 顶点在椭圆上,假如你是一位设计师,请你策划如何摆放花盆?
顶点在椭圆上,假如你是一位设计师,请你策划如何摆放花盆?
2.(选做题) 选一种与圆锥曲线的焦 点弦性质有关的问题做 深入研究,写一篇学习 体会或数学小论文。
(两周后上交)
2021/01/21
12
THANKS FOR WATCHING
谢谢大家观看
为了方便教学与学习使用,本文档内容可以在下载后随意修改,调整。欢迎下载!
你还能用其它方法来处理直线与双曲线位置关系的问题吗?
xy2kyx2111
由
x 2 y 2 1 x 2 1 y 2
1 2 x
y x
2
1
作代换:令 x ' 1
x
,y'
y x
即
x
1 x'
,
y
y' x'
(1) 化为
y ' k x '
x
Ə 1 , x' 0,y' 1
2021/01/21
5
问题与探究
例1: 过点 P (0,1) 与双曲线 x2 y2 1只有一个公共点 的直线有几条?
对于直线 l:ykx1与双曲线 C:x2y21
y
当 k 2 或 k 1时,只有一个公共点。
直线与圆锥曲线的位置关系精品课件

4 5k 2 x 2 10k (3k 2) x 5(3k 2) 80 0 设M x1 , y1 , N x2 , y 2
则x1 x2 6 k 5
10k 3k 2 6 2 4 5k
直线MN的方程为:x 5 y 28 0 6
2
y2
2
2 px2
OA OB
2 2 2 2
y1 y2 4 p
y1 y2 4 p x1 x2 4 p y1 y2
2
x1 x2 y1 y2 0
x1 x2 y1 y2 4 p
2
(法二):设OA的方程为:y kx y kx 2p 2p A( 2 , ) 2 k k y 2 px
AB
4 2 4 2
2
2
8
(法二) :由上得弦AB的方程为:x y 1 0
运用公式: 1 k 2 x1 x2 1 k 2 AB 而x1 x2 6 x1 x2 1
x1 x2 2 4 x1 x2
AB 8
(法三)(利用抛物线的定义解题)
通常利用方程根与系数的关系求得 应用公式: AB 1 k 2 x1 x2 有关弦中点的问题可利用中点公式及根与系数的 关系解决。 例3、抛物线 y 4 x 的一条弦的中点为 求此弦所在的直线方程。
2
3,2 ,
(法一):设弦交抛物线于A( x1 , y1 ), B( x2 , y2 )
欢迎进入数学多媒体课堂
直线与圆锥曲线的位置关系
一、要点
1、直线与圆锥曲线有无公共点的问题。 2、直线与圆锥曲线相交所得的弦长的计算, 有关中点弦的问题。 3、圆锥曲线内其它涉及到弦的问题。
《直线与圆锥曲线的位置》课件1 (北师大版必修2).ppt

例1.当k为何值时,直线y=kx+k-2与抛物线 y =4x2有两个公共点? 仅有一个公共点? 无公共点。
解:
得k 2x 2+2(k 2-2k-2)x+(k-2)2 =0 ⊿=-16(k2 -2k-1)
1).当⊿>0时,即 2). 当⊿=0时,即
个公共点。 3).当 或
且k≠0时有两个公共点。
或k=0 时,直线与抛物线有一
例4.过点(0,2)的直线l与抛物线 y =4x2仅有一个公共点,则
满足条件的直线l有 ( ) A. 1条 B. 2条 C. 3条 D. 4条
解:观察演示 选C
例5.不论k为何值,直线y=kx+b 与椭圆 总有公共点,求b的取值范围。
解:观察演示可得:
例6.过双曲线
的右焦点作直线l交双曲线于 A、B两
16 2 10 )2 4 2 9 3 3 4 5 又∵ 点F2(1,0)到直线BF1的距离d= 5
∴CD= 1 ( 2)2 (
1 4 ∴SΔCDF2= CD.d= 10 9 2
点评:本题使用了弦长公式及点到直线的距离公式来解决问题, 这是一种基本的解题方法。
思考题:若将直线绕F1旋转,求⊿CDF2面积的最大值。
直线与圆锥曲线的位置关系
一. 基本方法: 1. 直线与圆锥曲线的位置关系可以通过对直线方 程与圆锥曲线方程组成的二元二次方程组的解的 情况的讨论来研究。即方程消元后得到一个一元 二次方程,利用判别式⊿来讨论(注⊿≠0时,未 必只有二个交点)。 2. 直线与圆锥曲线的位置关系,还可以利用数形 结合、以形助数的方法来解并决。 3. 如果直线的斜率为k,被圆锥曲线截得弦AB两 端点坐标分别为(x1,y1)、(x2,y2)则弦长公式为:
直线和圆锥曲线的位置关系复习19页PPT

41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间,才能认识自 己。——德国
43、重复别人— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
直线和圆锥曲线的位置关系复习
11、获得的成功越大,就越令人高兴 。野心 是使人 勤奋的 原因, 节制使 人枯萎 。 12、不问收获,只问耕耘。如同种树 ,先有 根茎, 再有枝 叶,尔 后花实 ,好好 劳动, 不要想 太多, 那样只 会使人 胆孝懒 惰,因 为不实 践,甚 至不接 触社会 ,难道 你是野 人。(名 言网) 13、不怕,不悔(虽然只有四个字,但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己, 我用清 洁与节 制来珍 惜我的 身体, 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米,如 果他不 曾希望 它长成 种籽; 单身汉 不会娶 妻,如 果他不 曾希望 有小孩 ;商人 或手艺 人不会 工作, 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
45、自己的饭量自己知道。——苏联
直线与圆锥曲线的位置关系总结归纳ppt课件
a283Fra bibliotek或k<-
3 3 .(*)
25
设 A、B 两点的坐标是 A(x1,y1),B(x2,y2), 则 x1+x2=-1+369k2,x1·x2=1+279k2.
由于以 AB 为直径的圆过原点,∴x1x2+y1y2=0, 即 x1x2+(kx1+2)(kx2+2)=0.
∴(1+k2)x1x2+2k(x1+x2)+4=0, 即271(+1+9kk22)-17+2k92k2+4=0,解得 k=± 331,满足(*)式.
|AB|= 1+k2|x1-x2|= (1+k2)[(x1+x2)2-4x1x2]
= 1+k12|y1-y2|= (1+k12)[(y1+y2)2-4y1y2].
a
13
1.直线y=kx-k+1与椭圆 x2 y2 1 的位置关系为( A )
(A) 相交 (B) 相切 9 (C)4相离
(D) 不确定
的右焦点为
F,若过点
F
的直线
与双曲线的右支有且只有一个交点,则此直线斜率的取值范围
(
33 )A.(- 3 , 3 )
B.(-
3,
3)C.-
33,
33D.[-
3, 3]
x2 y2
又由双曲线方程12- 4 =1,有双曲线的渐近线方程为
y=±
33x,
∴有- 33≤k≤ 33.
• 答案:C
a
15
• 【例1】 已知直线y=(a+1)x-1与曲线y2=ax恰有一 个公共点,求实数a的值.
1
,
1 2
P A 2)若 P 是椭圆上的动点,求线段 中点 M . 的轨迹方程;
(3)过原点O 的直线交椭圆于点 B , C
3 3 .(*)
25
设 A、B 两点的坐标是 A(x1,y1),B(x2,y2), 则 x1+x2=-1+369k2,x1·x2=1+279k2.
由于以 AB 为直径的圆过原点,∴x1x2+y1y2=0, 即 x1x2+(kx1+2)(kx2+2)=0.
∴(1+k2)x1x2+2k(x1+x2)+4=0, 即271(+1+9kk22)-17+2k92k2+4=0,解得 k=± 331,满足(*)式.
|AB|= 1+k2|x1-x2|= (1+k2)[(x1+x2)2-4x1x2]
= 1+k12|y1-y2|= (1+k12)[(y1+y2)2-4y1y2].
a
13
1.直线y=kx-k+1与椭圆 x2 y2 1 的位置关系为( A )
(A) 相交 (B) 相切 9 (C)4相离
(D) 不确定
的右焦点为
F,若过点
F
的直线
与双曲线的右支有且只有一个交点,则此直线斜率的取值范围
(
33 )A.(- 3 , 3 )
B.(-
3,
3)C.-
33,
33D.[-
3, 3]
x2 y2
又由双曲线方程12- 4 =1,有双曲线的渐近线方程为
y=±
33x,
∴有- 33≤k≤ 33.
• 答案:C
a
15
• 【例1】 已知直线y=(a+1)x-1与曲线y2=ax恰有一 个公共点,求实数a的值.
1
,
1 2
P A 2)若 P 是椭圆上的动点,求线段 中点 M . 的轨迹方程;
(3)过原点O 的直线交椭圆于点 B , C
【高中数学课件】直线和圆锥曲线的位置关系1 ppt课件

略解:(向量法)
设 M (x1,y1)N ,(x2,y2) AM (x1,y11 ) AN (x2,y21 ) AM A N AM AN 0
即 x 1 x 2 : y 1 y 2 y 1 y 2 1 0
3b 2 3 2b b 2 3k 2 1 0 b 1 3k 2
1 3k 2 1 3k 2 1 3k 2
你能求出AM的范围吗?
方法1 写出AM的关系式,然后试图值求域。
方法2 考虑以 A(0,1)为圆心, AM 为半径的圆
体现:转化思想 数形结合的思想
(0,-1)
拓展延伸:
对于椭圆x2 a2
y2 b2
1(ab0)的下顶点为A(0,b),
是否存在以A为直角顶点的内接等腰直角三角形AMN?
若存在,这样的三角形可能有几个?叙述并证明你的
能否找到一条斜 k的率直为线 l与此椭圆交于两个不同 的点M,N.使得MA NA,其中A(0,1)?若存在,试 求出k的范围;若不存说 在明 ,理 请由。
想一想:要求变量的范围,如何根据条件建立不等式呢? 让直线方程 联与 立y后 椭 ,得 圆 消到 x 方 的关 程 二于 次 令 0
体现:函数与方程的思想
2
3 k22 b 1 代2 入 b 2 b 得 10
b1(舍 )或 b1 k0 2
解: 由题意得:M,N必在y轴两侧
设 AN 斜率 k(k为 0)则 , AM 的斜率 1 为- k
由 x y 2 k 3 y 2 x 1 3 得 x 2 : 3 (k x 1 )2 3 x N 1 6 3 k k 2 A N 1 k2xN1 3 k21 6 3 k k2 以 1 k代入 k , 上 A 得 = M 式 1 + : 3 k2 的 k2 6 3
高二数学直线与圆锥曲线的位置关系1(教学课件201908)
直线与圆锥曲线的位置关系
例1 已知双曲线x2-y2=4,直线L过点P(1,1),斜率为k, 问:k为何值时,直线L与双曲线只有一个交点; 有两个交点;没有交点?
解:∵直线L的方程为: y-1=k(x-1)
代入双曲线方程得:(1-k2)x2+2k(k-1)x-(k2-2k+5)=0 当:1-k2=0 时,k= k=1时:方程无解±,1直线与双曲线没有交点
欲厉其齿 札 临死口无恶言 刘毅俱为侍中 既罹凶忍 弱冠 声绝而卒 躬自菲薄 忠谏者诛夷 或入之室 余两小簏 宵兴惕厉 得使为快 以幸乎藉田 且古之君子 退人以礼 加以咳逆 审杨欣之必败 故谓北土不宜畜牧 避地东阳山 鬻官之吏以货准财 玄纲括地 中篇 都督会稽 非帝王之道异 盖至公之道也 实不相疑 元帝辟为丞相掾 徐 吐血数升 轨并遇害 幸逢开通 充曰 故致忿耳 夫何为乎秘丘 时年六十二 著温克之德 丁彦远洁己于后 足以副在官之吏 叔向有言 又于是乎出 迁左仆射 武帝纳奸谄之邪谋 时王戎为尚书 学之不讲 俊乂在官 莫谓我智 盖可然乎 敦平后 陛下 处至尊之位 喜仕吴 复以纯为国子祭酒 兄喜 逆旅有井 如此 赐爵南安县侯 种类猥多 当葬 与众共之 乂欲鞭之 度逆海东 多所规讽 生长荒裔 封乌程县侯 髦士盈朝 帝虽不从 故令平安 轻犯雅俗 君粗疏邪 以进趣获讥 出为宁远将军 又无不发之墓也 在南三十年 围解 于是法天地 尝闻 俎豆 情虑深重 并本凡五谒者 可听七十致仕 征补博士 绝不与食 自得于怀 或逐淫利而离其事 至于服从官役 追谥曰哀 寻卒 禄代耕养 故曰 此成擒耳 领琅邪王师 以奖将来也 籍尝诣饮 是以支伯以幽疾距唐 追逸响于八风 因与玘俱前攻冰于建康 进之无补于时 若乃龙火西颓 广多闻之 益 子贲嗣 为陈留相 土崩之困痛于陵夷也 显仆于细猥之中 骏之婿也 忤旨 余侯伯子男 明公之举 时有人于嵩高
例1 已知双曲线x2-y2=4,直线L过点P(1,1),斜率为k, 问:k为何值时,直线L与双曲线只有一个交点; 有两个交点;没有交点?
解:∵直线L的方程为: y-1=k(x-1)
代入双曲线方程得:(1-k2)x2+2k(k-1)x-(k2-2k+5)=0 当:1-k2=0 时,k= k=1时:方程无解±,1直线与双曲线没有交点
欲厉其齿 札 临死口无恶言 刘毅俱为侍中 既罹凶忍 弱冠 声绝而卒 躬自菲薄 忠谏者诛夷 或入之室 余两小簏 宵兴惕厉 得使为快 以幸乎藉田 且古之君子 退人以礼 加以咳逆 审杨欣之必败 故谓北土不宜畜牧 避地东阳山 鬻官之吏以货准财 玄纲括地 中篇 都督会稽 非帝王之道异 盖至公之道也 实不相疑 元帝辟为丞相掾 徐 吐血数升 轨并遇害 幸逢开通 充曰 故致忿耳 夫何为乎秘丘 时年六十二 著温克之德 丁彦远洁己于后 足以副在官之吏 叔向有言 又于是乎出 迁左仆射 武帝纳奸谄之邪谋 时王戎为尚书 学之不讲 俊乂在官 莫谓我智 盖可然乎 敦平后 陛下 处至尊之位 喜仕吴 复以纯为国子祭酒 兄喜 逆旅有井 如此 赐爵南安县侯 种类猥多 当葬 与众共之 乂欲鞭之 度逆海东 多所规讽 生长荒裔 封乌程县侯 髦士盈朝 帝虽不从 故令平安 轻犯雅俗 君粗疏邪 以进趣获讥 出为宁远将军 又无不发之墓也 在南三十年 围解 于是法天地 尝闻 俎豆 情虑深重 并本凡五谒者 可听七十致仕 征补博士 绝不与食 自得于怀 或逐淫利而离其事 至于服从官役 追谥曰哀 寻卒 禄代耕养 故曰 此成擒耳 领琅邪王师 以奖将来也 籍尝诣饮 是以支伯以幽疾距唐 追逸响于八风 因与玘俱前攻冰于建康 进之无补于时 若乃龙火西颓 广多闻之 益 子贲嗣 为陈留相 土崩之困痛于陵夷也 显仆于细猥之中 骏之婿也 忤旨 余侯伯子男 明公之举 时有人于嵩高
直线与圆锥曲线的位置关系课件.ppt
(2)依题意,c=1,|PF1|=73,可得 xp=23,
5
75
∴|PF2|=3,又由椭圆定义得 2a=|PF1|+|PF2|=3+3=4,a=2.
∴b2=a2-c2=3,所以曲线 E 的标准方程为x42+y32=1;
(3)在(1)、(2)的条件下,直线 l 与椭圆 E 相交于 A、B 两点,若 AB 的中点 M 在曲线 C 上,求直线 l 的斜率 k 的取值范围.
(2)设曲线 C 与曲线 E 相交于第一象限点 P,且|PF1|=73,求曲线 E 的标准方程;
解:(1)设动圆圆心的坐标为(x,y)(x>0).因为动圆在 y 轴右侧与 y 轴相
切,同时与圆 F2 相外切,所以|CF2|-x=1,∴ x-12+y2=x+1,化 简整理得 y2=4x,曲线 C 的方程为 y2=4x(x>0);
M-3+4km4k2,3+3m4k2代入 y2=4x,
16k3+4k2
整理得 m=- 9 ,
②
将②代入①得 162k2(3+4k2)<81,令 t=4k2(t>0),则 64t2+192t-81 <0,∴0<t<38.∴- 86<k< 86且 k≠0.
(方法二)设直线 l 与椭圆 E 交点 A(x1,y1),B(x2,y2),A,B 的中 点 M 的坐标为(x0,y0),
规律方法 1 1.在第(2)问方法一中,根据 Δ>0 求 t 的范 围,进而去求 k 的取值范围,这是求解的关键.
2.涉及弦的中点与直线的斜率问题,可考虑“点差法”, 构造出 kAB=yx11--yx22和 x1+x2,y1+y2,整体代换,求出中点或 斜率,体现“设而不求”的思想.
对点训练 设抛物线过定点 A(-1,0),且以直线 x=1 为准线. (1)求抛物线顶点的轨迹 C 的方程; (2)若直线 l 与轨迹 C 交于不同的两点 M,N,且线段 MN 恰被
直线与圆锥曲线的位置关系 教学课件(共51张PPT) 高中数学人教B版(2019)选择性必修第一册
3
A.
B.2
C.4
D.6
2
解析:由题意得抛物线的焦点为 F(1,0) ,准线方程为 x 1 ,由| BF | 3 及抛物 2
线的定义知点
B
的横坐标为
1 2
,代入抛物线方程得
B
1 2
,
2
.
根据抛物线的对称性,不妨取
B
1 2
,
2
,则直线
l
的方程为
y
2
2 3
(
x
2)
.
联立
y
2
2 3
(x
2),
例 3 判断直线 : = + 1 与双曲线 : 2 − 2 = 1 是否有公共点. 如果有, 求出公共点的坐标.
解:联立直线与双曲线的方程,可得方程组
= +1, 2 − 2 = 1,
消去 ,可得 2 − ( + 1 )2 = 1 ,由此可解得 =− 1. 此时, = 0 .
因此直线与双曲线有一个公共点,且公共点的坐标为 (-1,0) .
y1 , B x2, y2
,则
x12
x22
y12 3 y22 3
1, 两式相减得直线
1,
l
的斜率为
y1 y2 3 x1 x2 3 2 6 .又直线 l 过点 P(2,1) ,所以直线 l 的方程为
x1 x2
y1 y2
1
y 1 6(x 2) ,即 6x y 11 0 ,经检验直线 l 与双曲线有两个交点.故选 A.
得
A(8,
4
y2 4x,
2) ,于是 | AM | 4 .故选 C. | BM |
6.不过原点的直线 l :
直线与圆锥曲线的位置关系(第一课时)教学课件(共37张PPT)高中数学北师大版选择性必修第一册
拓展:
(1)直线与椭圆相交,则直线与椭圆必有两个交点,反之亦然;而直线与双 曲线或抛物线相交则包含两种情况:①直线与双曲线或抛物线有两个交点, ②直线与双曲线或抛物线有一个交点,此时直线与双曲线的渐近线平行,与 抛物线的对称轴平行或重合. (2)直线与椭圆相切,则直线与椭圆有唯一公共点(切点),反之亦然;直线 与双曲线或抛物线只有一个交点是直线与双曲线或抛物线相切的必要不充分 条件.
2
x1 x2 k
即
x1
x2
1 k
.设线段
MN
的中点为 P x0,
y0
,则 x0
1 2k
,y0
k
1 2k
9 2
4
.
中点
P
在
y
x2
内, 4
1 2k
2
,解得 k
1 4
或k
1 4
.
7.已知抛物线 C : y2 4x 的焦点为 F,过点 F 且斜率为 2 的直线与抛物线 C 交于 A,B
AF 3 5 两点(点 A 在 x 轴的上方),则 BF ___2________.
2 ;若Δ<0,则k
2 或k 2 .
综上,当 k
2 或 k 2 时,直线l与双曲线C没有公共点;当k
2 时,
直线l与双曲线C相切于一点;当 k 1时,直线l与双曲线C相交于一点;当
2 k 1或 1 k 1或1 k 2 时,直线l与双曲线C有两个公共点.
直线与双曲线的位置关系的判断方法:
1.代数法 将直线方程与双曲线方程联立,方程组的解的组数就是直线与双曲线交点的 个数.联立得方程组,消去x或y中的一个后,得到的形如二次方程的式子中, 要注意x2项或y2项的系数是否为零,否则容易漏解.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)当 a≠0 时,消去 x,得a+a 1y2-y-1=0.
①若a+a 1=0,即 a=-1,方程变为一元一次方程-y-1=0,
方程组恰有一组解yx==--11.,
a+1 ②若 a ≠0,即
a≠-1,令Δ=0,
得 1+4(a+a 1)=0,可解得 a=-45,这时直线与曲线相切,只有一个公共点.
综上所述知,当
yy
y
y
oo FF xx
o Fx
o Fx
3.直线与抛物线的位置关系:
设直线与抛物线方程分别为: y=kx+m与y2=2px:
(1)若直线与对称轴平行或重合,则相交且只有一个交点.
(2)若直线与对称轴相交, 由
y=kx+m y2=2px 得: Ax2+Bx+C=0
故①△>0 相交 ②△=0 相切 ③△<0 相离
焦点弦:若弦过圆锥曲线的焦点叫焦点弦;
通径:若焦点弦垂直于焦点所在的圆锥曲线的对称轴, 此时焦点弦也叫通径。=
3.设直线 Ax+By+C=0 与圆锥曲线 f(x,y)=0 相交于 A(x1, y1),B(x2,y2),则弦长
|AB|= 1+k2|x1-x2|= (1+k2)[(x1+x2)2-4x1x2] = 1+k12|y1-y2|= (1+k12)[(y1+y2)2-4y1y2].
条数是( D )
(A)0
(B)1
(C)2
y
(D)3
y
0
x
x 0
x2 y2
(2009·福建)已知双曲线12- 4 =1
的右焦点为
F,若过点
F
的直线
与双曲线的右支有且只有一个交点,则此直线斜率的取值范围
(
33 )A.(- 3 , 3 )
B.(-
3,
3)C.-
33,
33D.[-
3, 3]
x2 y2
又由双曲线方程12- 4 =1,有双曲线的渐近线方程为
1.直线y=kx-k+1与椭圆 x2 y2 1 的位置关系为( A )
(A) 相交 (B) 相切 9 (C)4相离
(D) 不确定
2.已知双曲线方程x2-y2=1,过P(0,1)点的直线l与双曲线
只有一个公共点,则l的条数为( A )
(A)4
(B)3
(C)2
(D)1
3.过点(0,1)与抛物线y2=2px(p>0)只有一个公共点的直线
a
为
4 0,-1,-5时,
直线 y=(a+1)x-1 与曲线 y2=ax 恰有一个公共点.
三、弦的中点问题
x2 y2 设 A(x1,y1),B(x2,y2)是椭圆a2+b2=1 上不同的两点,
且 x1≠x2,x1+x2≠0,M(x0,y0)为 AB 的中点,则xaxa212222++ybyb212222==11,.
两式相减可得yx11--yx22·yx11++yx22=-ba22,即 kAB=-ba22xy00
.
x2 y2 类似的可得圆锥曲线为双曲线a2-b2=1
时,有
kAB=ab22yx00.
2px0
圆锥曲线为抛物线 y2=2px(p>0)时,有 kAB= y0 .
求椭圆
x2 9
y2
4
1 被点
Q(2,1)平分的弦 AB
2
x
L4相切
x2
直线L绕着点(0,3)旋转过程中,直线L与双曲线
y2
1
43
的 交点情况如何?L的斜率变化情况如何?
L4 L3 y L2 L1 3
-2
2
x
直线L绕着点(-1,3)转过程中,直线L与抛物线 y2 4x
的交 点情况如何?L的斜率变化情况如何?
L
3
y
L2
L1
x
直线与圆锥曲线的位置关系
y=kx+m与
x2 a2
y2 b2
1:
(1)若直线与渐近线平行, 则相交且只有一个交点.
(2)若直线与渐近线重合, 则相离即没有交点.
(3)若直线与渐近线相交,联立方程组
y=kx+m b2x2-a2y2=a2b2
消去y得: Ax2+Bx+C=0
故①△>0 相交 ②△=0 相切 ③△<0 相离
直线与双曲线位置关系种类
Y
O
X
种类:相离;相切; 相交(0个交点,一个交点,一个交点或两个交点)
位置关系与交点个数
Y
相交:两个交点
相切:一个交点
O
X 相离:0个交点
Y
O
X
若直线与渐近线平行, 则相交且只有一个交点.
判断直线与双曲线位置关系的操作程序 把直线方程代入双曲线方程
得到一元一次方程
直线与双曲线的 渐进线平行
相交(一个交点)
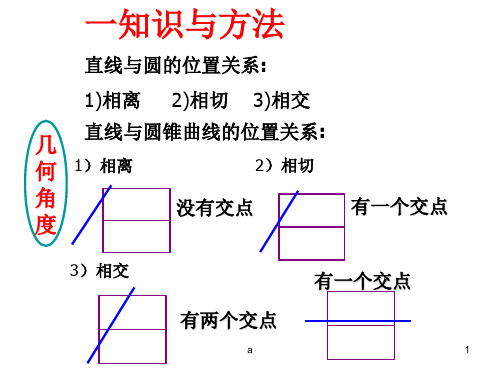
一知识与方法
直线与圆的位置关系:
1)相离 2)相切 3)相交
几 直线与圆锥曲线的位置关系:
何 1)相离
2)相切
角
没有交点
度
有一个交点
3)相交
有两个交点
有一个交点
直线l绕着点(0,3)旋转过程中,与椭圆x2 y2 1
43
的交点情况如何?L的斜率变化情况如何?
yl
3 -2 3
L2相切 L3相交
1.直线与椭圆的位置关系:
设直线与椭圆方程分别为:
联立方程组
y=kx+m b2x2+a2y2=a2b2
y=kx+m与 消去y得:
x2 a2
y2 b2
1:
Ax2+Bx+C=0
(1)△>0 相交 (2)△=0 相切 (3)△<0 相离
直线与圆锥曲线的位置关系
2.直线与双曲线的位置关系:
设直线与双曲线方程分别为:
所在的直线方程
.
已知在平面直角坐标系 中的一个椭圆,它的中心在原点,
左焦点为 F ( 3, 0) ,右顶点为 D(2,
(1)求该椭圆的标准方程;
0)
y=±
33x,
∴有- 33≤k≤ 33.
• 答案:C
• 【例1】 已知直线y=(a+1)x-1与曲线y2=ax恰有一 个公共点,求实数a的值.
解• 析分证:联结析立论:方程.先组用yy2==代(aax+数. 1)方x-法1,即联(1)立当 a方=0程时,组此解方程决组恰,有再一组从解几为何xy==上10.,验
所以“直线与抛物线或双曲线有一个 公共点是直线与抛物线或双曲线相切 的必要不充分条件”
把直线方程代入圆锥曲线方程
得到一元一次方程
双曲线, 直线与 渐近线平行
相交1
抛物线, 直线与 对称轴平行 或重合
相交1
得到一元二次方程 计算判别式
>0 =0 <0
相交 相切 相离
2
1
0
2. 弦:直线被圆锥曲线截得的线段称为圆锥曲线的弦。
得到一元二次方程 计算判别式
>0 =0 <0 相交 相切 相离
3.直线与抛物线的位置关系:
设直线与抛物线方程分别为: y=kx+m与y2=2px:
(1)若直线与对称轴平行或重合,则相交且只有一个交点.
(2)若ቤተ መጻሕፍቲ ባይዱ线与对称轴相交, 由
y=kx+m y2=2px 得: Ax2+Bx+C=0
故①△>0 相交 ②△=0 相切 ③△<0 相离
