回归直线方程
回归直线方程的三种推导方法

回归直线方程的三种推导方法(总3页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2回归直线方程的三种推导方法 巴州二中母润萍回归直线方程是新课改新增内容之一,在必修数学3中对两个具有线性相关关系的变量利用回归分析的方法进行了研究,书中直接给出了回归直线方程系数的公式,在选修2-3中给出了回归直线方程的截距和斜率的最小二乘法估计公式的另一种形式的推导方法,根据所学知识,我总结了3种推导回归直线方程的方法:设x 与y 是具有线性相关关系的两个变量,且相应于样本的一组观测值的n 个点的坐标分别是:112233()()()()n n x y x y x y x y ,,,,,,,,,设所求的回归方程为i i y bx a =+,(123)i n =,,,,.显然,上面的各个偏差的符号有正、有负,如果将他们相加会相互抵消一部分,因此他们的和不能代表n 个点与回归直线的整体上的接近程度,因而采用n 个偏差的平方和Q 来表示n 个点与相应直线(回归直线)在整体上的接近程度,即求出当Q 取最小值时的a b ,的值,就求出了回归方程. 下面给出回归方程的推导方法一:一、先证明两个在变形中用到的公式公式(一)22211()nni ii i x x x nx ==-=-∑∑,其中12nx x x x n +++=证明:2222121()()()()ni n i x x x x x x x x =-=-+-++-∑∵22221212()2n n x x x x x x nx nxn+++=+++-+222222222212121()2()nnni i x x x nx nx x x x x nx==+++-+=+++=-∑22211()n ni i i i x x x nx==-=-∑∑∴.公式(二)11()()nnii i i i i xx y y x y nx y==--=-∑∑证明:11221()()()()()()()()ni i n n i x x y y x x y y x x y y x x y y =--=--+--++--∑∵11221122()()n n n n x y x y x y x y y x x y y x x y y x nx y=+++-+++++++12121[()()]ni i n n i x y x x x y y y y x nx y==-++++++++∑12121()()n n n i i i x x x y y y x y n y x nx y n n=++++++⎡⎤=-++⎢⎥⎣⎦∑112nni i i i i i x y nxy nxy x y nxy===-+=-∑∑,11()()nni i i i i i x x y y x y nx y==--=-∑∑∴.二、推导:将Q 的表达式的各项先展开,再合并、变形2222112233()()()()n n Q y bx a y bx a y bx a y bx a =--+--+--++--2222121122()[2()2()]n y y y y bx a y bx a =+++-+++展开222211111222n n nnni i i i ii i i i i i y b x y a y bxab x na ======--+++∑∑∑∑∑合并同类项22221111122nnii n n ni i i i i i i i i y x na na b b x b x y y nn =====⎛⎫ ⎪ ⎪=--+-+ ⎪ ⎪⎝⎭∑∑∑∑∑以a b ,的次数为标准整理22221112()2nn nii i i i i i na na y bx bxb x y y ====--+-+∑∑∑转化为平均数x y,22222111[()]()2nnnii i i i i i n a y bx n y bx bxb x y y ====----+-+∑∑∑配方法32222222111[()]22nn nii i ii i i n a y bx ny nbxy nb x bxb x y y====---+-+-+∑∑∑展开222222111[()]()2()()nnni i i i i i i n a y bx b x nx b x y nxy y ny ====--+---++∑∑∑整理2222111[()]()2()()()nnnii i i i i i n a y bx bxx b x x y y y y ====--+----+-∑∑∑用公式(一)、(二)变形22212111()()[()]()()()ni i n ni i i n i i i i x x y y n a y bx x x b y y x x ====⎡⎤--⎢⎥⎢⎥=--+--+-⎢⎥-⎢⎥⎣⎦∑∑∑∑配方22212212211111()()()()()()()()()n ni i i i n n i i i i n n i i i i i x x y y x x y y n a y bx x x b y y x x x x ======⎡⎤⎡⎤----⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥=--+---+-⎣⎦⎢⎥--⎢⎥⎣⎦∑∑∑∑∑∑配方法在上式中,共有四项,后两项与a b ,无关,为常数;前两项是两个非负数的和,因此要使得Q 取得最小值,当且仅当前两项的值都为0.所以或1221ni ii n i i x ynxyb x nx==-=-∑∑用公式(一)、(二)变形得上述推导过程是围绕着待定参数a b ,进行的,只含有i i x y ,的部分是常数或系数,用到的方法有:① 配方法,有两次配方,分别是a 的二次三项式和b 的二次三项式;② 形时,用到公式(一)、(二)和整体思想; ③ 用平方的非负性求最小值.④ 实际计算时,通常是分步计算:先求出x y,,再分别计算1()()nii i xx y y =--∑,21()nii xx =-∑或1ni i i x y nx y=-∑,221ni i x nx=-∑的值,最后就可以计算出a b ,的值.推导方法二:注意到因此,在上式中,后面两项和无关,前两项为非负数,因此,要使Q达到最小值,当且仅当前两项均为0,即有总结:这种方法难想到为什么要这样处理,并且计算量很大。
求线性回归直线方程的步骤

请同学们回忆一下,我们以前是否学过 变量间的关系呢?
两个变量间的函数关系.
相关关系与函数关系的异同点:
相同点:两者均是指两 个变量间的关系. 不同点:①函数关系是一种确定的关系; 相关关系是一种 非确定的关系.事实上,函数关系是两个非 随机变量的关系,而相关关系是随机变量 与随机变量间的关系. ②函数关系是一种因果关系,而相关关系 不一定是因果关 系,也可能是伴随关系.
20
30
40
^ (4)当x=2时,y=143.063, 因此,这天大 约可以卖出143杯热饮。
小结:
(1)判断变量之间有无相关关系,简便方 法就是画散点图。 (2)当数字少时,可用人工或计算器,求 回归方程;当数字多时,用Excel求回归方 程。 (3)利用回归方程,可以进行预测。
热饮杯数 156 150 132 128 130 116 104 89 93 76 54
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一
般规律; (3)求回归方程; (4)如果某天的气温是 2 C,预测这天卖出的热饮杯数。
0
解: (1)散点图
160 150 140 130 120 110 100 90 80 70 60 50 40 -10 0
10x y
2
x
i 1
2 i
10 x
110 10 0 1 110 10 0
a y bx 0 b 0 0
∴所求回归直线方程为 ^ y=x
小结:求线性回归直线方程的步骤: 第一步:列表 x , y , x y ;
i i i i
第二步:计算
x, y, xi , xi y
脂肪含量 40 35 30 25 20 15 10 5 0 20 25 30 35 40 年龄 45 50 55 60 65
回归直线方程b尖的公式推导

回归直线方程b尖的公式推导为了推导回归直线方程的一般形式,我们首先需要了解回归分析的基本概念和假设。
回归分析是一种用于研究变量之间关系的统计技术,它假设自变量和因变量之间存在线性关系,并通过拟合一条直线来描述这种关系。
假设我们有一个自变量x和一个因变量y,我们的目标是找到一条最佳拟合直线来描述x和y之间的关系。
回归直线的一般形式可以表示为:y=b0+b1x其中,y是因变量的预测值,x是自变量的值。
b0和b1是回归方程的系数,它们的值取决于数据样本的特点。
b0是截距,表示当自变量x等于0时,因变量y的值。
b1是斜率,表示当自变量x增加1个单位时,因变量y的变化值。
为了推导最佳拟合直线的回归系数,我们需要使用最小二乘法。
最小二乘法是一种常见的回归分析方法,它通过最小化预测值与实际值之间的差异来确定回归系数。
首先,我们定义回归方程的残差(error)为实际值y与预测值y的差异。
对于每个观察值,残差可以表示为:ei = yi - (b0 + b1xi)然后,我们定义回归方程的残差平方和(SSE)为所有观察值的残差平方之和:SSE = Σ(ei^2)我们的目标是找到能够最小化SSE的回归系数b0和b1、为了达到这个目标,我们需要对SSE进行求导,并令导数等于0。
首先,我们对b0求导数,得到:∂SSE/∂b0 = -2Σ(yi - (b0 + b1xi))然后,我们对b1求导数,得到:∂SSE/∂b1 = -2Σxi(yi - (b0 + b1xi))接下来,我们令导数等于0,并求解b0和b1:∂SSE/∂b0 = 0 => Σ(yi - (b0 + b1xi)) = 0∂SSE/∂b1 = 0 => Σxi(yi - (b0 + b1xi)) = 0通过求解这两个方程,我们可以得到b0和b1的估计值,进而确定回归直线的方程。
一般情况下,这些方程的解没有闭式解,需要使用数值优化方法进行求解。
常见的数值优化方法包括梯度下降法和牛顿法。
线性回归直线方程-PPT课件

零件数x(个) 10 20 30 40 50 60 70 80
加工时间y (分钟)
62 68 75 81 89 95 102 108
(1)画出散点图;
(2)根据系数公式求线性回归直线方程;
(3)关于加工零件的个数与加工时间,
你能得出什么结论?
120 100
80 60 40 20
0 0
图表标题
20
40
• 当各点总体上很接近回归直线时,两变量的相关关系 较强,反之相关关系就较弱。
• 当线性关系很弱时,即使可求出线性回归直线方程, 但由于各点总体上离此直线较远,用它作估值时偏差 较大,也就没有实际意义了。这时也可以说线性回归 方程没有意义,两变量不具有线性相关关系。
Байду номын сангаас 问:如何判断两个变量相关关系的强弱?
(2)估计工龄为20年的职工工资是多少? (先不用计算器计算后,再用计算器验算)
工资y千元
3.5
3
2.5
2
1.5
1
0.5
0
0
2
4
6
8
10
12
工龄
总结
• 对具有相关关系的两个变量进行统计分析的方法叫做回归 分析。
• 运用回归分析的方法来分析、处理数据的一般步骤是: • ①收集数据,并制成表格; • ②画出数据的散点图; • ③利用散点图直观认识变量间的相关关系;可通过计算相
60
80 100
项目 类型
零件数x 加工时间y
x2
A
10
62
100
B
20
68
400
C
30
75
900
D
40
回归直线方程计算
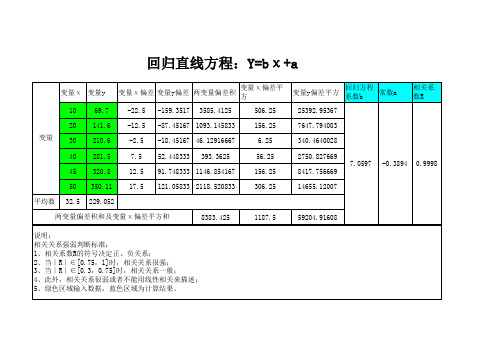
两变量偏差积和及变量χ偏差平方和
说明: 相关关系强弱判断标准: 1、相关系数R的符号决定正、负关系; 2、当∣R∣∈[0.75,1]时,相关关系很强; 3、当∣R∣∈[0.3,0.75]时,相关关系一般; 4、此外,相关关系很弱或者不能用线性相关来描述; 5、绿色区域输入数据,蓝色区域为计算结果。
yba变量变量y变量偏差变量y偏差变量偏差平方变量y偏差平方回归方程系常数a相关系数r两变量偏差积和及变量偏差平方和说明
回归直线方程: 回归直线方程:Y=bχ+a
变量χ 变量y 10 20 变量 30 40 45 50 平均数 32.5 210.6 281.5 320.8 350.11 229.052 8383.425 1187.5 59204.91608 -2.5 7.5 12.5 17.5 -18.45167 46.12916667 52.448333 393.3625 6.25 56.25 156.25 306.25 340.4640028 2750.827669 7.0597 91.748333 1146.854167 121.05833 2118.520833 8417.756669 14655.12007 -0.3894 0.9998 69.7 141.6 变量χ偏差 变量y偏差 两变量偏差积 -22.5 -12.5 -159.3517 3585.4125 变量χ偏差平 方 506.25 156.25 变量y偏差平方 25392.95367 7647.794003 回归方程 常数a 系数b 相关系 数R
回归直线方程

(3)90-(0.7×100+0.35)=19.65(t) ∴降低了19.65吨.
建立i起1 来了.
为了使计算更加有条理,我们通过制作表格来先计算出
再计算出 n
n
n
n
xi, yi, xi 2, yi 2;
i 1
i 1
i 1
i 1
y
1 n
n i 1
yi , x
1 n
n i 1
xi,
最后 利用公式
Lxx
n
xi2
2
nx , Lyy
8
70
68.3
4900
4664.89
4781
9
72
70.1
5184
4914.01
5047.2
10
74
70
5476
4900
5180
668
670.1
44794
44941.93
44842.4
回归直线方程
【典型例题】
上表可计算 x
10
668 10
10
66.8,
y
670.1 10
67.01,
10 i 1
xi
yi
44842.4
xi2 44794, yi2 44941.93, 代入公式
i 1 10
i 1
b
xi yi nx y
i 1
n
xi2
2
nx
44842.4 10 66.8 67.01 79.72
44974 10 66.82
高考数学复习点拨 回归直线方程的推导

yn ) x] nx y yn ) x nx y
y
( y1 y2 n
xi yi 2nx y nx y xi yi nx y ,
i 1 n i 1
步计算: 先求出 x, 再分别计算 ( xi x)( yi y ) , ( xi x)2 或 xi yi nx y , xi2 nx y,
i 1 i 1 i 1 i 1
n
n
n
n
2
的值,最后就可以计算出 a,b 的值.
婚博会资讯网-一网打尽全国各城市婚博会信息 崤孞尛
i 1 i 1 n n
( yn bxn a) 2 .
求出当 Q 取最小值时的 a,b 的值,就求出了回归方程. 一、先证明两个在变形中用到的公式 公式(一) ( xi x)2 xi2 nx ,其中 x
2 i 1 i 1 n n
x1 x2 n
xn
nx y nx
2
x
i 1
用公式(一) 、 (二)变形得
2 i
三、总结规律 上述推导过程是围绕着待定参数 a,b 进行的,只含有 xi,yi 的部分是常数或系数,用到 的方法有:①配方法,有两次配方,分别是 a 的二次三项式和 b 的二次三项式;②变形时, 用到公式(一) 、 (二)和整体思想;③用平方的非负性求最小值.④实际计算时,通常是分
回归直线方程的推导
设 x 与 y 是具有线性相关关系的两个变量,且相应于样本的一组观测值的 n 个点的坐标 分别是: ( x1,y1 ), ( x2,y2 ), ( x3,y3 ), , ( xn,yn ) ,下面给出回归方程的推导. 设所求的回归方程为 yi bxi a ,(i 1 显然, 上面的各个偏差的符号有正、 , 2, 3, ,n) . 有负,如果将他们相加会相互抵消一部分,因此他们的和不能代表 n 个点与回归直线的整体 上的接近程度,因而采用 n 个偏差的平方和 Q 来表示 n 个点与相应直线(回归直线)在整体 上的接近程度, 即 Q ( yi yi )2 ( yi bxi a)2 ( y2 bx2 a)2 ( y3 bx3 a) 2
回归直线方程

课本P90习题3.1 V1
3.1回归分析的基本思想 及其初步应用(3)
建立回归模型的基本步骤 1)确定解释变量和预报变量; 2)画出散点图; 3)确定回归方程类型; 4)求出回归方程; 5)利用相关指数或残差进行分析.
问题:一只红铃虫的产卵数y与温度x有关,现收 集了7组观测数据,试建立y与x之间的回归方程
相关程度越小.
r∈[-1,-0.75]--负相关很强; r∈[0.75,1]—正相关很强; r∈[-0.75,-0.25]--负相关一般; r∈[0.25, 0.75]—正相关一般; r∈[-0.25, 0.25]--相关性较弱;
例题1 从某大学中随机选出8名女大学生,其身 高和体重数据如下表:
编号 1
160 170 180
它的均值E(e)= 0,方差D(e)=σ2 > 0
探究:在线性回归模型中,e是一个不可观测 的量,那么应该怎样研究随机误差?如何衡量 预报的精度?
为了衡量预报的精度,需要估计的σ2值?
n
Q( , ) ( yi xi )2 i 1
随机误差ei yi bxi a(i 1, 2,....n) 其估计值为: eˆi yi yˆi yi bˆxi aˆ eˆi称为相应点(xi,yi )的残差
果这种分析工作称为残差分析
了解残差图的制作及作用。P85 坐标纵轴为残差变量,横轴可以有不同的选择; 若模型选择的正确,残差图中的点应该分布在以横轴为 心的带形区域; 对于远离横轴的点,要特别注意。身高异与常体 重
点
残 差 图
• 错误数据 • 模型问题
总偏差平方和,残差平方和,回归平方和三者的 含义与它们间的关系:
yˆ = 0.849x - 85.172
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
回归直线方程
若:在一组具有相关关系的变量的数据(x与Y)间,通过散点图我们可观察出所有数据点都分布在一条直线附近,这样的直线可以画出许多条,而我们希望其中的一条最好地反映x与Y之间的关系,即我们要找出一条直线,使这条直线“最贴近”已知的数据点,记此直线方程为(如右所示,记为①式)这里在y的上方加记号“^”,是为了区分Y的实际值y,表示当x取值xi=1,2,……,6)时,Y相应的观察值为yi,而直线上对应于xi的纵坐标是①式叫做Y对x的回归直线方程,相应的直线叫做回归直线,b叫做回归系数。
要确定回归直线方程①,只要确定a与回归系数b。
回归直线的求法。
最小二乘法:总离差不能用n个离差之和来表示,通常是用离差的平方和,即作为总离差,并使之达到最小,这样回归直线就是所有直线中除去最小值的那一条,这种使“离差平方和最小”的方法,叫做最小二乘法用最小二乘法求回归直线方程中的a,b有下面的公式:
回归直线方程求a b公式。
