一半径为的均匀带电圆环

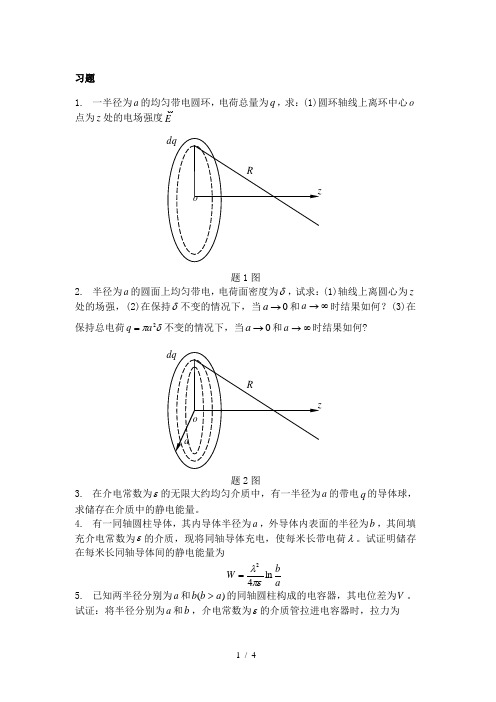
习题1. 一半径为a 的均匀带电圆环，电荷总量为q ，求：(1)圆环轴线上离环中心o点为z 处的电场强度E题1图解：(1)如图所示，环上任一点电荷元dq 在P 点产生的场强为204R dqE d πε=由对称性可知，整个圆环在P 点产生的场强只有z 分量，即()23220204cos za zdq RzR r dq E d E d z +===πεπεθ积分得到()()()()2322023220232202322042444za qza za z dlza z dq za z E lz +=+=+=+=⎰⎰πεππελλπεπε2. 半径为a 的圆面上均匀带电，电荷面密度为δ，试求：(1)轴线上离圆心为z 处的场强，(2)在保持δ不变的情况下，当0→a 和∞→a 时结果如何？(3)在保持总电荷δπ2a q =不变的情况下，当0→a 和∞→a 时结果如何?题2图解：(1)如图所示，在圆环上任取一半径为r 的圆环，它所带的电荷量为δπdr dq 2=由习题2．1的结果可知该回环在轴线上P 点处的场强为()()23222322024zrrdrz zr zdq E d +=+=εδπε则整个均匀带电圆面在轴线上P 点出产生的场强为()⎪⎪⎭⎫⎝⎛+-=+=⎰22002322122z a z zrrdrz E az εδεδ （2）若δ不变，当0→a 时，则0)11(20=-=εδz E ； 当∞→a ，则002)01(2εδεδ=-=z E (3)若保持δπ2a q =不变，当0→a 时，此带电圆面可视为一点电荷。

则204z q E z πε=。

当∞→a 时，0→δ，则0=z E。

3. 在介电常数为ε的无限大约均匀介质中，有一半径为a 的带电q 的导体球，求储存在介质中的静电能量。

解：导体在空间各点产生的电场为)()0(02a r rr qE a r E r w >=<<=πε故静电能量为a q dr r r q dVE dV E D W VV πεππεεε84421212122222=⎪⎭⎫ ⎝⎛==•=⎰⎰⎰∞4. 有一同轴圆柱导体，其内导体半径为a ，外导体内表面的半径为b ，其间填充介电常数为ε的介质，现将同轴导体充电，使每米长带电荷λ。

试证明储存在每米长同轴导体间的静电能量为ab W ln 42πελ=证：在内外导体间介质中的电场为)(2b r a rE <<=πελ沿同轴线单位长度的储能为ab dr r e dVE edV D E W ln 422222122πελππελ=⎪⎭⎫ ⎝⎛==•=⎰⎰⎰ 5. 已知两半径分别为a 和)(a b b >的同轴圆柱构成的电容器，其电位差为V 。

试证：将半径分别为a 和b ，介电常数为ε的介质管拉进电容器时，拉力为ab V F ln )(20εεπ-=证：内外导体间的电场为ab r V E r ln=插入介质管后的能量变化为ab zV dz dr r a b rB dV E W z b a v ln )(ln 2)(21)(21200222020εεππεεεε-=⎪⎭⎫ ⎝⎛-=-=⎰⎰⎰ 式中z 为介质管拉进电容器内的长度。

故拉力为ab V z W F V ln )(20εεπ-=∂∂=不变6. 求均匀极化介质圆球的极化电荷分布。

++--题6图 均匀极化介质解：圆球表面上存在极化电荷，在半个球面上为正电荷，另半个球面上为负电荷，分布不均匀。

以平行于P的直径为z 轴，如题6图所示，则与z 轴夹角为θ的地方，极化电荷面密度为θσcos P P n =='7. 真空中一半径为R 的圆球空间内，分布有体密度为ρ的电荷，ρ为常量。

试求静电能量。

解：应用高斯通量定理，得出电场强度)(3)(32030R r r R E R r r E r r >=<=ερερ故52024205202202222154494922R dr r r R dr r r dV E W R RVe ρεππερπερεε=⎥⎦⎤⎢⎣⎡+==⎰⎰⎰⎰⎰∞8. 今有一球形薄膜导体，半径为R ，其上带电荷q 。

求薄膜单位面积上所受膨胀力。

解：孤立导体球电容R Rq qqC 0044/πεπεϕ===采用球坐标，原点置于球心，选g 为R ，则20222222284222R qC q R C C q F g C C q F R g πεπε==∂∂=∂∂=R F 的方向与R 增大的方向相同，为膨胀力。

单位面积上的力为DE ER q R F F S S R R 21212)4(240222022====='ρερπεπ该膨胀力是由于电荷同号相斥面产生的。

9. 在半径为a 的球体内，均匀分布着电荷，总电荷量为q ，求各点的电场E，并计算电场E的散度和旋度。

题9图 电荷的球体分布解：由于电荷分布的球对称性，电场E只有沿r 方向的分量，并且在与带电球同心的球面上电场E的值处处相同。

因此，在a r >的区域内，可取半径为r 的同心球面为高斯面，如题9图所示。

高斯面上各点的电场E 与面元dS 的方向相同。

于是，由高斯定理，有024επq E r dS E dS E r S r ===•⎰⎰ 所以204r q E r πε=矢量形式为)(430a r rqr E >=πε在a r <的区域内，同样可作出半径为r 的球面为高斯面。

于是，有24επq E r dS E S d E r S r '===•⎰⎰ 式中q '为高斯面内的电荷，其值为(a) （b ）333333/43434aqr a q r r q =⎪⎭⎫ ⎝⎛=='ππρπ 所以)(443030a r a r q E aqr E r <==πεπε或当a r =时，由上面的推导结果得出相同的E 值为204a q πε；当a r >时，即超过这个表面时电场是连续的。

关于上面的结果示于题9图（b ）上。

下面计算电场的散度和旋度。

在a r >的区域内，有4043030=⎪⎭⎫⎝⎛⨯∇=⨯∇=⎪⎭⎫⎝⎛•∇=•∇r r q E r r q E πεπε 而在a r <的区域内，有44340300=⨯∇=⨯∇==•∇=•∇r q E a q r q Eπεερπεπε10. 已知电场强度如下式所示，求体电荷密度)(ερ电容率e 。

),(0033为常数E a a E ae E r <≤=ρρ解：因为E D D e ερ==•∇，所以320334)(E aE a E e ερρρρρεερ=⎪⎪⎭⎫⎝⎛∂∂=•∇=11. 真空中有一电荷线密度为l ρ的圆环形均匀带电线，其半径为a 。

试求圆环轴线上任一场点P 处的电场强度。

题11图解：采用圆柱坐标系，取圆环中心为原点，并使圆环的轴线与z 轴重合，如图所示。

在圆环上任取一线电荷元，即''ϕρρad dl dQ l l ==，它在场点P 处所产生的场强元为R e R dQ E d204πε=其中：22a z R +=。

由于电荷分布对称，场点P 处场强元的径向r 分量r dE 相互抵消，故只需计算场强元的z 分量，于是()'44cos 2322020ϕπερπεαd a z az R zR dQ dE dE l z +=== 在求整个带电圆环在P 点所产生的场强时，应将场点坐标暂时视为常量，而只对源点坐标积分，但积分后场强仍是场点坐标的函数，这和数学中的累积分（偏积分）类似，即()()2322020232202'4az azd az azE l l z +=+=⎰ερϕπερπ故()z l e a z azE 232202+=ερ12. 半径为R 的空心球金属薄壳内，有一点电荷q ，离球小距离为b ，R b <，如图所示。

巳知球壳为个性，即壳内外表面总电荷为零。

求壳内外的电场。

ε0+题12图（a ）解：点电荷q 在壳内表面产生感应电荷为q q -=1金属球壳既然为中性，必须壳外表面有感应电荷q q +=2。

由于金属中电场强度为零，即无电力线穿过金属，故该壳有屏蔽作用。

壳内电场强度仅由点电荷q 和感应电荷1q 决定，而与感应电荷2q 无关。

壳外电场强度仅由感应电荷2q 决定，而与点电荷q 和感应电荷1q 无关。

计算壳内电场强度时，采用镜象法将1q 的作用用镜象电荷t q 1来代替，如图所示。

t q 1距球心为d ，b R d 2=，即q 与t q 1的位置对球心互为反演关系。

t q 1的量值为q bR q R d q t -=-=1 根据q 和t q 1即可计算出壳内电场强度。

1t题12图（b ）计算壳外电场强度时，可视力q 和t q 1皆不存在。

由于2q 为均匀分布，将2q 集中于球心是等效的。

13. 真空中，电荷按体密度⎪⎪⎭⎫⎝⎛-=2201a r ρρ分布在半径为a 的球形区域内，其中0ρ为常数。

试计算球内、外的电场强度和电位函数。

解：由于电荷分布具有球对称分布，电场也应具有球对称分布，因此，E沿半径方向，且只是r 的函数。

作一半径为r 的同心球面S ，应用高斯定律的积分形式可得。

当a r >时02224επQ E r S d E S ==•⎰ 而Q 为球面S 包围的总电荷，即球形区域内的总电荷。

()30024200215844a dr a r r dr r r Q aaπρπρπρ=⎪⎪⎭⎫ ⎝⎛-==⎰⎰因此20302152raa E rερ = 当a r <时()⎪⎪⎭⎫⎝⎛-===•⎰⎰25300200121534414a r r dr r r E r S d E rSεπρπρεπ ⎪⎪⎭⎫⎝⎛-=2300133a r r a E r ερ 取无穷远的电位为零，得球外的电位分布为()rar d E r 030022152ερφ=•=⎰∞球面上()a r =的电位为20152ερφa S =当a r <时()⎪⎪⎭⎫ ⎝⎛+-=•+=⎰2422001110322a r r a r d E r arS ερφφ 由于()30158a Q πρ=，在球外，电场和电位还可以写成20241r Q a E rπε =rQ 0241πεφ=14. 已知空间某一区域内的电位分布为()()z ch y ax 32sin 2=φ，求此空间内的体电荷分布及电场强度E。

解：先求电荷体密度ρ把已知电位分布()()z ch y ax 32sin 2=φ，代入泊松方程，得()()()02232sin 52ερφ-=+=∇z ch y a x ()()()z ch y a x 32sin 2520+-=ερ再求电场强度E由z z y y x x z y x E e E e E e z e y e xe E ++=⎥⎦⎤⎢⎣⎡∂∂+∂∂+∂∂-=-∇=φφφφ ()()z ch y ax x E x 32sin 2••-=∂∂-=φ()()z ch y ax y E y 32cos 22••-=∂∂-=φ()()z sh y ax zE z 32sin 32••-=∂∂-=φ15. 将介电常数为ε、内外半径分别为a 和b 的介质球壳从无限远处移至真空中点电荷Q 的电场中，并设点电荷Q 位于坐标原点处。