(精编资料推荐)三种常见坐标系中梯度散度旋度的计算公式
圆柱坐标系的梯度散度旋度公式
圆柱坐标系的梯度散度旋度公式在数学和物理学中，圆柱坐标系是一种常用的坐标系，特别适用于具有圆柱对称性的问题。
在三维空间中，圆柱坐标系由径向、方位角和高度三个坐标轴组成。
在圆柱坐标系下，梯度、散度和旋度是描述矢量场性质的重要概念。
下面我们将探讨在圆柱坐标系下梯度、散度和旋度的计算公式。
圆柱坐标系下的梯度在圆柱坐标系下，一个标量函数$$ f(\\rho, \\phi, z) $$的梯度可以用下式表示：$$ \ abla f = \\frac{\\partial f}{\\partial \\rho} \\hat{\\rho} + \\frac{1}{\\rho} \\frac{\\partial f}{\\partial \\phi} \\hat{\\phi} + \\frac{\\partial f}{\\partial z}\\hat{z} $$其中$$ \\hat{\\rho} $$、$$ \\hat{\\phi} $$和$$ \\hat{z} $$分别是径向、方位角和高度方向的单位矢量。
圆柱坐标系下的散度对于一个矢量场$$ \\mathbf{F}(\\rho, \\phi, z) = F_\\rho \\hat{\\rho} + F_\\phi \\hat{\\phi} + F_z \\hat{z} $$，在圆柱坐标系下的散度计算公式为：$$ \ abla \\cdot \\mathbf{F} = \\frac{1}{\\rho} \\frac{\\partial}{\\partial\\rho}(\\rho F_\\rho) + \\frac{1}{\\rho} \\frac{\\partial F_\\phi}{\\partial \\phi} + \\frac{\\partial F_z}{\\partial z} $$圆柱坐标系下的旋度对于一个矢量场$$ \\mathbf{F}(\\rho, \\phi, z) $$，在圆柱坐标系下的旋度计算公式为：$$ \ abla \\times \\mathbf{F} = \\left( \\frac{1}{\\rho} \\frac{\\partialF_z}{\\partial \\phi} - \\frac{\\partial F_\\phi}{\\partial z} \\right) \\hat{\\rho} + \\left( \\frac{\\partial F_\\rho}{\\partial z} - \\frac{\\partial F_z}{\\partial \\rho} \\right) \\hat{\\phi} + \\frac{1}{\\rho} \\left( \\frac{\\partial}{\\partial\\rho}(\\rho F_\\phi) - \\frac{\\partial F_\\rho}{\\partial \\phi} \\right) \\hat{z} $$这三个公式是描述在圆柱坐标系下梯度、散度和旋度的基本公式，它们在解决圆柱对称性问题时具有重要的应用价值。
梯度散度和旋度——定义及公式
梯度散度和旋度——定义及公式梯度、散度和旋度是矢量场的重要属性，它们帮助我们理解和描述矢量场的变化特征。
梯度表示了矢量场的变化率和方向，散度表示了矢量场的流出或流入程度，旋度表示了矢量场的循环或旋转程度。
在物理学、工程学和应用数学等领域，梯度、散度和旋度被广泛应用于描述流体力学、电磁场和温度分布等问题。
首先，让我们来看看梯度的定义和公式。
梯度表示了矢量场在一个点上的最大变化率和该变化的方向。
对于一个标量场（只有大小没有方向的场），梯度是一个矢量场。
设f(x,y,z)是一个三维空间中的标量场，梯度∇f(x,y,z)可以表示为：∇f(x,y,z)=(∂f/∂x,∂f/∂y,∂f/∂z)其中，∂f/∂x、∂f/∂y和∂f/∂z分别表示f对x、y和z的偏导数。
梯度的大小表示了函数在该点上变化最快的方向。
接下来，我们来看看散度的定义和公式。
散度表示了矢量场的流出或流入程度。
对于一个三维矢量场F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))，它的散度∇·F可以表示为：∇·F=∂P/∂x+∂Q/∂y+∂R/∂z其中，∂P/∂x、∂Q/∂y和∂R/∂z分别表示F的各个分量对x、y和z的偏导数。
散度的值正表示流出，负表示流入。
最后，我们来看看旋度的定义和公式。
旋度表示了矢量场的循环或旋转程度。
对于一个三维矢量场F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))，它的旋度∇×F可以表示为：∇×F=(∂R/∂y-∂Q/∂z,∂P/∂z-∂R/∂x,∂Q/∂x-∂P/∂y)其中，∂R/∂y-∂Q/∂z、∂P/∂z-∂R/∂x、∂Q/∂x-∂P/∂y分别表示F的各个分量对x、y和z的偏导数之差。
旋度的大小表示了场的循环或旋转的强度。
梯度、散度和旋度提供了一种描述矢量场的数学工具，帮助我们分析矢量场的性质和行为。
通过计算这些属性，我们可以得到关于矢量场的重要信息，如流体的速度分布、电磁场的演化和温度场的变化。
散度和梯度的计算公式
散度和梯度的计算公式散度和梯度是微积分中的重要概念，它们在物理、工程和计算机图像处理等领域中有着广泛的应用。
本文将为您介绍散度和梯度的计算公式及其应用。
一、散度散度是一个向量场的量化描述，表示了向量场在某一点上的发散程度。
它可以理解为向量场的源和汇的总和。
在三维空间中，散度的计算公式为：div(F) = ∂Fx/∂x + ∂Fy/∂y + ∂Fz/∂z其中，F = (Fx, Fy, Fz) 是一个向量场，∂Fx/∂x、∂Fy/∂y 和∂Fz/∂z 分别表示 F 关于 x、y 和 z 的偏导数。
散度可以用来描述物质的流动情况。
当散度为正时，表示物质从该点流出；当散度为负时，表示物质流向该点；当散度为零时，表示物质在该点没有流动。
例如，在流体力学中，散度可以用来描述流体的流量分布情况。
二、梯度梯度是一个标量场的变化率，表示了标量场在某一点上的最大变化方向。
它可以理解为标量场的斜率或者是变化速度最快的方向。
在三维空间中，梯度的计算公式为：grad(f) = (∂f/∂x, ∂f/∂y, ∂f/∂z)其中，f 是一个标量场，∂f/∂x、∂f/∂y 和∂f/∂z 分别表示 f 关于 x、y 和 z 的偏导数。
梯度可以用来描述标量场的变化情况。
在物理学和工程学中，梯度可以用来描述电场、温度场、压力场等的变化情况。
例如，在地理学中，梯度可以用来描述地形的陡峭程度。
三、散度和梯度的应用散度和梯度在物理、工程和计算机图像处理等领域中有着广泛的应用。
在物理学中，散度可以用来描述电场的散发和电荷的分布情况。
梯度可以用来描述温度场的变化和热量的传导情况。
在工程学中，散度可以用来描述流体力学中的流速分布情况和质量守恒定律。
梯度可以用来描述压力场的变化和力的分布情况。
在计算机图像处理中，散度可以用来描述图像的纹理和边缘信息。
梯度可以用来进行图像的边缘检测和特征提取。
总结：散度和梯度是微积分中的重要概念，它们在物理、工程和计算机图像处理等领域中有着广泛的应用。
梯度、发散和旋度——定义及公式
梯度、发散和旋度——定义及公式梯度、发散和旋度是矢量场分析中常用的概念，它们用于描述矢量场的特性和变化。
以下是它们的定义及相关公式：1. 梯度（Gradient）梯度表示矢量场在给定点上最大变化的方向和速率。
我们可以将一个标量场（Scalar field）与一个矢量场（Vector field）的梯度进行计算。
梯度的定义：$$\nabla f = \frac{\partial f}{\partial x}\mathbf{i} + \frac{\partialf}{\partial y}\mathbf{j} + \frac{\partial f}{\partial z}\mathbf{k}$$其中，$\nabla$ 表示梯度算子，$f$ 表示标量场，$\mathbf{i}$，$\mathbf{j}$，$\mathbf{k}$ 表示坐标轴的单位向量。
2. 发散（Divergence）发散用于描述矢量场的流出和流入情况，它表示在给定点的矢量场流量的变化率。
发散的定义：$$\nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} +\frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}$$其中，$\nabla$ 表示梯度算子，$\cdot$ 表示点乘，$\mathbf{F}$ 表示矢量场。
3. 旋度（Curl）旋度用于描述矢量场的旋转和循环性质，它表示在给定点的矢量场环量的变化率。
旋度的定义：$$\nabla \times \mathbf{F} = \left(\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}\right)\mathbf{i} + \left(\frac{\partialF_x}{\partial z} - \frac{\partial F_z}{\partial x}\right)\mathbf{j} +\left(\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partialy}\right)\mathbf{k}$$其中，$\nabla$ 表示梯度算子，$\times$ 表示叉乘，$\mathbf{F}$ 表示矢量场。
矢量运算(梯度、散度、旋度)与拉普拉斯算符公式整理
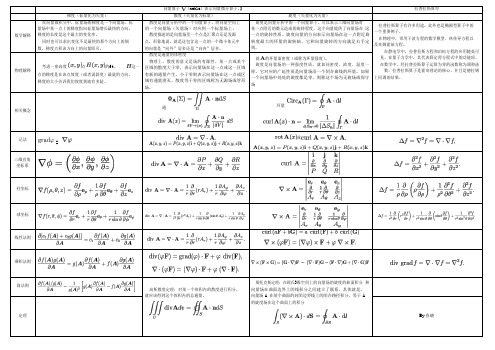
向量算子 （nabla ）表示向量微分算子。
】拉普拉斯算符梯度（标量化为矢量）散度（矢量化为标量）旋度（矢量化为矢量）数学解释在向量微积分中，标量场的梯度是一个向量场。
标量场中某一点上的梯度指向标量场增长最快的方向，梯度的长度是这个最大的变化率。
同时也可以求出变化不是最快的那个方向上的倒数，梯度点积该方向上的向量即可。
散度是向量分析中的一个向量算子，将向量空间上的一个向量场（矢量场）对应到一个标量场上。
散度描述的是向量场里一个点是汇聚点还是发源 点，形象地说，就是这包含这一点的一个微小体元中 的向量是“向外”居多还是“向内”居多。
旋度是向量分析中的一个向量算子，可以表示三维向量场对 某一点附近的微元造成的旋转程度。
这个向量提供了向量场在 这一点的旋转性质。
旋度向量的方向表示向量场在这一点附近旋转度最大的环量的旋转轴，它和向量旋转的方向满足右手定则。
拉普拉斯算子有许多用途，此外也是椭圆型算子中的 一个重要例子。
在物理中，常用于波方程的数学模型、热传导方程以 及亥姆霍兹方程。
在静电学中，拉普拉斯方程和泊松方程的应用随处可见。
在量子力学中，其代表薛定谔方程式中的动能项。
在数学中，经拉普拉斯算子运算为零的函数称为调和函 数；拉普拉斯算子是霍奇理论的核心，并且是德拉姆 上同调的结果。
物理解释考虑一座高度 点 的ft 。
这一 点的梯度是在该点坡度（或者说斜度）最陡的方向。
梯度的大小告诉我们坡度到底有多陡。
散度是通量的体密度物理上，散度的意义是场的有源性。
某一点或某个区域的散度大于零，表示向量场在这一点或这一区域有新的通量产生，小于零则表示向量场在这一点或区域有通量湮灭。
散度等于零的区域称为无源场或管形场。
就 的环量面密度（或称为环量强度）。
旋度是向量场的一种强度性质，就如同密度、浓度、温度一 样，它对应的广延性质是向量场沿一个闭合曲线的环量。
如果一个向量场中处处的旋度都是零，则称这个场为无旋场或保守场相关概念通环量记法=或三维直角坐标系柱坐标球坐标线性法则乘积法则商法则高斯散度定理：对某一个体积内的散度进行积分， 就应该得到这个体积内的总通量。
1-3梯度-散度-旋度
∂ ∂φ
如何记忆？
d ⇒∇ dl
笛卡儿坐标系中微分长度 G G
G
G
dl = axdx + aydy + azdz
∇
=
G ax
∂ ∂x
+
G ay
∂ ∂y
+
G az
∂ ∂z
dU ⇒ ∇ dl
柱面坐标系中微分长度
G dl
=
G ar
dr
+
G aφ
(
r
⋅
dφ
)
+
G az
dz
∇
=
G ar
∂ ∂r
+
G aφ
1 r
v∫
GG A • dS
=
∫ (∇ •
AG) dV
=
∫ 源dV
S
V
V
Example: Net positive flux
v∫
G A
•
G dS
>
0
S
Streamlines are directed away from the origin
4
矢量的“环量”
矢量的环量：该矢量沿闭合路径的标量线积分
G
GG
∫ 矢量 A沿G闭合路径 C的环量＝ A •dl
G ∇×B
=
G∂ ax(∂y
Bz
−
∂ ∂z
By)
G +ay
∂ ( ∂z
Bx
−?Bz
)
+aGz(∂∂x
By
−?Bx)
∇
=
G ax
∂ ∂x
+
G ay
梯度旋度散度
梯度、散度和旋度梯度、散度和旋度是矢量分析里的重要概念。
之所以是“分析”，因为三者是三种偏导数计算形式。
这里假设读者已经了解了三者的定义。
它们的符号分别记作如下：从符号中可以获得这样的信息：①求梯度是针对一个标量函数，求梯度的结果是得到一个矢量函数。
这里φ称为势函数；②求散度则是针对一个矢量函数，得到的结果是一个标量函数，跟求梯度是反一下的；③求旋度是针对一个矢量函数，得到的还是一个矢量函数。
这三种关系可以从定义式很直观地看出，因此可以求“梯度的散度”、“散度的梯度”、“梯度的旋度”、“旋度的散度”和“旋度的旋度”，只有旋度可以连续作用两次，而一维波动方程具有如下的形式(1)其中a为一实数，于是可以设想，对于一个矢量函数来说，要求得它的波动方程，只有求它的“旋度的旋度”才能得到。
下面先给出梯度、散度和旋度的计算式：(2)(3)(4)旋度公式略显复杂。
这里结合麦克斯韦电磁场理论，来讨论前面几个“X度的X 度”。
I.梯度的散度：根据麦克斯韦方程有：而(5)则电势的梯度的散度为这是一个三维空间上的标量函数，常记作(6)称为泊松方程，而算符▽2称为拉普拉斯算符。
事实上因为定义所以有当然，这只是一种记忆方式。
当空间内无电荷分布时，即ρ=0，则称为拉普拉斯方程当我们仅需要考虑一维情况时，比如电荷均匀分布的无限大平行板电容器之间（不包含极板）的电场，我们知道该电场只有一个指向，场强处处相等，于是该电场满足一维拉普拉斯方程，即这就是说如果那边平行板电容器的负极板接地，则板间一点处的电压与该点距负极板的距离呈线性关系。
II.散度的梯度：散度的梯度，从上面的公式中可以看到结果会比较复杂，但是它的物理意义却是很明确的，因为从麦克斯韦方程可以看出空间某点处电场的散度是该点处的电荷密度，那么再求梯度就是空间中电荷密度的梯度。
这就好比说清水中滴入一滴红墨水，起初水面红色浓度最高，杯底浓度最低，这样水面与杯底形成一个浓度梯度，红墨水由水面向杯底扩散，最后均匀。
梯度、散度和旋度——定义及公式
梯度、散度和旋度——定义及公式1 哈密顿算子（Hamiltion Operator ）哈密顿算子本身没有含义，只有作用于后面的量才有实际意义；它是一个微分算子，符号为∇。
三维坐标系下，有=i j k x y z∂∂∂∇++∂∂∂ 或者 (,,)x y z ∂∂∂∇=∂∂∂ 其中,,i j k 分别为xyz 方向上的单位矢量。
2 梯度（Gradient ） 2.1 梯度的定义梯度是哈密顿算子直接作用于函数f 的结果（f 可以是标量和向量）。
(,,)f f f f f f grad f f i j k x y z x y z ∂∂∂∂∂∂=∇=++=∂∂∂∂∂∂ 标量场的梯度是向量，标量场中某一点的梯度指向标量场增长最快的地方，梯度的长度是最大变化率。
2.2 梯度的性质∇c=0∇(RS)= ∇R+∇S21()(),0R S R R S S S S∇=∇-∇≠ [()]()f S f S S '∇=∇其中，C 为常数，R 、S 为两个标量场，f 为一连续可微函数。
3 散度（Divergence ）散度是哈密顿算子与矢量函数f 点积的结果，是一个标量。
设矢量函数=(,,)x y z x y z f f i f j f k f f f =++则散度表示为： (,,)(,,)y x z x y z f f f div f f f f f x y z x y z∂∂∂∂∂∂=∇==++∂∂∂∂∂∂ 散度是描述空气从周围汇合到某一处或从某一处散开来程度的量。
它可用于表征空间各点矢量场发散的强弱程度，物理上，散度的意义是场的有源性。
当0div f >，该点有散发通量的正源（发散源）；当0div f <，该点有吸收通量的负源（洞或汇）； 当=0div f ，该点无源。
4 旋度（Curl, Rotation ）旋度是哈密顿算子与矢量函数f 叉积的结果，是一个矢量，设矢量函数=(,,)x y z x y z f f i f j f k f f f =++则旋度：=rot ()()()y y x x z z x y zij k f f f f f f curl f f f i j k xy z y zz x x y f f f ∂∂∂∂∂∂∂∂∂=∇⨯==-+-+-∂∂∂∂∂∂∂∂∂ 旋度是矢量分析中的一个矢量算子，可以表示三维矢量场对某一点附近的微元造成的旋转程度。
实用文档之三种常见坐标系中梯度散度旋度的计算公式
实用文档之三种常见坐标系中梯度散度旋度的计算公式在物理、数学和工程学等领域，常常会遇到需要计算梯度、散度和旋度的问题。
梯度、散度和旋度是描述矢量变量随空间坐标变化的变化率的重要工具。
在实用文档中，对于三种常见的坐标系下的梯度、散度和旋度计算公式进行详细说明，使读者能够理解和应用这些公式。
一、笛卡尔坐标系笛卡尔坐标系是三维空间中经常使用的坐标系。
在笛卡尔坐标系下，梯度、散度和旋度的计算公式如下：1.梯度：梯度用于描述标量函数在空间各个方向上的变化率。
对于标量函数f(x,y,z)，其梯度可表示为：∇f=(∂f/∂x)i+(∂f/∂y)j+(∂f/∂z)k其中，∂f/∂x、∂f/∂y和∂f/∂z分别表示f对x、y和z的偏导数，i、j 和k分别是笛卡尔坐标系的基底单位矢量。
2.散度：散度描述矢量场在其中一点的流入或流出情况。
对于矢量场F(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k，其散度可表示为：∇·F=∂P/∂x+∂Q/∂y+∂R/∂z其中，∂P/∂x、∂Q/∂y和∂R/∂z分别表示F的每个分量对应坐标的偏导数。
3.旋度：旋度描述矢量场的旋转情况。
对于矢量场F(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k，其旋度可表示为：∇×F=(∂R/∂y-∂Q/∂z)i+(∂P/∂z-∂R/∂x)j+(∂Q/∂x-∂P/∂y)k其中，∂P/∂x、∂Q/∂y和∂R/∂z分别表示F的每个分量对应坐标的偏导数。
二、柱坐标系柱坐标系适用于具有圆柱对称性的问题，在极坐标的基础上，引入了z轴方向的坐标。
在柱坐标系下，梯度、散度和旋度的计算公式如下：1.梯度：梯度的计算公式同样适用于柱坐标系，∇f的表达式保持不变。
2.散度：散度的计算公式在柱坐标系下为：∇·F=(1/ρ)∂(ρP)/∂ρ+(1/ρ)∂Q/∂φ+∂R/∂z其中，P、Q和R为矢量场F的每个分量。
梯度、散度和旋转速度——定义及公式
梯度、散度和旋转速度——定义及公式梯度、散度和旋转速度是在向量微积分中经常出现的概念。
它们在研究物理、计算机图形学以及其他领域中都有广泛的应用。
以下是对这些概念的定义和相应的公式。
梯度：梯度表示向量场在某一点上的变化率方向和大小。
对于二维向量场而言，梯度是一个二维向量，可以表示为∇f=(∂f/∂x, ∂f/∂y)，其中f为标量函数，∂f/∂x和∂f/∂y分别表示f关于x和y的偏导数。
散度：散度表示向量场在某一点上的流入流出情况。
对于二维向量场而言，散度是一个标量，可以表示为div F=∇·F=∂F1/∂x + ∂F2/∂y，其中F=(F1, F2)为二维向量场，∂F1/∂x和∂F2/∂y分别表示F1和F2关于x和y的偏导数。
旋转速度：旋转速度表示向量场在某一点上的旋转情况。
对于二维向量场而言，旋转速度是一个标量，可以表示为curl F=∇×F=∂F2/∂x -∂F1/∂y，其中F=(F1, F2)为二维向量场，∂F1/∂x和∂F2/∂y分别表示F1和F2关于x和y的偏导数。
在三维空间中，梯度、散度和旋转速度的定义和公式与二维类似，只是涉及到更多的坐标和偏导数。
这些概念和公式对于研究向量场的性质和行为非常重要，能够帮助我们理解向量场的变化和流动规律。
在实际应用中，通过计算梯度、散度和旋转速度，我们可以获得有关向量场的关键信息，从而进行更深入的分析和建模。
总结：- 梯度表示向量场在某一点上的变化率方向和大小，公式为∇f=(∂f/∂x, ∂f/∂y)。
- 散度表示向量场在某一点上的流入流出情况，公式为divF=∇·F=∂F1/∂x + ∂F2/∂y。
- 旋转速度表示向量场在某一点上的旋转情况，公式为curlF=∇×F=∂F2/∂x - ∂F1/∂y。
希望这份文档能够帮助你更好地了解梯度、散度和旋转速度的定义及其公式。
如有任何疑问，请随时向我提问。
旋度和散度计算公式
旋度和散度计算公式旋度和散度是向量分析中的两个重要概念，它们可以帮助我们更好地理解和描述物理现象。
本文将介绍旋度和散度的计算公式及其应用。
一、旋度旋度是一个向量场的旋转程度，它描述了向量场在某一点的旋转强度和旋转方向。
旋度的计算公式如下：旋度 = ∇ × F其中，∇表示向量微分算子，F表示向量场。
旋度的结果是一个向量，它的大小表示旋转强度，方向表示旋转方向。
旋度在物理学中有广泛的应用，例如在电磁学中，旋度可以用来描述电场和磁场的相互作用。
在流体力学中，旋度可以用来描述流体的旋转和涡旋。
二、散度散度是一个向量场的发散程度，它描述了向量场在某一点的扩散强度和扩散方向。
散度的计算公式如下：散度 = ∇ · F其中，∇表示向量微分算子，F表示向量场。
散度的结果是一个标量，它的大小表示扩散强度，正负号表示扩散方向。
散度在物理学中也有广泛的应用，例如在流体力学中，散度可以用来描述流体的流量和流速。
在电磁学中，散度可以用来描述电场和磁场的源和汇。
三、应用举例1. 电场和磁场的相互作用在电磁学中，电场和磁场的相互作用可以用旋度来描述。
电场和磁场的旋度分别为：旋度(E) = -∂B/∂t旋度(B) = μ0J + ε0μ0∂E/∂t其中，E表示电场，B表示磁场，J表示电流密度，μ0表示真空磁导率，ε0表示真空电容率。
2. 流体的流量和流速在流体力学中，散度可以用来描述流体的流量和流速。
流体的速度场为：v = (u, v, w)其中，u、v、w分别表示流体在x、y、z方向上的速度分量。
流体的流量为：流量= ∫∫S v· n dS其中，S表示流体的流过的面积，n表示面积法向量。
流体的流速为：流速 = ∇ · v其中，∇表示向量微分算子。
旋度和散度是向量分析中的两个重要概念，它们可以帮助我们更好地理解和描述物理现象。
旋度和散度的计算公式可以应用于各种物理学领域，例如电磁学、流体力学等。
1.2 散度-旋度-梯度
u u( x, y, z) u(r ) C
如同温层，等位面，等高线
a
b
等值面
d c
2
方向导数
如何了解标量场 中某一点的标量 函数U沿某一方 向的变化情况？
b a
等值面
d c
方向导数：标量函数在给定点沿 某一方向对距离的变化率
U l
3
方向导数
z
ez
z
U l
M ( x 0 x , y0 y, z 0 z )
1 1 ( ) 的梯度 R R
z
r
Q ( x , y , z ) R
o
r
P ( x, y, z )
y
x
16
源点与场点
• 源点： • 场点：
( x, y, z) ( x, y, z )
源点 r'
R
场点
r
O
17
例题
1 1 距离矢量 R r r ，求标量场 R 的梯度 ( ) R z Q ( x , y , z )
数学描述：矢量 A 沿某一有向曲面 S 的面积分
A dS A en dS A cos θdS
s s s
通量(Flux)
dS en dS
S
C
有向曲面：开表面， 右螺旋
闭合曲面，外法线
通量：穿过曲面s的矢量线的总数
22
通量的应用
• 判断闭合曲面内源的性质
ey ez 直角坐标系中： ex x y z 1 柱面坐标系中： e e ez z 1 1 球面坐标系中： eR e e R R R sin
梯度散度和旋转速度——定义及公式
梯度散度和旋转速度——定义及公式梯度是标量场的一个向量值函数，它描述了函数在其中一点的变化率和方向。
对于一个标量场 f(x, y, z)，其梯度可以表示为∇f 或grad(f)，其中∇=（∂/∂x，∂/∂y，∂/∂z）是称为向量微分算子的 nabla符号。
梯度的每个分量表示相应方向上的变化率，即变化最快的方向和速率的大小。
梯度的公式可以表示为：∇f=(∂f/∂x，∂f/∂y，∂f/∂z)其中，∂f/∂x，∂f/∂y和∂f/∂z是f对各个坐标的偏导数。
梯度的长度表示函数在其中一点的变化率大小，即梯度的模表示了函数在该点的变化速率。
因此，梯度可以用来描述场的变化方向和速率。
散度是矢量场的一个标量值函数，它描述了矢量场的发散和收敛情况。
对于一个矢量场 F(x, y, z) = (F_x, F_y, F_z)，其散度可以表示为∇·F 或 div(F)。
散度描述了矢量场在其中一点的源头和汇聚情况，即矢量场的流入和流出情况。
散度的公式可以表示为：∇·F=(∂F_x/∂x+∂F_y/∂y+∂F_z/∂z)其中，∂F_x/∂x，∂F_y/∂y和∂F_z/∂z分别是F_x，F_y和F_z对各个坐标的偏导数。
散度的大小表示了场在其中一点的流入和流出速率，正值表示流出速率大于流入速率，负值表示流入速率大于流出速率。
旋转速度是矢量场的一个矢量值函数，它描述了矢量场的旋转和曲率情况。
对于一个矢量场 F(x, y, z) = (F_x, F_y, F_z)，其旋转速度可以表示为∇×F 或 curl(F)。
旋转速度描述了矢量场的环流和涡旋情况，即矢量场围绕其中一点或曲线旋转的程度和方向。
旋转速度的公式可以表示为：∇×F=((∂F_z/∂y-∂F_y/∂z),(∂F_x/∂z-∂F_z/∂x),(∂F_y/∂x-∂F_x/∂y))其中，∂F_z/∂y-∂F_y/∂z，∂F_x/∂z-∂F_z/∂x和∂F_y/∂x-∂F_x/∂y分别是F_x，F_y和F_z对各个坐标的偏导数之差。
三种常见坐标系中梯度散度旋度计算公式
圆柱坐标系中梯度、散度和旋度在圆柱塑标系下*圆1主坐标(rho- theta^ z)与直角坐标(x ＞严h)的变换方程九x = pcos9, y = psinQ, z = z直角坐标的至微分沏dx = cosfidp — psin^dQ. d y = sinfldp + p 匚osBdB dz = dz无穷小距蔼的平方为ds A 2=dx A 2 4-(ly A 2 + dz A 2=dp A 2 亠(pdfl)A 2 + dz A2所以，标jaia 子为hp = 1J h° = pi h z = 1在正交坐标系下的三维徽分算子育 梯度Ci 59 e 2 dtp e 3 dipV<p = ----- + --- -- + -11丄如 h 2aq 2 h 3 9q 3「ji d 厲(Fjhjh^) + -— (Fjhjhj) + 気［0 h 2h 3 lSq 201並f(h 2F 2)d v a十2h 』-加 OhFj-e 3 d a十」-Lr(h 2F 2)-—VXF =11V F =——hjhLdq\d ,. a a r K齐(叫)+西F°+芜(pF»旋產由梯度和散度组合可段容易的得到拉普拉斯算子。
梯度 Sepdpap舸度ddz(pF 』+ 算子 正交半标罠丘梯虔» .5 .1 滩-1 海V<P =&i~ ------- F 切 j 小 + 电 Aj 闵 1 b(A/3 A S tlya7^-( Fj/j2^1)十 7^- ( ^2^1) + (眄力 1免) j a(12 內 n认隠伽斫佥(閱)1 +Dh 、h 血［如血E) -詬伽两V 34> =—-h 、h^h A 也i0 (九2血jI E (&住 h\ &qjd(j2 \ b 如。
梯度、散度、旋度表达式的推导精编版
是一封闭曲线，我们在积分号中加一
小圆圈Ñ ，并称之为矢量 a 沿封闭回
线 L 的环量。
3．旋度
b.旋度
1) 定义：
矢量 a 的矢量旋度rota在 n 方向的投影：
Ñ ar • rd r
r
no
tl iaL s0
m S
注意：1）L 为封闭曲线，即积分为封闭
积分
2）S 的界面为 L
3．旋度
b.旋度
2) 表示形式
2. 散度
b. 散度 2) 表示形式
利用高斯公式把面积分转化为体积分上 式可得：
Ñ (ax ay az )dV
x y z
所以，最后可得
Ñ Ñ lim
ar
•
r dS
lim
( ax x
ay y
az )dV z
ax
ay
az
•
r a
ai
v0 V
v0
V
x y z
xi
2. 散度
b. 散度
3）面积分与体积分的转换
1.梯度
g. 梯度的单位
由定义可知
x
n
(nr ,
xr )
x
所以
x
r i
y
r j
z
r k
上式即为 在直角坐标系中的表示。
h. 性质 • drr d
证明：
•
drr
xi
• dxi
x
dx
y
dy
z
dz
2. 散度
a . 通量 给定一矢量 a(r , t)，在场内取一曲面 S,它可以
是封闭的也可以是不封闭的，在 S 面上取一面积元 素 d S ,在 d S 上任取一点 M,作 S 面在 M 点的法线， 令 n 表示 S 面上法线方向的单位矢量，a 表示 M 点 上的矢量函数的值，则
三度三定理
笛卡儿坐标系中：
柱面坐标系中：
通量：矢量沿某一有向曲面的面积分称为通过的通量，以标量
散度：当闭合面向某点无限收缩时，矢通过该闭合面的通量与该闭合面包围的体积之比的极限称为矢量场在该点
在直角坐标系中
∫∫⋅=⋅∇S
V V d d S A A r r r
的闭合面上
笛卡儿坐标系中：圆柱坐标系中：圆球坐标系中：
矢量场沿一条闭合有向曲线线积分称为矢量场沿该曲线的环量，以环量用来描述矢量场的旋涡特性
表示矢量的旋度，则其方向是使矢量具有最大环量强度的
两个特殊的场分量之和
两个特殊的场分量之和。