机械振动大作业-求初始激励的自由振动响应
哈工大机械振动基础大作业

《机械振动基础》大作业(2015年春季学期)题目基于MATLAB求系统特性姓名学号班级专业机械设计制造及其自动化报告提交日期哈尔滨工业大学报告要求1.请根据课堂布置的2道大作业题,任选其一,拒绝雷同和抄袭;2.报告最好包含自己的心得、体会或意见、建议等;3.报告统一用该模板撰写,字数不少于3000字,上限不限;4.正文格式:小四号字体,行距为倍行距;5.用A4纸单面打印;左侧装订,1枚钉;6.课程报告需同时提交打印稿和电子文档予以存档,电子文档由班长收齐,统一发送至:。
7.此页不得删除。
评语:成绩(15分):教师签名:年月日解多自由度矩阵的认识体会。
二、MATLAB程序图:>> m=[];k1=[];k=[];c=[];c1=[];for i=1:9a=input('输入质量矩阵m:');m(i,i)=a;end ;for j=1:9b=input('输入刚度系数k:');k1(1,j)=b;endfor l=1:8k(l,l)=k1(l)+k1(l+1);k(9,9)=k1(9);k(l+1,l)=-k1(l+1);k(l,l+1)=-k1(l+1);k(9,8)=-k1(9);k(8,9)=-k1(9);end ;syms w;B=k-w^2*m %系统的特征矩阵BY=det(B); %展开行列式W=solve(Y); %求解whlW=length(W);[V,D]=eig(k,m);for I=1:9for J=1:9V(J,I)=V(J,I)/V(5,I);endendVW三 MATLAB结果输入输出:程序输入内容:输入质量矩阵m:1输入质量矩阵m:2输入质量矩阵m:3输入质量矩阵m:4输入质量矩阵m:5输入质量矩阵m:6输入质量矩阵m:7输入质量矩阵m:8输入质量矩阵m:9输入刚度系数k:10输入刚度系数k:11输入刚度系数k:12输入刚度系数k:13输入刚度系数k:14输入刚度系数k:15输入刚度系数k:16输入刚度系数k:17输入刚度系数k:18Matlab 输出界面截图:输出结果:B =[ 21-w^2, -11, 0, 0, 0, 0, 0, 0, 0][ -11, 23-2*w^2, -12, 0, 0, 0, 0, 0, 0][ 0, -12, 25-3*w^2, -13, 0, 0,0, 0, 0][ 0, 0, -13, 27-4*w^2, -14, 0, 0, 0, 0][ 0, 0, 0, -14, 29-5*w^2, -15, 0, 0, 0][ 0, 0, 0, 0, -15, 31-6*w^2, -16, 0, 0][ 0, 0, 0, 0, 0, -16,33-7*w^2, -17, 0][ 0, 0, 0, 0, 0, 0, -17, 35-8*w^2, -18][ 0, 0, 0, 0, 0, 0, 0, -18, 18-9*w^2]V =W =.224079.403四. 心得体会:(一)利用Matlab 进行多自由度振动分析的体会:MATLAB是一种高性能软件平台,是一种面向科学与工程的高级语言,它集数值分析、矩阵运算、信号处理和图形显示于一体,构成了一个功能强大、方便、界面友好的用户环境。
1-《机械振动基础》大作业,基于matlab的多自由度振动讲解

《机械振动基础》大作业(2016年春季学期)题目多自由度振动系统的固有频率和固有阵型姓名学号班级专业报告提交日期哈尔滨工业大学报告要求1.请根据课堂布置的2道大作业题,任选其一,拒绝雷同和抄袭;2.报告最好包含自己的心得、体会或意见、建议等;3.报告统一用该模板撰写,字数不少于3000字,上限不限;4.正文格式:小四号字体,行距为1.25倍行距;5.用A4纸单面打印;左侧装订,1枚钉;6.课程报告需同时提交打印稿和电子文档予以存档,电子文档由班长收齐,统一发送至:liuyingxiang868@。
7.此页不得删除。
评语:成绩(15分):教师签名:年月日基于MATLAB的对多自由度振动系统的固有频率和固有阵型的分析一、利用MATLAB编程求七自由度系统的固有频率和固有振型模型如下图所示系统中各质量为(kg):m1=2;m2=4;m3=5;m4=6;m5=5;m6=4;m7=2;各处弹性系数为(N/m)k1=5;k2=5;k3=5;k4=5;k5=5;k6=5;k7=5;二、实验程序如下:clearclosem1=2;m2=4;m3=5;m4=6;m5=5;m6=4;m7=2;k1=5;k2=5;k3=5;k4=5;k5=5;k6=5;m=[m1,0,0,0,0,0,0;0,m2,0,0,0,0,0;0,0,m3,0,0,0,0;0,0,0,m4,0,0,0;0,0,0,0,m5,0,0;0,0,0,0,0,m6,0;0,0,0,0,0,0,m7];k=[k1+k2,-k2,0,0,0,0,0;-k2,k2+k3,-k3,0,0,0,0;0,-k3,k3+k4,-k4,0,0,0;0,0,-k4,k4+k5,-k5,0,0;0,0,0,-k5,k5+k6,-k6,0;0,0,0,0,-k6,k6+k7,-k7; 0,0,0,0,0,-k7,k7];[V,D]=eig(k,m)for j=1:1:7w(j)=sqrt(D(j,j));for i=1:1:7absV(i,j)=abs(V(i,j)); endendmax=(absV);for j=1:1:7for i=1:1:7V(i,j)=V(i,j)/max(j);endwfigurex=1:7;for a=1:7subplot(3,4,a),plot(x,V(x,a));hold on;grid on;title('振型图');end三、将程序在MATLAB上运行,得到结果如下图(1)多自由度系统的固有频率得到振型图如下图(2)多自由度系统的固有阵型图(2)中分别为本实验条件下,模拟出来小车的振动的阵型图。
机械振动考题及答案
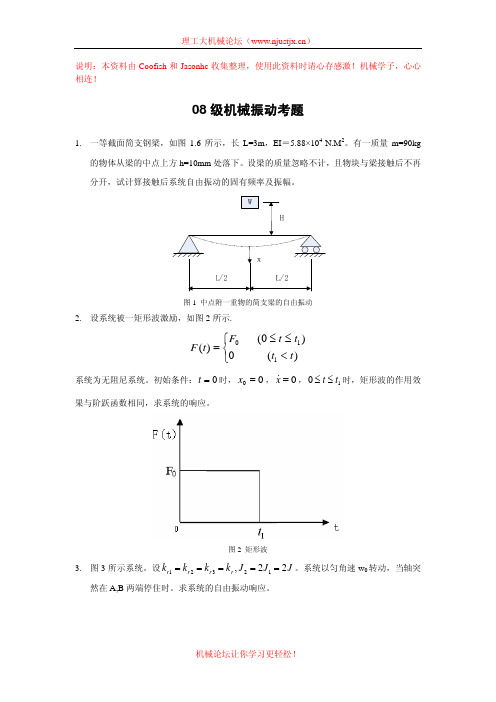
⎛
M
M
M ⎞
T
将 ω2 = ω3 =
k 代回主振型的线性方程组,得: m
M ⎛ ⎜3− m ⎜ ⎜ −1 ⎜ −1 ⎜ ⎜ −1 ⎝
⎞ −1 −1 −1⎟ ⎛ φ1i ⎞ ⎛ 0 ⎞ ⎟ ⎜φ ⎟ ⎜ 0 ⎟ 0 0 0 ⎟ ⎜ 2i ⎟ = ⎜ ⎟ , ( i = 2,3) ⎜φ ⎟ ⎜ 0 ⎟ 0 0 0 ⎟ ⎜ 3i ⎟ ⎜ ⎟ ⎟ φ ⎝ 4i ⎠ ⎝ 0 ⎠ 0 0 0⎟ ⎠
x ( t ) = x ( t1 ) cos ωn ( t − t1 ) +
x ( t1 )+ 0
•
ωn
sin ωn ( t − t1 )
机械论坛让你学习更轻松!
欢迎光临机械论坛(南京理工大学)
=
F0 F 1 − cos ωn t1 ) cos ωn ( t − t1 ) + 0 2 sin ωn t1 sin ωn ( t − t1 ) 2 ( mωn mωn F0 ⎡ cos ωn ( t − t1 ) − cos ωn t ⎤ ⎦ mωn 2 ⎣
⎛M ⎜ T 由于 φ2 M φ3 = ( 0 1 1 −2 ) ⎜ ⎜ ⎜ ⎝ ⎞⎛ 0 ⎞ ⎟⎜ ⎟ m ⎟ ⎜ 1 ⎟ = 3m ≠ 0 ⎟⎜ 0 ⎟ m ⎟⎜ ⎟ m ⎠ ⎝ −1 ⎠
T
T
′ = φ2 + cφ3 = ( 0 1 + c 1 −2 − c ) 强迫 φ3′ 与 φ2 正交。 取 φ3 ⎛M ⎜ T ′ = ( 0 1 1 −2 ) ⎜ 即: φ2 M φ3 ⎜ ⎜ ⎝ ∴ c = −2 ⎞⎛ 0 ⎞ ⎟⎜ ⎟ m ⎟ ⎜ 1 + c ⎟ = 3m ( c + 2 ) = 0 ⎟⎜ 1 ⎟ m ⎟⎜ ⎟ m ⎠ ⎝ −2 − c ⎠
单自由度系统响应编程作业报告

《振动与机器动力学》 单自由度系统响应编程报告 组别: 组员:一、单自由度系统对初始条件和谐波激励的全响应1、 任意假设系统的参数(刚度,质量,阻尼)(每个小组不可以一样,也不可和下面参数数据一样) 假设k=22、 激振函数形式为()0sin F t ω,任意假设激振参数(激振力大小,频率)3、 任意假设初始条件(初始位移,初始速度)4、 写出求解系统全解()()()120cos sin sin n t d d x t e A t A t B t ζωωωβωϕ-=++-的过程,包括如何求参数A1,A2,放大系数,滞后角。
(此处若需要,可以自行添加公式,流程图等说明) 已知:()()()120cos sin sin n t d d x t e A t A t B t ζωωωβωϕ-=++-的解为:x=x 1+x 2。
已知:112()(cos sin )n td d x te A t A t ζωωω-=+5、 绘制系统瞬态响应,稳态响应和全响应波形图。
稳定响应全响应图1:系统响应图以下结果作为检验程序正确性的参考: k=1;%系统刚度 m=1;%系统质量 c=0.3;%系统阻尼 w=1.5;%激振频率 x0=2;%初始位移 v0=2;%初始速度F0=1;%激振力,激振力形式为sinwt 计算结果为:120.7527 2.796 2.255 3.4395A A βϕ====二、单自由度系统任意激励的响应(卷积)1、 简单介绍利用卷积求解系统响应的基本原理(将输入细分从为脉冲,输出为脉冲响应的叠加)(需要图示)2、 输入函数和脉冲响应函数介绍:(需要图示)脉冲响应函数为上面的有阻尼单自由度系统的脉冲响应函数。
激励函数的频率w=3,大小为1,激振力形式为sinwt 波形如图2所示图2:脉冲响应函数与激励力函数3、 将输入细分成脉冲,利用脉冲响应进行移位叠加法进行计算系统的响应,简要说明计算过程,绘制流程图。
05机械振动作业及参考答案2015(1)分析

2015-2016(1)《大学物理 A(2)》作业参考答案提示:两根劲度系数分别为 k1和k2的两个轻质弹簧串联后,可看成一根弹簧,其弹第十三章机械振动选择题:并联,系统的劲度系数为 6k .C 】2 (基础训练4) 一质点作简谐振动,周期为T .当它由平衡位置向 x 轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的时间为(A) T /12.(B) T /8.(C) T /6.(D) T /4.提示:从从二分之一最大位移处到最大位移处这段路程在旋转矢量图上,矢量转过的1角位移为,对应的时间为T/6.3[B ] 3、(基础训练8)图中所画的是两个简谐振动的振动曲线•若这两个简谐振动可叠加,则合成的余弦振动的初相为(B)二 (C)丄二.(D) 0.2提示:使用谐振动的矢量图示法,-A2,初相位为…[D ] 4、(自测提高4)质量为m 的物体,由劲度系数为k 1和k 2的两个轻质弹簧串联后 连接到固定端,在光滑水平轨道上作微小振动,则振动频率为:(A)k 1 k 2(B )(C )v=丄]人严22 \ m&k 2(D )k 1k 21 2 \ m(k 1 k 2)【D 】1 (基础训练2) 一劲度系数为k 的轻弹簧截成三等份,取出 其中的两根,将它们并联,下面挂一质量为 m 的物体,如图13-15所示。
则振动系统的频率为(A)(C)「k二二、3m-3km(B)(D) k二,m :6k - I ]二 \ m图 13-15提示:劲度系数为 k 的轻弹簧截成三等份,每份的劲度系数为变为 3k ,取出其中2份合振动的初始状态为(A)性系数满足: k 二k1k2,可计算得到v m(k「k2)【B】5、(自测提高5)一简谐振动曲线如图所示•则振动周期是(A) 2.62 s. (B) 2.40 s. (C) 2.20 s.2.00s.提示:使用谐振动的矢量图示法,初始状态旋转矢量位于第四象限,初始相位为…,到第一次回到平衡位置时,旋转矢量转过的角度为35 5……=…,此过程经历时间为1s,可得•等到周期为2.4s2 3 6 6【D】6、(自测提高所做的功为:(A kA26)弹簧振子在水平光滑桌面上作简谐振动,其弹性力在半个周期内)1 2 1 2B kAC kAD 02 4提示:振动方程为x=Acos(・t「0),经过半个周期,质点偏离平衡位置的位移为Ax = Acos(t \ ■ ■),这两个位置弹簧所具有的弹性势能E p= -kx2相同,所以所做的2功为零。
机械震动--单自由度体系的自由振动

y sy(t)机械振动分析------单自由度无阻尼系统的自由振动机械振动是物体(或物体的一部分)在平衡位置(物体静止时的位置)附近作的往复运动。
可分为自由振动、受迫振动。
又可分为无阻尼振动与阻尼振动。
常见的简谐运动有弹簧振子模型、单摆模型等。
振动在机械中的应用非常普遍,例如在振动筛分行业中基本原理系借电机轴上下端所安装的重锤(不平衡重锤),将电机的旋转运动转变为水平、垂直、倾斜的三次元运动,再把这个运动传达给筛面。
若改变上下部的重锤的相位角可改变原料的行进方向。
物体受到初干扰后,仅在系统的恢复力作用下在其平衡位置附近的振动称为无阻尼自由振动。
其中仅需用一个独立坐标就可确定振体位置的系统为单自由度系统。
单自由度系统的振动理论是振动理论的基础。
研究单自由度系统的振动有着非常普遍的实际意义,因为工程上有许多问题通过简化,用单自由度系统的振动理论就能得到满意的结果。
而同时对多自由度系统和连续系统的振动,在特殊坐标系中考察时,显示出与单自由度系统类似的性态。
因此,揭示单自由度振动系统的规律、特点,为进一步研究复杂振动系统奠定了基础。
影响振动作用的因素是振动频率、加速度和振幅。
现在我们就此方面展开对单自由度无阻尼振动的讨论。
主要包括两部分:单自由度无阻尼系统的自由振动和单自由度无阻尼系统的受迫振动。
一、单自由度无阻尼系统的自由振动如下图,设此梁上的集中质量为m ,其重量为W mg ,梁由于质量的重力引起的质量处的静力位移用s y 表示,与s y 相应的质量位置称为质量的静力平衡位置。
若此质量受到扰动离开了静力平衡位置,当扰动除去后,则体系将发生振动,这样的振动称为体系的自由振动。
由于振动的方向与梁轴垂直,故称为横向振动。
在此,只讨论微小振幅的振动,由振动引起的内力限于材料的弹性极限以内,用以表示质量运动的方程将为线性微分方程。
1、建立运动方程建立运动方程常用的基本原理是达朗伯原理(亦称惯性力法或动静法)。
机械动力学第五章作业(答案)
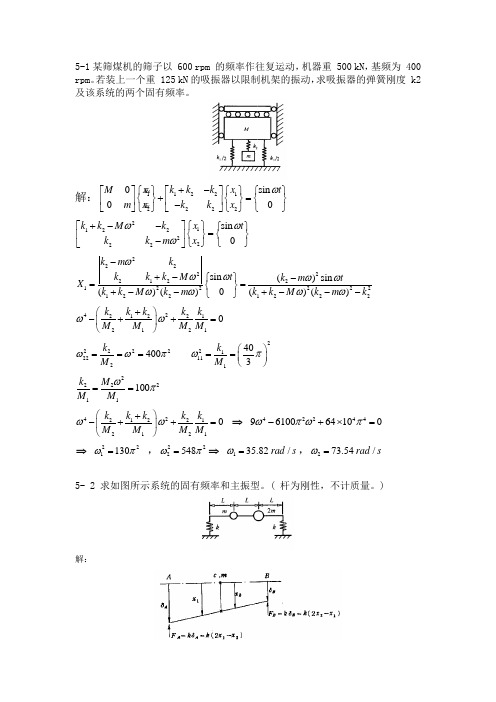
5-1某筛煤机的筛子以 600 rpm 的频率作往复运动,机器重 500 kN ,基频为 400 rpm 。
若装上一个重 125 kN 的吸振器以限制机架的振动,求吸振器的弹簧刚度 k2 及该系统的两个固有频率。
解:1122122220sin 00x k k k x M t x k k x m ω+-⎧⎫⎡⎤⎧⎫⎡⎤⎧⎫+=⎨⎬⎨⎬⎨⎬⎢⎥⎢⎥-⎣⎦⎩⎭⎩⎭⎣⎦⎩⎭&&&& 211222222sin 0x t k k M k x k k m ωωω⎡⎤+--⎧⎫⎧⎫=⎨⎬⎨⎬⎢⎥-⎩⎭⎩⎭⎣⎦ 2222221221222221221222sin ()sin 0()()()()k m k t k k k M k m tX k k M k m k k M k m k ωωωωωωωωω-+-⎧⎫-==⎨⎬+--+---⎩⎭ 422122121210k k k k k M M M M ωω⎛⎫+-++=⎪⎝⎭ 2222222400k M ωωπ=== 221111403k M ωπ⎛⎫== ⎪⎝⎭222211100k M M M ωπ== 422122121210k k k k k M M M M ωω⎛⎫+-++=⎪⎝⎭ ⇒ 422449610064100ωπωπ-+⨯= ⇒ 221130ωπ= ,222548ωπ=⇒ 135.82/rad s ω=,273.54/rad s ω=5- 2 求如图所示系统的固有频率和主振型。
( 杆为刚性,不计质量。
)解:22222()2()333l J m l m ml =+= 12x x l θ-=由1212212(2)(2)mx mx k x x k x x +=----&&&& 得 121220mx mx kx kx +++=&&&&由12211224545()(2)(2)33333B A l l l lJ ml x x F F k x x k x x θ=-=-=---&&&&&& 得 12122214130mx mx kx kx -+-=&&&&所以[]112220221413x x m m k k x x m m k k ⎡⎤⎡⎤⎡⎤⎡⎤+=⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦&&&&10.8110k m ω= 2 2.6158kmω= 21121121221111120.6577()0.9214(0.6577)X m k k kX k m k k ωω--⨯===--- ,120.921.00X X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 2112212222111122 6.8423() 2.3423( 6.8423)X m k k kX k m k k ωω--⨯===----,12 2.341.00X X -⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 所以[]111.0850.427u ⎡⎤=⎢⎥-⎣⎦5- 3选如图所示均质杆的质心C 点向下移动的位移 x 及杆顺时针方向转角θ为广义坐标,求系统的固有圆频率和主振型。
机械振动

数学上,单位脉冲必须具有零脉冲宽度、单 位面积和无限的高度。这样的脉冲模型不可能在 现实应用中实现。
在具体系统的脉冲试验中,若激励的持续时 间同系统的固有周期(T=1/f )相比时非常的短,则 激励就可以考虑为一个脉冲。
具有上述特性的任何函数(并不一定是矩形 脉冲),都可用来作为一个脉冲,而且称为函数。
dx e
n
F ( )d sin d md
1 x(t ) md
t 0
F ( )e n (t ) sin d t d
对任何初始条件的响应 6、需要数学上的支持,引 入 函数 对零初始条件的脉冲响应
x n x0 x(t ) e nt x0 cosd t 0 sin d t d 1 t F ( )e n (t ) sin d (t )d md 0
0 0 0
因为
0 0
ˆ F (t )dt
0 0 0
0
ˆ F (t )dtdt
(3.8-6)
ˆ ˆ F (t )dt F
ˆ (t )dt F 常量 (3.8-7)
则方程(3.8-6)中的左端第二项、第三项、右端项的积分值均为无限小量,可以 略去不计。解释 0 0 0
例3.8-1 设一单自由度无阻尼系统受到的简 谐激励如下: F0 sin t (t 0) F (t ) (t 0) 0 试用卷积积分计算其响应。 解:在方程(3.8-16)中,令ζ=0,d=n,则 1 t x(t ) 0 F ( ) sin n (t )d m n F0 t 0 sin sin n (t )d m n F0 1 sin t sin nt 2 k 1 n n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图示系统中, m1=m2=m3=m, k1=k2=k3=k, 设初始位移为1, 初始速度为0, 求初始激励的自由振动响应。
要求:
(1)利用影响系数法求解刚度阵K和质量阵M,建立控制方程;(15分) (2)求解系统固有频率和基准化振型;(13分)
(3)求解对初始激励的响应(运动方程);(12分)
(4)利用软件仿真对初始激励响应曲线(Matlab,simulink,excel均可),给出仿真程序(或框图)、分析结果;尝试对m、k赋值,分析曲线变化;
(10分)
(5)浅谈对本课程的理解、体会,对授课的意见、建议;(10分)
字迹清晰,书写规整。
(10分)
(1)利用影响系数法求解刚度阵K 和质量阵M ,建立控制方程;
①求解刚度矩阵K 令[]T
00
1
=X
,则弹簧变形量δ=[1 1 0]T
,
在此条件下系统保持平衡,按定义需加于三物块的力312111、、k k k 如图所示
根据平衡条件可得
0,,2312222121221111=-=-=-==+=+=k k k k k k k k k k k δδδ
同理,令[]T
010=X 得
k k k k k k k k k k -=-==+=-=-=3323222212,2,
令[]T
100=X 得
k k k k k k k ===-==33332313,-,0
故刚度矩阵为
②求解质量矩阵M
令[
]T
001=X 得m m m ==111,021=m ,031=m 令[]T
010=X 得012=m ,m m m ==222,032=m
令[]T 100=X 得013=m ,023=m ,m m m ==333
故质量矩阵为
③建立控制方程 应用叠加原理可得:
002020
00000
321321=⎥⎥⎥
⎦
⎤
⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣
⎡----+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣
⎡x x x k k
k k k k k x x x m m
m
(2)求解系统固有频率和基准化振型;
①求解固有频率 令
则
33
233322323123123
22322
222212211321312
21211211=---------m k m k m k m k m k m k m k m k m k ωωωωωωωωω
将
代入解得
②求解基准化振型
将ω1、ω2、ω3分别代入([K]-ω2[M]){X}=0得:
则
(3)求解对初始激励的响应(运动方程);对初始条件标准化:
标准坐标下的初始激励响应:
广义坐标下的初始激励响应
(4)利用软件仿真对初始激励响应曲线(Matlab,simulink,excel 均可),给出仿真程序(或框图)、分析结果;尝试对m、k赋值,分析曲线变化;
利用MATLAB对初始激励响应曲线在m=1, k=1; m=1, k=10; k=10, m=1; m=1,
k=10 四种情况下进行仿真,仿真源程序与仿真结果见附录。
当m=1,k=1时,仿真结果如图1所示,可以看出x1,x2,x3均呈现周期性变化;当m=1,k=10时,仿真结果如图2所示,1、2两图相比较可知,变化周期与k负相关;当m=10,k=1时,仿真结果如图3所示,1、3两图相比较可知,变化周期与m正相关;当m=10,k=10时,仿真结果如图4所示,1、4两图相比较可知,m、k增大倍数相同时,变化周期不变。
附录:MATLAB仿真程序
①k=1 m=1 时的初始激励响应曲线仿真
程序如下:
clear all
close all
clc
k=1;m=1;
w1=sqrt(0.198*k/m)
w2=sqrt(1.555*k/m)
w3=sqrt(3.247*k/m)
t=linspace(0,100,10000);
x1=0.543.*cos(w1.*t)+0.349.*cos(w2.*t)+0.107.*cos(w3.*t) x2=0.979.*cos(w1.*t)+0.155.*cos(w2.*t)-0.134.*cos(w3.*t) x3=0.122.*cos(w1.*t)-0.28.*cos(w2.*t)+0.059.*cos(w3.*t) plot(t,x1,'m-',t,x2,'r-',t,x3,'k-');
title('k=1 m=1时的初始激励响应曲线');
xlabel('t/s');
ylabel('x(t)/m');
legend('x1','x2','x3');
②k=1 m=10时的初始激励响应曲线
clear all
close all
clc
k=1;m=10;
w1=sqrt(0.198*k/m)
w2=sqrt(1.555*k/m)
w3=sqrt(3.247*k/m)
t=linspace(0,100,10000);
x1=0.543.*cos(w1.*t)+0.349.*cos(w2.*t)+0.107.*cos(w3.*t) x2=0.979.*cos(w1.*t)+0.155.*cos(w2.*t)-0.134.*cos(w3.*t) x3=0.122.*cos(w1.*t)-0.28.*cos(w2.*t)+0.059.*cos(w3.*t) plot(t,x1,'m-',t,x2,'r-',t,x3,'k-');
title('k=1 m=10时的初始激励响应曲线'); xlabel('t/s');
ylabel('x(t)/m');
legend('x1','x2','x3');
③k=10 m=1时的初始激励响应曲线clear all
close all
clc
k=10;m=1;
w1=sqrt(0.198*k/m)
w2=sqrt(1.555*k/m)
w3=sqrt(3.247*k/m)
t=linspace(0,100,10000);
x1=0.543.*cos(w1.*t)+0.349.*cos(w2.*t)+0.107.*cos(w3.*t) x2=0.979.*cos(w1.*t)+0.155.*cos(w2.*t)-0.134.*cos(w3.*t) x3=0.122.*cos(w1.*t)-0.28.*cos(w2.*t)+0.059.*cos(w3.*t) plot(t,x1,'m-',t,x2,'r-',t,x3,'k-');
title('k=10 m=1时的初始激励响应曲线');
xlabel('t/s');
ylabel('x(t)/m');
legend('x1','x2','x3');
④k=10 m=10时的初始激励响应曲线
clear all
close all
clc
k=10;m=10;
w1=sqrt(0.198*k/m)
w2=sqrt(1.555*k/m)
w3=sqrt(3.247*k/m)
t=linspace(0,100,10000);
x1=0.543.*cos(w1.*t)+0.349.*cos(w2.*t)+0.107.*cos(w3.*t) x2=0.979.*cos(w1.*t)+0.155.*cos(w2.*t)-0.134.*cos(w3.*t) x3=0.122.*cos(w1.*t)-0.28.*cos(w2.*t)+0.059.*cos(w3.*t) plot(t,x1,'m-',t,x2,'r-',t,x3,'k-');
title('k=10 m=10时的初始激励响应曲线');
xlabel('t/s');
ylabel('x(t)/m');
legend('x1','x2','x3');。
