2021高考数学一轮复习考点规范练53算法初步(含解析)

合集下载

2021年高考数学第一轮复习课后练习册子及其答案和详细解析

高考Байду номын сангаас复习课程--2021 年高考数学第一轮总复习
强化练习题
目录
第 1 讲集合与简易逻辑...........................................................................................................................- 1 第 2 讲函数及其性质经典精讲 ...............................................................................................................- 2 第 3 讲函数及其性质 2019 高考真题赏析 .............................................................................................- 3 第 4 讲函数及其性质 2018 高考真题赏析 .............................................................................................- 4 第 5 讲平面向量.......................................................................................................................................- 5 第 6 讲三角函数与三角恒等变换经典精讲 ............................................................

2021高考数学一轮复习专练53随机抽样含解析文新人教版

专练53 随机抽样命题范围：简单随机抽样、系统抽样、分层抽样基础强化一、选择题1．[2020·陕西榆林高三测试]某方便面生产线上每隔15分钟抽取一包进行检验，该抽样方法为①，从某中学的40名数学爱好者中抽取5人了解学习负担情况，该抽样方法为②，那么①和②分别为( )A．①系统抽样，②分层抽样B．①分层抽样，②系统抽样C．①系统抽样，②简单随机抽样D．①分层抽样，②简单随机抽样2．对一个容量为N的总体抽取容量为n的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为P1，P2，P3，则( ) A．P1＝P2<P3B．P2＝P3<P1C．P1＝P3<P2 D．P1＝P2＝P33．[2020·山西太原高三测试]某中学有高中生960人，初中生480人，为了了解学生的身体状况，采用分层抽样的方法，从该校学生中抽取容量为n的样本．其中高中生有24人，那么n等于( )A．12 B．18C．24 D．364．在一次马拉松比赛中，35名运动员的成绩(单位：分钟)的茎叶图如图所示.若将运动员按成绩由好到差编为1～35，再用系统抽样方法从中抽取7人，则成绩在区间[139,151]上的运动员的人数为( )A．3 B．4C．5 D．65．“双色球”彩票中红色球的号码由编号为01,02，…，33的33个个体组成，一位彩民利用下面的随机数表选取6组数作为6个红色球的编号，选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字，则选出来的第6个红色球的编号为( )49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 916457 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 0676C．02 D．176．[2020·江西宜春高三测试]某中学高一年级560人，高二年级540人，高三年级520人，用分层抽样的方法抽取容量为81的样本，则在高一、高二、高三三个年级抽取的人数分别为( )A．28,27,26 B．28,26,24C．26,27,28 D．27,26,257．[2019·全国卷Ⅰ]某学校为了解1 000名新生的身体素质，将这些学生编号为1,2，…，1 000，从这些新生中用系统抽样方法等距抽取100名学生进行体质测验．若46号学生被抽到，则下面4名学生中被抽到的是( )A ．8号学生B ．200号学生C ．616号学生D ．815号学生8．[2020·宣城一中高三测试]一支田径队共有运动员98人，其中女运动员42人，用分层抽样的方法抽取一个样本，每名运动员被抽到的概率都是27，则男运动员应抽取( ) A ．18人 B ．16人C ．14人D ．12人9．[2020·江西师大附中高三测试]一个总体中有100个个体，随机编号为0,1,2，…，99.依编号顺序平均分成10个小组，组号依次为一，二，三，…，十．现用系统抽样方法抽取一个容量为10的样本，如果在第一组随机抽取的号码为m ，那么在第k 组中抽取的号码个位数字与m ＋k 的个位数字相同．若m ＝6，则在第七组中抽取的号码是( )A ．63B ．64C ．65D ．66二、填空题10．某公司有大量客户，且不同年龄段客户对其服务的评价有较大差异．为了解客户的评价，该公司准备进行抽样调查，可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样，则最合适的抽样方法是________．11．某校高一年级有900名学生，其中女生400名．按男女比例用分层抽样的方法，从该年级学生中抽取一个容量为45的样本，则应抽取的男生人数为________．12．[2020·南昌八一中学高三测试]某校高三(2)班现有64名学生，随机编号为0,1,2，…，63，依编号顺序平均分成8组，组号依次为1,2,3，…，8.现用系统抽样方法抽取一个容量为8的样本，若在第1组中随机抽取的号码为5，则在第6组中抽取的号码为________．能力提升13．从2 007名学生中选取50名学生参加全国数学联赛，若采用以下方法选取：先用简单随机抽样方法从2 007名学生中剔除7名学生，剩下的2 000名学生再按系统抽样的方法抽取，则每名学生入选的概率( )A ．不全相等B ．均不相等C ．都相等，且为502 007D ．都相等，且为14014．我国古代数学专著《九章算术》中有一衰分问题：今有北乡八千一百人，西乡七千四百八十八人，南乡六千九百一十二人，凡三乡，发役300人，则北乡遣( )A ．104人B ．108人C ．112人D ．120人15．某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200,400,300,100件．为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取________件．16．为了研究雾霾天气的治理，某课题组对部分城市进行空气质量调查，按地域特点把这些城市分成甲、乙、丙三组，已知三组城市的个数分别为4，y ，z ，依次构成等差数列，且4，y ，z ＋4成等比数列，若用分层抽样抽取6个城市，则乙组中应抽取的城市个数为________．专练53 随机抽样1．C 由随机抽样的特征可知①为等距抽样，为系统抽样；②是简单随机抽样．2．D 在简单随机抽样、系统抽样和分层抽样中，每个个体被抽中的概率均为n N，故P 1＝P 2＝P 3. 3．D 由分层抽样可知n 960＋480＝24960，得n ＝36. 4．B 由题可知分段间隔为357＝5，而在[130,138]范围内有10人，故从[130,138]范围内抽2人，在[152,153]范围内有5人，故在[152,153]内抽取1人，在[139,151]上抽取7－2－1＝4人．5．C 依题意选出的6个红色球的编号依次为21,32,09,16,17,02，故选出的第6个红色球的编号为02.6．A 设高一、高二、高三三个年级抽取的人数分别为x ，y ，z ，由题意可得x 560＝y 540＝z 520＝81560＋540＋520，得x ＝28，y ＝27，z ＝26. 7．C 本题考查系统抽样；考查了数据处理能力；考查的核心素养为数据分析．将1 000名学生分成100组，每组10人，则每组抽取的号码构成公差为10的等差数列{a n }，由题意知a 5＝46，则a n ＝a 5＋(n －5)×10＝10n －4，n ∈N *，易知只有C 选项满足题意．故选C.8．B ∵田径队共有运动员98人，其中女运动员有42人，∴男运动员有56人，∵每名运动员被抽到的概率都是27， ∴男运动员应抽取56×27＝16(人)，故选B. 9．A 因为m ＝6，所以在第7组中抽取的号码个位数字与13的个位数字相同，而第7组中的编号依次为60,61,62,63，…，69，故在第7组中抽取的号码是63.10．分层抽样11．25解析：男生人数为900－400＝500.设应抽取男生x 人，则由45900＝x 500，得x ＝25.即应抽取男生25人． 12．46解析：∵分段间隔为648＝8，又第1组中随机抽取的号码为6，∴第6组中抽取的号码为6＋8×5＝46.13．C 从N 个个体中抽取M 个个体，每个个体被抽到的概率都等于M N，因此应选C.14．B 由题意知，这是一个分层抽样问题，其中北乡应抽取的人数为300×8 1008 100＋7 488＋6 912＝300×8 10022 500＝108. 15．18解析：设从丙种型号的产品中抽取x 件，由题意得60200＋400＋300＋100＝x 300， ∴x ＝18.16．2解析：由题意可得⎩⎪⎨⎪⎧ 2y ＝4＋z ，y 2＝4z ＋4，解得⎩⎪⎨⎪⎧y ＝8，z ＝12，则乙组中应抽取的城市个数为6×84＋8＋12＝2.。

2021年高考数学一轮复习算法初步课时作业理(含解析)新人教A版

2021年高考数学一轮复习算法初步课时作业理（含解析）新人教A版一、选择题1．(xx·汕头市质量测评(二))执行下边的框图，若输出的结果为12，则输入的实数x的值是( )A.14B.32C.22D.2解析：x>1时，log2x＝12得x＝2成立，而x<1时，x－1＝12得x＝32>1与x<1矛盾，故选D.答案：D第1题图第2题图2．(xx·天津卷)阅读上边的程序框图，运行相应的程序．若输入x的值为1，则输出S的值为( )A ．64B ．73C ．512D ．585解析：第1次循环，S ＝1，不满足判断框内的条件，x ＝2；第2次循环，S ＝9，不满足判断框内的条件，x ＝4；第3次循环，S ＝73，满足判断框内的条件，跳出循环，输出S ＝73.答案：B3．(xx·浙江卷)某程序框图如图所示，若该程序运行后输出的值是95，则( )A ．a ＝4B ．a ＝5C ．a ＝6D ．a ＝7解析：k ＝1，S ＝1＋1－12＝32；k ＝2，S ＝1＋1－13＝53；k ＝3，S ＝1＋1－14＝74；k ＝4，S ＝1＋1－15＝95.输出结果是95，这时k ＝5>a ，故a ＝4.答案：A第3题图第4题图4．(xx·湖北七市联考)已知全集U ＝Z ，Z 为整数集，如上图程序框图所示，集合A ＝{x |框图中输出的x 值}，B ＝{y |框图中输出的y 值}；当x ＝－1时，(∁U A )∩B ＝( )A ．{－3，－1,5}B ．{－3，－1,5,7}C ．{－3，－1,7}D ．{－3，－1,7,9}解析：由程序框图的运行程序可知，集合A ＝{0,1,2,3,4,5,6}，B ＝{－3，－1,1,3,5,7,9}，所以(∁U A)∩B＝{－3，－1，7,9}，故选D.答案：D5．(xx·辽宁大连第一次模拟)如图是用模拟方法估计椭圆x24＋y2＝1面积的程序框图，S表示估计的结果，则图中空白处应该填入( )A．S＝N250B．S＝N125C．S＝M250D．S＝M125解析：区间0～2构成边长为2的正方形，其面积为4，由程序框图的运行程序可知在2 000个点中落在椭圆第一象限内的点共有M个，而椭圆自身是关于x轴、y轴、原点对称的，故空白处应填入M2 000×4×4＝M125，故选D.答案：D6．(xx·辽宁卷)执行如图所示的程序框图，若输入n＝10，则输出S＝( )A.511B.111C.3655D.7255解析：S＝122－1＋142－1＋162－1＋182－1＋1102－1＝511.答案：A第6题图第7题图7．(xx·重庆六区高三调研抽测)一个算法的程序框图如图所示，若该程序输出的结果为910，则判断框内应填入的条件是( ) A．i>9 B．i≥9 C．i>10 D．i≥8解析：S＝11×2＋12×3＋…＋1n n＋1＝1－12＋12－13＋…＋1n－1n＋1＝nn＋1，由S＝910，得n＝9，故选A.答案：A8．(xx·山西适应性训练考试)执行如图所示的程序框图，输入m＝1 173，n＝828，则输出的实数m的值是( )A．68B．69C．138D．139解析：1 173÷828＝1…345,828÷345＝2…138，354÷138＝2…69,138÷69＝2…0，∴m＝n＝69，n＝r＝0.∴输出的实数m的值为69.答案：B9．(xx·石家庄第二次模拟)定义min{a1，a2，…，a n}是a1，a2，…，a n中的最小值，执行程序框图(如图)，则输出的结果是( )A.15B.14C.13D.23解析：n＝2时，a2＝2，n＝3时，a3＝1a2＝12；n＝4时，a4＝a2＋1＝3，n＝5时，a5＝1a4＝13；n ＝6时，a 6＝a 3＋1＝32，n ＝7时，a 7＝1a 6＝23；n ＝8时，a 8＝a 4＋1＝4，T ＝min⎩⎨⎧⎭⎬⎫1，2，12，3，13，32，23，4＝13. 答案：C第9题图第10题图10．(xx·云南昆明高三调研)某班有24名男生和26名女生，数据a 1，a 2，…，a 50是该班50名学生在一次数学学业水平模拟考试中的成绩(成绩不为0)，如图所示的程序用来同时统计全班成绩的平均数：A ，男生平均分：M ，女生平均分：－W .为了便于区别性别，输入时，男生的成绩用正数，女生的成绩用其成绩的相反数，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的( )A ．T >0？，A ＝M ＋W50B ．T <0？，A ＝M ＋W50 C ．T <0？，A ＝M －W50D ．T >0？，A ＝M －W50解析：依题意得，全班成绩的平均数应等于班级中所有的学生的成绩总和除以总人数，注意到当T>0时，输入的成绩表示的是某男生的成绩；当T<0时，输入的成绩表示的是某女生的成绩的相反数．因此结合题意得，选D.答案：D二、填空题11．(xx·广东卷)执行如图所示的程序框图，若输入n的值为4，则输出s的值为________．解析：第1次循环：s＝1＋(1－1)＝1，i＝1＋1＝2；第2次循环：s＝1＋(2－1)＝2，i＝2＋1＝3；第3次循环：s＝2＋(3－1)＝4，i＝3＋1＝4；第4次循环：s＝4＋(4－1)＝7，i＝4＋1＝5.循环终止，输出s的值为7.答案：7第11题图第12题图12．(xx·山东卷)执行上面的程序框图，若输入的ε的值为0.25，则输出的n的值为________．解析：逐次计算的结果是F1＝3，F0＝2，n＝2；F1＝5，F0＝3，n＝3，此时输出，故输出结果为3.答案：313．(1)(xx·宁德质检)运行下图所示的程序，输入3,4时，则输出________．INPUTa ，bIF a >b THENm ＝aELSE m ＝bEND IFPRINT mENDS ←0n ←0While S ≤1 023S ←S ＋2nn ←n ＋1End WhilePrint n第(1)题图第(2)题图(2)(xx·常州市高三教学期末调研测试)根据上图所示的算法，可知输出的结果为________．解析：(1)程序的功能是比较两个数的大小且输出较大的数，所以输入3,4时输出4. (2)根据算法语句可知这是一个循环结构，S n 是一个以1为首项，2为公比的等比数列的前n 项和，即：S n ＝1－2n1－2＝2n－1，可见n ＝10时，S 10＝1 023，所以n ＝10时进行最后一次循环，故n ＝11.答案：(1)4 (2)11 [热点预测]14．(1)(xx·安徽省“江南十校”高三联考)下图是寻找“徽数”的程序框图．其中“S mod 10”表示自然数S 被10除所得的余数，“S /10”表示自然数S 被10除所得的商．则根据上述程序框图，输出的“徽数S ”为( )A ．18B ．16C ．14D ．12第(1)题图第(2)题图(2)(xx·江西重点中学第一次联考)如图所示的程序框图中，令a ＝tan θ，b ＝sin θ，c ＝cos θ，若在集合⎩⎨⎧⎭⎬⎫θ|－π4<θ<3π4，θ≠0，π4，π2中，给θ取一个值，输出的结果是sin θ，则θ的值所在范围为( )A.⎝ ⎛⎭⎪⎫－π4，0 B.⎝⎛⎭⎪⎫0，π4C.⎝ ⎛⎭⎪⎫π2，3π4D.⎝ ⎛⎭⎪⎫π4，π2 解析：(1)法一：S ＝10，则x ＝S MOD 10＝10，y ＝S /10＝1,3(x ＋y ＋1)＝6，不符合判断条件，S ＝11，则x ＝1，y ＝1，3(x ＋y ＋1)＝9，不符合判断条件．S ＝12，则x ＝2，y ＝1，3(x ＋y ＋1)＝12，符合判断条件，输出S ＝12，选D.法二：由题意知，此程序的功能是寻找“徽数”，所谓“徽数”的定义是个位数与S 被10除所得的商的和加1后，再乘以3等于这个数本身，所以从选项验证可知D 正确．(2)由程序框图可知，本程序的功能是输入的三个数中输出最大的一个，现在tan θ，sin θ，cos θ，输出了sin θ，所以sin θ是最大的，在集合⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫θ⎪⎪⎪－π4<θ<3π4，θ≠0，π4，π2中θ的取值范围是⎝ ⎛⎭⎪⎫π2，34π.答案：(1)D (2)C [ '24966 6186 憆t929516 734C 獌t-29431 72F7 狷26668 682C 栬21394 5392 厒%35320 89F8 觸39170 9902 餂。

2021高考数学一轮复习课时作业53曲线与方程理(含答案及解析)

高考数学一轮复习：课时作业53 曲线与方程[基础达标]一、选择题1．已知点P 是直线2x －y ＋3＝0上的一个动点，定点M (－1,2)，Q 是线段PM 延长线上的一点，且|PM |＝|MQ |，则Q 点的轨迹方程是( )A ．2x ＋y ＋1＝0B ．2x －y －5＝0C ．2x －y －1＝0D ．2x －y ＋5＝0解析：由题意知，M 为PQ 中点，设Q (x ，y )，则P 为(－2－x,4－y )，代入2x －y ＋3＝0得2x －y ＋5＝0.答案：D2．方程|x |－1＝1－y －12所表示的曲线是( )A ．一个圆B ．两个圆C ．半个圆D ．两个半圆解析：由题意得⎩⎪⎨⎪⎧|x |－12＋y －12＝1，|x |－1≥0，即⎩⎪⎨⎪⎧x －12＋y －12＝1，x ≥1或⎩⎪⎨⎪⎧x ＋12＋y －12＝1，x ≤－1.故原方程表示两个半圆．答案：D3．设点A 为圆(x －1)2＋y 2＝1上的动点，PA 是圆的切线，且|PA |＝1，则P 点的轨迹方程为( )A ．y 2＝2x B ．(x －1)2＋y 2＝4 C ．y 2＝－2x D ．(x －1)2＋y 2＝2解析：如图，设P (x ，y )，圆心为M (1,0)．连接MA ，则MA ⊥PA ，且|MA |＝1. 又∵|PA |＝1，∴|PM |＝|MA |2＋|PA |2＝2，即|PM |2＝2，∴(x －1)2＋y 2＝2. 答案：D4．[2020·珠海模拟]已知点A (1,0)，直线l ：y ＝2x －4，点R 是直线l 上的一点，若RA →＝AP →，则点P 的轨迹方程为( )A ．y ＝－2xB ．y ＝2xC ．y ＝2x －8D ．y ＝2x ＋4解析：设P (x ，y )，R (x 1，y 1)，由RA →＝AP →知，点A 是线段RP 的中点，∴⎩⎪⎨⎪⎧x ＋x12＝1，y ＋y12＝0，即⎩⎪⎨⎪⎧x 1＝2－x ，y 1＝－y .∵点R (x 1，y 1)在直线y ＝2x －4上，∴y 1＝2x 1－4，∴－y ＝2(2－x )－4，即y ＝2x . 答案：B5．[2020·福建八校联考]已知圆M ：(x ＋5)2＋y 2＝36，定点N (5，0)，点P 为圆M 上的动点，点Q 在NP 上，点G 在线段MP 上，且满足NP →＝2NQ →，GQ →·NP →＝0，则点G 的轨迹方程是( )A.x 29＋y 24＝1B.x 236＋y 231＝1C.x 29－y 24＝1 D.x 236－y 231＝1 解析：由NP →＝2NQ →，GQ →·NP →＝0知GQ 所在直线是线段NP 的垂直平分线，连接GN ， ∴|GN |＝|GP |，∴|GM |＋|GN |＝|MP |＝6>25，∴点G 的轨迹是以M ，N 为焦点的椭圆，其中2a ＝6,2c ＝25，∴b 2＝4，∴点G 的轨迹方程为x 29＋y 24＝1，故选A.答案：A 二、填空题6．在△ABC 中，A 为动点，B ，C 为定点，B ⎝ ⎛⎭⎪⎫－a 2，0，C ⎝ ⎛⎭⎪⎫a2，0(a ＞0)，且满足条件sinC －sin B ＝12sin A ，则动点A 的轨迹方程是________．解析：由正弦定理得|AB |2R －|AC |2R ＝12×|BC |2R ，即|AB |－|AC |＝12|BC |，故动点A 是以B ，C 为焦点，a2为实轴长的双曲线右支．即动点A 的轨迹方程为16x 2a 2－16y23a 2＝1(x ＞0且y ≠0)．答案：16x 2a 2－16y23a2＝1(x ＞0且y ≠0)7．[2020·河南开封模拟]如图，已知圆E ：(x ＋3)2＋y 2＝16，点F (3，0)，P 是圆E 上任意一点．线段PF 的垂直平分线和半径PE 相交于Q .则动点Q 的轨迹Γ的方程为________________．解析：连接QF ，因为Q 在线段PF 的垂直平分线上，所以|QP |＝|QF |，得|QE |＋|QF |＝|QE |＋|QP |＝|PE |＝4.又|EF |＝23＜4，得Q 的轨迹是以E ，F 为焦点，长轴长为4的椭圆，则方程为x 24＋y2＝1.答案：x 24＋y 2＝18．[2020·江西九江联考]设F (1,0)，点M 在x 轴上，点P 在y 轴，且MN →＝2MP →，PM →⊥PF →，当点P 在y 轴上运动时，则点N 的轨迹方程为________．解析：设M (x 0,0)，P (0，y 0)，N (x ，y )，由MN →＝2MP →，得⎩⎪⎨⎪⎧x －x 0＝－2x 0，y ＝2y 0，即⎩⎪⎨⎪⎧x 0＝－x ，y 0＝12y ，因为PM →⊥PF →，PM →＝(x 0，－y 0)，PF →＝(1，－y 0)，所以(x 0，－y 0)·(1，－y 0)＝0，所以x 0＋y 20＝0，即－x ＋14y 2＝0，所以点N 的轨迹方程为y 2＝4x .答案：y 2＝4x 三、解答题9．在平面直角坐标系xOy中，点B与点A(－1,1)关于原点O对称，P是动点，且直线AP与BP的斜率之积等于－13.求动点P的轨迹方程．解析：因为点B与点A(－1,1)关于原点O对称．所以点B的坐标为(1，－1)．设点P的坐标为(x，y)，由题设知直线AP与BP的斜率存在且均不为零，则y－1x＋1·y＋1x－1＝－13，化简得x2＋3y2＝4(x≠±1)．故动点P的轨迹方程为x24＋y243＝1(x≠±1)．10．如图所示，已知圆A：(x＋2)2＋y2＝1与点B(2,0)，分别求出满足下列条件的动点P的轨迹方程．(1)△PAB的周长为10；(2)圆P与圆A外切，且过B点(P为动圆圆心)；(3)圆P与圆A外切，且与直线x＝1相切(P为动圆圆心)．解析：(1)根据题意，知|PA|＋|PB|＋|AB|＝10，即|PA|＋|PB|＝6>4＝|AB|，故P点轨迹是椭圆，且2a＝6,2c＝4，即a＝3，c＝2，b＝ 5.因此其轨迹方程为x29＋y25＝1(y≠0)．(2)设圆P的半径为r，则|PA|＝r＋1，|PB|＝r，因此|PA|－|PB|＝1.由双曲线的定义知，P点的轨迹为双曲线的右支，且2a＝1,2c＝4，即a＝12，c＝2，b ＝152，因此其轨迹方程为4x2－415y2＝1⎝⎛⎭⎪⎫x≥12.(3)依题意，知动点P到定点A的距离等于到定直线x＝2的距离，故其轨迹为抛物线，且开口向左，p＝4.因此其轨迹方程为y2＝－8x.[能力挑战]11．已知圆C 1的圆心在坐标原点O ，且恰好与直线l 1：x －y －22＝0相切． (1)求圆的标准方程；(2)设点A 为圆上一动点，AN ⊥x 轴于点N ，若动点Q 满足OQ →＝mOA →＋(1－m )ON →(其中m 为非零常数)，试求动点Q 的轨迹方程．解析：(1)设圆的半径为r, 圆心到直线l 1的距离为d ，则d ＝|－22|12＋12＝2. 因为r ＝d ＝2，圆心为坐标原点O ，所以圆C 1的方程为x 2＋y 2＝4. (2)设动点Q (x ，y )，A (x 0，y 0)， ∵AN ⊥x 轴于点N ，∴N (x 0,0)，由题意知，(x ，y )＝m (x 0，y 0)＋(1－m )·(x 0,0)，解得⎩⎪⎨⎪⎧x ＝x 0，y ＝my 0，即⎩⎪⎨⎪⎧x 0＝x ，y 0＝1m y .将点A ⎝ ⎛⎭⎪⎫x ，1m y 代入圆C 1的方程x 2＋y 2＝4，得动点Q 的轨迹方程为x 24＋y 24m 2＝1.。

2021高三数学(理)一轮复习专练53抛物线含解析

2021高三数学（理）人教版一轮复习专练53抛物线含解析专练53抛物线命题范围：抛物线的定义、标准方程与简单的几何性质[基础强化］一、选择题1．抛物线y＝14x2的焦点到其准线的距离为(）A．1 B．2C。

12D。

错误!2．已知抛物线y2＝2px（p〉0）的准线经过点（－1，1),则该抛物线的焦点坐标为(）A．（－1,0) B．（1,0)C．(0，－1) D．(0，1）3．动点M到点F(2，1)的距离和到直线l：3x＋4y－10＝0的距离相等，则动点M的轨迹为（）A．抛物线B．直线C．线段D．射线4．若抛物线y2＝2px的焦点与双曲线错误!－y2＝1的右焦点重合，则p的值为（）A．－4 B．4C．－2 D．25．若抛物线y2＝2px（p〉0)上横坐标为6的点到此抛物线焦点的距离为10，则该抛物线的焦点到准线的距离为（）A．4 B．8C．16 D．326．［2019·全国卷Ⅱ]若抛物线y2＝2px（p〉0)的焦点是椭圆错误!＋错误!＝1的一个焦点，则p＝（）A．2 B．3C．4 D．87。

如图，过抛物线y2＝2px（p>0)的焦点F的直线依次交抛物线及准线于点A，B,C，若｜BC|＝2|BF|，且|AF｜＝4，则抛物线的方程为()A．y2＝8xB．y2＝4xC．y2＝2xD．y2＝x8．设坐标原点为O,抛物线y2＝2x与过焦点的直线交于A,B两点，则错误!·错误!等于()A。

错误!B．－错误!C．3 D．－39．已知抛物线y2＝2px(p〉0）的焦点为F，准线为l,过点F 的直线交抛物线于A，B两点，过点A作准线l的垂线，垂足为E，当A点坐标为(3,y0）时,△AEF为正三角形，则此时△OAB的面积为(）A.错误!B。

错误!C.错误!D.错误!二、填空题10．已知抛物线的顶点是原点,对称轴为坐标轴，并且经过点P(－2，－4)，则该抛物线的标准方程为______________．11．过抛物线y2＝4x的焦点的直线l交抛物线于P（x1，y1），Q(x2,y2)两点，若x1＋x2＝6，则|PQ|＝________。

高优指导2021数学理人教B版一轮考点规范练53基本计数原理

考点规范练53基本计数原理考点规范练A 册第39页基础巩固组1.已知两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为()A.40B.16C.13D.10答案:C解析:分两类状况争辩:第1类,直线a分别与直线b上的8个点可以确定8个不同的平面;第2类,直线b分别与直线a上的5个点可以确定5个不同的平面.依据分类加法计数原理知,共可以确定8+5=13个不同的平面.2.有a,b,c,d,e共5个人,从中选1名组长和1名副组长,但a不能当副组长,不同选法的种数是()A.20B.16C.10D.6答案:B解析:当a当组长时,则共有1×4=4种选法;当a不当组长时,又由于a也不能当副组长,则共有4×3=12种选法.因此共有4+12=16种选法.3.教学大楼共有五层,每层均有两个楼梯,由一层到五层的走法有()A.10种B.25种C.52种D.24种答案:D解析:共分4步:一层到二层2种,二层到三层2种,三层到四层2种,四层到五层2种,一共有24种.4.将3张不同的电影票分给10名同学中的3人,每人1张,则不同分法的种数是()A.2 160B.720C.240D.120答案:B解析:分步来完成此事.第1张电影票有10种分法;第2张电影票有9种分法;第3张电影票有8种分法,共有10×9×8=720种分法.5.(2021广东汕头模拟)如图,用6种不同的颜色把图中A,B,C,D四块区域涂色分开,若相邻区域不能涂同一种颜色,则不同涂法的种数为()A.400B.460C.480D.496答案:C解析:从A开头,有6种方法,B有5种,C有4种,D,A若同色有1种,D,A若不同色有3种,则有6×5×4×(1+3)=480种不同涂法.6.(2021银川模拟)已知集合P={x,1},Q={y,1,2},其中x,y∈{1,2,3,…,9},且P⊆Q.把满足上述条件的一对有序整数对(x,y)作为一个点的坐标,则这样的点的个数是()A.9B.14C.15D.21〚导学号92950566〛答案:B解析:∵P={x,1},Q={y,1,2},且P⊆Q,∴x∈{y,1,2}.∴当x=2时,y=3,4,5,6,7,8,9,共有7种状况;当x=y时,x=3,4,5,6,7,8,9,共有7种状况.故共有7+7=14种状况,即这样的点的个数为14.7.高三班级的三个班去甲、乙、丙、丁四个工厂参与社会实践,但去何工厂可自由选择,甲工厂必需有班级要去,则不同的安排方案有() A.16种B.18种C.37种D.48种答案:C 解析:三个班去四个工厂不同的安排方案共43种,甲工厂没有班级去的安排方案共33种,因此满足条件的不同的安排方案共有43-33=37(种).8.在平面直角坐标系内,点P(a,b)的坐标满足a≠b,且a,b都是集合{1,2,3,4,5,6}中的元素.又点P到原点的距离|OP|≥5,则这样的点P的个数为.答案:20解析:依题意可知:当a=1时,b=5,6,两种状况;当a=2时,b=5,6,两种状况;当a=3时,b=4,5,6,三种状况;当a=4时,b=3,5,6,三种状况;当a=5或6时,b各有五种状况.所以共有2+2+3+3+5+5=20种状况.9.(2021河北邯郸二模)我们把中间位数上的数字最大,而两边依次减小的多位数称为“凸数”.如132,341等,那么由1,2,3,4,5可以组成无重复数字的三位凸数的个数是.〚导学号92950567〛答案:20解析:依据“凸数”的特点,中间的数字只能是3,4,5,故分三类,第一类,当中间数字为“3”时,此时有2种(132,231);其次类,当中间数字为“4”时,从1,2,3中任取两个放在4的两边,故有A32=6种;第三类,当中间数字为“5”时,从1,2,3,4中任取两个放在5的两边,故有A42=12种;依据分类计数原理,得到由1,2,3,4,5可以组成无重复数字的三位凸数的个数是2+6+12=20种.10.已知集合N={a,b,c}⊆{-5,-4,-2,1,4},若关于x的不等式ax2+bx+c<0恒有实数解,则满足条件的集合N的个数是.答案:8解析:依题意知,集合N最多有10个,其中对于不等式ax2+bx+c<0没有实数解的状况可转化为需要满足a>0,且Δ=b2-4ac≤0,因此只有当a,c同号时才有可能,共有2种状况,因此满足条件的集合N的个数是10-2=8.11.三边长均为正整数,且最大边长为11的三角形的个数是.答案:36解析:另两边长用x,y(x,y∈N+)表示,且不妨设1≤x≤y≤11,要构成三角形,必需x+y≥12.当y取11时,x可取1,2,3,…,11,有11个三角形;当y取10时,x可取2,3,…,10,有9个三角形;…;当y取6时,x只能取6,只有1个三角形.所以所求三角形的个数为11+9+7+5+3+1=36.12.如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有种.答案:12解析:先涂三棱锥P-ABC的三个侧面,然后涂三棱柱的三个侧面,共有C31×C21×C11×C21=3×2×1×2=12种不同的涂法.力量提升组13.(2021陕西商洛一模)某体育彩票规定:从01至36共36个号中抽出7个号为一注,每注2元.某人想从01至10中选3个连续的号,从11至20中选2个连续的号,从21至30中选1个号,从31至36中选1个号组成一注,则这人把这种特殊要求的号买全,至少要花()A.3 360元B.6 720元C.4 320元D.8 640元答案:D解析:从01至10中选3个连续的号共有8种选法;从11至20中选2个连续的号共有9种选法;从21至30中选1个号有10种选法;从31至36中选一个号有6种选法,由分步乘法计数原理知共有8×9×10×6=4 320(种)选法,故至少需花4 320×2=8 640(元).14.如图所示,一个地区分为5个行政区域,现给该地区的地图涂色,要求相邻区域不得使用同一种颜色,现有4种颜色可供选择,则涂色方法共有的种数为()A.72B.46C.60D.78〚导学号92950568〛答案:A解析:由于区域1与其他4个区域都相邻,首先考虑区域1,有4种涂法,然后再按区域2,4同色和不同色,分为两类: 第1类,区域2,4同色,有3种涂法,此时区域3,5均有2种涂法,共有4×3×2×2=48种涂法;第2类,区域2,4不同色,先涂区域2,有3种涂法,再涂区域4,有2种涂法,此时区域3,5都只有1种涂法,共有4×3×2×1×1=24种涂法.依据分类加法计数原理,共有48+24=72种满足条件的涂色方法.15.(2021河北保定调研)已知集合M={1,2,3,4},集合A,B为集合M的非空子集,若对∀x∈A,y∈B,x<y恒成立,则称(A,B)为集合M的一个“子集对”,则集合M的“子集对”共有个.〚导学号92950569〛答案:17解析:A={1}时,B有23-1=7种状况;A={2}时,B有22-1=3种状况;A={3}时,B有1种状况;A={1,2}时,B有22-1=3种状况;A={1,3},{2,3},{1,2,3}时,B均有1种状况,故满足题意的“子集对”共有7+3+1+3+3=17个.16.(2021辽宁大连二十四中高考模拟)某工程队有5项工程需要单独完成,其中工程乙必需在工程甲完成后才能进行,工程丙必需在工程乙完成后马上进行,那么支配这5项工程的不同排法种数是.(用数字作答)答案:12解析:支配甲工程放在第一位置时,乙丙与剩下的两个工程共有A33种方法,同理甲在其次位置共有2×2种方法,甲在第三位置时,共有2种方法.由加法原理可得:A33+4+2=12种.17.(2021湖南十二校联考)用红、黄、蓝三种颜色去涂图中标号为1,2,…,9的9个小正方形(如图),使得任意相邻(有公共边)的小正方形所涂颜色都不相同,且标号为1,5,9的小正方形涂相同的颜色,则符合条件的全部涂法共有种.〚导学号92950570〛答案:108解析:把区域分为三部分,第一部分1,5,9,有3种涂法.其次部分4,7,8,当5,7同色时,4,8各有2种涂法,共4种涂法;当5,7异色时,7有2种涂法,4,8均只有1种涂法,故其次部分共4+2=6种涂法.第三部分与其次部分一样,共6种涂法.由分步乘法计数原理,可得共有3×6×6=108种涂法.18.一个旅游景区的巡游线路如图所示,某人从P点处进,Q点处出,沿图中线路巡游A,B,C三个景点及沿途风景,则不重复(除交汇点O外)的不同巡游线路有种.〚导学号92950571〛答案:48 解析:从P点处进入结点O以后,巡游每一个景点所走环形路线都有2个入口(或2个出口),若先巡游完A景点,再进入另外两个景点,最终从Q点处出有(4+4)×2=16种不同的方法;同理,若先巡游B景点,有16种不同的方法;若先巡游C景点,有16种不同的方法.因而所求的不同巡游线路有3×16=48种.。

2021年高考数学一轮复习第53讲排列与组合

第一节排列与组合[考纲传真] 1.理解分类加法计数原理和分步乘法计数原理.2.能正确区分“类”和“步”，并能利用两个原理解决一些简单的实际问题.3.理解排列的概念及排列数公式，并能利用公式解决一些简单的实际问题.4.理解组合的概念及组合数公式，并能利用公式解决一些简单的实际问题．1．两个计数原理分类加法计数原理分步乘法计数原理条件完成一件事有两类不同方案，在第1类方案中有m种不同的方法，在第2类方案中有n种不同的方法完成一件事需要两个步骤，做第1步有m种不同的方法，做第2步有n种不同的方法结论完成这件事共有N＝m＋n种不同的方法完成这件事共有N＝mn种不同的方法排列的定义从n个不同元素中取出m(m≤n)个元素按照一定的顺序排成一列组合的定义合成一组排列数组合数定义从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数公式A m n＝n(n－1)(n－2)…(n－m＋1)＝n！n－m！C m n＝A m nA m m＝n n－1n－2…n－m＋1m！性质A n n＝n！，0！＝1C m n＝C n－mn，C m n＋C m－1n＝Cmn＋11．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)所有元素完全相同的两个排列为相同排列．( )(2)在分类加法计数原理中，每类方案中的方法都能直接完成这件事．( )(3)在分步乘法计数原理中，每个步骤中完成这个步骤的方法是各不相同的．( )(4)k C k n＝n C k－1n－1. ( )[答案](1)×(2)√(3)√(4)√2．(教材改编)图书馆的一个书架有三层，第一层有3本不同的数学书，第二层有5本不同的语文书，第三层有8本不同的英语书，现从中任取1本书，不同的取法有( ) A．12 B．16C．64 D．120B[书架上共有3＋5＋8＝16本不同的书，从中任取一本共有16种不同的取法，故选B.]3．(教材改编)用数字1,2,3,4,5组成无重复数字的四位数，其中偶数的个数为( ) A．8 B．24C．48 D．120C[末位只能从2,4中选一个，其余的三个数字任意排列，故这样的偶数共有A34C12＝4×3×2×2＝48个．故选C.]4．某市委从组织机关10名科员中选3人担任驻村第一书记，则甲、乙至少有1人入选，而丙没有入选的不同选法的种数为( )A．85 B．56C．49 D．28C[法一(直接法)：甲、乙两人均入选，有C17C22种方法，甲、乙两人只有1人入选，有C12C27种方法，由分类加法计数原理，共有C22C17＋C12C27＝49种选法．法二(间接法)：从9人中选3人有C39种方法，其中甲、乙均不入选有C37种方法，∴满足条件的选排方法有C39－C37＝84－35＝49种．]5．将6名教师分到三所中学任教，一所1名，一所2名，一所3名，则有________种不同的分法．360 [将6名教师分组，分3步完成：第1步，在6名教师中任取1名作为一组，有C16种取法；第2步，在余下的5名教师中任取2名作为一组，有C25种取法；第3步，余下的3名教师作为一组，有C33种取法．根据分步乘法计数原理，共有C16C25C33＝60(种)取法．将这三组教师分配到三所中学，有A33＝6(种)分法，故共有60×6＝360(种)不同的分法．]两个计数原理的综合应用【例1】(1)从甲地到乙地每天有直达汽车4班，从甲到丙地，每天有5个班车，从丙地到乙地每天有3个班车，则从甲地到乙地不同的乘车方法有( )A．12种B．19种C．32种D．60种(2)如图，用6种不同的颜色分别给图中A，B，C，D四块区域涂色，若相邻区域不能涂同一种颜色，则不同的涂法共有( )A．400种B．460种C．480种D．496种(1)B(2)C[(1)分两类：一类是直接从甲到乙，有n1＝4种方法；另一类是从甲经丙再到乙，可分为两步，有n2＝5×3＝15种方法．由分类计数原理可得：从甲到乙的不同乘车方法n＝n1＋n2＝4＋15＝19.故选B.(2)完成此事可能使用4种颜色，也可能使用3种颜色．当使用4种颜色时：从A开始，有6种方法，B有5种，C有4种，D有3种，完成此事共有6×5×4×3＝360种方法；当使用3种颜色时，A，D使用同一种颜色，从A，D开始，有6种方法，B有5种，C有4种，完成此事共有6×5×4＝120种方法．由分类加法计数原理可知：不同的涂法有360＋120＝480(种)．][规律方法]与两个计数原理有关问题的解题策略1在综合应用两个原理解决问题时，一般是先分类再分步，但在分步时可能又会用到分类加法计数原理.2对于较复杂的两个原理综合应用的问题，可恰当地画出示意图或列出表格，化抽象为直观.种数为________．五名学生争夺四项比赛的冠军(冠军不并列)，则获得冠军的可能性有________种．(2)用0,1,2,3,4,5,6这7个数字可以组成________个无重复数字的四位偶数．(用数字作答)(1)4554(2)420[(1)五名学生参加四项体育比赛，每人限报一项，可逐个学生落实，每个学生有4种报名方法，共有45种不同的报名方法．五名学生争夺四项比赛的冠军，可对4个冠军逐一落实，每个冠军有5种获得的可能性，共有54种获得冠军的可能性．图(1)(2)①当末位数字是0时，如图(1)所示，共有A 36个不同的四位偶数；图(2)②当末位数字是2或4或6时，如图(2)所示，共有A 15A 25C 13个不同的四位偶数；即共有A 36＋A 15A 25C 13＝120＋5×5×4×3＝420个无重复数字的四位偶数．] 排列问题【例2】 3(1)若女生全排在一起，有多少种排法？(2)若女生都不相邻，有多少种排法？(3)若女生不站两端，有多少种排法？(4)其中甲必须排在乙左边(可不邻)，有多少种排法？(5)其中甲不站最左边，乙不站最右边，有多少种排法？[解] (1)(捆绑法)由于女生排在一起，可把她们看成一个整体，这样同5名男生合在一起有6个元素，排成一排有A 66种排法，而其中每一种排法中，3名女生之间又有A 33种排法，因此共有A 66·A 33＝4 320种不同排法．(2)(插空法)先排5名男生，有A 55种排法，这5名男生之间和两端有6个位置，从中选取3个位置排女生，有A 36种排法，因此共有A 55·A 36＝14 400种不同排法．(3)法一(位置分析法)：因为两端不排女生，只能从5名男生中选2人排，有A 25种排法，剩余的位置没有特殊要求，有A 66种排法，因此共有A 25·A 66＝14 400种不同排法．法二(元素分析法)：从中间6个位置选3个安排女生，有A 36种排法，其余位置无限制，有A 55种排法，因此共有A 36·A 55＝14 400种不同排法.(4)8名学生的所有排列共A 88种，其中甲在乙左边与乙在甲左边的各占12，因此符合要求的排法种数为12A 88＝20 160. (5)甲、乙为特殊元素，左、右两边为特殊位置．法一(特殊元素法)：甲在最右边时，其他的可全排，有A 77种不同排法；甲不在最右边时，可从余下6个位置中任选一个，有A 16种．而乙可排在除去最右边位置后剩余的6个中的任一个上，有A 16种，其余人全排列，共有A 16·A 16·A 66种不同排法．由分类加法计数原理知，共有A77＋A16·A16·A66＝30 960种不同排法．法二(特殊位置法)：先排最左边，除去甲外，有A17种排法，余下7个位置全排，有A77种排法，但应剔除乙在最右边时的排法A16·A66种，因此共有A17·A77－A16·A66＝30 960种排法．法三(间接法)：8名学生全排列，共A88种，其中，不符合条件的有甲在最左边时，有A77种排法，乙在最右边时，有A77种排法，其中都包含了甲在最左边，同时乙在最右边的情形，有A66种排法．因此共有A88－2A77＋A66＝30 960种排法．[规律方法]求解排列应用问题的六种常用方法直接法把符合条件的排列数直接列式计算优先法优先安排特殊元素或特殊位置捆绑法相隔问题把相邻元素看作一个整体与其他元素一起排列，同时注意捆绑元素的内部排列插空法对不相邻问题，先考虑不受限制的元素的排列，再将不相邻的元素插在前面元素排列的空当中定序问题除法处理对于定序问题，可先不考虑顺序限制，排列后，再除以定序元素的全排列间接法正难则反、等价转化的方法A．144 B．120C．72 D．24(2)旅游体验师小明受某网站邀请，决定对甲、乙、丙、丁这四个景区进行体验式旅游，若不能最先去甲景区旅游，不能最后去乙景区和丁景区旅游，则小李可选的旅游路线数为( )A．24 B．18C．16 D．10(1)D(2)D[(1)先把3把椅子隔开摆好，它们之间和两端共有4个位置，再把3人带椅子插放在4个位置，共有A34＝24(种)方法．故选D.(2)分两种情况，第一种：最后体验甲景区，则有A33种可选的路线；第二种：不在最后体验甲景区，则有C12·A22种可选的路线．所以小李可选的旅游路线数为A33＋C12·A22＝10.故选D.]组合问题【例3】队长．现从中选5人主持某种活动，依下列条件各有多少种选法？(1)只有一名女生当选；(2)两队长当选；(3)至少有一名队长当选；(4)至多有两名女生当选．[解](1)只有一名女生当选等价于有一名女生和四名男生当选．故共有C15·C48＝350种．(2)两队长当选，共有C22·C311＝165种．(3)至少有一名队长当选含有两类：只有一名队长当选，有两名队长当选．故共有C12·C411＋C22·C311＝825种．(或采用排除法：C513－C511＝825(种))．(4)至多有两名女生当选含有三类：有两名女生当选，只有一名女生当选，没有女生当选．故选法共有C25·C38＋C15·C48＋C58＝966种．[规律方法]组合问题的常见类型与处理方法1“含有”或“不含有”某些元素的组合题型：“含”，则先将这些元素取出，再由另外元素补足；“不含”，则先将这些元素剔除，再从剩下的元素中选取.2“至少”或“至多”含有几个元素的题型：若直接法分类复杂时，逆向思维，间接求解.人值班1天．若6位员工中的甲不值9日，乙不值11日，则不同的安排方法共有( ) A．30种B．36种C．42种D．48种(2)现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张，从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多1张，不同取法的种数为( ) A．232 B．252C．472 D．484(1)C(2)C[(1)若甲在11日值班，则在除乙外的4人中任选1人在11日值班，有C14种选法，9日、10日有C24C22种安排方法，共有C14C24C22＝24(种)安排方法；若甲在10日值班，乙在9日值班，余下的4人有C14C13C22种安排方法，共有12种安排方法；若甲、乙都在10日值班，则共有C24C22＝6(种)安排方法．所以总共有24＋12＋6＝42(种)安排方法．(2)分两类：第一类，含有1张红色卡片，不同的取法共有C14C212＝264(种)；第二类，不含有红色卡片，不同的取法共有C312－3C34＝220－12＝208(种)．由分类加法计数原理知，不同的取法有264＋208＝472(种)．]1．(2017·全国卷Ⅱ)安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有( )A．12种 B．18种C．24种D．36种D[由题意可得其中1人必须完成2项工作，其他2人各完成1项工作，可得安排方式为C 13·C 24·A 22＝36(种)，或列式为C 13·C 24·C 12＝3×4×32×2＝36(种)．故选D.]2．(2016·全国卷Ⅱ)如图，小明从街道的E 处出发，先到F 处与小红会合，再一起到位于G 处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为( )A ．24B ．18C ．12D ．9B [从E 到G 需要分两步完成：先从E 到F ，再从F 到G .从F 到G 的最短路径，只要考虑纵向路径即可，一旦纵向路径确定，横向路径即可确定，故从F 到G 的最短路径共有3条．如图，从E 到F 的最短路径有两类：先从E 到A ，再从A 到F ，或先从E 到B ，再从B 到F .因为从A 到F 或从B 到F 都与从F 到G 的路径形状相同，所以从A 到F ，从B 到F 最短路径的条数都是3，所以从E 到F 的最短路径有3＋3＝6(条)．所以小明到老年公寓的最短路径条数为6×3＝18.]3．(2018·全国卷Ⅰ)从2位女生，4位男生中选3人参加科技比赛，且至少有1位女生入选，则不同的选法共有________种．(用数字填写答案)16 [法一：可分两种情况：第一种情况，只有1位女生入选，不同的选法有C 12C 24＝12(种)；第二种情况，有2位女生入选，不同的选法有C 22C 14＝4(种)．根据分类加法计数原理知，至少有1位女生入选的不同的选法有16种．法二：从6人中任选3人，不同的选法有C 36＝20(种)，从6人中任选3人都是男生，不同的选法有C 34＝4(种)，所以至少有1位女生入选的不同的选法有20－4＝16(种)．]。

21高考数学理导学大一轮人教A广西专用考点规范练53 算法初步含解析

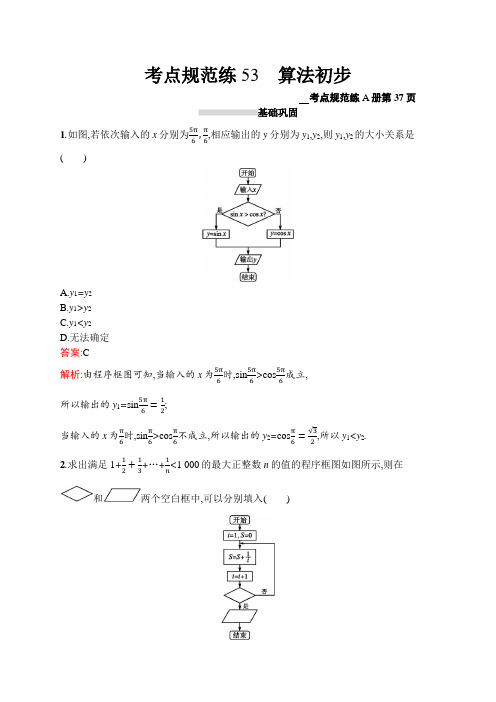
考点规范练53算法初步考点规范练A册第37页基础巩固1.如图,若依次输入的x分别为5π6,π6,相应输出的y分别为y1,y2,则y1,y2的大小关系是()A.y1=y2B.y1>y2C.y1<y2D.无法确定答案:C解析:由程序框图可知,当输入的x为5π6时,sin5π6>cos5π6成立,所以输出的y1=sin5π6=12;当输入的x为π6时,sinπ6>cosπ6不成立,所以输出的y2=cosπ6=√32,所以y1<y2.2.求出满足1+12+13+…+1n<1 000的最大正整数n的值的程序框图如图所示,则在和两个空白框中,可以分别填入()A .“S<1 000?”和“输出i-1”B .“S<1 000?”和“输出i-2”C .“S ≥1 000?”和“输出i-1”D .“S ≥1 000?”和“输出i-2” 答案:D解析:执行程序框图,S=0,i=1,得到S=1,i=2,不满足判断框中的条件时继续循环,所以判断框中应填“S ≥1 000?”.S=1+12,i=3,不满足判断框中的条件;S=1+12+13,i=4,不满足判断框中的条件;…,S=1+12+…+1i ,i=i+1,满足判断框中的条件,则“输出i-2”,故选D . 3.(2019天津,理4)阅读右面的程序框图,运行相应的程序,输出S 的值为( )A.5B.8C.24D.29 答案:B解析:i=1,为奇数,S=1; i=2,为偶数,S=1+2×21=5;i=3,为奇数,S=8;i=4,此时4≥4,满足要求, 输出S=8. 故选B .4.(2019广东广州高三二模)执行如图所示的程序框图,则输出z 的值是( )A.21B.22C.23D.24答案:A解析:执行程序框图,x=1,y=2,z=1+2=3;x=2,y=3,z=2+3=5;x=3,y=5,z=3+5=8;x=5,y=8,z=5+8=13;x=8,y=13,z=13+8=21>20,输出z=21,选A .5.一个程序框图如图所示,令y=f (x ),若f (a )>1,则a 的取值范围是( )A.(-∞,2)∪(2,5]B.(-∞,-1)∪(1,+∞)C.(-∞,2)∪(2,+∞)D.(-∞,-1)∪(1,5] 答案:D解析:根据程序框图可知f (x )={x 2,x ≤2,2x -3,2<x ≤5,1x ,x >5.由f (a )>1,得{a ≤2,a 2>1或{2<a ≤5,2a -3>1或{a >5,1a>1.由上述三个不等式组可解得a<-1或1<a ≤5,即a 的取值范围为(-∞,-1)∪(1,5],故选D .6.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.利用秦九韶算法求某多项式值的一个实例的程序框图如图所示.若输入n ,x 的值分别为3,2,则输出v 的值为( )A.9B.18C.20D.35答案:B解析:程序运行如下,n=3,x=2→v=1,i=2≥0→v=1×2+2=4,i=1≥0→v=4×2+1=9,i=0≥0→v=9×2+0=18,i=-1<0,结束循环,输出v=18,故选B.7.为了在运行如图所示的程序之后得到结果y=16,则输入的x应该是()IF x<0THENy=(x+1) (x+1)ELSEy=(x-1)(x-1)END IFA.±5B.5C.-5D.0答案:A解析:∵f(x)={(x+1)2,x<0, (x-1)2,x≥0,∴当x<0时,令(x+1)2=16,∴x=-5;当x≥0时,令(x-1)2=16,∴x=5,∴x=±5.8.执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为()A.0,0B.1,1C.0,1D.1,0答案:D解析:若输入x=7,则b=2(b2<x,且x不能被b整除)→b=3(b2>x)→输出a=1;若输入x=9,则b=2(b2<x,且x不能被b整除)→b=3(b2=x,但x能被b整除)→输出a=0.故选D.9.执行如图所示的程序框图,若输出的S=2524,则判断框内填入的条件可以是()A.k≥7B.k>7C.k≤8D.k<8答案:D解析:由程序框图可知,第一次循环:k=2,S=12;第二次循环:k=4,S=12+14;第三次循环:k=6,S=12+14+16;第四次循环:k=8,S=12+14+16+18=2524.此时不满足条件,退出循环,输出S的值为2524.结合选项可得判断框内填入的条件可以是k<8.故选D.10.某算法的程序框图如图所示,若输入区间[1,19]上的实数x,则输出的x大于49的概率为.答案:23解析:第一次循环得x=2x-1,n=2;第二次循环得x=2(2x-1)-1=4x-3,n=3;第三次循环得x=2(4x-3)-1=8x-7,n=4;结束循环,输出8x-7.由8x-7>49,得x>7,所以当输入的x∈[1,19]时,输出的x大于49的概率为19-719-1=23.11.执行如图所示的程序框图,若输入的a,b的值分别为0和9,则输出的i的值为.答案:3解析:第一次循环:a=1,b=8;第二次循环:a=3,b=6;第三次循环:a=6,b=3;满足条件,结束循环,此时,i=3.12.运行如图所示的程序,当输入a,b分别为2,3时,最后输出的m的值为.答案:3解析:∵a=2,b=3,∴a<b,应把b的值赋给m,∴m的值为3.能力提升13.(2019河北唐山一模)如图是根据南宋数学家杨辉的“垛积术”设计的程序框图,该程序所能实现的功能是()A.求1+3+5+…+(2n-1)B.求1+3+5+…+(2n+1)C.求12+22+32+…+n2D.求12+22+32+…+(n+1)2答案:C解析:根据题意,得a=0,S=0,i=1;a=1,S=1,i=2;a=4,S=1+4,i=3;a=9,S=1+4+9,i=4;a=16,S=1+4+9+16,i=5,……依次写出S的表达式,总结规律,选项C满足要求.故选C.}的前100项和,则赋值框和判断框中可分别填14.若用如图所示的程序框图求数列{n+1n入()A.S=S+i+1i,i ≥100B.S=S+i+1i ,i ≥101C.S=S+ii -1,i ≥100 D.S=S+ii -1,i ≥101 答案:B解析:题中程序框图的功能是求数列{n+1n}的前100项和S=1+11+2+12+3+23+…+100+1100的运算.数列{n+1n}的通项应为i+1i的形式,则处理框内应填S=S+i+1i;计数变量i 的初值为1,步长值为1,故最后一次进行循环时i 的值为100,即当i ≥101时,满足判断框中的条件,退出循环,故判断框中的条件应为i ≥101.故选B .15.2017年国庆期间,全国接待国内游客7.05亿人次,其中某30个景区日均实际接待人数与最大接待人数比值依次记为a i (i=1,2,…,30),若该比值超过1,则称该景区“爆满”,否则称为“不爆满”,则如图所示的程序框图的功能是( )A.求30个景区的爆满率B.求30个景区的不爆满率C.求30个景区的爆满数D.求30个景区的不爆满数答案:B解析:根据题意得,程序框图中只有当a i≤1时,才计数一次,并且进入循环,进入下一次判断,而a i≤1这一条件表示不爆满,故程序框图的功能是求30个景区的不爆满率.故选B.16.根据如图所示的算法语句,可知输出的结果S为.答案:7解析:开始:S=1,I=1;第一次循环:S=S+2=1+2=3,I=I+3=1+3=4<8;第二次循环:S=S+2=3+2=5,I=I+3=4+3=7<8;第三次循环:S=S+2=5+2=7,I=I+3=7+3=10>8.故S=7.高考预测17.若如图所示的程序框图输出的S是126,则条件①可以为()A.n≤5?B.n≤6?C.n≤7?D.n≤8?答案:B解析:该程序是输出S=2+22+…+2n的值.由于S=2+22+…+26=126,因此①中应填n≤6.故选B.。

2021年高考数学一轮复习：53 算法与程序框图

2021年高考数学一轮复习：53 算法与程序框图姓名:________ 班级:________ 成绩:________一、单选题 (共14题；共28分)1. （2分）执行如图的程序框图，则输出的s=（）A .B . -C .D . -2. （2分）(2019·西宁模拟) 若某程序框图如图所示，则该程序运行后输出的值是（）A . 5B . 4C . 3D . 23. （2分） (2019高二上·南充期中) 若正整数N除以正整数m后的余数为r，则记为，例如 .如图所示的程序框图的算法源于我国古代数学名著《孙子算经》中的“中国剩余定理”，则执行该程序框图输出的（）A . 8B . 18C . 23D . 384. （2分） (2018高二下·惠东月考) 执行如图所示的程序框图，若输出的，则判断框内可以填入（）A .B .C .D .5. （2分）(2017·新课标Ⅲ卷理) 执行如图的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为（）A . 5B . 4C . 3D . 26. （2分）执行如图所示的程序框图,若输入n的值为7,则输出的s的值为（）A . 22B . 16C . 15D . 117. （2分）如图是一个结构图，在□处应填入（）A . 对称性B . 解析式C . 奇偶性D . 图象交换8. （2分）某程序框图如图所示，现将输出值依次记为：若程序运行中输出的一个数组是则数组中的（）A . 32B . 24C . 18D . 169. （2分）若如图所示的程序框图输出的S是30，则在判断框中M表示的“条件”应该是（）A . n≥3B . n≥4C . n≥5D . n≥610. （2分）(2018·鞍山模拟) 执行如图所示的程序框图，则输出的最大值为（）A .B .C . 2D .11. （2分）如图所示为某公司的组织结构图，总经理的直接下属是（）A . 总工程师和专家办公室B . 开发部C . 总工程师、专家办公室和开发部D . 总工程师、专家办公室和七个部12. （2分）(2018·陕西模拟) 某程序框图如右图所示，该程序运行输出的值是（）A . 9B . 8C . 7D . 613. （2分） (2019高二上·四川期中) 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入，分别为2，8，则输出的等于（）A . 4B . 0C . 2D . 1414. （2分）程序框图，如果输入三个实数a、b、c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的（）A . c >xB . x >cC . c >D . b >c二、填空题 (共6题；共6分)15. （1分）如图是某算法的程序框图，则程序运行后输出的结果是________16. （1分）若a=11时，下面的程序段输出的结果是________.IF a<10 THENy=2* (a-1)ELSEy=a MOD 10END IFPRINT yEND17. （1分） (2016高一下·和平期末) 如图所示，如果执行如图所示的程序框图，输入n=6，m=4，那么输出的p=________．18. （1分）(2017·临沂模拟) 阅读如图的程序框图，若运行此程序，则输出S的值为________．19. （1分）已知函数y＝|x－3|，如图所示程序框图表示的是给定x值，求其相应函数值的算法．请将该程序框图补充完整．其中①处应填________，②处应填________．20. （1分）(2017·南京模拟) 根据如图所示的伪代码，输出S的值为________．三、解答题 (共1题；共15分)21. （15分） (2017高二上·抚州期末) 调查某车间20名工人的年龄，第i名工人的年龄为ai，具体数据见表：i1234567891011121314151617181920ai2928301931283028323130312929313240303230（1）作出这20名工人年龄的茎叶图；（2）求这20名工人年龄的众数和极差；（3）执行如图所示的算法流程图（其中是这20名工人年龄的平均数），求输出的S值．参考答案一、单选题 (共14题；共28分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、填空题 (共6题；共6分)15-1、16-1、17-1、18-1、19-1、20-1、三、解答题 (共1题；共15分)21-1、21-2、21-3、。

高优指导2021数学文人教A版一轮考点规范练53 合情推理与演绎推理

考点规范练53 合情推理与演绎推理考点规范练A 册第42页基础巩固组1.下面几种推理是合情推理的是( ) ①由圆的性质类比出球的有关性质;②由直角三角形、等腰三角形、等边三角形的内角和是180°,归纳出全部三角形的内角和都是180°; ③某次考试张军成果是100分,由此推出全班同学成果都是100分; ④三角形的内角和是180°,四边形的内角和是360°,五边形的内角和是540°,由此得出n 边形的内角和是(n-2)·180°. A.①② B.①③ C.①②④ D.②④ 答案:C解析:①是类比推理,②④是归纳推理,③是非合情推理.2.“由于对数函数y=log a x 是增函数(大前提),而y=lo g 14x 是对数函数(小前提),所以y=lo g 14x 是增函数(结论)”,以上推理的错误是( )A.大前提错误导致结论错误B.小前提错误导致结论错误C.推理形式错误导致结论错误D.大前提和小前提均错误导致结论错误答案:A解析:当a>1时,函数y=log a x 是增函数;当0<a<1时,函数y=log a x 是减函数.故大前提错误导致结论错误.3.(2021山东临沂模拟)观看(x 2)'=2x,(x 4)'=4x 3,(cos x)'=-sin x,由归纳推理得:若定义在R 上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)=( ) A.f(x) B.-f(x) C.g(x) D.-g(x)答案:D解析:由已知得偶函数的导函数为奇函数,故g(-x)=-g(x).4.观看下列各式:a+b=1,a 2+b 2=3,a 3+b 3=4,a 4+b 4=7,a 5+b 5=11,…,则a 10+b 10等于( ) A.28 B.76 C.123 D.199答案:C解析:从给出的式子特点观看可推知,等式右端的值,从第三项开头,后一个式子的右端值等于它前面两个式子右端值的和,照此规律,则a 10+b 10=123. 5.已知数列{a n }的前n 项和为S n ,a 1=-23,满足S n +1S n+2=a n (n ≥2),则S 2 015=( )A.-20222021B.-20212022C.-20222021D.-20222021〚导学号32470543〛答案:D解析:利用归纳推理求解.由S n +1S n+2=a n =S n -S n-1,得1S n =-S n-1-2(n ≥2). 又S 1=a 1=-23,所以S 2=-34,S 3=-45,S 4=-56.由归纳推理可得S 2 015=-20222021. 6.(2021浙江,文8)设实数a,b,t 满足|a+1|=|sin b|=t.( )A.若t 确定,则b 2唯一确定B.若t 确定,则a 2+2a 唯一确定C.若t 确定,则sin b 2唯一确定 D.若t 确定,则a 2+a 唯一确定答案:B解析:当t=0时,sin b=0,即b=k π,k ∈Z ,所以b 2不确定,故A 错;sin b 2=sin kπ2=0或1或-1,故C 错;当t=2时,|a+1|=2,解得a=1或a=-3,所以a 2+a=2或a 2+a=6,故D 错;由于|a+1|=t,所以a 2+2a=t 2-1;当t 确定时,t 2-1唯一确定,即a 2+2a 唯一确定,故B 正确.7.(2021郑州模拟)从1开头的自然数按如图所示的规章排列,现有一个三角形框架在图中上下或左右移动,使每次恰有九个数在此三角形内,则这九个数的和可以为( )A.2 011B.2 012C.2 013D.2 014〚导学号32470544〛答案:B解析:依据题干图所示的规章排列,设第一层的一个数为a,则其次层的三个数为a+7,a+8,a+9,第三层的五个数为a+14,a+15,a+16,a+17,a+18,这9个数之和为a+3a+24+5a+80=9a+104. 由9a+104=2 012,得a=212,是自然数.故选B.8.甲、乙、丙三位同学被问到是否去过A,B,C 三个城市时, 甲说:我去过的城市比乙多,但没去过B 城市; 乙说:我没去过C 城市;丙说:我们三人去过同一城市.由此可推断乙去过的城市为 . 答案:A解析:由丙的说法“三人去过同一城市”知乙至少去过一个城市,而甲说去过的城市比乙多,且没去过B 城市,因此甲肯定去过A 城市和C 城市.又乙没去过C 城市,所以三人共同去过的城市必为A,故乙去过的城市就是A. 9.在平面几何中有如下结论:正三角形ABC 的内切圆面积为S 1,外接圆面积为S 2,则S 1S 2=14,推广到空间可以得到类似结论:已知正四周体P-ABC 的内切球体积为V 1,外接球体积为V 2,则V 1V 2= . 答案:12710.若集合{a,b,c,d}={1,2,3,4},且下列四个关系:①a=1;②b ≠1;③c=2;④d ≠4有且只有一个是正确的,则符合条件的有序数组(a,b,c,d)的个数是 .〚导学号32470545〛答案:6解析:依据题意可分四种状况:(1)若①正确,则a=1,b=1,c ≠2,d=4,符合条件的有序数组有0个;(2)若②正确,则a ≠1,b ≠1,c ≠2,d=4,符合条件的有序数组为(2,3,1,4)和(3,2,1,4); (3)若③正确,则a ≠1,b=1,c=2,d=4,符合条件的有序数组为(3,1,2,4);(4)若④正确,则a ≠1,b=1,c ≠2,d ≠4,符合条件的有序数组为(2,1,4,3),(4,1,3,2),(3,1,4,2). 所以共有6个.故答案为6.力量提升组。

课时规范练53 算法初步

课时规范练53算法初步基础巩固组1.如图,若依次输入的x分别为5π6,π6,相应输出的y分别为y1,y2,则y1,y2的大小关系是()A.y1=y2B.y1>y2C.y1<y2D.无法确定答案:C解析:由算法框图可知,当输入的x为5π6时,sin5π6>cos5π6成立,所以输出的y1=sin5π6=12;当输入的x为π6时,sinπ6>cosπ6不成立,所以输出的y2=cosπ6=√32,所以y1<y2.2.(2021河南六市一模)已知[x]表示不超过x的最大整数.执行如图所示的算法框图,若输入x的值为2.4,则输出z的值为()A.1.2B.0.6C.0.4D.-0.4答案:D解析:执行该算法框图,输入x=2.4,y=2.4,x=[2.4]-1=1,满足x≥0,x=1.2,y=1.2,x=[1.2]-1=0,满足x≥0,x=0.6,y=0.6,x=[0.6]-1=-1,不满足x≥0,终止循环,z=-1+0.6=-0.4,输出z的值为-0.4.3.(2021河北石家庄四模)如图是计算1+13+15+…+131的值的算法框图,则图中①②处可以填写的语句分别是()A.n=n+2,i>16B.n=n+2,i≥16C.n=n+1,i>16D.n=n+1,i≥16 答案:A解析:式子1+13+15+…+131中所有项的分母构成公差为2的等差数列1,3,5,…,31,则①处填n=n+2.令31=1+(k-1)×2,k=16,共16项,而1到129共15项,需执行最后一次循环,此时i=16,所以②中应填“i>16”.故选A.4.秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的算法框图如图所示,若输入的a0,a1,a2,…,a n分别为0,1,2,…,n.若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为()A.248B.258C.268D.278答案:B解析:该算法框图是计算多项式f(x)=5x5+4x4+3x3+2x2+x当x=2时的值,f(2)=258,故选B.5.某算法框图如图所示,运行该程序后输出S=()A.53B.74C.95D.116答案:D解析:根据算法框图可知其功能为计算:S=1+11×2+12×3+…+1n(n+1)=1+1-12+12−13+…+1n−1n+1=1+1-1n+1=2n+1n+1,初始值为n=1,当n=6时,输出S,可知最终赋值S时n=5,所以S=2×5+15+1=116,故选D.6.(2021湖北武汉模拟)元朝时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个算法框图,若输入的a,b分别为5,2,则输出的n=()A.2B.3C.4D.5 答案:C解析:执行算法框图得n=1,a=152,b=4,a ≤b 不成立;n=2,a=454,b=8,a ≤b 不成立;n=3,a=1358,b=16,a ≤b 不成立;n=4,a=40516,b=32,a ≤b 成立.故输出的n=4,故选C .综合提升组7.执行如图的算法框图,如果输入的x ∈-π4,π,则输出y 的取值范围是( )A.[-1,0]B.[-1,√2]C.[1,2]D.[-1,1]答案:B解析:流程图计算的输出值为分段函数:y={2cos2x+sin2x-1,x<π2,cos2x+2sinx-1,x≥π2,原问题即求解函数在区间[-π4,π]上的值域.当-π4≤x<π2时,y=2cos2x+sin 2x-1=cos 2x+1+sin 2x-1=√2sin(2x+π4),-π4≤x<π2,则-1 4π≤2x+π4<54π,此时函数的值域为[-1,√2].当π2≤x≤π时,y=cos2x+2sin x-1=-sin2x+2sin x,π2≤x≤π,则0≤sin x≤1,此时函数的值域为[0,1].综上可得,函数的值域为[-1,√2]∪[0,1],即[-1,√2].即输出y的取值范围是[-1,√2].故选B.8.(2021河南开封一模)我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的算法框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的语句是()A.i<7,s=s-1i,i=2iB.i≤7,s=s-1i,i=2iC.i<7,s=s2,i=i+1D.i≤7,s=s2,i=i+1答案:D解析:由题意可知第一天后剩下12,第二天后剩下122……由此得出第7天后剩下127,结合选项分析得,①应为i ≤7,②应为s=s 2,③应为i=i+1,故选D .9.如图所示的程序,若最终输出的结果为6364,则在程序中“ ”处应填入的语句为( )A.i>=8B.i >=7C.i <7D.i <8答案:B解析:S=0,n=2,i=1,执行S=12,n=4,i=2;S=12+14=34,n=8,i=3;S=34+18=78,n=16,i=4;S=78+116=1516,n=32,i=5;S=1516+132=3132,n=64,i=6;S=3132+164=6364,n=128,i=7.此时满足题目条件输出的S=6364,∴“ ”处应填上i >=7.故选B .10.根据某校10位高一同学的身高(单位:cm)画出的茎叶图(图1),其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,设计一个算法框图(图2),用A i (i=1,2,…,10)表示第i 个同学的身高,计算这些同学身高的方差,则算法框图①中要补充的语句是( )图1图2A.B=B+A iB.B=B+A i 2C.B=(B+A i -A )2D.B=B 2+A i 2答案:B 解析:由s 2=(x 1-x )2+(x 2-x )2+…+(x n -x )2n=x 12+x 22+…+x n2-2(x 1+x 2+…+x n )x+nx 2n=x 12+x 22+…+x n 2-2nx 2+nx 2n=x 12+x 22+…+x n 2n−x 2,循环退出时i=11,知x 2=(Ai -1)2.所以B=A 12+A 22+…+A 102,故算法框图①中要补充的语句是B=B+A i 2.故选B .11.执行如图所示的算法框图,若输入的m ,n 分别为385,105(图中“m MOD n ”表示m 除以n 的余数),则输出的m= .答案:35解析:执行算法框图,可得m=385,n=105,r=70,m=105,n=70,不满足条件r=0; r=35,m=70,n=35,不满足条件r=0;r=0,m=35,n=0,满足条件r=0,退出循环,输出的m 值为35.创新应用组12.(2021河南郑州二模)执行如图的算法框图,如果输入的ε为0.01,则输出s 的值为( )A.2-124 B.2-125 C.2-126 D.2-127 答案:C解析:执行算法框图,s=1,x=12,不满足条件x<0.01; s=1+12,x=122,不满足条件x<0.01;s=1+12+122,x=123,不满足条件x<0.01; ……由于126>0.01,而127<0.01,可得当s=1+12+122+…+126,x=127时,满足条件x<0.01,输出s=1+12+122+…+126=2-126.故选C .13.(2021河南郑州模拟)我们可以用随机数法估计π的值,如图所示的算法框图表示其基本步骤(函数RAND 是产生随机数的函数,它能随机产生(0,1)内的任何一个实数),若输出的结果为521,则由此可估计π的近似值为( )A.3.119B.3.126C.3.132D.3.151答案:B解析:在空间直角坐标系O-xyz 中,不等式组{0<x <1,0<y <1,0<z <1表示的区域是棱长为1的正方体区域,相应区域的体积为13=1;不等式组{0<x <1,0<y <1,0<z <1,x 2+y 2+z 2<1表示的区域是棱长为1的正方体区域内的18球形区域,相应区域的体积为18×43π×13=π6,因此π6≈5211 000,即π≈3.126,故选B.。

人教高中理科数学考点规范练53算法初步(含答案)

考点规范练53算法初步基础巩固1.如图,若依次输入的x分别为5π6,π6,相应输出的y分别为y1,y2,则y1,y2的大小关系是()A.y1=y2B.y1>y2C.y1<y2D.无法确定答案:C解析:由程序框图可知,当输入的x为5π6时,sin5π6>cos5π6成立,所以输出的y1=sin5π6=12;当输入的x为π6时,sinπ6>cosπ6不成立,所以输出的y2=cosπ6=√32,所以y1<y2.2.求出满足1+12+13+…+1n<1 000的最大正整数n的值的程序框图如图所示,则在和两个空白框中,可以分别填入()A.“S<1 000?”和“输出i-1”B.“S<1 000?”和“输出i-2”C .“S ≥1 000?”和“输出i-1”D .“S ≥1 000?”和“输出i-2” 答案:D解析:执行程序框图,S=0,i=1,得到S=1,i=2,不满足判断框中的条件时继续循环,所以判断框中应填“S ≥1000?”.S=1+12,i=3,不满足判断框中的条件;S=1+12+13,i=4,不满足判断框中的条件;…,S=1+12+…+1i ,i=i+1,满足判断框中的条件,则“输出i-2”,故选D . 3.执行下边的程序框图,如果输入的ε为0.01,则输出s 的值等于( )A.2-124 B.2-125C.2-126 D.2-127答案:C解析:x=1,s=0,s=0+1,x=12>0.01,s=0+1+12,x=14>0.01,…,s=0+1+12+…+126,x=127<0.01,终止循环,输出s=1+12+…+126=1-1271-12=2-126.故选C .4.执行如图所示的程序框图,若输入的x=2 017,则输出的i=( )A.2B.3C.4D.5答案:B解析:根据题意,得a=2017,i=1,b=-12016,i=2,a=-12016,b=20162017,i=3,a=20162017,b=2017,不满足b ≠x ,退出循环,输出i=3.故选B .5.一个程序框图如图所示,令y=f (x ),若f (a )>1,则a 的取值范围是( )A.(-∞,2)∪(2,5]B.(-∞,-1)∪(1,+∞)C.(-∞,2)∪(2,+∞)D.(-∞,-1)∪(1,5] 答案:D解析:根据程序框图可知f (x )={x 2,x ≤2,2x -3,2<x ≤5,1x,x >5.由f (a )>1,得{a ≤2,a 2>1或{2<a ≤5,2a -3>1或{a >5,1a>1.由上述三个不等式组可解得a<-1或1<a ≤5,即a 的取值范围为(-∞,-1)∪(1,5],故选D .6.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.利用秦九韶算法求某多项式值的一个实例的程序框图如图所示.若输入n ,x 的值分别为3,2,则输出v 的值为( )A.9B.18C.20D.35答案:B解析:程序运行如下,n=3,x=2→v=1,i=2≥0→v=1×2+2=4,i=1≥0→v=4×2+1=9,i=0≥0→v=9×2+0=18,i=-1<0,结束循环,输出v=18,故选B.7.为了在运行如图所示的程序之后得到结果y=16,则输入的x应该是()A.±5B.5C.-5D.0答案:A解析:∵f(x)={(x+1)2,x<0, (x-1)2,x≥0,∴当x<0时,令(x+1)2=16,∴x=-5;当x≥0时,令(x-1)2=16,∴x=5,∴x=±5.8.执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为()A.0,0B.1,1C.0,1D.1,0答案:D解析:若输入x=7,则b=2(b2<x,且x不能被b整除)→b=3(b2>x)→输出a=1;若输入x=9,则b=2(b2<x,且x不能被b整除)→b=3(b2=x,但x能被b整除)→输出a=0.故选D.9.执行如图所示的程序框图,若输出的S=2524,则判断框内填入的条件可以是()A.k≥7B.k>7C.k≤8D.k<8答案:D解析:由程序框图可知,第一次循环:k=2,S=12;第二次循环:k=4,S=12+14;第三次循环:k=6,S=12+14+16;第四次循环:k=8,S=12+14+16+18=2524.此时不满足条件,退出循环,输出S的值为2524.结合选项可得判断框内填入的条件可以是k<8.故选D.10.某算法的程序框图如图所示,若输入区间[1,19]上的实数x,则输出的x大于49的概率为.答案:23解析:第一次循环得x=2x-1,n=2;第二次循环得x=2(2x-1)-1=4x-3,n=3;第三次循环得x=2(4x-3)-1=8x-7,n=4;结束循环,输出8x-7.由8x-7>49,得x>7,所以当输入的x∈[1,19]时,输出的x大于49的概率为19-719-1=23.11.执行如图所示的程序框图,若输入的a,b的值分别为0和9,则输出的i的值为.答案:3解析:第一次循环:a=1,b=8;第二次循环:a=3,b=6;第三次循环:a=6,b=3;满足条件,结束循环,此时,i=3.12.运行如图所示的程序,当输入a,b分别为2,3时,最后输出的m的值为.答案:3解析:∵a=2,b=3,∴a<b,应把b的值赋给m,∴m的值为3.能力提升13.执行如图所示的程序框图,则输出的n等于()A.1B.2C.3D.4答案:C解析:程序框图运行如下:初始化数据:n=0,x=13π12;第一次循环:a=sin x=sin13π12≠√32,执行n=n+1=1,x=x-2n-112π=π;第二次循环:a=sin x=sinπ≠√32,执行n=n+1=2,x=x-2n-112π=π-3π12=9π12;第三次循环:a=sin x=sin9π12≠√32,执行n=n+1=3,x=x-2n-112π=9π12−5π12=4π12=π3;第四次循环:a=sin x=sin π3=√32,此时跳出循环,输出n=3.故选C .14.下图是求12+12+12的程序框图,图中空白框中应填入( )A.A=12+A B.A=2+1AC.A=11+2AD.A=1+12A答案:A解析:执行第1次,A=12,k=1≤2,是,第一次应该计算A=12+12=12+A ,k=k+1=2;执行第2次,k=2≤2,是,第二次应该计算A=12+12+12=12+A ,k=k+1=3;执行第3次,k=3≤2,否,输出,故循环体为A=12+A ,故选A .15.某年国庆期间,全国接待国内游客7.05亿人次,其中某30个景区日均实际接待人数与最大接待人数比值依次记为a i (i=1,2,…,30),若该比值超过1,则称该景区“爆满”,否则称为“不爆满”,则如图所示的程序框图的功能是( )A.求30个景区的爆满率B.求30个景区的不爆满率C.求30个景区的爆满数D.求30个景区的不爆满数答案:B解析:根据题意得,程序框图中只有当a i≤1时,才计数一次,并且进入循环,进入下一次判断,而a i≤1这一条件表示不爆满,故程序框图的功能是求30个景区的不爆满率.故选B.16.根据如图所示的算法语句,可知输出的结果S为.答案:7解析:开始:S=1,I=1;第一次循环:S=S+2=1+2=3,I=I+3=1+3=4<8;第二次循环:S=S+2=3+2=5,I=I+3=4+3=7<8;第三次循环:S=S+2=5+2=7,I=I+3=7+3=10>8.故S=7.高考预测17.若如图所示的程序框图输出的S是126,则条件①可以为()A.n≤5?B.n≤6?C.n≤7?D.n≤8?答案:B解析:该程序是输出S=2+22+…+2n的值.由于S=2+22+…+26=126,因此①中应填n≤6.故选B.。

2021版新高考数学一轮复习课时规范练53 古典概型与几何概型新人教A版.docx

基础巩固组1.(2019山东德州模拟,4)如图,在边长为2的正方形中,随机撒1 000粒豆子,若按π≈3计算,估计落到阴影部分的豆子数为()A.125B.150C.175D.2002.(2019山东菏泽一模拟,6)《九章算术》勾股章有一“引葭赴岸”问题“今有饼池径丈,葭生其中,出水两尺,引葭赴岸,适与岸齐,问水深,葭各几何?”,其意思是:有一个直径为一丈的圆柱形水池,池中心生有一颗类似芦苇的植物,露出水面两尺,若把它引向岸边,正好与岸边齐,问水有多深,该植物有多高?其中一丈等于十尺,如图,若从该葭上随机取一点,则该点取自水下的概率为()A.1213B.1314C.2129D.14153.(2019广东一模,4)古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出已知线段的黄金分割点,具体方法如下:①取线段AB=2,过点B作AB的垂线,并用圆规在垂线上截取BC=12AB,连接AC;②以C为圆心,BC为半径画弧,交AC于点D;③以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为()(参考数据:√5≈2.236)A.0.236B.0.382C.0.472D.0.6184.(2019广东深圳六校联考)在区间[-π,π]上随机取两个实数a,b,记向量OO⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(a,4b),OO⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(4a,b),则OO⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·OO⃗⃗⃗⃗⃗⃗⃗⃗⃗ ≥4π2的概率为()A.1-π8B.1-π4C.1-π2D.1-3π45.(2019安徽芜湖模拟,8)中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他民俗活动的民间艺术,蕴含了极致的数学美和丰富的传统文化信息.现有一幅剪纸的设计图,其中的4个小圆均过正方形的中心,且内切于正方形的两邻边.若在正方形内随机取一点,则该点取自黑色部分的概率为()A.3π32B.(3-2√2)π2C.(2-√2)π4D.π86.安排甲、乙、丙、丁四人参加周一至周六的公益活动,每天只需一人参加,其中甲参加三天活动,乙、丙、丁每人参加一天,那么甲连续三天参加活动的概率为()A.115B.15C.14D.127.(2019江西名校(临川一中、南昌二中)联考,8)如图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设DF=3AF=3,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是()A.37B.√217C.413D.2√13138.某校有包括甲、乙两人在内的5名大学生自愿参加该校举行的A,B两场国际学术交流会的服务工作,这5名大学生中有2名被分配到A场交流会,另外3名被分配到B场交流会,如果分配方式是随机的,那么甲、乙两人被分配到同一场交流会的概率为.9.(2019河南焦作四模,14)记[m]表示不超过m的最大整数.若在x∈(18,12)上随机取1个实数,则使得[log2x]为偶数的概率为.10.锅中煮有芝麻馅汤圆6个,花生馅汤圆5个,豆沙馅汤圆4个,这三种汤圆的外部特征完全相同,从中任意舀取4个汤圆,则每种汤圆都至少取到1个的概率为.综合提升组11.如图所示的图形中,每个三角形上各有一个数字,若六个三角形上的数字之和为20,则称该图形是“和谐图形”,已知其中四个三角形上的数字之和为14.现从1,2,3,4,5中任取两个数字标在另外两个三角形上,则恰好使该图形为“和谐图形”的概率为()A.310B.15C.110D.32012.(2019湖南师范大学附中模拟,8)中华人民共和国国旗是五星红旗,旗面左上方缀着的五颗黄色五角星,四颗小五角星环拱于大星之右,象征中国共产党领导下的革命人民大团结和人民对党的衷心拥护.五角星可通过正五边形连接对角线得到,且它具有一些优美的特征,如O2O2O1O2=O1O2O1O1=O1O1O1O1且等于黄金分割比√5-12,现从正五边形A1B1C1D1E1内随机取一点,则此点取自正五边形A2B2C2D2E2内部的概率为()A.7-3√52B.√5-22C.3-√52D.√5-1213.已知O,A,B三地在同一水平面内,A地在O地正东方向2 km处,B地在O地正北方向2 km处,某测绘队员在A,B之间的直线公路上任选一点C作为测绘点,用测绘仪进行测绘,O地为一磁场,距离其不超过√3 km的范围内会对测绘仪等电子仪器形成干扰,使测量结果不准确,则该测绘队员能够得到准确数据的概率是()A.1-√22B.√22C.1-√32D.1214.(2019河南郑州联考,8)将曲线x2+y2=|x|+|y|围成的区域记为Ⅰ,曲线x2+y2=1围成的区域记为Ⅱ,曲线x2+y2=1与坐标轴的交点分别为A,B,C,D,四边形ABCD围成的区域记为Ⅲ,在区域Ⅰ中随机取一点,此点取自Ⅱ,Ⅲ的概率分别记为p1,p2,则()A.p1+p2>1B.p1+p2<1C.p1+p2=1D.p1=p215.(2019河北衡水模拟,14)已知数列{a n}满足a1=2,a n+1=-2a n(n∈N*).若从数列{a n}的前10项中随机抽取一项,则该项不小于8的概率是.创新应用组16.在区间[1,e]上任取实数a,在区间[0,2]上任取实数b,使函数f(x)=ax2+x+14b有两个相异零点的概率是()A.12(e-1)B.14(e-1)C.18(e-1)D.116(e-1)17.已知实数a,b满足0<a<1,-1<b<1,则函数y=13ax3+ax2+b有三个零点的概率为.参考答案课时规范练53古典概型与几何概型1.A由题意知圆的半径为1,则圆的面积近似为3,又正方形面积为4,则阴影部分面积为12×(4-3)=12.设落到阴影部分的豆子数为n,则O1000=124,n=125.故选A.2.C由题意知BC=2,B'C=5,设AC=x,则AB=AB'=x+2,在Rt △ACB'中,列勾股方程得52+x 2=(x+2)2,解得x=214,所以从该葭上随机取一点,则该点取自水下的概率为P=O O +2=214214+2=2129,故选C .3.A 由勾股定理可得AC=√5≈2.236,由图可知BC=CD=1,AD=AE=√5-1≈1.236,BE ≈2-1.236=0.764,则0.764≤AF ≤1.236,由几何概型可得,使得BE ≤AF ≤AE 的概率约为1.236-0.7642=0.236,故选A .4.B 在区间[-π,π]上随机取两个实数a ,b ,则点(a ,b )在以2π为边长的正方形内,因为OO ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(a ,4b ),OO ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(4a ,b ),则OO ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·OO ⃗⃗⃗⃗⃗⃗⃗⃗⃗ =4a 2+4b 2.因为OO ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·OO ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ≥4π2,所以a 2+b 2≥π2,点(a ,b )在以原点为圆心,以π为半径的圆外,且在以2π为边长的正方形内,所以OO ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·OO ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ≥4π2的概率为P=4π2-π34π2=1-π4,故选B .5.B 如图所示,设正方形的边长为2,其中的4个圆过正方形的中心,且内切正方形的两邻边的小圆的半径为r ,故BE=O 2E=O 2O=r ,∴BO 2=√2r.∵BO 2+O 2O=BO=12BD=√22,∴√2r+r=√22,∴r=2-√22.∴黑色部分面积S=π(2-√22)2=3-2√22π,正方形的面积为1,∴在正方形内随机取一点,则该点取自黑色部分的概率为3-2√22π,故选B .6.B 由题意分析可得甲连续三天参加活动的所有情况为:第1~3天,第2~4天,第3~5天,第4~6天,共4种,故所求概率P=4·A 33C 63·A 33=15.故选B .7.A 由题,DF=3AF=3,可得AF=BD=1,AD=4,且∠ADB=120°,所以在三角形ADB中,cos ∠ADB=OO 2+OO 2-OO 22OO ·OO,解得AB=√21,所以概率为P=√34OO 2√34OO =921=37,故选A .8.25 记其余3名大学生分别为丙、丁、戊,则5名大学生分别被分配到A 场交流会、B 场交流会的所有基本事件有:①A (甲、乙),余下的人分配到B 场交流会,下同,②A (甲、丙),③A (甲、丁),④A (甲、戊),⑤A (乙、丙),⑥A (乙、丁),⑦A (乙、戊),⑧A (丙、丁),⑨A (丙、戊),⑩A (丁、戊),共10个,其中甲、乙两人被分配到同一场交流会的基本事件是:①⑧⑨⑩,故所求概率为410=25.9.23 若x ∈(18,12),则log 2x ∈(-3,-1). 要使得[log 2x ]为偶数, 则log 2x ∈[-2,-1).所以x ∈[14,12),故所求概率P=12-1412-18=23.10.4891 P=C 62C 51C 41+C 61C 52C 41+C 61C 51C 42C 154=4891.11.B 由题意可知,若该图形为“和谐图形”,则另外两个三角形上的数字之和恰为20-14=6.从1,2,3,4,5中任取两个数字的所有情况有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共10种,而其中数字之和为6的情况有(1,5),(2,4),共2种,所以所求概率P=15.故选B .12.A 根据题意知,正五边形A 1B 1C 1D 1E 1∽正五边形A 2B 2C 2D 2E 2,可得O 2O 2O 1O 2=O 1O 2O 1O 1=O 1O 1O 1O 1=√5-12, 所以O 2O 2O 1O 1=O 1O 2O 1O 1=O 1O 2O 1O 1·O 1O 1O 1O 1=(√5-12)2,所以由面积比的几何概型,可得所求的概率为P=(√5-12)4=7-3√52,故选A .13.A 由题意,△AOB 是直角三角形,OA=OB=2,所以AB=2√2,O 地为一磁场,距离其不超过√3km 的范围为14个圆,与AB 相交于C ,D 两点,作OE ⊥AB ,则OE=√2,所以CD=2,所以该测绘队员能够得到准确数据的概率是1-OOOO =1-=1-√22.故选A .14.C 由方程x 2+y 2=|x|+|y|,得{O ≥0,O ≥0,(O -12)2+(O -12)2=12或{O ≥0,O <0,(O -12)2+(O +12)2=12或{O <0,O ≥0,(O +12)2+(O -12)2=12或{O <0,O <0,(O +12)2+(O +12)2=12,所以曲线x 2+y 2=|x|+|y|围成的区域Ⅰ,Ⅱ,Ⅲ,如图.可知区域Ⅰ的面积为S 正方形ABCD +2π×(√22)2=2+π;区域Ⅱ的面积为π×12=π;区域Ⅲ的面积为(√2)2=2;所以由几何概率公式得p 1=π2+π,p 2=22+π,故p 1+p 2=1.故选C .15.25 由题意可知a n =2·(-2)n-1,故前10项中,不小于8的只有8,32,128,512,共4项,故所求概率是410=25.16.A 设事件A={使函数f (x )=ax 2+x+14b 有两个相异零点},方程ax 2+x+14b=0有两个相异实根,即Δ=1-ab>0,即ab<1,所有的试验结果Ω={(a ,b )|1≤a ≤e,且0≤b ≤2},对应区域面积为2(e -1);事件A={(a ,b )|ab<1,1≤a ≤e ,且0≤b ≤2},对应区域面积S=∫e 11Od a=1,则事件A 的概率P (A )=12(e -1).故选A .17.516 对y=13ax 3+ax 2+b 求导数可得y'=ax 2+2ax ,令ax 2+2ax=0,可得x=0或x=-2,0<a<1,x=-2是极大值点,x=0是极小值点,所以函数y=13ax 3+ax 2+b ,有三个零点,可得{-83O +4O +O >0,O <0,即{4O +3O >0,O <0.画出可行域如图,满足函数y=13ax3+ax2+b有三个零点,如图深色区域,实数a,b满足0<a<1,-1<b<1,为长方形区域,所以长方形的面积为2,深色区域的面积为12×1+14=58,所以所求概率为P=582=516,故答案为516.。

高考数学一轮复习课时作业(五十三)第53讲算法初步文(2021年整理)

2019年高考数学一轮复习课时作业（五十三）第53讲算法初步文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2019年高考数学一轮复习课时作业（五十三）第53讲算法初步文）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2019年高考数学一轮复习课时作业（五十三）第53讲算法初步文的全部内容。

课时作业（五十三）第53讲算法初步时间/ 45分钟分值/ 75分基础热身1.［2017·石嘴山三中四模]图K53-1是一个算法程序框图,若输入的x=3,则输出的y的值为()A. —2B. 6C。

0 D。

—1图K53—1图K53—22.[2017·广西五市联考]某程序框图如图K53-2所示，则该程序运行后输出的B的值是()A。

15 B。

29C。

31 D。

633。

执行如图K53-3所示的程序框图，若输入a=—7，d=3，则输出的S的值为（）A. —12B. —11C. -10D. -6图K53—3图K53—44.［2017·湛江二模］运行如图K53-4所示的程序框图，若输入的n=3,x=2,则输出的y的值为（）A. 9B. 18C。

20 D. 355.［2017·北京西城区一模]执行如图K53-5所示的程序框图，当输入的x=ln 时，输出的y的值为.图K53—5能力提升6。

［2017·贵阳模拟］执行如图K53—6所示的程序框图，则该程序运行后输出的值是()A。

0B。

—1C. —2D。

-8图K53—6图K53—77。

［2017·咸阳二模]设x∈[0，3］，执行如图K53—7所示的程序框图,从输出的结果中随机取一个数a，则“a≤5"的概率为（）A.B。

考点53 算法初步典型高考数学试题解读与变式(解析版)

相等，则这样的 x 的个数是（
）
A．1
B．2
【答案】C
C．3
D．4
（二）根据程序框图求输入数据例 2 【2017 课标 3】执行右图的程序框图，为使输出 S 的值小于 91，则输入的正整数 N 的最小值为（）
A．5 【答案】D
B．4
C．3
D．2
【解析】阅读流程图，程序运行如下：首先初始化数值： t = 1, M = 100, S = 0 ，然后进入循环体：此时
【方法技巧归纳】算法初步与数列的交汇主要表现为与数列求和综合，求和时通常涉及到利用裂项相消法、
错位相减法、分组求和法等方法．此类试题有时为根据输出结果来确定程序框图中涉及到的参数的值，解
答时可有两类方法：（1）如果循环运算次数不多时，则可逐步写出每一步的结果与要求进行比较；（2）
如果循环运行次数多，则要通过数列求和，求出所涉及到的数列的前 n 项和，然后根据条件建立方程来解
别为 495，125，则输出的 m= （
）
A． 0
B． 5
【答案】B
C． 25
D．120
【变式 2】【变为《孙子算经》中的分鹿问题】《孙子算经》中有道算术题：“今有百鹿入城，家取一鹿不尽，又三家共一鹿适尽，问城中家几何？”，意思是有 100 头鹿，若每户分一头则还有剩余，再每三户
分一头则正好分完，问共有多少户人家？涉及框图如下，则输出 i 的值是（）
若输出 i 的值为 2 ，则输入 x 的最大值是（
）
A． 22
B．11
C． 6
D． 5
【答案】A
【解析】由程序框图知：第一次循环 i = 1, x = 0.5x −1 ；第二次循环 i = 2, x = 0.5 (0.5x −1) − 2 ；∵输

2021届高考数学一轮复习方案第53讲统计案例课时作业新人教B版

课时作业(五十三) [第53讲统计案例](时间：45分钟分值：100分)基础热身1．分类变量X和Y的列联表如下：A．ad－bc越小，说明X与Y关系越弱B．ad－bc越大，说明X与Y关系越强C．(ad－bc)2越大，说明X与Y关系越强D．(ad－bc)2越接近于0，说明X与Y关系越强2．为了研究色盲与性别的关系，调查了1 000人，得到了如下数据，则( )A.99.9%B．99%的把握认为色盲与性别有关C．95%的把握认为色盲与性别有关D．90%的把握认为色盲与性别有关3．[2012·商丘一中二模] 对于回归分析，下列说法错误的是( )A．在回归分析中，变量间的关系若是非确定关系，那么因变量不能由自变量唯一确定B．线性相关系数可以是正的，也可以是负的C．在回归分析中，如果r2＝1，说明x与y之间完全相关D．样本相关系数r∈(－1，1)4．下面是一个2×2列联表，请填上表中空缺：能力提升5．摘取部分国家13岁学生数学的授课天数与测验平均分数如下：A．一定存在B．可能存在也可能不存在C．一定不存在D．以上都不正确6．在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是( )A．若χ2的观测值为k＝6.635，我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病B．从独立性检验可知，有99%的把握认为吸烟与患肺病有关时，我们说某人吸烟，那么他有99%的可能患有肺病C．若从统计量中求出有95%的把握认为吸烟与患肺病有关系，是指有5%的可能性使得推断出现错误D．以上三种说法都不正确7．[2012·唐山一中月考] 变量X与Y相对应的一组数据为(10，1)，(11.3，2)，(11.8，3)，(12.5，4)，(13，5)；变量U与V相对应的一组数据为(10，5)，(11.3，4)，(11.8，3)，(12.5，2)，(13，1)．r1表示变量Y与X之间的线性相关系数，r2表示变量V与U之间的线性相关系数，则( )A．r2<r1<0 B．0<r2<r1C．r2<0<r1 D．r2＝r18．冶炼某种金属可以用旧设备和改造后的新设备，为了检验用这两种设备生产的产品中所含杂质的关系，调查结果如下表所示：根据以上数据，则( A ．含杂质的高低与设备改造有关 B ．含杂质的高低与设备改造无关C ．设备是否改造与含杂质的高低不一定有关D ．以上答案都不对9.．．．A ．商品销售收入与商品的广告支出经费之间具有相关关系B ．线性回归方程对应的直线y ^＝b ^x ＋a ^至少经过其样本数据点(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )中的一个点C ．在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高D ．在回归分析中，R 2为0.98的模型比R 2为0.80的模型拟合的效果好10．利用独立性检验来考虑两个分类变量X 和Y 是否有关系时，通过查阅下表来确定“X 和Y 有关系”的可信度．如果k >5.024，那么认为“X 和Y 有关系”的犯错率不超过________．①若χ2的观测值为k ＝6.635，我们有99%的把握认为吃零食与性别有关系，那么在100个吃零食的人中必有99人是女性；②从独立性检验可知有99%的把握认为吃零食与性别有关系时，我们说某人吃零食，那么此人是女性的可能性为99%；③若从统计量中求出有99%的把握认为吃零食与性别有关系，是指有1%的可能性使得出的判断出现错误．12．为了了解患慢性气管炎与吸烟的关系，调查了228人，其中每天的吸烟支数在10支以上20支以下的调查者中，患者人数有98人，非患者人数有89人；每天的吸烟支数在20支及以上的调查者中，患者人数有25人，非患者人数有16人，试问患慢性气管炎与吸烟量________(填“是”或“不是”)相互独立．13．为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：.认为喜爱打篮球与已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为5性别有关的把握为________(用百分数表示)．下面的临界值表供参考：，其中n＝a＋b＋c＋d.) (参考公式：χ2＝（a＋b）（c＋d）（a＋c）（b＋d）14．(10分)[2012·石家庄质检] 某工科院校对A，B两个专业的男女生人数进行调查，得到如下的列联表：(1)从B少？(2)能否在犯错误的概率不超过0.05的前提下，认为工科院校中“性别”与“专业”有关系呢？15．(13分)[2012·南阳二联] 第11届全国人大五次会议于2012年3月5日至3月14日在北京召开，为了搞好对外宣传工作，会务组选聘了16名男记者和14名女记者担任对外翻译工作，调查发现，男、女记者中分别有10人和6人会俄语．(1)根据以上数据完成以下2×2列联表：参考数据：(2)会俄语的名女记者中随机抽取2人做同声翻译，则抽出的2人都在俄罗斯工作过的概率是多少？难点突破16．(12分)某食品厂为了检查甲乙两条自动包装流水线的生产情况，随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位：克)，重量值落在(495，510]的产品为合格品，否则为不合格品．下表是甲流水线样本频数分布表，图K53－1是乙流水线样本的频率分布直方图．图K53－1(1)根据上表数据作出甲流水线样本的频率分布直方图；(2)若以频率作为概率，试估计从两条流水线分别任取1件产品，该产品恰好是合格品的概率分别是多少；(3)由以上统计数据完成下面2×2列联表，并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”．参考公式：χ2＝，其中n＝a＋b＋c＋d.（a＋b）（c＋d）（a＋c）（b＋d）课时作业(五十三)【基础热身】1．C [解析] 因为χ2＝n （ad －bc ）2（a ＋b ）（a ＋c ）（b ＋d ）（c ＋d ），当(ad －bc )2越大时，χ2越大，说明X 与Y 关系越强．故选C.2．A [解析] χ2＝1 000×（442×6－38×514）2956×44×480×520≈27.139>10.828.3．D [解析] 样本相关系数r ∈[－1，1]，所以D 错．4．52 54 100 [解析] 73－21＝52，52＋2＝54，54＋46＝100. 【能力提升】5．A [解析] 作出散点图可知授课天数与分数存在回归关系． 6．C [解析] 根据独立性检验的思想知，选项C 正确．7．C [解析]对于变量Y 与X 而言，Y 随X 的增大而增大，故Y 与X 正相关，即r 1>0；对于变量V 与U 而言，V 随U 的增大而减小，故V 与U 负相关，即r 2<0.∴r 2<0<r 1.故选C.8．A [解析] 由已知数据得到如下2×2列联表：由公式 χ2＝382158×224×59×323≈13.11.由于13.11＞10.828，故有99.9%的把握认为含杂质的高低与设备是否改造是有关的．故选A.9．B [解析] 根据变量的相关关系的概念知选项A 正确；根据残差的概念和相关系数的概念知选项C ，D 正确；线性回归方程经过样本点中心(x ，y )，B 错．10．0.025 [解析] P (χ2≥5.024)＝0.025，那么认为“X 与Y 有关系”的犯错率就不会超过0.025.11．③ [解析] 由独立性检验的基本思想可得，只有③正确． 12．是 [解析] 由已知条件得出如下2×2列联表：χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ）＝228×（98×16－89×25）2123×105×187×41≈0.994.由于0.994<2.706，所以没有理由认为患慢性气管炎与吸烟量有关．即认为患慢性气管炎与吸烟量无关，是相互独立的．13．99.5% [解析] 列联表补充如下：因为χ2＝5030×20×25×25≈8.333>7.879，所以有99.5%的把握认为喜爱打篮球与性别有关．14．解：(1)设B 专业的4名女生为甲、乙、丙、丁，随机选取两个共有(甲，乙)，(甲，丙)，(甲，丁)，(乙，丙)，(乙，丁)，(丙，丁)6种可能，其中选到甲的共有3种可能，则女生甲被选到的概率是P ＝36＝12.(2)根据列联表中的数据χ2＝100×（12×46－4×38）216×84×50×50≈4.762，由于4.762>3.841，因此在犯错误的概率不超过0.05的前提下认为工科院校中“性别”与“专业”有关系．15．解：(1)如下表：χ2＝30×（10×8－6×6）216×14×16×14≈1.157 5<2.706.所以在犯错的概率不超过0.10的前提下不能判断会俄语与性别有关．(2)会俄语的6名女记者，分别设为A ，B ，C ，D ，E ，F ，其中A ，B ，C ，D 曾在俄罗斯工作过，则从这6人中任取2人有AB ，AC ，AD ，AE ，AF ，BC ，BD ，BE ，BF ，CD ，CE ，CF ，DE ，DF ，EF 共15种，其中2人都在俄罗斯工作过的是AB ，AC ，AD ，BC ，BD ，CD 共6种，所以抽出的女记者中，2人都在俄罗斯工作过的概率是P ＝615＝25.【难点突破】16．解：(1)甲流水线样本的频率分布直方图如下：(2)由表1知甲样本中合格品数为8＋14＋8＝30，由图1知乙样本中合格品数为 (0.06＋0.09＋0.03)×5×40＝36，故甲样本合格品的频率为3040＝0.75，乙样本合格品的频率为3640＝0.9，据此可估计从甲流水线任取1件产品，该产品恰好是合格品的概率为0.75，从乙流水线任取1件产品，该产品恰好是合格品的概率为0.9.(3)2×2列联表如下：∵χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ）＝80×（120－360）266×14×40×40≈3.117>2.706，∴有90%的把握认为产品的包装质量与两条自动包装流水线的选择有关．附：高考各科的答题技巧一、掌握好基础知识掌握基础知识没有捷径，俗话说“巧妇难为无米之炊”，没有基础知识，再多的答题技巧也没有用，有了基础知识，才能在上面“玩一些复杂的花样”，让自己分数提高一个层次，其实很简单，上课认真听讲，放学再温习一两遍足矣。