第四章 习题解答
第4章 习题解答

第4章 习题与答案4-1作简谐振动的物体,每次通过同一位置时,不一定相同的量是 [ ] (A) 位移 ; (B) 速度 ; (C) 加速度; (D) 能量。
[答案:B ]4-2 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为 [ ](A) π; (B) π/2; (C) 0; (D) θ [答案:C ]4-3 谐振动的振动曲线如题4-3图所示,则有[ ] (A )A 超前π/2; (B )A 落后π/2; (C )A 超前π; (D )A 落后π。
[答案:A ]4-4 一个质点作简谐振动,振辐为A ,在起始时刻质点的位移为A /2,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为题4-4图 中哪一个? [ ][答案:B ]4-5 两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点恰在最大负位移处。
则第二个质点的振动方程为 [ ] (A) )π21cos(2++=αωt A x ; (B) )π21cos(2-+=αωt A x ; (C) )π23cos(2-+=αωt A x ; (D) )cos(2π++=αωt A x 。
[答案:A ]4-6 已知某简谐振动的振动曲线如题4-6图所示。
则此简谐振动的振动方程(SI )为 [ ](A) 题4-4图题4-3图(A )220.02cos()33x t =π+π;(B )220.02cos()33x t =π-π;(C )420.02cos()33x t =π+π;(D )420.02cos()33x t =π-π。
[答案:C ]4-7 弹簧振子作简谐振动,先后以相同的速度依次通过A 、B 两点,历时1秒,质点通过B 点后再经过1秒又第二次通过B 点,在这2秒内质点通过的总路程为12cm ,则质点的振动周期和振幅分别为 [ ](A )3s 、12cm ; (B )4s 、6cm ; (C )4s 、9cm ; (D )2s 、8cm 。
原子物理学第四章习题解答

第四章习题解答4-1 一束电子进入1.2T 的均匀磁场时,试问电子的自旋平行于和反平行于磁场的电子的能量差为多大?解:∵磁矩为μu r 的磁矩,在磁场B u r中的能量为:U = -μu r ·B u r= -sz μ B电子自旋磁矩 sz μ=±B μ∴电子自旋平行于和反平行于磁场的能量差u =B μ B – (-B μB) =2B μ B ∴u = 2B μ B =2 ×0.5788×410-eV ·1T -× 1.2 T = 1.39 ×410- eV4-2 试计算原子处于23/2D 状态的磁矩μ及投影μz 的可能值. 解:由23/2D 可知 S=12 J=32L=2 ∴j g =32+12(1)(1)(1)S S L L J J +-++=32+121323223522⨯-⨯⨯=45又j μ=j g Bμ45B μ =1.55 B μ∴μ=1.55 B μ又,j z j j B m g μμ= 又3113,,,2222j m =--∴,142×255j z B B μμμ=±=±或,346×255j z B B μμμ=±=±即,6226(,,,)5555j z B μμ=--4-3 试证实:原子在63/2G 状态的磁矩等于零,并根据原子矢量模型对这一事实作出解释.解:由63/2G 可知:S =52 J = 32L = 4∴5745 31(1)(1)3122··03522(1)22×22JS S L LgJ J⨯-⨯+-+=+=+=+∴(1)0J j Bj j gμμ=+=即原子在63/2G状态的磁矩等于零。
解释:∵原子的总角动量为J L S=+u r u r u r,而处于63/2G态原子各角动量为:(1)4(41)20 4.47L L L=+=+==h h h h5535(1)(1) 2.9622S S S=+=+==h h h h3315(1)(1) 1.94222J J J=+=+==h h h h则它们的矢量关系如图示:Lu r和Su r同时绕Ju r旋进,相对取项保持不变由三角形余弦定理可知:22222211()[(1)(1)(1)]22L J L J S L L J J S S⋅=+-+++-+u r u rh h h=22355715[45]222222=⨯+⨯-⨯=hh而222221573515()(45)2222224S J S J L⋅=+-=⨯+⨯-⨯=-u r u r hh∴相应的磁矩2B BS Sg S Sμμμ=-=-u r u r u rh hB B Lg L L μμμ∆=-=-u ru r u r hhS L μμμ=+u r u ru r由于磁矩μu r 随着角动量绕J u r 旋进,因而对外发生效果的是μu r在J u r 方向上的分量。
功和能习题解答

第四章 功和能一 选择题1. 一辆汽车从静止出发,在平直公路上加速前进时,若发动机功率恒定,则正确的结论为:( )A. 加速度不变B. 加速度随时间减小C. 加速度与速度成正比D. 速度与路径成正比 解:答案是B 。
简要提示:在平直公路上,汽车所受阻力恒定,设为F f 。
发动机功率恒定,则P =F v ,其中F 为牵引力。
由牛顿运动定律得a m F F =-f ,即:f F P/m -v a =。
所以,汽车从静止开始加速,速度增加,加速度减小。
2. 下列叙述中正确的是: ( ) A. 物体的动量不变,动能也不变. B. 物体的动能不变,动量也不变. C. 物体的动量变化,动能也一定变化. D. 物体的动能变化,动量却不一定变化. 解:答案是A 。
3. 一颗卫星沿椭圆轨道绕地球旋转,若卫星在远地点A 和近地点B 的角动量与动能分别为L A 、E k A 和L B 、E k B ,则有:( )A. L B > L A , E k B > E k AB. L B > L A , E k B = E k AC. L B = L A , E k B > E k A地球BA选择题3图D. L B = L A , E k B = E k A 解:答案是C 。
简要提示:由角动量守恒,得v B > v A ,故E k B > E k A 。
4. 对功的概念有以下几种说法:(1) 保守力作正功时,系统内相应的势能增加. (2) 质点运动经一闭合路径,保守力对质点作的功为零.(3) 作用力和反作用力大小相等、方向相反,所以两者所作功的代数和必为零. 在上述说法中: ( )A. (1)、(2)是正确的;B. (2)、(3)是正确的;C. 只有(2)是正确的;D. 只有(3)是正确的. 解:答案是C 。
5. 如图所示,足够长的木条A 置于光滑水平面上,另一木块B 在A 的粗糙平面上滑动,则A 、B 组成的系统的总动能:( )A. 不变B. 增加到一定值C. 减少到零D. 减小到一定值后不变 解:答案是D 。
量子力学周世勋习题解答第四章

第四章习题解答4.1.求在动量表象中角动量x L 的矩阵元和2x L 的矩阵元。
解:⎰⋅⋅'-'-=τπd e p z p y e L r p i y z rp i p p x)ˆˆ()21()(3 ⎰⋅⋅'--=τπd e zp yp e r p i y z rp i)()21(3 ⎰⋅⋅'-∂∂-∂∂-=τπd e p p p p i e rp i zy y z r p i))(()21(3⎰⋅'-∂∂-∂∂-=τπd e p p p p i r p p i z y y z)(3)21)()(()()(p p p p p p i y z z y'-∂∂-∂∂= δ ⎰''=τψψd L x L p x p p p x 2*2)()( ⎰⋅⋅'--=τπd e p z p y e r p i y z r p i23)ˆˆ()21( ⎰⋅⋅'---=τπd e p z p y p z p y e r p i y z y z rp i)ˆˆ)(ˆˆ()21(3 ⎰''-∂∂-∂∂-=τπd e p p p p i p z p y e rp i yz z y y z r p i))()(ˆˆ()21(3 ⎰⋅⋅'--∂∂-∂∂=τπd e p z p y e p p p p i r p i y z rp i y z z y)ˆˆ()21)()((3 ⎰⋅'-∂∂-∂∂-=τπd e p p p p r p p i y z z y)(322)21()()()(22p p p p p p yz z y'-∂∂-∂∂-= δ #4.2 求能量表象中,一维无限深势阱的坐标与动量的矩阵元。
解:基矢:x a n a x u n πsin 2)(=能量:22222a n E n μπ =对角元:2sin 202a xdx a m x a x a mm ==⎰π 当时,n m ≠ ⎰⋅⋅=a mn dx ax x a m a x 0)(sin )(sin 2π[][]1)1()(4)(1)(11)1(])(sin )()(cos )([])(sin )()(cos )([1)(cos )(cos 12222222022202220---=⎥⎦⎤⎢⎣⎡+----=⎥⎥⎦⎤+++++-⎢⎢⎣⎡--+--=⎥⎦⎤⎢⎣⎡+--=--⎰n m n m a aa n m mnan m n m a x a n m n m ax x a n m n m a x a n m n m ax x a n m n m a a dx x a n m x a n m x a ππππππππππππ[][]a n m mn i n m n m a a n i x a n m n m a x a n m n m a a n i dxx a n m x a n m a n i xdxa n x a m an i xdxan dx d x a m a i dx x u p x u p n m nm aa a a n m mn )(21)1(]1)1()(1)(1 )(cos)()(cos )()(sin )(sin cos sin 2sin sin 2)(ˆ)(2220202020*---=--⎥⎦⎤⎢⎣⎡-++=⎥⎦⎤⎢⎣⎡--+++=⎥⎦⎤⎢⎣⎡-++-=⋅-=⋅-==--⎰⎰⎰⎰πππππππππππππππ#4.3 求在动量表象中线性谐振子的能量本征函数。
弹性力学(徐芝纶)第四章习题答案

第四章 习题解答4-14-2、解:本题为轴对称应力问题,相应的径向位移为: ()()()()()θ+θ+⎥⎦⎤⎢⎣⎡υ-+υ-+-υ-+υ+-=sin cos ln K I Cr 12Br 311r Br 12r A 1E 1u r (1) 轴对称应力通式为()()02ln 232ln 2122=+++-=+++=θθτσσr r C r B rAC r B r A由应力边界条件()()()()0,00,===-=====b r r b r r a r r a r r q θθτστσ并结合位移单值条件可知B=0,求得:22222222ab qa C a b qb a A -=--= 因半径的改变与刚体位移I ,K 无关,且为平面应变问题,将A 、B 、C 代入(1)式,并将υυυυ-→-→1,12EE 得:内半径的改变:()()()⎪⎪⎭⎫⎝⎛-+-+-=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛--+-⎪⎭⎫ ⎝⎛-+-=∆=υυυυυυυυ11*111112222222222222a b a b Eqa a a b qa a a b q b a E u ar r外半径的改变:()()()2222222222221*11111a b ab E qa b a b qa b a b q b a Eu br r --=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛--+-⎪⎭⎫ ⎝⎛-+-=∆=υυυυυυ 圆筒厚度的改变:()()()⎪⎪⎭⎫⎝⎛-++---=∆-∆=∆==υυυ112a b a b E qa u u R ar r b r r4-2另解:半径为r 的圆筒周长为r π2,受载后周长则为 ()θθεπεππ+=+1222r r r , 于是半径为 ()θε+1r ,半径的改变量则为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛+--=⎪⎭⎫⎝⎛---=C r A C rA r E E r r r 212111*2222υυυσυυσυεθθ将对应的A 、C 及r=a,b 分别代入,可求出内外半径的改变及圆筒厚度的改变。
(解答)《随机过程》第四章习题

第四章 二阶矩过程、平稳过程和随机分析 习题解答1、 设∑=-=Nk k k kn U n X 1)cos(2ασ,其中k σ和k α为正常数,)2,0(~πU U k ,且相互独立,N k ,,2,1 =,试计算},1,0,{ ±=n X n 的均值函数和相关函数,并说明其是否是平稳过程。
解:计算均值函数和相关函数如下0)}{cos(2)cos(2}{)(11=-=⎭⎬⎫⎩⎨⎧-==∑∑==Nk k k k N k k k k n X U n E U n E X E n ασασμ∑∑∑∑∑∑======-=--=--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-⋅⎥⎦⎤⎢⎣⎡-=Ni i i N i i i i i i Ni Nj j j i i j i N j j j j N i i i i X m n U m U n E U m U n E U m U n E m n R 12121111)](cos[)}cos(){cos(2)}cos(){cos(2)cos(2)cos(2),(ασαασαασσασασ因此可知,},1,0,{ ±=n X n 是平稳随机过程。
2、 设有随机过程))(cos()(t t A t X πηω+=,其中0>ω为常数,}0),({≥t t η是泊松过程,A 是与)(t η独立的随机变量,且2/1}1{}1{===-=A P A P 。
(1) 试画出此过程的样本函数,并问样本函数是否连续? (2) 试求此过程的相关函数,并问该过程是否均方连续? 解:(1)样本函数不连续。
(2)令:012≥>t t ,下面求相关函数:)(221)(212210)(1212211212121211212212122112221122121121212cos cos )]}(cos[)]({cos[21!)]([)]}(cos[)]({cos[)1(21))]}()(()(cos[))]()(()(2)({cos[21))]}()(()(cos[))]()(()({cos[21))}(cos())({cos(}{))}(cos())(cos({)}()({),(t t t t k t t k kX e t t e t t t t e k t t t t t t t t t t t t t t t E t t t t t t t t E t t t t E A E t t t t A E t X t X E t t R ----∞=--⋅=⋅-++=⋅-⋅-++-=-+-+-+++=-+-++++=++⋅=++==∑λλλωωωωλωωηηπωηηππηωηηπωηηπωπηωπηωπηωπηω因为:t t t R ωξ2cos ),(=因此该过程是均方连续的随机过程。
第4章 习题解答
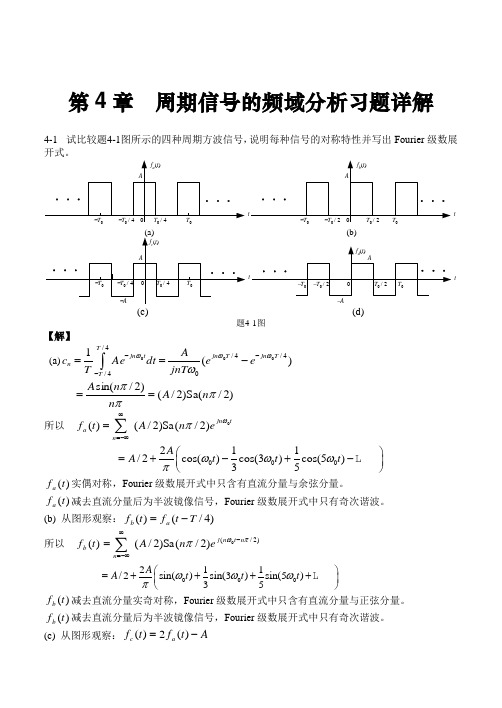
第4章 周期信号的频域分析习题详解4-1 试比较题4-1图所示的四种周期方波信号,说明每种信号的对称特性并写出Fourier 级数展开式。
tt(b)tt-A(c) (d)题4-1图【解】 (a))(14/4/04/4/000T jn T jn tjn T T n eejnT A dt AeTc ωωωω----==⎰)2/(Sa )2/()2/sin(πππn A n n A ==所以 tjn n a e n A t f 0)2/(Sa )2/()(ωπ∑∞-∞==000211/2cos()cos(3)cos(5)35A A t t t ωωωπ⎛⎫=+-+- ⎪⎝⎭)(t f a 实偶对称,Fourier 级数展开式中只含有直流分量与余弦分量。
)(t f a 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(b) 从图形观察:)4/()(T t f t f a b -=所以 )(t f b )2/(0)2/(Sa )2/(πωπn t n j n en A -∞-∞=∑=000211/2sin()sin(3)sin(5)35A A t t t ωωωπ⎛⎫=++++ ⎪⎝⎭)(t f b 减去直流分量实奇对称,Fourier 级数展开式中只含有直流分量与正弦分量。
)(t f b 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(c) 从图形观察:A t f t f a c -=)(2)(第4章 周期信号的频域分析 83所以 tjn n n c en A t f 0)2/(Sa )(0,ωπ∑∞≠-∞==000411c o s ()c o s (3)c o s (5)35A t t t ωωωπ⎛⎫=-+- ⎪⎝⎭)(t f c 实偶对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的余弦分量。
(d) 从图形观察:)4/()(T t f t f c d -=所以 )2/(0,0)2/(Sa )(πωπn t n j n n d en A t f -∞≠-∞=∑=000411sin()sin(3)sin(5)35A t t t ωωωπ⎛⎫=++- ⎪⎝⎭)(t f d 实奇对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的正弦分量。
大学电路习题第4章
第四章(电路定律)习题解答一、选择题1.受控源是不同于独立源的一类电源,它一种激励。
A.是; b.不是2.下列电路定理、定律中,仅能用于线性电路的有。
A.KVL 和KCL ; B.叠加定理;C.替代定理; D.戴维南定理和诺顿定理3.甲乙两同学对图4—1所示电路应用替代定理求电流I 。
甲画了图4—2(a )电路,乙画了图4—2(b )电路,后来他们认为图是不可行的,其理由是。
A.不满足“置换前后电路应具有唯一解”这一条件;B.电路中不存在电阻;C.电流等于零了;D.电流等于无限大了4.图4—3所示电路的诺顿等效电路如图4—4,则s I 、eq G 分别为。
a.S 403A 1,;b.S 340A 1,;c.S 403A 2,;d.S 103A 2,5.图4—5(a )所示电路的端口特性如图4—5(b ),其戴维南等效电路如图4—5(c ),则oc u 、i R 分别为。
A.Ω-20V 20,;B.Ω20V 20,;C.Ω-20V 20,; C.Ω10V 10,二、填空题1.线性一端口电路N 如图4—6所示。
当0=R 时,A 5=i ;当∞→R 时V 10=u 。
如果Ω=5R ,则=u ,=i 。
2.图4—7所示电路中,N 为线性电路,且Ω=10R 。
当0=s u ,0=s i 时,V 5=u ;当A 2=s i ,0=s u 时,V 8=u ;当0=s i ,V 10=s u 时,V 6=u 。
那么,当A 6=s i ,V 4=s u 时,=i 。
3.图4—8(a )所示电路的戴维南等效电路如图4—8(b ),那么=s U ,=eq R 。
4.图4—9(a )所示电路的戴维南等效电路如图4—9(b ),则=s U ,=eq R 。
5.在图4—10(a )所示的电路中,i u 1024-=(i 的单位用安培时,u 的单位为伏特),其戴维南等效电路如图4—10(b ),则=s u ,=0R 。
三、计算题1.用叠加定理计算图4—11所示电路中的u 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4-1 如图是用频率为1 000 kHz 的载波信号同时传输两路信号的频谱图。
试写出它的电压表达式,并画出相应的实现方框图。
计算在单位负载上的平均功率P av 和频谱宽度BW AM 。
解:(1)为二次调制的普通调幅波。
第一次调制:调制信号:F = 3 kHz载频:f 1 = 10 kHz ,f 2 = 30 kHz第二次调制:两路已调信号叠加调制到主载频f c = 1000 kHz 上。
令 Ω = 2π ⨯ 3 ⨯ 103 rad/sω1 = 2π ⨯ 104 rad/s ω2= 2π ⨯ 3 ⨯ 104 rad/s ωc = 2π ⨯ 106 rad/s第一次调制:v 1(t ) = 4(1 + 0.5cos Ωt )cos ω1tv 2(t ) = 2(1 + 0.4cos Ωt )cos ω2t第二次调制:v O (t ) = 5 cos ωc t + [4(1 + 0.5cos Ωt )cos ω1t + 2(1 + 0.4cos Ωt )cos ω2t ] cos ωc t = 5[1+0.8(1 + 0.5cos Ωt )cos ω1t + 0.4(1 + 0.4cos Ωt )cos ω2t ] cos ωc t(2) 实现方框图如图所示。
(3) 根据频谱图,求功率。
○1 载频为10 kHz 的振幅调制波平均功率 V m01 = 2V ,M a1 = 0.5W 5.4)211(2W 22121a 01av1201m 01=+===M P P V P ;○2 f 2 = 30 kHz V m02 = 1V ,M a2 = 0.4W 08.1)211(2W 5.02122a 02av2202m 02=+===M P P V P ; ○3 主载频f c = 1000 kHz V m0 = 5VW 5.122120m 0==V P总平均功率P av = P 0 + P av1 + P av2 = 18.08 W ○4 BW AM 由频谱图可知F max = 33 kHz得 BW AM = 2F = 2(1033 -1000) = 66 kHz4-3 试画出下列三种已调信号的波形和频谱图。
已知ωc >>Ω (1) v (t ) = 5cos Ωt cos ωc t (V); (2) v (t ) = 5cos(ωc +Ω) t ;(3) v (t ) = (5 + 3cos Ωt ) cos ωc t 。
解:(1) 双边带调制信号(a);(2) 单边带调制信号(b);(3) 普通调幅信号(c)。
4-6 何谓过调幅?为何双边带调制信号和单边带调制信号均不会产生过调幅? 答:调制信号振幅大于载波信号振幅的情况称为过调幅。
因为双边带和单边带调制信号已经将载波信号抑制,故均不会产生过调幅。
4-8 一非线性器件的伏安特性为⎩⎨⎧≤>=00Dv v v g i式中v = V Q 十v 1+ v 2 = V Q +V 1m cos ω1t +V 2m cos ω2t 。
若V 2m 很小,满足线性时变条件,则在V Q = -V 1m /2、0、V 1m 三种情况下,画出g (v 1)波形,并求出时变增量电导g (v 1)的表示式,分析该器件在什么条件下能实现振幅调制、解调和混频等频谱搬移功能。
解:根据伏安特性画出增量电导随v 的变化特性g (v )如图所示。
(1)1m Q 21V V -=时,画出g (t ) 波形如图所示。
图中通角由,2121cos m m==V V θ求得3π=θ D 3π3πD031d 2π1g t g g ==⎰-ω )3πsin(π2d cos π1D 3π3πD n n n g t t n g g ==⎰-ωωt n n n g g t g n 11D D cos )3πsin(1π231)(ω∑∞=+= (2) V Q = 0时,画出g (v ) 的波形如图所示。
])12(cos π)12(2)1(21[)cos33π2cos π221()()(111D 11D 11D t n n g t t g t K g t g n n ωωωω---+=⋅⋅⋅+-+==∑∞=-(3) V Q = V 1m ,g (t ) = g D ,如图所示。
可见,(1)、(2)中g (t ) 含有基波分量,能实现频谱搬移功能,而(3)中g (t )仅有直流分量,故无法实现频谱搬移功能。
为实现消除一些有害无用的组合频率分量,使输出有用信号的质量提高,在实现频谱搬移功能时,应遵循有用信号较弱,参考信号较强的原则。
调制时:v 1 = V cm cos ωc t (载波),v 2 = V Ωm cos Ωt (调制信号)解调时:v 1 = V cm cos ωc t (参考信号),v 2 = V sm (1 + M a cos Ωt )cos ωc t (调幅信号) 混频时:v 1 = V Lm cos ωL t (本振信号),v 2 = V sm (1 + M a cos Ωt )cos ωc t (调幅信号)4-9 在如图所示的差分对管调制电路中,已知v c (t ) = 360cos10π ⨯ 106t (mV ),v Ω (t ) = 5cos2π ⨯ 103t (mV ),V CC =|V EE |= 10 V ,R EE =15 k Ω,晶体三极管 β 很大,V BE(on)可忽略。
试用开关函数求i C =(i C1 - i C2)值。
解:由教材(4-2-14)可知i C = i C1 - i C2 = )2(th Tc 0V vi令,TCM c V Vx =i 0 = I 0 + i Ω(t )其中mA))(10π2cos(1031)()(mA 31V 533EE EEEE 0t R t v t i R V I ΩΩ⨯⨯=≈=-≈-, mA))](10π2cos(101[31330t i ⨯+=-又1085.13mV26mV360T cm c >===V V x 则⋅⋅⋅-+-=≈t t t t K t x c c c c 2c c 5cos 5π43cos 3π4cos π4)()cos 2(th ωωωωω 所以)mA ]()10π50cos(084.0)10π30cos(14.0)10π10cos(42.0)][10π2cos(101[)()]10π2cos(101[31)cos 2(th 66633c 233c c 0C ⋅⋅⋅-⨯+⨯-⨯⨯+=⨯+≈=--t t t t t K t t x i i ωω4-11一双差分对平衡调制器如图所示,其单端输出电流kTqv R v I kT qv i i I i 2th 22th 221E 201650I +≈-+=试分析为实现下列功能(不失真),两输人端各自应加什么信号电压?输出端电流包含哪些频率分量,输出滤波器的要求是什么?(1)混频(取ωI =ωL - ωC );(2)双边带调制;(3)双边带调制波解调。
解:(1) 混频:v 1(t ) = v L (t ) =V Lm cos ωL t ,v 2(t ) = v S (t ) = V sm cos ωc t ,当V Lm > 260 mV ,V sm < 26 mV 工作在开关状态时,产生的组合频率分量有ωL ± ωc ,3ωL ± ωc ,⋅⋅⋅,(2n +1)ωL ± ωc ,输出采用中心频率为 ωI 的带通滤波器。
(2) 双边带调制:v 1(t ) = v c (t ) = V cm cos ωc t ,v 2(t ) = v Ω(t ) = V Ωm (t )cos Ωt 。
工作在开关状态时,产生的组合频率分量有ωc ± Ω,3ωc ± Ω,⋅⋅⋅,(2n +1)ωc ± Ω。
输出采用中心频率为 ωc ,BW 0.7 > 2F 的带通滤波器。
(3) 双边带调制波解调:v 1(t ) = v r (t ) = V rm cos ωc t ,v 2(t ) = v S (t ) = V m0cos Ωt cos ωc t 。
开关工作时,产生的组合频率分量有Ω,2ωc ± Ω,4ωc ± Ω,⋅⋅⋅,2n ωc ± Ω。
输出采用低通滤波器,BW 0.7 > 2F 。
4-16 采用双平衡混频组件作为振幅调制器,如图所示。
图中v c (t ) = V cm cos ωc t ,v Ω(t ) = V Ωm cos Ωt 。
各二极管正向导通电阻为R D ,且工作在受v C (t )控制的开关状态。
设R L >>R D ,试求输出电压v O (t )表达式。
解:作混频器,且v C >> v Ω,各二极管均工作在受v C 控制的开关状态。
当 v C > 0,D 1、D 2导通,D 3、D 4截止 当 v C < 0,D 3、D 4导通,D 1、D 2截止 (1) 当 v C > 0时,等效电路,i I = i 1 - i 2 回路方程为:⎩⎨⎧=-+--=-++-②①00)(C D 2L I L 21D 1C v R i R i v R i i R i v v ΩΩ ○1 - ○2 2( i 1 - i 2)R L + 2 v Ω + ( i 1 - i 2)R D = 0DL 21I 22R R v i i i Ω+-=-= 考虑v C 作为开关函数K 1(ωc t )所以 )(2)(2c 1DL I t K R R t v i Ωω+-=(2) 同理可求v C < 0时i Ⅱ)π(2)(2c 1D L 43-+-=-=t K R R t v i i Ωω(3) R L 总电流 i = i Ⅰ- i Ⅱ)(2)(2)]π()([2)(2c 2DL c 1c 1D L t K R R t v t K t K R R t v ΩΩωωω+-=--+-=(4) v O (t ) ∵ R L >> R D ∴)()()()(22)(c 2c 2DL LO t K t v t K t v R R R t v ΩΩωω-≈+-=4-23 晶体三极管混频器的输出中频频率为f I = 200 kHz ,本振频率为f L = 500 kHz ,输人信号频率为f c = 300 kHz 。
晶体三极管的静态转移特性在静态偏置电压上的幂级数展开式为i C = I 0+av be +2be bv +3be cv 。
设还有一干扰信号v M =V Mm cos (2π×3.5×105t ),作用于混频器的输人端。
