出行分布预测
4 四步骤交通需求预测模型(1)概述与出行生成预测

出行生成 出行分布 方式划分
交通分配
“四阶段”模型内容描述(2)
出行分布(Trip Distribution)
对每个交通小区,它所产生的这 些出行量究竟到那个分区去了? 它所吸引的这些出行量又究竟 来自哪里?出行分布也就是要 预测未来规划年各个分区之间 出行的交换量
出行生成 出行分布 方式划分
交通分配
根据以上划分可以看出,伦敦1963年规划把家庭 划分为6×6×3=108类
1 出行生成预测:相关基本概念
(4)出行生成的两种量化表达
出行产生量(Trip Generation)
单位时间内某一个交通小区的出行产生量等于家 庭端点在这个分区的由家出行数,与起点在这个 分区的非由家出行和货物出行的出行数之和
出行吸引量(Trip Attraction)
单位时间内某一个交通小区的出行吸引量等于非 家庭端点在这个分区的由家出行数,与终点在这 个分区的非由家出行数和货物出行数之和
起讫点与产生吸引点的区别
A B 公司和饭店
家
C 客户
1 出行生成预测:相关基本概念
(3)区分出行产生点、吸引点与出行起讫点的意义 由于一个交通小区的交通出行发生量主要是由这 个小区的土地利用形态决定的,而起讫点的概念 与用地形态没有关系 例如:居住用地,其既可以是出行的起点(去上 班),也可以是出行的讫点(下班回家) 从起讫点的概念出发,无法由交通小区未来的用 地模式预测该小区的交通出行发生量
将各交通小区之间出行分布量分 配到交通网络的各条边上去的过 程,预测交通需求PA分布各组成 部分流量具体在道路交通网络上 的交通流量
出行生成 出行分布 方式划分
交通分配
“四阶段”模型功能说明
“四阶段”模型用于进行交通需 求预测,以用地和社会经济等 相关数据作为输入,通过“四 阶段”模型进行处理,得到未 来年每个路段的交通流量数据, 以预测的未来年路段交通流量 数据为基础进行新建道路或者 道路拓宽等交通设施建设依据
3-2-交通分布预测

例3-7:利用基础年的OD矩阵和目标年发生交通 量的预测值求目标年OD矩阵
D O
1
2
3 合计 预测值
1
17.0 7.0
4.0 28.0 38.6
2
7.0 38.0 6.0 51.0 91.9
3
4.0 5.0 17.0 26.0 36.0
合计 28.0 50.0 27.0 105.0 166.5
现状的O-D分布 增长系数法预测 重力模型法预测
•即使没有完整的现状OD表也能进行预测。
(其基本假设为交通区 i 到交通区 j的出行分布量与i区 的出行发生量O(i)、j区的出行吸引量D(j)成正比, 与 i区和 j区之间的出行阻抗成反比。)
•重力模型法是交通规划中使用最广泛的 交通分布预测模型。
比较各种增长率模型的基本假设、计算方法和应用 条件。
➢ 常增长率模型? ➢ 平均增长率模型? ➢ Detroit模型(底特律法)? ➢ Fratar模型(福莱特法)? ➢ Furness模型(佛尼斯法)?
增长系数法的特点:
•当土地利用、交通源布局等有较大变化、
预测区域交通设施状况有较大变化时,误 差较大。
不收敛转步骤二,循环进行
4、Fratar模型福莱特法
福莱特法假设i,j小区间分布交通量qij的增长系数 不仅与i小区的发生增长系数和j小区的吸引增长系 数有关,还与整个规划区域的其他交通小区的增长 系数有关。
fF
(FOmi ,
FDmj )
FOmi
FDmj
( Li Lj 2
)
Li
Oim qimj FDmj
D O
1
2
3 合计
第七讲 出行分布预测3

19
误差小于3%,停止迭代,得到:
0.8957, K4 1.0643,K5 1.2618 K1 0.002996, K2 0.003501, K3
第三步: P\A 1 2 3 147.6 402.4 4 95.7 104.3 5 56.7 193.3 小计 300.0 700.0
f
R R
ij
ij
指数型
f
R exp b R
ij ij
–指数型只含一个参数,比较容易标定,较常使用。
半钟型
1 f Rij a bRij
8
–半钟型含两个以上参数,使用的较少
(幂与指数)复合型
f
R e
ij
bRij
R
1 1Leabharlann 代入,求得0.003*300 0.003499*700 K3 0.8958 3 3 0.003*300 0.003499*700 K4 1.0640 2 5
1
1
第一次 迭代
0.003*300 0.003499*700 K5 1.2621 5 4
i
14
1、参数的标定——
Step1: 1
f Rij Rij
Step2:
求Ki、K j
2-1: 令K j 1 j 1, 2, , n
1 ,求得Ki 2-2: 把K j j 1, 2 , n 代入Ki K j Aj f Rij
小计
550.0
200.0
250.0
1000
20
第四步:
150*3 100*2 50*5 400*3 100*5 200*4 R 3.4 1000 147.6*3 95.7*2 56.7*5 402.4*3 104.3*5 193.3*4 ˆ R 3.3996 1000 ˆ / R 3%, 可认为 1可以接受 因为 R R
TransCAD实验三 出行分布预测

实验三:重力模型用于出行分布预测一、实验的输入与输出文件1、输入文件➢地理文件:小区地理文件(njZone.dbd)、线类型地理文件(njroad.dbd);➢矩阵文件:现状出行分布矩阵(BaseOD.mtx);2、输出文件➢地理文件:质心地理文件(Center.dbd);➢网络文件:道路网络();➢矩阵文件:小区质心间最短出行时间阻抗矩阵(SPMAT.mtx)、出行分布预测矩阵(CGRAV.MTX);➢数据表文件:重力模型参数标定输出数据表文件(Summary.bin);二、实验过程1、创建质心连杆和交通网络(1)创建质心地理文件在TransCAD中打开njZone.dbd小区地理文件,选择Tools/Export菜单项,弹出Export Zone Geography对话框。
在该对话框中,To后选择Standard Geographic File,ID Field后选择ZoneID,同时勾选Exports as Centroid points,点击OK进行确定,并将其保存为Center.dbd地理文件。
(2)质心连杆点击顶部工具栏按钮,弹出Layers对话框,点击Add layer按钮,分别打开njroad.dbd和Center.dbd地理文件,选中njroad point图层,点击Show Layer按钮,完成后点击Close按钮,关闭对话框。
将njroad point 置为当前层,选择Dataview/Modify Table菜单项,在弹出的对话框中为节点图层地理文件添加一个名为Index(Integer型)的属性字段。
将njZone置为当前层,选择Tools/Map Editing/Connect菜单项,弹出Connect对话框。
在该对话框中,选择Fill选项卡,在Node Field后的下拉列表框中选择Index,同时勾选IDs from Zone layer单选框,点击OK,完成小区质心与现有路网的连接。
出行分布预测(第五章)

21
二、预测方法
[例题5] D.第1次迭代计算结果
A P
1 20.744 11.165 4.902 36.811
2 10.991 77.987 7.885 96.862
3 4.753 9.318 20.287 34.358
合计 36.478 98.470 33.074 168.031
1 2 3 合计
1 0 q32 q32 Fp03 Fa02 /(Q / Q 0 ) 5.0 1.3846 1.8060 / 1.5857 7.885
1 0 q33 q33 Fp03 Fa03 /(Q / Q 0 ) 17.0 1.3846 1.3667 / 1.5857 20.287
0 0 0 q1 q ( F F 23 23 p2 a 3 ) / 2 6.0 (1.8020 1.3667 ) / 2 9.506
1 0 q31 q31 ( Fp03 Fa0 1 ) / 2 4.0 (1.3846 1.4036 ) / 2 5.576
0 0 0 0 q1 q F F /( Q / Q ) 6.0 1.8020 1.3667 / 1.5857 9.318 23 23 p2 a3
1 0 0 q31 q31 Fp03 Fa0 /( Q / Q ) 4.0 1.3846 1.4036 / 1.5857 4.902 1
j j
B.特点评价:该方法是在底特律市1956年规划首次被开发 利用,收敛速度较快;等效于使用现状出行分布表的同时 概率最大化方法理论求解结果。
17
二、预测方法
[例题5]:已知3个交通小区的现状PA表和规划年各小区的产生 量和吸引量,试用底特律法求解规划年PA矩阵。设定收敛标 准为3% 。
交通规划 第五章 交通分布
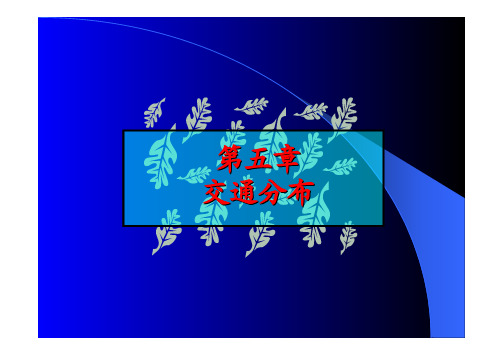
j
i
三、交通分布预测方法
根据各交通小区未来年份产生量、吸引量以及现 状OD矩阵求解未来OD矩阵; (增长系数法)
用未来年份产生量、吸引量以及交通区之间的交 通阻抗矩阵求解未来OD矩阵; (重力模型法)
根据出行产生、吸引量、交通区间阻抗、各小区 吸引概率,求解未来OD矩阵; (介入机会法)
根据交通小区划分和路段交通流量,反推交通小
作用 解决:预测每个交通小区的产生量去向 何方?吸引量来自哪里?政策依据。
tij
i
j
二、出行分布矩阵特性
出行分布矩阵的行数与列数一般相同,如 果行数与列数不相同,即m*n形式,属于 Hitchcock问题。
矩阵单元格:tij为以i小区为产生点以j小区 为吸引点的出行量。
矩阵的行表示产生,列表示吸引。矩阵的 行和表示产生量,列和表示吸引量。
差 大
FO13 U 3 / O3 36 / 33.074 1.0885
于
FD11 V1 / D1 39.3 / 36.8 1.0676
FD12 V2 / D2 90.3 / 96.9 0.9323
FD13 V3 / D3 36.9 / 34.4 1.074
T/X=1.01
3%
结
3
4.9 7.9 20.3 33.1 36.0
果
总计 36.8 96.9 34.4 168.1
未来 V 39.3 90.3 36.9
166 .5
(2)重新计算FO和FD、T/X
FO11 U1 / O1 38.6 / 36.5 1.0579
误
FO12 U 2 / O2 91.9 / 98.5 0.9333
2
7.0 38.0 6.0 51.0 91.9
完整word版,交通出行分布预测
交通出行分布预测作业二零一五年六月九号1. 分别采用平均增长率法、Fratar法对5月20日的OD调查表进行交通出行分布预测。
解:(1)现状OD表的绘制及未来出行发生/吸引量的预测1)考虑到实际调查中可能出现的偏差,现对5月20日和6月1日调查的原始数据进行如下规则的处理:1. 若不同站点统计人数有所偏差,以韵苑、喻园以及南大门询问统计的人数为准;2. 在不违背现有站点已统计总数的前提下,各个站点现有交通产生量/吸引量即为各站点统计的下车人数/上车人数;3. 各站点之间的交通量按照上/下行车站点顺序,对其上/下车人数进行推算(如:从喻园到集贸的交通量因其之间只隔1段,故为喻园车的下车人数);4. 其他未统计站点按照实际情况合理补充和调整;5. 由于第一次未安排喻园站的统计,故两次统计结果偏差较大;6. 因统计结果不全,且实际该时段东九的交通量可忽略不计,故不考虑该站的上/下车人数。
2)在测算设定未来发生量和吸引量时,参照如下依据:1. 根据近几年华科招生人数变化以及工科专业人数比例(考虑到工科专业的实验及大学物理等要搭乘校车的课程)。
网上显示,2015年预计招生7180人,虽比2014年的7300人少,但考虑到有3个新增的工科专业以及未来校区总人数的增长,故对各个站点下午上课时段的交通量影响不大,且预计会有少量增加;2. 对于现状站点交通量为0的站点,为方便计算,可将其增长忽略不计,即仍视为0;3. 由于集贸以及绝望坡的餐饮业发展,预计人流量会有相对较大的增长;4. 考虑到人们出行需求的增长,南大门站作为从学校到光谷的出口,交通量增长相对较大。
最终结果整理如下表(答案不唯一):(2)根据第一次的OD 表,用平均增长率法进行交通出行分布预测。
1) 数学原理平均增长率法属于增长率法,其原理可表示为:未来分布=现状分布*增长系数。
假设站点i 和j 之间的现状交通量为t ij (0),i 站点现状的产生交通量为G i (0),未来的产生交通量为G i ,站点j 现状的产生交通量为A i (0),未来的产生交通量为A i ,增长率计算过程:1. 计算未来交通量第一次近似值:t ij (1)=t ij (0)f2. 得到第1次预测各小区的发生交通量和吸引交通量:G i(0)=∑t ij (1)jA i(0)=∑t ij (1)i3. 计算调整系数:αi =G i (0)G i(1)βi =A j(0)A j(1)4. 若两个调整系数均收敛到1左右,则停止计算,相应的t ij (1)即为所求的分布;否则迭代。
第四章 出行分布预测
q ij = α O i D j f ( c ij )
重力模型的标定
重力模型的特点 • 重力模型具有以下优点: 重力模型具有以下优点: (1)模型形式直观,可解释性强,易被规划人员理解 模型形式直观, 模型形式直观 可解释性强, 和接受; 和接受; (2)能比较敏感地反映交通供给变化对出行的影响, 能比较敏感地反映交通供给变化对出行的影响, 能比较敏感地反映交通供给变化对出行的影响 适用于中长期需求预测; 适用于中长期需求预测; (3)不需要完整的基年 不需要完整的基年O-D矩阵,如果有可信赖的模 矩阵, 不需要完整的基年 矩阵 型参数,甚至不需要基年O-D矩阵; 矩阵; 型参数,甚至不需要基年 矩阵 (4)特定小区(如新开发区)之间的分布量为零时, 特定小区( 特定小区 如新开发区)之间的分布量为零时, 也能进行预测 重力模型最主要的缺点是难以准确预测小区内出 行分布量、采用幂型、指数型函数时, 行分布量、采用幂型、指数型函数时,由于区内 出行距离很小,预测结果往往比实际偏高。 出行距离很小,预测结果往往比实际偏高。
i i ij j
j j ij i
Tij = tij a i b j (
Li + L j 2
)
Li =
∑t ∑tபைடு நூலகம்b
ij j ij j
Lj =
j
∑t ∑t a
ij i ij i
i
• Fratar 法计算过程较为繁琐,但收敛速度快,是 法计算过程较为繁琐,但收敛速度快, 实际规划工作中应用较多的一种方法。 实际规划工作中应用较多的一种方法。 • 总之,增长系数法结构简单,易于理解,且直接 总之,增长系数法结构简单,易于理解, 使用观测出行矩阵来预测出行增长, 使用观测出行矩阵来预测出行增长,不需要其他 额外的数据。但该方法有很多缺点,包括: 额外的数据。但该方法有很多缺点,包括: (1) 增长系数法要求有完整的现状出行分布矩阵,而 增长系数法要求有完整的现状出行分布矩阵, 得到这种基础数据的成本很高; 得到这种基础数据的成本很高; (2)增长系数法对于基年出行矩阵精度的依耐性较大, 增长系数法对于基年出行矩阵精度的依耐性较大, 增长系数法对于基年出行矩阵精度的依耐性较大 任何出行在基年出行矩阵中的误差将在计算过程 中被放大; 中被放大; (3)如果基年矩阵中有零元素,那么预测矩阵中对应 如果基年矩阵中有零元素, 如果基年矩阵中有零元素 的部分也为零, 的部分也为零,即这种方法无法补充观测矩阵中
第四章 出行分布预测
佛莱特法( 佛莱特法(Fratar method) )
• 佛莱特法是 佛莱特法是Fratar 1954年发表的一种方法。主要 年发表的一种方法。 年发表的一种方法 引进一个和各交通分区有关的数量关系, 引进一个和各交通分区有关的数量关系,作为其 增长率之修正依据。它基于两项基本假设: 增长率之修正依据。它基于两项基本假设: O (1)未来的出现空间分布与出行产生的增长率 (1)未来的出现空间分布与出行产生的增长率 ∑ t = a D 均成正比关系; 和出行吸引的增长率 ∑ t = b 均成正比关系; (2)未来的出现空间分布与两区间的出行阻扰因素成 未来的出现空间分布与两区间的出行阻扰因素成 反比关系, 反比关系,此处出行的阻扰因素可表示为 L i + L j 2 其基本公式为: 其基本公式为:
i i ij j
j j ij i
Tij = tij a i b j (
Li + L j 2
)
Li =
∑t ∑t b
ij j ij j
Lj =
j
∑t ∑t a
ij i ij i
i
• Fratar 法计算过程较为繁琐,但收敛速度快,是 法计算过程较为繁琐,但收敛速度快, 实际规划工作中应用较多的一种方法。 实际规划工作中应用较多的一种方法。 • 总之,增长系数法结构简单,易于理解,且直接 总之,增长系数法结构简单,易于理解, 使用观测出行矩阵来预测出行增长, 使用观测出行矩阵来预测出行增长,不需要其他 额外的数据。但该方法有很多缺点,包括: 额外的数据。但该方法有很多缺点,包括: (1) 增长系数法要求有完整的现状出行分布矩阵,而 增长系数法要求有完整的现状出行分布矩阵, 得到这种基础数据的成本很高; 得到这种基础数据的成本很高; (2)增长系数法对于基年出行矩阵精度的依耐性较大, 增长系数法对于基年出行矩阵精度的依耐性较大, 增长系数法对于基年出行矩阵精度的依耐性较大 任何出行在基年出行矩阵中的误差将在计算过程 中被放大; 中被放大; (3)如果基年矩阵中有零元素,那么预测矩阵中对应 如果基年矩阵中有零元素, 如果基年矩阵中有零元素 的部分也为零, 的部分也为零,即这种方法无法补充观测矩阵中
交通规划 5出行分布预测
Pi qij
Aj qij
,
j
i
Q Pi Aj qij qij
i
j
ij
ji
式中,(i,j=1, … ,n)
5
二、预测方法
1、预测方法种类 我们通过交通调查资料的分析和预测,可以找到和利用的数
据有:现状PA表,两个分区之间的交通阻抗矩阵。至今开发的出 行分布预测方法有:增长率法、引力模型法、机会模型法等。我 们详细介绍前面两种,第三种因为理论依据不足且难以实用,不 做详细介绍。预测方法的大体结构如下所示:
《交通规划》
四阶段模型——出行分布预测
蒋阳升 教授 2011~2012年第二学期
西南交通大学交通运输与物流学院 交通工程专业
1
一、基本概念
1、出行分布量 出行分布量是指分区i与分区j之间平均单位时间内的出行量。
单位时间可以是一天、一周、一月等,也可以是专指高峰小时 。 qij——以分区i为产生点(不一定是出行的起点),以分区j为吸引点
3
36.0
合计 28.0 51.0 26.0 105.0
合计 39.3 90.3 36.9 166.5
11
二、预测方法
[例.求各小区产生量和吸引量的增长率,k=0
Fp01
P1 P10
38.6 28.0
1.3786
Fa01
A1 A10
39.3 28.0
1.4036
,
Fp02
P2 P20
10
二、预测方法
[例题4]:已知3个交通小区的现状PA表和规划年各小区的产生量 和吸引量,试用平均增长率法求解规划年PA矩阵。设定收敛 标准为3% 。
现状PA
A1
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章出行分布预测§5.1 概念从出行发生预测可以得知对象区域各个分区出行产生量和出行吸引量。
下面的问题是:就某个分区而言,它所产生的这些出行量究竟到那个分区去了?它所吸引的这些出行量又究竟来自哪里?也就是要预测未来规划年各个分区之间出行的交换量。
我们把分区之间的出行的交换量叫做“出行分布量”,本章就来研究出行分布量的预测问题。
5.1.1 出行分布量出行分布量是指:分区i 与分区j 之间平均单位时间内的出行量,单位时间可以是一天、一周、一月等,也可以是专指高峰小时。
就一对分区i 和j 而言,它由两部分q ij 、q ji 组成:q ij ——以分区i 为产生点(注:不一定是出行的起点),以分区j 为吸引点(不一定是出行的终点)的出行量。
q ji ——以分区j 为产生点,分区i 为吸引点的出行量。
如同一个分区的产生量不一定等于吸引量一样,q ij 不一定等于q ji 。
从下面的例子可以看出这一点。
例5-1 如图5-1所示的两分区之间的六次出行中;q ij =4(出行1、2、5、6)q ji =2(出行3、4)但以i 为起点的出行数=3(出行1、4、5);以j 为起点的出行数=3(出行2、3、6)。
5.1.2 出行分布矩阵(PA 矩阵)出行分布矩阵是一个二维表(矩阵),行坐标为吸引分区号(Absorbing zone ),列坐标为产生分区号(Producing zone ),元素为出行分区量。
如表5-1所示,表5-1中的行数和列数相等。
从理论的严格意义上讲,产生区和吸引区不一定相同,甚至某些分区只是产生区,但不吸引任何出行,因而不是吸引区,如纯住宅区,也可能有某些分区只是吸图例:h —家庭;s —学校;f —工厂图5-1 (例5-1)两个分区间的六次出行引区,但不是产生区。
但是,实际中,绝大多数分区既是产生区又是吸引区,为了叙述简便起见,我们一般假定产生区和吸引区数相同,用n 表示。
但在后面也给出两者不相同的实例(例5-5)。
对于城市交通而言,由于市民在市内的出行都是当天返回的,因此一分区出行的起点数总是等于讫点数,所以基于起讫点的出行量矩阵(OD 矩阵)是对称的。
早期的分布矩阵是指这种OD 矩阵,但正如第四章所指出的,由于以起讫点作为出行端点进行分析不便于出行的预测,所以OD 矩阵现在交通规划中基本不用。
由于一个分区的出行产生点和吸引点不一定相等,所以基于产生点、吸引点的出行量矩阵不一定是对称的,这一点是要特别注意的。
可是,已有的交通规划书籍仍习惯将这种基于产生点——吸引点的矩阵称做“OD 矩阵”。
这是不准确的,后来以讹传讹,一直传至今天,这很容易引起理解上的失误,这种基于产生点——吸引点的分布矩阵正确的简称应该是“PA 矩阵”。
今后我们就使用这个新的简称。
与第四章的产生量和吸引量相比,产生量P i 、吸引量A j 是两个不带方向的量(标量)。
而本节的出行分布量q ij 是一个带有方向性的量(矢量),它有两个下标。
本书规定:第一个为产生分区号,第二个为吸引分区号。
它们关系式是:),,1,(n j i q A q P iijj jij i ===∑∑,(5-1)总出行量:∑∑∑∑∑∑====ijjiij ij jj ii q q A P Q (5-2)5.1.3 分布量预测本章的问题是在前一章得出的各分区产生量、吸引量预测值的基础上,求PA 分布矩阵中各个元素q ij ,即已知PA 表小计列和小计行中各元素的值,求其它元素的值。
从数学上来说,这是用2n 个方程(5-1)式求n ×n 个未知数的问题。
数学常识告诉我们,当n >2时,这是没有唯一解的。
为此,我们必须借用其它的一些条件,但是从后面的进一步的研究可以发现,即使是借用了其它条件,仍很难求出精确的解来,而只能求出近似解。
我们通过对调查资料的分析和预测,可以找到和利用的数据有:现状的PA 表:][0ij q (1≤i ,j ≤n );两个分区之间的交通阻抗矩阵[R ij ]。
至今已开发的方法有:增长率法、引力模型法、机会模型法。
我们详细介绍前两种,第三种因理论依据不足,且难于实用,不作详细介绍。
§5.2 增长率法增长率法是一种比较简单的预测方法,包括两大类:增长函数方法和Fueness 约束条件方法。
增长函数方法是指一大类方法,具体地,它又包括:常增长率法、平均增长率法、Detroit (底特律法)、Frator (弗雷德)法。
5.2.1 增长函数方法的思路具体的增长函数方法有多种,它们的基本思路相同,不同的是各自采用不同的增长函数。
首先我们给出描述共同基本思路的算法,然后就不同的增长函数讨论各个具体的增长函数方法。
增长函数的基本思路可用以下算法描述: 算法5-1:步1:用0ij q 表现状分布量,i P 0、j A 0表现状产生量、吸引量: P i 、A j 表由第四章预测方法得到的规划年产生量、吸引量的预测值,令k =0。
步2:计算各分区第0次产生增长率、吸引增长率:000jj aj i i pi A A F P P F ==,;(5-3) 步3:设),(aj gi F F f 为增长函数,计算第(k +1)次预测值:),(kaj k pi k ij k ij F F f q q ⋅=+1;(5-4) 步4:检验预测结果:计算新的产生量和吸引量∑∑++++==ik ij k jjk ij k i q A q P 1111,,(5-5) 令1111++++==k jj k aj k ii k pi AA F P P F ,(5-6)在允许一定误差率(如3%)的前提下,对所有的i 和j 考察:11≈≈k aj k pi F F ,?若是,1+k ijq为之所求,今1+=k ij ij q q ,停止;否则进行下一步迭代,令k =k +1,转至第3步继续。
下面就各种不同的增长函数提出各种具体的增长率法。
5.2.2各种增长函数法1 常增长率法该方法认为,q ij 的增长仅与i 区的产生量增长率有关。
增长函数为()0,ii pi aj pi P PF F F f ==常(5-7)这种方法只单方面考虑产生量增长率对增长函数的影响,忽视了吸引量增长率的影响。
由于产生量与吸引量的不对称性,因此这种方法的预测精度不高,是一种最粗糙的方法,有时甚至不能保证算法5-1的迭代过程一定能收敛。
2 平均增长率法该方法认为:q ij 的增长与i 区产生量的增长及j 分区吸引量的增长同时相关,而且相关的程度也相同。
即()()ai pi aj pi F F F F f +=21,平(5-8)此法明显比第一种方法合情理一些,这是一种最常用的方法。
在实际运用时,因迭代步数较多,使计算速度稍慢,但有计算机帮忙也很好用。
3 Detroit 法此法认为,q ij 的增长与i 分区产生量增长率pi F 成正比,而且还与j 分区吸引量增长占整个区域吸引量增长的相对比率成正比。
全区域在现年和规划年的吸引总量分别为∑jjA0、∑jj A ,因此全区域的吸引量增长率为∑∑jjjjAA 0。
于是Detroit 增长函数为()∑∑⋅=⋅=jjjj j j i i ajpi aj pi D A A A A P P Q Q F F F F f 0000,(5-9) 该方法是在底特律市1956年规划首次被开发利用,收敛速度较快。
4 Frator 法1954年Frator 提出了分别从产生区和吸引区两个角度分析计算q ij ,然后平均的方法。
先从产生区考虑:①Frator 认为,q ij 与 i 区出行量中j 分区的“相对吸引增长率” b ij 成正比。
由于规划年从i 区产生的出行量中被分区j 吸引去的出行量为aj ij F q 0,因此,这个相对吸引增长率为:∑=jajij ajij ij F qF q b 00(5-10)②Frator 还认为:q ij 也应与i 分区规划年的产生量)(00ij ij i F P P =成正比; ③综上两点,得∑⋅⋅⋅⋅=⋅=jajijajij pii ij i ijFqF q F P b P q 0000001'(5-11)再从吸引区j 分区的角度分析,同样,类似于以上三步,得∑⋅⋅⋅⋅=jpi ij piij ajjijF q F q F A q 0000001"(5-12) 由于上两式的'1ij q 、"1ijq 是表示同一个量1ij q ,故预测值应取其平均值: ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⋅⋅⋅+⋅⋅=+=∑∑⋅i pi ij pi ij aj j j aj ij aj ij pi i ij ij ij F q F q F A F q F q F P q q q 00000000000011121]"'[21 220000000000000j i aj pi ij i pi ij jj aj ij i ij piaj L L F F q F q A F q P q F F +⋅⋅=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⋅⋅⋅⋅=∑∑(5-13) 其中:∑=jkajk ij k i k piF q P L 、∑=ik pikijk jk aj Fq A L ——分别称为第k 轮分区i 的“产生位置系数”、分区j 的“吸引位置系数”。
故Frator 增长函数为:2),(k ajk pi k ajk pi k aj kpi F L L F F F F f +⋅⋅=(5-14)Frator 法的计算比较麻烦,但它的收敛速度快,应用还是比较广泛的。
例5-2 表5-2(1)是一个只有四个分区的现状PA 表,表5-2(2)给出了规划年的各个分区的出行产生量和吸引量。
试分别用平均增长率法和Frator 法求出规划年PA 矩阵。
表5-2 例5-2的已知数据表(1)现状PA 表 (2)规划年产生量和吸引量解:1)平均增长率法。
用式(5-3)算得第0次的三个分区产生增长率0pi F 分别为了:2.500,1.667,3.125;三个分区的吸引量增长率0aj F 分别为2.778, 1.800, 2.444。
从而,算得各个平均增长率(即增长函数),(00aj pi F F f )如表5-3(1)所示。
由式(5-5)可得第1次迭代值如表5-3(2)。
从表5-3(2)可见,第1次迭代值的行和列的小计与表5-2(2)中规划年的产生量、吸引量差别较大,故须进一步进行第2次迭代运算。
一直进行了6次迭代运算后,得到的结果与表5-2(2)中的值基本一致,收敛误差小于1%。
结果见表5-3(3),所以此表即为所求的规划年出行分布预测结果。
表5-3 例5-2平均增长率法计算结果表(2)平均增长率法第1次迭代结果 (3)平均增长率法第6次迭代结果2)Frator 法。
