通用版高考理科数学培优专题二解三角形
培优专题02 与三角形有关的线段和角的问题-解析版

培优专题02 与三角形有关的线段和角的问题1.(2022·全国·八年级专题练习)如图,在ABC V 中,20AB =,18AC =,AD 为中线.则ABD △与ACD △的周长之差为( )A .1B .2C .3D .4【答案】B 【分析】利用三角形中线的定义、三角形的周长公式进行计算即可得出结果.【详解】Q 在ABC V 中,AD 为中线,BD CD \=.ABD C AB BD AD =++Q △,ACD C AC CD AD =++△,20182ABD ACD C C AB AC \-=-=-=V V .故选:B .【点睛】本题考查三角形的中线的理解与运用能力.三角形中,连接一个顶点和它所对边的中点的线段叫做三角形的中线.明确三角形的中线的定义,运用两个三角形的周长的差等于两边的差是解本题的关键.2.(2022·全国·八年级专题练习)如图,ABC V 的面积是2,AD 是ABC V 的中线,13AF AD =,12CE EF =,则CDE △的面积为( )A .29B .16C .23D .49【答案】A【分析】根据中线的性质即可求出S △ACD ,然后根据等高时,面积之比等于底之比,即可依此求出3.(2022·四川成都·七年级期中)如图,ABC V 中,12Ð=Ð,G 为AD 中点,延长BG 交AC 于E ,F 为AB 上一点,且CF AD ^于H ,下列判断,其中正确的个数是( )①BG 是ABD V 中边AD 上的中线;②AD 既是ABC V 中BAC Ð的角平分线,也是ABE V 中BAE Ð的角平分线;③CH 既是ACD V 中AD 边上的高线,也是ACH V 中AH 边上的高线.A .0B .1C .2D .3【答案】C【分析】根据三角形的高,中线,角平分线的定义可知.【详解】解:①G 为AD 中点,所以BG 是ABD △边AD 上的中线,故正确;②因为12Ð=Ð,所以AD 是ABC V 中BAC Ð的角平分线,AG 是ABE △中BAE Ð的角平分线,故错误;③因为CF AD ^于H ,所以CH 既是ACD △中AD 边上的高线,也是ACH V 中AH 边上的高线,故正确.故选:C .【点睛】熟记三角形的高,中线,角平分线是解决此类问题的关键.4.(2018·江苏省江阴市第一中学七年级期中)如图,在长方形网格中,每个小长方形的长为2,宽为1,A 、B 两点在网格格点上,若点C 也在网格格点上,以A 、B 、C 为顶点的三角形面积为1,则满足条件的点C 个数是( )A .5B .6C .7D .8【答案】B 【分析】据三角形ABC 的面积为1,可知三角形的底边长为2,高为1,或者底边为1,高为2,可通过在正方形网格中画图得出结果.【详解】解:C 点所有的情况如图所示:由图可得共有6个,故选:B .【点睛】本题考查了三角形的面积的求法,此类题应选取分类的标准,才能做到不遗不漏,难度适中.5.(2022·江苏·七年级专题练习)如图, D 、E 分别在∆ABC 的边 BC 、AC 上,13CD BC =,13CE AC =,CD = 1 ,CE = 1 ,AC , AD 与 BE 交于点O ,已知∆ABC 的面积为 12,则∆ABO 的面积为()A .4B .5C .6D .76.(2019·天津市静海区第二中学八年级期中)如图,在△ABC 中,∠B=70°,∠C=40°,AD 是BC 边上的高,AE 是∠BAC 的平分线,则∠DAE 的度数是()A .15°B .16°C .70°D .18°7.(2021·安徽·中考真题)两个直角三角板如图摆放,其中90BAC EDF Ð=Ð=°,45E Ð=°,30C Ð=°,AB 与DF 交于点M .若//BC EF ,则BMD Ð的大小为( )A .60°B .67.5°C .75°D .82.5°【答案】C 【分析】根据//BC EF ,可得45FDB F Ð=Ð=°,再根据三角形内角和即可得出答案.【详解】由图可得6045B F Ð=°Ð=°,,∵//BC EF ,∴45FDB F Ð=Ð=°,∴180180456075BMD FDB B Ð=°-Ð-Ð=°-°-°=°,故选:C .【点睛】本题考查了平行线的性质和三角形的内角和,掌握平行线的性质和三角形的内角和是解题的关键.8.(2022·广西贵港·七年级期末)如图7,AB ⊥BC ,AE 平分∠BAD 交BC 于E ,AE ⊥DE ,∠1+∠2=90°,M ,N 分别是BA ,CD 延长线上的点,∠EAM 和∠EDN 的平分线交于点F .下列结论:①AB ∥CD ;②∠AEB +∠ADC =180°;③DE 平分∠ADC ;④∠F =135°,其中正确的有( )A .1个B .2个C .3个D .4个【答案】C 【分析】先根据AB ⊥BC ,AE 平分∠BAD 交BC 于点E ,AE ⊥DE ,∠1+∠2=90°,∠EAM 和∠EDN 的平分线交于点F ,由三角形内角和定理以及平行线的性质即可得出结论.【详解】解:标注角度如图所示:∵AB ⊥BC ,AE ⊥DE ,∴∠1+∠AEB =90°,∠DEC +∠AEB =90°,∴∠1=∠DEC ,又∵∠1+∠2=90°,∴∠DEC +∠2=90°,∴∠C =90°,∴∠B +∠C =180°,9.(2022·全国·八年级课时练习)如图,将ABC V 沿DH HG EF 、、翻折,三个顶点恰好落在点O 处.若140Ð=°,则2Ð的度数为( )A .12B .60°C .90°D .140°【答案】D【分析】根据翻折变换前后对应角不变,故∠B =∠EOF ,∠A =∠DOH ,∠C =∠HOG ,∠1+∠2+∠HOD +∠EOF +∠HOG =360°,进而求出∠1+∠2的度数.【详解】解:∵将△ABC 三个角分别沿DE 、HG 、EF 翻折,三个顶点均落在点O 处,∴∠B =∠EOF ,∠A =∠DOH ,∠C =∠HOG ,∠1+∠2+∠HOD +∠EOF +∠HOG =360°,∵∠HOD +∠EOF +∠HOG =∠A +∠B +∠C =180°,∴∠1+∠2=360°-180°=180°,∵∠1=40°,∴∠2=140°,故选:D .【点睛】此题主要考查了翻折变换的性质和三角形的内角和定理,根据已知得出∠HOD +∠EOF +∠HOG =∠A +∠B +∠C =180°是解题关键.10.(2022·全国·八年级专题练习)如图,a b ∥,一块含45°的直角三角板的一个顶点落在直线b 上,若15854¢Ð=°,则∠2的度数为( )A .1036¢°B .1046¢°C .10354¢°D .10454¢°【答案】C 【分析】设∠2的同位角为∠3,∠3的邻补角为∠5,三角板的一个锐角为∠4,根据等腰三角板的特点可求出∠4,根据三角形内角和即可求出∠5,再根据平角的性质即可求出∠3,进而根据两直线平行同位角相等即可求出∠2.【详解】设∠2的同位角为∠3,∠3的邻补角为∠5,三角板的一个锐角为∠4,如图,∵直角三角板含一个45°的锐角,∴该三角板为等腰三角形,∴∠4=45°,∵∠1=58°54′,又∵在三角形中有∠1+∠4+∠5=180°,∴∠5=180°-(∠1+∠4)=180°-(58°54′+45°)=180°-103°54′=76°6′,∵∠3+∠5=180°,∴∠3=180°-∠5=180°-76°6′=103°54′,∵a b ∥,∴∠2=∠3,∴∠2=103°54′,故选:C .【点睛】本题主要考查了平行线的性质以及三角形的内角和等知识,掌握两直线平行同位角相等是解答本题的关键.11.(2022·江苏·盐城市初级中学七年级期中)如图,AD 是ABC V 的高,45BAD Ð=°,65C =°∠,则BAC Ð=________.【答案】70°【分析】先由直角三角形的性质求得∠DAC ,然后再根据线段的和差求解即可.【详解】解:AD Q 是ABC V 的高,90ADC °\Ð=,∵65C =°∠=9025DAC C °\Ð-Ð=o ,254570BAC DAC BAD °°°\Ð=Ð+Ð=+=.故答案为:70°.【点睛】本题主要考查了角的和差、直角三角形的性质、三角形高的性质等知识点,掌握直角三角形两锐角互余是解答本题的关键.12.(2022·江苏·扬州中学教育集团树人学校七年级期中)如图,在△ABC 中,点D 在BC 上,点E 、F 在AB 上,点G 在DF 的延长线上,且∠B =∠DFB ,∠G =∠DEG ,若29BEG Ð=°,则∠BDE 的度数为_____.【答案】58°【分析】设BED x Ð=,则29G DEG x Ð=Ð=+°,再根据三角形的内角和定理可得1222EDG x Ð=°-,根据三角形的外角性质可得122B DFB x Ð=Ð=°-,然后在BDE V 中,根据三角形的内角和定理即可得.【详解】解:设BED x Ð=,29BEG Ð=°Q ,29BED G DEG BEG x Ð=Ð=Ð=++\а,1801222EDG G DEG x \Ð=°-Ð-Ð=°-,122BED B DFB EDG x \Ð=Ð=Ð=а-+,()()180********BED BDE B x x Ð+=\Ð=°-а-°-=+°,故答案为:58°.【点睛】本题考查了三角形的内角和定理、三角形的外角性质,熟练掌握三角形的内角和定理是解题关键.13.(2022·江苏·扬州市江都区第三中学七年级阶段练习)如图,∠A =45°,∠BCD =135°,∠AEB 与∠AFD 的平分线交于点P .下列结论:①EP ⊥FP ;②∠AEB +∠AFD =∠P ;③∠A =∠PEB +∠PFD .其中正确的结论是______.∵∠AEB与∠AFD的平分线交于点∴12BEPAEP AEB=Ð=ÐÐ∵∠BCD=135°,∴∠BCF=180°-∠BCD=45°14.(2022·全国·八年级专题练习)如图,在△ABC中,AM是△ABC的角平分线,AD是△ABC的高线.猜想∠MAD、∠B、∠C之间的数量关系,并说明理由.15.(2022·全国·八年级单元测试)在△ABC中,BC=8,AB=1;(1)若AC是整数,求AC的长;(2)已知BD是△ABC的中线,若△ABD的周长为10,求△BCD的周长.【答案】(1)8(2)17【分析】(1)根据三角形三边关系“两边之和大于第三边,两边之差小于第三边”得7<AC<9,根据AC是整数得AC=8;(2)根据BD是△ABC的中线得AD=CD,根据△ABD的周长为17和AB=1得AD+BD=9,即可求解.(1)由题意得:BC﹣AB<AC<BC+AB,∴7<AC<9,∵AC是整数,∴AC=8;(2)如图所示:∵BD是△ABC的中线,∴AD=CD,∵△ABD的周长为10,∴AB+AD+BD=10,∵AB=1,∴AD+BD=9,∴△BCD的周长=BC+BD+CD=BC+AD+CD=8+9=17.【点睛】本题考查的是三角形的三边关系、三角形的中线的定义,掌握三角形两边之和大于第三边、两边之差小于第三边是解题的关键.16.(2022·河南周口·七年级期末)如图.AD为△ABC的中线,BE为△ABD的中线,EF⊥BC于点F.(1)在△BEF中,请指出边EF上的高;(2)若BD=5,EF=2,求△ACD的面积;(3)若AB=m,AC=n,若△ACD的周长为a,请用含m,n,a的式子表示△ABD的周长.【答案】(1)边EF上的高是BF;(2)S△ACD=10;(3)△ABD的周长为m+a-n.【分析】(1)根据三角形高的定义即可得出边EF上的高是BF;(2)先求得△BDE的面积,然后根据三角形的中线将三角形分成两个三角形得到S△ABE=S△BDE=5,进一步得到S△ACD=S△ABD=10;(3)利用三角形周长公式即可求得.(1)解:∵EF⊥BC于点F,17.(2022·陕西渭南·七年级期末)如图,点A 在CB 的延长线上,点F 在DE 的延长线上,连接AF ,分别与BD 、CE 交于点G 、H .已知∠1=52°,∠2=128°.(1)探索BD 与CE 的位置关系,并说明理由;(2)若∠C =78°,求∠A 的度数.【答案】(1)BD CE ∥,理由见解析(2)50°【分析】(1)由152DGF Ð=Ð=°,∠2=128°,得到∠DGF +∠2=180°,利用“同旁内角互补,两直线平行”可证出BD CE ∥;(2)由BD CE ∥得到78ABD C Ð=Ð=°,由三角形内角和定理求解即可.(1)BD CE ∥,理由:∵152DGF Ð=Ð=°,∠2=128°,∴252128180DGF Ð+Ð=°+°=°,∴BD CE ∥.(2)∵BD CE ∥,∵78ABD C Ð=Ð=°,∴1801180785250A ABD Ð=°-Ð-Ð=°-°-°=°.【点睛】本题考查了平行线的判定与性质、三角形内角和定理,解题的关键是熟练掌握相关性质和定理.18.(2022·江苏·兴化市乐吾实验学校七年级阶段练习)(1)【问题背景】如图1的图形我们把它称为“8字形”,请说明A B C D Ð+Ð=Ð+Ð;(2)【简单应用】如图2,AP 、CP 分别平分BAD Ð、BCD Ð,若35ABC Ð=°,15ADC Ð=°,求P Ð的度数;(3)【问题探究】如图3,直线AP 平分BAD Ð的外角FAD Ð,CP 平分BCD Ð的外角BCE Ð,若35ABC Ð=°,29ADC Ð=°,请猜想P Ð的度数,并说明理由;(4)【拓展延伸】在图4中,若设C a Ð=,B b Ð=,13CAP CAB Ð=Ð,13CDP CDB Ð=Ð,试问P Ð与C Ð、B Ð之间的数量关系为:___.(用a 、b 表示P Ð,不必说明理由)【答案】(1)见解析(2)25P Ð=°(3)32P Ð=°;理由见解析。
高中数学培优——解三角形

解三角形课 题:正弦定理(两课时) 教学目的:⑴使学生掌握正弦定理⑵能应用解斜三角形,解决实际问题。
教学过程: 一、引言:在直角三角形中,由三角形内角和定理、勾股定理、锐角三角函数,可以由已知的边和角求出未知的边和角。
那么斜三角形怎么办?(创设情景)早在1671年,两个法国天文学家就测出了地球与月亮之间的距离大约是385400公里,你能设计一种近似的测量方法吗?——提出课题:正弦定理二、讲解新课:正弦定理:在任一个三角形中,各边和它所对角的正弦比相等, 即A a sin =B b sin =Ccsin =2R (R 为△ABC 外接圆半径) 1.直角三角形中:sinA=c a ,sinB=cb, sinC=1 即 c=A a sin , c=B b sin , c=Ccsin . ∴A a sin =B b sin =Cc sin 2.斜三角形中证明一:(等积法)在任意斜△ABC 当中 S △ABC =A bcB acC ab sin 21sin 21sin 21== 两边同除以abc 21即得:A a sin =B b sin =Ccsin证明二:(外接圆法) 如图所示,∠A=∠D∴R CD Da A a 2sin sin === 同理B b sin =2R ,Ccsin =2R 证明三:(向量法)过A 作单位向量垂直于由 AC +CB =AB两边同乘以单位向量 得 •(AC +CB )=•AB 则j •AC +j •CB =j •AB∴||•||cos90︒+||•||cos(90︒-C)=||•||cos(90︒-A) ∴A c C a sin sin = ∴A a sin =Ccsin 同理,若过C 作垂直于得:C c sin =B b sin ∴A a sin =B b sin =Ccsin 正弦定理的应用 从理论上正弦定理可解决两类问题: 1.两角和任意一边,求其它两边和一角;2.两边和其中一边对角,求另一边的对角,进而可求其它的边和角。
新广东高考数学理科步步高二轮复习热点突破3.2三角变换与解三角形(含答案解析)

第2讲 三角变换与解三角形热点一 三角变换例1 (1)已知sin(α+π3)+sin α=-435,-π2<α<0,则cos(α+2π3)等于( )A .-45B .-35C.45D.35(2)(2014·课标全国Ⅰ)设α∈(0,π2),β∈(0,π2),且tan α=1+sin βcos β,则( )A .3α-β=π2B .2α-β=π2C .3α+β=π2D .2α+β=π2思维启迪 (1)利用和角公式化简已知式子,和cos(α+23π)进行比较.(2)先对已知式子进行变形,得三角函数值的式子,再利用范围探求角的关系. 答案 (1)C (2)B解析 (1)∵sin(α+π3)+sin α=-435,-π2<α<0,∴32sin α+32cos α=-435, ∴32sin α+12cos α=-45, ∴cos(α+2π3)=cos αcos 2π3-sin αsin 2π3=-12cos α-32sin α=45.(2)由tan α=1+sin βcos β得sin αcos α=1+sin βcos β,即sin αcos β=cos α+cos αsin β, ∴sin(α-β)=cos α=sin(π2-α).∵α∈(0,π2),β∈(0,π2),∴α-β∈(-π2,π2),π2-α∈(0,π2),∴由sin(α-β)=sin(π2-α),得α-β=π2-α,∴2α-β=π2.思维升华 (1)三角变换的关键在于对两角和与差的正弦、余弦、正切公式,二倍角公式,三角恒等变换公式的熟记和灵活应用,要善于观察各个角之间的联系,发现题目所给条件与恒等变换公式的联系,公式的使用过程要注意正确性,要特别注意公式中的符号和函数名的变换,防止出现张冠李戴的情况.(2)求角问题要注意角的范围,要根据已知条件将所求角的范围尽量缩小,避免产生增解.设函数f (x )=cos(2x +π3)+sin 2x .(1)求函数f (x )的最小正周期和最大值;(2)若θ是第二象限角,且f (θ2)=0,求cos 2θ1+cos 2θ-sin 2θ的值.解 (1)f (x )=cos(2x +π3)+sin 2x =cos 2x cos π3-sin 2x sin π3+1-cos 2x 2=12-32sin 2x .所以f (x )的最小正周期为T =2π2=π,最大值为1+32.(2)因为f (θ2)=0,所以12-32sin θ=0,即sin θ=33,又θ是第二象限角, 所以cos θ=-1-sin 2θ=-63. 所以cos 2θ1+cos 2θ-sin 2θ=cos 2θ-sin 2θ2cos 2θ-2sin θcos θ=θ+sin θθ-sin θ2cos θθ-sin θ=cos θ+sin θ2cos θ=-63+33-63=6-326=2-24.热点二 解三角形例2 在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,满足a =2sin A ,cos B cos C +2a c +bc =0.(1)求边c 的大小;(2)求△ABC 面积的最大值.思维启迪 (1)将cos B cos C +2a c +bc =0中的边化成角,然后利用和差公式求cos C ,进而求c .(2)只需求ab 的最大值,可利用cos C =a 2+b 2-c 22ab 和基本不等式求解.解 (1)∵cos B cos C +2a c +bc=0, ∴c cos B +2a cos C +b cos C =0,∴sin C cos B +sin B cos C +2sin A cos C =0, ∴sin A +2sin A cos C =0, ∵sin A ≠0,∴cos C =-12,∵C ∈(0,π)∴C =2π3,∴c =a sin A·sin C = 3.(2)∵cos C =-12=a 2+b 2-32ab,∴a 2+b 2+ab =3,∴3ab ≤3,即ab ≤1. ∴S △ABC =12ab sin C ≤34.∴△ABC 的面积最大值为34. 思维升华 三角形问题的求解一般是从两个角度,即从“角”或从“边”进行转化突破,实现“边”或“角”的统一,问题便可突破. 几种常见变形:(1)a ∶b ∶c =sin A ∶sin B ∶sin C ;(2)a =2R sin A ,b =2R sin B ,c =2R sin C ,其中R 为△ABC 外接圆的半径; (3)sin(A +B )=sin C ,cos(A +B )=-cos C .(1)(2014·广东)在△ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,已知b cos C+c cos B =2b ,则ab=________.(2)(2014·江西)在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若c 2=(a -b )2+6,C =π3,则△ABC 的面积是( ) A .3 B.932C.332 D .3 3答案 (1)2 (2)C解析 (1)方法一 (1)因为b cos C +c cos B =2b ,所以b ·a 2+b 2-c 22ab +c ·a 2+c 2-b 22ac =2b ,化简可得ab=2.方法二 因为b cos C +c cos B =2b , 所以sin B cos C +sin C cos B =2sin B , 故sin(B +C )=2sin B ,故sin A =2sin B ,则a =2b ,即ab=2.(2)∵c 2=(a -b )2+6,∴c 2=a 2+b 2-2ab +6.① ∵C =π3,∴c 2=a 2+b 2-2ab cos π3=a 2+b 2-ab .②由①②得ab =6.∴S △ABC =12ab sin C =12×6×32=332.热点三 正、余弦定理的实际应用例3 (2013·江苏)如图,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为50 m/min.在甲出发2 min 后,乙从A 乘缆车到B ,在B 处停留1 min 后,再从B 匀速步行到C .假设缆车匀速直线运动的速度为130 m/min ,山路AC 长为1 260 m ,经测量cos A =1213,cos C =35.(1)求索道AB 的长;(2)问:乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内? 思维启迪 (1)直接求sin B ,利用正弦定理求AB .(2)利用余弦定理和函数思想,将甲乙距离表示为乙出发后时间t 的函数.解 (1)在△ABC 中,因为cos A =1213,cos C =35,所以sin A =513,sin C =45.从而sin B =sin[π-(A +C )]=sin(A +C ) =sin A cos C +cos A sin C=513×35+1213×45=6365.由正弦定理AB sin C =ACsin B ,得 AB =AC sin B ×sin C =1 2606365×45=1 040(m).所以索道AB 的长为1 040 m.(2)假设乙出发t 分钟后,甲、乙两游客距离为d ,此时,甲行走了(100+50t )m ,乙距离A 处130t m , 所以由余弦定理得d 2=(100+50t )2+(130t )2-2×130t ×(100+50t )×1213=200(37t 2-70t +50),由于0≤t ≤1 040130,即0≤t ≤8,故当t =3537 min 时,甲、乙两游客距离最短.(3)由正弦定理BC sin A =ACsin B,得BC =AC sin B ×sin A =1 2606365×513=500(m).乙从B 出发时,甲已走了50×(2+8+1)=550(m),还需走710 m 才能到达C . 设乙步行的速度为v m/min ,由题意得-3≤500v -71050≤3,解得1 25043≤v ≤62514,所以为使两位游客在C 处互相等待的时间不超过3 min ,乙步行的速度应控制在⎣⎡⎦⎤1 25043,62514(单位:m/min)范围内.思维升华 求解三角形的实际问题,首先要准确理解题意,分清已知与所求,关注应用题中的有关专业名词、术语,如方位角、俯角等;其次根据题意画出其示意图,示意图起着关键的作用;再次将要求解的问题归结到一个或几个三角形中,通过合理运用正、余弦定理等有关知识建立数学模型,从而正确求解,演算过程要简练,计算要准确;最后作答.如图,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A 地侦察发现,在南偏东60°方向的B 地,有一艘某国军舰正以每小时13海里的速度向正西方向的C 地行驶,企图抓捕正在C 地捕鱼的中国渔民.此时,C 地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C 地救援我国渔民,能不能及时赶到?(2≈1.41,3≈1.73,6≈2.45)解 过点A 作AD ⊥BC ,交BC 的延长线于点D .因为∠CAD =45°,AC =10海里, 所以△ACD 是等腰直角三角形.所以AD =CD =22AC =22×10=52(海里). 在Rt △ABD 中,因为∠DAB =60°,所以BD =AD ×tan 60°=52×3=56(海里). 所以BC =BD -CD =(56-52)(海里).因为中国海监船以每小时30海里的速度航行,某国军舰正以每小时13海里的速度航行, 所以中国海监船到达C 点所用的时间t 1=AC 30=1030=13(小时),某国军舰到达C 点所用的时间t 2=BC 13=6-213≈-13=0.4(小时).因为13<0.4,所以中国海监船能及时赶到.1.求解恒等变换问题的基本思路一角二名三结构,即用化归转化思想“去异求同”的过程,具体分析如下:(1)首先观察角与角之间的关系,注意角的一些常用变换形式,角的变换是三角函数变换的核心.(2)其次看函数名称之间的关系,通常“切化弦”. (3)再次观察代数式的结构特点. 2.解三角形的两个关键点(1)正、余弦定理是实现三角形中边角互化的依据,注意定理的灵活变形,如a =2R sin A ,sin A =a2R (其中2R 为三角形外接圆的直径),a 2+b 2-c 2=2ab cos C 等,灵活根据条件求解三角形中的边与角.(2)三角形的有关性质在解三角形问题中起着重要的作用,如利用“三角形的内角和等于π”和诱导公式可得到sin(A +B )=sin C ,sin A +B 2=cos C2等,利用“大边对大角”可以解决解三角形中的增解问题等.3.利用正弦定理、余弦定理解决实际问题的关键是如何将实际问题转化为数学问题,抽象出三角形模型.。
2020年高考理科数学 《解三角形》题型归纳与训练及答案解析

2020年高考理科数学 《解三角形》题型归纳与训练【题型归纳】题型一 正弦定理、余弦定理的直接应用例1ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知2sin()8sin2BA C +=. (1)求cos B(2)若6a c +=,ABC ∆面积为2,求b . 【答案】(1)15cos 17B =(2)2b =. 【解析】由题设及A B C π++=得2sin 8sin2BB =,故sin 4(1cos )B B =-. 上式两边平方,整理得217cos 32cos 150B B -+=, 解得cos 1B =(舍去),15cos 17B =.(2)由15cos 17B =得8sin 17B =,故14sin 217ABC S ac B ac ∆==. 又2ABC S ∆=,则172ac =. 由余弦定理及6a c +=得22222cos ()2(1cos )b a c ac B a c ac B =+-=+-+1715362(1)4217=-⨯⨯+=. 所以2b =.【易错点】二倍角公式的应用不熟练,正余弦定理不确定何时运用 【思维点拨】利用正弦定理列出等式直接求出例2 ABC △的内角,,A B C 的对边分别为,,a b c ,若2cos cos cos b B a C c A =+,则B = . 【答案】π3【解析】1π2sin cos sin cos sin cos sin()sin cos 23B B AC C A A C B B B =+=+=⇒=⇒=.【易错点】不会把边角互换,尤其三角恒等变化时,注意符号。
【思维点拨】边角互换时,一般遵循求角时,把边换成角;求边时,把角转换成边。
例3在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,若b =1,c =3,C =23π,则S △ABC =________.【答案】34【解析】因为c >b ,所以B <C ,所以由正弦定理得b sin B =c sin C ,即1sin B =3sin 2π3=2,即sin B =12,所以B=π6,所以A =π-π6-2π3=π6.所以S △ABC =12bc sin A =12×3×12=34. 【易错点】大边对大角,应注意角的取值范围【思维点拨】求面积选取公式时注意,一般选取已知角的公式,然后再求取边长。
高三理科数学培优专题——三角函数(含答案)

三角函数专题一、方法总结:1.三角函数恒等变形的基本策略。
(1)注意隐含条件的应用:1=cos 2x +sin 2x 。
(2)角的配凑。
α=(α+β)-β,β=2βα+-2βα-等。
(3)升幂与降幂:主要用2倍角的余弦公式。
(4)化弦(切)法,用正弦定理或余弦定理。
(5)引入辅助角。
asinθ+bcosθ=22b a +sin (θ+ϕ),这里辅助角ϕ所在象限由a 、b 的符号确定,ϕ角的值由tan ϕ=ab确定。
2.解答三角高考题的策略。
(1)发现差异:观察角、函数运算间的差异,即进行所谓的“差异分析”。
(2)寻找联系:运用相关公式,找出差异之间的内在联系。
(3)合理转化:选择恰当的公式,促使差异的转化。
二、例题集锦: 考点一:三角函数的概念1.(2011年东城区示范校考试15)设A 是单位圆和x 轴正半轴的交点,Q P 、是单位圆上的两点,O 是坐标原点,6π=∠AOP ,[)παα,0,∈=∠AOQ .(1)若34(,)55Q ,求⎪⎭⎫ ⎝⎛-6cos πα的值; (2)设函数()f OP OQ α=⋅u u u r u u u r ,求()αf 的值域.考点二:三角函数的图象和性质2.(2014年课标I ,7)在函数①cos 2y x =,②cos y x =,③cos(2)6y x π=+,④tan 24y x π⎛⎫=- ⎪⎝⎭中,最小正周期为π的所有函数为 ( )A.①②③B. ②③④C. ②④D. ①③3.(2012年课标全国,9)已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减,则ω的取值范围是( )A.15[,]24B.13[,]24C.10,2⎛⎤ ⎥⎝⎦D.()0,24.(2011年课标全国,11)设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π,且()()f x f x -=,则( )A. ()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减B. ()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 C. ()f x 在0,2π⎛⎫ ⎪⎝⎭单调递增 D. ()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增5.将函数()()sin 22f x x πϕϕ⎛⎫=+<⎪⎝⎭的图象向左平移6π个单位长度后,所得函数()g x 的图象关于原点对称,则函数()f x 在0,2π⎡⎤⎢⎥⎣⎦的最小值为 A .12- B .12C.6.(2011年东城区期末15)函数()sin()(0,0,||)2f x A x A ωφωφπ=+>><部分图象如图所示.(Ⅰ)求()f x 的最小正周期及解析式;(Ⅱ)设()()cos 2g x f x x =-,求函数()g x 在区间[0,]2x π∈上的最大值和最小值.考点三、四、五:同角三角函数的关系、 诱导公式、三角恒等变换7.已知函数2()2sin cos 2cos f x x x x ωωω=-(0x ω∈>R ,),相邻两条对称轴之间的距离等于2π. (Ⅰ)求()4f π的值; (Ⅱ)当02x π⎡⎤∈⎢⎥⎣⎦,时,求函数)(x f 的最大值和最小值及相应的x 值.8.已知向量(cos ,sin ),a x x =r 向量(cos ,sin ),()b x x f x a b =-=⋅r r r(1)求函数()()sin 2g x f x x =+的最小正周期和对称轴方程; (2)若x 是第一象限角且'3()2()f x f x =-,求tan()4x π+的值.考点六:解三角形9.ABC ∆中,角,,A B C成等差数列是sin sin )cos C A A B =+成立的 ( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件10.已知函数()cos f x x =,,,a b c 分别为ABC ∆的内角,,A B C 所对的边,且22233a b c +-4ab =,则下列不等式一定成立的是A .()()sin cos f A fB ≤ B .()()sin cos f A f B ≥C .()()sin sin f A f B ≥D .()()cos cos f A f B ≤ 11.(2014年课标I ,16)已知,,a b c 分别为ABC ∆三个内角,,A B C 的对边,2a =,且(2)(sin sin )()sin b A B c b C +-=-,则ABC ∆面积的最大值为 .12.(2014年河南焦作联考)在ABC ∆中,已知sin sin cos sin sin cos sin sin cos A B C A C B B C A =+,若,,a b c 分别是角,,A B C 所对的边,则2abc 的最大值为 . 13.(2015河北秦皇岛一模,17,12分)在ABC ∆中,角A B C ,,所对的边分别为,,a b c ,满足()222.AB AC a b c ⋅=-+u u u r u u u r(1)求角A 的大小; (2)求24sin()23C B π--的最大值,并求取得最大值时角,B C 的大小.14.(2009全国II , 17,10分) 设ABC ∆的内角A B C ,,的对边分别为,,a b c ,3cos()cos 2A CB +=-,2b ac =.求B ∠的大小.14.(2015课标II ,17,12分)△ABC 中,D 是BC 上的点,AD 平分BAC ∠,ABD ∆的面积是ADC ∆面积的2倍. (1)求sin sin BC∠∠;(2)若1,2AD DC ==,求BD 和AC 的长.15、(2011东城一模15)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c 分,且满足2cos cos c b Ba A-=. (Ⅰ)求角A 的大小;(Ⅱ)若a =ABC 面积的最大值.例题集锦答案:1.(2011年东城区示范校考试理15)如图,设A 是单位圆和x 轴正半轴的交点,Q P 、是 单位圆上的两点,O 是坐标原点,6π=∠AOP ,[)παα,0,∈=∠AOQ .(1)若34(,)55Q ,求⎪⎭⎫ ⎝⎛-6cos πα的值;(2)设函数()f OP OQ α=⋅u u u r u u u r ,求()αf 的值域.★★单位圆中的三角函数定义解:(Ⅰ)由已知可得54sin ,53cos ==αα……………2分6sin sin 6cos cos 6cos παπαπα+=⎪⎭⎫⎝⎛-∴………3分1043321542353+=⨯+⨯=…………4分(Ⅱ)()f OP OQ α=⋅u u u r u u u r ()cos ,sin cos ,sin 66ππαα⎛⎫=⋅ ⎪⎝⎭………6分ααsin 21cos 23+=………………7分 sin 3πα⎛⎫=+⎪⎝⎭………………8分[0,)απ∈Q 4[,)333πππα∴+∈………9分 sin 123πα⎛⎫-<+≤ ⎪⎝⎭ (12)分()αf ∴的值域是⎛⎤ ⎥ ⎝⎦ (13)分2.(2011年西城期末理15)已知函数2()22sin f x x x =-.(Ⅰ)若点(1,P在角α的终边上,求()f α的值; (Ⅱ)若[,]63x ππ∈-,求()f x 的值域.★★三角函数一般定义解:(Ⅰ)因为点(1,P 在角α的终边上,所以sin α=,1cos 2α=, ………………2分 所以22()22sin cos 2sin f αααααα=-=-………………4分21(2(32=⨯-⨯=-. ………………5分 (Ⅱ)2()22sin f x x x =-cos 21x x =+- ………………6分2sin(2)16x π=+-, ………………8分因为[,]63x ππ∈-,所以65626πππ≤+≤-x , ………………10分所以1sin(2)126x π-≤+≤, ………………11分所以()f x 的值域是[2,1]-. ………………13分 3.(2011年东城区期末理15)函数()sin()(0,0,||)2f x A x A ωφωφπ=+>><部分图象如图所示.(Ⅰ)求()f x 的最小正周期及解析式;(Ⅱ)设()()cos 2g x f x x =-,求函数()g x 在区间[0,]2x π∈上的最大值和最小值.解:(Ⅰ)由图可得1A =,22362T πππ=-=,所以T =π. ……2分 所以2ω=.当6x π=时,()1f x =,可得 sin(2)16ϕπ⋅+=, 因为||2ϕπ<,所以6ϕπ=. ……5分 所以()f x 的解析式为()sin(2)6f x x π=+. ………6分 (Ⅱ)()()cos 2sin(2)cos 26g x f x x x x π=-=+-sin 2cos cos 2sin cos 266xx x ππ=+- 12cos 22x x =- sin(2)6x π=-. ……10分 因为02x π≤≤,所以52666x πππ-≤-≤. 当262x ππ-=,即3x π=时,()g x 有最大值,最大值为1;当266x ππ-=-,即0x =时,()g x 有最小值,最小值为12-.……13分2T =相邻平衡点(最值点)横坐标的差等;2||T =πω ;()max min 12y y A =- ;φ----代点法 4.(2010年海淀期中文16)已知函数x x x f 2cos )62sin()(+-=π.(1)若1)(=θf ,求θθcos sin ⋅的值;(2)求函数)(x f 的单调增区间.(3)求函数的对称轴方程和对称中心 解:(1)22cos 16sin2cos 6cos2sin )(xx x x f ++-=ππ...3分(只写对一个公式给2分) 212sin 23+=x ....5分 由1)(=θf ,可得332sin =θ ......7分 所以θθθ2sin 21cos sin =⋅ ......8分 63= .......9分 (2)当Z k k x k ∈+≤≤+-,22222ππππ,换元法 ..11即Z k k k x ∈++-∈],4,4[ππππ时,)(x f 单调递增.所以,函数)(x f 的单调增区间是Z k k k ∈++-],4,4[ππππ... 13分5.(2011年丰台区期末理15)已知函数2()2sin cos 2cos f x x x x ωωω=- (0x ω∈>R ,),相邻两条对称轴之间的距离等于2π.(Ⅰ)求()4f π的值;(Ⅱ)当02x π⎡⎤∈⎢⎥⎣⎦,时,求函数)(x f 的最大值和最小值及相应的x 值.解:(Ⅰ)()sin 2cos 212sin(2)14f x x x x π=--=--ωωω. ω意义 ……4分因为 22T π=,所以 T =π,1ω=. ……6分所以 ()2sin(2)14f x x π=--.所以 ()04f π= ………7分(Ⅱ)()2sin(2)14f x x π=--当 0,2x π⎡⎤∈⎢⎥⎣⎦时, 32444x πππ-≤-≤, 无范围讨论扣分所以 当242x ππ-=,即8x 3π=时,max ()21f x =-, …10分当244x ππ-=-,即0x =时,min ()2f x =-. ………13分6、(2011朝阳二模理15)已知函数2()2sin sin()2sin 12f x x x x π=⋅+-+ ()x ∈R .(Ⅰ)求函数()f x 的最小正周期及函数()f x 的单调递增区间;(Ⅱ)若02()23x f =,0ππ(, )44x ∈-,求0cos 2x 的值. 解: 2()2sin cos 2sin 1=⋅-+f x x x x ……………………………………1分 sin 2cos2=+x x ……………………………………2分π2sin(2)4x =+. 和差角公式逆用 ………………3分 (Ⅰ)函数()f x 的最小正周期2ππ2T ==. ……………………………………5分 令πππ2π22π242k x k -++≤≤()k ∈Z , ……………………………………6分所以3ππ2π22π44k x k -+≤≤. 即3ππππ88k x k -+≤≤.所以,函数()f x 的单调递增区间为3ππ[π, π]88k k -+ ()k ∈Z . ……………8分(Ⅱ)解法一:由已知得0002()sin cos 23x f x x =+=, …………………9分 两边平方,得021sin 29x += 同角关系式 所以 07sin 29x =-…………11分 因为0ππ(, )44x ∈-,所以0π2(, )22x π∈-. 所以20742cos 21()99x =--=. ……………………………………13分 解法二:因为0ππ(, )44x ∈-,所以0ππ(0, )42x +∈. …………………………9分 又因为000ππ2()2)2)2244x x f x =⋅+=+=,得 0π1sin()43x +=. ……………………………………10分 所以20π122cos()1()43x +=-=……………………………………11分 所以,00000πππcos 2sin(2)sin[2()]2sin()cos()2444x x x x x π=+=+=++ 122422339=⋅⋅=. 诱导公式的运用7、(2011东城二模理15)(本小题共13分)已知πsin()410A+=,ππ(,)42A∈.(Ⅰ)求cos A的值;(Ⅱ)求函数5()cos2sin sin2f x x A x=+的值域.解:(Ⅰ)因为ππ42A<<,且πsin()410A+=,πcos()410A+=-.ππππcos()cossin()sin4444A A+++31021025=-⋅+=.所以3cos5A=.………6分(Ⅱ)由(Ⅰ)可得4sin5A=.212sin2sinx x=-+2132(sin)22x=--+,x∈R.因为sin[1,1]x∈-,所以,当1sin2x=时,()f x取最大值32;当sin1x=-时,()f x取最小值3-.所以函数()f x的值域为3[3,]2-.8.(2011年朝阳期末理15)已知△ABC中,2sin cos sin cos cos sinA B C B C B=+.(Ⅰ)求角B的大小;(Ⅱ)设向量(cos,cos2)A A=m,12(, 1)5=-n,求当⋅m n取最小值时,)4tan(π-A值.解:和差角公式逆用所以2sin cos sin()sin()sinA B B C A A=+=π-=. ……… 3分因为0A p<<,所以sin0A¹.所以1cos2B=. ……… 5分3Bπ=. …………7分(Ⅱ)因为12cos cos25A A⋅=-+m n,………………… 8分所以2212343cos2cos12(cos)5525A A A⋅=-+-=--m n. …10分所以当3cos5A=时,⋅m n取得最小值.同角关系或三角函数定义……12分所以tan11tan()4tan17AAAπ--==+. …………… 13分9.(2011年石景山期末理15)已知函数23cossinsin3)(2-+=xxxxf()Rx∈.(Ⅰ)求)4(πf的值;(Ⅱ)若)2,0(π∈x,求)(xf的最大值;(Ⅲ)在ABC∆中,若BA<,21)()(==BfAf,求ABBC的值.解:(Ⅰ)234cos4sin4sin3)4(2-+=ππππf21=. 4分(Ⅱ)2)2cos1(3)(xxf-=+232sin21-xxx2cos232sin21-=)32sin(π-=x.…6分2π<<xΘ,32323πππ<-<-∴x.∴当232xππ-=时,即125π=x时,)(xf的最大值为1.…8分(Ⅲ)Θ)32sin()(π-=xxf,若x是三角形的内角,则π<<x令21)(=xf,得解得4π=x或127π=x.……10分由已知,BA,是△ABC的内角,BA<且21)()(==BfAf,∴4π=A,127π=B,∴6π=--π=BAC.…11分又由正弦定理,得221226sin 4sinsin sin ==ππ==C A AB BC . ……13分 10、(2011东城一模理15)(本小题共13分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c 分,且满足2cos cos c b Ba A-=. (Ⅰ)求角A 的大小;(Ⅱ)若a =ABC 面积的最大值. 解:(Ⅰ)因为2cos cos c b Ba A-=, 所以(2)cos cos c b A a B -⋅=⋅由正弦定理,得(2sin sin )cos sin cos C B A A B -⋅=⋅.边化角 整理得2sin cos sin cos sin cos C A B A A B ⋅-⋅=⋅. 所以2sin cos sin()sin C A A B C ⋅=+=. 在△ABC所以1cos 2A =,3A π∠=.(Ⅱ)由余弦定理2221cos 22b c a A bc +-==,a = 所以2220220b cbc bc +-=≥- 均值定理在三角中的应用 所以20bc ≤,当且仅当b c=时取“=” . 取等条件别忘 所以三角形的面积1sin 2S bc A =≤. 所以三角形面积的最大值为 ……………………13分11、(2011丰台一模理15). 在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且b 2+c 2-a 2=bc .(Ⅰ)求角A 的大小;(Ⅱ)设函数2cos 2cos 2sin 3)(2x x x x f +=,当)(B f 取最大值23时,判断△ABC的形状.解:(Ⅰ)在△ABC 中,因为b2+c 2-a 2=bc 可得cos A =12.(余弦定理或公式必须有一个,否则扣1分) ……3分 ∵, (或写成A 是三角形内角) ……………………4分 ∴3A π=.……………………5分 (Ⅱ)2cos2cos 2sin 3)(2x x x x f +=11cos 222x x =++ …7分 1sin()62x π=++, ……9分∵3A π=∴2(0,)3B π∈(没讨论,扣1分)…10分 ∴当62B ππ+=,即3B π=时,()f B 有最大值是23. …11分 又∵3A π=, ∴3C π= ∴△ABC 为等边三角形. ……13分12、(2011海淀一模理15). (本小题共13分)在ABC ∆中,内角A 、B 、C 所对的边分别为,,a b c ,已知1tan 2B =,1tan 3C =,且1c =. (Ⅰ)求tan A ; (Ⅱ)求ABC ∆的面积. 解:(I )因为1tan 2B =,1tan 3C =,tan tan tan()1tan tan B C B C B C ++=-, …………………1分代入得到,1123tan()111123B C ++==-⨯ . …………………3分 因为180A B C =--o , …………………4分角关系 ………5分 (II )因为0180A <<o o ,由(I )结论可得:135A =o . …………………7分因为11tan tan 023BC =>=>,所以090C B <<<o o . …………8分所以sin B =sin C =. …………9分 由sin sin a cA C=得a = …………………11分 所以ABC ∆的面积为:11sin 22ac B =. ………………13分 13、(2011石景山一模理15).在ABC ∆中,角A ,B ,C 所对应的边分别为a ,b ,c ,且274sin cos222A B C +-=. (Ⅰ)求角C 的大小;(Ⅱ)求sin sin A B +的最大值.解:(Ⅰ)∵ A 、B 、C 为三角形的内角, ∴ π=++C B A .∵ 三角形中角的大小关系∴ …………2分 ∴ 27)1cos 2(2cos 142=--+⋅C C .即 021cos 2cos 22=+-C C . ……4分∴ 21cos =C . 又∵ π<<C 0 , ∴ 3π=C . …7分(Ⅱ)由(Ⅰ)得 32π=+B A .∴ A A A sin 32cos cos 32sinsin ⋅-⋅+=ππ)6sin(3cos 23sin 23π+=+=A A A .…10分 ∵ 320π<<A ,∴ 6566πππ<+<A .∴ 当26ππ=+A ,即 3π=A 时,B A sin sin +取得最大值为3.…………13分。
22版:高考专题突破二 高考中的解三角形问题(步步高)

高考专题突破二 高考中的解三角形问题题型一 利用正、余弦定理解三角形例1 (10分)(2020·新高考全国Ⅰ)在①ac =3,②c sin A =3,③c =3b 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c 的值;若问题中的三角形不存在,说明理由.问题:是否存在△ABC ,它的内角A ,B ,C 的对边分别为a ,b ,c ,且sin A =3sin B ,C =π6,________? 注:如果选择多个条件分别解答,按第一个解答计分.规范解答解 方案一:选条件①.由C =π6和余弦定理得a 2+b 2-c 22ab =32.[2分] 由sin A =3sin B 及正弦定理得a =3b . 于是3b 2+b 2-c 223b 2=32,[6分] 由此可得b =c .[7分]由①ac =3,解得a =3,b =c =1.[9分]因此,选条件①时问题中的三角形存在,此时c =1.[10分]方案二:选条件②.由C =π6和余弦定理得a 2+b 2-c 22ab =32.[2分] 由sin A =3sin B 及正弦定理得a =3b . 于是3b 2+b 2-c 223b 2=32,[6分] 由此可得b =c ,B =C =π6,A =2π3.[7分] 由②c sin A =3,得c =b =23,a =6.[9分]因此,选条件②时问题中的三角形存在,此时c =2 3.[10分]方案三:选条件③.由C =π6和余弦定理得a 2+b 2-c 22ab =32.[2分]由sin A =3sin B 及正弦定理得a =3b .于是3b 2+b 2-c 223b 2=32,[6分] 由此可得b =c .[7分]由于③c =3b ,与b =c 矛盾.[9分]因此,选条件③时问题中的三角形不存在.[10分]第一步:根据C =π6及余弦定理得出a ,b ,c 的关系; 第二步:根据条件sin A =3sin B 得出a ,b 的关系,从而得出b ,c 的关系;第三步:结合自然条件即可求出各边长;第四步:下结论,判断三角形解的情况.[高考改编题] 在①cos 2B -3sin B +2=0;②2b cos C =2a -c ;③b a =cos B +13sin A三个条件中任选一个,补充在下面问题中,并加以解答.已知△ABC 的内角A ,B ,C 所对的边分别是a ,b ,c ,若________,且a ,b ,c 成等差数列,则△ABC 是否为等边三角形?若是,写出证明;若不是,说明理由.注:如果选择多个条件分别解答,按第一个解答计分.解 选条件①.因为cos 2B =1-2sin 2B ,所以2sin 2B +3sin B -3=0,即(2sin B -3)(sin B +3)=0,解得sin B =-3(舍去)或sin B =32. 因为0<B <π,所以B =π3或2π3. 又因为a ,b ,c 成等差数列,所以2b =a +c ,所以b 不是三角形中最大的边,即B =π3. 由b 2=a 2+c 2-2ac cos B ,得a 2+c 2-2ac =0,即a =c ,从而a =b =c ,故△ABC 是等边三角形.选条件②.由正弦定理可得2sin B cos C =2sin A -sin C ,故2sin B cos C =2sin(B +C )-sin C ,整理得2cos B sin C -sin C =0.因为0<C <π,所以sin C >0,即cos B =12. 因为0<B <π,所以B =π3. 又因为a ,b ,c 成等差数列,所以2b =a +c .由余弦定理b 2=a 2+c 2-2ac cos B ,可得a 2+c 2-2ac =0,即a =c .故△ABC 是等边三角形.选条件③.由正弦定理得sin B sin A =cos B +13sin A. 因为sin A ≠0,所以3sin B -cos B =1,即sin ⎝⎛⎭⎫B -π6=12. 因为0<B <π,所以-π6<B -π6<5π6, 即B -π6=π6,可得B =π3. 又因为a ,b ,c 成等差数列,所以2b =a +c ,由余弦定理b 2=a 2+c 2-2ac cos B ,可得a 2+c 2-2ac =0,即a =c .故△ABC 是等边三角形.跟踪训练1 (2019·全国Ⅰ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,设(sin B -sin C )2=sin 2A -sin B sin C .(1)求A ;(2)若2a +b =2c ,求sin C .解 (1)由已知得sin 2B +sin 2C -sin 2A =sin B sin C ,故由正弦定理得b 2+c 2-a 2=bc ,由余弦定理得cos A =b 2+c 2-a 22bc =12, 因为0°<A <180°,所以A =60°.(2)由(1)知B =120°-C ,由题设及正弦定理得2sin A +sin(120°-C )=2sin C ,即62+32cos C +12sin C =2sinC , 可得cos(C +60°)=-22. 由于0°<C <120°,所以sin(C +60°)=22, 故sin C =sin(C +60°-60°)=sin(C +60°)cos 60°-cos(C +60°)sin 60° =6+24. 题型二 平面几何中的解三角形问题例2 (八省联考)在四边形ABCD 中,AB ∥CD ,AD =BD =CD =1.(1)若AB =32,求BC ; (2)若AB =2BC ,求cos ∠BDC .解 (1)在△ABD 中,cos ∠ABD =12+⎝⎛⎭⎫322-122×1×32=34, 因为AB ∥CD ,所以∠CDB =∠ABD , 所以cos ∠CDB =34, 在△BDC 中,BC 2=DC 2+DB 2-2CD ·DB cos ∠CDB =12+12-2×34=12,所以BC =22. (2)设BC =x ,则AB =2x ,所以cos ∠ABD =12+(2x )2-124x=x , cos ∠CDB =12+12-x 22=1-12x 2, 因为AB ∥CD ,所以∠CDB =∠ABD , 故x =1-12x 2,x 2+2x =2, 又x >0,所以x =3-1,所以cos ∠BDC =cos ∠ABD =3-1.思维升华 平面几何中解三角形问题的求解思路(1)把所提供的平面图形拆分成若干个三角形,然后在各个三角形内利用正弦、余弦定理求解.(2)寻找各个三角形之间的联系,交叉使用公共条件,求出结果.跟踪训练2 (2020·河南、河北重点中学联考)如图,在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知c =4,b =2,2c cos C =b ,D ,E 均为线段BC 上的点,且BD =CD ,∠BAE =∠CAE .(1)求线段AD 的长;(2)求△ADE 的面积.解 (1)因为c =4,b =2,2c cos C =b ,所以cos C =b 2c =14. 由余弦定理得cos C =a 2+b 2-c 22ab =a 2+4-164a =14, 所以a =4,即BC =4.在△ACD 中,CD =2,AC =2,所以AD 2=AC 2+CD 2-2AC ·CD ·cos C =6,所以AD = 6.(2)因为AE 是∠BAC 的平分线,所以S △ABE S △ACE =12AB ·AE ·sin ∠BAE 12AC ·AE ·sin ∠CAE =AB AC =2, 又S △ABE S △ACE =BE EC,所以BE EC =2, 所以CE =13BC =43,DE =DC -EC =2-43=23. 又因为cos C =14,所以sin C =1-cos 2C =154. 所以S △ADE =S △ACD -S △ACE =12AC ·CD sin C -12AC ·EC sin C =12AC ·(CD -EC )sin C =12DE ·AC sin C =156.即△ADE 的面积为156. 题型三 解三角形中的最值与范围问题例3 (2021·湖北七市联考)在锐角三角形ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且cos A a +cos B b =23sin C 3a. (1)求角B 的大小;(2)若b =23,求a +c 的取值范围.解 (1)由已知条件,得b cos A +a cos B =233b sin C . 由正弦定理,得sin B cos A +cos B sin A =233sin B sin C , 即sin(A +B )=233sin B sin C . 又在△ABC 中,sin(A +B )=sin C ≠0, 所以sin B =32.因为B 是锐角,所以B =π3. (2)由正弦定理,得a sin A =c sin C =b sin B =2332=4, 则a =4sin A ,c =4sin C .所以a +c =4sin A +4sin C =4sin A +4sin ⎝⎛⎭⎫2π3-A =6sin A +23cos A =43sin ⎝⎛⎭⎫A +π6. 由0<A <π2,0<2π3-A <π2,得π6<A <π2, 所以π3<A +π6<2π3,所以32<sin ⎝⎛⎭⎫A +π6≤1, 所以6<a +c ≤4 3.故a +c 的取值范围为(6,43].思维升华 本题涉及求边的取值范围,一般思路是(1)利用正弦定理把边转化为角,利用三角函数的性质求出范围或最值.(2)利用正、余弦定理把角转化为边,利用不等式求出范围或最值.跟踪训练3 给出两个条件:①2c -3b =2a cos B ;②(2b -3c )cos A =3a cos C ,从中选出一个条件补充在下面的问题中,并以此为依据求解问题.(选出一种可行的条件解答,若两个都选,则按第一个解答计分)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 所对的边. (1)求A ;(2)若a =3-1,求△ABC 面积的最大值.解 (1)选①2c -3b =2a cos B ,由正弦定理可得,2sin C -3sin B =2sin A cos B ,即2sin ()A +B -3sin B =2sin A cos B ,∴2cos A sin B =3sin B ,∵B ∈()0,π,∴sin B ≠0,∴2cos A =3,即cos A =32, 又A ∈()0,π,∴A =π6. 选②()2b -3c cos A =3a cos C ,由正弦定理可得,()2sin B -3sin C cos A =3sin A cos C , ∴2sin B cos A =3sin ()A +C =3sin B ,∵B ∈()0,π,∴sin B ≠0,∴cos A =32, 又A ∈()0,π,∴A =π6. (2)由余弦定理得,a 2=b 2+c 2-2bc cos A =b 2+c 2-3bc , 又b 2+c 2≥2bc ,当且仅当“b =c ”时取“=”,∴a 2≥()2-3bc ,即()3-12≥()2-3bc ,∴bc ≤2,∴S △ABC =12bc sin A =14bc ≤12, ∴△ABC 的面积的最大值为12.。
解三角形题型培优(学生版)
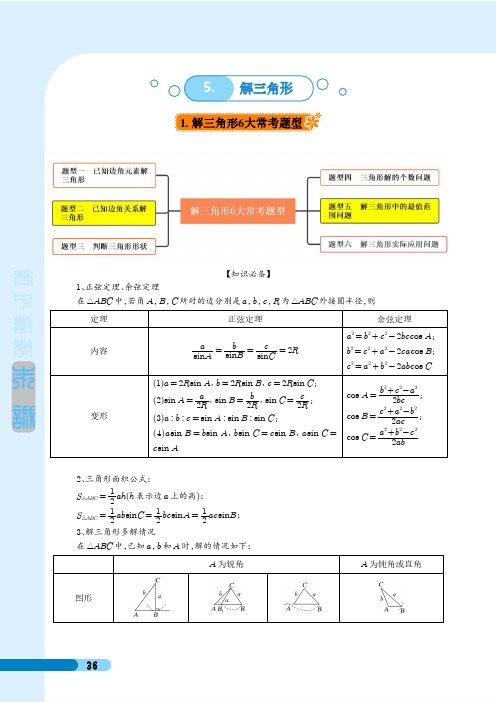
5.解三角形1.解三角形6大常考题型【知识必备】1、正弦定理、余弦定理在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则定理正弦定理余弦定理内容asin A=bsin B=csin C=2Ra2=b2+c2-2bc cos A;b2=c2+a2-2ca cos B;c2=a2+b2-2ab cos C变形(1)a=2R sin A,b=2R sin B,c=2R sin C;(2)sin A=a2R,sin B=b2R,sin C=c2R;(3)a∶b∶c=sin A∶sin B∶sin C;(4)a sin B=b sin A,b sin C=c sin B,a sin C=c sin Acos A=b2+c2-a22bc;cos B=c2+a2-b22ac;cos C=a2+b2-c22ab2、三角形面积公式:S△ABC=12ah(h表示边a上的高);S△ABC=12ab sin C=12bc sin A=12ac sin B;3、解三角形多解情况在△ABC中,已知a,b和A时,解的情况如下:A为锐角A为钝角或直角图形a =b sin A b sin A <a <b a ≥关系式b a >b a ≤b解的个数一解两解一解一解无解4、实际应用(1)仰角和俯角在视线和水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫俯角(如图①).(2)方位角从指北方向顺时针转到目标方向线的水平角,如B 点的方位角为α(如图②).(3)方向角:相对于某一正方向的水平角.(1)北偏东α,即由指北方向顺时针旋转α到达目标方向(如图③).(2)北偏西α,即由指北方向逆时针旋转α到达目标方向.(3)南偏西等其他方向角类似.(4)坡角与坡度(1)坡角:坡面与水平面所成的二面角的度数(如图④,角θ为坡角).(2)坡度:坡面的铅直高度与水平长度之比(如图④,5、相关应用(1)正弦定理的应用①边化角,角化边⇔a :b :c =sin A :sin B :sin C②大边对大角大角对大边a >b ⇔A >B ⇔sin A >sin B ⇔cos A <cos i 为坡度).坡度又称为坡比.Ba +b +c③合分比:sin A +sin B +sin Ca +b =sin A +sin B b +c =sin B +sin C a +c =sin A +sin C a =sin A b =sin B c =sin C=2R (2)△ABC 内角和定理:A +B +C =π①sin C =sin (A +B )=sin A cos B +cos A sin B ⇔c =a cos B +b cos A 同理有:a =b cos C +c cos B ,b =c cos A +a cos C .②-cos C =cos (A +B )=cos A cos B -sin A sin B ;A +tan ③斜三角形中,-tan C =tan (A +B )=1Btan -tan ⋅A tan B⇔tan A +tan B +tan C =tan A ⋅tan B ⋅tan C④sin A +2B =cos C 2;cos A +2B=sin C 2⑤在ΔABC 中,内角A ,B ,C 成等差数列⇔B =π3,A +C =2π3.Z 【题型精讲】题型一:【已知边角元素解三角形】必备技巧已知边角元素解三角形技巧正弦定理、余弦定理的作用是在已知三角形部分元素的情况下求解其余元素,基本思想是方程思想,即根据正弦定理、余弦定理列出关于未知元素的方程,通过解方程求得未知元素.1.1(多选)(山东济南一模)在ΔABC中,角A,B,C所对的边分别为a,b,c,下列结论正确的是()A.a2=b2+c2-2bc cos AB.a sin B=b sin AC.a=b cos C+c cos BD.a cos B+b cos A=sin C1.2(多选)(重庆市高三二模)已知在△ABC中,角A,B,C所对的边分别为a,b,c,且A=60°,b=2,c=3+1,则下列说法正确的是A.C=75°或C=105°B.B=45°C.a=6D.该三角形的面积为3+1 21.3在△ABC中,角A,B,C所对的边分别为a,b,c若sin A=35,A=2B,角C为钝角,b=5.(1)求sin(A-B)的值;(2)求边c的长.Z【跟踪精练】1.3.1在△ABC中,角A,B,C所对的边分别为a,b,c,若(a+b)2-c2=ab,则C=()A.π6 B.π3或2π3 C.2π3 D.π6或5π61.3.2在△ABC中,内角A,B,C所对的边分别是a,b,c.若A=π3,a=23,b=22,则B=()A.π4 B.π3 C.π4或3π4 D.π3或2π31.3.3△ABC的内角A、B、C的对边分别为a、b、c,若a=4,b=3,c=2,则中线AD的长为()A.5B.10C.52 D.102题型二:【已知边角关系解三角形】必备技巧已知边角关系解三角形正弦定理、余弦定理的另一个作用是实现三角形边角关系的互化,解题时可以把已知条件化为角的三角函数关系,也可以把已知条件化为三角形边的关系.1.1在△ABC中,内角A,B,C的对边分别为a,b,c,已知2cos C a cos B+b cos A=c.(1)若cos A=64,求sin2A+C的值;(2)若c=7,△ABC的面积为332,求边a,b的值.21a △ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知△ABC 1.2的面积为2-b 2sin C .(1)证明:sin A =2sin B ;(2)若a cos C =32b ,求cos A .Z 【跟踪精练】ΔABC 的内角A ,B ,C 的对边分别为a ,b ,c .设(sin B -sin C )2=sin 2A 1.2.1-sin B sin C .(1)求A ;(2)若2a +b =2c ,求sin C .在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,b tan A +b tan B 1.2.2=3ccos A.(1)求角B ;(2)D 是AC 边上的点,若CD =1,AD =BD =3,求sin A 的值.题型三:【判断三角形形状】必备技巧判断三角形形状的方法(1)化边:通过因式分解、配方等得出边的相应关系.(2)化角:通过三角恒等变换,得出内角的关系,此时要注意应用A +B +C =π这个结论.在△ABC 中,已知a 2+b 2-c 2=ab ,且2cos A sin B =sin C 1.1,则该三角形的形状是()A.直角三角形B.等腰三角形C.等边三角形D.钝角三角形在△ABC 中,已知(b +c -a )(b +c +a )=3bc ,且2cos B sin C =sin A ,则△ABC 1.2的形状为()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形Z 【跟踪精练】对于△ABC ,有如下四个命题1.2.1:①若sin2A =sin2B ,则△ABC 为等腰三角形,②若sin B =cos A ,则△ABC 是直角三角形③若sin 2A +sin 2B <sin 2C ,则△ABC 是钝角三角形④若acos 2A =b cos 2B =cC cos 2,则△ABC 是等边三角形.其中正确的命题序号是1.2.2a在△ABC 中,已知a +b =tan Ab +tan B ,则△ABC 的形状一定是()A.等腰三角形B.直角三角形C.等边三角形D.等腰或直角三角形题型四:【三角形解的个数问题】1.1已知在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,则根据条件解三角形时恰有一解的一组条件是()A.a =3,b =4,A =π6 B.a =4,b =3,A =π3C.a =1,b =2,A =π4D.a =2,b =3,A =2π31.2△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,A =30°,a =3,若这个三角形有两解,则b 的取值范围是()A.3<b ≤6B.3<b <6C.b <6D.b ≤6Z 【跟踪精练】1.2.1在△ABC 中,根据下列条件解三角形,则其中有两个解的是()A.b =10,A =45°,C =70°B.a =60,c =48,B =60°C.a =5,b =7,c =8D.a =14,b =16,A =45°1.2.2在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若,满足条件a =3,A =60°的三角形有两个,则b 的取值范围是()A.2,3B.3,33C.3,23D.22,23题型五:【解三角形中的最值范围问题】方法技巧解三角形中最值范围问题基本处理方法1、用余弦定理结合基本不等式求解,2、要求的量转化为某角的三角函数,求函数的最值或值域。
高考数学第05周解三角形周末培优试题理新人教A版(2021学年)

2017-2018学年高考数学第05周解三角形周末培优试题理新人教A 版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017-2018学年高考数学第05周解三角形周末培优试题理新人教A版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017-2018学年高考数学第05周解三角形周末培优试题理新人教A版的全部内容。
第05周 解三角形(测试时间:60分钟,总分:90分)班级:____________ 姓名:____________ 座号:____________ 得分:____________一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.在ABC △中,角,,A B C 的对边分别为,,a b c ,30,则B =A .60或120 ﻩﻩ B.60C.120 ﻩ ﻩﻩﻩﻩﻩD .30或150 【答案】A∵b a >,∴60B =︒或120,故本题选A。
2.在ABC △中,角,,A B C 的对边分别为,,a b c ,若2c =,221a b =+,则cos a B =ﻩﻩﻩ ﻩﻩ C ﻩ ﻩﻩ D.5【答案】B【解析】由余弦定理得,2222212cos 154cos a b a c ac B a a B=+=+-+=+-554cos 0cos 4a B a B ⇒-=⇒=,故选B.3.若ABC △的内角,,A B C 所对的边分别为,,a b c ,已知2sin23sin b A a B =,且2c b =,A ﻩﻩ ﻩ BC ﻩﻩﻩ ﻩﻩ【答案】B【解析】2sin 23sin b A a B =4sin cos 3sin 4sin sin cos 3sin sin b A A a B B A A A B ⇒=⇒=2224cos 343,2b c a A bc+-⇒=⇒⋅=22c b a b =∴=,,选B。
