实验八回归分析
数学建模实验报告

湖南城市学院数学与计算科学学院《数学建模》实验报告专业:学号:姓名:指导教师:成绩:年月日目录实验一 初等模型........................................................................ 错误!未定义书签。
实验二 优化模型........................................................................ 错误!未定义书签。
实验三 微分方程模型................................................................ 错误!未定义书签。
实验四 稳定性模型.................................................................... 错误!未定义书签。
实验五 差分方程模型................................................................ 错误!未定义书签。
实验六 离散模型........................................................................ 错误!未定义书签。
实验七 数据处理........................................................................ 错误!未定义书签。
实验八 回归分析模型................................................................ 错误!未定义书签。
实验一 初等模型实验目的:掌握数学建模的基本步骤,会用初等数学知识分析和解决实际问题。
实验内容:A 、B 两题选作一题,撰写实验报告,包括问题分析、模型假设、模型构建、模型求解和结果分析与解释五个步骤。
主成分回归多重共线性
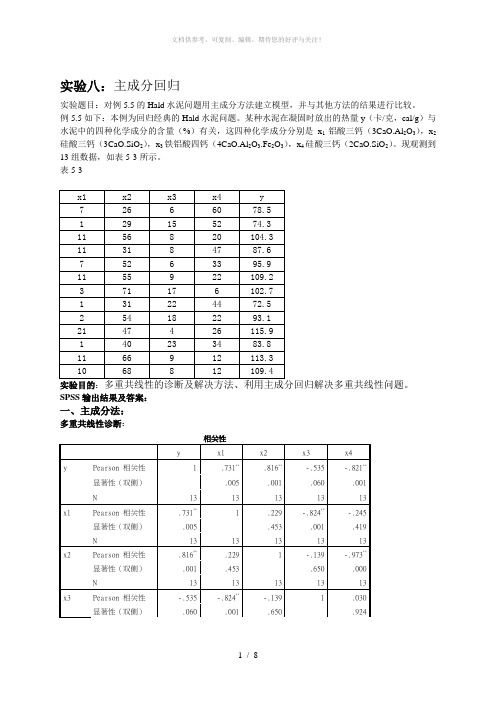
实验八:主成分回归实验题目:对例5.5的Hald水泥问题用主成分方法建立模型,并与其他方法的结果进行比较。
例5.5如下:本例为回归经典的Hald水泥问题。
某种水泥在凝固时放出的热量y(卡/克,cal/g)与水泥中的四种化学成分的含量(%)有关,这四种化学成分分别是x1铝酸三钙(3CaO.Al2O3),x2硅酸三钙(3CaO.SiO2),x3铁铝酸四钙(4CaO.Al2O3.Fe2O3),x4硅酸三钙(2CaO.SiO2)。
现观测到13组数据,如表5-3所示。
表5-3实验目的:SPSS输出结果及答案:一、主成分法:多重共线性诊断:N 13 13 13 13 13 x4 Pearson 相关性-.821**-.245 -.973**.030 1显著性(双侧).001 .419 .000 .924N 13 13 13 13 13**. 在 .01 水平(双侧)上显著相关。
由表可知,x1,x2,x4的相关性都比较大,较接近,所以存在多重共线性主成分回归:解释的总方差成份初始特征值提取平方和载入合计方差的 % 累积 % 合计方差的 % 累积 %1 2.236 55.893 55.893 2.236 55.893 55.8932 1.576 39.402 95.294 1.576 39.402 95.2943 .187 4.665 99.959 .187 4.665 99.9594 .002 .041 100.000 .002 .041 100.000提取方法:主成份分析。
输出结果显示有四个特征根,最大的是λ1=2.236,最小的是λ4=0.002。
方差百分比显示第一个主成分Factor1的方差百分比近56%的信息量;前两个主成分累计包含近95.3%的信息量。
因此取两个主成分就已经足够。
由于前两个主成分的方差累计已经达到95.3%,故只保留前两个主成分。
成份矩阵a成份1 2 3 4x1 .712 -.639 .292 .010x2 .843 .520 -.136 .026x3 -.589 .759 .275 .011x4 -.819 -.566 -.084 .027提取方法:主成分a.已提取了 4 个成份。
回归分析课程设计

回归分析课程设计一、教学目标本节课的教学目标是让学生掌握回归分析的基本概念、原理和方法,能够运用回归分析解决实际问题。
具体来说,知识目标包括:了解回归分析的定义、原理和应用;掌握一元线性回归和多元线性回归的分析方法;理解回归模型的评估和优化。
技能目标包括:能够使用统计软件进行回归分析;能够解释和分析回归结果;能够根据实际问题选择合适的回归模型。
情感态度价值观目标包括:培养学生的数据分析能力和科学思维;激发学生对回归分析的兴趣和好奇心;培养学生的团队合作意识和问题解决能力。
二、教学内容本节课的教学内容主要包括回归分析的基本概念、原理和方法。
具体来说,教学大纲如下:1.回归分析的定义和原理–介绍回归分析的定义和基本原理–解释一元线性回归和多元线性回归的概念2.回归模型的建立和评估–介绍回归模型的建立方法和步骤–讲解如何评估和优化回归模型3.回归分析的应用–介绍回归分析在实际问题中的应用案例–引导学生运用回归分析解决实际问题三、教学方法为了达到本节课的教学目标,将采用多种教学方法进行教学。
具体包括:1.讲授法:通过讲解回归分析的基本概念、原理和方法,使学生掌握相关知识。
2.案例分析法:通过分析实际案例,让学生了解回归分析在实际问题中的应用。
3.讨论法:学生进行小组讨论,培养学生的团队合作意识和问题解决能力。
4.实验法:引导学生使用统计软件进行回归分析,提高学生的实践操作能力。
四、教学资源为了支持本节课的教学内容和教学方法的实施,将准备以下教学资源:1.教材:选用权威、实用的统计学教材,作为学生学习的基础资料。
2.参考书:推荐学生阅读相关领域的参考书籍,丰富学生的知识体系。
3.多媒体资料:制作精美的PPT,展示回归分析的原理、方法和应用案例。
4.实验设备:准备计算机、统计软件等实验设备,方便学生进行实际操作。
五、教学评估本节课的评估方式将采用多元化、全过程的评价体系,以全面、客观、公正地评估学生的学习成果。
回归分析数据

回归分析数据回归分析是一种经济学和统计学中常用的方法,用于研究两个或更多变量之间的关系。
这种分析方法广泛应用于各个领域,包括市场研究、金融分析、经济预测等。
在此文档中,我们将介绍回归分析数据以及如何使用它们进行分析和解释。
回归分析的基本概念是研究一个或多个自变量对某个因变量的影响。
自变量是独立变量,而因变量则是依赖于自变量的变量。
通过分析自变量与因变量之间的关系,我们可以得出它们之间的数学模型,用于预测或解释因变量。
在进行回归分析之前,我们首先需要收集回归分析数据。
这些数据包括自变量和因变量的观测值。
通常,我们会收集一组样本数据,其中包含自变量和对应的因变量的数值。
这些数据可以是经过实验或观测得到的,也可以是从其他来源获取的。
一旦我们收集到回归分析数据,接下来就可以使用统计软件或编程语言进行数据分析。
常见的回归分析方法包括简单线性回归、多元线性回归和非线性回归。
在简单线性回归中,我们将自变量和因变量之间的关系建模为一条直线。
在多元线性回归中,我们可以考虑多个自变量对因变量的影响。
非线性回归则允许我们考虑更复杂的关系模型。
回归分析的结果通常包括回归方程、参数估计和统计显著性检验。
回归方程描述了自变量和因变量之间的数学关系。
参数估计给出了回归方程中的系数估计值,用于解释自变量与因变量之间的关系。
统计显著性检验则用于判断回归方程的有效性和模型的拟合度。
当我们得到回归分析的结果后,我们可以进行解释和预测。
通过解释回归方程中的系数估计值,我们可以了解自变量与因变量之间的关系强度和方向。
通过预测模型,我们可以根据自变量的数值预测因变量的数值。
回归分析数据在许多实际应用中具有重要的价值。
在市场研究中,回归分析数据可以帮助我们理解产品价格与销售量之间的关系。
在金融分析中,回归分析数据可以用于预测股票价格或汇率变动。
在经济预测中,回归分析数据可以用于预测GDP增长率或失业率。
总而言之,回归分析数据是一种强大的工具,用于研究自变量与因变量之间的关系。
SPSS实验8-二项Logistic回归分析
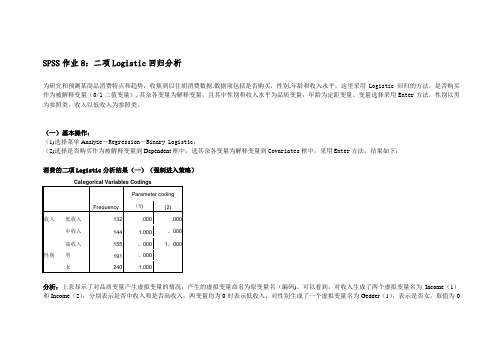
SPSS作业8:二项Logistic回归分析为研究和预测某商品消费特点和趋势,收集到以往胡消费数据.数据项包括是否购买,性别,年龄和收入水平。
这里采用Logistic回归的方法,是否购买作为被解释变量(0/1二值变量),其余各变量为解释变量,且其中性别和收入水平为品质变量,年龄为定距变量。
变量选择采用Enter方法,性别以男为参照类,收入以低收入为参照类。
(一)基本操作:(1)选择菜单Analyz e-Regression-Binary Logistic;(2)选择是否购买作为被解释变量到Dependent框中,选其余各变量为解释变量到Covariates框中,采用Enter方法,结果如下:消费的二项Logistic分析结果(一)(强制进入策略)Categorical Variables CodingsFrequency Parameter coding (1) (2)收入低收入132 .000 .000中收入144 1.000 。
000高收入155 。
000 1。
000性别男191 。
000女240 1.000分析:上表显示了对品质变量产生虚拟变量的情况,产生的虚拟变量命名为原变量名(编码)。
可以看到,对收入生成了两个虚拟变量名为Income(1)和Income(2),分别表示是否中收入和是否高收入,两变量均为0时表示低收入;对性别生成了一个虚拟变量名为Gedder(1),表示是否女,取值为0时表示为男。
消费的二项Logistic 分析结果(二)(强制进入策略)Block 0: Beginning BlockClassification Table a,bObserved Predicted是否购买 Percentage Correct不购买购买Step 0是否购买不购买 269 0 100。
购买162。
0 Overall Percentage62。
4a 。
Constant is included in the model 。
实验八 气相色谱法测定甲醇中的苯系物

ห้องสมุดไป่ตู้氢气流量:空气流量:氮气流量:
分析项目
保留时间min
保留时间min
2.数据处理
以色谱峰面积为纵坐标,标准溶液的浓度为横坐标,绘制标准曲线,计算回归方程a、b、r值,及未知苯系物的含量。
1)苯的含量:
2)甲苯含量:
广东环境保护工程职业学院
班级:
学号:《仪器分析技术》实验(实习)报告
姓名:成绩:
组别评阅老师:
同组人姓名:日期:
实验名称:实验八气相色谱法测定甲醇中的苯系物
[实验目的]:
[实验原理]:
[仪器与试剂]
[实验步骤]:
[数据记录与结果报告表]:
1.数据记录
分析日期:年月日进样体积:μL
标准曲线浓度范围:
气化室温度:分流比:柱温条件:柱流量:
岭回归
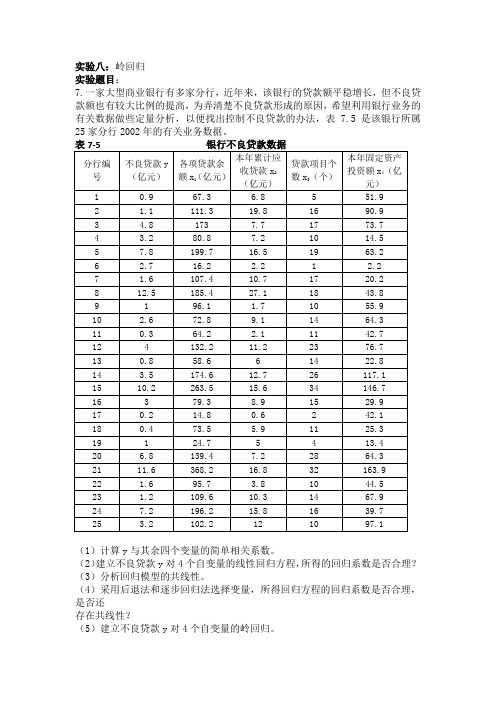
实验八:岭回归实验题目:7.一家大型商业银行有多家分行,近年来,该银行的贷款额平稳增长,但不良贷款额也有较大比例的提高,为弄清楚不良贷款形成的原因,希望利用银行业务的有关数据做些定量分析,以便找出控制不良贷款的办法,表7.5是该银行所属25家分行2002年的有关业务数据。
(1)计算y与其余四个变量的简单相关系数。
(2)建立不良贷款y对4个自变量的线性回归方程,所得的回归系数是否合理?(3)分析回归模型的共线性。
(4)采用后退法和逐步回归法选择变量,所得回归方程的回归系数是否合理,是否还存在共线性?(5)建立不良贷款y对4个自变量的岭回归。
(6)对第4步剔除变量后的回归方程再做岭回归。
(7)某研究人员希望做y对各项贷款余额,本年累计应收贷款贷款项目个数这三个变量的回归,你认为这种做是否可行,如果可行应该如何做?实验目的:利用岭估计解决多重共线性问题SPSS主要操作:需要编程序,进入Syntax语法窗口,录入以下命令:INCLUDE’c:Program Files\spss 10.0\Ridge regression.sps’.(该命令因spss安装的路径不同而要作相应的修改)Ridgereg enter=x1 x2 x3/dep=y(在选出k,比如k=0.5,再增加一条命令/k=0.5)SPSS输出结果及答案:(1)计算y与其余四个变量的简单相关系数。
由结果得到,Y与四个自变量的相关系数分别为:0.844, 0.732, 0.7, 0.519,且都通过了显著性检验,说明y与其余4个变量是显著线性相关的。
同时也可以看出变量之间也存在一定的线性相关性。
(2)建立不良贷款y对4个自变量的线性回归方程,所得的回归系数是否合理?回归方程为:y=0.04x1+0.148x2+0.015x3-0.029x4-1.022从上表可看出,方程的自变量x3,x4,x5未通过t检验,说明回归方程不显著,而且由实际意义出发,x4的系数不能是负的。
实验设计与数据处理第八章例题及课后习题答案doc资料
0
428
0 1.162084
492
0 1.162084
512
0
0
509
0
0
Signific ance F
7.93E-05
Lower Upper 下限 上限
95%
95% 95.0% 95.0%
465.4405 471.5595 465.4405 471.5595
5.242078 12.93644 5.242078 12.93644
0.002795085 2.593838854 0.122018
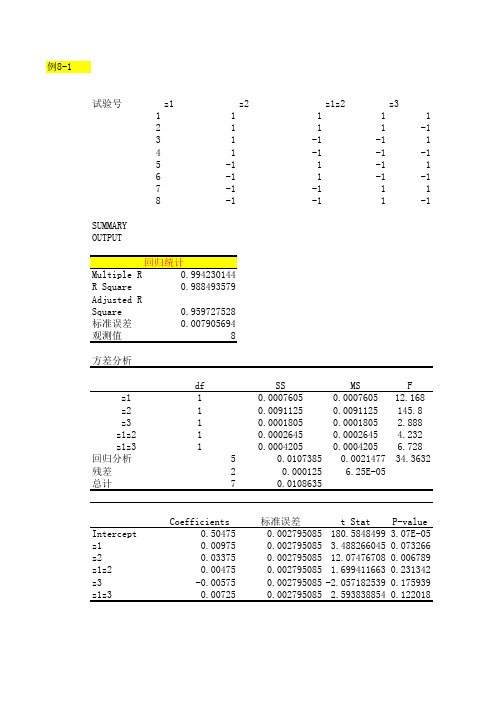
例8-2
回归方程: 由该回归方程 中偏回归系数 绝对值的大 小,可以得到 各因素和交互 作用的主次顺 序为:
y=0.50475+0.00 975z1+0.03375z 2+0.00475z1z20.00575z3+0.00 725z1z3
0 0 -41.73590203
y=468.5+9.09z1 -26.56z2+z3
标准误差
t Stat P-value
1.10193312 425.1619191 1.84E-10
1.385649972 6.55956341 0.002794
1.385649972 -19.17042163 4.36E-05
SS 0.0091125
0.001626 0.0108635
MS
F
0.0091125 33.62546
0.000271
试验号
z1 1 2 3 4 5 6 7 8 9 10 11
z2 1 1 1 1 -1 -1 -1 -1 0 0 0
z3 1 1 -1 -1 1 1 -1 -1 0 0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试用版
t -1.306
Sig. .206 .001 .075 .863 .067
.891 .260 .034 -.325
3.837 1.879 .175 -1.937
(注:ecxel 加载宏出了问题,用 spss 软件进行回归分析) 表三 人均 GDP 的回归分析
系数 模型 非标准化系数 B 1 VAR00001 a. 因变量: VAR00002 1127.855 (常量) -2190.007
2、表8-2是1990-2009年人均GDP数据,根据最小二乘法确定人均GDP(Yt)与时间序列t的直线趋势 方程,计算各期的预测值和预测误差,预测2010年的人均GDP,并将原序列和各期的预测值序列绘 制成图形进行比较。 表8-2 1990-2009年人均GDP数据
年份 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 人均GDP(元) 1644.0 1892.8 2311.1 2998.4 4044.0 5045.7 5845.9 6420.2 6796.0 7158.5 7857.7 8621.7 9398.1 10542.0 12335.6 14185.4 16499.7 20169.5 23707.7 25575.5
4
表二
SPSS 输出的多元回归分析结果
系数 a 非标准化系数 标准 误 标准系数
模型 1 (常量) VAR00002 VAR00003 VAR00004 VAR00005 a. 因变量: VAR00001
B -1.022 .040 .148 .015 -.029
差 .782 .010 .079 .083 .015
1
表8-1
分行 编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 不良贷款 (亿元) 0.9 1.1 4.8 3.2 7.8 2.7 1.6 12.5 1.0 2.6 0.3 4.0 0.8 3.5 10.2 3.0 0.2 0.4 1.0 6.8 11.6 1.6 1.2 7.2 3.2 各项贷款余额 (亿元) 67.3 111.3 173.0 80.8 199.7 16.2 107.4 185.4 96.1 72.8 64.2 132.2 58.6 174.6 263.5 79.3 14.8 73.5 24.7 139.4 368.2 95.7 109.6 196.2 102.2
原序列和各期的预测值序列绘制成图五,可以看出人均 GDP 的变化趋势是逐年上升的,预测值与实 际值折线之间的差距较小,说明回归方程拟合的较好。
7
8
a
标准系数 试用版
t
Sig.
标准 误差 1148.703 95.892
-1.907 .941 11.762
.073 .000
5
表四
人均 GDP 线性趋势预测
图五
实际值与预测值对比图 30000 25000 20000 15000 10000 5000 0 -5000 人均GDP实际值 人均GDP预测值
b1 1127.86 表示:时间每增加一年,人均 GDP 平均增加 1127.86 元。将 t=1,2…….带入方程得到
各期预测值(见表四 )预测值的误差由表也可见 将 t=21 带入趋势方程即可得到 2010 年人均 GDP 的预测值,即
ˆ 2190.011127.86 21 21494.96 Y 2010
某商业银行2002年的主要业务数据
本年累计应收贷 款(亿元) 6.8 19.8 7.7 7.2 16.5 2.2 10.7 27.1 1.7 9.1 2.1 11.2 6.0 12.7 15.6 8.9 0.6 5.9 5.0 7.2 16.8 3.8 10.3 15.8 12.0 贷款项目个 数(个) 5 16 17 10 19 1 17 18 10 14 11 23 14 26 34 15 2 11 4 28 32 10 14 16 10 本年固定资产投资额 (亿元) 51.9 90.9 73.7 14.5 63.2 2.2 20.2 43.8 55.9 64.3 42.7 76.7 22.8 117.1 146.7 29.9 42.1 25.3 13.4 64.3 163.9 44.5 67.9 39.7 97.1
不良贷款
系列1
3
图三
不良贷款与贷款项目个数散点图 14 12 10 8 6 4 2 0 0 5 10 15 20 25 贷款项目个数 30 35 40
不良贷款
系列1
图四
不良贷款与固定资产投资额散点图 14 12 10 8 6 4 2 0 0 50 100 固定资产投资额 150 200
不良贷款
系列1
实验要求 1、每题要写出操作过程。 2、图表格式美观,数据准确。 3、独立完成实验报告。
二、实验内容和原理
实验内容(所有题目显著性水平 0.05 ) 1、 表8-1是一家大型商业银行各分行不良贷款与各项贷款余额、 本年累计应收贷款、 贷款项目个数、 本年固定资产投资额的数据。 (1)分别绘制不良贷款与各项贷款余额、本年累计应收贷款、贷款项目个数、本年固定资产投资 额的散点图,从散点图的分布情况,说明不良贷款与哪项数据的线性关系比较密切。 (2)用EXCEL软件计算不良贷款与各项贷款余额、本年累计应收贷款、贷款项目个数、本年固定资 产投资额的相关系数,并分析不良贷款与这些指标相关性的强弱。 (3)在EXCEL中,利用多元线性回归,试建立不良贷款(y)与各项贷款余额(x1)、本年累计应收 贷款(x2)、贷款项目个数(x3)、本年固定资产投资额(x4)的线性回归方程,并解释各回归系数的含 义。
(3)在EXCEL中,利用多元线性回归,试建立线性回归方程,并解释各回归系数的含义。 根据表二的结果,得到建立不良贷款(y)与各项贷款余额(x1)、本年累计应收贷款(x2)、贷款 项目个数(x3)、本年固定资产投资额(x4)的线性回归方程为:
ˆ 1.021640 0.040039x1 0.148034x2 0.014529x3 0.029194x4 y
重庆科技学院学生实验报告
课程名称 经济预测与决策 开课学院及实验室 学生姓名 指导教师 张佐明 学号 实验项目名称 实验日期 专业班级 实验成绩 相关及回归分析 2015-7-9
一、实验目的和要求
实验目的 1、掌握相关系数的求解方法和含义; 2、掌握一元线性回归、多元线性回归方程的求解方法及各回归系数的含义; 3、掌握如何用EXCEL软件得出回归分析的结果,并知道各数据的含义。
表一不良贷款与各项贷款余额、本年累计应收贷款、贷款项目个数、本年固定资产投资额的相关性 相关系数分析 列 1 列 2 列 3 列 4 列 5 1 列 1 0.843571 1 列 2 0.731505 0.678772 1 列 3 0.700281 0.848416 0.585831 1 列 4 0.518518 0.779702 0.472431 0.746646 1 列 5
0.014529
ˆ 0.029193 表示,在其他条件不变的情况下,贷款项目个数每增加一亿元,不良贷款平均减少 4
0.029193
2、预测 2010 年的人均 GDP,并将原序列和各期的预测值序列绘制成图形进行比较。 根据最小二乘法求得的线性趋势法方程为
ˆ 2190.01 1127.86t Y t
各回归参数的实际意义为
ˆ 0.040039 表示,在其他条件不变的情况下,贷款余额每增加一亿元,不良贷款平均增加 1
0.040039
ˆ 0.148034 表示,在其他条件不变的情况下,累计应收贷款每增加一亿元,不良贷款平均增加 2
0.148034
ˆ 0.014529 表示,在其他条件不变的情况下,贷款项目个数每增加一亿元,不良贷款平均增加 3
五、实验记录与处理(数据、图表、计算等) 图一
不良贷款与贷款余额散点图 14 12 10 8 6 4 2 0 0 50 100 150 200 贷款余额 250 300 350 400
不良贷款
系列1
图二
不良贷款与累计营收贷款散点图 14 12 10 8 6 4 2 0 0 5 10 15 累计营收贷款 20 25 30
2
三、主要仪器设备
电脑一台; Microsoft EXCEL 2007 软件一套;
四、实验操作方法和步骤
1、在【插入】————【图表】————【散点图】------框中相应区域------【确定】 2、在【工具】--------【数据分析】------【相关系数】------框中相应区域-----【确定】 3、在【工具】--------【数据分析】------【回归分析】------框中相应区域-----【确定】 4、在表中输入年份、实际值、预测值、绝对误差、相对误差字段,依次求出各字段的数据,并进行 分析,并比较实际值与预测值。
19 90
19 92
19 94
19 96
19 98
20 00
20 02
20 04
20 06
年份
六、实验结果及分析
1、 (1)从散点图的分布情况,说明不良贷款与哪项数据的线性关系比较密切。 从散点图可以看出,不良贷款与各项贷款余额、本年累计应收贷款、贷款项目个数、本年固定
6
20 08
资产投资额都具有一定线性相关关系。从各散点图的分布情况可以看出不良贷款与各项贷款余额的 线性关系关系比较密切,而与固定资产投资额之间的关系最不密切。 (2)并分析不良贷款与这些指标相关性的强弱 从相关分析矩阵中可以看出:不良贷款与各项贷款余额的相关系数为0.843571;不良贷款与本 年累计应收贷款的相关系数为0.731505;不良贷款与贷款项目个数的相关系数为0.700281;不良贷 款本年固定资产投资额的相关系数0.518518。不良贷款与贷款余额的相关系数最大,固定投资额的 相关系数最小。
