工程流体力学-牛顿内摩擦定律(简明易懂)
工程流体力学 第4章 粘性流体动力学基础

沿程损失水头 (hf):
hf
LV2 D 2g
达西(Darcy)公式
λ:为沿程损失系数,与流动状态、管壁的粗糙度等有关
hf不仅与管段长度成正比,还与管道直径成反比
2020年1月10日
FESTO气动中心
局部阻力水头损失 :当流体在运动中遇到局部障 碍(半开阀门、管道弯头、粗细管接口、滤网等)时, 流线会发生局部变形,并且由于流动分离、二次流等 原因产生漩涡运动,从而耗散一部分机械能,造成水 头损失。
2020年1月10日
FESTO气动中心
解 :(1)求管中心最大流速 umax 2V 2 6.35 12.7cm/s
(2)离管中心 r=20mm 处的流速
u
umax
p
4L
r2
当r=50mm时,管轴处u=0,则有
0 12.7 p 52
4L
p 0.51
4L
则r=20mm在处的流速 u 12.7 0.51 22 10.7cm/s
LV2
d 2g
64 / Re
2020年1月10日
FESTO气动中心
克服沿程阻力而消耗的功率
W
ghf Q
pQ
128 LQ 2 d 4
动能修正系数
1
R2
R u 32rdr 2
0 V
2020年1月10日
FESTO气动中心
例: 设有一恒定有压均匀管流,已知管径d=20mm,管长l=20m, 管 中 水 流 流 速 V=0.12m/s , 水 温 t=10℃ 时 水 的 运 动 粘 度 ν=1.306×10-6m2/s。求沿程阻力损失
二维牛顿内摩擦定律公式

二维牛顿内摩擦定律公式二维牛顿内摩擦定律公式在物理学中可是个相当重要的概念呢!咱们先来说说啥是牛顿内摩擦定律。
简单来讲,牛顿内摩擦定律说的是流体内部相邻两层之间的摩擦力和它们的速度梯度以及接触面积成正比,和两层之间的距离成反比。
那二维牛顿内摩擦定律公式就把这个关系更精确地表达出来啦。
想象一下,你在一个大游泳池里游泳。
当你在水里缓慢游动的时候,是不是感觉水的阻力不是特别大?但要是你加速游动,就会明显感觉到水对你的阻碍变强了。
这其实就和牛顿内摩擦定律有关系。
咱们再具体看看这个公式。
二维牛顿内摩擦定律公式通常写作:$\tau = \mu \frac{\partial u}{\partial y}$ 。
这里的 $\tau$ 表示切应力,也就是咱们说的摩擦力啦;$\mu$ 是动力粘度,这就好比是流体本身的一种“脾气”,不同的流体这个值可不一样哦;$\frac{\partial u}{\partialy}$ 则是速度梯度。
比如说,咱们想象有一层薄薄的油在一个平板上流动。
这层油的厚度很薄,就像一张纸那么薄。
油在平板上流动的速度不是处处相同的,靠近平板的地方慢一点,离平板远的地方快一点。
这速度的变化率,也就是速度梯度,就和产生的摩擦力大小密切相关。
在实际生活中,这个定律的应用可多了去了。
比如汽车发动机里的润滑油,要是润滑油的粘度不合适,就可能导致零件之间的摩擦过大,影响发动机的性能,甚至还可能损坏发动机呢。
再比如说,在一些工业生产过程中,需要控制流体的流动速度和摩擦力,这时候就得依靠对二维牛顿内摩擦定律公式的准确理解和运用。
工程师们会根据具体的情况,选择合适的流体材料和流动条件,以达到最佳的生产效果。
还有啊,在气象学中,研究大气的流动也会用到这个定律。
大气可不是静止不动的,而是时刻在流动和变化。
了解大气中不同层次之间的摩擦力和速度变化,对于预测天气、研究气候变化都非常重要。
总之,二维牛顿内摩擦定律公式虽然看起来有点复杂,但它在我们的生活和科学研究中真的是无处不在,发挥着重要的作用。
牛顿黏性流体定律表达式

牛顿黏性流体定律表达式
牛顿粘性定律表达式是:f=ηA(du/dy)。
式中:η是比例系数(即动力黏度系数)。
1687年英国科学家牛顿从实验发现此规律。
描述一类流体内摩擦力(剪应力)与剪切率关系的定律。
可表述为:当流体的流动为层流时,平行平板中流体层间的摩擦阻力(f)与流体层的面积(A)和剪切率(du/dy)成正比。
牛顿粘性定律指出:
1、内摩擦力正比于流层移动的相对速度。
2、内摩擦力正比于流层间的接触面积。
3、内摩擦力随流体的物理性质而改变。
4、内摩擦力与正压力无关。
关于牛顿内摩擦定律及流体粘度
利用量纲分析法可以得到:
( Re ,
d
)
式中: — 粗糙度
d
— 相对粗糙度
根据实验,得到莫狄(Moody)摩擦系数图。
0.1 0.09 0.08 0.07 0.06 0.05
e/l
0.05 0.04 0.03 0.02 0.015 0.01 0.008 0.006 0.0045
(1)流体阻力的表示方法
对应于机械能衡算的三种形式,流体阻力损失亦有三种表达形式:
R
h
f
kJ/kg m Pa
R g
p
f
R
阻力损失与压力差的区别: △pf —— 流体流经两截面间的机械能损失;
△p —— 任意两点间的压力差。
二者之间的关系:
u2 p We gz p f 2
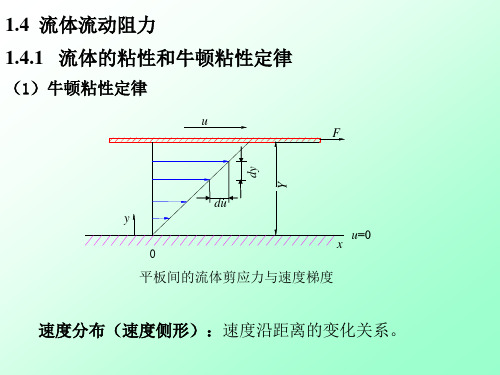
1.4 流体流动阻力
1.4.1 流体的粘性和牛顿粘性定律
(1)牛顿粘性定律
u F dy
du
y 0 x u=0
平板间的流体剪应力与速度梯度
速度分布(速度侧形):速度沿距离的变化关系。
Y
平板间的流体剪应力与速度梯度
实测发现:
F u A Y
牛顿粘性定律:
du dy
意义:剪应力的大小与速度梯度成正比。
1.4.2 流体流动的类型---层流及湍流
(1)雷诺实验
1883年, 英国物理学家Osbone Reynolds作了如下实验。
C 墨水流线 A 玻璃管
D
B
雷诺实验
(2)雷诺实验现象
用红墨水观察管中水的流动状态 层流
(a)
过渡流
(b)
湍流
(c)
工程流体力学考研期末简答题名词解释汇总

工程流体力学考研期末简答题名词解释汇总1.理想流体:实际的流体都是有粘性的,没有粘性的假想流体称为理想流体。
2.水力光滑与水力粗糙管:流体在管内作紊流流动时(1分),用符号△表示管壁绝对粗糙度,δ0表示粘性底层的厚度,则当δ0>△时,叫此时的管路为水力光滑管;(2分)当δ0<△时,叫此时的管路为水力粗糙管。
(2分)3.边界层厚度:物体壁面附近存在大的速度梯度的薄层称为边界层;(2分)通常,取壁面到沿壁面外法线上速度达到势流区速度的99%处的距离作为边界层的厚度,以δ表示。
(3分)4.卡门涡街:流体绕流圆柱时,随着雷诺数的增大边界层首先出现分离,分离点不断的前移;(2分)当雷诺数大到一定程度时,会形成两列几乎稳定的、非对称性的、交替脱落的、旋转方向相反的旋涡,并随主流向下游运动,这就是卡门涡街。
(3分)1、雷诺数:是反应流体流动状态的数,雷诺数的大小反应了流体流动时,流体质点惯性力和粘性力的对比关系。
2、流线:流场中,在某一时刻,给点的切线方向与通过该点的流体质点的刘速方向重合的空间曲线称为流线。
3、压力体:压力体是指三个面所封闭的流体体积,即底面是受压曲面,顶面是受压曲面边界线封闭的面积在自由面或者其延长面上的投影面,中间是通过受压曲面边界线所作的铅直投影面。
4、牛顿流体:把在作剪切运动时满足牛顿内摩擦定律的流体称为牛顿流体。
5、欧拉法:研究流体力学的一种方法,是指通过描述物理量在空间的分布来研究流体运动的方法。
6、拉格朗日法:通过描述每一质点的运动达到了解流体运动的方法称为拉格朗日法。
7、湿周:过流断面上流体与固体壁面接触的周界称为湿周。
17水力当量直径——非圆截面的流道计算阻力损失时以水力当量直径代替圆管直径,其值为4倍的流道截面积与湿周之比。
8、恒定流动:流场中,流体流速及由流速决定的压强、粘性力、惯性力等也不随时间变化的流动。
9、附面层:粘性较小的流体在绕过物体运动时,其摩擦阻力主要发生在紧靠物体表面的一个流速梯度很大的流体薄层内,这个薄层即为附面层。
流体的牛顿内摩擦定律表达式

流体的牛顿内摩擦定律表达式流体的牛顿内摩擦定律,是描述流体内部分子间相互作用的一种定律。
在流体内部存在着分子间的相互作用,其中最重要的一种是内摩擦,这种相互作用能够导致流体的黏性,即阻止流体分子沿着相互平行的方向运动。
牛顿内摩擦定律表达了流体内部分子间相互作用的大小与流体剪切速率的关系。
该定律的表达式为:τ = μ × dv/dy其中,τ表示剪切应力,μ表示黏度,dv/dy表示速度梯度。
这个定律的含义是,当流体内部发生剪切运动时,其所受到的剪切应力与速度梯度成正比,而比例系数就是黏度。
这个定律的表达式形式简单明了,但是背后的物理原理却非常复杂。
黏度是描述流体黏性的物理量,它是指单位面积上下层流体之间的滑动速度差与所需要的剪切应力之比。
黏度的单位是帕秒(Pa·s),也可以用毫帕秒(mPa·s)表示。
不同的流体其黏度值也是不同的,比如说水的黏度值是0.001 Pa·s,而蜂蜜的黏度值则要高得多,约为200 Pa·s。
流体的黏性是由于其分子间相互作用引起的。
在流体内部,分子之间存在着相互吸引力和相互排斥力。
当流体受到外力作用时,流体内部的分子就会发生相对运动,而这种相对运动必须克服分子间的相互作用力才能实现。
这个过程中,分子间的相互作用力就表现出了流体的黏性。
黏度是流体内部分子间相互作用的重要表现形式,它对于流体的流动和传热过程都有着重要的影响。
比如说,在工业生产中,黏度的大小会影响流体的输送和混合过程;在生物学中,黏度的大小则会影响血液的流动和细胞的运动。
流体的牛顿内摩擦定律是描述流体内部分子间相互作用的一种定律,它表达了流体内部分子间相互作用的大小与流体剪切速率的关系。
黏度是描述流体黏性的物理量,它对于流体的流动和传热过程都有着重要的影响。
广义牛顿内摩擦定理

广义牛顿内摩擦定理
广义牛顿内摩擦定理(Newton’s Generalized Internal Friction Law)是牛顿在他的《力学原理》中提出的一个定理,它可以用来描述物体在受力作用下的内摩擦力的大小。
牛顿内摩擦定理解释了物体移动时的摩擦力,并将其表示为力的一部分,它是物体运动的重要因素之
牛顿内摩擦定理是以下形式:当物体在受力作用下移动时,内摩擦力(f)与速度(v)成正比,即f = kv,其中k是一个
常数,可以通过实验测量得出。
此外,k是物体材料和几何形
状的函数,k值越大,内摩擦力越大,反之亦然。
牛顿内摩擦定理的重要性在于,它可以帮助我们更好地理解物体运动的机理。
牛顿内摩擦定理可以用来计算物体的内摩擦力,这对于工程设计有重要意义,例如,在设计机械设备时,可以根据该定理计算出滑动部件的最佳尺寸和材料,以保证机械设备的运行稳定。
此外,牛顿内摩擦定理还可以用于制定有效的机械设备保养计划,例如,可以根据该定理设置机械设备的定期检查和维护,以减少机械设备的磨损和损坏,从而提高机械设备的使用寿命。
总之,牛顿内摩擦定理是一个重要的物理定理,它不仅可以用来计算物体的内摩擦力,还可以用于设计机械设备,以及
制定有效的机械设备保养计划。
因此,牛顿内摩擦定理对于我们更好地理解物体运动有重要意义。
牛顿流体与非牛顿流体

牛顿流体与非牛顿流体一、牛顿流体是指在受力后极易变形,且切应力与变形速率成正比的低粘性流体。
凡不同于牛顿流体的都称为非牛顿流体。
牛顿内摩擦定律表达式:τ=μγ式中:τ--所加的切应力;γ--剪切速率(流速梯度);μ--度量液体粘滞性大小的物理量,简称为黏度,物理意义是产生单位剪切速率所需要的剪切应力。
从流体力学的角度来说,凡是服从牛顿内摩擦定律的流体称为牛顿流体,否则称为非牛顿流体。
所谓服从内摩擦定律是指在温度不变的条件下,随着流速梯度的变化,μ值始终保持一常数。
水、酒精等大多数纯液体、轻质油、低分子化合物溶液以及低速流动的气体等均为牛顿流体;高分子聚合物的浓溶液和悬浮液等一般为非牛顿流体。
二、牛顿流体与非牛顿流体依据内摩擦剪应力与速度变化率的关系不同,粘性流体又分为牛顿流体和非牛顿流体。
牛顿内摩擦定律表示:流体内摩擦剪应力和单位距离上的两层流体间的相对速度成比例。
比例系数µ称为流体动力粘度,常简称为粘度。
它的值取决于流体的性质、温度和压力大小。
若µ为常数,则称为牛顿流体,否则为非牛顿流体。
空气、水等均为牛顿流体;聚合溶液、含有悬浮粒杂质或纤维的流体为非牛顿流体三、要说非牛顿流体就得先说牛顿流体,牛顿流体的精确定义涉及到流体力学的术语,我就不说了,通俗来讲,牛顿流体不管怎么搅拌都能保持”流体“的性质,几乎我们日常见到的所有液体都是牛顿流体。
而非牛顿流体只要一搅拌就会出现一个能一直维持形状的“洞”,呈现出一定“固体”的性质。
最常见的非牛顿流体就是玉米淀粉加水泡成的糊在震动下的形态(比如放在音响喇叭上),网上有很多视频。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
x
• 设F为各层间产生的内摩擦力,大量 实验证明,内摩擦力F与流体的性质 du 有关,与接触面积A、速度梯度 dy 成正比,而与接触面积的压力无关, du 即F∝ A dy 。若乘以比例系数μ则 有
y
•
F μA
du dy
(1.2.5)
• 令г为单位面积上的内摩擦力,即摩 擦应力(又称切应力),于是 • F du г μ A dy • (1.2.6)
(1)牛顿内摩擦定律
• 图1.1给出的时平板实验示意图 • 在宽度和长度都足够大, 其边缘条件可以略去不计的互 相平行的平板Ⅰ和Ⅱ之间充满 某种液体。若板Ⅱ固定,拉动 板Ⅰ以某一等度V向右移动,这 时由于流体附着力的作用,附 着在板Ⅱ上的流体层的速度则 为零。而板Ⅰ和Ⅱ之间的各层 流体由于质点间的内摩擦力的 作用,其速度沿y方向的变化规 律如图1.1所示。
x
• 式中
F——内摩擦力,N;
•
• •
•Hale Waihona Puke • •г——单位面积上的内摩擦力,N/㎡; A ——流体层的接触面积,㎡; du dy 速度梯度,即速度在垂直于该速度方向 1 上的变化率,S ; μ——与流体性质有关的比例系数,称为 动力粘性系数,或称动力粘度, Pa * s 。 式(1.2.5)、(1.2.6)的表达式称为牛顿内摩擦定 律或粘性定律。 若两板间的距离h很小,两板间的速度分布近似为线 性,即 du 。 dy
