第二章 量子力学初步
合集下载
量子力学第二章知识点
量子力学第二章知识点基本概念波粒二象性量子力学中的粒子既可以表现出粒子性，也可以表现出波动性。
这种既是粒子又是波动的性质被称为波粒二象性。
波函数波函数是量子力学中描述粒子状态的数学函数。
波函数的模的平方表示在某一位置发现粒子的概率密度。
叠加原理量子力学中，两个波函数的线性叠加仍然是一个有效的波函数。
这个原理被称为叠加原理。
量子态所有可能的状态（波函数）构成了量子力学中的量子态。
一个量子态可以通过线性叠加得到另一个量子态。
算符和测量算符算符是描述量子系统性质变化的数学操作。
在量子力学中，算符通常用来描述物理量的测量和演化。
算符的本征值和本征态对于一个算符，它的本征值是测量该物理量时可能得到的值；而本征态是对应于这些本征值的一组特定的波函数。
观测量和平均值观测量是指用来测量物理量的实际实验装置，而平均值则是对同一量子态进行多次测量得到的结果的平均值。
不确定性原理不确定性原理是量子力学的基本原理之一，它描述了在某些物理量的测量中，有些对应物理量无法同时精确确定的限制。
氢原子壳层和轨道氢原子中，电子围绕原子核运动的轨道被称为壳层。
氢原子的壳层用主量子数 n 来标记。
能级和能量氢原子中电子的能量是量子化的，称为能级。
能级由主量子数 n 决定，能级越高，能量越大。
轨道角动量氢原子中，电子的轨道运动导致了其具有轨道角动量。
轨道角动量用量子数 l 来标记。
磁量子数氢原子中，轨道角动量的分量在某一方向上的投影用磁量子数 m 来标记。
自旋和电子态自旋自旋是粒子固有的一种角动量，与粒子的旋转运动无关。
电子具有自旋角动量。
自旋量子数自旋量子数用 s 来标记，对于电子，其自旋量子数为 1/2。
自旋态自旋态是描述粒子自旋状态的波函数。
对于电子，自旋态可以是自旋向上的态，记作|↑⟩，也可以是自旋向下的态，记作|↓⟩。
自旋磁量子数自旋磁量子数用 m_s 来标记，对于电子，其自旋磁量子数可以是 1/2 或 -1/2。
总结本文介绍了量子力学第二章的知识点，包括波粒二象性、波函数、叠加原理、量子态、算符和测量、算符的本征值和本征态、观测量和平均值、不确定性原理、氢原子的壳层和轨道、能级和能量、轨道角动量、磁量子数、自旋和电子态等内容。
原子物理――量子力学初步精品PPT课件
• 因此可认为，光学是经典物理学向近代物理学（包 括量子论和相对论）过渡和发展的纽带和桥梁。
海森伯不确定关系的讨论
• 经典粒子：可以同时有确定的位置、 速度、动量、能量…… 其运动是可以用轨迹来描述的。
• 经典波：有确定的波长，但总是在空 间扩展，没有确定的位置
• 波粒二象性：不可能同时具有确定的 位置和动量。如何来确定它们位置、 动量等物理量？
• 粒子在其中以驻波的形式存在 • 匣子壁是驻波的波节 • 匣子的长度是半波长的整数倍
匣子 长度
Ln
2
p h
p nh 22m
n2h2 8mL2
束缚粒子的能 量是量子化的
如果将匣子等效为核的库仑势场
• 其中的粒子就是核外电子，电子沿轨道运动一周后回到起点
• 轨道的周长为匣子长度的2倍
资料仅供参考约恩逊clausjnsson实验1961年50kv005a缝间距基本数据89年日立公司的电子双棱镜实验单电子干涉实验20029物理世界最美丽的十大物理实验让电子通过特制的金属狭缝资料仅供参考1989年日立公司的akiratonomura等人作了更精确的实实际测量证明每秒钟只有少于1000个电子入射到双棱镜中所以不可能有两个或两个以上的电子同时到达接收装置上因而不存在干涉是两个电子相互作用的结果20029物理世界最美丽的十大物理实验资料仅供参考如果让入射电子数减弱每次仅有一个电子射出经过一段时间后仍能得到稳定的双缝干涉花样
1926 年玻恩提出 德布罗意波是概率波 .
统计解释：在某处德布罗意波的强度是与粒子在该 处邻近出现的概率成正比的 .
概率概念的哲学意义：在已知给定条件下，不可能 精确地预知结果，只能预言某些可能的结果的概率 .
三、量子态—波粒二象性的必然结果
海森伯不确定关系的讨论
• 经典粒子：可以同时有确定的位置、 速度、动量、能量…… 其运动是可以用轨迹来描述的。
• 经典波：有确定的波长，但总是在空 间扩展，没有确定的位置
• 波粒二象性：不可能同时具有确定的 位置和动量。如何来确定它们位置、 动量等物理量？
• 粒子在其中以驻波的形式存在 • 匣子壁是驻波的波节 • 匣子的长度是半波长的整数倍
匣子 长度
Ln
2
p h
p nh 22m
n2h2 8mL2
束缚粒子的能 量是量子化的
如果将匣子等效为核的库仑势场
• 其中的粒子就是核外电子，电子沿轨道运动一周后回到起点
• 轨道的周长为匣子长度的2倍
资料仅供参考约恩逊clausjnsson实验1961年50kv005a缝间距基本数据89年日立公司的电子双棱镜实验单电子干涉实验20029物理世界最美丽的十大物理实验让电子通过特制的金属狭缝资料仅供参考1989年日立公司的akiratonomura等人作了更精确的实实际测量证明每秒钟只有少于1000个电子入射到双棱镜中所以不可能有两个或两个以上的电子同时到达接收装置上因而不存在干涉是两个电子相互作用的结果20029物理世界最美丽的十大物理实验资料仅供参考如果让入射电子数减弱每次仅有一个电子射出经过一段时间后仍能得到稳定的双缝干涉花样
1926 年玻恩提出 德布罗意波是概率波 .
统计解释：在某处德布罗意波的强度是与粒子在该 处邻近出现的概率成正比的 .
概率概念的哲学意义：在已知给定条件下，不可能 精确地预知结果，只能预言某些可能的结果的概率 .
三、量子态—波粒二象性的必然结果
大学量子力学课件第二章
v dW (r , t ) v v 2 w(r , t ) = = c Φ (r , t ) —几率密度。 几率密度。 dτ
上式中左边是粒子性表示， 右边是波性表示， 该式是实物粒子波 上式中左边是粒子性表示， 右边是波性表示， 粒二象性的又一表示（德布罗意关系是一表示） 。 粒二象性的又一表示（德布罗意关系是一表示）
本章三重点： 本章三重点： 1. 微粒的状态由波函数完全描写 2. 状态随时间的变化遵从薛定谔方程（掌握、会用） 状态随时间的变化遵从薛定谔方程（掌握、会用） 3. 举例说明量子力学处理问题的方法和结果的特征
一、状态的描述
v v v 1.经典力学中质点的状态由 1.经典力学中质点的状态由 r , p( v) 描写 v v v 两基本量来描写质点的状态。 经典力学中用 r , p( v) 两基本量来描写质点的状态。 v v v (1)每个时刻 都有完全确定的数值， 变化； (1)每个时刻 t 该 r , p( v) 都有完全确定的数值，且随 t 变化； v v v v (2)质点的其它力学量 质点的其它力学量， (2) 质点的其它力学量 ， 如 E k、 V ( r )、 E 总、 L 等全是 r , p 的函
因此，对一个光子来说， 因此，对一个光子来说，光波在某点的强度 Ψ 与一个光子
2
出现在包含该点在内的单位体积内的几率（几率密度）成正比。 出现在包含该点在内的单位体积内的几率（几率密度）成正比。
2.微粒的波粒二象性的统一 2.微粒的波粒二象性的统一
微粒具有波动性。 微粒具有波动性。物质波在某点的强度 Φ 2 与一个粒子出现
(3) Ψ 归一化后仍有一不定相因子 e iδ ， Ψe iδ 与 Ψ 描写同一状 态，且均归一化，因为： 且均归一化，因为：
量子力学第二章
ν , λ 一定
Ψ(x, t) = Ψ e 0
i − ( Et− px ⋅x) ℏ
推广 ：三维自由粒子波函数
二、波函数的物理意义 波函数的物理意义
Ψ(r , t ) = Ψ0e
i − ( Et− p⋅r ) ℏ
如何理解波函数和粒子之间的关系？ 如何理解波函数和粒子之间的关系？ 1 物质波就是粒子的实际结构？即三维空间连续分 物质波就是粒子的实际结构？ 布的物质波包，那就会扩散，粒子将会越来越胖。 布的物质波包，那就会扩散，粒子将会越来越胖。再 衍射时，电子就会被分开。夸大了波动性， 者，衍射时，电子就会被分开。夸大了波动性，抹煞 了粒子性。 了粒子性。 2 大量粒子空间形成的疏密波？电子衍射实验， 大量粒子空间形成的疏密波？电子衍射实验， 电子流很弱时，时间足够长，仍会出现干涉图样。 电子流很弱时，时间足够长，仍会出现干涉图样。单 个电子就具有波动性。 个电子就具有波动性。 3 波函数的统计解释（Born 1926）:波函数在空间 波函数的统计解释（ ） 波函数在空间 某点的强度（振幅绝对值的二次方） 某点的强度（振幅绝对值的二次方）和该点找到粒子 的几（ 率成比例。即物质波是几率波。 的几（概）率成比例。即物质波是几率波。
2 2 x 2
2 2
i ( p⋅r − Et ) ℏ
2 px = − 2Ψ ℏ
pz2 ∂ 2Ψ = − 2Ψ 2 ∂z ℏ
2
p ∂Ψ ∂Ψ ∂Ψ 2 + 2 + 2 = ∇ ψ = − 2Ψ 2 ℏ ∂x ∂y ∂z
由
p2 E= 2µ
(2.3-3)
得
i i p2 i − ℏ2 2 ∂Ψ Ψ =− = − EΨ = − ∇Ψ ℏ ℏ 2µ ℏ 2µ ∂t
量子力学基础入门
CHENLI
形式二：
t E
2
若粒子在能量状态E 只能停留时间Δt ，那么这段时间内 粒子的能量状态不能完全确定，只有当粒子的停留时间为无 限长时(定态)，它的能量状态才是完全确定的(ΔE = 0)。
由于粒子的波动性，它在客观上不能同时具有确定的坐 标位置位置和相应的动量。
CHENLI
2012年的两位物理学奖获得者能够映射到当外 界环境参与时量子猫的状态。他们设计了创新 实验，详细说明观测这一行为实际上如何导致 量子状态的崩溃并失去其叠加特性的。阿罗什 和 维因兰德并没有用猫，而是将势阱中的离子
放入薛定谔假设的叠加态中。这些量子物体尽 管宏观上没有猫那样的形状，但相对于量子尺 度仍然足够大。
利用相似的方法，阿罗什和他的团队可以数空腔内的光子。光子不容易数，任何和外 界接触就会破坏。借助这个方法，阿罗什和他的团队设计后期方案一步一步实现单个量子 状态的测量。
CHENLI
CHENLI
量子力学悖论
量子力学描绘了一个肉眼无 法观测的微观世界，很多与我们 的期望和在经典物理中的经验相 反。
量子世界本身具有不确定性。 例如叠加态，一个量子可以有多 重形态。我们通常不会认为一块 大理石同时是“这样”也是“那 样”，除非是一块量子大理石。 叠加态的大理石只能确切地告诉 我们大理石是每一种形态的概率。
1929年,德布罗意获 诺贝尔物理学奖.
1924年11月，德布罗意在其博士论文里首次提出所有物 质粒子具有波粒二象性的假设。
质量为m 的粒子，以速度 v 匀速运动时，一方面可以用 能量E 和动量P 对它作粒子的描述，另一方面也可以用频 率ν，波长λ作波的描述，其关系为：
E h
p
h
/
h h
形式二：
t E
2
若粒子在能量状态E 只能停留时间Δt ，那么这段时间内 粒子的能量状态不能完全确定，只有当粒子的停留时间为无 限长时(定态)，它的能量状态才是完全确定的(ΔE = 0)。
由于粒子的波动性，它在客观上不能同时具有确定的坐 标位置位置和相应的动量。
CHENLI
2012年的两位物理学奖获得者能够映射到当外 界环境参与时量子猫的状态。他们设计了创新 实验，详细说明观测这一行为实际上如何导致 量子状态的崩溃并失去其叠加特性的。阿罗什 和 维因兰德并没有用猫，而是将势阱中的离子
放入薛定谔假设的叠加态中。这些量子物体尽 管宏观上没有猫那样的形状，但相对于量子尺 度仍然足够大。
利用相似的方法，阿罗什和他的团队可以数空腔内的光子。光子不容易数，任何和外 界接触就会破坏。借助这个方法，阿罗什和他的团队设计后期方案一步一步实现单个量子 状态的测量。
CHENLI
CHENLI
量子力学悖论
量子力学描绘了一个肉眼无 法观测的微观世界，很多与我们 的期望和在经典物理中的经验相 反。
量子世界本身具有不确定性。 例如叠加态，一个量子可以有多 重形态。我们通常不会认为一块 大理石同时是“这样”也是“那 样”，除非是一块量子大理石。 叠加态的大理石只能确切地告诉 我们大理石是每一种形态的概率。
1929年,德布罗意获 诺贝尔物理学奖.
1924年11月，德布罗意在其博士论文里首次提出所有物 质粒子具有波粒二象性的假设。
质量为m 的粒子，以速度 v 匀速运动时，一方面可以用 能量E 和动量P 对它作粒子的描述，另一方面也可以用频 率ν，波长λ作波的描述，其关系为：
E h
p
h
/
h h
量子力学课件第二章
2 dW ( p, t ) | c( p, t ) | dp t时刻粒子出现在动量 点附近 p dp体积元内的几率。
2.2 态叠加原理
若(r , t )是归一化的，则 p, t 也是归一化的 c
若 ( r , t ) ( r , t )dr 1
率成比例。
量子力学的第一条基本假定（或公设）
强度大 强度小 或为0 粒子出现 的概率大
粒子出现 的概率小
2.1 波函数的统计解释
假设衍射波用 (x) 描述，衍射花样的强度则用振
幅的平方
2 描述。就可以得到粒子在空间任意 ( r ) ( r ) ( r ) *
一点出现的概率。
波函数（概率幅）描写体系的量子状态（态或状态）
动量算符
2 2 i t 2m
2.3 薛定谔方程
三、力场中粒子的波函数方程
P2 力场中E U(r ) 2m P2 E 【 U(r )】 2m
p i，E i t
2 2 i (r , t ) [ U(r , t )] (r , t ) t 2m
波叠加原理称为态叠加原理。
解释电子双缝干涉
S1 Ψ= C1Ψ1 + C2Ψ2 也是电子可能状态。
电子源
Ψ1
P
S2
Ψ2
感 光 屏
空间找到电子的几率则是： |Ψ|2 = |C1Ψ1+ C2Ψ2|2
= (C1*Ψ1*+ C2*Ψ2*) (C1Ψ1+ C2Ψ2)
= |C1 Ψ1|2+ |C2Ψ2|2 + [C1*C2Ψ1*Ψ2 + C1C2*Ψ1Ψ2*]
薛定谔波动方程
2.2 态叠加原理
若(r , t )是归一化的，则 p, t 也是归一化的 c
若 ( r , t ) ( r , t )dr 1
率成比例。
量子力学的第一条基本假定（或公设）
强度大 强度小 或为0 粒子出现 的概率大
粒子出现 的概率小
2.1 波函数的统计解释
假设衍射波用 (x) 描述，衍射花样的强度则用振
幅的平方
2 描述。就可以得到粒子在空间任意 ( r ) ( r ) ( r ) *
一点出现的概率。
波函数（概率幅）描写体系的量子状态（态或状态）
动量算符
2 2 i t 2m
2.3 薛定谔方程
三、力场中粒子的波函数方程
P2 力场中E U(r ) 2m P2 E 【 U(r )】 2m
p i，E i t
2 2 i (r , t ) [ U(r , t )] (r , t ) t 2m
波叠加原理称为态叠加原理。
解释电子双缝干涉
S1 Ψ= C1Ψ1 + C2Ψ2 也是电子可能状态。
电子源
Ψ1
P
S2
Ψ2
感 光 屏
空间找到电子的几率则是： |Ψ|2 = |C1Ψ1+ C2Ψ2|2
= (C1*Ψ1*+ C2*Ψ2*) (C1Ψ1+ C2Ψ2)
= |C1 Ψ1|2+ |C2Ψ2|2 + [C1*C2Ψ1*Ψ2 + C1C2*Ψ1Ψ2*]
薛定谔波动方程
第二章 量子力学初步-3 薛定谔方程
粒子在一维势场中的运动可以通过薛定谔方程来描述。薛定谔方程是量子力学的基本方程，用于描述微观粒子的运动规律。对于一维势场中的粒子，其薛定谔方程具有特定形式，涉及粒子的波函数、势能函数以及时间空间微分。要求解粒子的定态能级和归一化波函数，首先需要确定势能函数U(x)，然后将其代入一维势场中的薛定谔方程。通归一化波函数则需要满足一定的条件，即波函数在全空间的积分为1。这通常涉及对波函数进行一定的数学变换，以确保其满足归一化条件。虽然文档提及了薛定谔方程的建立及其在描述微观粒子运动中的重要性，但并未详细展开如何具体求解一维势场中粒子的定态能级和归一化波函数。因此，需要进一步参考相关量子力学教材或咨询专业人士以获取更详细的求解步骤和方法。
原子物理学第三次作业答案 (8)
第二章 量子力学初步为什么要学？量子力学已经从理论物理的一个分支学科，发展成为技术专家手中的一门有力的工具：纳米（10－9M ）科学与技术, STM 和AFM ，…对物理专业的学生，导论和准备；对应用物理专业的学生，掌握量子力学的基本知识。
为什么在这时候学？在波尔与索末菲的旧量子理论中：问题1：L （轨道角动量数值）＝n ϕℏ，L z （轨道角动量的方向）= m ℏ；即：定态条件，作为“规定”的量子化条件引入。
这种强制性“规定”不符合数学逻辑。
问题2：氢原子基态的电子空间分布： 波尔理论：n =1的“轨道”，r n ＝n 2a 1＝a 1＝0.53A ； 中学物理中的“电子云”。
孰是孰非？“电子云”概念是正确的，“轨道”概念是错误的。
正确的原子概念的建立，必须学习量子力学。
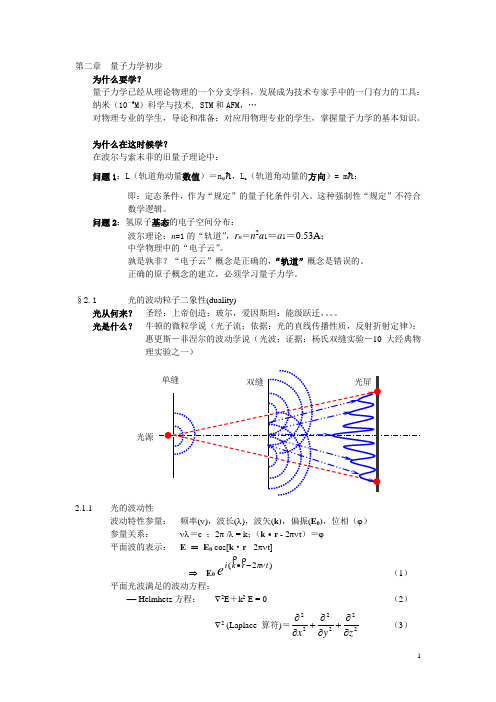
§2.1 光的波动粒子二象性(duality)光从何来？ 圣经：上帝创造；玻尔，爱因斯坦：能级跃迁，。
光是什么？ 牛顿的微粒学说（光子流；依据：光的直线传播性质，反射折射定律）；惠更斯－菲涅尔的波动学说（光波；证据：杨氏双缝实验－10大经典物理实验之一）2.1.1 光的波动性波动特性参量： 频率(ν)，波长(λ)，波矢(k)，偏振(E 0)，位相（ϕ） 参量关系： νλ＝c ；2π /λ = k ；（k ·r - 2πνt ）＝ϕ 平面波的表示： E ＝ E 0 cos[k ·r - 2πνt]⇒ E 0)2(t r k i eπν-∙（1）平面光波满足的波动方程：− Helmhetz 方程： ∇2E ＋k 2 E = 0 （2）∇2(Laplace 算符)＝222222zy x ∂∂+∂∂+∂∂（3）光源2.1.2光的粒子性粒子特性参量：能量E ，动量p 。
粒子特性参量（E ，p ）和波动特性参量（ν，λ)由Einstein 关系联系起来： E ＝ h ν ＝hc / λ （4）p ＝ h / λ ＝ h ν / c ＝ ℏk（5） p ＝ℏk ＝ (h / λ) k 0 (k 0 ：光传播的方向)（5'）光子能量（4）式的实验证实：光电效应实验装置：结果：仅当入射光的频率 ν > νmin ，才有光电流（光电子）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.3薛定谔波动方程的应用
• 2.3.2无限深势阱（变为驻波方程）
与时间无关的波动方程为：
2 x 2m 2 E V x x 0 2 x
2.13
由于E有限，所以区域I和III中：
x =0
2 x 2mE 2 x 0 2 x
区域II与时间无关的波动方程为：
2.13
2.3薛定谔波动方程的应用
x A1cosKx+A2sinKx
边界条件： x 0 x a 0
x a 0 A2sinKa
a
2.28
2.30
2.31
2mE K 2
A1 0
热辐射是不连续的假设，即量子。)
Ｅ＝hv (普郎克常数h=6.625x10-34J-s) 1905年爱因斯坦提出光量子概念（光子）解释了光 电效应(光波也是由分立的粒子组成的假设，即光量子。)
光电子的最大动能：
Tmax
1 2 mv hv h 0 2
0
入射光子能量
功函数：电子逸出表面吸收的最小能量
2.2 薛定谔波动方程
/p-240652226806.html
1926年薛定谔结合了普朗克的量子化原理和德布罗意的波粒 二相性原理，提出了波动力学理论，来描述电子的运动。 2.2.1 波动方程
一维非相对论的薛定谔方程： 2 x, t 2 x, t V x x, t j 2.6 2 2m x t 其中，Ψ (x,t)为波函数，V(x)为与时间无关的势函数，m为 粒子的质量，j为虚常数。波函数Ψ(x,t)描述的是系统的状态. 分离变量： x, t x t
2.2.2 波函数的物理意义----几率波
整个波函数是与坐标有关（与时间无关）的函数和与时间有关的函数的乘积：
与时间性无关的概率 密度函数
即：
2.2 薛定谔波动方程
2.2.3 边界条件
x dx 1
2
(2.18)
归一化条件
要使能量E和势函数V(x)在任何位置均为有限值，则： 1、波函数Ψ(x)必须有限、单值和连续。 2、波函数Ψ(x)的一阶导数必须有限、单值和连续。
j / t
2.11
认为分离常数
η =E（粒子总能量）
正弦波的指数形式 角频率ω =η / 而
E h h / 2
薛定谔波动方 程可写为：
2 2
ω = E/
1 x V x E 2 2m x x
2.12
2.2 薛定谔波动方程
主要观点： （1）对于同一粒子不可能同时确定其坐标和动量。 若动量的不确定程度为△p，坐标的不确定程度为△x，则不确定关系为
=h/2π为修正普朗克常数。
（2）对于同一粒子不可能同时确定其能量和具有此能量的时间点。 若给定能量不确定程度为△E，而具有此能量的时间的不确定量为 △ t，则 不确定关系为： 注：当同时测量坐标与动量或同时测量能量与时间时，会出现一定程度的偏差。 无法确定一个电子的准确坐标，因而可以确定某个坐标位置可能发现电子的 概率。
2.1量子力学的基本原理
三个基本原理
能量量子化原理 波粒二相性原理 不确定原理（测不准原理）
2.1量子力学基本原理
2.1.1能量量子化原理
光电效应-----理论与实验的矛盾
2.1量子力学基本原理---能量量子化
光电效应理论与实验的矛盾 1900年普郎克提出热辐射量子化的概念(从加热表发出的
在单电子原子中，电子与质子间库仑力形成的势函数：
三维与时间无关的薛定谔波动方程：
在球坐标系中，波动方程还可写为：
n---主量子数，n=1,2,3,…
分离变量法求解：
L--角量子数，L=n-1,n-2,…，0
m—磁量子数，|m|=L,L-1,L-2,…,0 s—自旋量子数，s=1/2,-1/2
每一组量子数对应一个量子态的电子
/v6515991.htm
（１）主量子数n：决定体系能 量E或电子离核远近距离r。 n= 1，2，3，4，5，6，7…… 电子层数：K L M N O P Q （2）角量子数l:确定原子轨道的形
状并在多电子原子中和主量子数一起 决定电子的能级。 l = 0，1，2，3，4，5，6……n-1 相应的能级： s p d f g…… l = 0 球形对称 l = 1 原子轨道呈哑铃形分布 l = 2 其原子轨道呈花瓣形分布
（3）磁量子数m:决定原子轨 道在空间的取向的个数。 m=0，±1，±2…… ±L 共(2L+1) 个 （4）自旋量子数：只决定电子 运动状态与薛定谔方程无关。
s = ±1/2
2.4 原子波动理论的延伸
2.4.2 周期表
1.不同原子中电子数量不同，电子按电子态填充状态是一样的，
最终只是最外层出现未填满的状态;
m—磁量子数,|m|=L,L-1,L-2 ,…,0
s—自旋量子数，s=1/2,-1/2 核外电子排布原理一 ——最低能量原理
L=1,m=-1,s=1/2或-1/2 n=3,L=0,m=0,s=1/2或-1/2 ,2个状态,填2个电子 L=1 ,6个状态,填2个电子， 4个空状态
n l m s 四个量子数
P
h
h P
h为普郎克常数，P为粒子动量。
λ为物质波的德布罗意波长。
波粒二相性原理是利用波理论描述晶体中的电子的运动和状态的基础。
P23例2.2
电子的波动性实验
10
电磁波频谱
2.1量子力学的（三个）基本原理
2.1.3 不确定原理（测不准原理）
1927 年德国核物理学家沃纳-海森堡(Heisenberg)提出不确定原理
2.3薛定谔波动方程的应用
入射粒子能量小于势垒时也有一定概率穿过势垒 （与经典力学不同）
假设E<V0
2.3薛定谔波动方程的应用
2.3.3 阶跃势函数
穿透距离大约为两个硅晶格
2.3薛定谔波动方程的应用
2.3.4 矩形势垒 分别在三个区域中求解与时间无关的 薛定谔方程
假设E<V0
2.3薛定谔波动方程的应用
2.3薛定谔波动方程的应用
2.3.1 自由空间中的电子
在没有外力作用下的粒子，势函数V(x)为常量，且E>V(x)，设V(x) =0
说明自由空间中的粒子运动表现为行波。 沿方向+x运动的粒子： x, t A exp j kx t
2.23
h P
2.4 原子波动理论的延伸
2.4.1 单电子原子
电子的能量为：
1 13 .6 2 n
n为主量子数，式中能量为负表示电子被束缚在核的周围。n取值为整数， 说明总能量只能取分立值，能量的量子化。
，最小的能量状态，n=1,L=0,m=0,此时波函数：
氢原子能 级图
2.4 原子波动理论的延伸
径向概率密度函数：指电子出现在离核某个距离的概率。
2.3薛定谔波动方程的应用
能量量子化
2 n2 2 E En , 2 2ma n=1,2,3, (2.37)
波函数:
x 2 a sin Kx
(2.38)
n K a
粒子的能量是不连续的，其能量是各个分立
的能量确定值，称为能级，其值由主量子数n决定。
例2.3
K为波数=2π/λ, λ为波长。
h 2mE
2.3薛定谔波动方程的应用
是一个与坐标无关的常数，说明自由粒子在空间任意位置出现的概率相等。
行波与驻波： 形象的说就是一个行走一个停留（当然不是真正的停留） 行 波：就是波从波源向外传播； 驻 波：波在一个空间中来回反射，由于来回的距离等于1/4波长的奇数倍，于是反射 回来的波与后面传来的波发生干涉，形成稳定的干涉场，各处的振幅稳定不变。振幅 为零的地方叫波节，振幅最大的地方叫波腹。如果发生在一根绳子上我们就会看到一 个稳定的象莲藕一样的图像，似乎波"停止“了传播，所以叫驻波（驻留）。
2.原子的特性（化学活泼程度）取决于未填满的那一层，也就 是最外层的价电子数； 3.内层电子全部填满，所以是稳定的。
本章小结
2.5 小 结
• 量子力学的基本原理 能量量子化、波粒二象性、不确定原理 • 薛定谔波动方程——概率密度 • 束缚态粒子的能量是量子化的
2.4.2 元素周期表
• 根据电子自旋和泡利不相容原理：n l m s 四个量子数可以 推出元素周期表（框架） (每层可以容纳2n2个电子)
2.4 原子波动理论的延伸
2.4.2 周期表
电子自旋:电子具有量子化的本征角动量，它的值为两个可能值中的 一个，由量子数s确定，s=1/2或-1/2.
泡利不相容原理:在任意系统中，不可能有两个电子处于同一个量子 态，对于原子，不可能有两个电子具有相同的量子数组.
2.3薛定谔波动方程的应用
• 无限深势阱（前４级能量）
随着能量的增加，在任意 给定坐标值处发现粒子的概 率会渐趋一致
2.3薛定谔波动方程的应用
2.3.3 阶跃势函数
假设E<V0
定义反射系数：R=反射流/入射流。 在Ⅰ区域，E<V0的粒子流入射到势垒上将全部反射回来； 但E<V0时，区域Ⅱ中找到粒子的概率不为零； 在Ⅱ区由于 ≠0,说明入射粒子有一定的概率会穿过势垒到达区域Ⅱ。
能量E
n K 当Ka=nπ时成立，且n为正整数，称为量子数。 a
归一化边界条件:
2 2 A2 2 a A sin 0 2 Kxdx 1 2.33 波的表达式: x 2 a sin n x n=1,2,3, （驻波） a