高等数学的实验报告册答案
高数实验报告 (2)
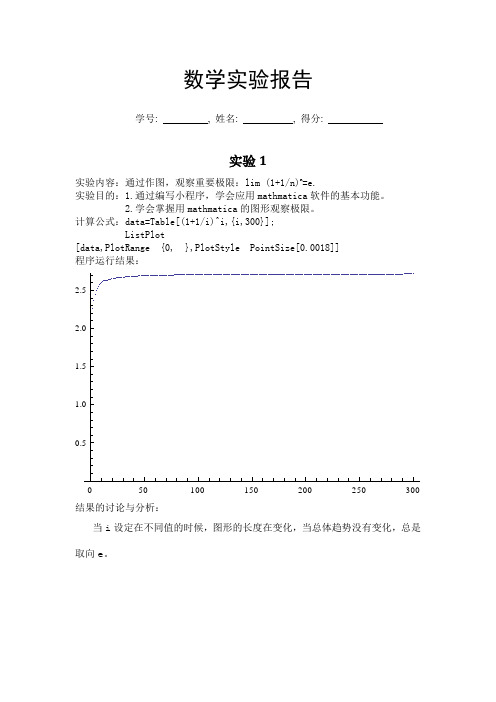
数学实验报告学号: , 姓名: , 得分:实验1实验内容:通过作图,观察重要极限:lim (1+1/n)n=e.实验目的:1.通过编写小程序,学会应用mathmatica软件的基本功能。
2.学会掌握用mathmatica的图形观察极限。
计算公式:data=Table[(1+1/i)^i,{i,300}];ListPlot[data,PlotRange {0, },PlotStyle PointSize[0.0018]]程序运行结果:结果的讨论与分析:当i设定在不同值的时候,图形的长度在变化,当总体趋势没有变化,总是取向e。
实验2实验内容:设数列{Xn}由下列递推关系式给出:x1=1/2,xn+1=xn2+xn(n=1,2………)观察数列1/(x1+1)+ 1/(x2+1) +…….+1/(xn+1)的极限。
实验目的和意义:1:掌握mathmatica数学实验的基本用法。
2:学会利用mathmatica 编程求数列极限。
3:了解函数与数列的关系。
计算公式:f[x_]:=x^2+x;xn=0.5;g[x_,y_]:=y+1/(1+x);y n=0;For[n=1,n 15,n++,xN=xn;yN=yn;xn=N[f[x N]];yn=N[g[xN,yN]]];Print[" y30=",yn]程序运行结果:y30= 2.结果与讨论:这个实验,当yn中n趋向无穷大的时候,能够更加接近极限,当取30以上时候,2就是极限值。
实验3实验内容:已知函数:f(x)=1/(x2+2x+c)(-5<=x<=4),作出并比较当c 取不同的值的时候(-1,0,1,2,3),并从图上观察出极值点,驻点,单调区间,凹凸区间和渐进线。
实验目的:1.通过实验掌握如何用mathmatica作图。
2.学会观察图像来求函数的相关数据。
计算公式:f[x_]=1/(x2+2 x+(-1))Plot[f[x],{x,-5,4},GridLines Automatic,Frame True,PlotStyle RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(0))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(2))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(3))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(3))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]程序运行结果:结果的讨论与分析:不同的c,函数的形态有较大的不同,也就是原方程=0什么情况下有解的问题,根据图像很容易的得到驻点,拐点,等相关信息。
大学数学实验报告答案

实验题目:线性方程组的求解实验目的:1. 理解线性方程组的概念和求解方法。
2. 掌握高斯消元法和矩阵求逆法求解线性方程组。
3. 熟悉MATLAB软件在数学实验中的应用。
实验时间:2021年X月X日实验地点:计算机实验室实验器材:1. 计算机2. MATLAB软件实验内容:一、实验原理线性方程组是数学中一类常见的方程组,其形式如下:\[ Ax = b \]其中,\( A \) 是一个 \( m \times n \) 的系数矩阵,\( x \) 是一个 \( n \) 维的未知向量,\( b \) 是一个 \( m \) 维的常数向量。
线性方程组的求解方法有多种,如高斯消元法、矩阵求逆法等。
本实验主要介绍高斯消元法和矩阵求逆法。
二、实验步骤1. 设计一个线性方程组,并记录系数矩阵 \( A \) 和常数向量 \( b \)。
\[ \begin{cases}2x + 3y - z = 8 \\-x + 2y + 3z = 1 \\4x - y + 2z = 3\end{cases} \]系数矩阵 \( A \) 和常数向量 \( b \) 如下:\[ A = \begin{bmatrix}2 &3 & -1 \\-1 & 2 & 3 \\4 & -1 & 2\end{bmatrix}, \quad b = \begin{bmatrix}8 \\1 \\3\end{bmatrix} \]2. 使用MATLAB软件进行高斯消元法求解线性方程组。
```matlabA = [2 3 -1; -1 2 3; 4 -1 2];b = [8; 1; 3];x = A\b;```3. 使用MATLAB软件进行矩阵求逆法求解线性方程组。
```matlabA_inv = inv(A);x_inv = A_invb;```4. 比较两种方法得到的解,并验证其正确性。
三、实验结果与分析1. 使用高斯消元法求解得到的解为:\[ x = \begin{bmatrix}2 \\1 \\1\end{bmatrix} \]2. 使用矩阵求逆法求解得到的解为:\[ x = \begin{bmatrix}2 \\1 \\1\end{bmatrix} \]两种方法得到的解相同,验证了实验的正确性。
数学实验全部答案(精品).doc

实验十:简单的鹿群增长问题•问题一:鹿群增长模型•问题二:养老保险问题•问题三:金融公司的支付基金流动•问题四:保险金问题摘要:本篇实验报告主要是针对实验十:简单的鹿群增长问题而建立的模型。
并且将此模型的求解方法,运用到其他的类似的模型当中。
对该模型的求解,运用斧分方程组和线性代数的有关知识,通过用matlab编程,实现对矩阵的特征值和特征向量的自动求解。
以及将已知矩阵进行对角化。
并且用该模型的建模思想和求解方法,对课后的四个实验任务,分别进行了模型的建立和求解。
具体的四个实验任务如下:(1)鹿群增长模型的建立,算法编程以及程序的可行性验证;(2)养老保险问题模型的建立与求解;(3)金融公司支付基金的流动模型的建立与求解;(4)人寿保险计划模型的建立与求解;针对这几个实验任务,我分别建立了不同的数学模型,运用Matlab编程进行求解。
通过书上给出的实际数据进行了算法的可行性检验,并且通过实际数据给出了该模型的优略性评价。
问题一:鹿群增长模型问题重述:假设在一个自然生态地区生长着一群鹿,在一段时间内鹿群的增长受资源制约的因素较小。
这里所说的资源包括:有限的食物、空间、水等。
试建立一个简单的鹿群增长模型,并以适当的数据给出结果。
给出数据一:x0=0.8 ,yO=l ,al=0.3 ,a2=1.5 ,bl=0.62 ,b2=0.75 ,s=0.8; 数据二:xO=2.8 ,y0=3.4 ,al=0.4 ,a2=1.8 ,b 1=0.61 ,b2=0.72 ,s=0.7; 情况下的结果模型假设:(1)只考虑母鹿,并将其分为两组,一岁以下为幼鹿组,其余的为成年组;(2)不考虑饱和状态,即在所考虑的时间段内,种群的增长基本上是不受自然资源的制约;(3)鹿的生育数与鹿的总数成正比。
符号说明:X fl:第“年幼鹿的数量;y n:第"年成年鹿的数量;%:幼鹿的生育率;a2:成年鹿的的生育率;也:幼鹿的存活率;b2 :成年鹿的存活率;A:系数矩阵;人:矩阵A的特征值;入:矩阵A的特征值;X o:开始时幼鹿的数量;%):开始时成年鹿的数量;S:刚出生的幼鹿在哺乳期的存活率;J 代入方程⑴中,可以得到:= Au模型的建立:问题分析:根据鹿群数量增长的关系模型,建立幼鹿和成年鹿的数量关系式(观测吋间取为一年),建立如下的线性斧分方程组:(1)问题转化为对(2)进行求解。
高等数学上机实验报告第5题2003
《高等数学》数学实验报告
姓
名
任课教师学号所在学部、院、班级
卢
佳
琦
张宏伟201365062 机械工程与材料能源学部材料1304
实
验
内
容
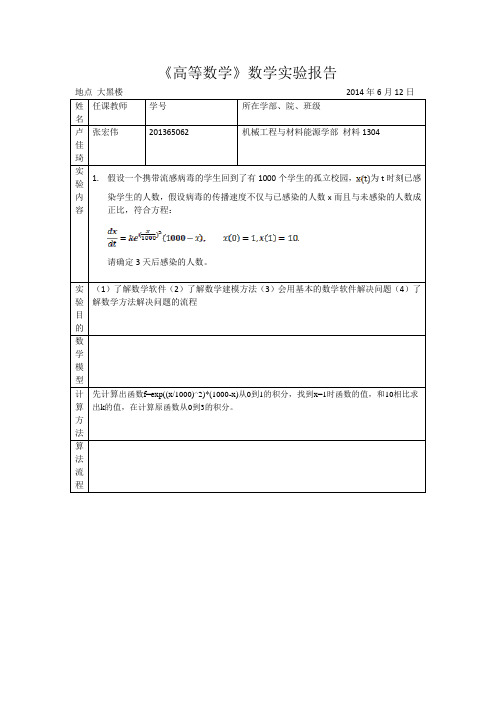
1.假设一个携带流感病毒的学生回到了有1000个学生的孤立校园,为t时刻已感
染学生的人数,假设病毒的传播速度不仅与已感染的人数x而且与未感染的人数成正比,符合方程:
请确定3天后感染的人数。
实
验
目
的
(1)了解数学软件(2)了解数学建模方法(3)会用基本的数学软件解决问题(4)了解数学方法解决问题的流程
数
学
模
型
计
算
方
法
先计算出函数f=exp((x/1000)^2)*(1000-x)从0到1的积分,找到x=1时函数的值,和10相比求出k的值,在计算原函数从0到3的积分。
算
法
流
程
实
验
结
果
与
分
析
当x=1时,y=1001,则k=10/1001
将函数从0到3积分,x=3的值为2997,乘以k,最后结果约为30 实
验
后
感
想。
东南大学高数实验报告(大一上)

高等数学数学实验报告
实验题目1:设数列{n x }由下列关系出: ),2,1(,2
1
211 =+==+n x x x x n n n ,观察数列
1
1
111121++
++++n x x x 的极限。
解:根据题意,编写如下程序求出数列的值
运行结果为:
0.66,
1.,
1.6,
1.9,
1.9,
1.9,,
,,,,
,,.
根据观察分析易得出,数列的极限为2.
实验题目2:已知函数)45(21
)(2
≤≤-++=x c
x x x f ,作出并比较当c 分别取-1,0,1,2,3时的图形,并从图上观察极值点、驻点、单调区间、凹凸区间以及渐进线。
解:根据题意,编写如下程序绘制函数
所得图像如下图所示,为c分别取-1,0,1,2,3时的图形:
c的值影响着函数图形上的极值点、驻点、单调区间、凹凸区间以及渐进线,c的值决定了函数图像。
实验题目3:对f(x)=cosx求不同的x处的泰勒展开的表达形式。
解:编写程序如下:
(1)
(2)
(3)
(4)
程序运行结果如下图所示:(1)
(2)
(3)
(4)
由图像可知,函数的泰勒多项式对于函数的近似程度随着阶数的提高而提高,但对于任意确定的次数的多项式,它只在展开点附近的一个局部范围内才有较好的近似精确度。
高等数学实验下(答案)

0.0.2 kt
中的参数 a,b,k
2) tdata=100:100:1000 cdata=1e-03*[4.54,4.99,5.35,5.65,5.90,6.10, 6.26,6.39,6.50,6.59]; x0=[0.2,0.05,0.05]; x=lsqcurvefit ('curvefun1',x0,tdata,cdata) f= curvefun1(x,tdata) plot(tdata,cdata,'*',tdata,f)
1)编写 M 文件 curvefun1.m function f=curvefun1(x,tdata) f=x(1)+x(2)*exp(-0.02*x(3)*tdata) %其中 x(1)=a; x(2)=b;x(3)=k;
11. 求
∑ 4n
n =1
∞
2
1 的值. + 8n + 3
syms n;
symsum(1/(4*n^2+8*n+3),1,inf) ans = 1/6 12. 求 ∑
7.求 z = xe − x
2
− y2
在区域 −2 ≤
x, y ≤ 2 ,步长为 0.2,画等高线梯度图
v=-2:.2:2; [x,y]=meshgrid(v); z=x.*exp(-x.^2-y.^2); [px,py]=gradient(z,.2,.2); contour(v,v,z),hold on; quiver(v,v,px,py),hold off
高等数学实验教材答案

高等数学实验教材答案高等数学实验教材答案是学习高等数学实验课程的重要参考资料。
在这篇文章中,我将为大家提供一份高等数学实验教材的答案,以帮助学生更好地理解和掌握相关知识。
一、微分与导数1.1 定义与性质1.2 基本微分法则1.3 乘积法则、商法则与链式法则1.4 高阶导数与隐函数求导1.5 几何应用:切线与法线二、积分与不定积分2.1 定义与性质2.2 基本积分法则2.3 分部积分法2.4 有理函数的积分2.5 几何应用:定积分与曲线下面积三、微分方程3.1 一阶常微分方程3.2 高阶常微分方程3.3 可降阶的高阶常微分方程3.4 几何应用:曲线的凹凸性与拐点四、级数与幂级数4.1 数项级数与收敛性4.2 幂级数的收敛半径与收敛区间4.3 函数展开为幂级数4.4 幂级数展开与微分、积分的关系五、多元函数与偏导数5.1 多元函数的概念与性质5.2 偏导数及其计算5.3 隐函数与参数方程求导5.4 多元函数的极值与条件极值5.5 几何应用:方向导数与梯度六、重积分6.1 重积分的定义与性质6.2 二重积分的计算6.3 三重积分的计算6.4 极坐标、柱坐标与球坐标下的积分6.5 几何应用:质量、重心与转动惯量七、曲线积分与曲面积分7.1 第一类曲线积分7.2 第二类曲线积分7.3 常见曲线的参数方程与弧长7.4 曲面积分的概念与性质7.5 几何应用:质量、重心与转动惯量的曲面积分表示八、常微分方程与拉普拉斯变换8.1 齐次与非齐次线性常微分方程8.2 求解常系数齐次线性常微分方程8.3 非齐次线性常微分方程的常数变易法8.4 拉普拉斯变换的定义与性质8.5 拉普拉斯变换与求解微分方程以上是高等数学实验教材的答案大纲。
希望这份答案对广大学生们学习和理解高等数学实验课程有所帮助。
请将这份答案作为参考,并结合教材中的练习题进行实践,以巩固所学知识。
祝大家在高等数学实验课程中取得好成绩!。
高数实验

试验报告1 基本计算与作图1 计算下列各式的值(要求有输入命令及输出结果)(1)1675 输入:75^16 输出:ans =1.0023e+030(2 输入: sqrt(1-3*i) 输出: ans =1.4426 - 1.0398i(3) sin 23输入:sin(23/180*pi) 输出:ans = 0.3907 (4) 2arcsin π 输入: asin(2/pi) 输出:ans = 0.6901(5) 88! 输入:prd=1; j=1; while j<=88 prd=prd*j; j=j+1; end prd 输出: prd =1.8548e+1342 2tan 3a b π==,计算: (1)2335235a ab a b +-输入: a=sqrt(exp(1)^exp(1)); b=tan(pi^2/3); 2*a^2+3*a*b^3-5*a^3*b^5输出: ans = 30.3255(2)sec(arctan())a 输入: a=sqrt(exp(1)^exp(1)); sec(atan(a)) 输出: ans = 4.01923 作图(写出输入格式,并画出草图)(1)做出13y x =的图像 输入:x=0:0.01:5; y=x.^(1/3);plot(x,y) 输出:00.51 1.52 2.53 3.54 4.5500.20.40.60.811.21.41.61.8(2)做出1()4x y 的图像 输入: x=-3:0.01:3; y=(1/4).^x;plot(x,y) 输出:-3-2-10123010203040506070(3)做出(,)sin(f x y π=的图像 输入:x=-5:0.01:5; y=x;[X,Y]=meshgrid(x,y);z=sin(pi*sqrt(X.^2+Y.^2));mesh(X,Y ,z) 输出:(4)做出sin(2)4y x π=+在一个周期内的图像 输入:x=0:0.01:pi; y=sin(2*x+pi/4);plot(x,y) 输出:00.51 1.52 2.53 3.5-1-0.8-0.6-0.4-0.20.20.40.60.81(5)做出c o s (3c o s )s i n (3c o s )s i n x t u y t u z u =+⎧⎪=+⎨⎪=⎩,其中(0,2),(0,2)t u ππ∈∈的图像 输入:t=0:0.01:2*pi; u=0:0.01:2*pi; x=cos(t.*(3+cos(u))); y=sin(t.*(3+cos(u))); z=sin(u); plot3(x,y,z) 输出:-11(6)在一个坐标内画出:,cos ,[0,]y x y x x π==∈和arccos .[1,1]y x x =∈-的图像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数学实验——高等数学分册》(郭科主编)---《实验报告册》参考答案------轩轩第5章1.(1)syms x y;f=(1-cos(x^2+y^2))/((x^2+y^2)*exp(x^2*y^2));limit(limit(f,x,0),y,0)ans =(2)syms x y;f=(log(x*exp(x)+exp(y)))/sqrt(x^2+y^2);limit(limit(f,x,0),y,0)ans =NaN另解syms x y;f=log(x*exp(x)+exp(y));g=sqrt(x^2+y^2);limit(limit(f/g,x,0),y,0)ans =NaN注:“()”多了以后,系统无法识别,但在matlab的语法上是合理的。
在有的一些matlab 版本上可以识别。
在以下的题目答案中同理。
(3)syms x y;f=(2*x*sin(y))/(sqrt(x*y+1)-1);limit(limit(f,x,0),y,0)ans =4另解syms x y;f=2*x*sin(y);g=sqrt(x*y+1)-1;limit(limit(f/g,x,0),y,0)ans =42.(1)syms x y;z=((x^2+y^2)/(x^2-y^2))*exp(x*y);zx=diff(z,x)zx =(2*x*exp(x*y))/(x^2 - y^2) - (2*x*exp(x*y)*(x^2 +y^2))/(x^2 - y^2)^2 + (y*exp(x*y)*(x^2 + y^2))/(x^2 - y^2) zy=diff(z,y)zy =(2*y*exp(x*y))/(x^2 - y^2) + (x*exp(x*y)*(x^2 +y^2))/(x^2 - y^2) + (2*y*exp(x*y)*(x^2 + y^2))/(x^2 -y^2)^2注:所有的x在高的版本中都可以替换为x。
(即,不用单引号,结果任然正确。
前提为:不与前面的函数冲突。
)(2)syms x y z;u=log(3*x-2*y+z);ux=diff(u,x)ux =3/(3*x - 2*y + z)uy=diff(u,y)uy =-2/(3*x - 2*y + z)uz=diff(u,'z')uz =1/(3*x - 2*y + z)(3)syms x y;z=sqrt(x)*sin(y/x);zx=diff(z,x)zx =sin(y/x)/(2*x^(1/2)) - (y*cos(y/x))/x^(3/2) zy=diff(z,y)zy =cos(y/x)/x^(1/2)(4)syms x y;z=asin(y*sqrt(x));zx=diff(z,x)zx =y/(2*x^(1/2)*(1 - x*y^2)^(1/2))zy=diff(z,y)zy =x^(1/2)/(1 - x*y^2)^(1/2)3.syms x y;f=x+y-sqrt(x^2+y^2);fx=diff(f,x);fy=diff(f,y);x=2;y=4;fx0=subs(fx)fx0 =0.5528fy0=subs(fy)fy0 =0.10564. syms x y z a;f=x^2+y^2+z^2-2*a*x*y*z;fx=diff(f,x);fy=diff(f,y);fz=diff(f,'z');dzx=-fx/fzdzx =-(2*x - 2*a*y*z)/(2*z - 2*a*x*y)dzy=-fy/fzdzy =-(2*y - 2*a*x*z)/(2*z - 2*a*x*y)5. syms x y u v R dux dvx duy dvy;f=x^2+y^2+u^2+v^2-R^2;g=x+y+u+v;fx=diff(f,x);fy=diff(f,y);fu=diff(f,'u');fv=diff(f,'v'); gx=diff(g,x);gy=diff(g,y);gu=diff(g,'u');gv=diff(g,'v'); ffx=fu*dux+fv*dvx+fx;ggx=gu*dux+gv*dvx+gx;[dux,dvx]=solve(ffx,ggx,'dux','dvx')dux =(v - x)/(u - v)dvx =-(u - x)/(u - v)ffy=fu*duy+fv*dvy+fy;ggy=gu*duy+gv*dvy+gy;[duy,dvy]=solve(ffy,ggy,'duy','dvy')duy =(v - y)/(u - v)dvy =-(u - y)/(u - v)6. syms x y z;f=x+y+z-exp(-(x+y+z));fx=diff(f,x);fz=diff(f,'z');dzx=-fx/fz;g=dzx;gy=diff(g,y);gz=diff(g,'z');dzxy=gy+gz*dzxdzxy =另解syms x y zf=x+y+z-exp(-(x+y+z));fx=diff(f,x);fz=diff(f,'z');dzx=-fx/fz;gy=diff(dzx,y);gz=diff(dzx,'z');dzxy=gy+gz*dzxdzxy =7. syms x y;z=x^2-x*y-2*y^2;zx=diff(z,x);zy=diff(z,y);fzx=inline(zx);fzy=inline(zy);a=pi/3;b=pi/6;f1=fzx(1,2)*cos(a)+fzy(1,2)*cos(b)f1 =-7.79428. syms t;x=sin(t);y=cos(t);z=t;dx=diff(x,'t');dy=diff(y,'t');dz=diff(z,'t'); x1=inline(dx);x2=inline(dy);x3=inline(dz);t=pi/4;a=sin(t);b=cos(t);c=t;x10=x1(a)x10 =0.7602x20=x2(b)x20 =-0.6496x30=x3(c)x30 =19. syms x y;f=x^2+y^2;fx=diff(f,x);fy=diff(f,y);x=1;y=2;fx0=subs(fx)fx0 =2fy0=subs(fy)fy0 =410. syms x y;f=x^3-y^3+3*x^2+3*y^2-9*x;fx=diff(f,x);fy=diff(f,y);[x0,y0]=solve(fx,fy)x0 =1-31-3y0 =22fxx=diff(diff(f,x),x) (此条可以写作:fxx=diff(f,x,2),类似的同理) fxx =6*x + 6fxy=diff(diff(f,x),y);fyy=diff(diff(f,y),y);delta=inline(fxy^2-fxx*fyy);delta(x0,y0)ans =-727272-72x=1;y=0;fmin=subs(f)fmin =-5x=-3;y=2;fmax=subs(f)fmax =3111. syms x y z lamda a;L=x*y*z+lamda*((x^2+y^2)/4+z^2-a^2);Lx=diff(L,x);Ly=diff(L,y);Lz=diff(L,'z');Llamda=diff(L,'lamda');[lamda x y z]=solve(Lx,Ly,Lz,Llamda)lamda =0 0 0 0 0 -(2*3^(1/2)*a)/3 (2*3^(1/2)*a)/3 (2*3^(1/2)*a)/3 (2*3^(1/2)*a)/3 (2*3^(1/2)*a)/3 -(2*3^(1/2)*a)/3 -(2*3^(1/2)*a)/3 -(2*3^(1/2)*a)/3 x =0 2*a 0 0 (-2)*a 0 (2*3^(1/2)*a)/3 (2*3^(1/2)*a)/3 -(2*3^(1/2)*a)/3 (2*3^(1/2)*a)/3 -(2*3^(1/2)*a)/3 -(2*3^(1/2)*a)/3 -(2*3^(1/2)*a)/3 (2*3^(1/2)*a)/3 y =0 0 2*a (-2)*a 0 0 (2*3^(1/2)*a)/3 -(2*3^(1/2)*a)/3 (2*3^(1/2)*a)/3 (2*3^(1/2)*a)/3 -(2*3^(1/2)*a)/3 (2*3^(1/2)*a)/3 -(2*3^(1/2)*a)/3 -(2*3^(1/2)*a)/3z =a-a(3^(1/2)*a)/3(3^(1/2)*a)/3(3^(1/2)*a)/3-(3^(1/2)*a)/3-(3^(1/2)*a)/3-(3^(1/2)*a)/3(3^(1/2)*a)/3-(3^(1/2)*a)/3V=x.*y.*zV =(4*3^(1/2)*a^3)/9-(4*3^(1/2)*a^3)/9-(4*3^(1/2)*a^3)/9-(4*3^(1/2)*a^3)/9-(4*3^(1/2)*a^3)/9(4*3^(1/2)*a^3)/9(4*3^(1/2)*a^3)/9(4*3^(1/2)*a^3)/9第6章1. syms x y;f=x*y;y1=2*x;y2=x^2+1;I=int(int(f,y,y1,y2),x,0,1)I =1/122. syms x y r t;x=r*cos(t);y=r*sin(t);f=exp(-(x^2+y^2));I=int(int(f*r,r,0,1),t,0,2*pi)I =-pi*(1/exp(1) - 1)3. syms x y z a A t r s;x=r*sin(s)*cos(t);y=r*sin(s)*sin(t);z=r*cos(s);f=x^2+y^2;I1=int(int(int(f*r^2*sin(s),s,0,1/2*pi),r,0,a),t,0,2*pi); I2=int(int(int(f*r^2*sin(s),s,0,1/2*pi),r,0,A),t,0,2*pi); I=I2-I1I =(4*pi*A^5)/15 - (4*pi*a^5)/154. syms x y z t r s;x=r*sin(s)*cos(t);y=r*sin(s)*sin(t);z=r*cos(s);f=(z*log(x^2+y^2+z^2+1))/(x^2+y^2+z^2+1);M=int(int(int(f*r^2*sin(s),s,0,1/2*pi),r,0,1),t,0,2*pi) M =-(pi*(log(2)^2 - log(16) + 2))/45.x=1/2:0.001:1;y=1./x;plot(x,y,k);xlabel(x);ylabel(y)syms x;f=1/x;fx=diff(f,x);I=int(x*sqrt(1+fx^2),x,1/2,1)I =int(x*(1/x^4 + 1)^(1/2), x = 1/2..1)6. syms x y r t;x=r*cos(t);y=r*sin(t);z=sqrt(x^2+y^2);zx=diff(z,x);zy=diff(z,y);f=(sqrt(x^2+y^2))*sqrt(1+zx^2+zy^2);M=int(int(f*r,r,0,1),t,0,2*pi)M =(2*pi)/38、syms x y a;p=exp(x)*sin(y)-y^2;q=exp(x)*cos(y)-1;f=diff(q,x)-diff(p,y);x1=0;x2=a;y1=0;y2=sqrt(a/4-(x-a/2)^2);f1=int(f,y,y1,y2);i=int(f1,x,x1,x2)i =-(a^2*(a - 3))/129、syms z t r;R=z^2;Rz=diff(R,z);t1=0;t2=2*pi;z1=0;z2=1;r1=0;r2=sqrt(z);f1=int(r*Rz,r,r1,r2);f2=int(f1,z,z1,z2);i=int(f2,t,t1,t2)i =(2*pi)/310.syms x y z;P=4*x;Q=-2*x*y;R=z^2; px=diff(P,x);qy=diff(Q,y);rz=diff(R,'z');x=1;y=1;z=3;px0=subs(px)px0 =4qy0=subs(qy)qy0 =-2rz0=subs(rz)rz0 =6。
