2-7带电体系的静电能与电场的势能
带电体系的静电能

中图分 类号 :0 4 . 41 1
一
文献 标识码 :A
文章编 号 :1 O — 6 2 2 0 )O —o 5 — o 8 1 9( 0 7 3 0 3 3 O
个 带 电体 系 的能量可 分为势 能和 动 能 。在 静 电学 中 ,由于 电荷 之 间处于相 对静 止状 态 ,无 需讨 论
或 Байду номын сангаас
q uz = 1 : -
_q q 2 l
由于这类 做功 改变 了体系 的静 电能 ,属于两 个 电荷 之 间相互 作用 能 的变 化 ,因而又 可 以用体 系的相 互作 用能来表示 ,即
Wm :
业
r
: (2ul+q u2 q 2 2 1 () ) 4
q刀 0
这一相互 作用 能 的积 累显 然 是 由外 力做功或 第一 个 电荷 的 电场 力做负 功转变 而来 的 ,故 这也 是体系 静 电能的另一 个称呼 。 3多个点 电荷 系统 的相互作 用 能 .
收 稿 日期 : 2 0 - l_ l 06- 2 3
作者简介:张进明 ( 91 ) 16- ,河北涿鹿人 ,张家口职业技术学院教育教学研 究室,副主任,副教授。
5 3
维普资讯
邢台职业技术学院学报
qz t 1 ql u z= q2
20 0 7年 第 3期
由上所 述不 难理解 ,电场 力做 功 与体系 的 电势 能完全 遵 守“ 能原 理” 功 而互 相转 化 ,若用 W 琳表示 外
力做功,其转换关系就是 h w =一 ( =一 q UA—UB =一 uA ) q B=q UB
带电体系的静电能
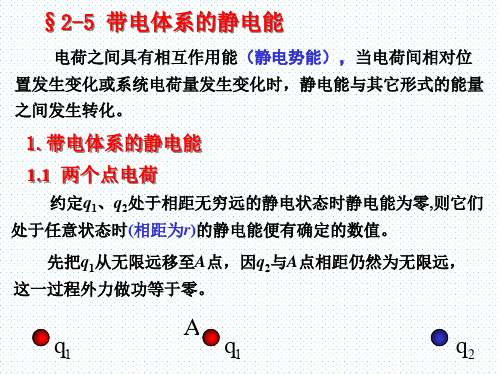
解:(1)根据空腔导体的静电性质和球对称性,两空腔内表面的 电荷面密度分别是
1
Q1
4R12
和 2
Q2
4R22
又根据电荷守恒定律,导体外表面的的电量Q=Q1+Q2,由于 球对称性,导体外表面的电荷面密度是
Q1 Q2
的电容分别为
C1
0
S d
,
C2
0
S 2d
板极上带电± Q时所储的电能为
W1
1 2
Q2
0C1
1 2
Q2d
0S
,W2
1 2
Q2 2d
0S
故两极板的间距拉开到2d后电容器中电场能量的增量 为
W=W2-W1
1 2
Q2d
0S
(2)设两极板之间的相互吸引力为F ,拉开两极板时 所加外力应等于F ,外力所作的功A=Fd ,所以
(c)圆柱电容器
C
2 0L
ln( R2 )
R1
(F)电容器的联接 (G)电容器的能量
(1)串联
1 1
C i Ci
(2)并联
C Ci
W
Q2
1 CU 2
i
1 QU
2C 2
2
(H) 点电荷系的静电能
1n W 2 i1 qiVi
4.例题
例1.如图所示,一个半径为R的中性导体球,内部有两个球 形空腔,半径分别为R1和R2,在空腔中心分别放置点电 荷Q1和Q2,试求:
F A W Q2
d d 20S
第二章小结
带电体系的静电能、带电体在外电场中的能量

解:相邻顶点之间的距离为b
面对角线长度为 2b
12对 12对
12e2k / b 12e2k /
1
4 0
2b
体对角线长度为 3b 4对 4e2k / 3b
中心到顶点距离 3b / 2 8对 8(2e2 )k / 3b / 2
总相 互作
用能
we
1
4 0
12e2 (
b
12e2 2b
4e2 3b
32e2 )
静
dq(U U ) u(t)dq
电
能
We
Q
u(t)dq
0
Q q(t) dq 1 Q2
0C
2C
电量 0——>Q
2013/3/13
电容器储能公式的推广
孤立导体
Q=CU
We
1 2
Q2 C
1 CU 2 2
1 QU 2
一组导体1、2、…、n
1
We 2
n i
1 QiUi 2
i
Ui edS
U (r l) U (r) U l l
U(r) l U
U (r l )
U (r )
W ql U P U p E(r) pE cos
2013/3/13
带电体系在外场中受的力或力矩与静电
势能的关系——虚功原理 p271/p61
设处在一定位形的带电体系的电势能为W,当它 的位形发生微小变化
3b
0.344e2
0b
2013/3/13
自能和相互作用能
相互作用能:把每一个带电体看作一个不 可分割的整体,将各带电体从无限远移到 现在位置所做的功等于它们的相互作用能。
自能:把全部电荷从无限分散的情况下聚 集到带电体上的过程中外力克服电场力所 做的功。
2.5带电体系的静电能

+ a
势能高 +q
b
势能低
W a W b A ab q
b
E dl
a
电势能也是一个相对量,要确定q在某点的电势能 值,必须选定参考点,并且,通常规定参考点的电势 能为零。如选b点为势能参考点,并令 W b 0 ,则
Wa Wa 0
参
qE dl
§2.5 带电体系的静电能
任何物体的带电过程,都是电荷之间的相对移动过 程,所以在形成带电系统的过程中,外力必须克服电 场力而做功,根据能量转化和守恒定律,外力对系统 所做的功,应等于系统能量的增量,所以任何带电系 统都具有能量。 a 一 带电体系的静电能 1、电势能
mg ha b
hb (1)重力势能(复习) 物体(质量为m的质点)只 在重力作用下,从a点移到b点时物体重力势能减少, 且重力在此过程中对物体所做的功等于物体重力势能 的减少。即
2、静电能 (1)单个带电体的自能 设想把这个带电体分割成无限多的小块(即使是点 电荷它也是一个带电体,也可无限分小)。把这个带 电体的每一小块无限远离时电场力所做的功;或把这 个带电体的每一小块从无限远离状态放到一起组成这 个带电体时外力所做的功,就是自能。
(2)带电体系的静电能 ① 每个带电体的自能:把这个带电体的每一小块 无限远离时电场力做的功。 ② 各带电体之间的互能:把各个带电体无限远离 时电场力做的功。 带电体系的静电能=单个带电体的自能+带电体 之间的互能
互能的一般公式的推导见书P72-73小字部分,自学。 二 电容器的静电能 电容器带电的过程可以看作是不 断地把微小电荷+dq从原来中性的B 板迁移到A板上的过程。 当电容器两极板已带电到某一q值 且两板间的电势差为u时,再把电荷 +dq从B板移到A板时,电场力做负功 (外力作功),其绝对值为
静电场的能量

= W互 + W自
5
W互是带电系统内N个带电体之间的相互作用能, 简称为系统的互能。
W自是每个带电体的静电能之和,简称为自能。
静电能 = 自能 + 相互作用能
⑵ 点电荷的自能
设想点电荷q是由半径为R( R → 0 )的均匀带电
球收缩半径而成,则球内一点产生的电势为
∫ ∫ ∫ U =
∞r r E ⋅ dl =
12
例1 如图所示,在一边长为d的立方体的每个顶 点上放有一个点电荷-e,立方体中心放有一个 点电荷+2e,求此带电系统的相互作用能量 。
解:法一
8个顶点上的负电荷的相 互作用能为12对,即
e2 12
4πε 0 d
6个面上对角顶点负电荷的相 互作用能为12对,即
12 e2 4πε0 2d
−e −e
R 0
Qr 4πε 0 R 3
2
4π
r 2dr
+
ε0 2
∞ R
Q 4πε 0 r 2
2
4π
r 2dr
= 3Q2
20πε 0 R
20
例4 球形电容器的内、外半径分别为R1和R2,所带电荷为Q。 若在两球壳间充以电容率为ε的电介质,求此电容器贮存 的电场能量。
解:由高斯定理, r
w1 = 0 (r < R1)
w4 = 0 (r > R2 )
w2
=
1 ε E2 2
=
32π
q2 2ε0ε r1r 4
(R1 < r < R)
w3
=
32π
q2 2ε 0ε r 2r 4
(R < r < R2 )
第10章静电场中的能量(单元知识清单)高二物理(人教版2019)

第10章必备知识清单§1电势能和电势1、在匀强电场中移动电荷时,静电力做的功与电荷的起始位置和终止位置有关,但与电荷经过的路径无关。
计算式:W电=qEd,其中d为带电体在沿电场方向的位移。
2、电势能(符号E P):电荷在电场中具有的势能,是标量3、静电力做功与电势能变化的关系:静电力做的功等于电荷电势能的减少量,即W AB=−∆E p=−(E pB−E pA)=E pA−E pB。
●当W AB>0,则E pA>E pB,表明电场力做正功,电势能减小;●当W AB<0,则E pA<E pB,表明电场力做负功,电势能增加。
4、电势能是相对的,具体数值与零势能面的选取有关。
通常把电荷在离场源电荷无限远处的电势能规定为0,或把电荷在大地表面的电势能规定为0。
5、电势能具有系统性,为电荷和对它作用的电场组成的系统共有。
●电荷在某点的电势能,等于把它从该点移动到零势能面时静电力所做的功。
●选择不同的零势能面,对于同一个带电体在同一点来说电势能大小是不相同的。
6、电势(符号 φ):电荷在电场中某一点的电势能与它的电荷量之比。
●定义式:φ=E pq●单位:伏特(V),1V=1J/C。
●电势是标量,有正负,负电势表示该处的电势比零电势低。
7、电势具有相对性,确定某点的电势,应先规定电场中某处电势为零,通常取大地或无穷远处的电势为零。
8、沿电场线方向,电势降低最快。
判断电势高低的基本方法:①沿电场线方向,电势越来越低。
②正电荷在电势能大的地方电势高,负电荷相反。
③静电力对正电荷做正功,则电势降低。
④离带正电的场源电荷越近的点,电势越高。
9、在等量异种点电荷的电场中,①沿点电荷的连线由正电荷到负电荷,电势逐渐降低。
②两点电荷连线中垂线上,电势均相等(若取无穷远处电势为0,则中垂线上电势处处为0)。
10、在等量同种正点电荷的电场中,①两电荷连线上,由正电荷到连线中点O电势逐渐降低,且关于O点对称。
②两电荷连线中垂线上,由中点O向两侧电势到无限远电势逐渐降低,且关于O点对称。
静电场的能量与电势能的计算

静电场的能量与电势能的计算引言:静电场是指电荷静止不动时所形成的电场。
在静电场中,电荷之间的相互作用是通过电势能来实现的。
本文将介绍静电场中能量的计算方法以及电势能与电量、距离之间的关系。
一、电场的能量计算公式在静电场中,电场的能量可以通过以下公式进行计算:E = (1/2) * ε * ∫E^2 dV其中,E表示电场的能量,ε为真空介电常数,E为电场的强度。
二、电势能的计算方法电势能是指电荷由于置于电场中而具有的能量。
对于单个点电荷q1和q2之间的电势能,可以使用以下公式进行计算:U = k * (q1 * q2) / r其中,k为库仑常数,q1和q2分别为电荷的大小,r为两电荷之间的距离。
三、电势能与电量和距离的关系1. 电势能与电量的关系对于一个点电荷q在电场E中的电势能U,可以使用以下公式进行计算:其中,V为电势差,也即电场中单位正电荷所具有的电势能。
2. 电势能与距离的关系电势能与距离之间满足一个倒数关系。
具体而言,当距离r增大时,电势能U减小;当距离r减小时,电势能U增大。
这一关系可以通过电势能的计算公式中的分母r来理解。
四、实例分析假设有两个点电荷q1和q2,它们的电量分别为3C和5C,两电荷之间的距离为2m。
现要计算它们在电场中的电势能。
根据电势能的计算公式:U = k * (q1 * q2) / r代入已知数值:U = 9 * 10^9 * (3 * 5) / 2U = 67.5 * 10^9 J因此,两个点电荷在电场中的电势能为67.5 * 10^9焦耳。
结论:本文介绍了静电场中能量的计算方法,以及电势能与电量、距离之间的关系。
通过学习和理解这些知识,我们可以更好地理解静电场的特性和现象,并应用于实际问题的计算和分析中。
[1] Griffiths, D. J. (2013). Introduction to electrodynamics. Cambridge University Press.[2] Purcell, E. M., & Morin, D. J. (2013). Electricity and magnetism. Cambridge University Press.。
带电粒子在电场中的势能

带电粒子在电场中的势能1. 介绍带电粒子在电场中的势能是物理学中一个重要的概念。
电场是由电荷产生的一种力场,而带电粒子在电场中具有势能。
本文将深入探讨带电粒子在电场中的势能的概念、计算方法以及相关的应用。
2. 带电粒子的势能带电粒子在电场中的势能可以通过以下公式计算:U=qV其中,U表示势能,q表示带电粒子的电荷量,V表示电场中的电势。
带电粒子的势能与其电荷量和所处电场的电势有关。
当带电粒子的电荷量增加或电场的电势增加时,势能也会增加。
带电粒子的势能是标量量,单位为焦耳(J)。
3. 电场中的势能变化当带电粒子在电场中移动时,它的势能也会发生变化。
带电粒子从一个位置移动到另一个位置时,它的势能的变化量可以通过以下公式计算:ΔU=qΔV其中,ΔU表示势能的变化量,ΔV表示电场的电势的变化量。
如果带电粒子沿着电场的力线方向移动,且电场是保守场,那么势能的变化量可以表示为:ΔU=−W其中,W表示带电粒子受到的电场力所做的功。
4. 电势能与力的关系带电粒子在电场中的势能与电场力之间存在着密切的关系。
根据能量守恒定律,带电粒子在电场中的势能的变化量等于所受力的负功。
根据定义可得:ΔU=−W根据力的定义可得:W=F⋅d其中,F表示带电粒子所受到的电场力,d表示带电粒子在电场中移动的距离。
将上述两个公式联立,可以得到:ΔU=−F⋅d根据牛顿第二定律可得:F=ma其中,m表示带电粒子的质量,a表示带电粒子在电场中的加速度。
将上述公式代入前面的公式,可以得到:ΔU=−ma⋅d因此,带电粒子在电场中的势能的变化量可以表示为:ΔU=−mad5. 应用带电粒子在电场中的势能的概念和计算方法在物理学中有着广泛的应用。
以下是一些常见的应用领域:5.1. 静电能带电粒子在电场中的势能也称为静电能。
静电能是带电粒子由于所处电场而具有的能量。
静电能的大小与带电粒子的电荷量和电场的电势有关。
在静电场中,带电粒子的势能可以通过以下公式计算:U=12 qV其中,U表示静电能,q表示带电粒子的电荷量,V表示电场中的电势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2-7 带电体系的静电能与电场的势能前面我们分析了有电介质存在时的电场和电势的一些行为,进一步的分析自然少不了有关能量的讨论。
在本节中,我们从较简单的点电荷系统开始分析,然后过渡到连续电荷分布的情形中去。
一、 点电荷系统的静电能我们从最简单的情形开始分析。
我们知道,在一定的电场中,若一个点电荷q 所在位置处的电势为U ,那么就可以说这个点电荷具有电势能W=qU ,这一点和我们熟知的重力势能很相象。
现在我们可以把电场说得更具体一些,最简单的,设这个电场是由另一个点电荷Q 产生的,于是点电荷q 具有的电势能可以写作rqQ W 041πε=(1)这里我们讨论的是在真空中的情形,所以介电常数是Q q r 和是,0ε的距离。
同样地,上式也表示了Q 在q 的电场中的电势能,于是我们可以说,由Q 和q 组成静电体系具有的静电能由(1)式给出。
⎪⎪⎭⎫⎝⎛+=r Qq rqQW 0414121πεπε对此式的解释是:我们不但考虑了在Q 形成的电场中q 所具有的电势能,而且还考虑了在q 形成的电场中Q 所具有的电势能,但是对于整个静电系统而言,其静电能只能由其中一项给出,所以要对上式右端的和乘以1/2。
我们之所以写出上面的表达式是因为希望进一步考虑由多个点电荷组成的静电系统。
设想空间中有多个点电荷,其带电量用i q 表示,相应的位置用i r 表示,任意两个点电荷间的距离可以由ij j i j r i =r =r -r 给出,我们来计算整个静电体系的静电能。
我们用一种类似于数学归纳法的办法来计算由N 个点电荷组成的静电体系的静电能。
当只有两个点电荷21q q 和时,静电能为1221041r q q W πε=现在引入第三个点电荷3q ,那么整个体系的静电能就应该在原有的基础上加上3q 与21q q 及之间的静电能,即⎪⎪⎭⎫⎝⎛++=233201331012210414141r q q r q q r q q W πεπεπε括号里的项正是由于引入第三个点电荷所引起的静电能的改变。
接着引入第四个点电荷,有⎪⎪⎭⎫⎝⎛++=233201331012210414141r q q r q q r q q W πεπεπε341424014024*********q q q q q q r r r πεπεπε⎛⎫+++ ⎪⎝⎭同样地,第二个括号里的项对应于第四个点电荷的引入所带来的静电能的变化。
重复以上过程,我们容易得到由N 个点电荷组成的静电系统的静电能为⎪⎪⎭⎫⎝⎛++=233201331012210414141r q q r q q r q q W πεπεπε+⎪⎪⎭⎫⎝⎛++344302442014410414141r q q r q q r q q πεπεπε+… (2) =∑∑≠==Nji ijj i Nji j i ijj i r q q r q q 01,0412141πεπε上式即为我们要求的结果,其最后一项表明对所有的满足j i ≠的下标求和。
我们可以对上述结果作进一步的分析,注意到对于某个特定的i ,∑≠Nij ijjr q41πε就是除了电荷i 以外的所有电荷在电荷i 处形成电势,令∑≠=Nij ijji r qU 041πε(3)则(2)式可以改写为iNiiU q W ∑=21(4)二、连续电荷分布的静电能以上我们讨论的是点电荷体系的静电能,可以很容易地将已有结论推广至连续分布的静电系统。
首先我们设想一个有限大小的带电体,其电荷密度为()ρr ,那么如果在该带电体内部且位置为r 处的电势可以用U (r )来表示——当然,所谓U (r ),是指在位置r 处的电势,而位置r 处的电荷对U (r )是没贡献的——则这一带电体所具有的静电能可以表示为1()()2VW U dV ρ=⎰⎰⎰r r (5)上式中V 表示整个带电体的体积,实际上,(5)式是(4)式的直接推广,是由离散的电荷分布过渡到连续的电荷分布,在表示上由求和过渡到积分。
图1(5)式确实能够从物理概念上解释静电能的意义:静电系统的每一部分所具有的电势能的总和。
但是,在实际问题中,直接利用(5)式求解静电能是很不易的。
只是因为计算各点的U (r )是件很麻烦的工作。
我们不妨从另一个角度考虑静电能。
对于一个有限体积的带电体,我们姑且不考虑其微观结构而只注意其静电性质,那么可以说,这一带电体之所以能够结合在一起,是需要外力维持的。
我们设想下面的过程来说明如何构成一个有限大小的带电体。
开始的时候,所有的电荷都位于无穷远处,我们人为地将一个个电荷从无穷远处极缓慢地移动到指定的位置,那么,在这个极缓慢的过程中我们对电荷所施加的力与电荷所受的的静电力想必是大小相等而方向相反的,我们所作的功就应该等于电荷的电势能的增量。
不断地重复这一过程,直到最终组成我们所要的有限大小的带电体,在整个过程中,我们所作的功就是静电体系的静电能。
这样,从功能原理的角度我们重新解释了静电能。
下面通过一个简单的例子来说明书这一过程。
图2我们来计算一个半径为R 的均匀带电球体的电势能。
如果按照公式(5)的要求,则要计算球体内每一点处的电势。
现在让我们从功能原理的角度考虑这个问题。
如图所示,为了构造一个半径为R 的带电球体,我们就要准静态地把电荷从无穷远处搬运到适当的位置,并组成球形。
假设在某个时候我们已经构成了如图所示的情形,即已经有了一个半径为r 的带电球体,接下来我们要继续从无穷远处搬运电荷,并将搬来的电荷均匀地分布在这个球体上。
我们每次搬运的电荷都是很少的,设电荷密度为ρ,那么每次搬运的电荷量可以表示为dr r ρπ24,而球表面的电势为rr23441πρπε⋅,无穷远处的电势为零,故在某一次的搬运过程中我们所作的功即为电量为dr r ρπ24的电荷的电势能的改变,它就是dr r rr2243441πρπρπε⋅⋅最后我们要组成半径为R 的带电球,于是该球体的电势能就是对上式的积分,即dr r rrW R2243441πρπρπε⋅⋅=⎰=41πε522513)4(R ρπ可以将电荷密度ρ表示为334RQπ,这里Q 是这个球体的带电量,于是上式化为RQW 24153πε=(6)这便是半径为R 带电量为Q 的均匀球体的静电能。
由于同种电荷是彼此排斥的,所以这一能量可以理解为维持这样的带电系统保持平衡所需要能量。
设想另外一种情形——引力,若有一个半径为R ,质量为M 的均匀球体,由于万有引力,其各部分是彼此吸引的,那么如果我们想击碎这一球体,需要多少能量才行呢?结合上面的过程,不难想象,所需能量为RM G253,其中G 是万有引力常数,大家可以对这一结果稍加分析。
下面我们来比较一下这样一些概念:静电能、相互作用能、自能。
在不少教科书及参考书中这些概念经常出现。
首先要重申,点电荷这一概念是数学上的抽象而不是物理上的实在,当用点电荷这一概念讨论物理问题时,我们不再关注已经被抽象成“点”的电荷的大小、形状及内部结构,转而关注这些“点”电荷对自身以外的空间或其它电荷的影响。
于是,对于由点电荷组成的静电系统,所谓的静电能就只能是各个点电荷之间的相互作用能,回顾(3)式和(4)式的推导,可以容易看出这一点。
对于那些有具体形状或大小的连续电荷分布,整体上的静电能可以分为自能和相互作用能两部分,让我们对此稍作分析。
上面我们计算了一个均匀带电球体的静电能,这个带电球体当然是一种连续的电荷分布,而且空间中除了这个带电球体外再没有别的带电体,这时我们可以说,这个带电球所具有的静电能就是其自身的自能。
再设想另有一个带电球体,那么,由这两个带电体组成的静电体系的总的静电能应该表示为:总的静电能=带电球1的自能+带电球2的自能+两个带电球间的相互作用能 其中相互作用能的计算是这样:把带电球1设想为源,它将在空间形成一定的电场,而带电球2位于该电场中,那么带电球2所具有的电势能便是二者间的相互作用能;当然,你也可以将球2设想为源,计算球1在带电球2形成电场中的电势能即可,二者只取其一,是不能相加的。
上面讨论的是没有电介质的空间,即真空中的情形,如果有电介质存在,那么静电能又会怎样呢?先考虑简单的情形,空间中充满一种均匀极化的电介质,设其相对介电常数为r ε,而这一空间中只有两个点电荷21,q q ,那么容易得到该体系的静电能为rq q W r21041επε==2211U q U q = (7) ()221121U q U q +=由此可以推广到任意多个点电荷组成的系统的静电能,其形式与(4)是一致,只是在计算i U 是要注意考虑相应的介电常数。
对于稍微复杂的情形,即空间中分布着不同的电介质,我们总可以不顾电介质的存在而得到空间各点的电位移矢量D (r );假设介质在空间的各个点是均匀极化的,但不同点处的介电常数可以不同,则有()()()ε=D r r E r ,这里()εr 是绝对介电常数,且与空间的位置有关,由此得到各点的场强,再由U =-∇E 得到空间各处的电势,于是电势能可以表示为1()()2freeVW U dV ρ=⎰⎰⎰r r (8)上式的电荷密度是针对自由电荷而言的,因为我们在计算电位移矢量时只涉及到自由电荷,积分区域V 可以是自由电荷所在的区域,也可以是全空间,对于后者,只要将不存在自由电荷的空间区域的自由电荷密度当作零就可以了。
可以看出,(8)式与(5)式在形式上是相似的。
三、电场能量与能量密度有了上面的讨论,我们来看看静电场能量的一般表述。
由(8)式,我们有()1()2VW U dV =∇⋅⎰⎰⎰D r11()22U dV U dV ∞∞=∇⋅-⋅∇⎰⎰⎰⎰⎰⎰D D1122S U dV →∞∞=⋅+⋅⎰⎰⎰⎰⎰D dS D E (9)12dV ∞=⋅⎰⎰⎰D E在上面的推导中,我们用到了关于微分算子∇的一些基本定理,而且,我们也用到了在无穷远处电势为零这一边界条件,其中出现的无穷大符号表明全空间的体积。
由(9)式可以看出,静电场的能量密度为12w =⋅D E (10)也就是说,静电场的静电能可以表示为W w dV∞=⎰⎰⎰。
从上面的讨论中可以看出,静电能储存在电场中,虽然我们是从电荷的带电量和电势的角度出发的,但结果显示,能量和电场有着不可分割的联系,这也从另一方面说明电场的物质性及客观上的存在性。
在一些特殊的情形下,(10)式可以写成更为简洁的形式。
例如,对于真空中的静电场,我们有0ε=D E ,于是该式变为221E w o ε=;在均匀的各向同性的介质中,有ε=D E ,故静电能的能量密度为221E w ε=。
我们可以利用静电能得到静电场中的静电力 。
分两种情形讨论: ① 带电体的电量不变 ② 带电体的电势不变。
