圆周角定理
圆周角定理 课件

与圆周角定理有关的线段的计算、角的计算,不仅可 以通过计算弧、圆心角、圆周角的度数来求相关的角、线 段,有时还可以通过三角形相似、解三角形等来计算.
1.如图,直径为 10 的⊙A 经过点 C(0,5)和点
O(0,0),B 是 y 轴右侧⊙A 弧上一点,则
cos∠OBC 的值为
()
A.12
B.
3 2
解:∵ AB= AC , ∴∠ADB=∠CDE. 又∵ BD= BD,∴∠BAD=∠ECD. ∴△ABD∽△CED. ∴ACDD=BEDD, 即63=E5D. ∴ED=2.5 (cm).
3.如图,△ABC 的角平分线 AD 的延长线交它 的外接圆于点 E. (1)证明:△A B E ∽△A DC; (2)若△ABC 的面积 S=1AD·AE, 2 求∠BAC 的大小. 解:(1)证明:由已知条件可得∠BAE=∠CAD. 因为∠AEB与∠ACB是同弧上的圆周角, 所以∠AEB=∠ACD. 故△ABE∽△ADC.
C.3
D.4
5
5
解析:法一:设⊙A与x轴另一个交点为D,
连接CD,如图所示.
因为∠COD=90°,
所以CD为⊙A的直径.
又因为∠CBO 与∠CDO 为圆弧 CO 所对 的圆周角, 所以∠CBO=∠CDO. 又因为 C(0,5), 所以 OC=5. 在 Rt△CDO 中,CD=10,CO=5, 根据勾股定理得 OD= CD2-OC2=5 3. 所以 cos∠OBC=cos∠CDO=OCDD=5103= 23,故选 B.
利用圆周角定理证明等量关系时,主要是分析圆周 角、圆心角、弧、弦之间的等量关系,有时需添加辅助线 构造等弧、等角、等弦的条件.
[例2] 如图,已知BC为半⊙O的直径, AD⊥BC,垂足为D,BF交AD于点E,且AE= BE.
圆周角定理推论

圆周角定理推论
中心角定理:如果一个三角形的三条边的长度都已知,则可以用这三条边到三角形的三个角的长度来求解出这个三角形的三个角的大小,这个定理又称为三角形钝角定理。
也可以称之为圆周角定理,它是圆周角的一种表示法,说明圆周角满足三角形的钝角定理。
即如果已知圆周角的三边长度,则可求出其三个内角。
例如,已知圆周角的三边长度分别为4,4,4,则可求出其三个内角分别为60°,60°,60°。
圆周角定理的公式是:若a、b、c分别为圆周角的三边长度,则有A = arccos((b2 + c2 - a2)/ 2bc),B = arccos((a2 + c2 - b2)/ 2bc),C = arccos((a2 + b2 - c2)/ 2bc)。
其中A,B,C分别为圆周角的三角形的三个内角。
圆周角定理及其证明

圆周角定理及其证明圆周角定理是几何中的一个重要定理,它描述了一个圆的圆周角与其对应的弧度之间的关系。
这个定理在解决与圆相关的问题时具有重要的应用价值。
下面将对圆周角定理及其证明进行详细介绍。
我们需要明确什么是圆周角。
圆周角是指以圆心为顶点的角,其两条边分别为相切于圆的两条弦。
在圆周角中,我们可以观察到一个有趣的现象:无论弦的长度如何变化,圆周角的大小始终保持不变。
这个现象被称为圆周角的度量唯一性。
为了形式化地描述圆周角定理,我们引入以下定义:当圆周角的两条弦分别与圆的直径相交时,这个圆周角被称为直径角。
根据圆周角的度量唯一性,我们可以得出结论:直径角恒等于180度或π弧度。
接下来,我们将证明圆周角定理。
证明:设圆的半径为r,圆周角对应的弧长为l,直径角对应的弧长为L。
根据圆的性质,我们知道圆的周长C等于2πr。
由于直径角等于半圆,所以L等于半圆的弧长,即L等于πr。
根据圆周角的度量唯一性,我们可以得出以下等式:l / C = L / 2πr将C和L的值代入上述等式,我们得到:l / 2πr = πr / 2πr经过简化后,我们得到:l / 2r = r / 2r进一步简化,我们得到:l = r由此可见,圆周角对应的弧长等于圆的半径。
这个结论可以推广到任意圆周角,无论弦的长度如何变化,圆周角的度量始终等于圆的半径。
通过上述证明,我们可以得出圆周角定理的结论:圆周角的度量等于圆的半径。
这个定理在解决与圆相关的问题时非常有用,可以帮助我们计算圆周角的度量,从而解决各种几何问题。
总结起来,圆周角定理描述了圆周角与其对应的弧度之间的关系。
通过证明,我们可以得出结论:圆周角的度量等于圆的半径。
这个定理在几何学中有重要的应用价值,可以帮助我们解决与圆相关的各种问题。
在实际应用中,我们可以根据圆周角定理来计算圆周角的度量,从而得到所需的几何信息。
圆周角定理和圆内四边形的性质典例精析
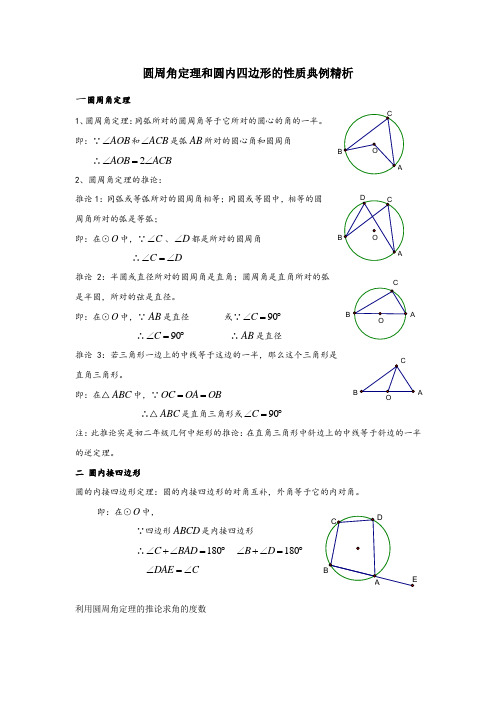
圆周角定理和圆内四边形的性质典例精析一圆周角定理1、圆周角定理:同弧所对的圆周角等于它所对的圆心的角的一半。
即:∵AOB ∠和ACB ∠是弧AB 所对的圆心角和圆周角 ∴2AOB ACB ∠=∠2、圆周角定理的推论:推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧;即:在⊙O 中,∵C ∠、D ∠都是所对的圆周角 ∴C D ∠=∠推论2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径。
即:在⊙O 中,∵AB 是直径 或∵90C ∠=︒ ∴90C ∠=︒ ∴AB 是直径推论3:若三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
即:在△ABC 中,∵OC OA OB ==∴△ABC 是直角三角形或90C ∠=︒注:此推论实是初二年级几何中矩形的推论:在直角三角形中斜边上的中线等于斜边的一半的逆定理。
二 圆内接四边形圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
即:在⊙O 中,∵四边形ABCD 是内接四边形∴180C BAD ∠+∠=︒ 180B D ∠+∠=︒ DAE C ∠=∠利用圆周角定理的推论求角的度数BABA O例1 (2016·四川眉山)如图,A、D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=()A.64° B.58° C.72° D.55°【分析】先根据圆周角定理求出∠B及∠BAC的度数,再由等腰三角形的性质求出∠OAB的度数,进而可得出结论.例2 (2016海南)如图,AB是⊙O的直径,AC、BC是⊙O的弦,直径DE⊥AC于点P.若点D在优弧上,AB=8,BC=3,则DP=.【考点】圆周角定理;垂径定理.【分析】解:由AB和DE是⊙O的直径,可推出OA=OB=OD=4,∠C=90°,又有DE⊥AC,得到OP∥BC,于是有△AOP∽△ABC,根据相似三角形的性质即可得到结论.例3(2016·山东省滨州市)如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD 分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是()A.②④⑤⑥B.①③⑤⑥C.②③④⑥D.①③④⑤【考点】圆的综合题.【分析】①由直径所对圆周角是直角,②由于∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角角,③由平行线得到∠OCB=∠DBC,再由圆的性质得到结论判断出∠OBC=∠DBC;④用半径垂直于不是直径的弦,必平分弦;⑤用三角形的中位线得到结论;⑥得不到△CEF和△BED中对应相等的边,所以不一定全等.利用圆周角定理的推论进行推理论证例4 (2015•烟台)如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且=.(1)试判断△ABC的形状,并说明理由.(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.例5 如图所示,BC是⊙O的直径,AD⊥BC,垂足为D,AB=AF,BF和AD相交于点E;求证:BE=AE.分析:由BC是⊙O的直径,根据直径所对的圆周角是直角,可得∠BAC=90°,又由AD⊥BC,即可得∠BAD=∠C,又由AB=AF,根据圆周角定理,易得∠ABF=∠F=∠C,则可证得∠ABF=∠BAD,继而证得结论.利用圆内接四边形的性质求度数例6(2015湖南邵阳第7题3分)如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC 的大小是()利用圆内接四边形的性质进行推理证明 例 7 (2015南京)(8分)如图,四边形ABCD 是⊙O 的内接四边形,BC 的延长线与AD 的延长线交于点E ,且DC=DE . (1) 求证:∠A=∠AEB .(2) 连接OE ,交CD 于点F ,OE ⊥ CD .求证:△ABE 是等边三角形.圆周角定理与相似三角形的综合例 8 (2016·天津市南开区·一模)如图,AB 是⊙O 的直径,C ,P 是上两点,AB=13,AC=5.(1)如图(1),若点P 是的中点,求PA 的长; (2)如图(2),若点P 是的中点,求PA 的长.(第26题)例 9 (肇庆市2012)如图7,在△ABC 中,AB =AC ,以AB 为直径的⊙O 交AC 于点E ,交BC 于点D ,连结BE 、AD 交于点P . 求证: (1)D 是BC 的中点; (2)△BEC ∽△ADC ; (3)AB ⋅ CE=2DP ⋅AD .圆内接四边形性质的综合应用例10 (2009•内江)如图,四边形ABCD 内接于圆,对角线AC 与BD 相交于点E ,F 在AC 上,AB =AD ,∠BFC =∠BAD =2∠DFC =β.求证:(1)∠ABD =90°-β (2)CD ⊥DF ; (3)BC=2CD .圆周角定理与函数的综合例 1 1 如图,AB 是圆O 的直径,CD 是弦,CD ⊥AB 于点E ,(1)求证:△ACE ∽△CBE ;(2)若AB=4,设OE=x (0<x <2),CE=y ,请求出y 关于x 的函数解析式图7。
圆周角定理的三种证明方法

圆周角定理的三种证明方法
圆周角定理是几何中著名的定理,亦即“每个三角形的外接圆的内切圆与它的最大外接圆所成的圆周角相等”。
此定理由古希腊数学家艾西法 (Euclid) 于其《几何原本》第六章首次提出数千年前,随着数学的发展,有许多其他的证明方法也被提出:
1、几何距离证明法:两个圆的圆心距离为2R的话,就可以让它们的相切线同时证明最大外接圆的圆周角和最小内切圆的圆周角相等。
可以用两等腰直角三角形向根据勾股定理来演算出,两个圆周角的圆心角度都是相等的。
2、数学归纳法:也就是艾西法于其《几何原本》所作的证明,即归纳法可以证明不论外接圆的半径有什么样的大小它们所成的圆周角都是相等的。
3、几何投影证明法:几何投影证明法通过找到三角形它的内切圆和最大外接圆,把两个圆投影到平面上,将圆心连线作为投影线,使投影线在它们之间形成一条射线,然后可以推出它们所成的圆周角相等。
圆周角定理

∵∠1=∠2,∴ = ,
∴BF=CG, = ,
∴∠FBD=∠GCE.
又 ∵BD=CE,∴△BFD≌△CGE,
∴∠F=∠G,∴ = ,
∴AB=AC.
题型一
题型二
题型三
题型三
易错辨析
易错点:误认为同弦或等弦所对圆周角相等而致错
【例3】 如图,若∠BAD=75°,则∠BCD=
分成两条弧:优弧和劣弧,若圆周角的顶点同在优弧上或同在劣弧
上,同弦或等弦所对的圆周角相等;若一个圆周角的顶点在优弧上,
另一个圆周角的顶点在劣弧上,则同弦或等弦所对的圆周角不相等,
它们互补(如本题).
(2)在圆周角定理的证明中,运用了数学中分类讨论和化归的思想
以及归纳的证明方法.这个定理是从特殊情况入手研究的,首先研
究当角的一边过圆心时,得到圆周角与同弧所对的圆心角的关系,
然后研究当角的一边不经过圆心时,圆周角与同弧所对的圆心角之
间的关系.当角的一边不经过圆心时,又有两种情况:一是圆心在圆
周角内部;二是圆心在圆周角外部.经过这样不同情况的讨论,最后
第二讲
直线与圆的位置关系
一
圆周角定理
1.了解圆心角定理,并能应用定理解决问题.
2.理解圆周角定理及其两个推论,并能应用定理解决有关问题.
圆周角定理的理解
剖析:(1)应用圆周角定理时,要注意的问题如下:
圆周角定理推论1中,同圆或等圆中,相等的圆周角所对的弧相等.
这一定理成立的前提是同圆或等圆,否则不成立.
角形,从而得到成比例线段,再列方程求得线段长.
题型一
题型二
题型三
【变式训练 1】 如图,已知△ABC 内接于☉O, = , 点是
圆周角定理 课件

要点三 直径上的圆周角 例 3 如图所示,已知 AB 为⊙O 的直径,AC
为弦,OD∥BC,交 AC 于 D,BC=4 cm. (1)试判断 OD 与 AC 的位置关系; (2)求 OD 的长; (3)若 2sin A-1=0,求⊙O 的直径.
解 (1)OD⊥AC.理由如下: ∵AB 为⊙O 的直径,∴∠ACB=90°. ∵OD∥BC,∴∠ADO=∠ACB=90°,∴OD⊥AC. (2)∵△AOD∽△ABC,∴OBCD=AAOB=12, ∴OD=12BC=2(cm). (3)∵2sin A-1=0,∴sin A=12.又∵sin A=BACB, ∴AB=2BC=8 cm,即⊙O 的直径为 8 cm.
圆周角定理
1.圆周角定理
文字语言
圆上一条弧所对的圆周角等于它所对的圆心
角的_一__半___
图形语言
符号语言 作用
在⊙O 中,B︵C所对的圆周角和圆心角分别是
∠BAC,∠BOC,则有∠BAC=_12_∠__B_O_C__
确定பைடு நூலகம்中两个角的大小关系
2.圆心角定理
文字语言
圆心角的度数等于它_所__对_弧___ 的度数
规律方法 此题充分利用了“直径所对的圆 周角是直角”这一特征,并在此基础上对前 面所学知识进行适当的综合.
1.圆周角定理揭示了圆周角与圆心角的关系,把角和 弧两种不同类型的图形联系起来.在几何证明的过程 中,圆周角定理为我们解决角和弧之间的问题提供 了一种新方法.
2.圆心角的度数等于它所对的弧的度数,它与圆的半 径无关,也就是说在大小不等的两个圆中,相同度 数的圆心角,它们所对的弧的度数相等;反过来, 弧的度数相等,它们所对的圆心角的度数也相等.
要点一 圆周角定理及其推论 例 1 在半径为 5 cm 的圆内有长为 5 3cm 的弦 AB,求此
圆周角定理 课件

3.关于圆周角定理推论的理解
(1)在推论1中,注意:“同弧或等弧”改为“同弦或等弦” 的话结论就不成立了,因为一条弦所对的圆周角有两种可 能,在一般情况下是不相等的.
(2)圆心角的度数和它所对的弧的度数相等,但并不是 “圆心角等于它所对的弧”.
(3)“相等的圆周角所对的弧也相等”的前提条件是“在 同圆或等圆中”.
【示例2】 如图,D,E分别为△ABC边AB,AC 的中点,直 线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明: (1)CD=BC; (2)△BCD∽△GBD.
证明 (1)因为D,E分别为AB,AC的中点,所以DE∥BC.又 已知CF∥AB,故四边形BCFD是平行四边形,所以CF=BD = AD. 而 CF∥AD , 连 接 AF , 所 以 ADCF 是 平 行 四 边 形 , 故 CD=AF.
证明 连结 CE、CF、EF,∵BC 为⊙O 的直径,∴∠BFC =90°,∠BEC=90°.又∵∠ACB=90°,∴∠BCE=∠A. 又∵∠BFE=∠BCE,∴∠BFE=∠A.又∵∠EBF=∠DBA, ∴△BEF∽△BDA.∴EBFE=ABDD. ∵∠BFC=∠BCA,∠CBD=∠CBD, ∴△CBF∽△DBC.∴CBCF=CBDD. 又∵AD=CD,∴EBFE=CBCF,∴BBCE=CEFF.
(4)在同圆或等圆中,由弦相等⇒弧相等时,这里的弧要求 同是优弧或同是劣弧,一般选劣弧.
题型一 圆中相关角度数的求解
【例 1】 在半径为 5 cm 的圆内有长为 5 3 cm 的弦 AB,求此弦
所对的圆周角.
[思维启迪] 对于弦所对的圆周角要考虑全面.
解 如图所示,过 O 点作 OD⊥AB 于点 D.因为 OD⊥AB,OD
反思感悟 弦所对的圆周角有两个,易丢掉120°导致错误,另外求圆周角时易应用到解三角形的知识.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
2
练习
求证:如果三角形一边上的中线等于这边的一半,那么这个三 角形是直角三角形。(提示:作出以这条边为直径的圆。)
已知:△ABC 中,CO为AB边上的中线,且CO= 1 AB
2 求证: △ABC 为直角三角形。
C
证明: 以AB为直径作⊙O
∵AO=BO,
CO=
1 2
AB
∴AO=BO=CO
A
·
B
O
∴点C在⊙O上
圆周角定理
足球场上有句顺口溜:”冲向球门跑,越近就越好;
歪着球门跑,射点要选好。”可见踢足球是有“学问”的, 以下我们将来学些几何知识来分析类似足球射门的问题。
请说说我们是如何给圆心角下定义的,试回答?
顶点在圆心,并且两边都和圆相交
的角叫圆心角。
考考你:你能仿照圆心角的定义, 给下图中象∠ACB 这样的角下个定义吗?
分线交⊙O于D,求BC、AD、BD的长。
解:∵AB是直径
∴ ∠ACB= ∠ADB=90°
C
在Rt△ABC中
BC AB 2 AC 2 102 62 8 A
O
பைடு நூலகம்
B
∵CD平分∠ACB
∴ ∠ACD= ∠BCD
D
∴AD=BD
又在Rt△ABD中,AD2+BD2=AB2
AD BD 2 AB 2 10 5 2(cm)
C2
推论
C1
半圆(或直径)所对的圆周
C3
角是直角; A 90°的圆周角所对的弦是直径。
·O
B
如图,已知△ABC内接于⊙O, , 的度数分别为80°和110°,则△ABC的三 个内角度数分别是多少度?
答: △ABC的三内角分别是 ∠A=55 °,∠B=85 ° ,∠C=40 °
例1 在绿茵场上,足球队员带球进攻,总是尽 力向球门AB冲近(如图1),你说为什么
(1)在圆周角的一条边上;
∵OA=OC,
A
O·
B
C
∴∠A=∠C. 又∠BOC=∠A+∠C
∴∠BOC=2∠A 即 A 1 BOC
2
(2)在圆周角的内部, 圆心O在∠BAC的内部,作直径AD,
利用(1)的结果,有
BAD 1 BOD 2
DAC 1 DOC 2
BAD DAC 1 (BOD DOC) 2
顶点在圆周上,并且两边都和圆相交的角
叫做圆周角。
探索:判断下列各图中,哪些是圆周角,为什么?
图1
图2
图3
图4
图5
图7
图8
图6 图9
重点观察下面三个图形中,圆心与圆周角的位置关系?
图1
图2
图3
在以上三个图形中,哪 个图形是特殊的,其它 图形可以转化为特殊
图形吗?
圆心角和圆周角都是和圆有关的角,圆心角的度数等于它所对弧的 度数。
解 :设球员在位于C处接到球,
他带球尽力向球门冲近到D, 此时不仅距离球门近了,射 门更为有力,而且对球门AB 的张角也扩大了,球更容易射 中.可以证明如下:
延长CD到E,则∠ADE>∠ACE,∠BDE>∠BCE 所以∠ADE+∠BDE>∠ACE+∠BCE 即∠ADB>∠ACB 这样,更容易射门得分
练习
如图,你能设法确定一个圆形纸片的圆心吗?你有多少
种方法?与同学交流一下。
方法三
方法一
O
A
B
C
O
方法二
A D
·
B
方法四
O
在同圆或等圆中,如果两个圆周角相等, 它们所对弧一定相等吗?为什么?
在同圆或等圆中,如果两个圆周角相等,它 们所对的弧一定相等。
例题
例2 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平
BAC 1 BOC
2
B
A
O·
C D
(3)在圆周角的外部,
圆心O在∠BAC的外部,作直径AD,
利用(1)的结果,有
BAD 1 BOD
2
DAC 1 DOC
2
DAC DAB 1 (DOC DOB)
A
2
BAC 1 BOC 2
O·
D
C B
定理
定理
在同圆或等圆中,同弧或等弧所对的圆周角 相等,都等于这条弧所对的圆心角的一半。
又∵AB为直径
∴∠ACB=
1 2
×180°=
90°
∴ △ABC 为直角三角形。
小结与作业 1、本节课我们学习了哪些知识? 2、圆周角定理及其推论的用途你 都知道了吗?
如果圆心角和圆周角所对的弧相同,那么 1、圆周角的度数与它所对弧的度数有什么关系呢? 2、圆周角与圆心角之间又有什么关系呢?
同学们可以大胆地说出你的猜想?
同弧所对圆周角与圆心角的关系
为了进一步探究上面的发现,如图在⊙O任取一个圆周角
∠BAC,将圆对折,使折痕经过圆心O和∠BAC的顶点A。由
于点A的位置的取法可能不同,这时折痕可能会:
