统计学原理计算题
统计学计算题
统计学原理复习1（计算题）1．某单位40名职工业务考核成绩分别为:68 89 88 84 86 87 75 73 72 6875 82 97 58 81 54 79 76 95 7671 60 90 65 76 72 76 85 89 9264 57 83 81 78 77 72 61 70 81单位规定:60分以下为不及格，60─70分为及格，70─80分为中,80─90分为良,90─100分为优.要求：（1)将参加考试的职工按考核成绩分为不及格、及格、中、良、优五组并编制一张考核成绩次数分配表;（2）指出分组标志及类型及采用的分组方法；(3）计算本单位职工业务考核平均成绩（4）分析本单位职工业务考核情况.解：(1）（2）分组标志为”成绩”，其类型为"数量标志";分组方法为：变量分组中的开放组距式分组,组限表示方法是重叠组限；（3)本单位职工业务考核平均成绩（4）本单位的职工考核成绩的分布呈两头小，中间大的”正态分布”的形态,说明大多数职工对业务知识的掌握达到了该单位的要求。
2．2004年某月份甲、乙两农贸市场农产品价格和成交量、成交额资料如下：试问哪一个市场农产品的平均价格较高?并说明原因.解：解：先分别计算两个市场的平均价格如下：甲市场平均价格()375.145.5/==∑∑=x m m X（元/斤） 乙市场平均价格325.143.5==∑∑=f xf X （元/斤）说明：两个市场销售单价是相同的，销售总量也是相同的，影响到两个市场平均价格高低不同的原因就在于各种价格的农产品在两个市场的成交量不同.3．某车间有甲、乙两个生产组，甲组平均每个工人的日产量为36件，标准差为9.6件;乙组工人日产量资料如下：要求：⑴计算乙组平均每个工人的日产量和标准差;⑵比较甲、乙两生产小组哪个组的日产量更有代表性？ 解：（1）50.291001345343538251515=⨯+⨯+⨯+⨯==∑∑fxf X （件）986.8)(2=-=∑∑ff X x σ（件） （2）利用标准差系数进行判断:267.0366.9===XV σ甲305.05.29986.8===X V σ乙因为0。
统计学原理试题及答案
统计学原理试题（6）一、单项选择题：（每小题1分,共20分)1。
设某地区有200家独立核算的工业企业,要研究这些企业的产品生产情况，总体是( )。
A.每一家工业企业 B。
200家工业企业C。
每一件产品 D.200家工业企业的全部工业产品2.有600家公司每位职工的工资资料，如果要调查这些公司的工资水平情况,则总体单位是（ )。
A。
600家公司的全部职工 B。
600家公司的每一位职工C.600家公司所有职工的全部工资D.600家公司每个职工的工资3.一个统计总体（）。
A。
只能有一个指标 B。
可以有多个指标C.只能有一个标志D.可以有多个标志4.以产品等级来反映某种产品的质量，则该产品等级是（ ).A.数量标志 B。
品质标志 C。
数量指标 D.质量指标5.在调查设计时,学校作为总体，每个班作为总体单位，各班学生人数是（ )。
A.变量值B.变量C.指标值 D。
指标6。
年龄是（）。
A。
变量值 B。
连续型变量 C.离散型变量D. 连续型变量,但在实际应用中常按离散型处理7.人口普查规定统一的标准时间是为了（）.A。
登记的方便 B。
避免登记的重复与遗漏C.确定调查的范围D.确定调查的单位8。
以下哪种调查的报告单位与调查单位是一致的( ）。
A.职工调查B.工业普查C.工业设备调查D.未安装设备调查9.通过调查大庆、胜利、辽河等油田，了解我国石油生产的基本情况.这种调查方式是（）.A.典型调查 B。
抽样调查 C.重点调查 D.普查10.某市进行工业企业生产设备普查，要求在10月1日至15日全部调查完毕，则这一时间规定是（ )。
A。
调查时间 B.登记期限 C.调查期限 D.标准时间11。
统计分组的关键问题是( ）。
A.确定分组标志和划分各组界限B.确定组距和组中值C.确定组距和组数D.确定全距和组距12。
某连续变量数列，其最小组为开口组,组限为400，又知其相邻组的组中值为500，则下开口组的组中值为（）。
A.200B.300 C。
《统计学原理》计算题
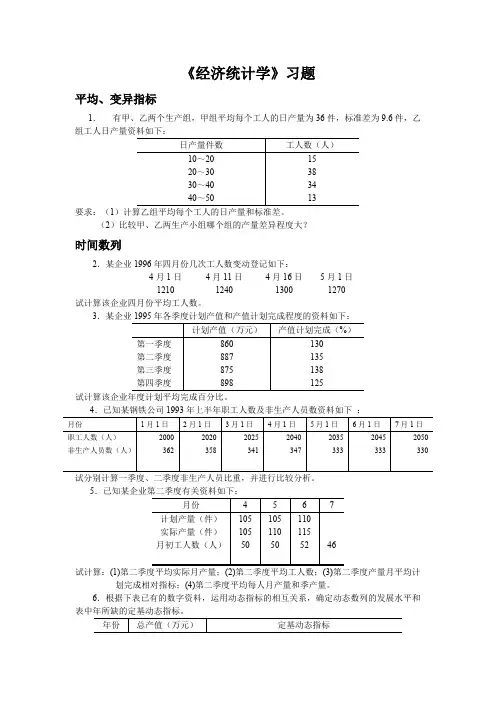
《经济统计学》习题平均、变异指标1．有甲、乙两个生产组，甲组平均每个工人的日产量为36件，标准差为9.6件，乙组工人日产量资料如下：日产量件数工人数（人）10～201520～303830～403440～5013要求：（1）计算乙组平均每个工人的日产量和标准差。
（2）比较甲、乙两生产小组哪个组的产量差异程度大？时间数列2．某企业1996年四月份几次工人数变动登记如下：4月1日4月11日4月16日5月1日1210124013001270试计算该企业四月份平均工人数。
3．某企业1995年各季度计划产值和产值计划完成程度的资料如下：计划产值（万元）产值计划完成（%）第一季度860130第二季度887135第三季度875138第四季度898125试计算该企业年度计划平均完成百分比。
4．已知某钢铁公司1993年上半年职工人数及非生产人员数资料如下：月份1月1日2月1日3月1日4月1日5月1日6月1日7月1日职工人数（人）2000202020252040203520452050非生产人员数（人）362358341347333333330试分别计算一季度、二季度非生产人员比重，并进行比较分析。
5．已知某企业第二季度有关资料如下：月份4567计划产量（件）105105110实际产量（件）105110115月初工人数（人）50505246试计算：(1)第二季度平均实际月产量；(2)第二季度平均工人数；(3)第二季度产量月平均计划完成相对指标；(4)第二季度平均每人月产量和季产量。
6．根据下表已有的数字资料，运用动态指标的相互关系，确定动态数列的发展水平和表中年所缺的定基动态指标。
年份总产值（万元）定基动态指标增长量(万元)发展速度(%)增长速度(%) 1986741－100－1987591988115.6198923.91990131.719912981992149.9199355.219944611995167.27．运用时间数列指标的相互关系，根据已知资料，确定某纺织厂棉布生产的各年发展水平、逐期增长量、环比发展速度、环比增长速度和增长１％的绝对值指标。
[统计学原理计算题答案]统计学计算题及答案
![[统计学原理计算题答案]统计学计算题及答案](https://img.taocdn.com/s3/m/b5b9d1f5c850ad02de8041dd.png)
[统计学原理计算题答案]统计学计算题及答案【试卷考卷】统计学计算题及答案篇(一):统计学试题及答案一、填空题(每空1分，共10分)1.从标志与统计指标的对应关系来看，标志通常与( )相同。
2.某连续变量数列，其首组为开口组，上限为80，又知其邻组的组中值为95，则首组的组中值为( )。
3.国民收入中消费额和积累额的比例为1：0.4，这是( )相对指标。
4.在+A的公式中，A称为( )。
5.峰度是指次数分布曲线项峰的( )，是次数分布的一个重要特征。
6.用水平法求平均发展速度本质上是求( )平均数。
7.按习惯做法，采用加权调和平均形式编制的物量指标指数，其计算公式实际上是( )综合指数公式的变形。
8.对一个确定的总体，抽选的样本可能个数与( )和( )有关。
9.用来反映回归直线代表性大小和因变量估计值准确程度的指标称( )。
二、是非题(每小题1分，共10分)1.统计史上，将国势学派和图表学派统称为社会经济统计学派。
2.统计总体与总体单位在任何条件下都存在变换关系统计学原理试题及答案统计学原理试题及答案。
3.学生按身高分组，适宜采用等距分组。
4.根据组距数列计算求得的算术平均数是一个近似值。
5.基尼系数的基本公式可转化为2(S1+S2+S3)。
6.对连续时点数列求序时平均数，应采用加权算术平均方法。
7.分段平均法的数学依据是Σ(Y-YC)2=最小值。
8.平均数、指数都有静态与动态之分。
9.在不重复抽样下，从总体N中抽取容量为n的样本，则所有可能的样本个数为Nn个10.根据每对x和y的等级计算结果ΣD2=0，说明x与y 之间存在完全正相关。
三、单项选择题(每小题2分，共10分)1.在综合统计指标分析的基础上，对社会总体的数量特征作出归纳、推断和预测的方法是A.大量观察法B.统计分组法C.综合指标法D.模型推断法2.对同一总体选择两个或两个以上的标志分别进行简单分组，形成A.复合分组B.层叠分组C.平行分组体系D.复合分组体系3.交替标志方差的最大值为A.1B.0.5C.0.25D.04.如果采用三项移动平均修匀时间数列，那么所得修匀数列比原数列首尾各少A.一项数值B.二项数值C.三项数值D.四项数值5.可变权数是指在一个指数数列中，各个指数的A.同度量因素是变动的B.基期是变动的C.指数化因数是变动的D.时期是变动的四、多项选择题(每小题2分，共10分)1.反映以经济指标为中心的三位一体的指标总体系包括A.社会统计指标体系B.专题统计指标体系C.基层统计指标体系D.经济统计指标体系E.科技统计指标体系2.典型调查A.是一次性调查B.是专门组织的调查C.是一种深入细致的调查D.调查单位是有意识地选取的E.可用采访法取得资料3.下列指标中属于总量指标的有A.月末商品库存额B.劳动生产率C.历年产值增加额D.年末固定资金额E.某市人口净增加数4.重复抽样的特点是A.各次抽选互不影响B.各次抽选相互影响C.每次抽选时，总体单位数逐渐减少D.每次抽选时，总体单位数始终不变E.各单位被抽中的机会在各次抽选中相等5.下列关系中，相关系数小于0的现象有A.产品产量与耗电量的关系B.单位成本与产品产量的关系C.商品价格与销售量的关系D.纳税额与收入的关系E.商品流通费用率与商品销售额的关系五、计算题(每小题10分，共60分)要求：(1)写出必要的计算公式和计算过程，否则，酌情扣分。
统计学原理计算题及参考答案
1、某生产车间30名工人日加工零件数（件）如下： 30 26 42 41 36 44 40 37 37 25 45 29 43 31 36 36 49 3447 33 43 38 42 32 34 38 46 43 39 35 要求：（1）根据以上资料分成如下几组：25—30，30—35，35—40，40—45，45—50，计算各组的频数和频率，编制次数分布表；（2） 根据整理表计算工人平均日产零件数。
（20分）则工人平均劳动生产率为：17.38301145===∑∑fxf x（2）当产量为10000件时，预测单位成本为多少元？（15分）xbx a y n x b n y a x x n y x xy n b c 5.2808010703125.232105.26151441502520250512503210128353)(222-=+==+=⨯+=-=-=-=--=-⨯⨯-⨯=--=∑∑∑∑∑∑∑因为，5.2-=b ，所以产量每增加1000件时，即x 增加1单位时，单位成本的平均变动是：平均减少2.5元 （2）当产量为10000件时，即10=x 时，单位成本为55105.280=⨯-=c y 元>课程的测试,甲班平均成绩为81分,标准差为9.5分;乙班的成绩分组资料如下: 计算乙班学生的平均成绩,并比较甲.乙两班哪个班的平均成绩更有代表性? 解：乙班学生的平均成绩∑∑=fxf x ，所需的计算数据见下表：75554125===∑∑fxf x （比较甲.乙两班哪个班的平均成绩更有代表性，要用变异系数σν的大小比较。
）甲班%65.207549.1549.152405513200)(2======-=∑∑xff x x σνσσ%73.11815.9===xσνσ 从计算结果知道，甲班的变异系数σν小，所以甲班的平均成绩更有代表性。
计算(1)产品产量总指数及由于产量增长而增加的总成本.(2)总成本指数及总成本增减绝对额. 解；（1）产品产量总指数为： %42.1112102342106351120605010060%10550%102100%12000==++=++⨯+⨯+⨯=∑∑qp qkp 由于产量增长而增加的总成本：∑∑=-=-242102340000qp q kp（2）总成本指数为：%62.10721022660501006046120011==++++=∑∑qp qp总成本增减绝对额：∑∑=-=-162102260011qp q p. 解：商品流转次数c=商品销售额a/库存额bba c =商品销售额构成的是时期数列，所以67.23837163276240200==++==∑na a 库存额b 构成的是间隔相等的时点数列，所以33.533160327545552453224321==+++=+++=b b b b b 第二季度平均每月商品流转次数475.433.5367.238===ba c 第二季度商品流转次数3*4.475=13.4251. 2008年某月份甲、乙两市场某商品价格和销售量、销售额资料如下：试分别计算该商品在两个市场上的平均价格. 解：甲市场的平均价格为：04.123270033220027001507001080007350011009007001100137900120700105==++=++⨯+⨯+⨯==∑∑fxf x乙市场的平均价格为74.1172700317900700800120031790013795900120960001051260009590096000126000==++=++++==∑∑xM M x。
统计学原理计算题例子及答案
例：根据下表资料计算销售额的变动并对其进行分析。
某商店三种商品的价格和销售量资料解：（1）销售额总变动元）增减销售额＝＝销售额指数＝(27150156000183150%4.1171560001831500.6100000.820000.1080005.6105000.925005.1088000011011=-=-=⨯+⨯+⨯⨯+⨯+⨯=∑∑∑∑p q p q pq p q（2）因素分析 ①销售量变动的影响∑∑∑∑=-==⨯+⨯+⨯=（元）＝—＝影响增减销售额销售量指数＝150001560001710006.1091560001710001560000.6105000.825000.1088000001001p q p q pq p q②商品价格变动的影响∑∑∑∑=-=-元）影响增减销售额＝＝＝价格指数＝(12150171000183150%1.1071710001831500111111p q p q p q p q③综合影响271501215015000%4.117%1.107%6.109=+=⨯由于销售量综合提高9.6%，同时由于价格综合上涨7.1%，二者共同作用，使销售额增长17.4%。
从绝对量看，销售量提高使销售额增加15000元，由于价格上涨使销售额增加12150元，从而使总销售额增加27150元。
例：以某月抽样调查的1000户农民家庭收入的分组资料计算平均数/标准差，见下表。
由表中资料可以计算：()元075.3541000354075===∑∑fxf x()()元126451000159902752==-=∑∑ffx x δ结果表明，该月1000户农民家庭人均纯收入为354.075元，人均纯收入标准差为126.45元。
例：对某型号的电子元件进行耐用性能检查，抽查的资料分组列表如下，要求以95%（t=1.96）的置信水平估计该批电子元件的平均耐用时数。
1.计算抽样平均数和样本标准差小时5.1055100105550_===∑∑fxf x 小时＝91.5112_=-⎪⎭⎫⎝⎛-∑∑i i i f f x x s()小时191.5==nsx σ 2.根据给定的置信水平95%（t=1.96），计算总体平均数的极限误差：()17.10191.596.1=⨯=•=∆x t σ因此小时上限小时下限7.10652.105.10553.10452.105.1055__=+=∆+==-=∆-=x x x x即可以以概率95 %的保证程度，估计该批电子元件的耐用时数在1045.3～1065.7之间。
统计学原理试题库(全)
统计学原理试题库（全）第一章一、单项选择题1、统计有三种涵义，其基础是（A）。
A、统计活动B、统计方法C、统计学D、统计资料2、一个统计总体（ C ）。
A、只能有一个指标B、只能有一个标志C、可以有多个指标D、可以有多个标志3、下列变量中，（D ）属于离散变量。
A、一个笔筒的直径B、一袋米的重量C、一个同学的身高D、一个县的人数4、全班同学统计学考试成绩分别为66分、76分和86分，这三个数字是（B ）。
A、标志B、标志值C、指标D、变量5、下列属于品质标志的是（D ）。
A、工人工资B、工人身高C、工人体重D、工人性别6、要了解某汽车公司的情况，该公司的产量和利润是（C ）。
A、连续变量B、离散变量C、前者是离散变量，后者是连续变量D、后者是离散变量，前者是连续变量7、劳动生产率是（C ）。
A、流量指标B、动态指标C、质量指标D、强度指标8、数理统计学的奠基人是（ C ）。
A、马克思B、威廉·配第C、凯特勒D、恩格尔9、指标是说明总体特征的，标志是说明单位特征的，所以（C ）。
A、指标和标志都是可以用数值表示的B、指标和标志之间没关系C、指标和标志之间在一定条件下可以相互变换D、指标和标志之间的关系是固定不变的10、统计研究的数量必须是（B ）。
A、抽象的量B、具体的量C、连续不断的量D、可直接相加的量11、构成统计总体的必要条件是（ D ）。
A、差异性B、综合性C、社会性D、同质性二、多项选择题1、对某市工业企业进行调查，则( BCE )。
A、该市工业企业总数是总体B、该市工业企业是总体C、该市工业企业总产值是指标D、该市工业企业总产值是数量标志E、每个工业企业总产值是数量标志2、某企业是总体单位，则下列属于数量标志的有( BCDE )。
A、所有制B、职工人数C、职工月平均工资D、年工资总额E、产品合格率3、下列指标哪些是质量指标（CDE）。
A、新产品数量B、高级职称人数C、考试及格率D、工人劳动生产率E、平均亩产量4、下列属于连续变量的有（ACE）。
统计学原理计算题例子及答案
例：根据下表资料计算销售额的变动并对其进行分析。
某商店三种商品的价格和销售量资料解：（1）销售额总变动元）增减销售额＝＝销售额指数＝(27150156000183150%4.1171560001831500.6100000.820000.1080005.6105000.925005.1088000011011=-=-=⨯+⨯+⨯⨯+⨯+⨯=∑∑∑∑p q p q pq p q（2）因素分析 ①销售量变动的影响∑∑∑∑=-==⨯+⨯+⨯=（元）＝—＝影响增减销售额销售量指数＝150001560001710006.1091560001710001560000.6105000.825000.1088000001001p q p q pq p q②商品价格变动的影响∑∑∑∑=-=-元）影响增减销售额＝＝＝价格指数＝(12150171000183150%1.1071710001831500111111p q p q p q p q③综合影响271501215015000%4.117%1.107%6.109=+=⨯由于销售量综合提高9.6%，同时由于价格综合上涨7.1%，二者共同作用，使销售额增长17.4%。
从绝对量看，销售量提高使销售额增加15000元，由于价格上涨使销售额增加12150元，从而使总销售额增加27150元。
例：以某月抽样调查的1000户农民家庭收入的分组资料计算平均数/标准差，见下表。
由表中资料可以计算：()元075.3541000354075===∑∑fxf x()()元126451000159902752==-=∑∑ffx x δ 结果表明，该月1000户农民家庭人均纯收入为354.075元，人均纯收入标准差为126.45元。
例：对某型号的电子元件进行耐用性能检查，抽查的资料分组列表如下，要求以95%（t=1.96）的置信水平估计该批电子元件的平均耐用时数。
1.计算抽样平均数和样本标准差小时5.1055100105550_===∑∑fxf x 小时＝91.5112_=-⎪⎭⎫⎝⎛-∑∑i i i f f x x s()小时191.5==nsx σ 2.根据给定的置信水平95%（t=1.96），计算总体平均数的极限误差：()17.10191.596.1=⨯=∙=∆x t σ因此小时上限小时下限7.10652.105.10553.10452.105.1055__=+=∆+==-=∆-=x x x x即可以以概率95 %的保证程度，估计该批电子元件的耐用时数在1045.3～1065.7之间。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、时间序列:1.某公司某年9月末有职工250人,10月上旬的人数变动情况就是:10月4日新招聘12名大学生上岗,6日有4名老职工退休离岗,8日有3名青年工人应征入伍,同日又有3名职工辞职离 岗,9日招聘7名营销人员上岗。
试计算该公司10月上旬的平均在岗人数。
解:1.2562122322591252225822623250=++++⨯+⨯+⨯+⨯+⨯==∑∑faf a要求:(1)具体说明这个时间序列属于哪一种时间序列。
(2)分别计算该银行2001年第一季度、第二季度与上半年的平均现金库存额。
解:2.(1)这就是个等间隔的时点序列(2)na a a a a a a nn 2213210++++++=-K 第一季度的平均现金库存额:)(480325204504802500万元=+++=a 第二季度的平均现金库存额:)(67.566325806005502500万元=+++=a 上半年的平均现金库存额:33.523267.566480,33.523625806005504802500=+==+++++=或K a 答:该银行2001年第一季度平均现金库存额为480万元,第二季度平均现金库存额为566、67万元,上半年的平均现金库存额为523、33万元、 要求计算:①第一季度平均人数;②上半年平均人数。
解:第一季度平均人数:)(10322122102010501210501002人=+⨯++⨯+=a上半年平均人数:1023321321008102022102010501210501002=++⨯++⨯++⨯+=a解:解:产品总产量∑=+++++=)(210005000040003000400030002000件a 产品总成本∑=+++++=)(1.1480.346.279.214.286.216.14万元b平均单位成本)/(52.70210001.148件元件万元总产量总成本==∑∑∑a bc或:平均单位成本)(52.706210001000061.148万元=⨯==ab c 答:该企业2001年上半年的产品平均单位成本为70.52元／件。
要求:(1)计算并填列表中所缺数字。
(2)计算该地区1997—2001年间的平均国民生产总值。
(3)计算1998—2001年间国民生产总值的平均发展速度与平均增长速度。
解:(1)计算表如下:某地区1996--2000年国民生产总值数据(2))(88.5459.61585.6811.459.40万元=++++==∑na a(3)平均发展速度:%91.1101091.19.409.6140====nn a a a 平均增长速度=平均发展速度-1=110.91％—1=10.91％答:该地区1996—2000年间的平均每年创造国民生产总值54.88亿元,1997—2000年期间国民生产总值的平均发展速度为110.91％,平均增长速度为10.91％。
平均在业人口数:)(28032270280285228022213210万人=+++=++++++=-n n a a a a a a a K 平均劳动力资源:)(68432686684685256802213210万人=+++=++++++=-n b b b b b b b nn K 平均在业人口比重:%94.40684280===ba c 答:该地区第四季度在业人口数占劳动力资源人口的平均比重为40.94％。
要求:(1)计算该企业第四季度的月平均劳动生产率。
(2)计算该企业第四季度劳动生产率。
解:(1)月平均劳动生产率cab 月平均人数平均月产值==)/(73.77703)205210200(310000)9.159168150(人元=÷++÷⨯++(2)季度劳动生产率ca b 季平均人数季度产值∑==)/(20.233123)205210200(10000)9.159168150(人元=÷++⨯++二、平均数:1、简单均值计算=NXNX X X X Ni iN∑==+++=121Λ2、加权均值计算=∑∑===++++++=Ki iKi iiNNN FFX F F F F X F X F X X 11212211ΛΛ&3、几何平均计算=N N M X X X G ⨯⨯⨯=Λ214、调与平均数(加权调与)=∑∑∑∑∑∑⇐⇒===ii i iii i i ii i M FF X XF X F X Xw w H 5、几何平均数=NNi iN N M XX X X G ∏==⨯⨯⨯=121Λ三、统计指数:二、综合指数的计算( 一)数量指标综合指数(拉氏)价格如果固定在基期,称为拉氏公式:∑∑=pq p q K q 0001价格如果固定在报告期,称为派氏公式:∑∑=pq p q K q111(二)质量指标综合指数(派氏)商品销售量,如果固定在基期,称为拉氏公式:∑∑=pq p q K p10如果固定在报告期,称为派氏公式:∑∑=pq p q K p 0111求商品销售额指数,并分析销售额变动受销售量与销售价格的影响分别就是多少。
1、销售额指数:%14.1174200049200011===∑∑qp q p K pq报告期与基期相比,销售额上升17、14%,增加的绝对数为:49200-42000=7200 2、受销量的影响为:%29.11442000480001===∑∑pq p q K q报告期与基期相比,销售上升14、29%,增加的绝对数为:48000-42000=6000 3、受销售价格的影响为%5.10248000492000111==∑∑=p q p q K p报告期与基期相比,销售价格上升2、5%,增加的绝对数为:49200-48000=1200 相对数:销售额指数 =销售量指数×销售价格指数 即117、14%= 114、29% × 102、5% 绝对数:7200=6000+1200(元)四、总体均值的区间估计(σ２已知)【例】某大学从该校学生中随机抽取100人,调查到她们平均每天参加体育锻炼的时间为26分钟。
试以95％的置信水平估计该大学全体学生平均每天参加体育锻炼的时间(已知总体方差为36小时)。
解:已知 ⎺x ＝26, σ=6,n =100, 1-α = 0、95,Ｚα/2=1、96()176.27,824.24100696.126,100696.126,22=⎪⎭⎫ ⎝⎛+-=⎪⎭⎫ ⎝⎛+-n Z x n Z x σσαα我们可以95％的概率保证平均每天参加锻炼的时间在24、824～27、176 分钟之间五、总体均值的区间估计(σ２未知)【例】从一个正态总体中抽取一个随机样本,n = 25 ,其均值`x = 50 ,标准差 s = 8。
建立总体均值m 的95%的置信区间。
解:已知Ｘ~N (μ,σ2),⎺x =50, s =8, n =25, 1-α = 0、95,t α/2=2、0639。
()3.53,69.462580639.250,2580639.250,1212=⎪⎭⎫ ⎝⎛+-=⎪⎭⎫ ⎝⎛+---n s t x n s t x n n αα我们可以95％的概率保证总体均值在46、69～53、30 之间六、样本容量的确定【例】一家广告公想估计某类商店去年所花的平均广告费用有多少。
经验表明,总体方差约为1800000元。
如置信度取95%,并要使估计处在总体平均值附近500元的范围内,这家广告公司应抽多大的样本？解:已知σ2=1800000,α=0、05, Z α/2=1、96,∆=500 应抽取的样本容量为2865.27500)1800000()96.1(222222≈==∆=σαZ n 总体均值的检验(大样本) 七、总体均值的检验(σ 2 已知)(双侧检验)【例】一种罐装饮料采用自动生产线生产,每罐的容量就是255ml ,标准差为5ml 。
为检验每罐容量就是否符合要求,质检人员在某天生产的饮料中随机抽取了40罐进行检验,测得每罐平均容量为255、8ml 。
取显著性水平α=0、05 ,检验该天生产的饮料容量就是否符合标准要求？• H 0 :μ = 255 • H1 :μ ≠ 255 α = 0、05 • n = 40 •临界值(c ):检验统计量:决策:不拒绝H0结论:样本提供的证据还不足以推翻“该天生产的饮料符合标准要求”的瞧法(左侧检验)【例】一种机床加工的零件尺寸绝对平均误差为1、35mm。
生产厂家现采用一种新的机床进行加工以期进一步降低误差。
为检验新机床加工的零件平均误差与旧机床相比就是否有显著降低,从某天生产的零件中随机抽取50个进行检验。
利用这些样本数据,检验新机床加工的零件尺寸的平均误差与旧机床相比就是否有显著降低？( =0、01)解:八、总体均值的检验(σ2 未知)(右侧检验)【例】某一小麦品种的平均产量为5200kg/hm2 。
一家研究机构对小麦品种进行了改良以期提高产量。
为检验改良后的新品种产量就是否有显著提高,随机抽取了36个地块进行试种,得到的样本平均产量为5275kg/hm2,标准差为120/hm2 。
试检验改良后的新品种产量就是否有显著提高？(α=0、05)解:九、总体均值的检验(小样本)【例】一种汽车配件的平均长度要求为12cm,高于或低于该标准均被认为就是不合格的。
汽车生产企业在购进配件时,通常就是经过招标,然后对中标的配件提供商提供的样品进行检验,以决定就是否购进。
现对一个配件提供商提供的10个样本进行了检验。
假定该供货商生产的配件长度服从正态分布,在0、05的显著性水平下,检验该供货商提供的配件就是否符合要求？解:十、估计方程的求法【例】求不良贷款对贷款余额的回归方程()⎪⎩⎪⎨⎧-=⨯-==-⨯⨯-⨯=8295.0268.120037895.0728.3ˆ037895.07.300637.516543252.937.300614.1708025ˆ021ββ 回归方程为:y = -0、8295 + 0、037895 x回归系数 =0、037895 表示,贷款余额每增加1亿元,不良贷款平均增加0、037895亿元十一、置信区间估计【例】求出贷款余额为100亿元时,不良贷款95%置信水平下的置信区间 解:根据前面的计算结果,已知n =25,s e=1、9799,t α2/(25-2)=2、069 置信区间为5744.154933)268.120100(2519799.1069.296.22-+⨯⨯± 8059.3)(1141.20≤≤y E当贷款余额为100亿元时,不良贷款的平均值在2、1141亿元到3、8059亿元之间。