19讲:锐角三角函数
河北省中考系统复习:第19讲锐角三角函数(8年真题训练)

第19讲 锐角三角函数命题点 解直角三角形1.(·承德模拟)如图,在Rt △ABC 中,∠C =90°,BC =8,tanB =12,点D 在BC 上,且BD =AD ,求AC 的长和cos∠ADC 的值.解:∵在Rt △ABC 中,BC =8,tanB =AC BC =12,∴AC =BC ·tanB =4.设AD =x ,则BD =x ,CD =8-x ,在Rt △ADC 中,(8-x)2+42=x 2,解得x =5. ∴AD =5,CD =8-5=3,∴cos ∠ADC =DC AD =35.2.(·河北模拟)如图,AD 是△ABC 的中线,tanB =13,cosC =22,AC = 2.求:(1)BC 的长;(2)sin ∠ADC 的值.解:(1)过点A 作AE ⊥BC 于点E. ∵cosC =22,∴∠C =45°. 在Rt △ACE 中,CE =AC ·cosC =1, ∴AE =CE =1.在Rt △ABE 中,tanB =13,即AE BE =13,∴BE =3AE =3.∴BC =BE +CE =4.(2)∵AD 是△ABC 的中线,∴CD =12BC =2.∴DE =CD -CE =1.∵AE ⊥BC ,DE =AE ,∴∠ADC =45°. ∴sin ∠ADC =22.重难点1 解直角三角形(·河北模拟)已知,在△ABC 中,∠ACB =90°,tanB =43,AB =5,D 在AB 上.(1)求BC 的长;(2)如图1,若∠CDB =∠B ,求sin ∠DCB 的值;(3)如图2,过点B 作BE ⊥CD 所在的直线,垂足为E ,BE 的延长线交直线AC 于点F. ①当tan ∠BCD =2时,求S △CBF ; ②当AF =54时,求线段AD 的长.【思路点拨】 (1)由正切的定义可知△ABC 是一个勾3,股4,弦5的直角三角形;(2)可通过过点D 作DE ⊥BC ,利用tanB 找到DE ,BE 的数量关系,再解直角△DCE ,求得sin ∠DCB 的值;(3)因为∠BCD =∠CFB :①利用tan ∠CFB 的值,求CF ,进而求S △CBF ;②可通过过点A 作BC 的平行线交CD 延长线于点G ,先求AG ,再利用相似求AD 的长. 【自主解答】 解:(1)在△ABC 中,∠ACB =90°,tanB =43,∴tanB =AC BC =43,∴AC =43BC.∵AC 2+BC 2=AB 2,∴(43BC)2+BC 2=52,∴BC =3.(2)过点D 作DE ⊥BC ,则tanB =43=DEBE ,∴BE =34DE ,∴CE =BC -BE =3-34DE.∵∠CDB =∠B ,∴CD =CB =3.∵CD 2=CE 2+DE 2,∴32=DE 2+(3-34DE)2,解得DE =7225.∴sin ∠DCB =DE DC =2425.(3)①∵∠BCD +∠FCE =90°,∠CFB +∠FCE =90°, ∴∠BCD =∠CFB.∴tan ∠BCD =tan ∠CFB =2.∵tan ∠CFB =BC CF =2,BC =3,∴CF =32.∴S △CBF =94.②当点F 在线段AC 上时,如图3,过点A 作AG ∥BC 交CD 延长线于点G , ∵tan ∠ACG =tan ∠CBF =AG AC =CF BC =1112,AC =4,∴AG =113.∵AG ∥BC ,∴AG BC =ADBD .∴119=AD 5-AD ,AD =114.图3 图4当点F 在线段CA 的延长线上,如图4,过点A 作AG ∥BC 交CD 延长线于点G. ∵tan ∠ACG =tan ∠CBF =AG AC =CF BC =74,AC =4,∴AG =7.∵AG ∥BC ,∴AG BC =AD BD .∴73=AD 5-AD .∴AD =72.方法指导1.解直角三角形,需知除直角以外的两个条件(一边和一角或两边),可求得其余的边或角.2.在求解时,一般选取既含未知边(角)又含有已知边(或角)的直角三角形,通过锐角三角函数的定义或勾股定理,建构已知或未知之间的桥梁;从而实现求解.3.若所求的线段(或角)不能直接求解,可以通过作出点到直线的距离或三角形高线,进而转化成直角三角形求解. 4.解直角三角形和相似三角形的性质,是几何求解中的重要工具.K,【变式训练1】 如图是由一个角为60°且边长为1的菱形组成的网格,每个菱形的顶点称为格点,点A ,B ,C 都在格点上,则tan ∠BAC =233.【变式训练2】(·上海)如图,已知在△ABC 中,AB =BC =5,tan ∠ABC =34.(1)求边AC 的长;(2)设边BC 的垂直平分线与边AB 的交点为D ,求ADDB的值.解:(1)过点A 作AE ⊥BC ,在Rt △ABE 中, tan ∠ABC =AE BE =34,AB =5,∴AE =3,BE =4.∴CE =BC -BE =5-4=1.在Rt △AEC 中,根据勾股定理,得AC =32+12=10.(2)如图,∵DF 垂直平分BC ,∴BD =CD ,BF =CF =52.∵tan ∠DBF =DF BF =34,∴DF =158.在Rt △BFD 中,根据勾股定理,得BD =(52)2+(158)2=258, ∴AD =5-258=158,则AD DB =35. 重难点2 解直角三角形的应用(1)如图1,为了游客的安全,某景点将原坡角为60°的斜坡AB 改为坡度为1∶3的斜坡AC ,已知AB =100米,BC 在同一水平线上,求改造后斜坡的坡脚向前移动距离BC 的长;(2)(·郴州)小亮在某桥附近试飞无人机,如图2,为了测量无人机飞行的高度AD ,小亮通过操控器指令无人机测得桥头B ,C 的俯角分别为∠EAB =60°,∠EAC =30°,且D ,B ,C 在同一水平线上.已知桥BC =30米,求无人机飞行的高度AD ;(精确到0.01米,参考数据:2≈1.414,3≈1.732)(3)(·湘西)如图3,某市郊外景区内一条笔直的公路l 经过A ,B 两个景点,景区管委会又开发了风景优美的景点C.经测量,C 位于A 的北偏东60°的方向上,C 位于B 的北偏东30°的方向上,且AB =10 km.①求景点B 与C 的距离;②为了方便游客到景点C 游玩,景区管委会准备由景点C 向公路l 修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)【思路点拨】这三个问题均可以通过过点A 作直线BC 的垂线,垂足为D ,再利用解直角三角形ABD 和直角三角形ACD 来解决.【自主解答】解:(1)过点A 作AD ⊥BC 于点D ,在Rt △ABD 中,∠ABD =60°,∴BD =AB ·cos ∠ABD =100×cos60°=50(米),AD =AB ·sin ∠ABD =503米. ∵AC 的坡度为1∶3, ∴AD ∶CD =1∶ 3.∴CD =150,BC =CD -BD =150-50=100(米).∴改造后斜坡的坡脚向前移动距离BC 的长是100 m. (2)由题意,得∠EAC =30°,∠EAB =60°,∵AE ∥BC ,∴∠EAC =∠ACB =30°,∠EAB =∠ABD =60°. ∵∠ABD =∠ACB +∠BAC ,∴∠BAC =∠ACB =30°. ∴AB =BC =30.在Rt △ABD 中,∴AD =AB ·sin ∠ABD =153≈25.98(米). (3)①由题意,得∠CAB =30°,∠ABC =90°+30°=120°, ∴∠C =180°-∠CAB -∠ABC =30°.∴∠CAB =∠C =30°. ∴BC =AB =10 km ,即景点B ,C 的距离为10 km.②过点C 作CD ⊥AB 于点D ,∵BC =10 km ,C 位于B 的北偏东30°的方向上,∴∠CBD =60°,在Rt △CBD 中,CD =32BC =5 3 km. 【变式训练3】(·常州)京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A ,B 和点C ,D ,先用卷尺量得AB =160 m ,CD =40 m ,再用测角仪测得∠CAB =30°,∠DBA =60°,求该段运河的河宽(即CH 的长).解:过点D作DE⊥AB于点E,可得四边形CHED为矩形,∴HE=CD=40 m.设CH=DE=x m,在Rt△BDE中,∠DBA=60°,∴BE=33x.在Rt△ACH中,∠BAC=30°,∴AH=3x.由AH+HE+EB=AB=160 m,得3x+40+33x=160,解得x=303,即CH=30 3 m.答:该段运河的河宽为30 3 m.方法指导1.对于解直角三角形的实际应用题,要灵活运用转化思想,通常是根据以下方法和步骤解决:(1)有图的要先将题干中的已知量在图中表示出来,找到与已知量和未知量相关联的三角形,画出平面几何图形,弄清已知条件中各量之间的关系;(2)若三角形是直角三角形,根据边角关系进行计算;若三角形不是直角三角形,可通过添加辅助线构造直角三角形来解决,其中作某边上的高是常用的辅助线.总的来说,解直角三角形的实际应用问题,关键是要根据实际情况建立数学模型,正确画出图形或作出辅助线并找准直角三角形.,模型建立)本题的三个题均可以抽象出如下图形:另外实际问题还可以抽象的几何图形为:1.(·孝感)如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于(A)A.35B.45C.34D.432.(·保定模拟)在△ABC中,∠A,∠B均为锐角,且(tanB-3)(2sinA-3)=0,则△ABC一定是(D) A.等腰三角形B.等边三角形C.直角三角形D.有一个角是60°的三角形3.(·唐山丰南区模拟)在△ABC 中,AB =AC =13,BC =24,则tanB 等于(B)A.513B.512C.1213 D.1254.(·贵阳)如图,A ,B ,C 是小正方形的顶点,且每个小正方形的边长为1,则tan ∠BAC 的值为(B)A.12B .1C.33D. 35.(·河北模拟)如图,△ABC 在边长为1个单位长度的方格纸中,它的顶点在小正方形的顶点位置.如果△ABC 的面积为10,且sinA =55,那么点C 的位置可以在(D) A .点C 1处B .点C 2处C .点C 3处D .点C 4处6.如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB 与墙MN 平行且距离为0.8米,一辆小汽车车门宽AO 为1.2米,当车门打开角度∠AOB 为40°时,车门是否会碰到墙?否;(填“是”或“否”)请简述你的理由点A 到OB 的距离小于OB 与墙MN 平行的距离.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)7.【分类讨论思想】(·无锡)已知在△ABC 中,AB =10,AC =27,∠B =30°,则△ABC 的面积等于153或10 3.8.(·贵阳)如图1,在Rt △ABC 中,以下是小亮探究a sinA 与bsinB之间关系的方法:∵sinA =a c ,sinB =b c ,∴c =a sinA ,c =b sinB .∴a sinA =bsinB ,根据你掌握的三角函数知识.在图2的锐角△ABC中,探究a sinA ,b sinB ,csinC之间的关系,并写出探究过程.解:a sinA =b sinB =c sinC.理由:过点A 作AD ⊥BC ,过点B 作BE ⊥AC , 在Rt △ABD 中,sinB =ADc ,即AD =c ·sinB ,在Rt △ADC 中,sinC =ADb ,即AD =b ·sinC ,∴c ·sinB =b ·sinC ,即b sinB =csinC .同理可得a sinA =csinC ,则a sinA =b sinB =c sinC.9.(·衡阳)一名徒步爱好者来衡阳旅行,他从宾馆C 出发,沿北偏东30°的方向行走2 000米到达石鼓书院A 处,参观后又从A 处沿正南方向行走一段距离,到达位于宾馆南偏东45°方向的雁峰公园B 处,如图所示.(1)求这名徒步爱好者从石鼓书院走到雁峰公园的途中与宾馆之间的最短距离;(2)若这名徒步爱好者以100米/分的速度从雁峰公园返回宾馆,那么他在15分钟内能否到达宾馆?解:(1)过点C 作CP ⊥AB 于点P ,由题意,得∠A =30°,AP =2 000米, 则CP =12AC =1 000米.(2)∵在Rt △PBC 中,PC =1 000,∠PBC =∠BCP =45°, ∴BC =2PC =1 0002米.∵这名徒步爱好者以100米/分的速度从雁峰公园返回宾馆, ∴他到达宾馆需要的时间为1 0002100=102<15. ∴他在15分钟内能到达宾馆.10.如图,在四边形ABCD 中,AB =8,BC =1,∠DAB =30°,∠ABC =60°,则四边形ABCD 的面积为53,AD 的长是23.提示:延长AD ,BC 相交于点E ,可得△ABE 为直角三角形.11.(·眉山)如图,在边长为1的小正方形网格中,点A ,B ,C ,D 都在这些小正方形的顶点上,AB ,CD 相交于点O ,则tan ∠AOD =2.提示:连接BE ,构造Rt △BOF ,根据△AOC ∽△BOK 可得OK 与CK 的数量关系,求出OF 与BF 的数量关系即可.12.如图,已知,在△ABC 中,AB =AC =25,sinB =255,D 为边BC 的中点,E 为边BC 的延长线上一点,且CE=BC.连接AE ,F 为线段AE 的中点.求:(1)线段DE 的长; (2)∠CAE 的正切值.解:(1)连接AD.∵AB =AC ,D 为BC 的中点, ∴AD ⊥BC , 即∠ADB =90°.∵AB =AC =25,sinB =255,∴AD AB =255.∴AD =4. 由勾股定理,得BD =2,∴DC =BD =2,BC =4. ∵CE =BC ,∴CE =4. ∴DE =DC +CE =2+4=6.(2)过点C 作CM ⊥AE 于点M, 则∠CMA =∠CME =90°. 在Rt △ADE 中,由勾股定理,得 AE =AD 2+DE 2=213.∵CM 2=AC 2-AM 2=CE 2-EM 2, ∴(25)2-AM 2=42-(213-AM)2, 解得AM =141313.∴CM =AC 2-AM 2=81313.∴tan ∠CAE =CM AM =47.13.(·河北模拟)阅读下面的材料:嘉嘉在数学课外小组活动中遇到这样一个问题:如果α,β都为锐角,且tan α=12,tan β=13,求α+β的度数.淇淇是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD =α,∠CBE =β,且BA ,BC 在直线BD 的两侧,连接AC ,可证得△ABC 是等腰直角三角形,因此可求得α+β=∠ABC =45°.请参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tan α=4,tan β=35时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α-β,由此可得α-β=45°.解:如图.。
锐角三角函数课件

45度角的余弦值
$cos 45^circ = frac{sqrt{2}}{2}$
30度角的余弦值
$cos 30^circ = frac{sqrt{3}}{2}$
60度角的正弦值
$sin 60^circ = frac{sqrt{3}}{2}$
45度角的正弦值
在工程学中的应用
结构设计
在建筑和机械设计中,锐角三角 函数用于计算结构件的角度和长
度。
控制系统
在控制系统的设计中,锐角三角函 数用于描述系统的传递函数和稳定 性。
信号处理
在信号处理中,锐角三角函数用于 频谱分析和滤波器的设计。
05
特殊角度的三角函数值
30度、45度、60度的三角函数值
30度角的正弦值
正切函数的图像在每 一个开区间(π/2+kπ, π/2+kπ), k∈Z内都是递增的。
04
锐角三角函数的应用
在几何学中的应用
01
02
03
计算角度
锐角三角函数可以帮助我 们计算出特定角度的三角 形的角度,例如直角三角 形中的锐角。
计算边长
通过已知的角度和边长, 我们可以使用锐角三角函 数来计算其他边的长度。
04
90度角的余弦值
$cos 90^circ = 0$
06
习题与解答
习题
题目1
已知直角三角形中,一个锐角为 30°,邻边长为3,求对边长。
题目2
在直角三角形中,已知一个锐角 为45°,斜边长为5,求邻边长。
题目3
已知直角三角形中,一个锐角为 60°,对边长为6,求斜边长。
答案与解析
01
锐角三角函数(公式、定理、结论图表) --中考数学知识必备
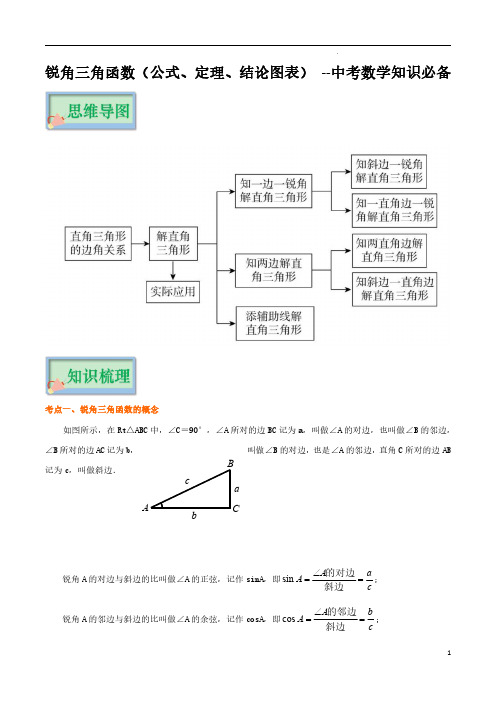
锐角三角函数(公式、定理、结论图表)--中考数学知识必备考点一、锐角三角函数的概念如图所示,在Rt△ABC 中,∠C=90°,∠A 所对的边BC 记为a,叫做∠A 的对边,也叫做∠B 的邻边,∠B 所对的边AC 记为b,叫做∠B 的对边,也是∠A 的邻边,直角C 所对的边AB记为c,叫做斜边.锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA,即sin A aA c ∠==的对边斜边;锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cosA,即cos A bA c∠==的邻边斜边;BCa c锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即tanA a AA b∠==∠的对边的邻边.同理sinB bBc∠==的对边斜边;cosB aBc∠==的邻边斜边;tanB bBB a∠==∠的对边的邻边.要点诠释:(1)正弦、余弦、正切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化.(2)sinA,cosA,tanA分别是一个完整的数学符号,是一个整体,不能写成,,,不能理解成sin与∠A,cos与∠A,tan与∠A的乘积.书写时习惯上省略∠A的角的记号“∠”,但对三个大写字母表示成的角(如∠AEF),其正切应写成“tan∠AEF”,不能写成“tanAEF”;另外,、、常写成、、.(3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.(4)由锐角三角函数的定义知:当角度在0°<∠A<90°之间变化时,,,tanA>0.典例1:(2022•扬州)在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,若b2=ac,则sin A的值为..【分析】根据勾股定理和锐角三角函数的定义解答即可.【解答】解:在△ABC中,∠C=90°,∴c2=a2+b2,∵b2=ac,∴c2=a2+ac,等式两边同时除以ac得:=+1,令=x,则有=x+1,∴x2+x﹣1=0,解得:x1=,x2=(舍去),当x=时,x≠0,∴x=是原分式方程的解,∴sin A==.故答案为:.【点评】本题主要考查了锐角三角函数,熟练掌握勾股定理和锐角三角函数的定义是解答本题的关键.考点二、特殊角的三角函数值利用三角函数的定义,可求出0°、30°、45°、60°、90°角的各三角函数值,归纳如下:要点诠释:(1)通过该表可以方便地知道0°、30°、45°、60°、90°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:sin0︒、、、、sin90︒的值依次为0、、、、1,而cos0︒、、、、cos90︒的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:当角度在0°<∠A<90°之间变化时,①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)②余弦值随锐角度数的增大(或减小)而减小(或增大).典例2:(2022•天津)tan45°的值等于()A.2B.1C.D.【分析】根据特殊角的三角函数值,进行计算即可解答.【解答】解:tan45°的值等于1,故选:B.【点评】本题考查了特殊角的三角函数值,熟练掌握特殊角的三角函数值是解题的关键.考点三、锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,;(2)平方关系:;(3)倒数关系:或;(4)商数关系:.要点诠释:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.考点四、解直角三角形在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:①三边之间的关系:a2+b2=c2(勾股定理).②锐角之间的关系:∠A+∠B=90°.③边角之间的关系:,,,,,.④,h为斜边上的高.要点诠释:(1)直角三角形中有一个元素为定值(直角为90°),是已知的值.(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.考点五、解直角三角形的常见类型及解法已知条件解法步骤Rt△ABC两边两直角边(a,b)由求∠A,∠B=90°-∠A,斜边,一直角边(如c,a)由求∠A,∠B=90°-∠A,一边一角一直角边和一锐角锐角、邻边(如∠A,b)∠B=90°-∠A,,锐角、对边(如∠A,a)∠B=90°-∠A,,斜边、锐角(如c,∠A)∠B=90°-∠A,,要点诠释:1.在遇到解直角三角形的实际问题时,最好是先画出一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2.若题中无特殊说明,“解直角三角形”即要求出所有的未知元素,已知条件中至少有一个条件为边.典例3:(2022•丹东)如图,AB是⊙O的直径,点E在⊙O上,连接AE和BE,BC平分∠ABE交⊙O于点C,过点C作CD⊥BE,交BE的延长线于点D,连接CE.(1)请判断直线CD与⊙O的位置关系,并说明理由;(2)若sin∠ECD=,CE=5,求⊙O的半径.【分析】(1)结论:CD是⊙O的切线,证明OC⊥CD即可;(2)设OA=OC=r,设AE交OC于点J.证明四边形CDEJ是矩形,推出CD=EJ=4,CJ=DE=3,再利用勾股定理构建方程求解.【解答】解:(1)结论:CD是⊙O的切线.理由:连接OC.∵OC=OB,∴∠OCB=∠OBC,∵BC平分∠ABD,∴∠OBC=∠CBE,∴∠OCB=∠CBE,∴OC∥BD,∵CD⊥BD,∴CD⊥OC,∵OC是半径,∴CD是⊙O的切线;(2)设OA=OC=r,设AE交OC于点J.∵AB是直径,∴∠AEB=90°,∵OC⊥DC,CD⊥DB,∴∠D=∠DCJ=∠DEJ=90°,∴四边形CDEJ是矩形,∴∠CJE=90°,CD=EJ,CJ=DE,∴OC⊥AE,∴AJ=EJ,∵sin∠ECD==,CE=5,∴DE=3,CD=4,∴AJ=EJ=CD=4,CJ=DE=3,在Rt△AJO中,r2=(r﹣3)2+42,∴r=,∴⊙O的半径为.【点评】本题考查解直角三角形,切线的判定,垂径定理,矩形的判定和性质,勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型考点六、解直角三角形的应用解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是:(1)弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解.拓展:在用直角三角形知识解决实际问题时,经常会用到以下概念:(1)坡角:坡面与水平面的夹角叫做坡角,用字母表示.坡度(坡比):坡面的铅直高度h和水平距离的比叫做坡度,用字母表示,则,如图,坡度通常写成=∶的形式.(2)仰角、俯角:视线与水平线所成的角中,视线中水平线上方的叫做仰角,在水平线下方的叫做俯角,如图.(3)方位角:从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角,如图①中,目标方向PA,PB,PC的方位角分别为是40°,135°,245°.(4)方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角,如图②中的目标方向线OA,OB,OC,OD的方向角分别表示北偏东30°,南偏东45°,南偏西80°,北偏西60°.特别如:东南方向指的是南偏东45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°,西北方向指的是北偏西45°.要点诠释:1.解直角三角形实际是用三角知识,通过数值计算,去求出图形中的某些边的长或角的大小,最好画出它的示意图.2.非直接解直角三角形的问题,要观察图形特点,恰当引辅助线,使其转化为直角三角形或矩形来解.例如:3.解直角三角形的应用题时,首先弄清题意(关键弄清其中名词术语的意义),然后正确画出示意图,进而根据条件选择合适的方法求解.典例4:(2022•黑龙江)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,山高为()米A.600﹣250B.600﹣250C.350+350D.500【分析】设EF=5x米,根据坡度的概念用x表示出BF,根据勾股定理求出x,根据正切的定义列出方程,解方程得到答案.【解答】解:设EF=5x米,∵斜坡BE的坡度为5:12,∴BF=12x米,由勾股定理得:(5x)2+(12x)2=(1300)2,解得:x=100,则EF=500米,BF=1200米,由题意可知,四边形DCFE为矩形,∴DC=EF=500米,DE=CF,在Rt△ADE中,tan∠AED=,则DE==AD,在Rt△ACB中,tan∠ABC=,∴=,解得:AD=600﹣750,∴山高AC=AD+DC=600﹣750+500=(600﹣250)米,故选:B.【点评】本题考查的是解直角三角形的应用—坡度坡角问题,掌握坡度是坡面的铅直高典例5:(2022•湖北)如图,有甲乙两座建筑物,从甲建筑物A点处测得乙建筑物D点的俯角α为45°,C 点的俯角β为58°,BC为两座建筑物的水平距离.已知乙建筑物的高度CD为6m,则甲建筑物的高度AB为16m.(sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,结果保留整数).【分析】过点D作DE⊥AB于点E,则BE=CD=6m,∠ADE=45°,∠ACB=58°,在Rt△ADE中,∠ADE=45°,设AE=xm,则DE=xm,BC=xm,AB=AE+BE=(6+x)m,在Rt△ABC中,tan∠ACB =tan58°=≈1.60,解得x=10,进而可得出答案.【解答】解:过点D作DE⊥AB于点E,如图.则BE=CD=6m,∠ADE=45°,∠ACB=58°,在Rt△ADE中,∠ADE=45°,设AE=xm,则DE=xm,∴BC=xm,AB=AE+BE=(6+x)m,在Rt△ABC中,tan∠ACB=tan58°=≈1.60,解得x=10,∴AB=16m.故答案为:16.【点评】本题考查解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键典例6:(2022•资阳)小明学了《解直角三角形》内容后,对一条东西走向的隧道AB进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东15°方向上,他沿西北方向前进100米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西60°方向上,(点A、B、C、D在同一平面内)(1)求点D与点A的距离;(2)求隧道AB的长度.(结果保留根号)【分析】(1)根据方位角图,易知∠ACD=60°,∠ADC=90°,解Rt△ADC即可求解;(2)过点D作DE⊥AB于点E.分别解Rt△ADE,Rt△BDE求出AE和BE,即可求出隧道AB的长.【解答】解;(1)由题意可知:∠ACD=15°+45°=60°,∠ADC=180°﹣45°﹣45°=90°,在Rt△ADC中,∴(米),答:点D与点A的距离为300米.(2)过点D作DE⊥AB于点E,∵AB是东西走向,∴∠ADE=45°,∠BDE=60°,在Rt△ADE中,∴(米),在Rt△BDE中,∴(米),∴(米),答:隧道AB的长为米.【点评】本题考查了解直角三角形的应用﹣方向角问题,掌握方向角的概念,掌握特殊角的三角函数值是解题的关键.考点七、解直角三角形相关的知识如图所示,在Rt△ABC 中,∠C=90°,(1)三边之间的关系:222a b c +=;(2)两锐角之间的关系:∠A+∠B=90°;(3)边与角之间的关系:sin cos a A B c ==,cos cos a A B c ==,cos sin b A B c ==,1tan tan a A b B==.(4)如图,若直角三角形ABC 中,CD⊥AB 于点D,设CD=h,AD=q,DB=p,则由△CBD∽△ABC,得a 2=pc;由△CAD∽△BAC,得b 2=qc;由△ACD∽△CBD,得h 2=pq;由△ACD∽△ABC 或由△ABC 面积,得ab=ch.(5)如图所示,若CD 是直角三角形ABC 中斜边上的中线,则①CD=AD=BD=12AB;②点D 是Rt△ABC 的外心,外接圆半径R=12AB.(6)如图所示,若r 是直角三角形ABC 的内切圆半径,则2a b c ab r a b c +-==++.直角三角形的面积:①如图所示,111sin 222ABC S ab ch ac B === △.(h 为斜边上的高)②如图所示,1()2ABCS r a b c=++△.典例7:(2022•黄石)我国魏晋时期的数学家刘徽首创“割圆术”:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长l6=6R,则π≈=3.再利用圆的内接正十二边形来计算圆周率,则圆周率π约为()A.12sin15°B.12cos15°C.12sin30°D.12cos30°【分析】利用圆内接正十二边形的性质求出A6A7=2A6M=2R×sin15°,再根据“圆周率等于圆周长与该圆直径的比”,即可解决问题.【解答】解:在正十二边形中,∠A6OM=360°÷24=15°,∴A6M=sin15°×OA6=R×sin15°,∵OA6=OA7,OM⊥A6A7,∴A6A7=2A6M=2R×sin15°,∴π≈=12sin15°,故选:A.【点评】本题主要考查了圆内接多边形的性质,解直角三角形等知识,读懂题意,计算出正十二边形的周长是解题的关键.。
《锐角三角函数》 讲义

《锐角三角函数》讲义一、锐角三角函数的定义在直角三角形中,我们把锐角的对边与斜边的比值叫做正弦(sin),锐角的邻边与斜边的比值叫做余弦(cos),锐角的对边与邻边的比值叫做正切(tan)。
以一个锐角为 A 的直角三角形为例,假设其对边为 a,邻边为 b,斜边为 c。
那么,sin A = a / c,cos A = b / c,tan A = a / b 。
需要注意的是,锐角三角函数的值只与角的大小有关,而与三角形的大小无关。
二、特殊角的三角函数值我们要牢记一些特殊角的三角函数值,这在解题中会经常用到。
30°角:sin 30°= 1 / 2,cos 30°=√3 / 2,tan 30°=√3 / 3 。
45°角:sin 45°=√2 / 2,cos 45°=√2 / 2,tan 45°= 1 。
60°角:sin 60°=√3 / 2,cos 60°= 1 / 2,tan 60°=√3 。
三、锐角三角函数的应用锐角三角函数在实际生活中有广泛的应用。
比如,测量物体的高度。
如果我们知道一个物体与我们的水平距离,以及我们观测物体顶部的仰角,就可以通过三角函数来计算物体的高度。
假设我们站在水平地面上,距离一个建筑物为 d 米,观测建筑物顶部的仰角为α,那么建筑物的高度 h 就可以通过tanα = h / d 来计算,即 h =d × tanα 。
再比如,测量河流的宽度。
我们可以在河的一岸选择一个点,然后测出对岸一个目标点与这个点的连线和河岸的夹角,以及这个点到河岸的垂直距离,从而计算出河流的宽度。
四、锐角三角函数的性质1、取值范围正弦和余弦的值域都在-1, 1之间,而正切的值域是全体实数。
2、增减性在锐角范围内,正弦函数值随着角度的增大而增大,余弦函数值随着角度的增大而减小,正切函数值随着角度的增大而增大。
锐角三角函数

锐角三角函数作为数学中的一个重要概念,锐角三角函数是我们学习三角函数的关键部分之一。
在几何学和三角学中,锐角指的是小于90度的角。
而锐角三角函数是以锐角作为自变量的三角函数。
一、正弦函数(sine function)在锐角三角函数中,正弦函数是最常见也是最重要的一个函数。
正弦函数可以表示为:sin(θ) = 对边/斜边其中,θ代表锐角的度数,对边代表锐角的对边长度,斜边代表锐角的斜边长度。
二、余弦函数(cosine function)余弦函数是锐角三角函数中的另一个核心函数,表示为:cos(θ) = 临边/斜边同样,θ代表锐角的度数,临边代表锐角的临边长度,斜边代表锐角的斜边长度。
三、正切函数(tangent function)正切函数是另一个重要的锐角三角函数,表达式为:tan(θ) = 对边/临边在这个公式中,θ代表锐角的度数,对边代表锐角的对边长度,临边代表锐角的临边长度。
四、余切函数(cotangent function)余切函数是正切函数的倒数,可以表示为:cot(θ) = 临边/对边θ代表锐角的度数,临边代表锐角的临边长度,对边代表锐角的对边长度。
五、正割函数(secant function)正割函数是余弦函数的倒数,可以表示为:sec(θ) = 斜边/临边θ代表锐角的度数,斜边代表锐角的斜边长度,临边代表锐角的临边长度。
六、余割函数(cosecant function)余割函数是正弦函数的倒数,可以表示为:csc(θ) = 斜边/对边在这个公式中,θ代表锐角的度数,斜边代表锐角的斜边长度,对边代表锐角的对边长度。
锐角三角函数在数学和实际应用中具有广泛的重要性。
无论是在几何学、物理学还是工程学中,锐角三角函数都扮演着重要的角色。
它们可以帮助我们计算和解决各种三角形和锐角相关问题。
在实际应用中,锐角三角函数还广泛应用于测量和建模等领域。
总结起来,锐角三角函数是数学中不可或缺的一部分。
通过掌握和理解正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数,我们可以更好地理解和解决与锐角有关的各种数学和实际问题。
锐角三角函数知识点

锐角三角函数知识点锐角三角函数:一、基本概念:1、什么是锐角三角函数:锐角三角函数是一类特殊的函数,涉及到角度和角度对应的三角函数值,用于计算平面向量在多边形中和求解三角形的面积。
2、锐角三角函数的定义:锐角三角函数是基于角度θ,从而定义的三角函数值。
一般情况下,它用半圆线直叙指函数如下所示:sinθ,cosθ,tanθ,cotθ,secθ,cscθ。
3、锐角三角函数的基本关系:cosθ= sin (π/2-θ);sinθ= cos (π/2-θ);tanθ=cot (π/2-θ);cotθ=tan (π/2-θ);secθ=csc(π/2-θ);cscθ=sec (π/2-θ)。
二、圆周角:1、什么是圆周角:圆周角是指以圆等分线在a轴上的量度,即由圆心和两个点确定的弧的长度。
圆周角定义在一个圆的周围,与半径的长度有关,可以用角度μ来表示。
2、单位:圆周角的单位是弧度rad,又称为radian,表示当一个圆的半径为1时,圆周角的长度。
三、锐角的余弦定理:1、锐角余弦定理是用弦和角定义的三角形问题,可以求解共有三角形A、B、C三个锐角所对应边长a、b、c满足关系:a²=b²+c²-2bc cosA;b²=a²+c²-2ac cosB;c²=a²+b²-2ab cosC。
2、此外,锐角余弦定理也可以利用三角形所有边长求解A、B、C三个锐角所对应的角度值,记为A=cos-1[(b²+c²-a²)/2bc];B=cos-1[(a²+c²-b²)/2ac];C=cos-1[(a²+b²-c²)/2ab]。
四、锐角的正弦定理:1、锐角正弦定理是求解三角形的已知一边和两个对边角的问题,满足条件如下:a=b sinA/sinB;b=a sinB/sinA;c=a sinC/sinA,c=bsinC/sinB。
《锐角三角函数》课件
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性,周期为2π。
正弦函数的相位表示函数在水平方向上的移动,通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1,表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线,呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算,通常转化为同角三角函数的除法运算,再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算,注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质,如取值范围、增减性等,以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下,一些特殊角的三角函数值,如0°、30°、45°、60°、90°等,以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
2022中考数学第一轮考点系统复习第四章三角形第19讲解直角三角形及其应用讲本课件
AB=AC=10,BC=12,则tan∠OBD的值是( )A
1 A.
B.2
C. 6
D.
6
2
3
4
命题点2 解直角三角形的应用
5.(2021·十堰)如图,小明利用一个锐角是30°的三角板测操场旗杆EC的高度
,已知他与旗杆之间的水平距离BC为15 m,AB为1.5 m(即小明的眼睛与地
面的距离),那么旗杆EC的高度是( D)
2 3
2 3.
CD 2 3 (2 3)(2 3)
类比这种方法,计算tan22.5°的值为( B )
A. 2+1 C. 2
B. 2-1
1 D. 2
1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月12日星期六下午2时3分37秒14:03:3722.3.12 2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给
那些善于独立思考的人,给那些具有锲而不舍的人。2022年3月下午2时3分22.3.1214:03March 12, 2022 3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022年3月12日星期六2时3分37秒14:03:3712 March 2022
谢谢观赏
You made my day!
在Rt△BCE中,BE=CE·tan∠BCE=6×tan60°= 6 3(m) .
在Rt△AFD中,∠AFD=45°,∴AD=DF=(3 3 +6)m, ∴AB=AD+DE-BE=3 3+6+2 3-6 3=6- 3 ≈4.3(m).
答:宣传牌的高度AB约为4.3m.
命题点1 直角三角形的边角关系
△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( D )
锐角三角函数课件
余弦函数
1
定义和公式
余弦函数描述直角三角形中的比例关系,其定义和公式为cos(x) = 邻边/斜边。
2
图像和性质
余弦函数的图像呈现波浪形状,具有周期性、振幅和相位差等性质。
3
应用举例
余弦函数在几何、物理、工程等领域有广泛的应用,如研究周期性现象和计算机 图形学。
正切函数
定义和公式 图像和性质 应用举例
和差化积公式
三角函数的和差化积公式可 以将两个三角函数的和、差 表达为一个三角函数的乘积。
倍角公式
三角函数的倍角公式用于计 算两倍角的三角函数值。
总结
特点和应用
锐角三角函数具有周期性、对称性和广泛的 应用,为解决实际问题提供了重要的数学工 具。
实际生活中的应用举例
锐角三角函数在摄影、测量、物理仿真等实 际生活中有广泛的应用。
ห้องสมุดไป่ตู้
扩展和推广
锐角三角函数的研究和应用正在不断扩展和 推广,涉及到更多领域和复杂情况。
未来发展和研究方向
锐角三角函数的未来发展将涉及到更多领域 的交叉研究和深入探索。
正切函数用来描述直角三角形中的比例关系, 其定义和公式为tan(x) = 对边/邻边。
正切函数的图像呈现周期性、无界和渐近线等 特点,其图像在某些范围内会无限逼近无穷。
正切函数在物理、工程、电子等领域中常用于 信号处理和电路分析等方面。
三角函数的关系式
基本关系式
正弦、余弦和正切函数之间 有一系列关系式,如sin²θ + cos²θ = 1等。
特点
锐角三角函数的值域在特 定区间内,具有周期性和 对称性等特点。
正弦函数
定义和公式
正弦函数用来描述直角三角形 中的比例关系,其定义和公式 为sin(x) = 对边/斜边。
2020年中考数学第一轮复习 第十九讲 解直角三角形 知识点+真题
2020年中考数学第一轮复习教案第三章图形的认识与三角形第十九讲解直角三角形【基础知识回顾】一、锐角三角函数定义:在Rt△ABC中,∠C=900, ∠A、∠B、∠C的对边分别为a、b、c,则∠A的正弦可表示为:sinA= ,∠A的余弦可表示为cosA= ∠A的正切:tanA= ,它们统称为∠A的锐角三角函数注意:1、sinA、∠cosA、tanA表示的是一个整体,是两条线段的比,没有单位,这些比值只与有关,与直角三角形的无关2、取值范围<sinA< ,cosA< ,tanA>注意:1、三个特殊角的三角函数值都是根据定义应用直角三角形性质算出来的,要在理解的基础上结合表格进行记忆2、正弦和正切值随着角度的增大而余弦值随着角度的增大而3、几个特殊关系:⑴sinA+cos2A= ,tanA=sin A()⑵若∠A+∠B=900,则sinA= ,tanA·tanB=三、解直角三角形:1、定义:由直角三角形中除直角外的个已知元素,求出另外个未知元素的过程叫解直角三角形2、解直角三角形的依据:Rt∠ABC中,∠C=900 三边分别为a、b、c⑴三边关系:⑵两锐角关系⑶边角之间的关系:sinA cosA tanAsinB cosB tanB注意:解直角三角形中已知的两个元素应至少有一个是当没有直角三角形时应注意构造直角三角形,再利用相应的边角关系解决3、解直角三角形应用中的有关概念⑴仰角和俯角:如图:在图上标上仰角俯角 ⑵坡度坡角:如图:斜坡AB 的垂直度h 和水平宽度l 的比叫做坡度,用i 表示,即i= 坡面与水平面得夹角为 用字母α表示,则i=tanα=hl。
⑶方位角:是指南北方向线与目标方向所成的小于900的水平角 如图:OA 表示 OB 表示 OC 表示OD 表示 (也可称东南方向)3、 利用解直角三角形知识解决实际问题的一般步骤:⑴把实际问题抓化为数学问题(画出平面图形,转化为解直角三角形的问题)⑵根据条件特点,选取合适的锐角三角函数去解直角三角形 ⑶解出数学问题答案,从而得到实际问题的答案注意:在解直角三角形实际应用中,先构造符合题意的三角形,解题的关键是弄清在哪个直角三角形中用多少度角的哪种锐角三角函数解决【中考真题考点例析】考点一:锐角三角函数的概念例1 (2019年威海)如图,一个人从山脚下的A 点出发,沿山坡小路AB 走到山顶B 点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角三角函数
【课前热身】
1.在△ABC 中,∠C =90°,BC =2,sinA
=2
3
,则AC 的长是( ) A
.3 C .
4
5
D 2.Rt ∆ABC 中,∠C=︒90,∠A ∶∠B=1∶2,则sinA A .21
B .22
C .23
D .1
3.如图,在平面直角坐标系中,已知点A (3,0),
点B (0,-4),则cos OAB ∠ 等于_______. 4.︒
+︒30sin 130cos =____________.
5.王英同学从A 地沿北偏西60º方向走100m 到B 地,再从B 地向正南方向走200m 到C 地,此时王英同学离A 地 ( )
A .150m
B .350m
C .100 m
D .3100m
【考纲解读】
1.理解并掌握锐角三角函数的定义、性质和特殊角的三角函数值
2.会利用直角三角函数值解直角三角形
3.能运用解直角三角形的一般步骤解决实际生活、生产中的问题 【考点扫描】
1.sin α,cos α,tan α定义
sin α=____,cos α=_______,tan α=______ . 2.特殊角三角函数值
3.锐角三角函数之间的关系
22sin sin cos 1,tan cos α
αααα
+==
4.解直角三角形
由直角三角形中除直角外的已知元素,求出所有未知元素的过程叫做解直角三角形 (直角三角形中,除直角外一共有5个元素,即三条边和两个锐角) 5.解直角三角形的应用问题
(1)俯角、仰角(2)坡度、坡角(3)方向角 6.解直角三角形的步骤方法
(1)根据题目的已知条件,画出平面几何图形,找出已知条件中各量之间的关系
(2)是直角三角形的,根据边角关系进行计算;若不是直角三角形,应大胆尝试添加辅助线,构造直角三角形进行解决
用直角三角形的方法解决实际问题的关键是要根据实际情况建立数学模型,正确的画出图形,找准三角形.
α
a b
c
【典型例题】
例1 在△ABC 中,∠C = 90°,tan A =1
3
,求sin B .
练1.1 若3
cos 4
A =,则下列结论正确的为( )
A . 0°< ∠A < 30°
B .30°< ∠A < 45°
C . 45°< ∠A < 60°
D .60°< ∠A < 90°
练1.2 在Rt ABC △中,90C ∠= ,5AC =,4BC =,则tan A = . 例2 计算
:4sin 304560︒︒︒.
练2.1 计算
45tan 30
cos 60sin - 练2.2 △ABC 中,若(sinA -
12
)2
+
-cosB|=0,求∠C 的大小.
练2.3 等腰△ABC 中,AB =AC =5,BC =8,求底角∠B 的四个三角函数值.
例3 图中有两个正方形,A ,C 两点在大正方形的对角线上,△HAC •是等边三角形,若AB=2,求EF
的长.
练3 矩形ABCD 中AB =10,BC =8, E 为AD 边上一点,沿BE 将△BDE 对折,点D 正好落在AB 边上,求 tan ∠AFE .
例4 海中有一个小岛P ,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A 测得小岛P 在北偏东60°方向上,航行12海里到达B 点,这时测得小岛P 在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
_ E
_ A _ F _
D _ C _
B _
O _ H _ G F
A
B
C D E
A
B C
a α
练4.1 为了农田灌溉的需要,某乡利用一土堤修筑一条渠道,在堤中间挖出深为1.2米,下底宽为2
米,坡度为1:0.8的渠道(其横断面为等腰梯形),并把挖出来的土堆在两旁,使土堤高度比原来增加了0.6米.(如图所示) 求:(1)渠面宽EF ;
(2)修200米长的渠道需挖的土方数.
练4.2 如图,在测量塔高AB 时,选择与塔底在同一水平面的同一
直线上的C 、D 两点,用测角仪器测得塔顶A 的仰角分别是30°和60°.已知测角仪器高CE=1.5米,CD=30米,求塔高AB .(保留根号)
【课后作业】 中考真题集锦
1.(2010年毕节地区)在正方形网格中,ABC △的位置如图
所示,则cos B ∠的值为( )
A .1
2
B
.
2
C
D
2.(2010年浙江省东阳市)如图,为了测量河两岸A 、B 两点的距离,在与AB 垂直的方向点C 处 测得AC =a ,∠ACB =α,那么AB 等于 ( )
A 、a ·sin α
B 、a ·tan α
C 、a ·cos α
D 、α
tan a
3.(2010日照市)如图,在等腰Rt △ABC 中,∠C =90o ,AC =6,D 是AC 上一点,若tan ∠DBA =5
1
,则
AD 的长为( )
(A ) 2 (B )3 (C )2 (D )1
(第2题) (第3题) (第4题)
A
米
4.(2010年辽宁省丹东市)如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE
为5m ,AB 为1.5m (即小颖的眼睛距地面的距离),那么这棵树高是( )
A .
2+)m B .
(32
)m C ..4m 5(2010江苏宿迁)小明沿着坡度为1:2的山坡向上走了1000m ,则他升高了( )
A .5200m
B .500m
C .3500m
D .1000m 6.(2010年湖北黄冈市)在△ABC 中,∠C =90°,sinA =4
5
,则tanB = ( ) A .
43 B .34 C .
35 D
.45
7(2010辽宁省丹东市)45sin 60)4
︒-︒+
= 8(2010江苏宿迁)如图,在Rt △ABC 中,∠C =90°, AM 是BC 边上的中
线,5
3
sin =∠CAM ,则B ∠tan 的值为 .
9.(2010福建泉州) 如图,先锋村准备在坡角为0
30=α山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB 为__________米.
10.(2010重庆市) 已知:如图,在Rt △ABC 中,∠C =90°,AC = 3 .点
D 为BC 边上一点,且BD =2AD ,∠AD C =60°求△ABC 的周长(结果保留根号)
11.(2010年眉山市)23.如图,在一次数学课外实践活动中,要求测教学楼的高度AB .小刚在D 处用高
1.5m 的测角仪CD ,测得教学楼顶端A 的仰角为30°,然后向教学楼前进40m 到达E ,又测得教学楼顶端A 的仰角为60°.求这幢教学楼的高度AB .
13.(2010年山东省青岛市)小明家所在居民楼的对面有一座大厦AB ,AB =80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C 处测得大厦顶部A 的仰角为37°,大厦底部B 的俯角为48°.求小明家所在居民楼与大厦的距离CD 的长度.(结果保留整数)
14.(2010江苏泰州)庞亮和李强相约周六去登山,庞亮从北坡山脚C 处出发,以24米/分钟的速度攀登,同时,李强从南坡山脚B 处出发.如图,已知小山北坡
的坡度31
∶ i ,山坡长为240米,南坡的坡角是45°.问李强以什么速度攀登才能和庞亮同时到达山顶A ?(将山路
AB 、AC 看成线段,结果保留根号)
15 (2010年浙江省绍兴市)如图,小敏、小亮从A ,B 两地观测空中C 处一个气球,分
别测得仰角为30°和60°,A ,B 两地相距100 m .当气球 沿与BA 平行地飘移10秒后到达C ′处时,在A 处测得气 球的仰角为45°.
(1)求气球的高度(结果精确到0.1m);
(2)求气球飘移的平均速度(结果保留3个有效数字).
第13题图
第20题图
第16题
图②
图① 16(2010年山东聊城)建于明洪武七年(1374年),高度33米的光岳楼是目前我国现存的最高大、最古老
的楼阁之一(如图①).喜爱数学实践活动的小伟,在30米高的光岳楼顶楼P 处,利用自制测角仪测得正南方向商店A 点的俯角为60,又测得其正前方的海源阁宾馆B 点的俯角为30(如图②).求商店与海源阁宾馆之间的距离(结果保留根号).
17.(2010年山东省济南市)我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC ∥AD ,斜坡AB =40米,坡角∠BAD =600,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过450时,可确保山体不滑坡,改造时保持坡脚A 不动,从坡顶B 沿BC 削进到E
处,问BE 至少是多少米(结果保留根号)?。
