第四章单元同步测试题

合集下载

人教版八年级地理上册第四章中国的经济发展单元测试(含答案)

第四章中国的经济发展单元测试题（含答案）一.选择题（4*15=60分）1.目前，我国最重要的运输方式是（）A．铁路 B．公路 C．航空 D．水运2.下列各种交通运输方式中，哪些属于现代交通运输方式？（）①牛马拉车②风帆行船③公路运输④铁路运输⑤航空运输⑥管道运输⑦手提肩扛A．①②③④⑤⑦ B．③④⑤⑥⑦ C．②③④⑤⑥⑦ D．③④⑤⑥3.运输速度最快的运输方式是A. 航空运输B. 公路运输C. 水路运输D. 铁路运输4.有一沙漠探险队经过京沪线，陇海线和兰新线来到南疆，这支探险队最有可能来自（）A．上海 B．北京 C．武汉 D．广州5.甲、乙、丙、丁四位同学选择的交通运输方式，你认为合适的是（）A．甲同学从石家庄到香港旅游，选择铁路运输B．乙同学从重庆到武汉观赏三峡风光，选择空运C．上海的丙同学急需骨髓移植，台北有捐献的骨髓要运到上海，选择水运D．丁同学爸爸将500公斤活鱼从郊区水库运到城区市场，丁同学帮爸爸选择铁路运输6.我国农业在国民经济中的地位是（）A. 国民经济的主导B. 国民经济的基础C. 国民经济的关键D. 经济发展的先行官7.下列地区中，油菜开花最早的是（）A. 藏南谷地B. 四川盆地C. 长江三角洲D. 珠江三角洲8.精准扶贫，园地制宜，适合湘西山区种植的经济作物有A. 柑橘、茶叶B. 荔枝、核桃C. 甘蔗、芒果D. 甜菜、菠萝9.我国北方地区在农业生产中流传着这样的话：“春耕、夏种、秋收、冬藏”，你认为形成这种农业生产模式的主要影响因素是（）A. 纬度位置B. 海陆位置C. 地形D. 气候变化10.在某超市的农产品销售处的标签上，产品原产地的标注错误．．的是（）A. 蔗糖——广西B. 花生油——山东C. 茶叶——新疆D. 面粉——河北11.下列生产过程，不属于工业生产过程的是（）A．开采铁矿B．将大米加工成雪米饼 C．生产化肥、农药D．人工养殖珍珠12.发展和建立新兴高新技术产业的最重要条件是（）A．自然资源丰富 B．科技力量雄厚 C．劳动力充足 D．位置优越13.“互联网+”就是互联网+各个传统行业，是利用通信信息技术以及互联网平台，让互联网与传统行业进行深度融合，创造新的发展生态。

人教版小学四年级数学上册《第四章三位数乘两位数》单元同步测试题(有答案)

人教版小学四年级数学上册《第四章三位数乘两位数》单元同步测试题一、填一填．1．游隼是世界上俯冲飞行速度最快的鸟，当它俯冲追击猎物时，速度每小时可达300千米，可写作．2．两个因数相乘的积是48．如果一个因数不变，另一个因数乘5，则积是．3．180×50的积的末尾有个0，304×50的积的末尾有个0．4．根据32×30＝960，直接写出得数．64×60＝64×30＝32×60＝32×＝4805．卡车在普通公路上以每小时50千米的速度行驶，4小时可行千米．轿车在高速公路上行驶的速度是卡车在普通公路上速度的2倍，轿车用同样的时间可行千米．二、辨一辨．（对的画“√”，错的画“×”）6．两个因数的末尾一共有2个0，积的末尾就一定有2个0．（判断对错）7．三位数乘两位数积一定是四位数．（判断对错）8．速度＝路程÷时间．．（判断对错）9．在一个乘法算式里，两个因数同时乘2，积不变．（判断对错）10．苹苹骑自行车的速度是250米/分，她1小时行15000米．（判断对错）三、选一选．（将正确答案的序号填在括号里）11．最大的三位数与最小的两位数的积是（）A．990B．9000C．999012．计算时，竖式中的2与437相乘的实际意义是（）A．2×437B．20×437C．200×43713．两个因数相乘，一个因数乘6，另一个因数不变，那么积（）A．乘6B．除以6C．不变14．两个数相乘的积是35，如果一个因数乘10，另一个因数除以10，那么积是（）A．350B．3500C．3515．如果2□7×□6是一个三位数乘两位数的算式，那么下面三个数中，（）可能是它的得数．A．6538B．10332C．100332四、解答题16．笔算下面各题．275×34＝428×57＝470×36＝740×50＝306×48＝409×60＝17．在□里填上合适的数．18．先补充条件或问题，再填空．（1）一棵樱花树苗82元，，一共需要多少元？已知和，要求的是．（2）一架飞机5小时飞行了4000千米，？已知和，要求的是．七、解决问题．19．一个坏水龙头每分钟要白白流掉168克水，一刻钟要浪费掉多少克的水？20．春风小学四年级师生共198人，准备包车去看潮．旅行车包车的价格是39元/人，老师带8000元钱包车，够吗？可以用估算的方法哟!21．苹苹和依依今天去公园划船，她们平均每分钟划18米，每划15分钟就休息一会儿．今天一共划了5次，一共划了多少米？22．东方广场有一块长方形草坪（如图），把草坪的宽增加到32米，长不变．扩大后的草坪面积是多少？23．苏华电器江汉路店开张啦!（1）这一天苏华电器江汉路店销售的浦金微波炉一共卖了多少元？（2）如果不优惠，按原价销售，这一天可以多卖多少元？24．一辆汽车往返于甲、乙两地，去时的速度为56千米/时，共用5小时，返回时只用了4小时，这辆汽车返回时的速度是多少？参考答案与试题解析一、填一填．1．解：游隼是世界上俯冲飞行速度最快的鸟，当它俯冲追击猎物时，速度每小时可达300千米，可写作300千米/时．故答案为：300千米/时．2．解：由分析得出：两个因数相乘的积是48，如果一个因数不变，另一个因数乘以5，积也乘5，所以是：48×5＝240．故答案为：240．3．解：（1）计算180×50时，可先计算18×5，然后将两个因数后面的0加在积的后面，18×5＝90，则180×50＝9000，即积后面有3个0．（2）计算304×50时，可先计算304×5，然后将因数后面的0加在积的后面，304×5＝1520，则304×50＝15200，即积后面有2个0．故答案为：3，2．4．解：根据32×30＝960，直接写出得数．64×60＝384064×30＝192032×60＝192032×15＝480故答案为：3840，1920，1920，15．5．解：50×4＝200（千米）50×2×4＝100×4＝400（千米）答：卡车4小时行驶200千米，轿车用同样的时间可行400千米．故答案为：200，400．二、辨一辨．（对的画“√”，错的画“×”）6．解：假设这两个因数是30与40；30×40＝12001200的末尾有2个0所以，两个因数末尾一共有2个0，这两个因数的积的末尾一定有2个0．故答案为：√．7．解：根据题意，假设三位数是700，两位数是50；700×50＝35000；35000是五位数；所以，两位数乘三位数积一定是四位数是错误的．故答案为：×．8．解：因为速度＝路程÷时间，所以题中说法正确．故答案为：√．9．解：根据积的变化规律可知，在一个乘法算式里，两个因数同时乘2，积就扩大2×2＝4倍．所以原题说法错误．故答案为：×．10．解：1小时＝60分，250×60＝15000（米）15000＝15000答：她1小时行15000米．故答案为：√．三、选一选．（将正确答案的序号填在括号里）11．解：999×10＝9990最大的三位数与最小的两位数的积是9990．故选：C．12．解：计算时，竖式中的2与437相乘的实际意义是20×437．故选：B．13．解：根据积的变化规律可得，两个因数相乘，一个因数乘6，另一个因数不变，那么积乘6；故选：A．14．解：由分析得：一个因数乘10也就是第一个因数扩大10倍，另一个因数除以10也就是第二个因数缩小10倍，所以积不变，还是35．故选：C．15．解：2□7×□6的积是四位或五位数，积的个位是2 2□7×□6得数可能是10332．故选：B．四、解答题16．解：（1）275×34＝9350；（2）428×57＝24396；（3）470×36＝16920；（4）740×50＝37000；（5）306×48＝14688；（6）409×60＝24540．17．解：18．解：（1）条件：妈妈买了5棵樱花树苗（答案不唯一）。

人教版七年级数学上册第四章同步测试题(含答案)

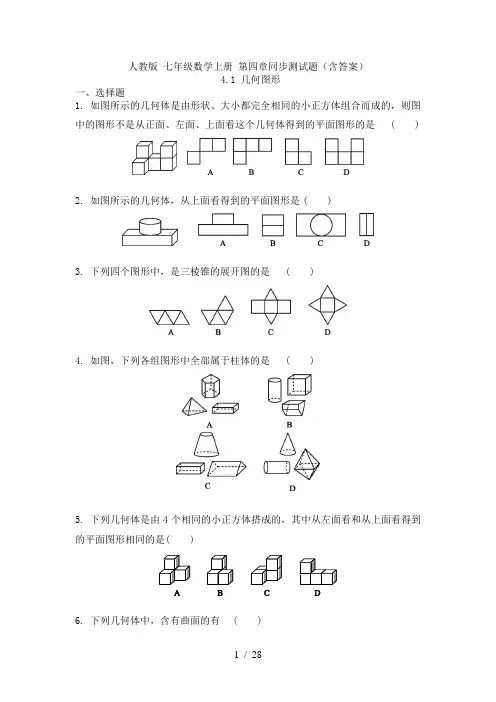
人教版七年级数学上册第四章同步测试题（含答案）4.1 几何图形一、选择题1. 如图所示的几何体是由形状、大小都完全相同的小正方体组合而成的，则图中的图形不是从正面、左面、上面看这个几何体得到的平面图形的是()2. 如图所示的几何体，从上面看得到的平面图形是()3. 下列四个图形中，是三棱锥的展开图的是()4. 如图，下列各组图形中全部属于柱体的是()5. 下列几何体是由4个相同的小正方体搭成的，其中从左面看和从上面看得到的平面图形相同的是( )6. 下列几何体中，含有曲面的有()A.1个B.2个C.3个D.4个7. 圆柱是由长方形绕着它的一边所在的直线旋转一周得到的，那么如图所示的几何体是图中的哪一个图形绕着直线旋转一周得到的()8. 将如图所示的长方体的表面展开，则得到的平面图形不可能是图中的 ()9. 如图，给定的是一个纸盒的外表面，图中的几何体能由它折叠而成的是()10. 如果一个棱柱有18条棱，那么它的底面一定是()A.十八边形B.八边形C.六边形D.四边形二、填空题11. 如图，观察生活中的物体，根据它们所呈现的形状，填出与它们类似的立体图形的名称：(1)______；(2)______；(3)__________；(4)________．12. 苏轼的诗句“横看成岭侧成峰，远近高低各不同”说明的现象是.13. 如图所示的图形中，是棱柱的有______．(填序号)14. 如图所示的8个立体图形中，是柱体的有，是锥体的有，是球的有.(填序号)15. 如图所示是某几何体的展开图，那么这个几何体是.16. 如图，把下列实物图和与其对应的立体图形连接起来.三、解答题17. 如图，有一个外观为圆柱形的物体，它的内部构造看不到，当分别用一组平面沿水平方向(自上而下)和竖直方向(自左而右)截这个物体时，得到了如图所示的(1)(2)两组形状不同的截面，请你试着说出这个物体的内部构造.18. 如图，是长方体的展开图，将其折叠成一个长方体，那么:(1)与点N重合的点是哪几个?(2)若AG=CK=14 cm，FG=2 cm，LK=5 cm，则该长方体的表面积和体积分别是多少?图19. 如图①是三个直立于水平面上的形状完全相同的几何体(下底面为圆，单位:cm)，将它们拼成如图②所示的新几何体，求新几何体的体积(结果保留π).人教版七年级数学上册 4.1 几何图形同步课时训练-答案一、选择题1. 【答案】A2. 【答案】C3. 【答案】A4. 【答案】B5. 【答案】B6. 【答案】B7. 【答案】A8. 【答案】C9. 【答案】B10. 【答案】C[解析] 一个棱柱有18条棱，则这个棱柱是六棱柱，六棱柱的底面是六边形.二、填空题11. 【答案】(1)圆柱(2)圆锥(3)圆柱、圆锥的组合体(4)球[解析] 立体图形实际上是由物体抽象得来的．12. 【答案】观察同一个物体，由于方向和角度不同，看到的图形往往不同13. 【答案】②⑥14. 【答案】①②⑤⑦⑧④⑥③15. 【答案】圆柱16. 【答案】①-C，②-B，③-D，④-E，⑤-A 连线略三、解答题17. 【答案】解:这个物体的内部构造为:圆柱中间有一球形空洞.18. 【答案】解:(1)与点N重合的点是点H，J.(2)由AG=CK=14 cm，LK=5 cm，可得CL=CK-LK=14-5=9(cm)，所以长方体的表面积为2×(9×5+2×5+2×9)=146(cm2)，体积为5×9×2=90(cm3).19. 【答案】解:π×22×(4+6)+[π×22×(4+6)]=40π+20π=60π(cm3).答:新几何体的体积为60π cm3.4.2直线、射线、线段同步练习试题（一）一．选择题1．平面上有三点A、B、C，如果AB＝10，AC＝7，BC＝3，那么（）A．点C在线段AB上B．点C在线段AB的延长线上C．点C在直线AB外D．点C可能在直线AB上，也可能在直线AB外2．下列四个生产生活现象，可以用公理“两点之间，线段最短”来解释的是（）A．用两个钉子可以把木条钉在墙上B．植树时，只要定出两棵树的位置，就能使同一行树坑在一条直线上C．打靶的时候，眼睛要与枪上的准星、靶心在同一直线上D．为了缩短航程把弯曲的河道改直3．有下列生活、生产现象：①从A地到B地架设电线，总是尽可能沿着线段AB架设．②用两个钉子就可以把木条固定在墙上．③植树时，只要确定两棵树的位置，就能确定同一行树所在的直线．④把弯曲的公路改直，就能缩短路程．其中能用“两点之间，线段最短”来解释的现象有（）A．①④B．②④C．①②D．③④4．已知点A，B，C在同一直线上，若AB＝20cm，AC＝30cm，点M、N分别是线段AB、AC中点，求线段MN的长是（）A．5cm B．5cm或15cm C．25cm D．5cm或25cm 5．已知点A，B，C为平面内三点，给出下列条件：①AC＝BC；②AB＝2BC；③AC ＝BC＝AB．选择其中一个条件就能得到“点C是线段AB中点”的是（）A．①B．③C．①或③D．①或②或③6．如图，点C是AB的中点，点D是BC的中点，下列结论：①CD＝AC﹣DB，②CD＝AB，③CD＝AD﹣BC，④BD＝2AD﹣AB，正确的有（）A．1个B．2个C．3个D．4个7．现实生活中“为何有人乱穿马路，却不愿从天桥或斑马线通过？”，请用数学知识解释图中这一现象，其原因（）A．两点之间，线段最短B．过一点有无数条直线C．两点确定一条直线D．两点之间线段的长度，叫做这两点之间的距离8．如图，某工厂有三个住宅区，A、B、C各区分别住有职工15人、20人、45人，且这三个区在一条大道上（A、B、C三点共线），已知AB＝1500m，BC＝1000m，为了方便职工上下班，该工厂打算从以下四处中选一处设置接送车停靠点，为使所有的人步行到停靠点的路程之和最小，那么该停靠点的位置应设在（）A．A住宅区B．B住宅区C．C住宅区D．B、C住宅区中间D处9．老爷爷从家到超市有甲、乙、丙三条路可以选择，在不考虑其它因素的情况下，他选择了乙路前往，则其中蕴含着的数学道理是（）A．两点确定一条直线B．两点之间线段最短C．连结直线外一点与直线上各点的所有线段中，垂线段最短D．在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线10．如图所示，某公司员工住在A，B，C三个住宅区，已知A区有2人，B区有7人，C区有12人，三个住宅区在同一条直线上，且AB＝150m，BC＝300m，D 是AC的中点．为方便员工，公司计划开设通勤车免费接送员工上下班，但因为停车位紧张，在A，B，C，D四处只能设一个通勤车停靠点，为使所有员工步行到停靠点的路程之和最小，那么停靠站应设在（）A．A处B．B处C．C处D．D处二．填空题11．如图所示是一段火车路线图，A、B、C、D、E是五个火车站，在这条线路上往返行车需要印制种火车票．12．点A到原点的距离为4，且位于原点的左侧，若一个点从A处向右移动2个单位长度，再向左移动7个单位长度，此时终点所表示的数为．13．如图，AE⊥AB于A点，DB⊥AB于B点，点P为线段AB上任意一点，若AE ＝2，DB＝4，AB＝8，则PE+PD的最小值是．14．曲桥是我国古代经典建筑之一，它的修建增加了游人在桥上行走的路程，有利于游人更好的观赏风光，如图，A、B两地间修建曲桥与修建直的桥相比，增加了桥的长度，其中蕴含的数学道理是．15．如图，建筑工人在砌墙时，经常用细线绳在墙的两端之间拉一条直的参照线，这样做的依据是．三．解答题16．如图所示，已知C、D是线段AB上的两个点，点M、N分别为AC、BD的中点．（1）若AB＝16cm，CD＝6cm，求AC+BD的长和M，N的距离；（2）如果AB＝m，CD＝n，用含m，n的式子表示MN的长．17．如图所示，把一根细线绳对折成两条重合的线段AB，点P在线段AB上，且AP：BP＝2：3．（1）若细线绳的长度是100cm，求图中线段AP的长；（2）从点P处把细线绳剪断后展开，细线绳变成三段，若三段中最长的一段为60cm，求原来细线绳的长．18．已知平面上点A，B，C，D（每三点都不在一条直线上）．（1）经过这四点最多能确定条直线．（2）如图这四点表示公园四个地方，如果点B，C在公园里湖对岸两处，A，D在湖面上，要从B到C筑桥，从节省材料的角度考虑，应选择图中两条路中的哪一条？如果有人想在桥上较长时间观赏湖面风光，应选择哪一条？为什么？19．已知如图，A，B，C三点在同一直线上，AB＝6，BC＝2．（1）已知点C在直线AB上，根据条件，请补充完整图形，并求AC的长；（2）已知点C在直线AB上，M，N分别是AB，BC的中点，根据条件，请补充完整图形，并求MN的长，直接写出MN与AC的长存在的数量关系；（3）已知点C在直线AB上，M，N分别是AC，BC的中点，根据条件，请补充完整图形，并求MN的长，直接写出MN与AB的长存在的数量关系．参考答案与试题解析一．选择题1．【解答】解：如图，在平面内，AB＝10，∵AC＝7，BC＝3，∴点C为以A为圆心，7为半径，与以B为圆心，3为半径的两个圆的交点，由于AB＝10＝7+3＝AC+BC，所以，点C在线段AB上，故选：A．2．【解答】解：A、根据两点确定一条直线，故本选项不符合题意；B、确定树之间的距离，即得到相互的坐标关系，故本选项不符合题意；C、根据两点确定一条直线，故本选项不符合题意；D、根据两点之间，线段最短，故本选项符合题意．故选：D．3．【解答】解：根据两点之间，线段最短，得到的是：①④；②③的依据是两点确定一条直线．故选：A．4．【解答】解：（1）当点C位于点B的右边时，MN＝（AC﹣AB）＝5cm，（2）当点C位于点A的左边时，MN＝（AC+AB）＝25cm故线段MN的长为5cm或25cm．故选：D．5．【解答】解：①点C在线段AB上，且AC＝BC，则C是线段AB中点故①不符合题意；②AB＝2BC，C不一定是线段AB中点故②不符合题意；③AC＝BC＝AB，则C是线段AB中点，故③符合题意．故选：B．6．【解答】解：∵点C是AB的中点，点D是BC的中点，∴AC＝BC＝AB，CD＝BD＝BC＝AC，∴①CD＝BC﹣DB＝AC﹣DB，正确；②CD＝BC＝AB，正确；③CD＝AD﹣AC＝AD﹣BC，正确；④BD＝AB﹣AD≠2AD﹣AB，错误．所以正确的有①②③3个．故选：C．7．【解答】解：现实生活中“为何有人乱穿马路，却不愿从天桥或斑马线通过？”，请用数学知识解释图中这一现象，其原因是两点之间，线段最短，故选：A．8．【解答】解：当停靠点在A区时，所有员工步行到停靠点路程和是：20×1500+45×2500＝142500m；当停靠点在B区时，所有员工步行到停靠点路程和是：15×1500+45×1000＝67500m；当停靠点在C区时，所有员工步行到停靠点路程和是：15×2500+20×1000＝57500m；当停靠点在D区时，设距离B区x米，所有员工步行到停靠点路程和是：15×（1500+x）+20x+45（1000﹣x）＝﹣10x+67500，由于k＝﹣10，所以，x越大，路程之和越小，∴当停靠点在C区时，所有员工步行到停靠点路程和最小．故选：C．9．【解答】解：图中三条路线，甲和丙是曲线，乙是线段，由两点间线段最短，∴乙最短，故选：B．10．【解答】解：BD＝（150+300）÷2﹣150＝75（m），以点A为停靠点，则所有人的路程的和＝7×150+12×（150+300）＝6450m，以点B为停靠点，则所有人的路程的和＝2×150+12×300＝3900m，以点C为停靠点，则所有人的路程的和＝2×（150+300）+7×300＝3000m，以点D为停靠点，则所有人的路程的和＝2×（150+300）÷2+7×75+12×（150+300）÷2＝3675m．故停靠点的位置应设在点C．故选：C．二．填空题11．【解答】解：图中线段有：AB、AC、AD、AE，BC、BD、BE，CD、CE、DE 共10条，∵每条线段应印2种车票，∴共需印10×2＝20种车票．故答案为：20．12．【解答】解：∵点A到原点的距离为4，且位于原点的左侧，∴点A表示的数为﹣4，∵一个点从A处向右移动2个单位长度，再向左移动7个单位长度，∴﹣4+2﹣7＝﹣9，故答案为：﹣9．13．【解答】解：过点D作DT⊥EA交EA的延长线于T，连接DE．∵AE⊥AB，DB⊥AB，DT⊥ET，∴∠B＝∠T＝∠BAT＝90°，∴四边形ABDT是矩形，∴BD＝AT＝4，AB＝DT＝8，∴ET＝AE+AT＝2+4＝6，∴DE＝＝＝10，∵PE+PD≥DE，∴PE+PD≥10，∴PE+PD的最小值为10．故答案为10．14．【解答】解：其中蕴含的数学道理是两点之间线段最短，故答案为：两点之间线段最短．15．【解答】解：建筑工人在砌墙时，经常用细线绳在墙的两端之间拉一条参照线，使垒的每一层砖在一条直线上，沿着这条线就可以砌出直的墙，则其中的道理是：两点确定一条直线．故答案为：两点确定一条直线．三．解答题16．【解答】解：（1）∵AB＝16cm，CD＝6cm，∴AC+BD＝AB﹣CD＝10cm，∴MN＝AB﹣（AM+BN）＝AB﹣（AC+BD）＝16﹣5＝11（cm）；（2）∵AB＝m，CD＝n，∴AC+BD＝AB﹣CD＝m﹣n，∴MN＝AB﹣（AM+BN）＝AB﹣（AC+BD）＝m﹣（m﹣n）＝．17．【解答】解：（1）∵AB＝100＝50，AP：BP＝2：3，∴AP＝20；（2）∵AP：BP＝2：3，∴设AP＝2x，BP＝3x，若一根绳子沿B点对折成线段AB，则剪断后的三段绳子中分别为2x，2x，6x，∴6x＝60，解得x＝10，∴绳子的原长＝2x+2x+6x＝10x＝100（cm）；若一根绳子沿A点对折成线段AB，则剪断后的三段绳子中分别为4x，3x，3x，∴4x＝60，解得x＝15，∴绳子的原长＝4x+3x+3x＝10x＝150（cm）；综上所述，绳子的原长为100cm或150cm．故答案为100cm或150cm．18．【解答】解：（1）经过这四点最多能确定6条直线：直线AB，直线AD，直线BC，直线CD，直线AC，直线BD，故答案为：6；（2）从节省材料的角度考虑，应选择图中路线2；如果有人想在桥上较长时间观赏湖面风光，应选择路线1，因为两点之间，线段最短，路线2比路线1短，可以节省材料；而路线1较长，可以在桥上较长时间观赏湖面风光．19．【解答】解：（1）如图，如图1，∵AB＝6，BC＝2．∴AC＝AB+BC＝8；如备用图1，AC＝AB﹣BC＝4．答：AC的长为8或4；（2）如图，∵M，N分别是AB，BC的中点，∴BM＝AB＝3，BN＝BC＝1，∴MN＝BM+BN＝3+1＝4，或MN＝BM﹣BN＝3﹣1＝2．答：MN的长为4或2；（3）如图，∵M，N分别是AC，BC的中点，∴MC＝AC＝4，NC＝BC＝1，∴MN＝MC﹣NC＝4﹣1＝34.3角同步练习试题（一）一．选择题1．如图，射线OA表示的方向是（）A．北偏东65°B．北偏西35°C．南偏东65°D．南偏西35°2．如图，∠AOC＝90°，OC平分∠DOB，且∠DOC＝22°36′，∠BOA度数是（）A．67°64′B．57°64′C．67°24′D．68°24′3．下列说法正确的是（）A．射线比直线短B．从同一点引出的两条射线所组成的图形叫做角C．若AP＝BP，则P是线段AB的中点D．两点之间的线段叫做这两点之间的距离4．下列语句错误的个数是（）①一个角的补角不是锐角就是钝角；②角是由两条射线组成的图形；③如果点C是线段AB的中点，那么AB＝2AC＝2BC；④连接两点之间的线段叫做两点的距离．A．4个B．3个C．2个D．1个5．按图1～图4的步骤作图，下列结论错误的是（）A．∠AOB＝∠AOP B．∠AOP＝∠BOPC．2∠BOP＝∠AOB D．∠BOP＝2∠AOP6．如图，用量角器度量∠AOB，可以读出∠AOB的度数为（）A．30°B．60°C．120°D．150°7．如图，小王从A处出发沿北偏东40°方向行走至B处，又从B处沿南偏东60°方向行走至C处，则∠ABC等于（）A．90°B．100°C．110°D．120°8．如图，将一副三角板按不同位置摆放，其中α和β互为余角的是（）A．B．C．D．9．如果∠1与∠2互补，∠2与∠3互余，那么∠1与∠3的关系是（）A．∠1＝90°+∠3 B．∠3＝90°+∠1 C．∠1＝∠3 D．∠1＝180°﹣∠310．为防止森林火灾的发生，会在森林中设置多个观测点，如图，若起火点M 在观测台B的南偏东46°的方向上，点A表示另一处观测台，若AM⊥BM，那么起火点M在观测台A的（）A．南偏东44°B．南偏西44°C．北偏东46°D．北偏西46°二．填空题11．若两个角互补，且度数之比为3：2，求较大角度数为．12．若∠A＝59.6°，则它的余角为°′．13．将一副三角板按如图方式摆放在一起，且∠1比∠2大20°，则∠1的度数等于．14．如图，点C在点B的北偏西60°的方向上，点C在点A的北偏西30°的方向上，则∠C等于度．15．如图，点A在点O的北偏西60°的方向上，点B在点O的南偏东20°的方向上，那么∠AOB的大小为°．三．解答题16．如图所示，O为直线上的一点，且∠COD为直角，OE平分∠BOD，OF平分∠AOE，∠BOC+∠FOD＝117°，求∠BOE的度数．17．如图，已知∠AOB＝128°，OC平分∠AOB，请你在∠COB内部画射线OD，使∠COD和∠AOC互余，并求∠COD的度数．18．已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD，OE．（1）如图①，当∠BOC＝40°时，求∠DOE的度数；（2）如图②，当射线OC在∠AOB内绕O点旋转时，OD，OE始终是∠AOC与∠BOC的平分线．则∠DOE的大小是否发生变化，说明理由；（3）当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时，OD，OE仍始终是∠AOC与∠BOC的平分线，直接写出∠DOE的度数（不必写过程）．19．如图①，点O为直线AB上一点，过点O作射线OC，将一直角三角板如图摆放（∠MON＝90°）．（1）若∠BOC＝35°，求∠MOC的大小．（2）将图①中的三角板绕点O旋转一定的角度得图②，使边OM恰好平分∠BOC，问：ON是否平分∠AOC？请说明理由．（3）将图①中的三角板绕点O旋转一定的角度得图③，使边ON在∠BOC的内部，如果∠BOC＝50°，则∠BOM与∠NOC之间存在怎样的数量关系？请说明理由．参考答案与试题解析一．选择题1．【解答】解：射线OA表示的方向是南偏东65°，故选：C．2．【解答】解：∵OC平分∠DOB，∴∠DOC＝∠BOC＝22°36′．∵∠AOC＝∠AOB+∠BOC＝90°，∴∠AOB＝∠AOC﹣∠BOC＝90°﹣22°36′＝67°24′．故选：C．3．【解答】解：A．射线和直线不可以比较长短，原说法错误，故本选项不符合题意；B．从同一点引出的两条射线所组成的图形叫做角，原说法正确，故本选项符合题意；C．若点P在线段AB上，AP＝BP，则P是线段AB的中点，原说法错误，故本选项不符合题意；D．两点之间的线段的长度叫做这两点之间的距离，原说法错误，故本选项不符合题意；故选：B．4．【解答】解：①直角的补角是直角，故原说法错误；②角是由有公共的端点的两条射线组成的图形，故原说法错误；③如果点C是线段AB的中点，那么AB＝2AC＝2BC，说法正确；④连接两点之间的线段的长度叫做两点的距离，故原说法错误．故错误的个数有①②④共3个．故选：B．5．【解答】解：∵OP是∠AOB的平分线，∴∠AOB＝2∠AOP＝2∠BOP，∠AOP＝∠BOP＝∠AOB，∴选项A、B、C均正确，选项D错误．故选：D．6．【解答】解：看内圈的数字可得：∠AOB＝120°，故选：C．7．【解答】解：如图：∵小王从A处沿北偏东40°方向行走至点B处，又从点B处沿南偏东60°方向行走至点C处，∴∠DAB＝40°，∠CBE＝60°，∵向北方向线是平行的，即AD∥BE，∴∠ABE＝∠DAB＝40°，∴∠ABC＝∠ABE+∠EBC＝40°+60°＝100°．故选：B．8．【解答】解：A、α和β互余，故本选项正确；B、α和β不互余，故本选项错误；C、α和β不互余，故本选项错误；D、α和β不互余，故本选项错误．故选：A．9．【解答】解：∵∠1+∠2＝180°∴∠1＝180°﹣∠2又∵∠2+∠3＝90°∴∠3＝90°﹣∠2∴∠1﹣∠3＝90°，即∠1＝90°+∠3．故选：A．10．【解答】解：如图：因为AM⊥BM，所以∠2+∠3＝90°，因为南北方向的直线平行，所以∠2＝46°，∠1＝∠3，所以∠3＝90°﹣∠2＝90°﹣46°＝44°，所以∠1＝44°，所以起火点M在观测台A的南偏西44°，故选：B．二．填空题11．【解答】解：因为两个角的度数之比为3：2，所以设这两个角的度数分别为（3x）°和（2x）°．根据题意，列方程，得3x+2x＝180，解这个方程，得x＝36，所以3x＝108．即较大角度数为108°．故答案为108°．12．【解答】解：∵∠A＝59.6°，∴∠A的余角为90°﹣59.6°＝30.4°＝30°24'，故答案为30；24．13．【解答】解：设∠2为x，则∠1＝x+20°；根据题意得：x+x+20°＝90°，解得：x＝35°，则∠1＝35°+20°＝55°；故答案为：55°．14．【解答】解：如图：根据题意可得：∠1＝60°，∠2＝30°，∵AE∥DB∥CF，∴∠BCF＝∠1＝60°，∠ACF＝∠2＝30°，∴∠ACB＝30°．故答案为：30．15．【解答】解：如图，∵点A在点O北偏西60°的方向上，∴OA与西方的夹角为90°﹣60°＝30°，又∵点B在点O的南偏东20°的方向上，∴∠AOB＝30°+90°+20°＝140°．故答案为：140．三．解答题16．【解答】解：设∠BOE＝α°，∵OE平分∠BOD，∴∠BOD＝2α°，∠EOD＝α°．∵∠COD＝∠BOD+∠BOC＝90°，∴∠BOC＝90°﹣2α°．∵OF平分∠AOE，∠AOE+∠BOE＝180°，∴∠FOE＝∠AOE＝（180°﹣α°）＝90°﹣α°，∴∠FOD＝∠FOE﹣∠EOD＝90°﹣α°﹣α°＝90°﹣α°，∵∠BOC+∠FOD＝117°，∴90°﹣2α°+90°﹣α°＝117°，∴α＝18，∴∠BOE＝18°．17．【解答】解：作OD⊥OA，则∠COD和∠AOC互余，如图所示．∵∠AOB＝128°，OC平分∠AOB，∴∠AOC＝∠AOB＝64°，∵∠COD和∠AOC互余，∴∠COD＝90°﹣∠AOC＝26°．18．【解答】解：（1）如图，∠AOC＝90°﹣∠BOC＝50°，∵OD、OE分别平分∠AOC和∠BOC，∴∠COD＝∠AOC＝25°，∠COE＝∠BOC＝20°，∴∠DOE＝∠COD+∠COE＝45°；（2）∠DOE的大小不变，理由是：∠DOE＝∠COD+∠COE＝∠AOC+∠BOC＝（∠AOC+∠BOC）∠AOB ＝45°；（3）∠DOE的大小分别为45°和135°，如图3，则∠DOE为45°；如图4，则∠DOE为135°．分两种情况：如图3所示，∵OD、OE分别平分∠AOC和∠BOC，∴∠COD＝∠AOC，∠COE＝∠BOC，∴∠DOE＝∠COD﹣∠COE＝（∠AOC﹣∠BOC）＝45°；如图4所示，∵OD、OE分别平分∠AOC和∠BOC，∴∠COD＝∠AOC，∠COE＝∠BOC，∴∠DOE＝∠COD+∠COE＝（∠AOC+∠BOC）＝×270°＝135°．19．【解答】解：（1）∵∠MON＝90°，∠BOC＝35°，∴∠MOC＝∠MON+∠BOC＝90°+35°＝125°．（2）ON平分∠AOC．理由如下：∵∠MON＝90°，∴∠BOM+∠AON＝90°，∠MOC+∠NOC＝90°．又∵OM平分∠BOC，∴∠BOM＝∠MOC．∴∠AON＝∠NOC．∴ON平分∠AOC．（3）∠BOM＝∠NOC+40°．理由如下：∵∠CON+∠NOB＝50°。

人教版八年级上册物理第四章单元测试题

人教版八年级上册物理第四章单元测试题姓名:________ 班级:________ 成绩:________一、单选题1 . 下列现象中，可用光的直线传播原理解释的是A．B．C．D．2 . 光沿与镜面15°角射到平面镜上，则反射角为A．15°B．30°C．60°D．75°3 . 下列有关光学的知识，叙述正确的是A．太阳光是由红、绿、蓝三种色光组成的B．光垂直入射到平面镜上，反射角是90度C．玻璃幕墙反射太阳光造成光污染是漫反射D．电视机的遥控器是利用红外线控制电视机4 . 如图示的现象中，属于光的反射现象的是A．水中倒影B．日食形成C．小孔成像D．铅笔“折断”5 . 如图是电磁波及其应用实例，下列说法正确的是A．紫外线是紫色的B．体检胸透用的X射线频率比无线电波低C．电视机遥控器用γ射线遥控D．可见光与无线电波在真空中的传播速度相同6 . 下列光现象中，与小孔成像原理相同的是（）A．大象在水中的倒影B．钢勺在水面处“折断”C．海市蜃楼D．手影7 . 如图是同学们探究“平面镜成像特点”的几种情景，下列说法正确的是（）A．若蜡烛A距玻璃板4cm，则蜡烛B距玻璃板8cm才能与蜡烛A的像完全重合B．若蜡烛A在玻璃板中的像偏高且倾斜，则丙图是产生该现象的原因C．若在玻璃板与蜡烛B之间放一块挡光板，则不能透过玻璃看到蜡烛A的像D．此实验选用玻璃代替平面镜，是因为玻璃不仅能反射光成像，还能透光便于找到像的位置8 . 下图中是物体在平面镜中成像的情况，正确的是（）A．B．C．D．9 . 如下短句或词语涉及到的知识与光的直线传播无关的是A．立竿见影B．一叶障目C．五彩缤纷D．坐井观天，所见甚小二、多选题10 . 如图所示，①②③④为物理学习中做的四个实验，abcd为应用实例，箭头表示实验和应用的对应关系，其中对应关系正确的是A．B．C．D．三、填空题11 . 射到平面镜上的平行光反射后___________平行的（选填“可能是”、“仍然是”、“不是”），称为________反射；电影院里，观众坐在不同位置都能看清幕布上的影像，是光的________反射．12 . 小明用蜡烛和玻璃板做探究“平面镜成像时物距和像距是否相等”，该实验需要做三次，这样做的目的是_______。

人教版高中化学选修4第四章《电化学基础》单元测试试题(含答案)

第四章《电化学基础》单元测试题一、单选题（每小题只有一个正确答案）1．利用反应 Zn+Cu2+= Zn2++ Cu 设计成原电池。

则该电池的负极、正极和电解质溶液选择合理的是（）A．Zn、 Cu、 ZnSO4 B． Cu、 Zn、 ZnCl 2C．Cu、 Zn、 CuCl2 D． Zn、 Cu、 CuSO42．控制适合的条件，将反应 2Fe3＋＋2I －2Fe2＋＋I 2设计成如下图所示的原电池。

下列判断不正确的是（）A．为证明反应的发生，可取甲中溶液加入铁氰化钾溶液B．反应开始时，甲中石墨电极上Fe3＋被还原，乙中石墨电极上发生氧化反应C．电流计读数为零时，在甲中溶入FeCl 2固体时，甲中的石墨电极为正极D．此反应正反应方向若为放热，电流计读数为零时，降低温度后乙中石墨电极为负极 3．某同学组装了如图所示的电化学装置，电极Ⅰ为Zn，其他电极均为Cu，电解质溶液都是 CuSO4 溶液，则下列说法正确的是（）A．电子移动：电极Ⅰ→电极Ⅳ→电极Ⅲ→电极ⅡB．电极Ⅰ发生还原反应C．电极Ⅳ逐渐溶解D．电极Ⅲ的电极反应： Cu－ 2e－=Cu2＋4．已知海水中含有的离子主要有Na+、 Mg2+、 Cl －、Br－，利用下图装置进行实验探究，列说法正确的是（）A． X为锌棒， K置于 M，可减缓铁的腐蚀，铁电极上发生的反应为2H＋＋ 2e－＝H2↑B．X 为锌棒， K置于 M，外电路电流方向是从 X到铁C．X 为碳棒， K置于 N，可减缓铁的腐蚀，利用的是外加电流的阴极保护法D．X 为碳棒， K置于 N，在 X电极周围首先失电子的是 Cl－5．下列解释事实的反应方程式不正确的是（）A.热的纯碱溶液可去除油污： CO32－ +2H2O H2CO3+2OH－B.钢铁发生吸氧腐蚀时，铁作负极被氧化： Fe－2e－＝ Fe2+C.以 Na2S为沉淀剂，除去溶液中的 Cu2+：Cu2++S2－＝CuS↓D.向电解饱和食盐水的两极溶液中滴加酚酞，阴极变红：2H2O+2e－==H2↑+2OH-6．化学与科学、技术、社会、环境密切相关。

第4章《光现象》单元测试卷(基础卷) 带解析

第四章《光现象》单元测试卷（基础卷）（解析版）（考试时间：90分钟试卷满分：100分）注意事项：1．测试范围：人教版八年级上册第4章。

第Ⅰ卷选择题一、选择题（本题共16小题，每小题2分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．中午12：00时，若太阳光垂直射入纸板上一个很小的“△”形孔，那么在地面上形成的光斑的形状是（）A．“”形B．“”形C．“△”形D．“”形【答案】A【分析】当光沿直线传播经过很小的孔时，就能形成物体倒立的像，这就是小孔成像；像的形状与物体的形状有关，与小孔的形状无关。

【解答】解：太阳光垂直照射在刻有一个很小的“Δ”形孔的纸板上，由于光沿直线传播，在地面上形成太阳的像，像的形状与太阳的形状一样，与小孔的形状无关；故A正确，BCD错误。

故选：A。

2．双阳“彩虹桥”的美丽夜景如图所示，其水中“倒影”的形成是由于（）A．光的反射B．光的折射C．光的直线传播D．光的色散【答案】A【分析】光遇到水面、玻璃以及其他许多物体的表面都会发生反射。

【解答】解：平静的水面上有“彩虹桥”的倒影，属于平面镜成像，属于光的反射现象。

故选：A。

3．2022年11月8日，延边出现了美丽的月食，下列现象中与月食成因相同的是（）A．雨后彩虹B．形影不离C．水中倒影D．池水变浅【答案】B【分析】光在同种均匀介质中沿直线传播，逐项分析各情景运用的光学知识进行作答。

【解答】解：月食的原理是光沿直线传播。

A．雨过天晴时，常在天空出现彩虹，这是太阳光通过悬浮在空气中细小的水珠折射而成的，白光经水珠折射以后，分成各种彩色光，这种现象叫做光的色散现象，所以说雨后的天空出现彩虹是由光的色散形成的，故A不符合题意；B．形影不离是由于光沿直线传播形成的，与月食成因相同，故B符合题意；C．水面相当于平面镜，水中倒影是平面镜成像现象，是由于光的反射形成的，故C不符合题意；D．水池变浅是因为光的折射形成的，故D不符合题意；故选：B。

人教版七年级数学上册第四章同步测试题及答案解析.doc

最新人教版七年级数学上册第四章同步测试题及答案解析课时作业（三十四）7[4」.1立体图形与平面图形]建议用时实际用时分值实际得分30分钟50分—、选择题（每小题4分，共计12分）1. 一个正方体的每个面都有一个汉字，其展开图如图所示，那么在该正方体中和“值”字相对的字是（A）A.记B.观C.心D.间解析：对于正方体的平面展开图中相对的面一定相隔一个小正方形，由图形可知，与“值”字相对的字是“记” •2.如图，不是三棱柱的展开图的是（C）解析：因为三棱柱的表面展开以后，两个底面不可能在侧面展开图的同一侧，所以选项C不是三棱柱的展开图.3.下面的三种形状图所对应的直观图是（C）解析：通过观察想象易知此物体由两部分组成，上方是一个扁圆柱，下方是一个长方体•故选C.二、填空题（每小题6分，共计12分）4.下列儿种儿何图形：①长方形；②梯形；③正方形；④圆柱；⑤圆锥；⑥球.其中是立体图形的是④⑤⑥（只填序号）.解析：圆柱、圆锥、球是立体图形.5.在如图所示的展开图中，分别填上数字1,2,3,4,5,6,使得折叠成正方体后，相对面上的数字之和相等，则tz = 6, b=2, c=4.513a cb解析：1与Q相对，5与b相对，3与c相对，•・T+a=5+b=3+c,六个面上的数字分别为1,2,3,4,5,6,三、解答题（共计26分）6.（满分8分）把下列立体图形与其对应的名称用线连起来.的形状图.解：从正面看，有3列，左边第1列有1层，第2列有3层，第3列有2层；从左面看，有3列，前面一列有2层，中间一列有3层，后面一列有1层；从上面看，有3列，从左面数第1列，有1个正方形，第2列有2个正方形，第3列有1个正方形.此几何体的三种形状图如图所解:圆柱圆锥正方体棱柱长方体示：从上面看8.（满分10分）小强在学习“丰富多彩的几何图形”吋，对探究正方体的平面展开图产生了浓厚的兴趣.他发现正方体的平面展开图是由6个大小相同的正方形拼接而成的，并在方格纸上先画出了如图所示的5个正方形（阴影部分），请你再画一个正方形，使它成为正方体的平面展开图.要求：①分别给出三种不同的画法；②将所画的正方形涂上阴影.解：如图所示:课时作业（三十五）[4」.2点、线、面、体]建议用时实际用时分值实际得分30分钟50分—、选择题（每小题6分，共计12分）1. 下面四个几何体中，含有曲面的个数是（B ）解析：球、圆锥都含有一个曲面，而正方体、棱柱中不含曲面.A. 12.如图将三角形绕直线/旋转一周，可以得到图（E）所示的是（B）解析：（1）和（3）有6个面，（2）有两个底面和一个侧面，共3个面，（4）只有一个面，（5）有两个面，（6）有4个面.4. 飞机表演“飞机拉线”，我们用数学知识可解释为点动成线.用数学知识解释下列现象:（1）一只蚂蚁行走的路线可以解释为点动成线；（2）自行车的辐条运动可解释为线动成面；（3） —个直角三角形纸板以它的一条直角边所在的直线为轴旋转可解释为竝成佐」解析：从实例中抽象出点、线、面、体，抓住点、线、面、体之间的关系进行解答.5. 如图，左排的平面图形绕轴旋转一周，可以得到右排的立体图形，那么与甲、乙、丙、丁各平面图形顺序对应的立体图形的编号应为③④①②.A.图(A) C.图(C)L LdI I III I a i ll(C)(D)D.图(D)解析：绕直角三角形一条直角边旋转可得到圆锥.本题要求得到两个圆锥的组合体，那么一定是两个直角三角形的组合体，两条直角边相对，绕另一直角边旋转而成的.故选B.二、填空题（每小题6分，共计18分）3.在下列几何体中，三个面的有辺，四个面的有⑹（填序号）.(E)甲乙丙丁丨①②③④解析：甲旋转后得到③，乙旋转后得到④，丙旋转后得到①，丁旋转后得到②.故与甲、乙、丙、丁各平面图形顺序对应的立体图形的编号应为③④①②.三、解答题（共计20分）6.（满分10分）一个五棱柱如图所示，它的底面边长都是4 cm,狈ij棱长6 cm,回答下列问题:(1)这个五棱柱一共有多少个面？它们分别是什么形状？哪些面的形状、面积完全相同？(2)这个五棱柱一共有多少条棱？它们的长度分别是多少？解：(1)这个五棱柱一共有7个面；其中5个是长方形，2个是五边形，2个五边形的底面形状、面积完全相同，所有的侧面形状、面积完全相同.(2)这个五棱柱一共有15条棱，5条侧棱长度彼此相等，都等于6cm;围成底面的所有棱长都相等，都等于4 cm.7.(满分10分)如图：将一个长方形沿它的长或宽所在的肓线旋转一周，回答下列问题：占 ----II⑴得到什么几何体？(2)长方形的长和宽分别为6 cm和4 cm,分别绕它的长或宽所在直线旋转一周，得到不同的几何体，它们的体积分别为多少？(结果保留町解：(1)得到的是圆柱；(2)绕宽旋转得到的圆柱的底面半径为6 cm,高为4 cm,体积=TC X62X4=144K (cm3): 绕长旋转得到的圆柱底面半径为4 cm,高为6 cm,体积=兀X4, X 6 = 96兀(cm3).课时作业(三十六)[4.2直线、射线、线段第1课时]—、选择题(每小题4分，共计12分)1.如图，小明的爸爸只用两枚钉子就把一根木条固定在墙上，下列语句能解释这个原理的是(B)A.木条是直的B.两点确定一条直线C.过一点可以画无数条直线D.一个点不能确定一条直线解析：根据两点确定一条直线，故选B.2-对于直线力仪线段CQ,射线EF,在下列各图中能相交的是(B)解析：B 选项中直线与射线能相交；A 选项中CQ 是线段不延长所以不和直线相交;C 选项中线段CD 与射线EF 不相交；D 选项直线和射线EF 不能相交.3. 延长线段到C,下列说法正确的是(B)A •点C 在线段MB 上 B.点C 在直线MB 上 C ・点C 不在直线MB 上D •点C 在直线必的延长线上解析：因为线段有两个端点，所以线段可以向两方延长，所以点C 不在线段AB ±，点 C 在直线上,故A, C 错误，B 正确，因为直线没有端点，可以向两方无限延伸，直线没有延长线的说法，故D 错误.故选B.二、填空题(每小题4分，共计12分)4•要在墙上钉一根小木条，至少要西个钉子，用数学知识解释为两点确定一条直线. 解析：根据直线的性质：经过两点有一条直线，并且只有一条直线，所以至少要两个钉子.5.如图所示，OA, 是两条射线，C 是CU 上一点，D, E 是上两点，则图中共有匕条线段，它们分别是OC, OD, ()E, CD, CE, DE ；图中共有丄条射线，它们分别是C4,OM, OB, DE, EB.ABD FCD6.平面内不同的两点确定一条直线，不同的三点最多确定三条直线.若平面内的不同的n个点最多可确定15条直线，则n的值为6.解析：平面两点画1条直线，三点最多确定3 = 1+2条直线，四点最多确定6=1+2 + 3 条直线，五点最多确定10=1+2 + 3+ 4条直线，六个点最多确定15 = 1+2 + 3+4+5条直线.三、解答题(共计26分)7.(满分8分)如图，直线上有4个点，问：图中有几条线段？几条射线？几条直线？A B C D解：线段力伏线段/1C,线段AD,线段BC,线段BD,线段CQ共6条；以每个点为端点的射线有两条，共8条；直线有1条.8.(满分8分)如图所示，读句画图.(1)连接/C和交于点O；(2)延长线段AD, BC,它们交于点(3)延长线段CD与AB的反向延长线交于点F.解：如图所示:9.(满分10分)动手画一画，再数数.(1)过一点/能画几条直线？(2)过两点力，〃能画几条直线？(3)己知平面上共有三个点B, C,过其中任意两点画直线，可画几条？(4)已知平面上共有四个点B, C, D,过其中任意两点画直线，那么可画多少条直线？(5)已知平面上共有77个点(〃为不小于3的整数)，其中任意三个点都不在同一直线上，那么连接任意两点，可画多少条直线？解：(1)过一点/能画无数条直线.(2)过两点力，B只能画一条直线.(3)①若三点共线则可画一条，②若三点不共线则可画三条，故可画1条或3条.(4)①若四点共线则可画1条，②若三点共线则可画4条，③若任意三点不共线则可画6 条，故可画1条或4条或6条.(5)根据过两点的直线有1条，过不在同一直线上的三点的直线有3条，过任何三点都不在一条直线上四点的直线有6条，按此规律由特殊到一般可得：根据过两点的直线有1条，过不在同一直线上的三点的直线有3条，过任何三点都不在一条直线上四点的直线有6条，按此规律可得共能画如(〃一1).课时作业(三十七)[4.2直线、射线、线段第2课时]—、选择题(每小题4分，共计12分)1.如图，长度为12 cm的线段的中点为M, C点将线段分成MC ： CB=\ : 2, 则线段/C的长度为(B)•• ••4 M C BA. 2 cmB. 8 cmC・ 6 cm D. 4 cm解析：J长度为12cm的线段的中点为M,:.AM=BM=(>, TC 点将线段⑷分成MC ：CB=\ : 2,・・・MC=2, CB=4,・・・/C=6+2 = 8.故选B.2.判断下列语句中：①线段就是B两点间的距离；②线段力3的一半就是线段力3的中点；③在所有连接两点的线中，直线最短；④如果AB=BC=CD,则AD=3AB.其中错误语句的个数是(D)A. 0个B. 2个C. 3个D. 4个解析：线段和线段的中点都是几何图形，而3两点间的距离和线段的一半都是数量，形与数不能划等号；③把线段与直线的性质混淆了；④中的三条线段可能不在一条直线上，因此，这四个语句都是错误的.3.如图所示，从力地到达E地，最短的路线是(B)C・Am D・A-C-GfEfB解析：由题意从/地到达B地，由图知，要先到E地再到B地，是一条直线，故最短•/到E 有四种选择，根据两点之间线段最短知：因为A,F,E在一条直线上，所以A-F-E 路线最短.二、填空题(每小题4分，共计12分)4・如图，若CB等于15 cm, DB等于23 cm, MD是/C的中点，则AC= 16 cm.I ______ I ______I ______________ IADC B解析：VC5=15 cm, DB=23 cm, :.DC=DB-CB = 23~15 = 8(cm),・.・Q 是力C 的中点，:.AC= 2DC= 2X8=16(cm).5.小明从家到学校有4条路可走，如图所示.若想走最短的路，应该选择第②条路，这是根据两点之间，线段最短.解析：根据两点之间，线段最短可得想走最短的路，应该选择第②条路.6.已知线段AB=8 cm,在直线AB上画线段3C使BC=3 cm,则线段AC= 5 cm 11 cm.解析：根据题意，点C可能在线段上，也可能在力B的延长线上.若点C在线段MB 上，则/C=/B—BC=8 — 3 = 5(cm);若点C在的延长线上，则/C=/B+BC=8 + 3 = 1 l(cm)・三、解答题(共计26分)7.(满分8分)如图所示，力，B是两个村庄，若要在河边/上修建一个水泵站往两村输水，问水泵站应修在河边的什么位置，才能使铺设的管道最短，并说明理由..4B解：如图，过点B作线段与直线/的交点尸即为所求水泵站的点，因为两点之间，线段最短.8.(满分8分)有两根木条，一根M长为80 cm,另一根CD长为130 cm,在它们的中点处各有一个小圆孔M, N(圆孔直径忽略不计，M, N抽彖成两个点)，将它们的一端重合, 放置在同一条直线上，此时两根木条的小圆孔之间的距离MN是多少？M/VI ............. a ............... I I o ------ 1A B C DA.Am B・A—F—EfB解：本题有两种情形：(1)当力，C(或3, D)重合,且剩余两端点在重合点同侧时，MN=CN-AM=^CD-^AB=65-40=25(cm);(2)当3, C(或D)重合,且剩余两端点在重合点两侧时，MN= CN+BM=^CD+^AB=65+40=105(cm)・故两根木条的小圆孔之间的距离MN是25 cm或105 cm.9.(满分10分)如图所示，某公司员工分别住B, C三个住宅区，力区有30人，B区有15人，C区有10人.三个区在同一条直线上，该公司的接送车打算在此间设一个停靠点，为使所有员工步行到停靠点的路程之和最小，那么停靠点的位置应设在哪个区？100 m 200 m•••.4 B C解：所有员工步行到停靠点/区的路程之和为：0X30+100X 15+(100+200)X 10= 0+1 500 + 3 000=4 500(m);所有员工步行到停靠点B区的路程之和为：100X30+0X 15+200X 10= 3 000+0+2 000=5 000(m);所有员工步行到停靠点C区的路程之和为：(100+200)X30+15X200+10X0= 9 000+3 000+0 =12 000(m).因为4 500<5 000<12 000,所以所有员工步行到停靠点/区的路程之和最小，所以停靠点的位置应设在力区.课时作业（三十八）[4.3.1 角]—、选择题（每小题4分，共计12分）1.下列关于角的说法正确的个数是（A）①角是由两条射线组成的图形；②角的边越长，角越大；③在角一边延长线上取一点④角可以看作由一条射线绕着它的端点旋转而形成的图形.A・1个 B. 2个C. 3个D・4个解析：①角是由有公共端点的两条射线组成的图形，故本选项错误；②角的大小与开口大小有关，角的边是射线，没有长短之分，故本选项错误；③角的边是射线，不能延长，故本选项错误；④角可以看作由一条射线绕着它的端点旋转而形成的图形，说法正确.所以只有④一个选项正确.故选A.2.4点10分，时针与分针所夹的小于平角的角为（B）A. 55°B・ 65°C. 70°D.以上结论都不对解析：因为时针和分针每分钟分别旋转0.5。

第四章光现象单元测试题

A BD C 第四章光现象单元测试题一、单项选择题1. 下列物体中,属于光源的是（）A. 放电影时所看到的银幕B. 放电视时看到的电视机画面C. 月亮D. 猫的眼睛 2. 关于光的传播，下列说法正确的是（）A. 光只有在空气中才沿直线传播B. 光在任何情况下都沿直线传播C. 光在玻璃中不是沿直线传播的D. 光在同种均匀介质里是沿直线传播的3. 如图所示，水平桌面上斜放着一个平面镜，桌面上有一个小球向右滚去。

要使平面镜中小球的像沿竖直方向下落，则镜面与桌面间的夹角α应为（） A. 30º B. 45º C. 60º D. 90º4. 如图所示，一只小鸭浮在平静的湖面上。

能正确表示小鸭和它在水中的“倒影”的是（）5. “猴子捞月”的寓言故事说，猴子看到井中有一个月亮，如图，以为月亮掉进水中了，就要去捞，结果什么也没捞到。

关于水中月亮离水面的远近，以下说法中正确的是（） A. 和天上月亮到水面的距离相等 B. 井有多深，月亮就有多深C. 月亮就在水的表面上D. 和猴子眼睛到水面的距离相等6. 光污染已成为21世纪人们十分关注的问题。

据测定，室内洁白、光滑的墙壁能将射到墙上的太阳光的80％反射，长时间在这样刺眼的环境中会感到很不舒服。

如果将墙壁表面做成凹凸不平，其作用之一可以使射到墙上的太阳光变成散射光，减少光污染，这是利用了（）A. 光的直线传播B. 光的镜面反射C. 光的漫反射D. 光的折射 7. 一束光线从空气斜射入水中时，如果入射角逐渐增大，则折射角（） A. 逐渐减小，且总大于入射角 B. 逐渐增大，且总小于入射角 C. 逐渐减小，且总小于入射角 D. 逐渐增大，且总大于入射角 8. 当光从一种介质射向另一种介质时，下列说法中正确的是（） A. 一定会发生偏折 B. 发生折射时，折射角一定小于入射角 C. 反射和折射不会同时发生 D. 只要光进入另一种介质，速度就一定改变9. 潜入水中工作的潜水员在水中看见岸上的路灯位置变高了。

2022-2023学年七年级下册科学第四章单元测试卷及答案浙教版

2022-2023学年七年级下册科学第四章单元测试卷及答案浙教版1．一场国际体育比赛在美国某地下午2时举行时，我们却要在半夜里起来观看这场比赛的电视直播。

造成中、美两地昼夜不同的原因是（）A．地球的公转B．地球的自转轴是倾斜的C．地球不透明、不发光D．地球的形状两极稍扁赤道略鼓【答案】C【解析】【详解】造成中、美两地昼夜不同的原因是地球不透明、不发光，因此在任何时候，太阳只能照亮地球的一半，这样就形成了昼夜现象，C选项正确，ABD选项错误。

故选C。

2．通常，将天枢与天璇连线并沿天枢方向五倍线延长可找到北极星。

古人根据北斗七星的位置变化总结出“斗柄东指，天下皆春；斗柄南指，天下皆夏；斗柄西指，天下皆秋；斗柄北指，天下皆冬。

”的规律。

某日夜晚一位天文爱好者打开观星软件将手机指向某一方向的天空，获得如图恒星与星座位置。

推测该天文爱好者此时观星的月份可能是（）A．3月B．6月C．9月D．12月【答案】A【解析】【详解】据图示信息可知，天枢、天璇、摇光所在的星座是北斗七星，摇光所指方向即北斗七星斗柄指向。

据材信息“斗柄东指，天下皆春；斗柄南指，天下皆夏；斗柄西指，天下皆秋；斗柄北指，天下皆冬”这个规律判断，此时斗柄指东，观测者所在地是春季，A选项正确。

故选A。

3．在行驶的汽车里看月亮，感觉“月亮跟着汽车跑”。

这是因为（）A．月球运动方向与汽车运动方向一致B．月球运动方向与地球自转方向一致C．月球运动方向与地球公转方向一致D．地月距离很大，而汽车移动距离很小【答案】D【解析】【详解】参照物及相对运动。

在行驶的汽车里看月亮，感觉月亮跟着汽车跑，主要是因为以汽车为参照物，地月距离很大，而汽车移动距离很小。

故D正确，ABC错误；4．如图中①-⑨代表太阳系中的八大行星和一个矮行星（即不再属于太阳系大行星），其中代表小行星带位置和地球的分别是（）A．⑤和⑥之间、⑧B．⑤和⑥之间、⑦C．④和⑤之间、⑦D．④和⑤之间、⑧【答案】B【解析】【分析】根据太阳系行星的分布，进行分析解答。

初中七年级上册数学第四章《几何图形初步》同步练习+单元测试题(含答案)

初中,七年级,上册,数学,第四章,《,七年级,七年级上册数学同步练习+单元测试题第四章《几何图形初步》4.1几何图形基础巩固1. （题型一）图4-1-1是一座房子的平面图，组成这幅图的几何图形有（）图4-1-1A.三角形、长方形B.三角形、正方形、长方形C.三角形、正方形、长方形、梯形D.正方形、长方形、梯形2. （知识点4）汽车上的雨刷把玻璃上的雨水刷干净，属于（）的实际应用.A.点动成线B.线动成面C.面动成体D.以上答案都不对3. （题型三）把如图4-1-2的图标折成一个正方体的盒子，折好后与“中”相对的字是（）图4-1-2A.祝B.你C.顺D.利4. （题型三）在下列四个展开图中，不能折叠成无盖的长方体盒子的是（）5. （题型一）在图4-1-3的图形中，是柱体的是.（填序号）___________.图4-1-36. （题型二）在一张桌子上放着几叠碗，图4-1-4的三幅图是李明分别从上面、前面、右面看所得到的图形，那么桌子上一共放着____个碗.图4-1-4能力提升7. （题型三）图4-1-5是一张硬纸片，结合所给数据，你能判断出它能否折叠成一个长方体盒子吗？若能，画出它的几何图形，并计算它的体积；若不能，请说明理由.图4-1-5答案基础巩固1. C 解析：题图中的几何图形有三角形、正方形、长方形及梯形.故选C.2. B 解析：汽车的雨刷可以看成是一条线段,通过运动把玻璃上的雨水刷干净,所以应是线动成面.故选B.3. C 解析：题图是一个正方体的展开图，共有六个面，其中“祝”与“利”相对，“你”与“考”相对，“中”与“顺”相对.故选C.4. A 解析：选项B，C，D都能折叠成无盖的长方体盒子，选项A不能折叠成无盖的长方体盒子.故选A.5. ②③⑥解析：①是圆锥，②是正方体，属于棱柱，③是圆柱，属于柱体，④是棱锥，⑤是球，⑥是三棱柱，属于柱体.6. 10 解析：首先由上面看到的图形可知一共有3叠碗，然后由前面、右面看到的图形可知第一排有2叠碗，每叠4个，第二排靠左面的一叠有2个碗，一共有4+4+2=10（个）碗.能力提升7. 解：能.如图D4-1-1，该长方体盒子的长为5 m,宽为1 m，高为3 m，故其体积为5×1×3=15图D4-1-14.2直线、射线、线段基础巩固1. （题型一）如图4-2-1，下列说法正确的是（）图4-2-1A.图中共有5条线段B.直线AB与直线AC是同一条直线C.射线AB与射线BA是同一条射线D.点O在直线AC上2. （知识点1）木工师傅用刨子可将木板刨平，如图4-2-2，经过刨平的木板上的两个点，就能弹出一条笔直的墨线，而且只能弹出一条墨线，用数学知识解释其道理正确的是（）图4-2-2A.两点确定一条直线B.两点之间，线段最短C.两条直线相交，只有一个交点D.不在同一条直线上的三点，确定一个平面3. （知识点6）已知C是线段AB上的一点，不能确定C是AB的中点的条件是（）A. AC=CBB. AC=ABC. AB=2BCD. AC+CB=AB4. （题型三）已知线段AB=8 cm，在直线AB上画线段BC，使它等于3 cm，则线段AC等于5. （题型四）经过任意三点中的两点可以画出的直线共有_____条.6. （题型六）如图4-2-3，由泰山到青岛的某一次单程列车，运行途中停靠的车站依次是泰山、济南、淄博、潍坊、青岛，那么需要为这次列车制作的火车票有_____种.图4-2-37. （题型三）如图4-2-4，线段AC=6 cm，线段BC=15 cm，M是AC的中点，在CB上取一点N，使得CN∶NB=1∶2，求MN的长.图4-2-48. （题型六）如图4-2-5，设A，B，C，D为四个居民小区，现要在四边形ABCD内建一个购物中心，试问应把购物中心建在何处，才能使4个居民小区到购物中心的距离之和最小？请用一句话说明理由.图4-2-59. （题型二）如图4-2-6，已知线段a，b,利用直尺和圆规画一条线段c，使它的长度等于3a-b.图4-2-6能力提升10. （题型三）如图4-2-7，在线段AF中，AB=a，BC=b，CD=c，DE=d，EF=e，则分别以A，B，C，D，E，F为端点的所有线段长度之和为（）图4-2-7A.5a+8b+9c+8d+5eB.5a+8b+10c+8d+5eC.5a+9b+9c+9d+5eD.10a+16b+18c+16d+10e11. （题型五）如图4-2-8，试确定各图中分别有几条线段、几条射线.（1）如图4-2-8（1），直线l上有1个点P1；（2）如图4-2-8（2），直线l上有2个点P1，P2；（3）如图4-2-8（3），直线l上有3个点P1，P2，P3；（4）如图4-2-8（4），直线l上有4个点P1，P2，P3，P4；（5）如图4-2-8（5），直线l上有n个点P1，P2，P3，…，Pn.图4-2-812. （题型三）如图4-2-9，线段AB=12，动点P从点A出发，以每秒2个单位长度的速度沿射线AB运动，M为AP的中点．（1）出发多少秒后，PB=2AM？（2）若点P在线段AB上运动时，试说明2BM-PB的值为定值．（3）当点P在AB的延长线上运动时，N为PB的中点，其他条件不变，下列两个结论：①MN 的长度不变；②AM+NP的值不变.请选择正确的结论，并说明理由．图4-2-9答案基础巩固1. B 解析：A.图中共有6条线段，故A错误；B.直线AB与直线AC是同一条直线，故B 正确；C.射线AB与射线BA不是同一条射线，故C错误；D.点O在直线AC外，故D错误.故选B.2. A 解析：经过刨平的木板上的两个点，就能弹出一条笔直的墨线，此操作的依据是两点确定一条直线.故选A.3. D 解析：A.若AC=CB，则C是线段AB的中点；B.若AC=1/2AB，则C是线段AB的中点；C.若AB=2BC，则C是线段AB的中点；D.若AC+BC=AB，则C是线段AB上任意一点，故不能确定C是AB的中点.故选D.4. 11 cm或5 cm 解析：根据题意可知，AB=8 cm,BC=3 cm.因为点C的位置不确定，所以要分两种情况分别进行讨论：如图D4-2-1（1），当点C在点B的右侧时，AC=AB+BC=8+3=11（cm）；如图D4-2-1（2），当点C在点B的左侧时，AC=AB-BC=8-3=5（cm）.综上所述，线段AC等于11 cm或5 cm.图D4-2-15. 1或3 解析：如图D4-2-2，可以画出1条或3条直线.图D4-2-26. 10 解析：如图D4-2-3，将泰山、济南、淄博、潍坊、青岛这五站分别用A，B，C，D，E表示，则有线段AB，AC，AD，AE，BC，BD，BE，CD，CE，DE，共10条，所以需要为这次列车制作的火车票有10种.图D4-2-37. 解：因为M是AC的中点，线段AC=6 cm，所以MC=AM=AC=×6=3（cm）.又因为CN∶NB=1∶2，线段BC=15 cm，所以CN=BC=×15=5（cm）.所以MN=MC+NC=3+5=8（cm）.8. 解：应建在AC，BD连线的交点处.理由：两点之间，线段最短.将A，B，C，D用线段连起来，在路程最短的两条线段的交点处建超市，则使4个居民小区到购物中心的距离之和最小.9. 解：（1）画射线AP，在射线AP上顺次截取AB=BC=CD=a；（2）以D为端点，在线段AD上截取DE=b.如图D4-2-4，线段AE的长度就是3a-b，设AE的长度为c，则c=3a-b.图D4-2-4能力提升10. A 解析：以A为端点的线段有AB，AC，AD，AE，AF，这些线段的长度之和为5a+4b+3c+2d+e；以B为端点的线段有BC，BD，BE，BF，这些线段的长度之和为4b+3c+2d+e；以C为端点的线段有CD，CE，CF，这些线段的长度之和为3c+2d+e；以D为端点的线段有DE，DF，这些线段长度之和为2d+e；以E为端点的线段有EF，线段的长度为e.所以分别以A，B，C，D，E，F 为端点的所有线段的长度之和为5a+8b+9c+8d+5e.故选A.11. 解：（1）题图（1）中有0条线段，2条射线.（2）题图（2）中有1条线段，4条射线.（3）题图（3）中有1+2=3（条）线段，6条射线.（4）题图（4）中有1+2+3=6（条）线段，8条射线.（5）题图（5）中有1+2+3+…+（n-1）=（条）线段，2n条射线.12. 解：（1）设出发t（t>0）秒后，PB=2AM.如图D4-2-5（1），由题意，得AP=2t，则PB=12-2t.因为M为AP的中点，所以AM=t.由PB=2AM，得12-2t=2t，解得t=3.故出发3秒后，PB=2AM.（2）设点P在AB上运动的时间为t（t >0）秒.如图D4-2-5（1），可得AP=2t，AM=t，所以BM=12-t.所以2BM-PB=2×（12-t）-（12-2t）=24-2t-12+2t=12.所以当点P在线段AB上运动时，2BM-BP的值为定值12.（3）结论①是正确的.理由如下：如图D4-2-5（2），设点P在AB的延长线上运动的时间为t（t>0）秒，则AP=2t，则AM=t，PB=2 t-.因为N为PB的中点，所以NP=PB=×（2t-12）=t-6.①MN=AP-AM-NP=2t-t-（t-6）=6.所以当点P在AB的延长线上运动时，MN的长度不变.所以结论①正确.②AM+NP=t+（t-6）=2t-6，所以当点P在AB的延长线上运动时，AM+PN的值会改变．所以结论②不正确．（1）（2）图D4-2-54.3角4.3.1角基础巩固1. （知识点1）下列说法正确的是（）A.周角是一条射线B.角的边越长，角越大C.大于直角的角叫作钝角D.两个直角的和一定是平角2. （知识点2）在下列四个图中，能用∠1，∠AOB，∠O三种方法表示同一个角的是（）3. （知识点3）将21.54°用度、分、秒表示为（）A.21°54′B.21°50′24″。

八年级物理上册第四章《光现象》单元综合测试题(含解

第四章《光现象》单元测试题一、单选题(每小题只有一个正确答案)1.光的色散现象说明（）A．太阳光是由三原色组成B．太阳光是由三色光组成C．白色光是单色光D．太阳光可以分成七种颜色色光2.利用紫外线的生理作用强可以（）A．杀菌B．使照相底片感光C．摄像D．验钞3.如图所示，一束光斜射到平面镜上，其中反射角是（）A．∠1B．∠2C．∠3D．∠44.夜晚，下列物体中放出红外线较多的是（）A．草木B．人C．岩石D．河水5.红外线波长较长，不容易被散射，在空气中传播距离较远，关于红外线的相关用途，下列说法中不正确的是（）A．战士用来观测夜间敌人的行动B．用来测量体温C．用来消毒杀菌D．用来进行遥控6.下列光现象的成因与池水变浅形成的原因不相同的是（）A．水中“折”笔B．手影C．露珠下的叶脉看起来变粗了D．大海中的“城市”7.如图所示，一束光线斜射入盛水的容器中，在容器底部形成一个光斑．打开阀门K，容器里的水逐渐流出的过程中，光斑将（）A．向左移动后静止B．向右移动后静止C．先向左移动再向右移动D．仍在原来位置8.如下应用事例中，哪一个不是利用红外线的热作用强的特性（）A．家庭用红外线烘烤食品B．工业用红外线烘干汽车表面的喷漆C．医疗上利用红外线对病人理疗D．生活中电视机利用红外线遥控调台9.下列说法中错误的是（）A．小灯泡放在凹面镜焦点上，灯泡发出的光线经过凹面镜反射后，成平行光射出B．用太阳灶烧水，壶应放在凹面镜的焦点上C．汽车的后视镜是凸面镜，司机可以从镜中观察到汽车后较大范围D．平面镜遵守光的反射定律，球面镜不遵守光的反射定律10.下列关于红外线的说法中正确的是（）A．红外线是可见光，不是电磁波B．十字路口的红灯发出的光是红外线C．红外线在真空中的传播速度要小于3×108m/sD．红外线的波长为105nm，则它的频率是3×1012Hz11.人眼看到斜插入水中的筷子向上折（如图），如图的四幅光路图中，能正确说明产生这一现象的原因的是（）A．B．C．D．12.下列现象中，属于光反射现象的是（）A．小孔成像B．水中的倒影C．影子D．日食、月食13.当一束光线垂直射向某透明介质表面时，（）A．入射角为0°，反射角为0°，折射光线垂直于入射光线B．入射角为0°，反射角为0°，光的传播方向不改变C．入射角为90°，反射角为90°，折射光线垂直于入射光线D．入射角为90°，反射角为90°，折射光线传播方向不改变14.下面四幅图，能正确表示渔民在岸边看到水中的鱼的光路图是（）A．B．C．D．15.在沙漠中赶路的人，有时正当非常口渴的时候，忽然一个碧波荡漾的大湖出现在眼前，当走近时，大湖消失得无影无踪，出现这种现象的原因是（）A．光在沙漠中发生漫反射的缘故B．光从云上反射下列的缘故C．光在不均匀的大气层中发生折射的缘故D．光在海水中发生折射的缘故二、多选题(每小题至少有两个正确答案)16.（多选）将绿色植物种植在盖有绿色玻璃的温室中，植物将（）A．更加翠绿B．仍正常生长C．颜色变浅D．不能正常生长17.（多选）关于实像和虚像，下列说法错误的是（）A．实像能用光屏呈现，虚像不能B．虚像是人的幻觉，并没有光线进入人眼，实像则相反C．实像一定是由光的折射现象形成的，虚像一定是由光的反射现象形成的D．实像有放大的，也有缩小的，而虚像都是放大的18.（多选）如图是光在不同表面发生反射的光路图，其中属于镜面反射的是（）A．B．C．D．19.（多选）关于光的反射，下列说法错误的是（）A．当入射光线与反射面的夹角为20°时，反射角也是20°B．入射光线靠近法线时，反射光线也靠近法线C．入射角增大5°时，反射光线与入射光线的夹角增大10°D．镜面反射遵守光的反射定律，漫反射不遵守光的反射定律三、填空题20.李东同学在桌面上的近视眼镜上看到自己身后同一个窗户的两个像，如图．这两个像是______ 像（填“实”、“虚”），是 ______ 面镜（填“平”、“凸”、“凹”）所成的像．其中较大的像是镜片上离李东较 ______ 的玻璃面（填“近”、“远”）所成的．21.通常情况下，夜间人的体温比野外木草、岩石的温度高，人体辐射的____________比它们强，人们根据这个原理制成了夜视仪．22.说起光速，人们总是感觉快得无法想象．其实科学家已经在实验室内将其降得很慢．请你设想一下，假如光速只有3m/s，我们的世界会发生什么变化?写出一个场景：．23.大厦玻璃幕墙强光刺眼是由于光的 ______ 反射造成的．24.平时我们能从不同的方向看清本身不发光的物体，这是因为光在该物体表面发生 ______ 反射的缘故．这种反射 ______ 光的反射定律．（填“遵循”或“不遵循”）四、实验题(共2小题,每小题分,共0分)25.如图所示“探究光的反射、折射规律”的实验装置：（1）将一束光贴着纸板A沿CO射到水面上的O点，同时观察到了反射光线OD、折射光线OE．若将纸板B向后折转一个角度，此时在纸板B上(选填“能”或“不能”)看到反射光线与折射光线，这样做的目的是探究反射光线、折射光线与入射光线是否在．（2）若将一束光贴着纸板B沿EO射到O点，光将沿图中的方向射出．26.小玲同学在探究平面镜成像时像与物的关系时，选择两根完全相同的蜡烛、一块较厚的玻璃板M（P、Q两个面都可以作为平面镜使用）．[进行实验与收集证据]她在桌面上铺一张大纸，竖立一块玻璃板：将蜡烛A放置在玻璃板的前面，点燃蜡烛A，然后将蜡烛B放置在玻璃板后面，如图甲所示，进行实验．小玲按照图乙中的测量方法，多次改变蜡烛A的位置，认真测量并记录了对应数据：[分析与论证]根据上述实验数据分析得出：像距 ______ （大于/等于/小于）物距．[交流与评估]这个结论与平面镜成像特点不相符，主要是选择了蜡烛A所成的像到反射面的距离______（填“正确”或“不正确”）；根据上面数据推算玻璃板的厚度为 ____ cm．小玲进一步思考：若保持A、B两支蜡烛的位置不变，多次改变玻璃板的位置，能发现B始终能与A的像重合吗？（能/不能） ______ ．四、计算题27.在田径运动会的百米赛跑项目中，小明和小江分别根据发令枪冒烟和听到枪声开始记时，同一运动员的跑步成绩（）A. 小明比小江多了0.294秒B. 小江比小明多了0.294秒C. 小明和小江的记录结果一样D. 小江记录的结果更准确28.一光源发出的一束光从地面上竖直向上投射到和它垂直的平面镜上，平面镜与地面距离为3米，如果把平面镜绕水平轴转过30°角，则地面上所成光点离光源多远？五、作图题29、如图7所示，平面镜前有一点光源S，S发出的一束光线被平面镜反射后经过A点，请作出该光线的光路图。

第四章《多彩的光》单元测试题

初中八年级物理（上）元测试题《多彩的光》班级：________姓名：________成绩：________一、选择题：（每小题3分，共45分）1、晴朗天空，在树阴下，我们常常可以看到地面上有许多圆形的光斑，它们是（）A．太阳的影子 B、太阳光照到树叶上小水珠而成的C、小孔成像所成的太阳的实像D、树叶形成的缝都是圆形的2、用激光器向月球发射激光信号，经过2.56秒接收到从月球返回的激光信号，则用此方法测得地球与月球之间的距离为（）A、7.68×108千米 B 7.68 ×105千米C 3.84 ×105千米D、3.84×108千米3、一条反射光线和镜面的夹角是30o，此时入射光线和反射光线的夹角是（）A、60oB、90oC、120oD、150o4、下列光学元件中都遵循光的折射规律的是（）A、平面镜，显微镜B凸面镜，凸透镜C、凹透镜，凸透镜D、潜望镜，望远镜5、一个身高1、80米的同学，要想站在平面镜前看到自己的全身像，此时平面镜被打坏了一半，问此同学在镜中像的高度（）A.大于1、80米 B、等于1.80米 C 、等于0、90米 D、小于1、80米6、如图所示，从平面镜里看到背后墙上电子钟示数，这时的时间应（A、21：05B、21：15C、20：15 D：20：057、图中的三角形PˊQˊRˊ是三角形PQR经平面镜所成的像，其中正确的是（）8、下列现象中，①人用放大镜看书；②在岸上看水中的鱼；③湖面上映出白云的“倒影”；④水中的筷子变弯；⑤教室里的同学都看到黑板上的字。

属于光的折射现象的是（）A、①②③B、②④⑤Ｃ、①②④Ｄ、③④⑤9、台上一演员上身着绿色衣服，下身着红色裙装，舞台上空红色追光灯的光照到她的身上后，台下观众看见她上装和下装的颜色是（）A、上装为绿色，下装为红色B、上下装都为红色C、上装为黑色，下装为红色D、上下装都是黑色10、“九寨沟”的镜海中有着“鱼在水中游的美景奇观，这水中画面的“鱼”是由于光的______形成的_______像，“鸟”是由于光的_______形成的________像A．折射，虚象；反射，实象； B、折射，实象；反射，实象C、反射、虚象，折射，虚象；D、折射，虚象；反射，虚象１０、幻灯机成像的特点是（）A、倒立、放大、实像B、正立、放大、实像C、正立、放大、虚像D、倒立、放大、虚像１１、物体通过凸透镜成像，下列说法中正确的是（）A、正立的一定是实象B、放大的都是实象C、倒立、缩小的一定是虚象D、倒立的一定是实象１２、凸透镜焦距为f，要使物体通过凸透镜成缩小的像，物距应满足条件是（）A、u<fB、f<u<2fC、u>2fD、u>f13、关于实象和虚象，下列说法正确的是（）A.虚象可成在光屏上，实象不能成在光屏上B.虚象只能用眼看，不能用光屏接收C.实象是清晰的，虚象是模糊的D.实象一般都是正立的1４、物体放在凸透镜前，在离透镜15厘米的光屏上得到物体清晰的放大的像，所使用的凸透镜的焦距可能是下列的哪一个数值（）Ａ、４厘米Ｂ、８厘米Ｃ、１２厘米Ｄ、１８厘米１５、蜡烛放在凸透镜１.５倍焦距的地方，当它向离透镜３倍焦距的地方移动时，它的像（）Ａ、先放大后缩小Ｂ、先缩小后放大Ｃ、逐渐变大Ｄ、逐渐变小二、填空题（每空１分，共20分）1、光的反射定律可以总结成三个简单的口诀，请写出它们的含义。

浙教版七年级第四章单元测试卷

浙教版七年级第四章单元测试卷一、单选题1．下列温州传统民俗活动中，主要涉及化学变化的是（）A．做糖画B．捣年糕C．酿米酒D．捏米塑2．在抗击新冠肺炎疫情的下列做法中，一定发生化学变化的是（）A．佩戴口罩B．保持通风C．杀菌消毒D．勤洗手3．砝码盒中最小的砝码为5g，用天平称物体质量时，发现加上5g这种砝码后指针偏右，减去这个砝码后，指针偏左。

接下来的操作是（）A．移动游码使天平横梁平衡后读数B．将被测物体转移至天平右盘，再测其质量C．调节横梁左边螺母，使天平横梁平衡D．在左盘加上5g砝码，设法使天平横梁平衡后读数4．纳米（nm）是一种长度单位，1nm=10−9m，纳米科技开辟了人类认识世界的新层面。

纳米材料科技是纳米科技最基本的组成部分，把固体物质加工到纳米级（1nm∼100nm）的超细粉末，即可得到纳米材料。

这种加工过程属于（）A．化学变化B．物理变化C．既有物理变化又有化学变化D．既不是物理变化又不是化学变化5．小明为了测盐水的密度，制定如下的实验计划：①测出空烧杯的质量；②将烧杯中一部分盐水倒入量筒中；③测出量筒中盐水的体积；④根据实验数据计算盐水的密度；⑤在烧杯中装入适量盐水，测出它们的总质量；⑥测出烧杯和剩余盐水的质量。

以上实验步骤安排最合理、误差最小的是（）A．①⑤②③④B．⑤②③⑥④C．⑤②③①④D．⑤⑥②③④6．如图为竖直放置的环形管，要使管中酒精发生对流且沿逆时针方向流动，最好把冰块放在（）A．甲处B．乙处C．丙处D．丁处7．图中的物态变化属于凝固的是（）A．湖水结冰B．雾气消散C．露珠形成D．冰雪消融8．如图是酒精沸腾时温度随时间变化的图像，下列说法正确的是（）A．酒精的沸腾属于液化现象B．酒精在沸腾过程中温度不变C．酒精沸腾过程中要放热D．酒精在任何情况下的沸点都是78∼9．小明同学家住桃园小区，目前家中煤气灶仍以瓶装煤气作为燃料。

他发现冬天到煤气公司购买时价格是55元/瓶，而夏天的价格则是51元/瓶。

高中生物必修一专题-第四章单元测试

第4章细胞物质输入和输出一、选择题(20×3分)1．下列叙述正确的是 ( )A．细胞膜是选择透过性膜B．小分子物质都能通过细胞膜，而大分子物质则不能C．原生质层包括细胞膜、细胞质和细胞核D．动物细胞一般不会吸水胀破，是因为细胞最外层有细胞壁2．下列关于细胞结构和功能的叙述，错误的是 ( )A.生物膜相互转化的基础是膜的组成和结构的相似性B.细胞膜的结构特点是选择透过性C.细菌和酵母菌都有细胞膜、核糖体、DNA、RNAD.细胞核能贮存遗传信息，也能对细胞的新陈代谢起调控作用3．甜菜根细胞的液泡中有花青素，使块根为红色。

将块根切成小块放在蒸馏水中，水无明显的颜色变化，但用盐酸处理后再放人蒸馏水中，则能使水变红。

其原因是 ( )A．花青素不溶于水而溶于盐酸 B．盐酸破坏了细胞膜的选择透过性C．盐酸破坏了原生质层的选择透过性 D．细胞壁被盐酸破坏4．右图为显微镜下洋葱表皮细胞在30％蔗糖溶液中的示意图。

下列叙述中错误的是（）A．若将细胞置于清水中，A基本不变B．若将该细胞置于20％蔗糖溶液中，B值将变小C．B／A值能表示细胞失水的程度 D．B／A值能表示液泡体积的变化5．下列物质进出细胞的过程消耗能量的是( )①水被胃黏膜吸收②氧气进入红细胞③肾小管壁上皮细胞吸收原尿中的Na+④小肠绒毛上皮细胞吸收氨基酸A．①② B．③④ C．②③④ D．①②③④6．有关生物膜结构和功能的下列叙述中，错误的是 ( )A.细胞膜上载体蛋白的种类和数量决定了植物根细胞对无机盐离子的吸收具有选择性B.甘油容易通过细胞膜，是因为磷脂双分子层构成了细胞膜的基本支架C.细胞器膜和核膜使得细胞内能够同时进行多种化学反应，而不会相互干扰D.B细胞对抗原的识别具有特异性，是因为B细胞膜上具有结合特定抗原的载体7.大肠杆菌在繁殖时，细胞内钾离子的浓度是培养液中的3 000倍。

如果在培养液中加入一种叫箭毒的药物，大肠杆菌细胞内钾离子浓度立即下降，这种药物很可能( )A．使细胞膜变成了全透性膜 B．抑制膜上载体的活动C．加快细胞膜的流动 D．使载体运动方向改变8.把蚕豆叶表皮浸泡在7％尿素溶液中，开始表皮细胞发生了质壁分离，然后又自动复原，发生自动复原的原因是( )A．原生质层破坏 B．尿素分子进入细胞C．细胞壁破坏 D．尿素溶液浓度低9.细胞膜的选择透过性主要取决于膜中的哪种成分（）A、磷脂分子B、核酸C、脂肪D、蛋白质10.囊性纤维病是由于有的细胞中某种蛋白质的结构异常，影响了一些离子的跨膜运输，使这些离子在细胞外积累过多造成的。

第四章物质的形态及其变化单元测试题(含答案)

第四章物质的形态及其变化单元测试题（总分100分时间100分钟）一、选择题（每小题3分，共30分）1.中华文化源远流长，诗词中蕴含丰富的物理知识。

以下有关物态变化的分析，正确的是（）A.“斜月沉沉藏海雾”——雾的形成是汽化，需要放热B.“露似真珠月似弓”——露的形成是液化，需要吸热C.“已是悬崖百丈冰”——冰的形成是凝固，需要吸热D.“霜叶红于二月花”——霜的形成是凝华，需要放热2.如图，将一个金属盖开口向上，放在表面平整的泡沫塑料块上，金属盖与泡沫塑料之间放少许水，再向金属盖内注入深约2毫米的少量乙醚，并用扇子对着乙醚扇，结果发现金属盖下的水会变成冰。

用手把金属盖往上提起来，泡沫塑料块不掉下来。

下面与此相关的说法不正确的是（）A.用扇子对着乙醚扇，加快了乙醚的蒸发速度B.此实验说明了蒸发具有致冷作用C.乙醚可能是一种沸点比较低的液体D.实验中涉及的两种物态变化都是吸热过程3.下面是八年级学生小明对日常生活的观察和体验，其中正确的是（）A.床头台灯的高度约为30dmB.淋浴时热水的温度约为80℃C.骑自行车上学的速度约为50m/sD.教室讲台前黑板的面积约为4.5 m24.根据下表中所列的物质的熔点，以下说法不正确的是（）C.液态钢的凝固点为1300℃D.在－256℃的氢是液态5.下列关于物态变化的说法中，正确的是（）A.冬天，汽车玻璃起“雾”影响视线，是车外空气液化形成的B.汽车水箱中加入适量酒精提高了水的凝固点，防止水凝固C.液化石油气是利用压缩体积的方式液化成液态的D.用久了的灯管两端变黑，是汽化造成的6.如图温度计使用正确的是（）A B C D7.我国自主研发的造雪机为北京冬奥营造完美雪道。

如图，造雪机将压缩空气与5℃以下的冷水混合后喷出，水雾在空气中凝结成雪花，“人造雪”具有更耐高温的优点。

下列说法正确的是（）A.“人造雪”的形成是凝华现象B.“人造雪”形成时需要放热C.“人造雪”的熔点低于自然雪D.造雪时空气温度须高于5℃8.如图所示物态变化的实例中，属于凝固的是（）A.湖水结冰B.叶尖上形成露珠C.冰雪消融D.草叶上形成白霜9.游泳时为了谨防抽筋现象，最适宜的水温是（）A.10℃B.20℃C.28℃D.40℃10.吃雪糕解暑，雪糕在口中所发生的物态变化是（）A.熔化B.汽化C.液化D.凝固二、填空题（每空1分，共21分）11.夏天，我们从冰箱中拿出冰棒，剥开包装纸看到冰棒直冒“白气”，根据你的观察，冰棒冒出的“白气”符合实际的是图，“白气”的形成是现象，产生的“白气”最后（后两空均填物态变化名称）到空气中看不见了。

财务管理第四章单元测试

第四章筹资管理（上）单元测试一、单项选择题1.为了优化资本结构和偿还到期债务而产生的筹资动机是（）。

A.创立性筹资动机B.支付性筹资动机C.扩张性筹资动机D.调整性筹资动机2.下列各项属于资金使用费用的是（）。

A.证券印刷费B.公证费C.律师费D.利息支出3.只有股份有限公司、国有独资企业、由两个以上的国有企业或者两个以上的国有投资主体投资设立的有限责任公司才有资格的筹资方式是（）。

A.吸收直接投资B.发行债券C.发行股票D.融资租赁4.筹资分为直接筹资和间接筹资两种类型是按照（）。

A.企业所取得资金的权益特性不同B.筹集资金的使用期限不同C.是否借助于金融机构为媒介来获取社会资金D.资金的来源范围不同5. 企业要充分利用各种筹资渠道，选择经济、可行的资金来源所涉及的筹资管理原则是（）。

A.筹措合法B.规模适当C.取得及时D.来源经济6.下列各项中，不属于股权筹资的是（）。

A.留存收益B.认股权证C.发行股票D.引入战略投资者7.相对于股权融资而言，长期银行借款筹资的缺点是（）。

A.财务风险大B.筹资速度快C.稳定公司的控制权D.资本成本低8.债券持有者可以在规定的时间内按规定的价格转换为发债公司股票的是（）。

A.不可转换债券B.可转换债券C．担保债券D.信用债券9.有一份融资租赁合同，标的资产是承租方售给出租方的，租赁合同约定除资产所有者的名义改变之外，其余情况均无变化，则这种融资租赁形式属于（）。

A.直接租赁B.售后回租C.杠杆租赁D.贷款租赁10.企业向租赁公司租入一台设备，价值1500万元，合同约定租赁期满时残值15万元归租赁公司所有，租期从2013年1月1日到2018年1月1日，租费率为12%，若采用先付租金的方式，则平均每年支付的租金为（）万元。

［（P/F，12%，5）=0.5674，（P/A，12%，4）=3.0373，（P/A，12%，5）=3.6048］A.371.54B.369.43C.413.75D.491.0611.下列各项属于融资租赁特点的是（）。

八年级物理单元同步达标测试(第四章)物态变化

八年级物理单元同步达标测试（第四章）物态变化
各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢
八年级单元同步达标测试
物理试卷
一、单项选择题
1、以下温度最接近25℃的是
A.冰水混合物的温度
B.人的正常体温
C.人感到舒适的房间温度
D.泉州盛夏中午的室外温度
2、物质的三态变化和温度有着密切的关系，下列物态变化中，吸热的一组是
A．熔化、液化、升华B．熔化、汽化、升华
C．升华、汽化、凝华D．液化、升华、汽化
3、夏天，从冰箱冷冻室取出的物品，放一会就会在物品上有一层白色的东西，这是
A.凝华所形成的霜
B.凝固所形成的霜
C.升华所形成的霜
D.汽化所形成的霜
4、测量液体的温度时，下列温度计的放置方法正确的是
八年级单元同步达标测试物态变化
相关阅读：
初二物理上册知识点汇总
苏科版八年级物理试题
八年级单元同步达标测试声现象
八年级单元同步达标测试光现象
八年级单元同步达标测试透镜及其应用
八年级单元同步达标测试电流和电路
各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢。

教科版八年级物理上册第四章在光的世界里单元测试题含答案

教科版八年级物理上册第四章在光的世界里单元测试题一、选择题(11×3分＝33分)1．如图所示的四种现象中，属于光的反射现象的是()A．叉鱼B．手影C．看到地上的书D．凸透镜使光线会聚2．下列光路图中，正确的是()3．在“五岳”之一泰山上，历史上曾多次出现“佛光”奇景。

据目击者说：“‘佛光’是一个巨大的五彩缤纷的光环，与常见的彩虹色彩完全一样。

”“佛光”形成的主要原因是()A．直线传播B．小孔成像C．光的反射D．光的色散4．人站在平面镜前，当他向平面镜走近时，下列说法正确的是()A．像变大，像到镜面的距离变小B．像变大，像到镜面的距离变大C．像不变，像到镜面的距离变小D．像不变，像到镜面的距离不变5．下列关于“光现象”的说法正确的是()A．池水看起来比实际浅，这是由于光的反射引起的B．浓密的树荫下出现很多圆形的光班，这是由于光的折射引起的C．路边建筑物的玻璃幕墙造成光污染，这是由于光的漫反射引起的D．因为光路可逆，所以甲从平面镜中看到乙的眼睛，乙也能从平面镜中看到甲的眼睛6．有一种自行车尾灯设计得很巧妙。

当后面汽车的灯光以任何方向射到尾灯时，它都能把光线“反向射回去”。

图中是四种尾灯的剖面示意图，其中用于反光的镜面具有不同的形状。

能产生上述效果的镜面是()7．一条光线AO从空气中斜射向平静的水面，如图甲所示。

在空气和水的分界面同时发生反射和折射。

在图乙中有四幅描述其反射和折射的光路图，其中正确的是()8．集体照相时，发现有些人没有进入镜头，为了使全体人员都进入镜头，应采取() A．人不动，照相机离人远一些，镜头往里缩一些B．人不动，照相机离人近一些，镜头往里缩一些C．人不动，照相机离人近一些，镜头往前伸一些D．照相机和镜头都不动，人站近一些9．在探究近视眼视力矫正问题时用如图所示的装置模拟眼睛，烧瓶中的着色液体相当于玻璃体，烧瓶左侧紧靠瓶壁的凸透镜相当于晶状体，右侧内壁相当于视网膜。

图中的四幅图是一些同学描绘近视眼矫正的方法和光路，其中能达到近视眼矫正目的的是()10．3D电影具有三维立体视觉效果，拍摄时，将两个摄像头按照人两眼间的距离放置，同时拍摄，制成胶片；放映时，两个放映机在银幕上呈现两个略有差异的画面，观看者带上特殊眼镜后，就和直接用双眼看到物体的效果一样。

人教版《第四章物态变化》单元测试题及答案

第四章单元同步测试题一、选择题1.O0C的冰和O0C的水相比较（）A、O0C的冰比O0C的水冷B、O0C的水比O0C的冰冷C、O0C的冰与O0C的水冷热程度相同D、无法比较2.在寒冷的冬天夜晚，用手摸室外的铁棍和木棍，感觉铁棍比木棍冷，则（）A、铁棍比木棍温度低B、木棍比铁棍温度低C、铁棍和木棍温度相同D、无法确定3.如图所示的四种“用温度计测水温”的实验操作，其中正确的是（）4.小明测体温时，忘了甩体温计，也没有读体温计的示数，直接用这个体温计去测体温，测量结果是37.50C。

下列说法中正确的是（）A、他的体温一定是37.50CB、他的体温一定高于37.50CC、他的体温可能是37.50C，也可能低于37.50CD、他的体温可能高于37.50C5.在1标准大气压下，将一支刻度模糊不清的温度计与一刻度尺平行地插入冰水混合物中，过适当时间温度计中水银面与刻度尺上的4cm刻度线对准，将这冰水混合物加热到沸腾时，水银面与204cm的刻度线对准，那么当沸水冷却到50℃时，水银面对准的刻度线是( )A、96cmB、100cmC、102cmD、104cm6.采用冷冻法可以把水与酒精从它们的混合液中分离出来，将混合液由常温降温直至产生冰晶，首先分离出来的晶体及原因是（）A．冰，水的凝固点比酒精的低 B．冰，水的凝固点比酒精的高C．酒精，酒精的凝固点比水的高 D．酒精，酒精的凝固点比水的低7.在寒冷的北方，河水上面结了厚厚的冰，若冰面上方气温是－10℃，那么下列说法中正确的是（）A．整个冰层的温度都是－10℃ B．冰层上表面为－10℃，下表面是0℃C．整个冰层的温度都是0℃ D．无法确定冰层两表面的温度8.把正在熔化的冰拿到0℃的房间里，下列说法中正确的是（）A．冰继续熔化，而熔化过程温度保持不变B．冰不再熔化，因为冰不能从周围吸收到热量C．因为熔化的温度高于0℃，所以冰不再继续熔化D．因为熔化的温度低于0℃，所以冰将继续熔化9.在寒冷的冬天，用手摸室外的金属，当手较潮湿时，会发生粘手的现象，好像手与金属表面之间有一层胶，下列说法中正确的是（）A．金属的温度低，而产生金属吸引皮肤的感觉B．金属的温度高，而产生金属吸引皮肤的感觉C．手上的水凝固，产生极薄的冰，将手粘在金属上D．这只是人的一种错觉10.关于晶体的熔化和凝固，下列说法正确的是（）A．晶体的温度达到熔点时一定熔化B．将食盐放到水中，一会儿水就变咸了，这是熔化现象C．晶体在凝固过程中要放出热量D．晶体在熔化过程中温度可能上升11．雨的形成是与自然界中水循环相关的复杂过程. 地球上的水升腾到高空变成水滴，成为云的主要组成部分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章物态变化知识点总结一、温度1、定义：温度表示物体的冷热程度。

2、单位：①国际单位制中采用热力学温度。

②常用单位是摄氏度（℃）规定：在一个标准大气压下冰水混合物的温度为0度，沸水的温度为100度，它们之间分成100等份，每一等份叫1摄氏度某地气温-3℃读做：零下3摄氏度或负3摄氏度③换算关系T=t + 273K3、测量——温度计（常用液体温度计）①温度计构造：下有玻璃泡，里盛水银、煤油、酒精等液体；内有粗细均匀的细玻璃管，在外面的玻璃管上均匀地刻有刻度。

②温度计的原理：利用液体的热胀冷缩进行工作。

③分类及比较：④常用温度计的使用方法：使用前：观察它的量程，判断是否适合待测物体的温度；并认清温度计的分度值，以便准确读数。

使用时：温度计的玻璃泡全部浸入被测液体中，不要碰到容器底或容器壁；温度计玻璃泡浸入被测液体中稍候一会儿，待温度计的示数稳定后再读数；读数时玻璃泡要继续留在被测液体中，视线与温度计中液柱的上表面相平。

练习：◇温度计的玻璃泡要做大目的是：温度变化相同时，体积变化大，上面的玻璃管做细的目的是：液体体积变化相同时液柱变化大，两项措施的共同目的是：读数准确。

二、物态变化填物态变化的名称及吸热放热情况：1、熔化和凝固2、①熔化：定义：物体从固态变成液态叫熔化。

晶体物质：海波、冰、石英水晶、非晶体物质：松香、石蜡玻璃、沥青、蜂蜡食盐、明矾、奈、各种金属熔化图象：熔化特点：固液共存，吸热，温度不变熔化特点：吸热，先变软变稀，最后变为液态温度不断上升。

熔点：晶体熔化时的温度。

熔化的条件：⑴达到熔点。

⑵继续吸热②凝固：③定义：物质从液态变成固态叫凝固。

凝固图象：凝固特点：固液共存，放热，温度不变凝固特点：放热，逐渐变稠、变黏、变硬、最后凝固点：晶体熔化时的温度。

成固体，温度不断降低。

同种物质的熔点凝固点相同。

凝固的条件：⑴达到凝固点。

⑵继续放热。

2、汽化和液化：①汽化：定义：物质从液态变为气态叫汽化。

定义：液体在任何温度下都能发生的，并且只在液体表面发生的汽化现象叫蒸发。

影响因素：⑴液体的温度；⑵液体的表面积⑶液体表面空气的流动。

作用：蒸发吸热（吸外界或自身的热量），具有制冷作用。

定义：在一定温度下，在液体内部和表面同时发生的剧烈的汽化现象。

沸点：液体沸腾时的温度。

沸腾条件：⑴达到沸点。

⑵继续吸热沸点与气压的关系：一切液体的沸点都是气压减小时降低，气压增大时升高②液化：定义：物质从气态变为液态叫液化。

方法：⑴降低温度；⑵压缩体积。

好处：体积缩小便于运输。

作用：液化放热3、升华和凝华：①升华：物质从固态直接变成气态的过程，吸热，易升华物质有：碘、冰、干冰、樟脑钨。

②凝华定义：物质从气态直接变成固态的过程，放热练习：☆要使洗过的衣服尽快干，请写出四种有效的方法。

⑴将衣服展开，增大与空气的接触面积。

⑵将衣服挂在通风处。

⑶将衣服挂在阳光下或温度教高处。

⑷将衣服脱水（拧干、甩干）。

气熔化吸热汽化吸热凝华放热蒸发沸腾☆解释“霜前冷雪后寒”？霜前冷：只有外界气温足够低，空气中水蒸气才能放热凝华成霜所以“霜前冷”。

雪后寒：化雪是熔化过程，吸热所以“雪后寒”。

第三章物态变化单元测试题姓名_________________班级___________一、选择题1.O0C的冰和O0C的水相比较（）A、O0C的冰比O0C的水冷B、O0C的水比O0C的冰冷C、O0C的冰与O0C的水冷热程度相同D、无法比较2.在寒冷的冬天夜晚，用手摸室外的铁棍和木棍，感觉铁棍比木棍冷，则（）A、铁棍比木棍温度低B、木棍比铁棍温度低C、铁棍和木棍温度相同D、无法确定3.如图所示的四种“用温度计测水温”的实验操作，其中正确的是（）4.小明测体温时，忘了甩体温计，也没有读体温计的示数，直接用这个体温计去测体温，测量结果是37.50C。

在满足一定条件时，该云团中的水滴先后要经历转变为水蒸气、小冰晶等过程，之后落向地面并形成雨滴。

那么，从该云团中的水滴到降雨的过程中，其先后经历的物态变化是A．液化、汽化、凝固 B．升华、凝华、熔化C．汽化、凝华、熔化 D．液化、凝固、熔化12.外科医生做小手术或紧急治疗运动员肌肉扭伤时，常用蒸发快的液态氯乙烷做麻醉剂，把液态氯乙烷喷到局部皮肤上，使皮肤快速冷却，在一段时间内失去疼痛感，这是由于氯乙烷A.汽化放热B.汽化吸热C.凝固放热D.熔化吸热13．用一支示数为39℃的体温计，没有甩就去测量一个38℃的发烧病人的体温，当时的气温为36℃，则体温计的示数是（）A．36℃B．38℃C．39℃D．以上都有可能14．房间里有甲、乙、丙三支温度计，其中有一支温度计的刻度不正确，将甲放在空气中，乙的玻璃泡插在密封于玻璃瓶中的酒精里，丙的玻璃泡用沾有酒精的棉花包裹后放在空气中，它们的示数恰巧都是15 ℃，那么，该房间里的实际温度（）A．等于15℃B．高于15℃C．低于15℃D．无法判断15．俗话说“霜前冷，雪后寒”，这句话从物理学的角度分析，这是（）A．霜形成之前的气温一定比下雪后的气温低B．霜形成的温度比雪形成的温度低C．霜后的气温一定比霜形成前高，雪后气温一定比雪落地前低D．霜是在地面形成的，气温必定在0℃以下；雪是在高空形成的，雪熔化要吸收大量的热量，使地面气温降低16．下列物态变化的事例中，正确的是（）A．电冰箱冷冻室内出现白色的霜，这是凝固现象B．夏天阴凉地方的石头比较潮湿，这是液化现象C．舞台上用干冰制作“云雾”，这是汽化现象D．衣柜中的樟脑丸，过一段时间变小或消失，这是汽化现象二、填空题17.家庭和实验室里常用的温度计是根据__________________的规律制成的。

18.摄氏温度计的刻度方法是把 _____________ 的温度规定为O0C，把通常情况下___________的温度规定为1000C，在O0C和1000C之间分成100等份，每一等份就是 ______0C。

19.如图所示是小明用温度计测液体温度的示意图，请你帮他指出测量中的两处错误。

（1）__________________ ；（2）__________________ 。

20.有三支温度计，其中甲温度计的测量范围是35℃～42℃，乙温度计的测量范围是－30℃～50℃，丙温度计的测量范围是-20℃～105℃，由此可知：________温度计是家庭用的寒暑表，________温度计是实验室用的温度计，________温度计是体温计。

21.有一种乳白色的固体物质，在250℃开始就熔化，直到温度升高到300℃时，才熔化结束，这种物质一定是__________(选填：“晶体”或“非晶体”)，此物质在熔化的过程中__________（选填：“吸热”或“不吸热”）。

22.把一盆浮着冰块的水放在室外，过一段时间后发现冰的质量增多了，由此可知水____________（填物态变化），说明室外的气温一定___________（“高于”、“低于”）0℃，在上述过程中水_________（“吸收”、“放出”）热量。

23.把盛有碎冰块的大试管插入杯里的碎冰块中，用酒精灯加热。

当烧杯中的冰块有大半熔化时，试管中的冰______（填“熔化”、“不熔化”）。

由此可知，晶体熔化必须满足两个条件：一是要达到___________ ，二是能继续____________。

24.请将与下列自然现象所对应的物态变化的名称填在相应的横线上：初春的早晨大雾弥漫 __________；炎热的夏天积水干涸________ ；寒冷的冬天滴水成冰___________ ；天气预报中说“…向北移动的暖湿气流与来自…地区的冷空气前锋相遇，将在我国×××至×××之间形成一条东西方向的降雨带……”。

暖湿气流携带较多的水分，而与冷空气相遇才会降雨是因为水蒸气遇冷_________所致。

25.下面有一些温度值，请在－18℃、37℃、42℃、100℃、200℃中选择正确的答案填在横线上：水沸腾时的温度是_______；人体的正常的体温是___；洗澡水的最佳温度约是______；冰箱冷冻室的温度是______；炸排骨时的油温是_____。

26．果农常用保鲜袋包水果，目的之一是减少水果中水份的_________。

夏天喜欢吃冰棒，是因为冰棒熔化时需要____________热，使人感到凉爽。

27．小明参加学校组织的生存夏令营，学到了许多野外生存的知识与技能。

⑴如何获得饮用水。

如图所示，用一个大塑料袋套在树叶浓密的嫩枝上，将袋口扎紧后，在下方开一个小孔，在小孔下方放上接水的容器，利用植物中水的不断___________和___________，经过一段时间，你就能获取可饮用的水了。