管理统计学习题参考答案第八章
《管理统计学》第八章

Ti2 1 2 852 1052 952 SSA T 5 5 5 5415 ni n 5455 5415 40 ∴ SSE SST SSA 232 40 192
SSA / s 1 40 / 2 ∴ F 1.22 SSE / n s 192 / 12
假设
H1A : 1,2, ,s 之间不完全相等 H1B : 1, 2, , n 之间不完全相等
分析因素A、B
1 2 SST x T ni (152 182 192 222 152 ) 3 5 5647 5415 232
(2) 2 服从 ((s 1)(n 1)) 分布
2
SSE
SSA
(3)当 H 0 A 成立时,有 (4)当 H 0B 成立时,有
SSB 2
2
2 (s 1) 分布 服从
2 (n 1) 分布 服从
(5)
(6)
SSA (n 1) SSA ( s 1) FA ~ F ((s 1), ( s 1)(n 1) SSE SSE ( s 1)(n 1) SSB ( s 1) SSB (n 1) FB ~ F ((n 1), ( s 1)(n 1) SSE SSE ( s 1)(n 1)
Sig . (2-tailed) .019 .000 .002 .000
a. The sum of the contrast coefficients is not zero.
Multiple Comparisons Dependent Variable: 当 工 前 资 Mean Difference (I-J) -$40666.78* $4,153.925* *********** *********** -$4,153.925* -$44820.71* -$40666.78* $4,153.925* *********** *********** -$4,153.925* -$44820.71*
《管理统计学》习题及标准答案

《管理统计学》作业集习题集及答案第一章导论*1-1 对50名职工的工资收入情况进行调查,则总体单位是(单选)( 3 )(1)50名职工(2)50名职工的工资总额(3)每一名职工(4)每一名职工的工资*1-2 一个统计总体(单选)( 4 )(1)只能有一个标志(2)只能有一个指标(3)可以有多个标志(4)可以有多个指标*1-3 某班学生数学考试成绩分别为65分、71分、80分和87分,这四个数字是(单选)( 4 ) (1)指标(2)标志(3)变量(4)标志值第二章统计数据的调查与收集*2-1 非全面调查包括(多项选择题)(12 4 )(1)重点调查(2)抽样调查(3)快速普查(4)典型调查(5)统计年报*2-2 统计调查按搜集资料的方法不同,可以分为(多项选择题)( 12 3 ) (1)采访法(2)抽样调查法(3)直接观察法(4)典型调查法(5)报告法*2-3 某市进行工业企业生产设备状况普查,要求在7月1日至7月5日全部调查完毕。
则规定的这一时间是(单项选择题)(2)(1) 调查时间(2) 调查期限(3) 标准时间(4) 登记期限*2-4 某城市拟对占全市储蓄额五分之四的几个大储蓄所进行调查,以了解全市储蓄的一般情况,则这种调查方式是(单项选择题)(4)(1) 普查(2) 典型调查(3) 抽样调查(4) 重点调查*2-5 下列判断中,不正确的有(多项选择题)(23 4 )(1)重点调查是一种非全面调查,既可用于经常性调查,也可用于一次性调查;(2)抽样调查是非全面调查中最科学的方法,因此它适用于完成任何调查任务;(3)在非全面调查中,抽样调查最重要,重点调查次之,典型调查最不重要;(4)如果典型调查的目的是为了近似地估计总体的数值,则可以选择若干中等的典型单位进行调查;(5)普查是取得全面统计资料的主要调查方法。
*2-6 下列属于品质标志的是(单项选择题)( 2 )(1)工人年龄(2)工人性别(3)工人体重(4)工人工资*2-7 下列标志中,属于数量标志的有(多项选择题)(3)(1)性别(2)工种(3)工资(4)民族(5)年龄*2-8 下列指标中属于质量指标的有(多项选择题)(13 4 )(1)劳动生产率(2)废品量(3)单位产品成本(1)资金利润率(5)上缴税利额第三章统计数据的整理*3-1 区分下列几组基本概念:(1)频数和频率;答:A、频数:在一组依大小顺序排列的测量值中,当按一定的组距将其分组时出现在各组内的测量值的数目。
统计学第五版第八章课后习题答案

由Excel制表得:
由图可知:
已知:α= 0、05,n1 = n2=12
=31、75 =28、67 =10、20 =6、06 t=1、72 t∈(-1、72,1、72)接受,否则拒绝。 t=(31 、75-28、67)/(8、08* 0、41)=0、93 0、 93∈(-1、72,1、72)
决策:在α= 0、05得水平上接受 。
已知包重服从正态分布,试检验该日打包机工作就是否正常 ( α
=0、) 。 解:
如图所示:
本题采用单样本t检验。
:μ=100 :μ≠100基
本统计量:
α=0、05,N=9, =99、978,
S=1、2122, =0、4041 检验结果: t=-0、005,自由度f=8, 双侧检验P=0、996,单侧检验P=0、498
:μ≥700
:μ<700
∵α=0、05∴
=-1、645
计算检验统计量: =(680-700)/(60/6)=-2
决策: ∵Z值落入拒绝域,
∴在α=0、05得显著水平上拒绝 ,接受 。
结论: 有证据表明这批灯泡得使用寿命低于700小时,为不合格产品。
8、3 某地区小麦得一般生产水平为亩产250公斤,其标准差为30 公斤。现用一种化肥进行试验,从25个小区抽样,平均产量为270
决策:在 α= 0、05得水平上拒绝 。
结论: 服用阿司匹林可以降低心脏病发生率。
8、14 某工厂制造螺栓,规定螺栓口径为7、0cm,方差为0、03cm。 今从一批螺栓中抽取80个测量其口径,得平均值为6、97cm,方差为 0、0375cm。假定螺栓口径为正态分布,问这批螺栓就是否达到规 定得要求 (a=0、05)?
双侧检验
《管理统计学》习题及答案

《管理统计学》作业集习题集及答案第一章导论*1-1 对50名职工的工资收入情况进行调查,则总体单位是(单选)( 3 )(1)50名职工(2)50名职工的工资总额(3)每一名职工(4)每一名职工的工资*1-2 一个统计总体(单选)( 4 )(1)只能有一个标志(2)只能有一个指标(3)可以有多个标志(4)可以有多个指标*1-3 某班学生数学考试成绩分别为65分、71分、80分和87分,这四个数字是(单选)( 4 ) (1)指标(2)标志(3)变量(4)标志值第二章统计数据的调查与收集*2-1 非全面调查包括(多项选择题)(12 4 )(1)重点调查(2)抽样调查(3)快速普查(4)典型调查(5)统计年报*2-2 统计调查按搜集资料的方法不同,可以分为(多项选择题)( 12 3 ) (1)采访法(2)抽样调查法(3)直接观察法(4)典型调查法(5)报告法*2-3 某市进行工业企业生产设备状况普查,要求在7月1日至7月5日全部调查完毕。
则规定的这一时间是(单项选择题)(2)(1) 调查时间(2) 调查期限(3) 标准时间(4) 登记期限*2-4 某城市拟对占全市储蓄额五分之四的几个大储蓄所进行调查,以了解全市储蓄的一般情况,则这种调查方式是(单项选择题)(4)(1) 普查(2) 典型调查(3) 抽样调查(4) 重点调查*2-5 下列判断中,不正确的有(多项选择题)(23 4 )(1)重点调查是一种非全面调查,既可用于经常性调查,也可用于一次性调查;(2)抽样调查是非全面调查中最科学的方法,因此它适用于完成任何调查任务;(3)在非全面调查中,抽样调查最重要,重点调查次之,典型调查最不重要;(4)如果典型调查的目的是为了近似地估计总体的数值,则可以选择若干中等的典型单位进行调查;(5)普查是取得全面统计资料的主要调查方法。
*2-6 下列属于品质标志的是(单项选择题)( 2 )(1)工人年龄(2)工人性别(3)工人体重(4)工人工资*2-7 下列标志中,属于数量标志的有(多项选择题)(3)(1)性别(2)工种(3)工资(4)民族(5)年龄*2-8 下列指标中属于质量指标的有(多项选择题)(13 4 )(1)劳动生产率(2)废品量(3)单位产品成本(1)资金利润率(5)上缴税利额第三章统计数据的整理*3-1 区分下列几组基本概念:(1)频数和频率;答:A、频数:在一组依大小顺序排列的测量值中,当按一定的组距将其分组时出现在各组内的测量值的数目。
大学统计学第八章课后题答案
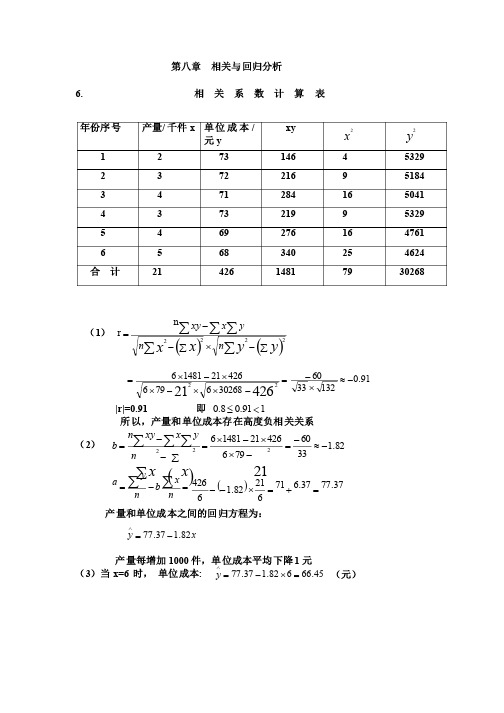
第八章 相关与回归分析 6. 相 关 系 数 计 算 表 (1) ()()åååååå-´å--=y yx x n n yx xy 2222nr 91.0132336030268679642621148164262122-»´-=-´´-´´-´= |r|=0.91 即 191.08.0<£ 所以,产量和单位成本存在高度负相关关系(2) ()82.133********211481621222-»-=-´´-´=å--=ååååx x n y x xy n b =-=åånx b ny a ()37.7737.67162182.16426=+=´-- 产量和单位成本之间的回归方程为: x y 82.137.77-=Ù 产量每增加1000件,单位成本平均下降1元 (3)当x=6 时, 单位成本: 45.66682.137.77=´-=Ùy (元) 年份序号 产量/千件x 单位成本/元y xy x 2 y 2 1 2 73 146 4 5329 2 3 72 216 9 5184 3 4 71 284 16 5041 4 3 73 219 9 5329 5 4 69 276 16 4761 6 5 68 340 25 4624 合 计 21 426 1481 79 30268 7. 相 关 系 数 计 算 表 序号 汽车使用年限/年x 年维修费用/元y xy x 2 y 2 1 2 400 800 4 160000 2 2 540 1080 4 291600 3 3 520 1560 9 270400 4 4 640 2560 16 409600 5 4 740 2960 16 547600 65 600 3000 25 360000 7 5 800 4000 25 640000 86 700 4200 36 490000 9 6 760 4560 36 577600 10 6 900 5400 36 810000 11 8 840 6720 64 705600 12 9 1080 9720 81 1166400 合 计 608520465603526428800()()åååååå-´å--=y yx x n n yx xy 2222n r=89.045552006244752064288001235212852060465601285206022»´=-´´-´´-´|r|=0.89 即 189.08.0<£所以,汽车使用年限与其维修费用间存在高度正相关关系(2) ()15.766244752035212852060465601260222==-´´-´=å--=ååååxx n y x xy n b =-=åån x b n y a 25.32975.380710126015.76128520=-=´- 汽车使用年限与其维修费用的回归方程为: x y 15.7625.329+=Ù(3) 当x=15时, 维修费用为: 5.14711515.7625.329=´+=Ùy8. (1) 相 关 系 数 计 算 表 序号 母亲身高/厘米x 女儿身高/厘米y xy x 2y 21 158 159 25122 24964 25281 2 159 160 25440 25281 256003 160 160 25600 25600 256004 161 163 26243 25921 265695 161 159 25599 25921 252816 155 154 23870 24025 237167 162 159 25758 26244 25281 8 157 158 24806 24649 24964 9 162 160 25920 26244 25600 10 150 157 23550 22500 24649 合计1585 1589251908251349252541()()åååååå-´å--=yy x x n n y x xy 2222nr=158915852225254110251349101589158525190810-´´-´´-´655.0»|r|=0.655 所以,母亲与女儿之间的关系为显著正相关(2) ()41.012655152513491015891585251908101585222»=-´´-´=å--=ååååxx n y x xy n b =-=åånx b n y a 915.93985.649.15810158541.0101589=-=´- 母亲与女儿之间的回归方程为: x y 41.0915.93+=Ù(3) 当x=170时, 女儿的身高为: 615.16317041.0915.93=´+=Ùy 9.(1) 由题知 n=9 å=546x å=260y å=16918xy 343622=åx()92.01114210302343629260546169189546222»=-´´-´=å--=ååååx x n yx xy n b =-=åånx b ny a 92.26954692.09260-=´-银行存款余额的直线回归方程: x y 92.092.26+-=Ù(2) 当x=400时,银行存款余额08.34140092.092.26=´+-=Ùy。
天津大学版管理统计学答案

天津⼤学版管理统计学答案管理统计学课后习题答案第⼀章题⽬1a调查规模为2500b定性c百分⽐d700题⽬2a定性b42.25%题⽬3a定量b定性c定性d定量题⽬4a定量b定量c定性d定量e定性题⽬5a40.00%b定性c略第⼆章题⽬1题⽬2ab33.00%c题⽬3abc上述数据显⽰了⼤多数⼈每周使⽤3-5.9⼩时计算机第三章题⽬1a平均数=38.75b Q1=29.5Q3=47.5题⽬2a国内平均数115.13中位数111.56国外平均数36.62083中位数36.695b国内全距86.24样本标准差26.81995变异系数0.232954国外全距42.96样本标准差11.398830.311266题⽬3题⽬4数据182168184190 a全距22b⽅差75.2c标准差8.671793355d变异系数0.04871794题⽬5标准差0.0126192〉0.005⽣产线要关闭题⽬6通话时间组中值频数组内和平⽅和4~7 5.5422184.968~119.5547.539.212~1513.5794.510.0816~1917.523554.0820~2321.5121.584.6424~2725.5125.5174.24合计20246547.2平均数12.3⽅差28.8标准差5.366563146第四章题⽬1a bc查表得78.12题⽬2a b c 题⽬3a 22.8b 7.757433711题⽬4a 200b 5c N(200,25)d中⼼极限定理题⽬5aN(250,50)b c 题⽬5a N(320,187.5)b 13.69306394c d第五章题⽬1=80S=10n=20总体⽅差未知,n=20<30,因此⽤t分布估计。
在90%置信度下,总体均值的置信区间为= 1.7291置信区间为[76.1336148683.86639]在95%置信度下,总体均值的置信区间为= 2.0933置信区间为[75.319238984.68076]题⽬2= 6.525S=0.5437443)20(t 05.0)19(t 025.0= 2.0933置信区间为[ 6.27048627 6.779514]题⽬3=22.4S=5n=61>30a= 1.96(正态分布表中查0.975所对应置信区间为[21.1452385823.65476]b=2置信区间为[21.119631223.68037]题⽬4=2000=0.05=an=61.4656取62bn=384.16取385cn=1536.64取1537题⽬5= 6.25=0.05=a n= 6.0025取7bn=150.0625取151题⽬6a=0.885714286b0.023569472c =1.645)60(t 025.0)19(t 025.0025.0µσα025.0µσα025.0µp =?05.0µ置信区间为[0.8659327650.905495807]题⽬7a 0.02=0.05n=2016.84取2017b =0.237977194c 单个总体⽐率的区间估计95%的置信区间为带⼊数据得[0.2193925270.256562]第六章题⽬1n=200S=1.5= 1.28:3:34.714045208> 1.28因此拒绝,收看电视的时间显著增加题⽬2a 拒绝规则为U<=b n=40S=1.2= 1.645:3:3-5.270462767<-1.645因此拒绝,减肥效果未达宣传值c p= 6.80401E-08近似为0题⽬3 n=45S=0.2:3=?αp01.0µ0H 1H >µ≤µ0H αµ-0H ≥µ<µ05.0µ0H 0H =µ≠µ:3==6.372793736> 1.28因此拒绝,该⼯序未达到标准题⽬4n=500S=0.2=-1.28:0.15:0.151.628183>因此接受,可实⾏新包装题⽬5an=30=2<24.24779435时拒绝原假设b=[ 3.417225575]=0.99968370.000316c =1H ≠µ01.0µ0H 0H 1H ≥p01.0µ-0H =0µσβΦ=ββ[0.678612788]=0.75130840.248692d=[-0.690693606]=0.24487910.755121题⽬6 n=30=0.8a 意味着冲⼊量未达标准但错认为达标从⽽b =得到〉[-5.383266[-1.463266Φ=ββΦ=β=0µσ2/αµΦΦ=β0.071697题⽬7=59令=<得到查表得= 1.285得到n=214.6225取215或由公式计算题⽬8=30385=0.02=0.11.285或由公式题⽬9=324=0.02=1-0.8==β=1µσ=-=-05.0µµα=βα=1µσβ=0µ=αµα=1µσβ=0µ=αµ=βµ2.0550.845或由公式75.69题⽬10设:看前、看后总体均值分别为因总体⽅差未知且是否相同未知,因此⾸先假设两总体⽅差是否相同::当显著性⽔平为0.1F= 1.484196880H 21µµ≥21,µµ=1S =2S 0H 1H 21σσ=21σσ≠⽅差分别为0.201739801n1=0.086756364n2=::当显著性⽔平为0.05时F= 5.407300359设湿路⼲路⽅差分别为32n1=16n2=a::当显著性⽔平为0.05时F=4〉F(29,29)=1.86b湿路不易刹车,应减速慢⾏题⽬13设两个⽣产部⽅差为 2.35.4:当显著性⽔平为0.1时21S ,S =1S =2S 0H 1H 21σσ=21σσ≠21S S >21S ,S =1S =2S 0H 1H 21σσ≤21σσ>2212S ,S =12S =22S 0H 1H 21σσ=21σσ≠F=0.425925926<所以拒绝原假设,认为两个⽣产部门产品有差异题⽬14国内航班⼀等舱⽐例pa1=0.045171国际航班⼀等舱⽐例pa2=0.079137⼀等舱总⽐例pa=0.055435H0:pa1=pa2 2.0674021拒绝H0,⼀等舱旅⾏⽐例与航班类型有关国内航班商务舱⽐例pb1=0.147975国际航班商务舱⽐例pb2=0.435252商务舱总⽐例pb=0.234783H0:pa1=pa29.4399796拒绝H0,商务舱旅⾏⽐例与航班类型有关国内航班经济舱⽐例pc1=0.806854国际航班经济舱⽐例pc2=0.485612经济舱总⽐例pc=0.709783025.02/µµα=025.02/µµα=025.02/µµα=H0:pc1=pc29.8583452拒绝H0,经济舱旅⾏⽐例与航班类型有关综上,机票类型与航班类型有关。
统计学第八章课后题及答案解析
第八章一、单项选择题1.时间数列的构成要素是()A.变量和次数 B.时间和指标数值C.时间和次数 D.主词和时间2.编制时间数列的基本原则是保证数列中各个指标值具有()A.可加性 B.连续性C.一致性 D.可比性3.相邻两个累积增长量之差,等于相应时期的()A.累积增长量 B.平均增长量C.逐期增长量 D.年距增长量4.统计工作中,为了消除季节变动的影响可以计算()A.逐期增长量 B.累积增长量C.平均增长量 D.年距增长量5.基期均为前一期水平的发展速度是()A.定基发展速度 B.环比发展速度C.年距发展速度 D.平均发展速度6.某企业2003年产值比1996年增长了1倍,比2001年增长了50%,则2001年比1996年增长了()A.33% B.50%C.75% D.100%7.关于增长速度以下表述正确的有()A.增长速度是增长量与基期水平之比 B.增长速度是发展速度减1C.增长速度有环比和定基之分 D.增长速度只能取正值8.如果时间数列环比发展速度大体相同,可配合()A.直线趋势方程 B.抛物线趋势方程C.指数曲线方程 D.二次曲线方程二、多项选择题1.编制时间数列的原则有()A.时期长短应一致 B.总体范围应该统一C.计算方法应该统一 D.计算价格应该统一E.经济内容应该统一2.发展水平有()A.最初水平 B.最末水平C.中间水平 D.报告期水平E.基期水平3.时间数列水平分析指标有()A.发展速度 B.发展水平C.增长量 D.平均发展水平E.平均增长量4.测定长期趋势的方法有()A.时距扩大法 B.移动平均法C.序时平均法 D.分割平均法E.最小平方法三、填空题1.保证数列中各个指标值的_______是编制时间数列的最主要规则。
2.根据采用的基期不同,增长量可以分为逐期增长量和_______增长量两种。
3.累积增长量等于相应的_______之和。
两个相邻的_______之差,等于相应时期的逐期增长量。
统计学第八章课后习题答案
8.1解:建立假设: H0:μ=4.55;H1:μ≠4.55这是双侧检验,并且方差已知,检验的统计量 Z 值为:=-1.833而=1.96>|-1.833|,因此不能拒绝原假设,即可认为现在生产的铁水平均含碳量为 4.558.2解:建立假设: H0:μ≥700;H1:μ<700这是左侧检验,并且方差已知,检验统计量 Z 为:Z==-2而-=-1.645>-2,因此拒绝原假设,即在显著性水平 0.05 下这批元件是不合格的。
8.3解:建立假设: H0:μ≤250;H1:μ>250这是右侧检验,并且方差已知,检验的统计量 Z 值为:Z==3.33 而=1.645<3.33,因此拒绝原假设,即这种化肥使小麦明显增产。
8.4解:建立假设: H0:μ=100;H1:μ≠1009/108.055.4484.4−=Z Z 025.036/60700680−Z 05.025/30250270−Z05.0由样本数据可得: ==99.978S===1.212这是双侧检验,并且方差未知,又是小样本,故采用 t 统计量,检验统计量的值为: t==-0.054而(8)=2.306>|-0.054|,因此不拒绝原假设,即该日打包机工作正常8.5、由题意先建立假设,显然不符合标准的比例越小越好,由于采用的是产品质量抽查,即使总体不合标准的比例没有超过5%,属于合格范围,采用右单侧检验。
P=6/50=12%属于单侧检验,当α=0.05时,有,因此拒绝原假设,即认为该批食品不能出厂n X ni ix∑==195.100....7.983.99+++1)(12−−∑=n x ni i x 8)978.995.100(...978.99-7.98978.99-3.99222−+++)()(9/2122.1100-978.99t025.0%5:%,5:1>≤ππH H o 27.250%)51(%5%5%12=−−−=Z 27.2645.105.0<=Z8.6、由题意建立假设:单侧检验,并且方差未知,n=15,属于小样本,故采用t 统计量,检验统计量的值为:α=0.05,,因此不能拒绝原假设,认为该厂家的广告不真实8.7、建立假设:,由样本数据可以得出,这是单侧检验,并且方差未知,是小样本,因此采用t 检验量,检验统计量的值为25000:,25000:10>≤μμH H 549.115/50002500027000/0=−=−=n s x t μ549.1761.1)14(05.0>=t 225,22510>≤H H 5.24116170485 (2121012801591)=++++++==∑=nxx ni i7.9815)5.241170(....)5.241280()5.241159(12221=−++−+−=−=∑=n xs ni in s x t /μ−=669.016/7.982255.241=−=通过查表可得出,,因此不能拒绝原假设,没有理由认为元件的平均寿命显著地大于225小时。
概率论与数理统计(经管类)第八章课后习题答案word
习题8.11.某天开工时,需检验自动装包机工作是否正常.根据以往的经验,其装包的重量在正常情况下服从正态分布N(100,1.52)(单位:公斤).现抽测了9包,其重量为:99.3 98.7 100.5 101.2 98.3 99.7 99.5 102.0 100.5问这天包装机工作是否正常?将这一问题化为一个假设检验问题,写出假设检验的步骤,设α=0.05.解: (1)作假设H0:μ=100,H1:μ≠100(2)选取检验统计量u=X−100σ√n⁄(3)查表知μα2=μ0.025=1.96, 拒绝域为|u|=|X−100σ√n⁄|≥1.96(4)由样本观测值有=99.97∴|u|=|X−100σ√n⁄|=|99.97−1001.5√9⁄|=0.06<1.96.不属于拒绝域,所以接受原假设H0,即认为这天包装机工作正常.2.设α,β分别是假设检验中犯第一,第二类错误的概率且H0,H1分别为原假设和备择驾驶,则(1)P{接受H0|H0不真}=β(2)P{拒绝H0|H0真}=α(3)P{拒绝H0|H0不真}=1−β(4)P{接受H0|H0真}=1−α习题8.21.某自动机生产一种铆钉,尺寸误差X~N(μ,1),该机正常工作与否的标志是检验μ=0是否成立.一日抽检容量n=10的样本,测得样本均值X=1.01.试问:在检验水平α=0.05下,该日自动机工作是否正常?解:检验假设H0:μ=μ0=0,H1:μ≠0∵X=1.01,n=10,σ=1∴|u|=|X−μσ√n⁄|=|1.01−01√10⁄|=3.194查表知μα2=μ0.025=1.96,由于|u|=3.194>1.96,故拒绝H0,即该日自动机工作不正常.2.假定考生成绩服从正态分布,在某地一次数学统考中,随机抽取了36位考生的成绩,算的平均成绩为X=66.5分,标准差S=15分,问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分?解: 检验假设H0:μ=μ0=70,H1:μ≠70选取检验统计量t =X−μ0S √n⁄−1)拒绝域为|t |=|X−70S √n ⁄≥t α2(n −1)=t 0.025(35)=2.0301将X =66.5,S =15,n =36代入得|t |=1.4<2.0301.故接受H 0.即在显著性水平0.05下, 可以认为这次考试全体考生的平均成绩为70分. 3. 某种产品的重量X~N (12,1)(单位:克).更新设备后,从新生产的产品中,随机地抽取100个,测得样本均值=12.5(克).如果方差没有变化,问设备更新后,产品的平均重量是否有显著变化(α=0.1)? 解: 检验假设H 0:μ=μ0=12,H 1:μ≠12 ∵ =12.5,n =100,σ=1∴|u |=|X −μσ√n⁄|=|12.5−121√100⁄|=5查表知μα2=μ0.05=1.645,由于|u |=5>1.645,故拒绝H 0.即设备更新后,产品的平均重量有显著变化.4. 一种燃料的辛烷等级服从正态分布,其平均等级为98.0,标准差为0.8,现从一批新油中抽25桶,算得样本均值为97.7.假定标准差与原来一样,问新油的辛烷平均等级是否比原燃料平均等级偏低(α=0.05). 解: 检验假设H 0:μ≤μ0=98,H 1:μ>98 ∵ =97.7,n =25,σ=0.8∴|u |=|X −μσ√n⁄|=|97.7−980.8√25⁄|=1.875查表知μα2=μ0.025=1.96,由于|u |=1.875<1.96,故接受H 0.即可以认为新油的辛烷平均等级比原燃料平均等级偏低.5. 从一批灯泡中随机抽取50个,分别测量其寿命,算得其平均值X =1900(小时),标准差S=490(小时).问能否认为这批灯泡的平均寿命为2000(小时)( α=0.01).(用大样本情况下的u 检验) 解: 检验假设H 0:μ=μ0=2000,H 1:μ≠2000 ∵ X =1900,n =50,s =490∴|u |=|X −μs √n⁄|=|1900−2000490√50⁄|=1.44查表知μα2=μ0.005=2.57,由于|u |=1.44<2.57,故接受H 0.即可以认为这批灯泡的平均寿命为2000(小时).6. 某批矿砂的五个样品中镍含量经测定为(%):3.25 3.27 3.24 3.263.24设测定值服从正态分布,问能否认为这批矿砂的镍含量为3.25%(α=0.05). 解: 检验假设H 0:μ=μ0=3.25,H 1:μ≠3.25 选取检验统计量t =X−μ0S √n⁄−1)经计算=3.252,S =0.013 拒绝域为|t |=|X−3.25S √n⁄|≥t α2(n −1)=t 0.025(4)=2.7764将X =66.5,S =15,n =5代入得|t |=0.344<2.7764.故接受H 0. 即可以认为这批矿砂的镍含量为3.25%.7. 有甲,乙两台机床加工同样产品,从这两台机床中随机抽取若干件,测得产品直径(单位:毫米)为:机床甲20.5 19.8 19.7 20.4 20.1 20.0 19.0 19.9 机床乙19.720.8 20.5 19.8 19.4 20.6 19.2 假定两台机床加工的产品直径都服从正态分布,且总体方差相等.问甲,乙两台车床加工的产品直径有无显著差异(α=0.05). 解:检验假设H 0:μ1=μ2,H 1:μ1≠μ2经计算X =19.925,y =20,S 12=1.5157,S 22=2.386∴|t |=|X −y S w √1m +1n|=||19.925−20√7∗1.5157+6∗2.3868+7−2∗√18+17||=0.265查表知t α2(m +n −2)=t 0.025(13)=2.1604,由于|t |=0.265<2.1604,故接受H 0.即甲,乙两台车床加工的产品直径无显著差异.8. 从甲地发送一个信号到乙地.设乙地接受到的信号值是一个服从正态分布N(μ,0.22)的随机变量,其中μ为甲地发送的真实信号值.现甲地重复发送同一信号5次,乙地接受到的信号值为 8.05 8.15 8.2 8.1 8.25 设接收方有理由猜测甲地发送的信号值为8.问能否接受这一猜测? (α=0.05) 解: 检验假设H 0:μ=μ0=8,H 1:μ≠8∵ =8.15,n =5,σ=0.2∴|u |=|X −μσ√n⁄|=|8.15−80.2√5⁄|=1.677查表知μα2=μ0.025=1.96,由于|u |=1.677<1.96,故接受H 0.即可以接受这一猜测. 习题8.31. 某纺织厂生产的某种产品的纤度用X 表示,在稳定生产时,可假定X~N(μ,σ2),其中标准差σ=0.048.现在随机抽取5跟纤维,测得其纤度为 1.32 1.55 1.36 1.40 1.44 试问总体X 的方差有无显著变化. (α=0.1) 解: 检验假设H 0:σ=0.048,H 1:σ≠0.048 检验统计量χ2=(n−1)S 2σ02~χ2(n −1)由α=0.1查表得χα22(n −1)=χ0.052(4)=9.488,χ1−α22(n −1)=χ0.952(4)=0.711于是得出拒绝域为W =(0,0.711)∪(9.488,+∞) 经计算S 2=0.31124代入χ2=(n−1)S 2σ02=4∗0.311240.048=13.51>9.488,故拒绝H 0.即总体X 的方差有显著变化.2. 设有来自正态总体X~N(μ,σ2),容量为100的样本,样本均值X =2.7,μ,σ2均未知,而∑(x i −x)2ni=1=225在α=0.05下,检验下列假设: (1) H 0:μ=3, H 1:μ≠3; (2) H 0:σ2=2.5, H 1:σ2≠2.5. 解: (1) 检验假设H 0:μ=3, H 1:μ≠3∵ X =2.7,n =100,S =√1n −1∑(x i −x)2ni=1=1.508 因此可用大样本情况的u 检验|u |=|X −μs √n⁄|=|2.7−31.508√100⁄|=1.99查表知μα2=μ0.025=1.96,由于|u |=1.99>1.96,故拒绝H 0.(同课后答案有争议)(2)该题无法查到χ0.0252(99)值故省略.(用χ2检验)3. 甲,乙两台机床加工某种零件,零件的直径服从正态分布,总体方差反映了加工精度.为比较两台机床的加工精度有无差别,现从各自加工的零件中分别抽取7件产品和8件产品,测得其直径为X(机床甲)16.2 16.4 15.8 15.5 16.7 15.6 15.8 Y(机床乙)15.9 16.0 16.4 16.1 16.5 15.8 15.7 15.0 问这两台机床的加工精度是否一致? 解:该题无α值,故省略.(用F 检验)4. 对两批同类电子元件的电阻进行测试,各抽6件,测得结果如下(单位:Ω)A 批0.140 0.138 0.143 0.141 0.144 0.137 B 批 0.135 0.140 0.142 0.136 0.138 0.141 已知元件电阻服从正态分布,设σ=0.05,问:(1) 两批电子元件电阻的方差是否相等; (2) 两批元件的平均电阻是否有差异.解: (1)检验假设H 0:σ12=σ22, H 1:σ12≠σ22经计算S 12=0.00272,S 22=0.00282由α=0.05查表得F α2(n 1−1,n 2−1)=F 0.025(5,5)=无法查F 0.025(5,5)对应值,故无法做. 习题8.4某厂使用两种不同的原料生产同一类产品,随机选取使用原料A 生产的产品22件,测得平均质量为X =2.36(kg),样本标准差S x =0.57(kg).取使用原料B 生产的样品24件,测得平均质量为y =2.55(kg),样本标准差S y =0.48(kg).设产品质量服从正态分布,这两个样本相互独立.问能否认为使用B 原料生产的产品平均质量较使用原料A 显著大?(取显著性水平α=0.05).解:检验假设H 0:μA ≥μB , H 0:μA <μB ; 选取检验统计量t =X −y S w √1m +1n+n −1)|t |=|X −y S w √1m +1n|=|2.36−2.55√21∗0.572+23∗0.48244∗√122+124|=1.226查表知t α2(m +n −2)=t 0.025(44)=2.0154,由于|t |=1.226<2.0154,故接受H 0.即使用B 原料生产的产品平均质量于使用原料A 生产的产品平均质量无显著大.自测题8 一、,选择题在假设检验问题中,显著性水平α的意义是 A . A. 在H 0成立的条件下,经检验H 0被拒绝的概率 B. 在H 0成立的条件下,经检验H 0被接受的概率 C. 在H 0不成立的条件下,经检验H 0被拒绝的概率 D. 在H 0不成立的条件下,经检验H 0被接受的概率 二、,填空题1. 设总体X 服从正态分布N (μ,σ2),其中μ未知,x 1,x 2,⋯,x n 为其样本.若假设检验问题为H 0:σ2=1, H 1:σ2≠1,则采用的检验统计量应为 χ2=(n−1)S 21.2. 设某假设检验问题的拒绝域为W,且当原假设H 0成立时,样本值x 1,x 2,⋯,x n 落入W 的概率为0.15,则犯第一类错误的概率为 0.15 .(参考page 169)3. 设样本,x 1,x 2,⋯,x n 来自正态分布N (μ,1),假设检验问题为H 0:μ=0,H 1:μ≠0,则在H 0成立的条件下,对显著性水平α,拒绝域W 应为 |u |>u α,其中u =X √n .(参考page 181表8-4)三、某型号元件的尺寸X 服从正态分布,其均值为3.278cm,标准差为0.002cm.现用一种新工艺生产此类元件,从中随机取9个元件,测量其尺寸,算得均值X =3.2795cm ,问用新工艺生产的元件尺寸均值与以往有无显著差异.(显著发生性水平α=0.05)(附u 0.025=1.96,u 0.05=1.645) 解: 检验假设H 0:μ=μ0=3.278,H 1:μ≠3.278 ∵ X =3.2795,n =9,σ=0.002∴|u |=|X −μσ√n⁄|=|3.2795−3.2780.002√9⁄|=2.25又因μα2=μ0.025=1.96,|u |=2.25>1.96故拒绝H 0,即用新工艺生产的元件尺寸均值与以往有差异.四、用传统工艺加工的某种水果罐头中,每瓶的平均维生素C的含量为19(单位:mg).现改变了加工工艺,抽查了16瓶罐头,测得维生素C的含量的平均值X=20.8,样本标准差S=1.617.假定水果罐头中维生素C的含量服从正态分布.问在使用新工艺后,维生素C的含量是否有显著变化(显著性水平α=0.01)?(附t0.005(15)=2.9467,t0.005(16)=2.9208)解: 检验假设H0:μ=μ0=19,H1:μ≠19∵=20.8,n=16,S=1.617∴|t|=|X−μS√n⁄|=|20.8−191.617√16⁄|=4.453又因tα2(n−1)=t0.005(15)=2.9467,|t|=4.453>2.9467故拒绝H0,即使用新工艺后,维生素C的含量有显著变化.。
管理统计学与SPSS-16.0应用课件习题及答案08
习题8(1)随着公司的持续发展,常常有滑入无效率困境的危险,假定若干年后公司的销售开始滑坡,但公司还是不停地招聘新人,这种情况在某个10年中的数据会与下表给出的数据相似。
根据这些数据,以销售额为自变量,员工数为因变量画出散点图,并建立一个回归模型,通过员工的数量来预测销售额。
根据你的分析结果回答:如果这个趋势继续下去,你对公司的管理层有何建议?你认为管理层应该关注什么?年序号销售额(百万美元)员工数1 20.2 1202 24.3 1353 28.6 1424 33.4 1505 35.2 1556 35.9 1687 36.3 1728 36.2 1709 36.5 17510 36.4 174解:得到的散点图如下图所示,由散点图看出两变量之间有明显的线性关系。
通过SPSS 操作,得到如下所示结果,操作步骤略(与书中案例同)。
由上表中判定系数为0.954,可知自变量与因变量的关系非常密切。
ANOVA bModel Sum of Squaresdf Mean Square F Sig. 1Regression 2958.627 1 2958.627 80.983.000aResidual 292.273 8 36.534Total3250.9009a. Predictors: (Constant), 销售额b. Dependent Variable: 员工数由上表中,统计量F=80.983,回归模型的Sig.值为0,说明该模型有显著的统计意义,自变量x 与因变量y 之间确有线性回归关系由上表,常数项和销售额所对应的系数其t 检验的Sig.值都为0,说明回归系数与0有显著差别,具有显著的统计学意义。
从表格中可以看出估计值及其检验结果,常数项689.56ˆ0=β,回归系数078.3ˆ1=β,回归系数检验统计量t=8.999。
所以得出例8-8的拟合结果为 x y078.3689.56ˆ+= 建议请读者独立思考,这里不多做解答。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章1. 解:(1)假设检验的基本思想是,样本平均数与总体平均数出现差异不外乎两种可能:一是改革后的总体平均长度不变,但由于抽样的随机性使样本平均数与总体平均数之间存在抽样误差;二是由于工艺条件的变化,使总体平均数发生了显著的变化。
因此,可以这样推断:如果样本平均数与总体平均数之间的差异不大,未超出抽样误差范围,则认为总体平均数不变;反之,如果样本平均数与总体平均数之间的差异超出了抽样误差范围,则认为总体平均数发生了显著的变化。
根据样本平均数的抽样分布定理,有x Z σx μ±=或Z /σμx x ≤-。
当0=Z 时,表明样本均值等于总体均值,即μx =;当Z 很大时,表明样本均值离总体均值很远,即∆很大。
后一种情况是小概率事件。
在正常情况下,小概率事件是不会发生的,那么在一次抽样中小概率事件居然发生了,我们就有理由认为样本均值是不正常的,它与原总体相比,性质已经发生变化,应该拒绝接受原假设。
(2)假设检验的一般步骤包括:① 提出原假设和备择假设;对每个假设检验问题,一般可同时提出两个相反的假设:原假设和备择假设。
原假设又称零假设,是正待检验的假设,记为H 0;备择假设是拒绝原假设后可供选择的假设,记为H 1。
原假设和备择假设是相互对立的,检验结果二者必取其一。
接受H 0,则必须拒绝H 1;反之,拒绝H 0则必须接受H 1。
② 选择适当的统计量,并确定其分布形式;不同的假设检验问题需要选择不同的统计量作为检验统计量。
在例中,我们所用的统计量是Z ,在H 0为真时,N Z ~(0,1)。
③选择显著性水平α,确定临界值;显著性水平表示H 0为真时拒绝H 0的概率,即拒绝原假设所冒的风险,用α表示。
假设检验就是应用了小概率事件实际不发生的原理。
这里的小概率就是指α。
但是要小到什么程度才算小概率? 对此并没有统一的标准。
通常取α=0.1,0.05,0.01。
给定了显著性水平α,就可由有关的概率分布表查得临界值,从而确定H 0的接受区域和拒绝区域。
临界值就是接受区域和拒绝区域的分界点。
④作出结论。
根据样本资料计算出检验统计量的具体值,并用以与临界值比较,作出接受或拒绝原假设H 0的结论。
如果检验统计量的值落在拒绝区域内,说明样本所描述的情况与原假设有显著性差异,应拒绝原假设;反之,则接受原假设。
2. 解:(1)抽样估计和假设检验都是统计推断的重要内容。
如果总体分布形式已知,只是总体参数未知,则统计推断问题就归结为推断总体参数的问题。
抽样估计或称参数估计是根据样本资料估计总体参数的真值,而假设检验是根据样本资料来检验对总体参数的先验假设是否成立。
区间估计通常求得的是以样本估计值为中心的双侧置信区间,而假设检验不仅有双侧检验也常常采用单侧检验,视检验的具体问题而定。
区间估计立足于大概率,通常以较大的把握程度(可信度)1-α去估计总体参数的置信区间。
而假设检验立足于小概率,通常是给定很小的显著性水平α去检验对总体参数的先验假设是否成立。
区间估计和假设检验虽各有其特点,但也有着紧密的联系。
两者都是根据样本信息对总体参数进行推断,都是以抽样分布为理论依据,都是建立在概率基础上的推断,推断结果都有一定的可信程度或风险;对同一实际问题的参数进行推断,使用同一样本、同一统计量、同一分布。
因而,两者可以相互转换,即区间估计问题可以转换成假设检验问题,假设检验问题也可以转换成区间估计问题。
这种相互转换形成了区间估计与假设检验的对偶性。
(2)根据置信区间进行假设检验的方法如下:以总体均值μ的区间估计和假设检验为例,当总体方差2σ已知时,n x /σσ=,由于统计量)/(00n σ/μx /σμx Z x -=-=~ N (0, 1)给定置信度1-α时,有αZ Z P α-=≤1)(2反之αα=>)(2Z Z P当总体均值μ可知时,可估计的μ置信度为1-α的置信区间为22/)-(αασμZ x Z x ≤≤-上式等价于Z 检验的接受区域:2αZ Z ≤若事先假设:0μμ=,可求出统计量Z 的具体值。
当2αZ Z ≤时,不属于小概率事件,应接受原假设;反之,当2αZ Z >时,小概率事件发生了,按假设检验的规则,应拒绝原假设。
可见,区间估计中的置信区间对应于假设检验中的接受区域,置信区间之外的区域就是拒绝区域。
对比率、方差等问题的区间估计和假设检验也同样存在这种对偶性。
3. 解:根据题意,提出假设:H 0:1000=μ,H 1:1000≥μ 检验统计量)//(/00n x x Z x σμσμ-=-=1.2)25/100/(1000-589==由α=0.02,查《正态分布分位表》(附录2表4)得临界值054.2=αZ由于Z = 2.1>αZ = 2.054,所以应拒绝H 0而接受H 1,即这批元件的使用寿命不低于1000小时,是合格品。
4. 解:根据题意,提出假设:H 0:500=μ,H 1:500<μ检验统计量)//(/00n x x Z x σμσμ-=-=5.2)100/20/(500-954==由α=0.05,查表得临界值645.1=αZ由于Z =2.5>Zα/2 =1.645,所以应拒绝H 0而接受H 1,即工艺改革后这批产品的使用寿命确有显著提高。
5. 解:第一类错误:当原假设H 0为真,但由于样本的随机性使样本统计量落入了拒绝区域,这时所作的判断是拒绝原假设。
这类错误称为第一类错误,亦称拒真错误,它实质上就是前面提到的显著性水平α,即P {拒绝H 0∣H 0为真}=α。
第二类错误:当原假设H 0为不真,但由于样本的随机性使样本统计量落入接受区域,这时的判断是接受原假设。
这类错误称为第二类错误,亦称取伪错误。
犯第二类错误的概率亦称取伪概率,用β表示,即P {接受H 0∣H 0不真}=β。
在一般场合,当n 固定时,减少α必然导致β增大;反之减少β必然会增大α。
以利用Z 统计量进行右侧检验的情况为例;α= P (Z >Z α∣H 0为真)β= P (Z≤Z α∣H 0为真)要使α小,则临界值 Z α增大,而 Z α增大必然导致β增大。
反之,要使β小,则必然导致α增大。
6. 解:正态分布是与自由度无关的一条曲线,t 分布是依自由度而变的一组曲线。
t 分布较正态分布顶部略低而尾部稍高。
在小样本情况下二者的区别较大,t 分布呈现尖峰后尾特征。
当自由度趋于无穷大时,t 分布曲线就成为标准正态分布曲线。
在总体方差未知的情况下,检验均值特征使用t 分布。
7. 解:根据题意,提出假设:H 0:800=μ,H 1:800≠μ 检验统计量)//(/00n x x Z x σμσμ-=-=333.1)16/60/(800208=-=由α=0.01,查表得临界值Z α=2.326由于Z =1.333<Z α=2.326,所以应拒绝H 0而接受H 1。
8. 解:假设H 0:0P =0.4,H 1:P <0.4。
样本比率P =m/n=76/200=0.38由于样本容量大,所以可近似采用Z 检验法,有331.20343.008.020062.038.03.038.0)1(0==⨯-=--=n p P P P Z给定α=0.05,查《正态分布分位表》(附录2表5)得645.1=αZ 。
由于αZ Z >,拒绝原假设,即认为报纸的订阅率显著降低了。
9. 解:已知250000=μ,10=n ,计算得25200=x ,666.332=S提出假设:H 0:25000=μ,H 1:25000≠μ检验统计量|t |=)//()(/)(00n S x x x μσμ-=-90.1)10/666.332/()2500025200(=-=由α=0.05,查《t 分布表》(附录2表5)得临界值2αt (n -1)= 025.0t (10-1)=2.262。
由于|t |=1.90<2αt (n -1) = 2.262,所以接受H 0,即认为该厂轮胎的耐用里程不存在显著差异。
10. 解:计算得00128.02=S假设H 0:20σ=0.03,H 1:20σ≠0.03统计量2χ=202/)1(σS n -=(6-1)0.00128/0.03=7.11α=0.1,查《2χ分布表》(附录2表6)得)5(205.0χ=2.015,故应拒绝H 0而接受H 1,即认为总体口径方差存在显著差异。
11. 解:(1)接受 (2)拒绝 (3)接受 (4)拒绝 (5)接受 (6)接受12. 解:(1)拒真错误 (2)没有错误 (3)取伪错误 (4)没有错误 (5)没有错误13. 解:对于甲乙厂放映时间方差的检验,首先建立假设:H 0:2221σσ=,H 1:2221σσ≠在n =5,m =7,α = 0.05时,025.0F (4, 6)=6.23,975.0F (4, 6)=0.161故拒绝域为{F ≤0.161或F ≥6.23}现由样本求得2x S =78.8,2y S =233.33,从而F =0.338,落入拒绝域,因而在α=0.05水平上可以认为两厂放映时间的方差存在显著差别。
对于甲乙厂放映时间均值的检验,首先建立假设:H 0:21μμ=,H 1:21μμ≠计算可得:甲厂:n =5,x =97.4,2x S =78.8;乙厂:m =7,y =100,2y S =233.33;α=0.05由于n 与m 都不大,且2x S 与2y S 又相差很大,故拟采用*t 统计量进行检验。
经计算,对应*t 分布的自由度为L =9.747,取整后为10。
在α=0.05时,)10(05.0t =1.8125,现由样本求得*t =-0.371<)10(05.0t ,故不拒绝H 0,认为甲乙厂放映时间的均值没有显著差别。
14. 解:对于A 、B 蛋白质含量方差的检验,首先建立假设:H 0:2221σσ=,H 1:2221σσ≠在n =10,m =5,α = 0.05时,)4,9(025.0F =8.9,212.0)9,4(1)4,9(025.0975.0==F F 故拒绝域为{F ≤0.212或F ≥8.9}由已知21S =1.621,22S =0.135,从而F =12.007,落入拒绝域,因而在α=0.05水平上可以认为A 、B蛋白质含量的方差存在显著差别。
对于A 、B 蛋白质含量均值的检验,首先建立假设:H 0:21μμ=,H 1:21μμ≠经计算,对应*t 分布的自由度为L =11.528,取整后为12。
在α=0.05时,)12(05.0t =1.782,现由样本求得*t =5.979>)12(05.0t ,故拒绝H 0,认为A 、B 蛋白质含量均值存在显著差别。
