4.4.2两个三角形相似的判定(二)
4.4.2探索三角形相似的条件(教案)

c. SAS(边角边)相似定理:如果两个三角形的两边和它们夹的角分别相等,则这两个三角形相似。
3.能够运用三角形相似的性质解决实际问题,例如:求三角形的面积、证明线段的比例关系等。
二、核心素养目标
本节课的核心素养目标旨在培养学生以下几方面的能力:
五、教学反思
今天在教授《4.4.2探索三角形相似的条件》这一章节时,我发现学生们对于三角形相似的概念和应用表现出很大的兴趣。在课堂上,我尝试通过引入日常生活中的例子,帮助他们理解相似三角形的实际意义。从学生的反应来看,这种方法是有效的,它使得抽象的几何知识变得具体而生动。
在讲授过程中,我注意到AA、SSS、SAS相似定理是学生们理解的难点。为此,我使用了多个图形示例,逐步引导他们识别对应角和对应边,并解释了成比例的概念。在这一点上,我感到可能需要更多的练习和实例来加深学生的理解,未来我计划设计一些更具挑战性的习题,以便他们能够更好地掌握这些定理。
-举例:通过具体图形,帮助学生理解什么是“对应”,如何找到相似三角形的对应角和对应边。
-难点二:AA相似定理的应用。学生需要掌握在没有给出边长信息的情况下,如何仅通过角度信息判断三角形相似。
-举例:给出两个三角形,其中一个三角形的两个角分别与另一个三角形的两个角相等,引导学生发现这两个三角形相似。
-难点三:SSS相似定理的理解。学生需要理解三边比例关系是判定三角形相似的关键,而不仅仅是三边相等。
通过这次教学,我更加坚信,结合生活实例和动手操作,能够有效提升学生对几何概念的理解和应用能力。在接下来的课程中,我会继续探索更多有效的教学方法,以期达到更好的教学效果。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
4.4 探索三角形相似的条件 第1课时 两角分别相等的两个三角形相似 (2)

4.4 探索三角形相似的条件
第1课时两角分别相等的两个三角形相似
学习目标:
1、掌握并会推导相似三角形的判定定理1.
2、会用相似三角形的判定定理1进行一些简单的判断、证明和计算.
学习重点:灵活运用相似三角形的判定定理1证明和解决有关问题.
预设难点:相似三角形的判定定理1的推导和应用.
☆预习导航☆
一、链接
1、一般地,两个相同的多边形,如果它们的对应角,对应边长度的比,那么这两个多边形叫做相似多边形;
2、定理:三角形一边的直线与其他两边(或)相交,截得的三角形与原三角形 .
二、导读
1、思考:根据定义判定两个三角形相似需要哪些条件?能否和判断三角形全等一样,也用很少的条件就能判定三角形相似呢?
2、有一个角对应相等的两个三角形相似吗?
有两个角对应相等的两个三角形相似吗?
3、结合课本写一写相似三角形的判定定理1的证明过程.
☆合作探究☆
1、如图,△ABC和△ADE的边BC、AD相交于点O,且∠1 = ∠2 = ∠3,点C在DE上,求证:△ABC ∽△ADE.
2、如图,正方形ABCD中,AB = 2,P是BC边上不与B、C重合的任意一点,DQ⊥AP于Q,试证明△DAQ∽△APB,当点P在BC上变动时,线段DQ也随之变化,设PA = x,DQ = y,求y与x之间的函数关系式.
☆归纳反思☆
本节课你有哪些收获?还存在哪些困惑?
☆达标检测☆
1、如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
..条件,使△ABC∽△AED.并说明理由.
2、如图,在△ABC中,AB = AC ,∠A = 36°,BD平分∠ABC,DE∥BC,那么图中与△ABC相似的三角形有哪些?写出来并说明理由.。
4.4.2 利用边角关系判定两三角形相似-课件

夯实基础·逐点练
当AADE=AABC时,∵∠A=∠A, ∴△ADE∽△ABC. 此时 AE=ACA·BAD=5×6 2=53. 故答案为152或53. 【答案】152或53
整合方法·提升练
10.【2018·上海】已知,如图,正方形 ABCD 中,P 是 BC 上一点,BE⊥AP,DF⊥AP,垂足分别是点 E,F.
整合方法·提升练
(2)连接 BF,如果ABFF=DADF,求证:EF=EP. 证明:如图,∵ABFF=DADF,AF=BE,
整合方法·提升练
∴BBEF=DADF, ∴DBEF=ABDF. 设BBEF=DADF=k,则 BE=kBF,DF=kAD,∴EF= BF2-BE2 = 1-k2BF,AF= AD2-DF2= 1-k2AD. ∴EAFF=ABDF.
探究培优·拓展练
13.如图,在矩形 ABCD 中, AB=10 cm,BC=20 cm,两 只小虫 P 和 Q 同时分别从 A, B 出发沿 AB,BC 向终点 B, C 方向前进,小虫 P 的速度为 1 cm/s,小虫 Q 的速度为 2 cm/s. 请问:它们同时出发多少秒时,以 P,B,Q 为顶点的三角 形与以 A,B,C 为顶点的三角形相似?
A.1 个 C.3 个
B.2 个 D.4 个
夯实基础·逐点练
5.在等边三角形 ABC 中,D,E 分别在 AC,AB 上,且AADC =13,AE=BE,则有( B ) A.△AED∽△BED B.△AED∽△CBD C.△AED∽△ABD D.△BAD∽△BCD
夯实基础·逐点练
6.【2017·潍坊】如图,在△ABC 中,AB≠AC,D,E 分别 为 AB,AC 上的点,AC=3AD,AB=3AE,点 F 为 BC 边上一点,添加一个条件:_D_F_∥_A_C_(_答_案__不_唯__一_)______,可 以使得△FDB 与△ADE 相似.(只需写出一个)
北师大九年级上册4.4.2 探索三角形相似的条件 教学设计
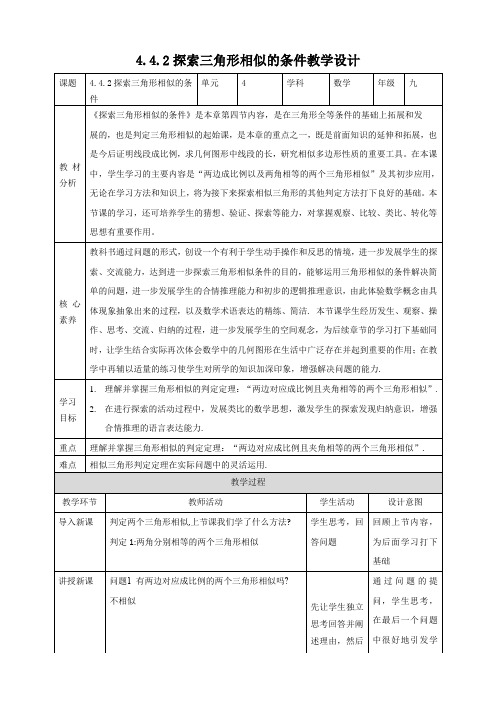
4.4.2探索三角形相似的条件教学设计问题2 类比三角形全等的判定方法(SAS,SSS ),猜想可以添加什么条件来判定两个三角形相似? 相似做一做利用刻度尺和量角器画△ABC 和△A ′B ′C ′,使∠A =∠A ′,ABA ′B′=ACA ′C′,量出∠B 与∠B ′的大小(或∠C 与∠C ′的大小),△ABC 和△A ′B ′C ′相似吗?两个三角形相似利用刻度尺和量角器画△ABC 和△A ′B ′C ′,使∠B =∠B ′,ABA ′B′=BCB ′C′,量出∠A 与∠A ′的大小(或∠C 与∠C ′的大小),△ABC 和△A ′B ′C ′相似吗?两个三角形相似猜想:两边成比例,且夹角相等的两个三角形相似 验证猜想:如图,在△ABC 与△A ′B ′C ′中,已知∠A= ∠A ′,AB A ′B′=ACA ′C′,求证:△ABC ∽△A ′B ′C ′.证明:在 △A ′B ′C ′的边 A ′B ′上截取点D , 使 A ′D = AB .过点 D 作DE ∥B ′C ′, 交 A ′C ′于点 E. ∵ DE ∥B ′C ′,∴ △A ′DE ∽△A ′B ′C ′. ∴A ′DA ′B′=A ′EA ′C′∵ A ′D=AB ,ABA ′B′=ACA ′C′ ∴A ′DA ′B′=A ′EA ′C′=AC A ′C′ ∴ A ′E = AC . 又 ∠A ′ = ∠A. ∴ △A ′DE ≌ △ABC , ∴ △A ′B ′C ′ ∽ △ABC. 归纳总结相似三角形的判定定理2定理:两边成比例且夹角相等的两个三角形相似. 符号语言:在△ABC 与△DEF 中,∵∠A=∠D ,AB AC =DEDF , ∴△ABC ∽△DEF.例2 如图,D ,E 分别是△ABC 的边 AC ,AB 上的点,AE =1.5,AC =2,BC =3,且ADAB =34,求 DE 的长.解:∵AE=1.5,AC=2,∴AEAC =34∵ADAB =34∴ADAB=AEAC又∵∠EAD=∠CAB,∴△ADE∽△ABC∴DEBC =ADAB=34∵BC =3,∴DE=34BC=34×3=94想一想:在三角形全等的判定中,有两个边和其中一边的对角相等的两个三角形全都吗?那么有两边成比例,其中一边的对角相等的两个三角形相似吗?△ABC与△DEF的两边成比例,其中一边的对角相等,那么,这两个三角形相似吗?下图是小明和小丽画的两个三角形,由此你能得出什么结论?和“有两条边和其中一边的对角相等的两个三角形不一定全都”一样,有两边成比例,其中一边的对角相等的两个三角形也不一定相似.1.下列条件不能判定△ABC与△ADE相似的是( )A.AEAD =ACABB. ∠B=∠ADEC.AEAC =DEBCD. ∠C=∠AED2.如图,点D是△ABC的边AC上的一点,根据下列条件,可以得到△ABC∽△BDC的是 ( ) A.AB·CD=BD·BC B.AC·CB=CA·CD C.BC2=AC·DC D.BD2=CD·DA3.如图,已知ADAE =ACAB,AD=3 cm,AC=6 cm,BC=8 cm,则DE的长为________cm.4.如图所示,在△ABC中,AB=6,AC=4,P是AC的中点,过点P的直线交AB于点Q,若以A,P,Q为顶点的三角形和△ABC相似,则AQ的长为.5. 如图,∠DAB =∠CAE,且AB ·AD = AE·AC,求证△ABC ∽△AED.。
北师大版数学九年级上册4.4.2探索三角形相似的条件教学设计

在情感态度方面,九年级学生正处于青春期,个性鲜明,对新鲜事物充满好奇。教师应充分利用学生的这一特点,设计富有挑战性和趣味性的教学活动,激发学生的学习兴趣,提高学生的参与度。
北师大版数学九年级上册4.4.2探索三角形相似的条件教学设计
一、教学目标
(一)知识与技能
1.理解相似三角形的定义及性质,掌握三角形相似的条件。
2.能够运用三角形相似的条件判断两个三角形是否相似,并求出相似比。
3.能够运用相似三角形的性质解决实际问题,如测量不可到达物体的高度、求解比例问题等。
4.学会使用尺规作图展示相似三角形,并能够通过作图发现相似三角相等、对应边成比例等,通过几何画板展示性质的直观效果。
2.教学目标:
(1)使学生掌握相似三角形的定义和判定条件,理解相似三角形的性质。
(2)培养学生运用几何画板等工具,观察、分析几何图形的能力。
(三)学生小组讨论
1.教学活动设计:
(1)将学生分成小组,每组分配一个探究任务,如探讨相似三角形的判定条件、性质和应用。
3.教学策略:
(1)关注学生的个体差异,实施分层教学,使每个学生都能在原有基础上得到提高。
(2)注重培养学生的动手操作能力,引导学生通过实践探索几何图形的性质。
(3)结合学生的认知规律,逐步引导学生从具体实例中抽象出一般性规律。
(4)加强师生互动,营造轻松、愉快的学习氛围,提高学生的学习兴趣。
4.教学评价:
(三)情感态度与价值观
数学相似三角形的知识点归纳

数学相似三角形的知识点归纳数学相似三角形的知识点归纳数学是人们认识自然、认识社会的重要工具。
它是一门古老而崭新的科学,是整个科学技术的基础。
随着社会的发展、时代的变化,以及信息技术的发展,数学在社会各个方面的应用越来越广泛,作用越来越重要。
以下是店铺整理的数学相似三角形的知识点归纳,希望帮助到您。
数学相似三角形的知识点归纳篇1本章有以下几个主要内容:一、比例线段1、线段比,2、成比例线段,3、比例中项————黄金分割,4、比例的性质:基本性质;合比性质;等比性质(1)线段比:用同一长度单位度量两条线段a,b,把他们长度的比叫做这两条线段的比。
(2)比例线段:在四条线段a,b,c,d中,如果线段a,b的比等于线段c,d的比,那么,这四条线段叫做成比例线段。
简称比例线段。
(3)比例中项:如果a:b=b:c,那么b叫做a,c的比例中项(4)黄金分割:把一条线段分成两条线段,如果较长线段是全线段和较短线段的比例中项,那么这种分割叫做黄金分割。
这个点叫做黄金分割点。
顶角是36度的等腰三角形叫做黄金三角形宽和长的比等于黄金数的矩形叫做黄金矩形。
(5)比例的性质基本性质:内项积等于外项积。
(比例=====等积)。
主要作用:计算。
合比性质,主要作用:比例的互相转化。
等比性质,在使用时注意成立的条件。
二、相似三角形的判定平行线等分线段——————平行线分线段成比例————————平行于三角形一边的直线截其他两边(或两边延长线),所截线段对应成比例——————(预备定理)平行于三角形一边的直线和其他两边(或两边延长线)相交,所截三角形与原三角形相似——————相似三角形的判定:类比于全等三角形的判定。
三、相似三角形的性质1、定义:相似三角形对应角相等对应边成比例。
2、相似三角形对应线段(对应角平分线、对应中线、对应高等)的比等于相似比3、相似三角形周长的比等于相似比4、相似三角形面积的比等于相似比的平方四、图形的位似变换1、几何变换:平移,旋转,轴对称,相似变换2、相似变换:把一个图形变成另一个图形,并保持形状不变的几何变换叫做相似变换。
( 浙教版)九年级数学上册课件:4.4(2)
OA边向点A以1cm/s的速度移动;点Q从
点B开始沿BO边向点O以1cm/s的速度移
动.如果P,Q同时出发,用t(s)表示移 B
动的时间(0≤t≤6),那么:
Q
(1)设△POQ的面积为y,求y关于t的函
数解析式;
OP A
(2)当△POQ的面积最大时,将△POQ 沿直线PQ翻折后得到△PCQ,试判断点 C是否落在直线AB上,并说明理由;
作△A´B´C´,使△A´B´C´
的边长为原来的2倍。
B
B’ A
问题:△ ABC与△A´B´C´
相似吗?
C
C’
相似三角形的判定方法:三边对应成比例
的两个三角形相似。
E 30
36
D
48 72
F
C 54
A 45 B
如图判断4×4方格中的两个三角形
是否相似,并说明理由. D
A
C EB
F
B
C
D
E
B
C
一般像上面的两个三角形结构,可以用
两边对应成比例,且夹角相等的 两个三角形
相似来证明两个三角形相似.
如图, D为⊿ ABC的边AB上一点若要使 ⊿ ACD与⊿ ABC相似,可以添加什么条 件?你有几种添加条件的不同方法?
A D
B C
思考题:
如图所示,在平面直角坐标系中,已知
AO=12cm,OB=6cm,点P从点O开始沿
• 两边对应成比例,且夹角相等两个三角 形相似。
如图已知点D,E分别在AB,AC上,
AD AB
AE AC
求证:DE‖BC.
A
D
E
B
C
ADEB NhomakorabeaC
相似三角形的判定口诀
相似三角形的判定口诀
两角对应相等,两个三角形相似。
两边对应成比例且夹角相等,两个三角形相似。
三边对应成比例,两个三角形相似。
三边对应平行,两个三角形相似。
斜边与直角边对应成比例,两个直角三角形相似。
1.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
(简叙为:两角对应相等,两个三角形相似。
)
2.如果两个三角形的两组对应边成比例,并且对应的夹角相等,那么这两个三角形相似。
(简叙为:两边对应成比例且夹角相等,两个三角形相似。
)
3.如果两个三角形的三组对应边成比例,那么这两个三角形相似。
(简叙为:三边对应成比例,两个三角形相似。
)
4.两三角形三边对应平行,则两三角形相似。
(简叙为:三边对应平行,两个三角形相似。
)
5.如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
(简叙为:斜边与直角边对应成比例,两个直角三角形相似。
)
6.如果两个三角形全等,那么这两个三角形相似(相似比为1:1)。
(简叙为:全等三角形相似)。
4.4 第2课时 利用两边及夹角判定三角形相似
且
AD = CD ,求证 ∠ACB=90°. CD BD
C
证明:∵ CD 是边 AB 上的高,
∴ ∠ADC =∠CDB =90°.
∵ AD CD, CD BD
AD
B
∴△ADC ∽△CDB,∴ ∠ACD =∠B,
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
方法总结:解题时需注意隐含条件,如垂直关系, 三角形的高等.
证明:
∵ △ABC 与 △ADE 是等腰三角形,
A
∴ AD =AE,AB = AC,
D
∴ AD AE .
AB AC
又 ∵∠DAB = ∠CAE,
B
E C
∴ ∠DAB +∠BAE = ∠CAE +∠BAE,
即 ∠DAE =∠BAC,∴△ABC ∽ △ADE.
例2 如图,D,E分别是 △ABC 的边 AC,AB 上的点,
随堂练习
1. 判断
(1) 两个等边三角形相似
(√)
(2) 两个直角三角形相似
(×)
(3) 两个等腰直角三角形相似
(√)
(4) 有一个角是50°的两个等腰三角形相似 (×)
2. 如图,D 是 △ABC 一边 BC 上一点,连接 AD,使
△ABC ∽ △DBA的条件是
( D)
A
A. AC : BC=AD : BD
A
又∵∠B=∠ACD,
D
∴ △ABC ∽ △DCA,
∴ AC BC 4,∴ AD 25 . B
C
AD AC 5
4
6. 如图,∠DAB =∠CAE,且 AB ·AD = AE·AC, 求证△ABC ∽△AED.
北师大版九年级上册4.探索三角形相似的条件课件
B
AB BD
=
BC AB
=
AC AD
A C
D
练一练
2. 如图,已知∠1=∠2,添加下列一个条件后,
仍然无法判定 △ABC ∽ △ADE是( B )
A.
AB AD
=
AC AE
B.
AB AD
=
BC DE
A
D
2
1
C. ∠B=∠D
B
C
E
D. ∠C=∠AED
练一练
3. 如图,AB,CD交于点O,且 OC=45, OD=30, OB=36, 当OA=__5_4__时,△AOC ∽ △BOD
第四章 图形的类似
4.4.2探索 三角形类似的条件(二)
温故知新
类似三角形
三角分别相等、三边成比例的两个三角形
叫做类似三角形.
A
类似三角形的判定定理:
两角分别相等的两个三角形类似. B
C
D
∵∠B=∠E
∠C=∠F
∴△ABC=△DEF
E
F
情境引入
有两边对应成比例的两个三角形类似吗?
5
5
33
类比三角形全等的判定方法(SAS,SSS), 猜想可以添加什么条件来判定两个三角形类似?
3
3
5
5
新知探究 8 25°
B
A
120° 6
35° C
12
D 4 120° 3 F E ∠E=25° 6 ∠F=35°
∠A=∠D
AB =2
DE
AC DF
=2
BC =2
EF
新知探究 探究类似三角形的条件
判定定理2:
两边成比例且夹角相等的两个三角形类似
