SPSS操作实例-重复测量
学会使用SPSS进行相关分析和重复测量ANOVA

学会使用SPSS进行相关分析和重复测量ANOVA相关分析和重复测量ANOVA是统计学中常用的分析方法之一。
本文将介绍如何使用SPSS软件进行相关分析和重复测量ANOVA的步骤和注意事项。
第一章:相关分析相关分析是用来研究两个或多个变量之间的关系的统计方法。
在相关分析中,我们可以计算变量之间的相关系数,来了解它们之间的相关性强度和方向。
1.1 数据准备在进行相关分析之前,首先需要确保数据的准备工作已经完成。
通过SPSS软件,我们可以导入数据集,并对数据进行预处理,包括数据的清洗和转换。
1.2 相关分析的基本步骤进行相关分析的基本步骤如下:1)打开SPSS软件并导入数据集;2)选择“分析”菜单中的“相关”选项;3)将要分析的变量移入“变量”框中;4)选择要计算的相关系数类型;5)点击“确定”按钮,进行数据处理和分析。
1.3 相关分析的结果解读在相关分析的结果中,我们关注的主要是相关系数的值和显著性水平。
相关系数的取值范围为-1到1,其中-1表示完全负相关,1表示完全正相关,0表示无相关性。
显著性水平则表明了相关系数的显著程度,一般取0.05作为显著性水平的界限。
第二章:重复测量ANOVA重复测量ANOVA是一种用于比较两个或更多相关样本组之间差异的统计方法。
在重复测量ANOVA中,我们可以通过比较不同因素或处理之间的差异来判断它们是否对研究对象产生了显著影响。
2.1 数据准备在进行重复测量ANOVA之前,同样需要进行数据的准备工作。
将数据导入SPSS软件,并进行必要的数据清洗和转换操作。
2.2 重复测量ANOVA的基本步骤进行重复测量ANOVA的基本步骤如下:1)打开SPSS软件并导入数据集;2)选择“分析”菜单中的“一元方差分析”选项;3)将要分析的变量移入“因子”框中;4)选择要比较的处理或因素;5)点击“确定”按钮,进行数据处理和分析。
2.3 重复测量ANOVA的结果解读在重复测量ANOVA的结果中,我们关注的主要是F值和显著性水平。
双因素重复测量方差分析spss

双因素重复测量方差分析spss
一、双因素重复测量方差分析(two-way repeated measures ANOVA)
双因素重复测量方差分析(Two-Way repeated measures ANOVA)可以用来检测一个
变量的变化在两个或多个独立变量的作用下是否发生变化。
在双因素重复测量方差分析中,变量1是因素1,因素1有若干水平,变量2是因素2,因素2也有若干水平。
双因素重
复测量方差分析可以检验两个因素是否共同影响变量1的变化,或者检测某个因素是否单
独地影响变量1的变化。
1、打开spss统计软件,点击文件、数据,从窗口中打开需要分析数据文件;
2、点击“分析”菜单,然后从子菜单中点击“多维分析”,再单击“双因素重复测
量方差分析”;
3、在弹出的窗口中,在“变量”框中选择需要分析的变量;
4、在“因素”框中,选择双因素,比如实验组和对照组;
5、点击“定义”按钮,设定因素的水平,比如实验组的水平为A,对照组的水平为B;
6、在“多重比较”框中,勾选“重复测量”框,并且可以设定多重比较的参数;
7、选择“显著性水平”框,设定检验的显著性,通常设定为0.05;
8、单击“OK”按钮,查看分析结果,该分析结果将显示两个因素及其交互作用对变
量1的影响情况。
SPSS数据分析—重复测量差分析

多因素方差分析中,每个被试者仅接受一种实验处理,通过随机分配的方式抵消个体间差异所带来的误差,但是这种误差并没有被排除。
而重复测量设计则是让每个被试接受所有的实验处理,这样我们就可以分离出个体差异所带来的误差,进而进一步细化因变量的变异来源,传统的方差分析只要分析处理因素对于因变量的影响,而重复测量方差分析需要分析处理因素、时间因素、处理和时间的交互作用三者对于因变量的影响。
具体而言就是传统方差分析的变异分解为:总变异=处理因素导致的变异(组间变异)+随机变异(组内变异)但是重复测量设计引入了重复测量因素,因此需要将这个因素的变异也考虑进去,调整为总变异=受试对象间变异+受试对象内变异=(处理因素导致的变异+个体间误差导致的变异)+(重复测量因素导致的变异+重复测量因素与处理因素的交互作用导致的变异+个体内误差导致的变异)关于重复测量资料,有以下两个特征1.处理因素g个水平,每个水平有n个试验对象,共有gn个试验对象2.时间因素m个水平,同一个试验对象在m个时间点获得的m个测量值,全部资料共有gnm个测量值由于分析因素的增多,重复测量方差分析的假设也增多,分别为1.对于处理因素而言H0:不同处理因素对于因变量的影响相同H1:不同处理因素对于因变量的影响相同2.对于时间因素而言H0:不同时间的因变量总体均值全相同H1:不同时间的因变量总体均值不全不同3.对于时间和处理因素的交互作用而言H0:处理因素和时间因素没有交互效应H1:处理因素和时间因素有交互效应重复测量方差分析和单因素方差分析这二者的区别我们结合数据资料的格式来看重复测量设计和完全随机区组设计的区别可以通过下图反映此外,单因素方差分析常将处理因素放在列,而个案放在行,重复测量方差分析常将重复测量因素放在列,而个案或者处理因素放在行,因此对于一些叫法,也有点区别,如下:从中我们可以看出几点区别1.单因素方差分析中,每个被试只接受一种处理,而重复测量方差分析每个被试要接受所有处理因素和不同处理因素水平下的重复测量因素。
SPSS syntax应用-重复观测值的处理
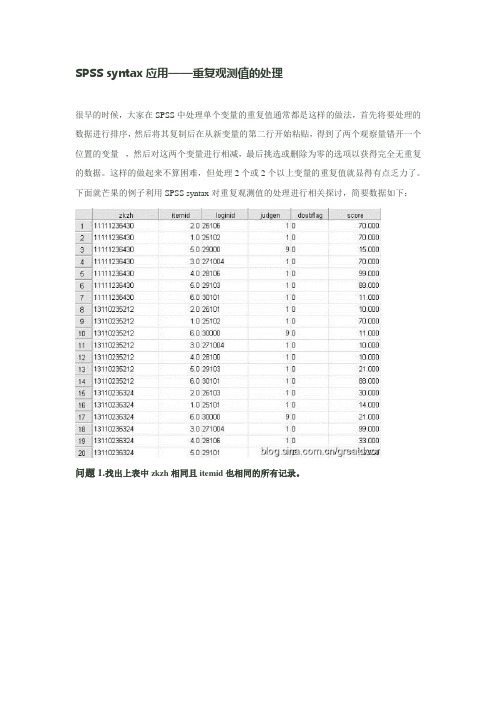
SPSS syntax应用——重复观测值的处理很早的时候,大家在SPSS中处理单个变量的重复值通常都是这样的做法,首先将要处理的数据进行排序,然后将其复制后在从新变量的第二行开始粘贴,得到了两个观察量错开一个位置的变量,然后对这两个变量进行相减,最后挑选或删除为零的选项以获得完全无重复的数据。
这样的做起来不算困难,但处理2个或2个以上变量的重复值就显得有点乏力了。
下面就芒果的例子利用SPSS syntax对重复观测值的处理进行相关探讨,简要数据如下:问题1.找出上表中zkzh相同且itemid也相同的所有记录。
上图是syntax命令及说明,关于sort cases/match files/filter等命令见下面小贴士的说明,首先看看数据处理结果:问题2. 如何快速的分离出被筛选的变量?还是利用上面的例子,我们利用dataset copy命令将被筛选出的观测值快速的筛选出来,形成一个新的数据集。
#1 Filter off.#2 Dataset copy shaixuanji.#3 DATASET ACTIVATE shaixuanji.#4 SELECT IF thesame=0.#5 EXECUTE .代码解析:第1行命令利用filter off命令清除上面的筛选效果。
第2行命令式将当前数据集复制到新的数据集shaixuanji中。
第3-4行命令是激活数据集shaixuanji,并且选择thesame变量中值为0的观测值(其他的默认删除)。
第5行命令是即时运算命令。
效果如下:如果不想要这么多的变量,可以使用save outfile.../keep(drop)命令选择自己需要的变量。
问题3.有时候我们并不知道如何筛选重复值,而是事先观察比较重复值的相关特性,然后做下一步的处理,那么如何选择输出重复值的相关信息呢?这里还是利用最初的数据进行说明,由于目的不同,这里筛选查找重复观测值的方式也不同。
问题1中采用的是match files命令来处理重复值,这里换一种方法,利用aggregate分类汇总命令来计量重复值,进而作进一步的汇总说明,具体代码如下:#1 AGGREGATE OUTFILE = * MODE = ADDVARIABLES#2 /BREAK = zkzh itemid#3 /sameCount = N.#4 SORT CASES BY sameCount (D).#5 COMPUTE filtervar=(sameCount > 1).#6 FILTER BY filtervar.#7 SUMMARIZE#8 /TABLES=zkzh itemid samecount#9 /FORMAT=LIST NOCASENUM TOTAL#10 /TITLE='重复值概述'#11 /CELLS=COUNT.代码解析:第1-3行命令利用aggregate命令在当前数据集中新增一个变量samecount记录分组变量zkzh 和itemid相同观测值的数目,类似于GUI操作中的data--aggregate.第4行命令对变量samecount进行降序排列.第5行命令计算新变量filtervar,对其满足条件samecount>1赋值1,否则赋值0.第6行命令对数据集按变量filtercar进行筛选,filtervar变量中值为0或缺失的都将被过滤.第7-11行是制表命令,等同于GUI菜单操作中的analyze--reports--case summarises,第8行选择表中的计量变量,这里选择了zkzh等3个变量,第9-10行则是对表格的格式及标题进行设置,第11行是相关统计量的选择,这里选择的是count,除此之外还可以选择maxrangesum等其他统计量。
案例分析两因素重复测量方差分析及SPSS操作

案例分析两因素重复测量方差分析及SPSS操作一.案例:(案例来源:中华护理杂志2016年4期)评价子午流注择时五音疗法在慢性心力衰竭(CHF)焦虑患者中的应用效果。
方法:将70例CHF焦虑患者随机分为实验组和对照组,各35例,实验组实施子午流注择时五行音乐疗法,对照组实施五行音乐疗法。
两组在干预前、干预后4周、8周和12周采用匹兹堡睡眠质量指数量表(PSQI)评价睡眠质量。
补充:PSQI量表包括主观睡眠质量、入睡时间、睡眠效率、睡眠时间、睡眠障碍、催眠药物、日间功能七个维度,得分越高,睡眠质量越差。
二.解析:该问题涉及两组研究对象,并且对每组对象进行了多次测量。
对于两组干预前的基线(T0)比较可以采用独立样本的t检验,整体组间、组内比较采用重复测量方差分析,因为共有四次测量时间,所以在进行重复测量方差时,干预前后组内需要进一步做两两比较,采用多重比较的方法进行分析。
三.SPSS操作1.操作步骤1.1先对干预前的基线进行差异性检验:将T0放入检验变量,分组放入分组变量,点击定义组,设置指定的组值。
1.2基线差异检验结果:由结果得:F=1.094,P=0.299>0.05,不能拒绝原假设,认为两组数据的方差是相等的。
所以t检验应该看第一行,t=0.306,P=0.760>0.05,因此不能拒绝原假设,认为两组数据的基线得分是不存在差异的。
1.3重复测量方差将主体内因子名改为时间,级别数框中填4;点击添加,然后点击定义。
将T0、T4、T8、T12放入主体内变量,分组放入主体间因子。
如下图所示:点击选项,出现如下对话框,显示栏中选择描述统计和齐性检验。
回到重复测量窗口,点击粘贴,出现如下语法编辑器,在“/METHOD=SSTYPE(3)”的下一行中插入简单效应语句:/EMMEANS=TABLES(时间*分组)COMPARE(时间)ADJ(SIDAK) /EMMEANS=TABLES(时间*分组)COMPARE(分组)ADJ(SIDAK) 点击红线所指处的箭头,确定。
重复测量资料的广义估计方程分析及SPSS实现

重复测量资料的广义估计方程分析及SPSS实现一、本文概述在统计学中,重复测量资料是一种常见的数据类型,通常涉及到同一观察对象在不同时间点或不同条件下的多次测量。
这类数据在医学、社会科学、心理学等领域的研究中尤为常见,例如追踪病人的病情发展、评估教育干预的效果、研究消费者的购买行为等。
为了有效分析这类数据,研究者需要采用适当的统计方法,以控制潜在的干扰因素,揭示数据间的内在关联。
广义估计方程(Generalized Estimating Equations,GEE)是一种适用于分析重复测量资料的统计方法。
它通过指定一个工作相关矩阵,来纠正观察对象间的相关性,并允许研究者根据数据的特性选择适当的相关结构。
GEE的优点在于其稳健性和灵活性,即使在数据分布不符合正态分布或观测次数不等的情况下,也能提供可靠的参数估计。
本文旨在介绍广义估计方程的基本原理及其在SPSS软件中的实现方法。
我们将首先概述广义估计方程的基本概念和数学模型,然后详细阐述如何在SPSS中运用GEE分析重复测量资料。
通过实例演示,读者将能够掌握从数据准备到结果解读的完整流程,从而提高对重复测量资料的分析能力。
本文还将讨论GEE分析中的一些常见问题及注意事项,以帮助研究者在实践中避免常见错误,确保分析结果的准确性和可靠性。
二、广义估计方程(GEE)的基本原理广义估计方程(GEE)是一种用于分析重复测量数据的方法,它扩展了传统的线性回归模型,允许处理复杂的数据结构,包括时间序列、聚类数据、纵向数据等。
GEE的核心在于其灵活性,它不需要指定数据的具体分布形式,只需要指定工作相关性结构,因此在实际应用中具有广泛的适用性。
构建工作相关性结构:在GEE中,研究者需要指定一个工作相关性矩阵,用于描述观测值之间的相关性。
这个矩阵可以根据数据的实际情况进行选择和构建,例如,如果数据是时间序列,可以选择一阶自回归(AR(1))模型;如果数据是聚类数据,可以选择交换相关(Exchangeable)模型等。
spss16.0重复测量数据分析步骤(原创)
应用SPSS16.0进行重复测量数据分析原始数据:Spss变量设置:导入数据:1.通过球形检验(Mauchly’s Test of Sphericity) 的结果判断重复测量数据之间是否存在相关性:Analyze→General Lineal Model→Repeated MeasuresWithin- subject factor name 框: 改为t “定义重复测量的变量名为t”Number of levels 框: 键入4: add “重复测量的次数为4 次”DefineWithin- subject variables 框: t1-t4 “t1-t4 代表4次测量结果”Between subject factor 框: groupModel:选中Custom “自定义模型”Within- subject Model 框: t “分析4次重复测量间有无趋 势”Between subject Model 框: group “只分析主效应” ContinueOK输出结果:Mauchly's Test of Sphericity bMeasure:MEASURE_1Epsilon a WithinSubjects Effect Mauchly's WApprox.Chi-Square df Sig.Greenhouse-Geisser Huynh-Feldt Lower-boundt .386 14.977 5.011.611.761 .333如果该检验P> 0. 05, 说明重复测量数据之间实际上不存在相关性, 数据符合Huynh-Feldt条件, 可按单因素方差分析方法来处理; 如果P < 0. 05, 说明重复测量数据之间存在相关性, 不可按单因素方差分析方法处理。
实际应用中的重复测量设计资料以后者多见, 应使用重复测量的方差分析模型。
球形检验的结果P< 0. 05, 说明4次重复测量的数据间存在高度的相关性, 宜用多元方差分析进行检验.Tests of Within-Subjects EffectsMeasure:MEASURE_1SourceType III Sum ofSquares df Mean Square F Sig. Sphericity Assumed 15607.63635202.54565.910 .000 Greenhouse-Geisser 15607.636 1.8328517.62265.910 .000 Huynh-Feldt 15607.636 2.2846832.46865.910 .000tLower-bound 15607.636 1.00015607.63665.910 .000Sphericity Assumed 3408.3116568.0527.197 .000 t * zbGreenhouse-Geisser 3408.311 3.665930.0167.197 .000Huynh-Feldt 3408.311 4.569746.0197.197 .000 Lower-bound 3408.311 2.0001704.1557.197 .005 Sphericity Assumed 4025.6185178.934Greenhouse-Geisser 4025.61831.151129.230Huynh-Feldt 4025.61838.834103.663Error(t)Lower-bound 4025.61817.000236.801此处t 和t* group 的P 值均< 0. 01, 时间因素以及时间因素和分组的交互作用有统计学意义, 说明测量指标有随时间变化的趋势并且时间因素的作用随着分组的不同而不同。
实验:单因素重复测量SPSS操作
华东师范大学
言语听觉(语言)研究生课程班实验报告
姓名:学号:实验时间:
班级:成绩:指导老师:_________
[实验名称] 单因素重复测量实验设计的SPSS操作
[实验目的]
1.复习巩固单因素重复测量实验设计的应用。
2.掌握单因素重复测量实验设计的SPSS操作。
3.正确分析单因素重复测量实验设计的结果。
[实验内容]
儿童名词理解能力测验分三组进行。
分别是指人名词、指物名词和抽象名词。
17名被试的成绩见下表。
要得出不同测验的成绩平均值差异是否显著应采用何种实验设计?
具体要求:
(1)将数据处理为相应的数据结构,输入到SPSS中,并定义好变量。
数据文件以.sav格式保存,命名为“单因素重复测量实验数据”
(2)对数据进行方差分析,
a)得出其描述性统计(均值、标准差、被试数),
b)说明方差是否齐性;
c)得出方差分析的结果;
d)如果差异显著,得出多重比较结果;
e)生成均值图。
f) f.结合方差分析结果比较平均值,将三种测验的平均成绩从高到低进行
排序。
所有操作步骤填在[实验步骤]里;将结果图表复制到[实验结果]里,然后说明。
[实验步骤]
[实验结果]。
单因素重复测量方差分析-SPSS教程
单因素重复测量方差分析-SPSS教程一、问题与数据研究者想知道锻炼对心率(Heart Rate,HR)的影响,招募了10名研究对象,并进行了6个月的锻炼干预。
HR共测量了3次,干预前的HR:HR_1,干预中(3个月):HR_2和干预后(6个月):HR_3。
部分数据如图1。
图1 部分数据二、对问题分析对于单因素重复测量的数据,可以使用One-way Repeated Measures Anova 进行分析,但需要考虑6个假设。
假设1:因变量唯一,且为连续变量;假设2:研究对象内因素(本例为干预的不同时间)有3个或以上的水平;假设3:研究对象内因素的各个水平中,因变量没有明显异常值;假设4:研究对象内因素的各个水平中,因变量需服从近似正态分布;假设5:对于研究对象内因素的各个水平组合而言,因变量的方差协方差矩阵相等,也称满足球形假设。
假设1、假设2与研究设计有关,本研究数据满足。
那么应该如何检验假设3、假设4和假设5,并进行单因素重复测量方差分析呢?三、SPSS操作3.1 检验假设3:研究对象内因素各个水平中,因变量没有明显异常值如果研究对象内因素某个水平中的某些因变量取值和其它值相比特别大或者特别小,则称之为异常值。
异常值会影响该水平的均数和标准差,因此会对最终的统计检验结果产生影响。
对于小样本研究,异常值的影响尤其显著,必须检查每组各个水平内是否存在明显异常值。
在主界面点击Analyze→Descriptive Statistics→Explore,把HR_1、HR_2和HR_3选入Dependent List框中。
如图2。
图2 Explore点击Plots,出现Explore: Plots对话框。
在Boxplots模块内选择Dependents together,在Descriptive模块内取消选择Stem-and-leaf,在下方勾选Normality plots with tests(执行Shapiro-Wilk's检验)。
重复测量方差分析spss
重复测量方差分析spss重复测量方差分析(RepeatedMeasuresAnalysisofVariance,简称RM ANOVA)是统计分析的一种重要方法,可以用来检验变量之间的关系,以及检查变量间的交互作用、顺序或临界影响。
它首先由英国心理学家 Ronald Fisher 于1935年提出,在统计学领域受到了广泛的引用和使用。
重复测量方差分析用于比较一个变量对另一个变量的效应,或者多个变量对另一变量的交互效应。
它可以用来检验一组连续性变量或一组分类变量与一个或多个因变量之间的关系,以及因变量之间的交互作用。
在实验中,它可以用来检测多次测量的结果是否有统计学意义。
此外,它还可以用来检验一组连续性变量或一组分类变量对一个或多个因变量的效应。
与其他类型的统计分析不同,重复测量方差分析只要求一组变量具有一致性,而不要求它们之间有固定的关系。
使用SPSS可以进行重复测量方差分析,通过该分析可以验证多次测量的结果是否具有统计学意义,进而判断变量之间的关系。
使用SPSS进行重复测量方差分析的步骤如下:第一步:打开SPSS软件,选择“分析”菜单,在其中选择“混合模型”。
第二步:在“混合模型”菜单中,选择“变量”子菜单,在其中选择“变量分解”,即可打开重复测量方差分析窗口。
第三步:在“变量分解”窗口中,首先将变量分别放入“因变量”、“自变量”和“重复测量”三个区域,然后选择“分析”按钮,即可开始重复测量方差分析。
第四步:重复测量方差分析完成后,SPSS会显示分析的结果,其中有统计量的计算结果,以及F值、概率值(p值)和其他辅助分析内容等。
重复测量方差分析是用来检验一组连续性变量或一组分类变量之间的关系的一种常用的统计分析方法。
它的使用只要求变量具有一致性,而不要求它们之间有固定的关系,因此它在实验中很常用。
使用SPSS可以很方便地完成重复测量方差分析,并获得统计学意义的结果。
本文详细介绍了如何使用SPSS进行重复测量方差分析的过程,为统计分析提供了有用的参考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 重复测方差分析实例操作
分析过程
1.数据格式
2.软件实验步骤
3.结果解释与描述
原始数据
group t0 t1 t2 t3 group t0 t1 t2 t3
1 1.17 1.14 0.89 1.77 0 1.35 0.74 0.6
2 0.61
1 0.66 0.58 0.75 0.68 0 1.66 1.39 1.1 0.75
1 0.63 0.67 0.69 0.97 0 0.71 0.63 0.49 0.52
1 1.8 2.
2 2.1
3 2.01 0 2.01 1.3 1.09 0.89
1 0.89 0.87 0.8
2 0.91 0 0.99 0.79 0.66 0.7
1 0.76 0.63 0.59 0.86 0 1.71 0.9 0.71 0.66
1 1.3
2 1.02 1.45 1.39 0 0.67 0.61 0.6 0.4
1 1.57 0.6
2 0.59 0.7 0 0.78 0.6
3 0.63 0.45
1 1.74 0.57 0.53 0.9
2 0 0.9
3 0.8
4 0.7 0.71
1 0.7 1.26 1.76 1.96 0 1.45 1.18 0.97 0.86
1 0.64 0.77 0.6
2 0.79 0 2.09 0.54 1.1 0.93
1 1.09 1.48 1.19 0.5
2 0 0.77 0.52 0.7
3 0.68
1 0.88 1.4
2 1.29 1.38 0 1.84 0.54 1.27 0.52
1 0.75 0.77 0.9 1.1 0 1.33 0.96 1.1
2 1.29
1 1.58 0.89 0.41 0.74 0 0.8 0.67 0.6 0.63
1 0.93 0.95 0.99 1.21 0 1.04 1.03 0.8 0.89
1 0.66 0.57 0.8 1.1
2 0 0.72 0.55 0.44 0.49
1 1.11 0.97 0.94 1.3
2 0 0.88 0.75 0.71 0.67
0 0.89 1.23 1.28 1.32 0 1.1 0.59 0.56 0.6
0 0.45 0.3 0.3 0.3 0 1.01 0.78 0.66 0.66
0 1.67 1.04 0.66 0.58 0 1.43 0.92 0.86 0.83
0 0.96 0.78 0.58 0.54 0 0.81 0.91 0.83 0.71
0 0.81 0.76 0.62 0.51 0 0.88 0.68 0.49 0.53
0 0.75 0.63 0.54 0.57 0 1.13 0.49 0.45 0.58
0 2.02 0.64 1.16 1.42 0 0.95 0.7 0.85 0.88
0 1.78 1.18 0.73 0.86 0 1.32 0.78 0.57 0.55
0 1.79 1.24 0.78 0.75 0 1.03 1.09 0.97 0.95
0 2.03 0.43 1.22 0.71 0 1.27 1.12 0.9 0.67
0 0.65 0.58 0.54 0.49 0 0.84 0.6 0.42 0.55
0 1.06 1 0.72 0.73 0 1.27 0.89 0.66 0.72
1.1 数据格式
1.2 软件实验步骤
些处的描述过程输出无标准差,
group=2时可用Analyze\ Explorer过程实现描述,
group=3时可用A nalyze→General Lineal Model→Multivariate去实现描述。
1.3 结果解释与描述
表1 有无合并症患者LC含量(s
x )
例数
重复测量时间
麻醉前麻醉后20分钟电切手术30分钟手术结束时
无合并症42 1.181±0.447 0.808±0.260 0.755±0.249 0.706±0.233 有合并症18 1.049±0.398 0.966±0.419 0.963±0.451 1.131±0.438
统计描述可以通过Analyze\ Explorer过程实现,该过程较简单不赘述。
SPSS.11_0统计分析教程.(高级篇)张文彤P37
也就是说,在分析时,我们首先要判断,重复测量的不同时间点之间的结果是否存在相关性,也就是进行球形检验,即Mauchly's Test of Sphericity 。
如果P<0.05,不符合Huynh-Feldt 条件,说明重复测量数据之间存在相关性,不可按单因素方差分析方法处理,需要进行多变量方差分析。
以多元检验结果为准。
SPSS.11_0统计分析教程.(高级篇)张文彤P41
如果P>0.05,符合Huynh-Feldt 条件,说明重复测量数据之间不存在相关性,可按单因素方差分析方法处理。
SPSS.11_0统计分析教程.(高级篇)张文彤P40
Table 2 Mauchly's Test of Sphericity
Within Subjects Effect Mauchly's W
Approx. Chi-Square df Sig. Epsilon a
Greenhouse-G eisser Huynh-Feldt Lower-b
ound Time
0.480 41.594
5
.000
0.680
0.717
0.333
本例由Table 2 Mauchly's Test of Sphericity可知,P<0.001,不符合Huynh-Feldt条件,说明重复测量数据之间存在相关性,不可按单因素方差分析方法处理,需要进行多变量方差分析,以多元检验结果为准。
Table 3 Multivariate Tests
Effect Value F Hypothesis df Error df Sig.
Time Pillai's Trace .271 6.952a 3.000 56.000 .000 Wilks' Lambda .729 6.952a 3.000 56.000 .000
Hotelling's Trace .372 6.952a 3.000 56.000 .000
Roy's Largest Root .372 6.952a 3.000 56.000 .000 Time * group Pillai's Trace .292 7.681a 3.000 56.000 .000 Wilks' Lambda .708 7.681a 3.000 56.000 .000
Hotelling's Trace .411 7.681a 3.000 56.000 .000
Roy's Largest Root .411 7.681a 3.000 56.000 .000 多变量方差分析结果如Table 3Multivariate Tests所示,四种检验结果Time和Time*group的P值均<0.05,说明时间因素以及时间因素和分组的交互作用有统计学意义,即测量指标有随时间变化的趋势并且时间因素的作用随着分组的不同而不同。
Table 4 Tests of Between-Subjects Effects
Source Type III Sum of Squares df Mean Square F Sig.
Intercept 179.966 1 179.966 617.964 .000
group 1.364 1 1.364 4.684 .035
Error 16.891 58 .291
表4组间效应的检验。
F=4.684,P=0.035,说明不同合并症患者的LC含量有差别。
综上,也就是说患者LC含量随手术时间的变化趋势不同,且这种变化趋势随着合并症(有/无)分组情况不同而不同。
如下图所示。
