高一数学限时训练试卷
高一数学限时训练试题3试题

限时检测题姓名___ _____.成绩 .一.选择题1. 向量(3,4),(sin ,cos )a b αα→→==,那么//,tan a b α→→=则( ) A.43 B.43- C.34 D.34-2. 设A 〔a,1〕,B 〔2,b 〕,C 〔4,5〕,为坐标平面上三点,O 为坐标原点,假设方向在与→→→OC OB OA 上的投影一样,那么a 与b 满足的关系式为( )A.354=-b aB.345=-b aC.1454=+b aD.1445=+b a3. 设,a b →→是非零向量,假设函数()()()f x x a b a x b →→→→=+⋅-的图象是一条直线,那么必有( )A. a b →→⊥B. a b →→∥C.||||a b →→=D.||||a b →→≠4. 如图,非零向量,,OA a OB b →→==且,BC OA C ⊥为垂足,设向量OC a λ→=,那么λ的值是( ) A.2||a ba →→→⋅ B. ||||ab a b →→→→⋅⋅ C. 2||a b b →→→⋅ D. ||||a b a b →→→→⋅⋅5.在ABC ∆中,M 是BC 的中点,AM=1,点P 在AM 上且满足学2PA PM =,那么()PA PB PC ⋅+等于( ) A.49 B.43 C.43- D.49-二.填空题6. 2,2cos120)a →=,那么与a →同向一共线的单位向量=____. O C A7. 关于平面向量,,a b c →→→.有以下三个命题:①假设a b a c →→→→⋅=⋅,那么b c →→=.②假设(1,),(2,6)a k b →→==-,//a b →→,那么3k =-. ③非零向量a →和b →满足||||||a b a b →→→→==-,那么a →与a b →→+的夹角为60.其中真命题的序号为__________.〔写出所有真命题的序号〕8. 平面上三点A 、B 、C 满足3AB =45,那么AB CA CA BC BC AB ⋅+⋅+⋅的值等于___________。
高一数学限时训练试题

高一数学必修1限时训练使用班级:高一级 使用时间:10月11日班级 姓名 成绩一.选择题(请将答案填写在答题卡,每题5分,共50分)1.集合},{b a 的子集有 ( ) A .2个B .3个C .4个D .5个2. 设集合{}|43A x x =-<<,{}|2B x x =≤,则AB = ( )A .(4,3)-B .(4,2]-C .(,2]-∞D .(,3)-∞ 3.已知()5412-+=-x x x f ,则()x f 的表达式是( )A .x x 62+ B .782++x x C .322-+x x D .1062-+x x4.函数f(x)=x21-的定义域是 ( )A 、[0,+∞)B 、(-∞,0)C 、(-∞,+∞)D 、(]0,∞-5.下列函数中,定义域为[0,∞)的函数是 ( ) A .x y =B .22x y -=C .13+=x yD .2)1(-=x y6.设,10<<<b a 则下列不等式正确的是( )b a b a A <. b a b b B <. a a b a C <. a b a b D <.7.指数函数y=a x 的图像经过点(2,16)则a 的值是 ( )A .41 B .21C .2D .4 8.若210,5100==b a,则b a +2=( )A 、0B 、1C 、2D 、3 9.已知0ab >,下面四个等式中: ①lg()lg lg ab a b =+; ②lglg lg aa b b=-; ③b ab a lg )lg(212= ; ④1lg()log 10abab =其中正确命题的个数为 ( )A .0B .1C .2D .310.定义运算a b ⊕,a b ⊕=⎩⎪⎨⎪⎧a ,a≤b,b ,a>b.例如:121⊕=,则函数12xy =⊕的值域为( )A 、(-∞,1)B 、(0,1)C 、[1,+∞)D 、(0,1]二 填空题(每空5分,共20分)11.若{}{}0,1,2,3,|3,A B x x a a A ===∈,则AB = .12.若函数2()1x af x x bx +=++在[]1,1-上是奇函数,则a = , b = .13、函数)10()(≠>=a a a x f x且在区间]2,1[上的最大值比最小值大2a,则a =__________14 .函数 y=log (x-1)(3-x) 的定义域是 。
高一数学基本不等式限时训练专题

高一数学基本不等式限时训练一、单选题(本大题共6小题,共30.0分)1.设x>2,则y=x+1x−2取得最小值时,x、y的值是()A. 4,3B. 3,4C. 3,3D. 4,42.已知正数x,y满足x+y=1,则11+x +11+2y的最小值是()A. 3328B. 76C. 3+2√25D. 653.已知a>0,b>0,3a+b=2ab,则a+b的最小值为()A. 2B. 3C. 2+√2D. 2+√34.若正数a,b满足1a +1b=1,则1a−1+9b−1的最小值为()A. 1B. 6C. 9D. 165.若实数a,b满足1a +4b=√ab,则ab的最小值为()A. √2B. 2C. 2√2D. 46.已知直线xa +4yb=1(a>0,b>0)过点(1,1),则a+b的最小值为()A. 2B. 4C. 7D. 9二、多选题(本大题共2小题,共10.0分)7.已知a>0,b>0,且a+2b=2,则下列正确的是()A. log2(a+2)+log2(b+1)的最大值为5B. 2√ab−a2−4b2的最大值为√2−2C. 3a+9b的最小值为6D. 2a +ab的最小值为2√2+18.已知x>0,y>0,且2x+y=2,则下列说法中正确的()A. xy的最大值为12B. 4x 2+y 2的最大值为2C. 4 x+2 y的最小值为4D. 2x +xy的最小值为4第II卷(非选择题)三、单空题(本大题共6小题,共30.0分)9.若x>0时,1−x−16x的最大值是.10.若正数a,b满足a+b=1,则9a +1b的最小值为.11.某公司一年购买某种货物600吨,每次购买x吨,运费为6万元/次,一年的总存储费用为4x万元.要使一年的总运费与总存储费用之和最小,则x的值是.12.已知a>1,b>2,a+b=5,则1a−1+9b−2的最小值为____________.13.函数f(x)=2x2−4x+5x−1(x>1)的最小值是__________.14.若a>0,b>0,3a+2b=1,则ab的最大值是.四、解答题(本大题共3小题,共36.0分)15.(1)已知a,b∈R,且a−3b+6=0,求2a+18b的最小值.(2)已知a,b是正数,且满足a+b=1,求1a +4b的最小值.16.(1)已知x>0,y>0,xy=4,求2x +1y的最小值;(2)已知x>0,y>0,x+2y=2,求2x +1y的最小值.17.(1)当x<2时,求函数y=x+92x−4的最大值;(2)设0<x<3,求函数y=√x(6−2x)的最大值.答案和解析1.【答案】B【解析】解:y =x +1x−2=x −2+1x−2+2≥2√(x −2)⋅1x−2+2=4,当且仅当x −2=1x−2,即x =3时取等, 故选:B .变形后用基本不等式可得.本题考查了基本不等式及其应用,属中档题.2.【答案】C【解析】解:∵正数x ,y 满足x +y =1,∴2x +2+2y +1=5,∴11+x +11+2y =15(2x +2+2y +1)(22+2x +11+2y) =15(3+2+4y2+2x +2+2x1+2y )⩾3+2√25, 当且仅当2+4y2+2x =2+2x1+2y ,即x =4−5√22,y =5√22−3时取等号,∴11+x +11+2y 的最小值为3+2√25.故选:C .根据条件可得2x +2+2y +1=5,再由11+x +11+2y =15(2x +2+2y +1)(22+2x +11+2y ),利用基本不等式求出11+x +11+2y 的最小值.本题考查了利用基本不等式求最值,考查了转化思想,属中档题.3.【答案】D【解析】 【分析】本题考查基本不等式的性质以及应用,关键是对3a +b =2ab 的变形.根据题意,由3a +b =2ab 可得32b +12a =1,进而分析可得a +b =(32b +12a )(a +b)=2+3a2b +b2a ,由基本不等式分析可得答案.解:根据题意,3a+b=2ab⇒32b +12a=1,则a+b=(32b +12a)(a+b)=2+3a2b+b2a≥2+2√3a2b⋅b2a=2+√3,当且仅当b=√3a且3a+b=2ab时等号成立,则a+b的最小值为2+√3,故选:D.4.【答案】B【解答】解:∵正数a,b满足1a +1b=1,∴b=aa−1>0,解得a>1.则1a−1+9b−1=1a−1+9aa−1−1=1a−1+9(a−1)≥2√9(a−1)·1a−1=6,当且仅当a=43时取等号(此时b=4).∴1a−1+9b−1的最小值为6.故选B.5.【答案】D【解析】【分析】本题考查了利用基本不等式求最值,属于基础题.利用基本不等式即可求解.【解答】解:实数满足1a +4b=√ab,∴a>0,b>0,∴1a +4b⩾2√1a·4b=2√4ab,∴√ab⩾2√4ab,即ab⩾4,当且仅当1a =4b时取等号,则ab的最小值为4.故选:D.【解析】解:由题意可知,1a +4b=1,∴a+b=(a+b)(1a +4b)=5+ba+4ab≥5+2√ba⋅4ab=9,当且仅当ba =4ab且1a+4b=1,即a=3,b=6时取等号,故a+b的最小值为9.故选:D.把已知点代入直线方程,然后利用“乘1法”与基本不等式的性质即可得出.本题考查了“乘1法”与基本不等式的性质,属于基础题.7.【答案】BCD【解析】对于A,因为log2(a+2)+log2(b+1)=log2(a+2)(b+1)=log2(ab+a+2b+2)=log2(ab+4)⩽log2[12(a+2b2)2+4]=log2(92),当且仅当a=2b=1时,等号成立.故A不正确;对于B,∵a+2b=2,a>0,b>0,∴由√(a)2+(2b)22≥a+2b2≥√2ab,可得√2ab≤1,a2+4b2≥2,∴2√ab−(a2+4b2)≤√2−2,当且仅当2b=a=1时取等号,∴最大值为√2−2.故B正确;对于C,3a+9b=3a+32b,∵a>0,b>0∴3a>1,32b>1,a+2b=2,∴3a+32b≥2√3a⋅32b=2√3a+2b=6,当且仅当3a=32b(a>0,b>0),即a=2b=1时,等号成立,故C正确;对于D,2 a +ab=a+2ba+ab=1+2ba+ab≥1+2√2ba·ab=2√2+1,当且仅当a=√2b时等号成立,故D正确;【解析】 【分析】本题考查利用基本不等式求最值,涉及不等式的性质,属中档题,根据已知条件,直接利用基本不等式可得xy 的最大值从而判定A ,套用2(a 2+b 2)⩾(a +b )2即可求得4x 2+y 2的最小值,从而判定B;4x +2y =22x +2y ⩾2√22x+y =4可判定C;2x +xy =2+(yx +xy ),再利用基本不等式求最值,即可判定D . 【解答】解:x ,y 是正数,在各选项这个大前提均成立, 由已知2=2x +y ,∵2x +y ≥2√2x ·y =2√2√xy , 当且仅当x =12,y =1时取等号, ∴√22⩾√xy ,∴xy ≤12,∴xy 最大值为12,当且仅当x =12,y =1时取到最大值12,故A 正确;对正数a ,b ,由不等式2(a 2+b 2)⩾(a +b )2可得:2(4x 2+y 2)⩾(2x +y )2=4, 即4x 2+y 2⩾12(2x +y )2=2, 当且仅当x =12,y =1时取等号, ∴4x 2+y 2的最小值为2,故B 错误; ∵4x +2y =22x +2y ⩾2√22x+y =4, 当且仅当x =12,y =1时取等号成立, 故4x +2y 的最小值为4,C 正确; 2x+xy =2x+y x+x y =2+(y x +x y )⩾2+2√x y ·yx =4,当且仅当x =y =23时取等号成立,故D 正确, 故选ACD .9.【答案】−7【分析】此题考查了利用基本不等式的性质求最值,可先变形为1−x−16x =1−(x+16x),再根据基本不等式性质可得到x+16x ≥2√x·16x,即可得到原式最大值.【解答】解:∵x+16x ≥2√x·16x,(x>0)即x+16x≥2√16,得到x+16x≥8,当且仅当x=16x,即x=4时取等号,∴1−x−16x⩽1−8,即1−x−16x⩽−7,故答案为−7.10.【答案】16【解析】【分析】本题主要考查基本不等式的应用,属于基础题.可对式子9a +1b乘以1,也即乘以a+b,再使用基本不等式即可求出答案.【解答】解:∵正数a,b满足a+b=1,∴9a +1b=(9a+1b)(a+b)=9+ab+9ba+1=10+ab+9ba≥10+2√ab⋅9ba=16,当且仅当{ab=9baa+b=1,也即当{a=34b=14时取“=”.故答案为:16.11.【答案】30 【解析】本题考查了基本不等式的性质及其应用,考查了推理能力与计算能力,属于基础题.由题意可得一年的总运费与总存储费用之和=600x×6+4x,利用基本不等式的性质即可得出.【解答】解:由题意可得:一年的总运费与总存储费用之和=600x ×6+4x≥4×2×√900x⋅x=240(万元).当且仅当x=30时取等号.故答案为:30.12.【答案】8【解析】【分析】本题考查了利用基本不等式求最值,“1”的应用,考查了运算求解能力,属于基础题.由条件有1a−1+9b−2=12[(a−1)+(b−2)](1a−1+9b−2),利用基本不等式可得答案.【解答】解:1a−1+9b−2=12[(a−1)+(b−2)](1a−1+9b−2)=12(1+9+b−2a−1+9×(a−1)b−2)≥12(10+2√b−2a−1⋅9×(a−1)b−2)=8当且仅当b−2a−1=9×(a−1)b−2,即a=32,b=72时,取得等号.故答案为:8 13.【答案】2√6【解析】【分析】由x>1,所以x−1>0,化简f(x)=2x2−4x+5x−1=2(x−1)2+3x−1=2(x−1)+3x−1,利用基本不等式求最小值.【解答】解:因为x>1,所以x−1>0,f(x)=2x2−4x+5x−1=2(x−1)2+3x−1=2(x−1)+3x−1,2(x−1)+3x−1≥2√2(x−1)·3x−1=2√6,当且仅当2(x−1)=3x−1,即x=1+√62,f(x)有最小值2√6,故答案为2√6.14.【答案】124【解析】【分析】本题考查了基本不等式的性质,属于基础题.利用基本不等式的性质即可得出.【解答】解:a>0,b>0,3a+2b=1,所以1=3a+2b≥2√6ab,当且仅当a=16,b=14,时取等号,所以ab≤124,所以ab的最大值是124,故答案为:124.15.【答案】解:(1)a−3b+6=0,即a−3b=−6,则2a+18b ≥2√2a⋅2−3b=2√2a−3b=14,当且仅当a =−3,b =1时,有最小值14;(2)a ,b 是正数,且满足a +b =1,则1a +4b =(a +b)(1a +4b )=5+b a+4a b ≥5+2√b a ⋅4a b =9, 当且仅当a =13,b =23时,有最小值9.【解析】(1)由题意可得a −3b =−6,再由基本不等式和指数的运算性质,可得所求最小值;(2)由a ,b 是正数,且a +b =1,可得1a +4b =(a +b)(1a +4b ),展开后运用基本不等式即可得到所求最小值.本题考查基本不等式的运用:求最值,考查指数的运算性质和变形能力,化简运算能力,属于基础题.16.【答案】解:(1)∵xy =4,且x >0,y >0,∴2x +1y ≥2√2xy =2√12=√2,当且仅当x =2√2,y =√2时取等号,即2x +1y 的最小值为√2.(2)∵x >0,y >0,x +2y =2,∴2(2x +1y )=(x +2y )(2x +1y )=4+4y x +x y ≥4+2√4y x ⋅x y =8, ∴2x +1y ≥4,当且仅当4y x =x y ,即x =2y =1时取等号,即2x +1y 的最小值为4.【解析】本题主要考查了运用基本不等式求最值,属于中档题.(1)直接利用基本不等式求得最小值.(2)2(2x +1y )=(x +2y)(2x +1y )整理后利用基本不等式求得最小值.17.【答案】解:(1)y =x +92x−4=x −2+92x−2+2=−[(2−x)+922−x ]+2,∵x <2,∴2−x >0, ∴(2−x)+922−x ≥2√92=3√2, ∴−[(2−x)+922−x ]+2≤2−3√2, 当且仅当2−x =922−x ,即x =4−3√22时,y 取最大值2−3√2. (2)y =√x(6−2x)=√−2(x −32)2+92(0<x <3), 设t =−2(x −32)2+92(0<x <3), ∴当x =32时,t 取最大值92,此时y 取得最大值√92=3√22.。
高中数学必修1课后限时训练30 阶段性检测卷1

高中数学必修1课后限时训练30 阶段性检测卷1本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分。
考试时间120分钟。
第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合M ={-2,-1,0,1,2},N ={x |12<2x +1<8,x ∈R },则M ∩N =( )A .{0,1}B .{-1,0}C .{-1,0,1}D .{-2,-1,0,1,2} 答案:C解析:因为N ={x |12<2x +1<8,x ∈R }={x |-2<x <2},所以M ∩N ={-1,0,1}.2.已知全集U =R ,A ={x |x ≤0},B ={x |x ≥1},则集合∁U (A ∪B )=( ) A .{x |x ≥0} B .{x |x ≤1} C .{x |0≤x ≤1} D .{x |0<x <1} 答案:D解析:A ∪B ={x |x ≤0或x ≥1},∁U (A ∪B )={x |0<x <1}. 3.下列函数中,定义域为(0,+∞)的是( )A .y =1x B .y =xC .y =1x 2D .y =12x答案:A4.已知f (x )=⎩⎪⎨⎪⎧2x (x ≥4)x +1(x <4)则f (f (3))=( )A .4B .2C .16D .8 答案:C解析:f (f (x ))=f (3+1)=f (4)=24=16.故选C.5.下列函数是偶函数,且在(-∞,0)上单调递减的是( )A .y =1xB .y =1-x 2C .y =1-2xD .y =1+x 2 答案:D6.下列函数中,既不是奇函数,也不是偶函数的是( )A .y =1+x 2B .y =x +1xC .y =2x +12x D .y =x +e x答案:D解析:y =1+x 2是偶函数,y =x +1x 是奇函数,y =2x +12x 是偶函数,y =x +e x 非奇非偶函数,故选D.7.化简(3+2)2 015(3-2)2 016=( ) A.3+2 B .2-3 C .1 D .-1 答案:B解析:(3+2)2015(3-2)2016=[(3+2)(3-2)]2015·(3-2)=2- 3.故选B.8.函数f (x )=ax +1x +2在区间(-2,+∞)上单调递增,则实数a 的取值范围是( )A .(0,12)B .(12,+∞)C .(-2,+∞)D .(-∞,-1)∪(1,+∞)答案:B解析:f (x )变形为f (x )=a +1-2a x +2,因为f (x )在(-2,+∞)上单调递增,所以1-2a <0,得a >12,故选B.9.定义运算a ⊗b =⎩⎪⎨⎪⎧a ,a ≤b ,b ,a >b ,则函数f (x )=x ⊗1x (x >0)的图象大致为( )答案:D解析:由题,知f (x )=x ⊗1x =⎩⎪⎨⎪⎧x ,0<x ≤1,1x ,x >1.其图象如下:故选D.10.若函数f (x ),g (x )分别是R 上的奇函数、偶函数,且满足f (x )-g (x )=e x ,e 是无理数,e =2.71828……,则有( )A .f (2)<f (3)<g (0)B .g (0)<f (3)<f (2)C .f (2)<g (0)<f (3)D .g (0)<f (2)<f (3) 答案:D解析:因为f (x )为R 上的奇函数,所以f (0)=0,由f (x )-g (x )=e x 得,g (0)=-1,因为g (x )为R 上的偶函数,故f (2)-g (2)=e 2,f (-2)-g (-2)=e -2,即-f (2)-g (2)=e -2,所以f (2)=e 2-e -22,同理可得f (3)=e 3-e -32,而e 3-e -3>e 2-e -2,故f (3)>f (2)>0>g (0). 11.f (x )是定义在R 上的奇函数,当x ≥0时,f (x )=2x +2x +b (b 为常数),则f (-1)=( ) A .3 B .1 C .-1 D .-3 答案:D解析:∵f (x )是定义在R 上的奇函数,且x ≥0时,f (x )=2x +2x +b ,∴f (0)=1+b =0,∴b =-1,∴f (1)=2+2-1=3,∴f (-1)=-f (1)=-3,故选D.12.函数f (x )=ax +1a(1-x ),其中a >0,记f (x )在区间[0,1]上的最小值为g (a ),则函数g (a )的最大值为( )A.12 B .0 C .1 D .2答案:C解析:f (x )=(a -1a )x +1a ,当a >1时,a >1a ,f (x )是增函数,f (x )最小值为f (0)=1a ,∴g (a )=1a,当a =1时,f (x )=1,∴g (a )=1,当0<a <1时,a -1a<0,f (x )最小值为f (1)=a ,∴g (a )=⎩⎪⎨⎪⎧a (0<a <1)1 (a =1)1a(a >1),因此g (a )最大值为1,选C.第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.已知函数f (x )=a x +b (a >0,a ≠1)的定义域、值域都是[-1,0],则a +b =________.答案:-32解析:当a >1时,f (x )=a x +b (-1≤x ≤0)的值域为[1a+b,1+b ],所以⎩⎪⎨⎪⎧ 1a +b =-11+b =0,解得b =-1,a 不存在.当0<a <1时,f (x )=a x +b (-1≤x ≤0)的值域为[1+b ,1a+b ],所以⎩⎪⎨⎪⎧1+b =-11a +b =0解得⎩⎪⎨⎪⎧a =12b =-2∴a +b =-32.14.函数f (x )=e x 2+2x 的增区间为________. 答案:[-1,+∞)解析:设f (x )=e t ,t =x 2+2x ,由复合函数性质得,f (x )=e x 2+2x 增区间就是t =x 2+2x 增区间[-1,+∞).故填[-1,+∞).15.设函数f (x )=x (e x +a e -x )(x ∈R )是偶函数,则实数a 的值为________. 答案:-1解析:因为函数f (x )=x (e x +a e -x )(x ∈R )是偶函数,所以设g (x )=e x +a e -x ,x ∈R ,由题意知,g (x )为奇函数,所以g (0)=0,则1+a =0,即a =-1.16.已知函数f (x )=⎩⎪⎨⎪⎧x 2+4x ,x ≥0,4x -x 2,x <0,若f (2-a )>f (a ),则a 的取值范围是________.答案:(-∞,1)解析:作出f (x )的图象,易知f (x )在R 上是增函数,由f (2-a )>f (a ),得2-a >a ,即2a <2,解得a <1.三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)(1)已知10a =2,10b =5,10c =3,求103a -2b +c 的值;(2)计算(2a 23 b 12 )2(-6a 12 b 32 )÷(-3a 16 b 56 )3.解析:(1)103a -2b +c =103a ·10c 102b =(10a )3·10c (10b )2=23×352=2425. (2)原式=22×(-6)(-3)3×a 23 ×2+12 -16 ×3b 12 ×2+32 -56 ×3=89a 43 b 0=89a 43 . 18.(本小题满分12分)已知集合A ={x |1≤2x ≤4},B ={x |x -a >0}. (1)若a =1,求A ∩B ,(∁R B )∪A ;(2)若A ∪B =B ,求实数a 的取值范围.解析:(1)∵1≤2x ≤4,∴20≤2x ≤22,∴0≤x ≤2, ∴A =[0,2],∴a =1,∴x >1,∴B =(1,+∞),所以A ∩B =(1,2].∴∁R B =(-∞,1],(∁R B )∪A =(-∞,2]. (2)∵A ∪B =B ,∴A ⊆B ,∴[0,2]⊆(a ,+∞), ∴a <0.19.(本小题满分12分)已知函数f (x )=x +ax,且f (1)=10.(1)求a 的值;(2)判断f (x )的奇偶性,并证明你的结论;(3)函数在(3,+∞)上是增函数,还是减函数?并证明你的结论. 解析:(1)f (1)=1+a =10,∴a =9.(2)∵f (x )=x +9x ,∴f (-x )=-x +9-x=-(x +9x )=-f (x ),∴f (x )是奇函数.(3)设x 2>x 1>3,f (x 2)-f (x 1)=x 2+9x 2-x 1-9x 1=(x 2-x 1)+(9x 2-9x 1)=(x 2-x 1)+9(x 1-x 2)x 1x 2=(x 2-x 1)(x 1x 2-9)x 1x 2,∵x 2>x 1>3,∴x 2-x 1>0,x 1x 2>9,∴f (x 2)-f (x 1)>0,∴f (x 2)>f (x 1),∴f (x )=x +9x在(3,+∞)上为增函数.20.(本小题满分12分)设函数f (x )=12-12x +1,(1)证明函数f (x )是奇函数;(2)证明函数f (x )在(-∞,+∞)内是增函数; (3)求函数f (x )在[1,2]上的值域.解析:(1)由题意,得x ∈R ,即函数的定义域关于原点对称,f (-x )=12-112x +1=12-2x2x +1=1-2x2(2x +1)=-12+12x +1=-f (x ),∴函数f (x )为奇函数.(2)设x 1,x 2是(-∞,+∞)内任意两实数,且x 1<x 2,则f (x 1)-f (x 2) =12-12x 1+1-12+12x 2+1 =2 x 1-2 x 2(2 x 1+1)(2 x 2+1)∵x 1<x 2,∴2x 1-2x 2<0,∴f (x 1)-f (x 2)<0,∴函数f (x )在(-∞,+∞)内是增函数. (3)∵函数f (x )在(-∞,+∞)内是增函数, ∴函数f (x )在[1,2]上也是增函数,∴f (x )min =f (1)=16,f (x )max =f (2)=310,∴函数f (x )在[1,2]上的值域为[16,310].21.(本小题满分12分)已知函数f (x )=2x -12|x |.(1)若f (x )=154,求x 的值;(2)若对于t ∈[1,2]时,不等式2t f (2t )+mf (t )≥0恒成立,求实数m 的取值范围.解析:(1)f (x )=154即2x -12|x |=154,当x ≥0时,2x -12x =154,去分母得4·4x -15×2x -4=0,∴2x =4或-14,又2x >0,∴2x =4,∴x =2,当x <0时,2x -12-x =154,即0=154不成立.综上,x =2. (2)∵2t (22t -122t )+m (2t -12t )≥0,∴2t (2t -12t )(2t +12t )+m (2t -12t )≥0化简得(2t -21t )(4t +1+m )≥0,∵t ∈[1,2],∴2t >12t ,∴4t +1+m ≥0恒成立,即m ≥-(4t +1)恒成立,也就是m 大于等于-(4t +1)的最大值-5,∴m ≥-5,因此m 的取值范围为[-5,+∞).22.(本小题满分12分)某市某企业决定从甲、乙两种产品中选择一种进行投资生产,打入国际市场.已x 2万美元的特别关税.(1)写出该企业分别投资生产甲、乙两产品的年利润y 1、y 2与生产相应产品的件数x (x ∈N *)之间的函数关系式;(2)分别求出投资生产这两种产品的最大年利润; (3)如何决定投资可获最大年利润?解析:(1)y 1=(10-a )x -20(1≤x ≤200,x ∈N *), y 2=-0.05x 2+10x -40(1≤x ≤120,x ∈N *). (2)∵10-a >0,故y 1为关于x 的增函数,∴x =200时,y 1取最大值,即生产甲产品听最大年利润S 1=(1980-200a )万美元. y 2=-0.05(x -100)2+460(1≤x ≤120,x ∈N *).∴x =100时,y 2取最大值,即生产乙产品的最大年利润S 2=460万美元.(3)S 1-S 2=200(7.6-a ),故当3≤a <7.6时,S 1>S 2,投资生产200件甲产品可获较大年利润;当a =7.6时,S 1=S 2,投资生产这两种产品获得的年利润相等;当7.6<a ≤8时,S 1<S 2,投资生产100件乙产品可获较大年利润.。
【高一数学试题精选】高一数学下册限时训练试题71

高一数学下册限时训练试题71
5 c 第38练班级姓名
1、在等比数列{an}中, =1, =3,则的值是
2、已知△ABc的三个内角A、B、c成等差数列,且AB=1,Bc =4,则边Bc上的中线AD的长为.
3、已知等差数列中,的值是
4、若全集U=R,集合=,S=,则
5、在数列中,,且对于任意正整数n,都有,则=________________
6、直线与圆在第一象限内有两个不同的交点,则的取值范围是
7、如图所示,平面、N互相垂直,棱a上有两点A、B,Ac ,BD N,且Ac⊥a,BD⊥a, AB=12c,Ac=3 c,BD=4c,则cD=____ ___.
8、在R上定义运算,若不等式成立,则实数a的取值范围是
9、如图,正方体ABcD—A1B1c1D1中,E在AB1上,
F在BD上,且B1E=BF
(1)求直线AB1 和平面A1B1c1D1 所成的角大小。
(2)求证EF∥平面BB1c1c
10、已知圆的半径为,圆心在直线上,圆被直线截得的弦长为,求圆的方程
5 c。
高中数学必修1课后限时训练31 阶段性检测卷2

高中数学必修1课后限时训练31 阶段性检测卷2本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分。
考试时间120分钟。
第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A ={y |y =log 3x ,x >1},B ={y |y =(13)x ,x >1},则A ∩B =( ) A .{y |0<y <13} B .{y |0<y <1} C .{y |13<y <1} D .Ø 答案:A解析:由x >1可得y =log 3x >log 31=0,y =(13)x <(13)1=13,因此A ={y |y >0},B ={y |0<y <13},所以A ∩B ={y |0<y <13},故选A. 2.若函数f (x )=⎩⎪⎨⎪⎧x 2+1,x ≤1,lg x ,x >1,则f (f (10))=( ) A .lg101 B .2C .1D .0答案:B解析:∵f (10)=lg10=1,∴f (f (10)=f (1)=12+1=2. 3.函数y =log 13 (1+x )+(1-x )-12 的定义域是( )A .(-1,0)B .(-1,1)C .(0,1)D .(0,1] 答案:B解析:函数y =log 13 (1+x )+(1-x ) -12 有意义应满足⎩⎪⎨⎪⎧ 1+x >01-x >0,∴-1<x <1,故选B.4.设a =log 0.50.6,b =log 1.10.6,c =1.10.6,则a ,b ,c 的大小关系是( )A .a <b <cB .b <c <aC .b <a <cD .c <a <b答案:C解析:a =log 0.50.6<log 0.50.5=1,又a =log 0.50.6>log 0.51=0,∴0<a <1.b =log 1.10.6<log 1.11=0,c =1.10.6>1.10=1,∴c >a >b ,故选C.5.设函数f (x )=ln(1+x )-ln(1-x ),则f (x )是( )A .奇函数,且在(0,1)上是增函数B .奇函数,且在(0,1)上是减函数C .偶函数,且在(0,1)上是增函数D .偶函数,且在(0,1)上是减函数答案:A解析:显然f (x )的定义域为(-1,1),关于原点对称,又∵f (-x )=ln(1-x )-ln(1+x )=-f (x ),∴f (x )是奇函数,显然f (x )在(0,1)上单调递增,故选A.6.已知函数f (x )的定义域为R ,f (x )在R 上是减函数,若f (x )的一个零点为1,则不等式f (2x -1)>0的解集为( )A .(12,+∞)B .(-∞,12) C .(1,+∞) D .(-∞,1) 答案:D解析:由f (x )是定义在R 上的减函数且f (x )的一个零点为1,易知当x <1时f (x )>0,所以f (2x -1)>0等价于2x -1<1,解得x <1,因此选D.8.函数y =e |-ln x |-|x -1|的图象大致是( )答案:D解析:当x ≥1时,y =1,当0<x <1时,y =1x+x -1, 故选D.9.函数f (x )=(2)x +3x 在区间( )内有零点( )A .(-2,-1)B .(0,1)C .(-1,0)D .(1,2)答案:C解析:f (0)=20+0×3=1,f (-1)=(2)-1-3=22-3<0,∴f (0)f (-1)<0,因此f (x )在(-1,0)上有零点,选C.10.某商店计划投入资金20万元经销甲或乙两种商品,已知经销甲商品与乙商品所获得的利润分别为P (万元)和Q (万元),且它们与投入资金x (万元)的关系是:P =x 4,Q =a 2x (a >0);若不管资金如何投放,经销这两种商品或其中的一种商品所获得的纯利润总不少于5万元,则a 的最小值应为( )A.5 B .5C .±5D .-5答案:A解析:设投放x 万元经销甲商品,则经销乙商品投放(20-x )万元,总利润y =P +Q =x 4+a 2·20-x . 令y ≥5,则x 4+a 2·20-x ≥5,所以a 20-x ≥10-x 2,即a ≥1220-x 对0≤x <20恒成立,而f (x )=1220-x 的最大值为5,且x =20时,a 20-x ≥10-x 2也成立,所以a min =5,故选A. 11.函数f (x )=|lg x |,则f (14)、f (13)、f (2)的大小关系是( ) A .f (2)>f (13)>f (14) B .f (14)>f (13)>f (2) C .f (2)>f (14)>f (13) D .f (13)>f (14)>f (2) 答案:B解析:f (14)=|lg 14|=|-lg4|=lg4,f (13)=|lg 13|=|-lg3|=lg3,∵lg4>lg3>lg2,∴f (14)>f (13)>f (2),故选B.12.定义在R 上的奇函数f (x )满足:当x >0时,f (x )=2015x +log 2015x ,则方程f (x )=0的实数根的个数是( )A .1B .2C .3D .4答案:C解析:f (x )=2015x +log 2015x ,在(0,+∞)上为增函数,又f (1)=2015>0,当x 无限接近零时,2015x 近似为1,log 2015x 是负数且无限小,因此函数值为负,所以f (x )在(0,+∞)上只有一根,又f (x )为奇函数,f (x )在(-∞,0)上递增且有一根,又f (0)=0,因此,f (x )在R 上有3个零点,故选C.第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.若幂函数y =f (x )的图象经过点(9,13),则f (25)的值是________. 答案:15解析:f (x )=x α,9α=13,∴α=-12,f (25)=25-12 =15. 14.设函数y =x 3与y =(12)x -2的图象的交点为(x 0,y 0),则x 0所在的区间是(n ,n +1),n ∈N +,则n =________.答案:1解析:设f (x )=x 3-(12)x -2 f (1)=-1<0,f (2)=7>0,又f (x )为增函数,∴x 0∈(1,2).15.对于函数f (x )=x -2-ln x ,我们知道f (3)=1-ln3<0,f (4)=2-ln4>0,用二分法求函数f (x )在区间(3,4)内的零点的近似值,我们先求出函数值f (3.5),若已知ln3.5=1.25,则接下来我们要求的函数值是________.答案:f (3.25)解析:由ln3.5=1.25且f (3.5)=3.5-2-ln3.5≈0.25>0,以及f (3)<0可知下一步应代入的x 值为3.5和3的平均数,即接下来我们需求的函数值为f (3.25).16.对于函数f (x )=log 2x 在其定义域内任意的x 1,x 2且x 1≠x 2,有如下结论:①f (x 1+x 2)=f (x 1)·f (x 2);②f (x 1·x 2)=f (x 1)+f (x 2);③f (x 1)-f (x 2)x 1-x 2>0;④f (x 1+x 22)<f (x 1)+f (x 2)2,上述结论中正确结论的序号是________.答案:②③解析:对于①,取x 1=2,x 2=4,可知f (x 1)·f (x 2)=log 22·log 24=2,而f (x 1+x 2)=log 26≠log 24=2,因此①不成立;对于②,由对数运算性质有f (x 1·x 2)=log 2(x 1·x 2)=log 2x 1+log 2x 2=f (x 1)+f (x 2),因此②成立;对于③,f (x 1)-f (x 2)x 1-x 2表示的正是两点(x 1,f (x 1)),(x 2,f (x 2))之间的变化率情况,由f (x )=log 2x 的图象易知其函数图象上任意两点之间的变化率必为正,因此③成立;对于④,取x 1=2,x 2=8,可知f (x 1)+f (x 2)2=log 22+log 282=2,f (x 1+x 22)=log 25, 而log 25>log 24=2,此时f (x 1+x 22)>f (x 1)+f (x 2)2, 因此④不成立.综上所述,应填②③.三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)求下列各式的值:(1)(279)12 -(23-π)0-(21027)-23 +0.25-32 ;(2)log 34273+lg25+lg4+7log 72. 解析:(1)原式=(259 )12 -1-(6427 )-23 +(14 )-32 =53-1-[(43 )3] -23 +[(12 )2] -32 =23-(43 )-2+(12 )-3=23-916+8=8548. (2)原式=log 33-14 +lg(25×4)+2=-14+2+2=154. 18.(本小题满分12分)已知函数f (x )=x 2+x +a 在区间(0,1)上有零点,求实数a 的取值范围.解析:函数f (x )=x 2+x +a 的对称轴方程为x =-12<0, 故f (x )在(0,1)上递增.由已知条件f (0)f (1)<0,即⎩⎪⎨⎪⎧ f (0)<0f (1)>0,故⎩⎪⎨⎪⎧a <02+a >0, 解得-2<a <0,故a 的取值范围为:(-2,0).19.(本小题满分12分)设函数f (x )=log 2(4x )·log 2(2x ),14≤x ≤4. (1)若t =log 2x 求t 的取值范围;(2)求f (x )的最值,并求出最值时,对应x 的值.解析:(1)∵t =log 2x ,14≤x ≤4,∴log 214≤t ≤log 24,∴-2≤t ≤2. (2)f (x )=(log 2x +log 24)(log 2x +log 22)=(log 2x +2)(log 2x +1)=log 22x +3log 2x +2,设log 2x =t ,∴y =t 2+3t +2=(t +32)2-14(-2≤t ≤2) 当t =-32,即log 2x =-32,x =2-32 =24时,f (x )min =-14当t =2即log 2x =2,x =4时,f (x )max =12.20.(本小题满分12分)定义在[-1,1]上的偶函数f (x ),已知当x ∈[0,1]时的解析式为f (x )=-22x +a ·2x (a ∈R ).(1)求f (x )在[-1,0]上的解析式.(2)求f (x )在[0,1]上的最大值h (a ).解析:(1)设x ∈[-1,0],则-x ∈[0,1],f (-x )=-2-2x +a ·2-x ,又∵函数f (x )为偶函数,∴f (x )=f (-x ),∴f (x )=-2-2x +a ·2-x ,x ∈[-1,0].(2)∵f (x )=-22x +a ·2x ,x ∈[0,1],令t =2x ,t ∈[1,2].∴g (t )=at -t 2=-(t -a 2)2+a 24. 当a 2≤1,即a ≤2时,h (a )=g (1)=a -1; 当1<a 2<2,即2<a <4时, h (a )=g (a 2)=a 24; 当a 2≥2,即a ≥4时,h (a )=g (2)=2a -4. 综上所述,h (a )=⎩⎪⎨⎪⎧ a -1, a ≤2,a 24, 2<a <4,2a -4, a ≥4.21.(本小题满分12分)已知函数f (x )=b ·a x (其中a ,b 为常数且a >0,a ≠1)的图象经过点A (1,6),B (3,24).(1)求f (x )的解析式;(2)若不等式(a b)x ≥2m +1在x ∈(-∞,1]上恒成立,求实数m 的取值范围. 解析:(1)由题意得⎩⎪⎨⎪⎧ a ·b =6b ·a 3=24⇒a =2,b =3, ∴f (x )=3·2x(2)设g (x )=(a b )x =(23)x , 则y =g (x )在R 上为减函数.(可以不证明)∴当x ≤1时g min (x )=g (1)=23, 因为(a b)x ≥2m +1在x ∈(-∞,1]上恒成立, 即g (x )min ≥2m +1,即2m +1≤23⇒m ≤-16,∴m 的取值范围为:m ≤-16. 22.(本小题满分12分)为了迎接世博会,某旅游区提倡低碳生活,在景区提供自行车出租.该景区有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每超过1元,租不出的自行车就增加3辆.为了便于结算,每辆自行车的日租金x (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用y (元)表示出租自行车的日净收入(日净收入=一日出租自行车的总收入-管理费用).(1)求函数y =f (x )的解析式及其定义域;(2)试问当每辆自行车的日租金定为多少元时,才能使日净收入最多?解析:(1)当x ≤6时,y =50x -115,令50x -115>0,解得x >2.3.∵x ∈N *,∴x ≥3,∴3≤x ≤6,x ∈N *.当x >6时,y =[50-3(x -6)]x -115.令[50-3(x -6)]x -115>0,得3x 2-68x +115<0.解得2≤x ≤20,又x ∈N *,∴6<x ≤20,x ∈N *,故y =⎩⎪⎨⎪⎧50x -115 (3≤x ≤6,x ∈N *),-3x 2+68x -115 (6<x ≤20,x ∈N *), 定义域为{x |3≤x ≤20,x ∈N *}.(2)对于y =50x -115(3≤x ≤6,x ∈N *),显然当x =6时,y max =185,对于y =-3x 2+68x -115=-3(x -343)2+8113(6<x ≤20,x ∈N *). 当x =11时,y max =270,∵270>185,∴当每辆自行车的日租金定为11元时,才能使日净收入最多.。
高一数学限时练1
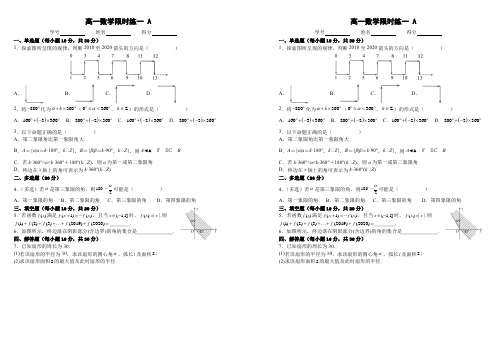
高一数学限时练一 A学号 姓名 得分一、单选题(每小题10分,共30分)1.探索图所呈现的规律,判断2018至2020箭头的方向是( )A .B .C .D . 2.将880-︒化为360k α+⨯︒(0360α︒≤<︒,Z k ∈)的形式是( )A .()1603360︒+-⨯︒B .()2002360︒+-⨯︒C .()1602360︒+-⨯︒D .()2003360︒+-⨯︒ 3.以下命题正确的是( ) A .第二象限角比第一象限角大B .A ={α|α=k ·180°,k ∈Z },B ={β|β=k ·90°,k ∈Z },则A BC .若k ·360°<α<k ·360°+180°(k ∈Z ),则α为第一或第二象限角D .终边在x 轴上的角可表示为k ·360°(k ∈Z ) 二、多选题(20分)4.(多选)若α是第三象限的角,则1802α-可能是( )A .第一象限的角B .第二象限的角C .第三象限的角D .第四象限的角三、填空题(每小题10分,共20分)5.若函数()f x 满足(1)()f x f x +=-,且当(1,1]x ∈-时,()||f x x =.则(1)(2)(3)(2019)(2020)f f f f f +++⋯++=________.6.如图所示,终边落在阴影部分(含边界)的角的集合是______________. 四、解答题(每小题10分,共30分) 7.已知扇形的周长为30.(1)若该扇形的半径为10,求该扇形的圆心角α,弧长l 及面积S ; (2)求该扇形面积S 的最大值及此时扇形的半径.高一数学限时练一 A学号 姓名 得分一、单选题(每小题10分,共30分)1.探索图所呈现的规律,判断2018至2020箭头的方向是( )A .B .C .D .2.将880-︒化为360k α+⨯︒(0360α︒≤<︒,Z k ∈)的形式是( )A .()1603360︒+-⨯︒B .()2002360︒+-⨯︒C .()1602360︒+-⨯︒D .()2003360︒+-⨯︒ 3.以下命题正确的是( )A .第二象限角比第一象限角大B .A ={α|α=k ·180°,k ∈Z },B ={β|β=k ·90°,k ∈Z },则A BC .若k ·360°<α<k ·360°+180°(k ∈Z ),则α为第一或第二象限角D .终边在x 轴上的角可表示为k ·360°(k ∈Z ) 二、多选题(20分)4.(多选)若α是第三象限的角,则1802α-可能是( )A .第一象限的角B .第二象限的角C .第三象限的角D .第四象限的角三、填空题(每小题10分,共20分)5.若函数()f x 满足(1)()f x f x +=-,且当(1,1]x ∈-时,()||f x x =.则(1)(2)(3)(2019)(2020)f f f f f +++⋯++=________.6.如图所示,终边落在阴影部分(含边界)的角的集合是______________. 四、解答题(每小题10分,共30分) 7.已知扇形的周长为30.(1)若该扇形的半径为10,求该扇形的圆心角α,弧长l 及面积S ; (2)求该扇形面积S 的最大值及此时扇形的半径.参考答案:1.C【解析】 【分析】根据探索图所呈现的规律,找出探索图的周期,再求出2018除4的余数即可求解. 【详解】由探索图易知,周期T =4, ∈201845042=⨯+,∈2018至2020箭头的方向和2至4的箭头方向相同, 故选:C. 2.D 【解析】 【分析】根据给定条件直接计算即可判断作答. 【详解】880200()3360-︒=︒+-⨯︒. 故选:D 3.B 【解析】 【分析】利用任意角的知识分析选项ACD 不正确,选项B 正确. 【详解】A 不正确,如-210°<30°.在B 中,集合A 表示终边在x 轴上的角的集合,集合B 表示终边在坐标轴上的角的集合,∈A B ,∈B 正确.在C 中,α为第一或第二象限角,或在y 轴的非负半轴上的角,∈C 不正确. 在D 中. 终边在x 轴上的角可表示为k ·180°(k ∈Z ),所以D 不正确. 故选:B 4.AC 【解析】 【分析】根据角限角的定义得出角的范围,再运用不等式的性质可得选项. 【详解】解:由于α是第三象限的角,故180360270360,k k k Z α,所以90180135180,2k k k Z α+⋅<<+⋅∈,所以4518018090180,2k k k Z α-⋅<-<-⋅∈.当k 为偶数时,1802α-为第一象限角; 当k 为奇数时,1802α-为第三象限角.所以1802α-可能是第一象限角,也可能是第三象限角.故选:AC. 5.1010 【解析】 【分析】推导出()()2f x f x +=,当(]1,1x ∈-时,().f x x =从而当x ∈N 时,()211f x +=,()20f x =,由此能求出结果.【详解】∈函数()f x 满足(1)()f x f x +=-, ∈()()2f x f x +=,∈当(]1,1x ∈-时,()f x x =.∈当x ∈N 时,()211f x +=,()20f x =,∈()()()()()123201*********f f f f f +++⋯++=. 故答案为:1010.6.{α|k ·360°-45°≤α≤k ·360°+120°,k ∈Z } 【解析】 【分析】写出终边在阴影部分的边缘的角即得解. 【详解】解:终边落在阴影部分第二象限最左边的角为360120,k k Z ⋅+∈, 终边落在阴影部分第四象限最左边的角为36045,k k Z ⋅-∈.所以终边落在阴影部分(含边界)的角的集合是{α|k ·360°-45°≤α≤k ·360°+120°,k ∈Z }. 故答案为:{α|k ·360°-45°≤α≤k ·360°+120°,k ∈Z } 7.(1)1α=,10l =,50S =; (2)2254,152. 【解析】【分析】(1)利用弧长公式,扇形面积公式即得;(2)由题可得()1122302S lr r r =-=,然后利用基本不等式即求. (1)由题知扇形的半径10r =,扇形的周长为30, ∈22030l r l +=+=, ∈10l =,10110l rα,1110105022S lr ==⨯⨯=.(2)设扇形的圆心角α,弧长l ,半径为r ,则230l r +=, ∈302l r =-,∈()()21522530112222154S lr r r r r r r -+⎛⎫--=⎪=⎭≤⎝== 当且仅当15r r -=,即152r =取等号, 所以该扇形面积S 的最大值为2254,此时扇形的半径为152.。
高一数学下册限时训练试题15.doc

第15练 班级 姓名
1、过点)4,3(-且在两坐标轴上的截距相等的直线方程为
2、已知数列{}n a 是等差数列,且,2,211-==d a 公差则这个数列的前n 项和n S 的最大值为
3、长方体的一个顶点上的三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积为
4、圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为π84,则圆台较小的底面的半径为
5、在ABC Rt ∆中,5,4.3===AC BC AB ,将三角形绕直角边AB 旋转一周所形成的几何体的体积为
6、若三个球的表面积之比为1:2:3,则它们的体积之比为
7、已知一个正方形的直观图是有一条边长为4的平行四边形,则此正方形的面积是 。
8、圆锥的轴截面是正三角形,则它的底面积与侧面积之比为
9、球内有相距cm 1的两个平行截面,截面的面积分别为2
285cm cm ππ和,球心不在截面之间,求球的表面积和体积。
10、P 为圆06422=-++y x y x 上一个动点,
(1)定点||),1,1(PQ Q 求-的最值;
(2)定点的最值求||),2,2(PN N -;
(3)到直线2=y 的距离最大的点P 的坐标;
(4)圆上到直线2=y 的距离为1的点有几个?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
贺兰一中高一数学限时训练(3)
出卷人 史艳妮
一.选择题
1.以下说法错误的是( )
A .零向量与任一非零向量平行 B.零向量与单位向量的模不相等 C.平行向量方向相同 D.平行向量一定是共线向量 2.下列四式不能化简为AD 的是( )
A .(
B .(
C .-+
D .;+ 3.已知a =(3,4),b =(5,12),a 与b 则夹角的余弦为( )
A .
6563 B .65 C .5
13
D .13 4. 已知a 、b 均为单位向量,它们的夹角为60°,那么|a + 3b | =( )
A .7
B .10
C .13
D .4
5.已知ABCDEF 是正六边形,且−→
−AB =→
a ,−→−AE =→
b ,则−→
−BC =( )
(A )
)(2
1
→→-b a (B ) )(2
1→→-a b (C ) →a +→b 2
1 (D ) )(2
1→
→+b a
6.设→
a ,→
b 为不共线向量,−→
−AB =→
a +2→
b ,−→−BC =-4→a -→b ,−→
−CD = -5→
a -3→
b ,则下列关系式中正确的是 ( )
(A )−→
−AD =−→−BC (B )−→−AD =2−→−BC (C )−→−AD =-−→−BC (D )−→−AD =-2−→
−BC 7.设x ,y ∈R ,向量a =(x,1),b =(1,y ),c =(2,-4),且a ⊥c ,b ∥c ,则|a +b |等于
( )
A. 5
B.10 C .2 5 D .10
8.在四边形ABCD 中,−→
−AB =−→−DC ,且−→−AC ·−→
−BD =0,则四边形ABCD 是( )
(A ) 矩形 (B ) 菱形 (C ) 直角梯形 (D ) 等腰梯形
9.已知M (-2,7)、N (10,-2),点P 是线段MN 上的点,且−→
−PN =-2−→
−PM ,则P 点的坐标为( )
(A ) (-14,16)(B ) (22,-11)(C ) (6,1) (D ) (2,4)
10.已知→a =(1,2),→b =(-2,3),且k →a +→b 与→a -k →
b 垂直,则k =( )
(A ) 21±-(B ) 12±(C ) 32±(D ) 23±
11、若平面向量(1,)a x =
和(23,)b x x =+- 互相平行,其中x R ∈.则a b -= ( )
A. 2-或0;
B.
C. 2或
D. 2或10.
12.在直角三角形ABC 中,点D 是斜边AB 的中点,点P 为线段CD 的中点,则|P A |2+|PB |2
|PC |2
等
于
( ) A .2
B .4
C .5
D .10
二. 填空题:
13、已知向量)2,1(,3==b a
,且b a ⊥,则a 的坐标是_________________。
14.已知向量a ,b 夹角为45°,且|a |=1,|2a -b |=10,则|b |=________.
15.如图,在矩形ABCD 中,AB =2,BC =2,点E 为BC 的中点,点F 在边CD 上,若AB →·AF →
=2,则AE →·BF →的值是________.
16 。
关于平面向量,,a b c .有下列三个命题:
①若
a b =a c ,则=b c . ②若(1)(26)k ==-,,,a b ,∥a b ,则3k =-.
③非零向量a 和b 满足||||||==-a b a b ,则a 与+a b 的夹角为60
.
其中真命题的序号为 .(写出所有真命题的序号) 三. 解答题:
17、设平面三点A (1,0),B (0,1),C (2,5).
(1)试求向量2+AC 的模; (2)试求向量与AC 的夹角; (3)试求与BC 垂直的单位向量的坐标.
18、已知向量)1,0(),0,1(,4,23212121==+=-=e e e e b e e a
其中
求 (1)b a b a
+⋅;的值; (2)a 与b 的夹角。
19.设两个向量e 1、e 2满足|e 1|=2,|e 2|=1,e 1、e 2的夹角为60°,若向量2t e 1+7e 2与向量e 1
+t e 2的夹角为钝角,求实数t 的取值范围.
20、 已知向量3(sin ,),(cos ,1).2
a x
b x ==-
(1)当//a b 时,求2
2cos sin 2x x -的值; (2)求b b a x f ⋅+=)()(在,02π⎡⎤-⎢⎥⎣⎦
上的
值域.
21.如图,
=(6,1),
,且。
(1)求x 与y 间的关系; (2)若 ,求x 与y 的值及四边形ABCD 的面积。
22.已知向量(cos ,sin )a αα= ,(cos ,sin )b ββ=
,a b -= .
(Ⅰ)求cos()αβ-的值; (Ⅱ)若02
π
α<<
,02
π
β-
<<,且5
sin 13
β=-
,求sin α的值.。
