第3章 刚体力学基础
第三章刚体力学基础

(2)轴通过棒的中心并与棒垂直;
dm
解:
J
r 2dm
dm dx m dx
o x dx
x
l
J l x2 m dx 1 m x3 l J 1 ml2
0l
3l 0
3
L
JC
2 L
x 2dx
mL2
/ 12
A
C
2
L/2
B
L/2
x
注:同一刚体,相对不同的转轴,转动惯量是不同的。
J ,r
质点A
T1 mg sin maA
质点B
mg T2 maB
滑轮(刚体) T2r T1r J
( T2 T2,T1 T1)
联系量 aA aB r
联立求解可得T1 、T2、 aA、 aB、
A
B
FN
T1 FR T1 mg T2
T2 m1g
为什么此时T1 ≠ T2 ?
mg
3、 平行轴定理与垂直轴定理
J11 J1 J2 2
ω
则B轮的转动惯量
J2
1 2 2
J1
n1 n2 n2
J1
20.0kg m2
(2)系统在啮合过程中机械能的变化为.
E
1 2
J1
J2
12
1 2
J112
1.32
104
J
质点的运动规律和刚体定轴转动规律的对比(一)
速度 加速度
质点v的运d动r
a
dt dv
dt
质量m, 力F
第一节 刚体运动的描述
一. 刚体
内部任意两点的距离在运动过程中始终保持不变的物 体,即运动过程中不发生形变的物体。
第3章刚体力学基础

描述质点系转动的动力学方程
z
取惯性坐标系
dt
oxyz
刚体所受的对
转轴的力矩
x
o
M r F
定义:在垂直于转轴的平 面轴内的,距外离力dF的与乘力积线到转
y z轴为固定转轴
z
M
F
F F
r
垂直转轴的外力分量产生沿
d
转轴方向的力矩, 平行于转
轴的外力分量产生的力矩被
轴承支承力的力矩所抵消
一 、作用于定轴刚体的合外力矩
相对于定轴的合外力矩
(力对转轴的力矩)
M z M iz ri Fi sin i
i
i
即作用在各质元的 力矩的 z 分量之和
二、刚体定轴转动定理
由于刚体只能绕 z 轴转动, 引起转动的力矩只有z方向,
因此转动动力学方程
Mz
dLz dt
dL M
dt
Li
Ri
m
i
v
i
oo ri
mi vi
解:
z
J z mi ri2
i
m i
x
2 i
y
2 i
i
Jy Jx
x
o
yi
ri
m
x
i
i
y
例 均质圆盘:m, R . 求以直径为轴的转动惯量 解:
J 1 mR2 4
例3-6(P181) 挂钟摆锤的转动惯量
解:
o
m1 l
J
1 3
m1l 2
1 2
m2 R2
m2 l
R2
m2 R
例 计算钟摆的转动惯量。(已知:摆锤质量为m,半 径为r,摆杆质量也为m,长度为2r)
大学物理第三章刚体力学基础习题答案培训课件

1 )
t2
下次上课内容:
§5-1 简谐运动 §5-2 旋转矢量表示法 §5-3 单摆和复摆 §5-4 振动的能量
角动量定理
t2 Mdt
t1
J2
J1
角动量守恒 M 0, J 恒矢量
力的功
W
r F
drr
力矩的功 W Md
动 能 1 mv2
2
动能定理
W
1 2
mv22
1 2
mv12
转动动能 1 J 2
2
转动动能定理W
1 2
J22
1 2
J12
习 题 课 (三)
3-1 一轻绳绕在有水平轴的定滑轮上,绳下端挂一
的角加速度 =
。从开始制动到 =1/3 0所经过
的时间t = 。
M k2 J
k 2 k02
J 9J
k2 J d
dt
t k dt
0J
1 3
0
d
0
2
t 2J
k0
3-6 一长为L的轻质细杆,两端分别固定有质量为
m 和2m 的小球,此系统在铅直平面内可绕过中心点
O且与杆垂直的水平固定轴转动。开始时杆与水平成
方向上,正对着杆的一端以相同的速率v相向运动,
如图所示。当两小球同时与杆的两端发生完全非弹性
碰撞后,就与杆粘在一起转动,则这一系统碰撞后的
转动角速度为
m
(A) 2v
4v (B)
v
3L
✓(C)
6v 7L
5L (D) 8v
9L
(E) 12v v m
o
7L
2mvL 1 mL2 2mL2
3
6v
7L
第三章-刚体力学基础

薄板对Z轴的转动惯量 J Z =
对X轴的转动惯量 J X
对Y轴的转动惯量 JY
Z
垂直轴定理
JZ JX JY
O
yi
Y
xi
ri
X
JZ miri2 mi xi2 mi yi2 Jx J y
五 刚体定轴转动的转动定律的应用
例1、一个质量为M、半径为R的定
滑轮(当作均匀圆盘)上面绕有细绳, 绳的一端固定在滑轮边上,另一端挂
分析: 由 每分钟150转 可知
0
t
2 150
60
5
rad
/ s
而已知 r=0.2m t=30s ω=0
可由公式求相应的物理量
解: (1) 0 0 5 (rad / s2 )
t
30
6
负号表示角加速度方向与角速度方向相反
(飞轮做匀减速转动)
2 02 2
(5 )2 2 ( )
末位置:
Ek
1 2
J 2
l
由刚体定轴转动的动能定理
1 mgl sin 1 J 2 0
2
2
mgl sin 3g sin
J
l
M
1 mgl cos
2
3g cos
J
1 ml2
2l
3
dm dl
gdm
(用机械能守恒定律解) 假设棒在水平位置时的重力势能为零势能
0 1 J2 (mg l sin ) O
动。最初棒静止在水平位置,求它由此下摆角时的
角加速度和角速度。(分别用动能定理和机械能守
恒定律求解)
解: (用动能定理解)
重力对轴的力矩为
M 1 mgl cos(M
O
大学物理第三章刚体力学基础习题答案

方向竖直向下
3-15 由角动量守恒得
mul J mvl 1 1 2 1 2 2 mu m v J 因弹性碰撞,系统机械能守恒: 2 2 2 1 1 2 2 又: J M 2l Ml 12 3 6mu M 3m u 联立可得: v M 3m l M 3m
2 2 2 1 mv l [m( l ) M l 2 ] 3 3 3
o
2 l 3
6mv (4m 3M ) l
v
m
A
3-9 电风扇在开启电源后,经过t1时间到达了额定 转速,此时相应的角速度为 0。当关闭电源后,经 过t2时间风扇停转。已知风扇转子的转动惯量为 J, 并假定摩擦力矩和电机的电磁力矩均为常量,试根据 已知量推算电机的电磁力矩。 解: 设电机的电磁力矩为M,摩擦力矩为Mf
1
0
t1
3-9 (1)
mg T ma
T mg sin 30 ma
g 2 a m/s 4
方向竖直向下
T2 N 2
mg
(2)
mg T1 ma
T2 mg sin 300 ma
T1r T2r J
a r
T1
1
mg
J k m r2
g 联立求解得: a 22 k
质点运动 m 质 量 力 F 刚体定轴转动 2 J r 转动惯量 m dm 力矩 M Fr sin
dp dL F m a F 第二定律 转动定律 M J M dt dt p mv 动 量 角动量 L J t t2 动量定理 t Fdt mv2 mv1 角动量定理 t Mdt J 2 J1 1 动量守恒 F 0, mv 恒矢量 角动量守恒 M 0, J 恒矢量 力矩的功 W Md 力 的 功 W F dr
刚体力学基础第三章

二、转动惯量J
对分立的质点系: J miri2
i
对刚体: 质量是连续分布
J r2dm
r 2dl 线分布,为线密度
J r 2ds 面分布,为面密度 r 2 dV 体分布,为体密度
z
dm
r
讨论
J r2dm
(1)转动惯量的物理意义:J表示刚体转动时惯性的大小
(2)转动惯量J的大小决定于
r 3dr
1 2
mR2
m
R 2
J
常 见 刚 体 的 转 动 惯 量
§3 刚体定轴转动定律
一、 力矩
使物体转动,必须给定一 个作用力,另外考虑转动与力 的作用点以及作用力的方向有 关,因此在研究物体转动中引
入力矩这一物理量。 (1)若刚体所受力 F在转动平面内
z
Od r
F
F
P
力臂:rsin = d 表示转轴到力作用线的垂直距离。
m
2(2
m
1
+
m
2
m 1+m 2
+
m
2
)g
T1
a m1 m1g T2 a m2 m2g
§4 力矩的功 动能定理
一、力矩的功
刚体在合外力矩作用下绕定轴转动而发生角位移时
d,A则力F矩 d对r刚体F作d了r功co。s F cos(900 )ds
F sin rd
Md
z
O d
dr
F
r P
元功:力矩对质点(或刚体)所作的 元功等于力矩和角位移的乘积
盘)。如A下降,B与水平桌面间的滑动摩擦系数为μ,
绳与滑轮之间无相对滑动,试求系统的加速度及绳中的
张力FT1和FT2。 受力分析 FT1
理论力学周衍柏第三章

(e) dT Fi dri
(e) 若 Fi dri dV 则 T V E
为辅助方程,可代替上述6个方程中任何一个
§3.5 转动惯量
一、刚体的动量矩 1. 某时刻刚体绕瞬轴OO’转动,则pi点的速度为
vi rii
动量矩为 2. 坐标表示
R Fi Fi 0 M M i ri Fi 0
2. 几种特例 1)汇交力系(力的作用线汇交于一点):取汇交点为 简化中心,则
Fix 0 R Fi 0 Fiy 0 Fiz 0
三、力偶力偶矩 1. 力偶:等大、反向、不共线的两个力组成的利系。
力 偶 所在平面角力偶面. 2. 力偶矩: 对任意一点O M rA F rB F (rA rB ) F r F M Fd
方向 : 右手法则 上式表明:
J z x mi zi xi y mi zi yi z mi ( xi2 yi2 )
I yy mi ( zi2 源自xi2 ) I zy mi zi yi I yz mi yi zi I xz mi xi zi
I zz mi ( xi2 yi2 )
面向新世纪课程教材大学物理大作业答案——刚体力学作业
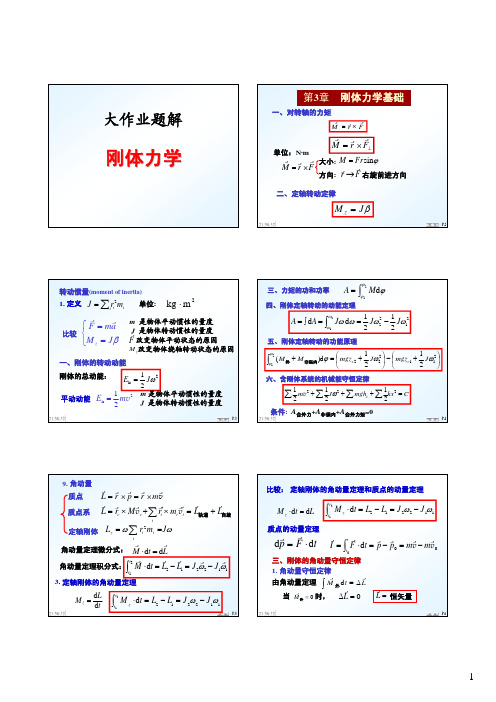
L2
−
L1
=
J 2ω2
−
J1ω1
质点的动量定理
dpr
=
r F
⋅
dt
∫ r
I
=
tr F ⋅ dt =
t0
pr − pr0 = mvr − mvr0
三、刚体的角动量守恒定律
1. 角动量守恒定律
∫ 由角动量定理
r M
当
r M外
=
0
时,
外
d
t r
ΔL
= =
Δ 0
r L
r L
=
恒矢量
P.6
1
区分两类冲击摆
(1)
大作业题解
刚体力学
第3章 刚体力学基础
一、对转轴的力矩
r M
=
rr
×
r F
单位:N·m
r M
=
rr
×
r F⊥
r M
=
rr
×
r F
大小: 方向:
M = Frsinϕ
rr
→
r F
右旋前进方向
二、定轴转动定律
M z = Jβ
P.2
转动惯量(moment of inertia)
∑ 1. 定义 J = iri2mi 单位: kg ⋅ m 2
l/4 O
[ A]
mg l = 1 Jω 2 J = 7 ml 2
22
48
⇒ ω = 4 3g 7l
P.11
9.如图所示,一人造卫星到地球中心C的最大距离和
最小距离分别为RA和RB。设人造卫星对应的角动量分
别为LA和LB,动能分别为EkA和EkB,则有
(A) LB > LA,EkB > EkA
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章 刚体力学基础一、基本要求1.理解质点及刚体转动惯量、角动量的概念,并会计算质点及刚体(规则形状刚体)的转动惯量、角动量; 2.理解刚体绕定轴转动的转动定律,并应用它来求解定轴转动刚体力矩和角加速度等问题; 3.会计算力矩的功、刚体的转动动能、刚体的重力势能,会应用机械能守恒定律解答刚体定轴转动问题;4.掌握刚体的角动量定理和角动量守恒定律,并会分析解决含有定轴转动刚体系统的力学问题(质点与刚体碰撞类问题等)。
二、基本内容(一)本章重点和难点:重点:刚体绕定轴转动定律及角动量守恒定律。
难点:刚体绕定轴转动系统的角动量守恒定律及其应用。
(二) 知识网络结构图:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧角动量守恒定律定轴转动定律基本定律转动动能角动量冲量矩转动惯量力矩基本物理量(三)容易混淆的概念:1.转动惯量和质量转动惯量反映刚体转动状态改变的难易程度,即刚体的转动惯性大小的量度;质量反映质点运动状态改变的难易程度,即质点的惯性大小的量度。
2.平动动能和转动动能平动动能是与质量和平动速度的平方成正比;转动动能是与转动惯量和角速度的平方成正比。
(四)主要内容:1.描述刚体定轴转动的角位置θ,角位移θ∆、角速度ω和角加速度α(β)等物理量t t d d ,d d ωαθω==角量与线量的关系:2n t ωαωθr a r a r v r s ====2.转动惯量--转动质点对转轴的转动惯量,等于转动质点的质量m 成以质点到转轴的距离r 的平方。
2Jm r =⋅(1)质量连续分布的刚体:⎰=mr J d 2线分布:dl dm ⋅=λ λ-质量线分布刚体,单位长度的质量。
面分布:dS dm ⋅=σ σ- 质量面分布刚体,单位面积的质量。
体分布:dV dm ⋅=ρ ρ 质量体分布刚体,单位体积的质量。
(2)质量离散分布刚体的转动惯量:2iJ m r=⋅∑(3)平行轴定理 2C J J md =+3.刚体绕定轴转动的转动定律—刚体的合外力矩等于转动惯量乘以角加速度。
t JJ M d d ωα==i i i M M r F ==⨯∑∑u u r u u v v u v力矩:F r M ϖϖϖ⨯=力对轴的力矩大小:θsin rF M =4.刚体绕定轴转动的动能定理--合外力矩对刚体所作的功,等于刚体转动动能的增量。
2122211122W Md J J θθθωω==-⎰ 21W Md θθθ=⎰ 力矩的功221ωJ E k =刚体绕定轴转动的转动动能:对于质点、刚体组成的系统,动能定理仍然适用,系统的动能包括系统内所有质点的平动动能和刚体的转动动能。
5.刚体转动系统机械能守恒定律--当转动刚体系统内力只有保守力矩作功,其他外力矩和非保守内力矩不作功或作的总功为零,则整个系统机械能守恒。
21常量2k p c E E J mgh ω+=+= P c E mgh = 刚体的重力势能6.角动量定理与角动量守恒定律 (1)角动量—质点位矢与动量的叉积。
运动质点对某一定点的角动量:v m r p r L ϖϖϖϖϖ⨯=⨯= 刚体绕定轴转动的角动量:ωJ L =(2)角动量定理--对一固定轴,作用于系统的合外力矩的冲量矩等于系统对该轴的角动量的增量。
⎰-=12ωωJ J Mdt21t t Mdt ⎰u u v冲量矩:力矩的时间积累效应。
(3)角动量守恒定律--若刚体所受合外力矩为零时,刚体的角动量守恒。
当0=M 时,常量==ωJ L (五)思考问答:问题1 以恒定角速度转动的飞轮上有两个点,一个点在飞轮的边缘,另一个点在转轴与边缘之间的一半处。
试问:在t ∆时间内,哪一个点运动的路程较长?哪一个点转过的角度较大?哪一个点具有较大的线速度、角速度、线加速度和角加速度?答:刚体绕定轴转动时,刚体内的任意各点具有相同的角速度、角加速度;各点的线速度、线加速度与角量之间的关系为:2,,ωαωτr a r a r v n ===。
所以飞轮边缘处的点的运动路程较长;两点转过的角度一样大;边缘的点具有较大的线速度、线加速度,两点的角速度、角加速度一样大。
问题2 如果一个刚体所受合外力为零,其合力矩是否也一定为零?如果刚体所受合外力矩为零,其合外力是否也一定为零?答: 合外力为零时,其合力矩不一定为零。
合外力矩为零时,其合外力不一定为零,刚体绕定轴O 在纸平面内转动,其中12212,2F F r r ==,其合力矩M=02211=-r F r F ,但其合力03121≠=+=F F F F 。
问题3 有两个飞轮。
一个是木制的,周围镶上铁质的轮缘。
另一个是铁质的,周围镶上木制的轮缘。
若这两个飞轮的半径相同,总质量相等,以相同的角速度绕通过飞轮中心的轴转动,哪一个飞轮的动量较大? 答:从转动动能221ωJ E k =可知,当两者ω相同时,J 越大的飞轮,其K E 也越大。
由 ⎰=dm r J 2可得木制飞轮的转动惯量为:222221m 21(m 21R M M R M R R M J ⎪⎭⎫⎝⎛-=+=+=木总铁木铁木木)而铁制飞轮的转动惯量为:2222212121R M M R m M R m R M J ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+=+=铁总木铁木铁铁由于两个飞轮的半径相同,且木铁M M 2121〉,所以铁木J J 〉,即木制的飞轮动能较大。
问题4 如果一个质点系的总角动量等于零,能否说此质点系中每一个质点都是静止的?如果一个质点系的总角动量为一常量,能否说作用在质点系上的合外力为零?答:由于()v m r P r L ϖϖρϖϖ⨯=⨯=,所以,角动量不仅取决于矢径r 、动量v m ϖ的量值,还取决于矢径与动量之间的夹角(取向),因此,总角动量为零,可以有两种情况:第一,每一个质点的角动量都不为零,但总和为零,则每一个质点不可能静止;第二,每一个质点的角动量都为零,此时,可以使每一个质点都静止,也可以是矢径与速度相互平行。
综上可知,每一质点不一定都静止。
此外,角动量守恒的条件是合外力矩为零,而合外力不一定是零。
问题 5 下面几个物理量中,那些与原点的选择有关?那些无关?(1)位矢;(2)位移;(3)速度;(4)角动量。
答:位移,速度与参考系选择有关,与坐标原点选择无关;位矢、角动量既与参考系选择有关,也与坐标原点选择有关。
问题6 转动惯量的物理意义是什么,大小和什么有关?答: 转动惯量的物理意义是:描述刚体作转动时保持其原运动状态的性质——转动惯性。
转动惯量的大小不仅与刚体的质量有关,也与转轴的位置有关,也就是说与刚体的总质量和相对于转轴的分布有关。
问题7 为什么在研究刚体运动时,要研究力矩的作用?力矩和哪些因素有关?答:一个静止的刚体能够获得平动加速度的原因是:相对它的质心而言所受的合外力不为零。
一个静止的刚体相对某一转轴能够获得角加速度的原因是:刚体所受到的相对转轴的合外力矩不为零。
因此,刚体的转动是与其受到的相对转轴的合外力矩密切相关的。
取z 轴为刚体转动的固定轴时,对转动有贡献的合外力矩是∑=izz MM ,其中i i i iz r F M θsin =,i F 是作用在刚体上的第i 个外力,在转动轴平面内的分量,而i r 是转轴(z 轴)到i F 作用点的距离,i θ是i r 与i F 间由右手定则决定的夹角。
所以,对z 轴的力矩不但与各外力在转动平面内分量的大小i F 有关,还与i F 的作用线和z 轴的垂直距离(力臂)i i i r d θsin =的值有关。
问题8 在定轴转动中,质点与刚体发生碰撞时动量是否守恒?答:质点与定轴转动的刚体发生碰撞时,转轴作用于刚体的力(外力)不为零,且比较大,不能忽略,故系统的动量不守恒。
只有在合外力矩为零时,角动量守恒。
问题9 在一个系统中,如果该系统的角动量守恒,动量是否一定会守恒?反之,如果该系统的动量守恒,角动量是否一定守恒?答:不一定。
当作用于一个系统的合外力矩为零时,合外力(即外力的矢量和)不一定为零,所以该系统的角动量守恒时,动量不一定守恒。
同理,当对一个系统作用的合外力为零时(即外力的矢量和),合外力矩不一定为零,所以该系统的动量守恒时,角动量也不一定守恒。
三、解题方法1.刚体绕定轴转动的特征:刚体内每个质点都在与转轴垂直的平面内作圆周运动,每个质点的角速度、角加速度均相同;但因每个质点距转轴的距离不同,即作圆周运动的半径不同,故各质点的线速度,线加速度不同。
2.类比方法:与质点动力学相似,刚体绕定轴转动存在一些与质点直线运动相对应的定理和定律(刚体绕定轴转动运动学公式与质点直线运动学公式、刚体绕定轴转动定律与牛顿第二定律),利用与质点动力学类比,便于对刚体绕定轴转动定理和定律的记忆和理解。
3.解动力学问题时,定理、定律的选择技巧:到目前为止,我们已学习了牛顿运动定律、动量定理、动量守恒定律、动能定理、功能原理、机械能守恒定律、角动量守恒定律等。
我们会迂到质点平动、刚体转动、综合等问题,在解这些动力学问题时,如何选择其中的某些定理、定律来解题呢?我们在解动力学问题过程中,通常是首先考虑能否用功能原理(或机械能守恒定律)求解;因功、能都是标量,而且都是状态量,可不考虑过程中发生的复杂细节。
其次,平动问题:考虑能否用动量定理或动量守恒定律求解;转动问题:考虑能否用角动量定理或角动量守恒定律求解。
因(角)动量是矢量,稍复杂一些。
再考虑能否用牛顿运动定律求解。
4.根据问题涉及物理量,确定解题路径:(1)如问题涉及到加速度,应首选动力学方法。
应用牛顿定律、转动定律以及运动学规律,可求得几乎所有的基本力学量。
(2)如问题不涉及加速度,但涉及时间,应选择(角)动量方法:考虑用动量定理和角动量定理处理问题。
(3)如问题不涉及加速度,又不涉及时间,应选择能量方法:考虑用动能定理或功能原理、机械能守恒定律处理问题。
(4)如问题不涉及加速度,又不涉及时间,且是碰撞等作用:应选择(角)动量守恒方法: 对平动问题:可首选考虑用动量守恒定律;对有转动问题:可首选考虑用角动量守恒定律处理问题。
注:1.动量守恒定律适用于平动问题;角动量守恒定律适用于转动问题。
2.分析问题要紧紧抓住运动过程和运动状态。
四、解题指导刚体转动惯量的计算(平行轴定理应用)1.如图所示,求大圆盘的实心部分对O 轴(垂直于盘面)的转动惯量。
(已知 r R 2= ,大盘质量为M ,小盘质量为m )[分析] 由于转动惯量有可加性,所以先分别求出大盘和小盘对O 轴的转动惯量,再把小盘的除去即得大盘实心部分对O 轴的转动惯量。
解:大盘对O 轴的转动惯量:2121MR J =;小盘对O 轴的转动惯量:2223mr J =。
所以实心部分对O 轴的转动惯量为:角动量守恒定律的应用2.匀质细棒,可绕其一端的水平光滑固定轴O 转动,原来静止悬挂在竖直位置,今有一质量为m 的小球以水平速度v 与其相碰撞,如图所示,则在碰撞过程中,小球和棒组成的系统对O 点的⎽⎽⎽⎽⎽⎽⎽守恒。
