合肥市2020届高三文科数学二模试卷含答案

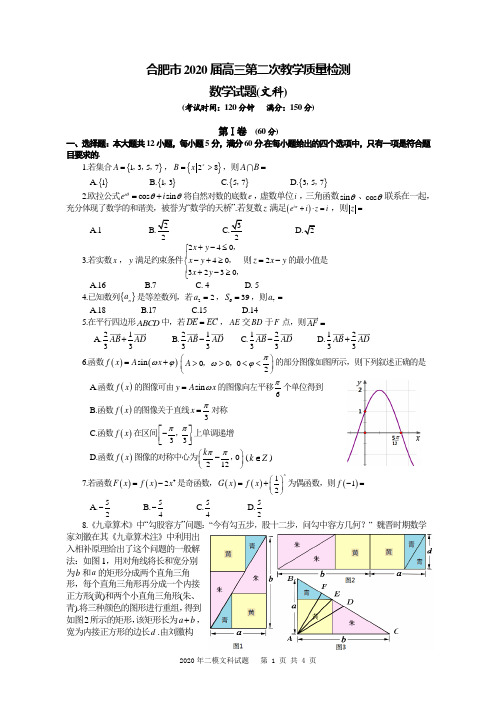
合肥市2020届高三第二次教学质量检测数学试题(文科)(考试时间：120分钟 满分：150分)第Ⅰ卷 (60分)一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若集合{}1 3 5 7A =，，，，{}28x B x =>，则A B = A.{}1 B.{}1 3，C.{}5 7，D.{}3 5 7，， 2.欧拉公式cos sin i e i θθθ=+将自然对数的底数e ，虚数单位i ，三角函数sin θ、cos θ联系在一起，充分体现了数学的和谐美，被誉为“数学的天桥”.若复数z 满足()i e i z i π+⋅=，则z =A.1B.2 C.32D.2 3.若实数x ，y 满足约束条件240 40 3230 x y x y x y +-≤⎧⎪-+≥⎨⎪+-≥⎩，，，则2z x y =-的最小值是 A.16 B.7 C.-4 D.-54.已知数列{}n a 是等差数列，若22a =，639S =，则7a = A.18 B.17 C.15 D.145.在平行四边形ABCD 中，若DE EC =，AE 交BD 于F 点，则AF =A.2133AB AD +B.2133AB AD -C.1233AB AD -D.1233AB AD +6.函数()()sin f x A x ωϕ=+00 02A πωϕ⎛⎫>><< ⎪⎝⎭，，的部分图像如图所示，则下列叙述正确的是A.函数()f x 的图像可由sin y A x ω=的图像向左平移6π个单位得到B.函数()f x 的图像关于直线3x π=对称C.函数()f x 在区间 33ππ⎡⎤-⎢⎥⎣⎦，上单调递增D.函数()f x 图像的对称中心为 0212k ππ⎛⎫- ⎪⎝⎭，(k Z ∈)7.若函数()()42F x f x x =-是奇函数，()()12xG x f x ⎛⎫=+ ⎪⎝⎭为偶函数，则()1f -=A.52-B.54-C.54D.528.《九章算术》中“勾股容方”问题：“今有勾五步，股十二步，问勾中容方几何？” 魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法：如图1，用对角线将长和宽分别为b 和a 的矩形分成两个直角三角形，每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组，得到如图2所示的矩形，该矩形长为a b +，宽为内接正方形的边长d .由刘徽构造的图形可以得到许多重要的结论，如图3.设D 为斜边BC 的中点，作直角三角形ABC 的内接正方形对角线AE ，过点A 作AF BC ⊥于点F ，则下列推理正确的是①由图1和图2面积相等可得abd a b=+；②由AE AF ≥可得22+22a b a b +≥； ③由AD AE ≥可得22+2112a b a b≥+； ④由AD AF ≥可得222a b ab +≥. A.①②③④ B.①②④ C.②③④ D.①③9.已知函数()22log 111x x f x x x >⎧=⎨-≤⎩，，，则()()1f x f x <+的解集为A.()1 -+∞，B.()1 1-，C.1 2⎛⎫-+∞ ⎪⎝⎭， D.1 12⎛⎫- ⎪⎝⎭，10.已知12F F ，为椭圆C ：221x y m+=的两个焦点，若C 上存在点M 满足120MF MF ⋅=，则实数m 取值范围是A.[)10 2 2⎛⎤+∞ ⎥⎝⎦，， B.[)1 122⎡⎫+∞⎪⎢⎣⎭，， C.(]10 1 22⎛⎤ ⎥⎝⎦，， D.(]1 11 22⎡⎫⎪⎢⎣⎭，， 11.为了实施“科技下乡，精准脱贫”战略，某县科技特派员带着A B C ，，三个农业扶贫项目进驻某村，对仅有的四个贫困户进行产业帮扶.经过前期走访得知，这四个贫困户甲、乙、丙、丁选择A B C ，，三扶贫项目 A B C 选择意向贫困户甲、乙、丙、丁甲、乙、丙丙、丁选择同一个扶贫项目的概率为A.38B.58C.516D.1212.某几何体是由一个半球挖去一个圆柱形成的，其三视图如图所示.已知半球的半径为6，则当此几何体的体积最小时，它的表面积为A.24πB.)1833π+C.21πD.()1842π+第Ⅱ卷 (90分)本卷包括必考题和选考题两部分.第13题—第21题为必考题，每个试题考生都必须作答.第22题、第23题为选考题，考生根据要求作答.二、填空题：本大题共4小题，每小题5分，满分20分. 第16题第一空2分，第二空3分. 把答案填在答题卡上的相应位置.13.曲线()2x f x ex e =-(e 是自然对数的底数)在1x =处的切线方程为 . 14.若数列{}n a 的首项为1-，12n n n a a +⋅=-，则数列{}n a 的前10项之和等于 . 15.已知双曲线22:12x C y -=的右焦点为点F ，点B 是虚轴的一个端点，点P 为双曲线C 左支上的一个动点，则BPF ∆周长的最小值等于 .16.在长方体1111ABCD A B C D -中，1123AB AD AA ===，，，点P 是线段1B C 上的一个动点，则：(1)1AP D P +的最小值等于 ；(2)直线AP 与平面11AA D D 所成角的正切值的取值范围为 .三、解答题：本大题共6小题，满分70分.解答应写出文字说明、证明过程或演算步骤．17.(本小题满分12分)已知ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，()tan 2cos sin cos 2sin A C A A C -=-. ⑴求角B 的大小；⑵若角B 为锐角，1b =，ABC ∆3，求ABC ∆的周长.18.(本小题满分12分)在矩形ABCD 中，E F ，在边CD 上，1BC CE EF FD ====，如图(1).沿BE AF ，将CBE ∆和DAF ∆折起，使平面CBE 和平面DAF 都与平面ABEF 垂直，连结CD ，如图(2).⑴证明：//CD AB ；⑵求三棱锥D BCE -的体积.19.(本小题满分12分)已知圆()()224425x y -+-=经过抛物线E :22y px =(0p >)的焦点F ，且与抛物线E 的准线l 相切.⑴求抛物线E 的标准方程；⑵设经过点F 的直线m 交抛物线E 于A B ，两点，点B 关于x 轴的对称点为点C ，若ACF ∆的面积为6，求直线m 的方程.20.(本小题满分12分)随着运动app 和手环的普及和应用，在朋友圈、运动圈中出现了每天1万步的健身打卡现象，“日行一万步，健康一辈子”的观念广泛流传.“健步达人”小王某天统计了他朋友圈中所有好友(共500人)的走路步数，并整理成下表：分组(单位：千步)[0，4) [4，8) [8，12) [12，16) [16，20) [20，24) [24，28) [28，32]频数60 240 100 60 20 18 0 2⑴请估算这一天小王朋友圈中好友走路步数的平均数(同一组中数据以这组数据所在区间中点值作代表)；⑵若用A 表示事件“走路步数低于平均步数”，试估计事件A 发生的概率；⑶若称每天走路不少于8千步的人为“健步达人”，小王朋友圈中岁数在40岁以上的中老年人共有300人，其中健步达人恰有150人，请填写下面2×2列联表.根据列联表判断，有多大把握认为，健步达人与年龄有关？健步达人 非健步达人 合计40岁以上 不超过40岁合计附：()()()()2n ad bc K a b c d a c b d -=++++.21.(本小题满分12分)已知函数()sin x f x e x =.(e 是自然对数的底数) ⑴求()f x 的单调递减区间；⑵若函数()()2g x f x x =-，证明()g x 在(0，π)上只有两个零点.(参考数据：2 4.8e π≈)请考生在第22、23题中任选一题作答.注意：只能做所选定的题目，如果多做，则按所做的第一个题目计分，作答时，请用2B 铅笔在答题卡上，将所选题号对应的方框涂黑.22.(本小题满分10分)选修4-4：坐标系与参数方程在直角坐标系xOy 中，曲线C 的参数方程为3cos 4sin 129cos sin 55x y ϕϕϕϕ=-⎧⎪⎨=+⎪⎩(ϕ为参数). 以坐标原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，直线l 的极坐标方程为sin 3πρθ⎛⎫+= ⎪⎝⎭.⑴曲线C 的普通方程和直线l 的直角坐标方程；⑵若直线l 与曲线C 交于P Q ，两点，M (2，0)，求MP MQ +的值.23.(本小题满分10分)选修4-5：不等式选讲 若不等式135x x m -+-<的解集为(32n ，). ⑴求n 的值；⑵若三个正实数a b c ，，满足a b c m ++=.证明：2222222b c c a a b a b c+++++≥.合肥市2020届高三第二次教学质量检测数学试题(文科)参考答案及评分标准一、选择题：本大题共12小题，每小题5分，共60分.二、填空题：本大题共4小题，每小题5分，共20分.13.y ex e =- 14.31 15.422+ 16.17，1133⎡⎤⎢⎥⎣⎦，(第一空2分，第二空3分)三、解答题：本大题共6小题，满分70分.17.(本小题满分12分)解：(1)∵()tan 2cos sin cos 2sin A C A A C -=-，∴222sin cos sin cos 2cos sin A C A A A C -=-. 化简得1sin cos cos sin 2A C A C +=，即()1sin 2A C +=，∴()1sin 2B π-=，即1sin 2B =. ∴6B π=或56B π=. ………………………………5分 (2)∵B 是锐角，∴6B π=，由13sin 2ABC S ac B ∆==得，3ac =.在ABC ∆中，由余弦定理得22222cos ()23b a c ac B a c ac ac =+-=+--∴()()22123313a c +=++=+，∴13a c +=+，∴ABC ∆的周长为23+ ………………………………12分18.(本小题满分12分)⑴证明：分别取AF BE ，的中点M N ，，连结DM CN MN ，，. 由图(1)可得，ADF ∆与BCE ∆都是等腰直角三角形且全等， ∴DM AF ⊥，CN BE ⊥，DM CN =.∵平面ADF ⊥平面ABEF ，交线为AF ，DM ⊂平面ADF ，DM AF ⊥， ∴DM ⊥平面ABEF .同理，CN ⊥平面ABEF ，∴//DM CN .又∵DM CN =，∴四边形CDMN 为平行四边形，∴//CD MN . ∵M N ，分别是AF BE ，的中点，∴//MN AB ，∴//CD AB . ………………………………5分 ⑵由图可知，D BCE B DCE V V =三棱锥－三棱锥－， ∵13EF AB ==，，∴2CD MN ==， ∴22B DCE B EFC C EFB V V V ==三棱锥－三棱锥－三棱锥－.由(1)知，CN ⊥平面BEF .∵2CN =，12BEF S ∆=，∴2C EFB V =三棱锥－，∴2D BCE V =三棱锥－. ………………………………12分题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CBDBDDCACAAD19.(本小题满分12分)解：⑴由已知可得：圆心(4，4)到焦点F 的距离与到准线l 的距离相等，即点(4，4)在抛物线E 上， ∴168p =，解得2p =.∴抛物线E 的标准方程为24y x =. ………………………………5分 ⑵由已知可得，直线m 斜率存在，否则点C 与点A 重合. 设直线m 的斜率为k (0k ≠)，则():1AB y k x =-.由()241y x y k x ⎧=⎪⎨=-⎪⎩消去y 得 ()2222220k x k x k -++=. 设A (11x y ，)，B (22x y ，)，∴12242x x k+=+，121x x =.………………………………7分由对称性可知，C (22 x y -，)，∴11AF x =+，21CF x =+.设直线m (AB )的倾斜角为α，则tan k α=， ∴()22222sin cos 2tan 2sin sin 2sin 22sin cos sin cos tan 11kAFC k αααπααααααα∠=-=====+++，∴()()()1212122111sin 2121AFCk S x x x x x x k α∆=++=+++⋅⎡⎤⎣⎦+4k =.……………………………10分 由已知可得46k =，解得23k =±. ∴直线m 的方程为()213y x =±-，即2320x y ±-=. ………………………………12分20.(本小题满分12分)解：⑴()12606240101001460182022183028.432500x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=，所以这一天小王500名好友走路的平均步数约为8432步.……………………………3分⑵()10.432602401000.62165004p A ⎛⎫=++⨯= ⎪⎝⎭， 所以事件A 的概率约为0.6216. ………………………………………………………5分 (3)……………………………………………………8分()()()()()()22250022500750031.2510.828200300300200n ad bc K a b c d a c b d --===>++++⨯⨯⨯，…………10分∴有99.9﹪以上的把握认为，健步达人与年龄有关. ………………………………12分21.(本小题满分12分)解：(1)()sin x f x e x =，定义域为R .()()sin cos sin 4x x f x e x x x π⎛⎫'=+=+ ⎪⎝⎭.由()0f x '<得sin 04x π⎛⎫+< ⎪⎝⎭，解得372244k x k ππππ+<<+(k Z ∈). ∴()f x 的单调递减区间为372 244k k ππππ⎡⎤++⎢⎥⎣⎦，(k Z ∈).………………………………5分 (2)∵()()sin cos 2x g x e x x '=+-，∴()2cos x g x e x ''=.∵()0x π∈，，∴当0 2x π⎛⎫∈ ⎪⎝⎭，时，()0g x ''>；当2x ππ⎛⎫∈ ⎪⎝⎭，时，()0g x ''<.∴()g x '在0 2π⎛⎫ ⎪⎝⎭，上单调递增，在2ππ⎛⎫⎪⎝⎭，上单调递减，又∵()0120g '=-<，2202g e ππ⎛⎫'=-> ⎪⎝⎭，()20g e ππ'=--<，∴()g x '在()0π，上图象大致如右图.∴10 2x π⎛⎫∃∈ ⎪⎝⎭，，22x ππ⎛⎫∈ ⎪⎝⎭，，使得()10g x '=，()20g x '=，且当()10x x ∈，或()2x x π∈，时，()0g x '<；当()12x x x ∈，时，()0g x '>.∴()g x 在()10x ，和()2x π，上单调递减，在()12x x ，上单调递增. ∵()00g =，∴()10g x <.∵202g e πππ⎛⎫=-> ⎪⎝⎭，∴()20g x >，又∵()20g ππ=-<，由零点存在性定理得，()g x 在()12x x ，和()2x π，内各有一个零点，∴函数()g x 在()0π，上有两个零点. ………………………………12分 22.(本小题满分10分)(1)曲线C 的参数方程3cos 4sin 129cos sin 55x y ϕϕϕϕ=-⎧⎪⎨=+⎪⎩消去参数ϕ得，曲线C 的普通方程为221259x y +=. ∵sin 33πρθ⎛⎫+= ⎪⎝⎭，∴3cos sin 230ρθρθ+-=，∴直线l 的直角坐标方程为3230x y +-=. ………………………………5分(2)设直线l 的参数方程为1223x t y t ⎧=-⎪⎪⎨⎪=⎪⎩(t 为参数)，将其代入曲线C 的直角坐标方程并化简得276630t t --=，∴1212697t t t t +==-，.∵点M (2，0)在直线l 上， ∴()21212123630243649MP MQ t t t t t t +=-=+-=+=. ………………………………10分23.(本小题满分10分)(1)由题意知，32为方程135x x m -+-=的根，∴391522m -+-=，解得1m =. 由1351x x -+-<解得，3724x <<，∴74n =. ………………………………5分 (2)由(1)知1a b c ++=，∴222222222b c c a a b bc ac ab a b c a b c +++++≥++. ()()()()22222222222222222221a b b c c a a b b c b c c a c a a b abc abc ⎡⎤=++=+++++⎣⎦，()()222122222abcab c bc a ca b a b c abc abc ≥++=++=， ∴2222222b c c a a b a b c+++++≥成立. ………………………………10分。