量子力学的矩阵形式及表象理论
量子力学的表象变换与矩阵形式

基矢变换的一个重要应用是求解量子力学中的本征值 问题。通过选择合适的基矢,可以将一个复杂的二次 型哈密顿量变为简单的形式,从而方便求解。
坐标表象与动量表象
01
坐标表象和动量表象是量子力学中最常用的两种表象。在 坐标表象中,波函数是坐标的函数,而在动量表象中,波 函数是动量的函数。
02 03
在坐标表象中,哈密顿量是一个关于坐标的二次型,而在 动量表象中,哈密顿量是一个关于动量的二次型。因此, 这两种表象适用于不同类型的问题。在求解一些与位置和 动量有关的物理问题时,选择合适的表象可以大大简化计 算过程。
表象变换
基矢变换
基矢变换的基本思想是通过线性组合的方式,将一组 旧的基矢变换为新的基矢。在量子力学中,这种变换 通常是通过一个可逆矩阵来实现的。
基矢变换是指在不同表象之间进行转换时,基矢的选 择会发生改变。在量子力学中,一个量子态由一个波 函数来描述,而波函数在不同的表象下会有不同的形 式。基矢变换就是用来描子计算
01
量子纠缠是量子力学中的一种现象,指两个或多个量子系统之 间存在一种特殊的关联,使得它们的状态无法单独描述。
02
量子纠缠在量子计算中具有重要作用,是量子并行性和量子算
法复杂性的基础。
利用量子纠缠,可以实现更高效的量子算法和量子通信协议。
03
量子通信与量子密码学
量子通信利用量子力学原理实现 信息的传输和保护,具有无条件
描述了密度矩阵的演化,其矩阵形式为密度矩阵与时间导数的乘积。
矩阵形式的测量与观测
量子测量
通过测量操作,将量子态投影到测量 算子的本征态上,其结果以概率的形 式给出。
观测结果
观测结果以概率分布的形式给出,反 映了量子态的测量结果与测量算子的 本征值的关联。
量子力学的矩阵形式和表象变换
§4.5 量子力学的矩阵形式和表象变换态和力学量算符的不同表示形式称为表象。
态有时称为态矢量。
力学量算符对态的作用实际上是对矢量量进行变换,因此可与代数中线性变换进行类比。
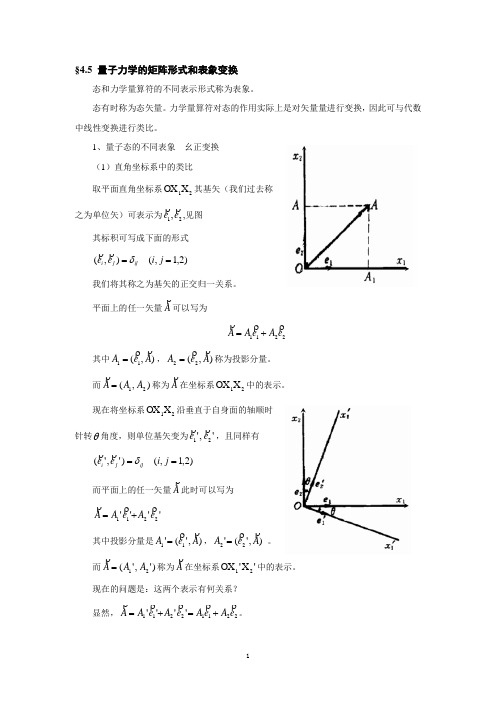
1、量子态的不同表象 幺正变换(1)直角坐标系中的类比取平面直角坐标系21X OX 其基矢(我们过去称之为单位矢)可表示为21,e e,见图其标积可写成下面的形式)2,1,(),(==j i e e ijj i δ我们将其称之为基矢的正交归一关系。
平面上的任一矢量A可以写为2211e A e A A +=其中),(11A e A =,),(22A e A=称为投影分量。
而),(21A A A = 称为A在坐标系21XOX 中的表示。
现在将坐标系21X OX 沿垂直于自身面的轴顺时针转θ角度,则单位基矢变为','21e e,且同样有)2,1,()','(==j i e e ijj i δ而平面上的任一矢量A此时可以写为 ''''2211e A e A A +=其中投影分量是),'('11A e A=,),'('22A e A =。
而)','(21A A A = 称为A在坐标系'X 'OX21中的表示。
现在的问题是:这两个表示有何关系?显然,22112211''''e A e A e A e A A+=+=。
用'1e 、'2e分别与上式中的后一等式点积(即作标积),有),'(),'('2121111e e A e e A A+= ),'(),'('2221212e e A e e A A+=表成矩阵的形式为⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛212212211121),'(),'(),'(),'(''A A e e e e e e e e A A由于'1e、1e及'2e、2e的夹角为θ,显然有⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛21212212211121cos sin sin cos ),'(),'(),'(),'(''A A A A e e e e e e e e A A θθθθ或记为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛2121)(''A A R A A θ 其中⎪⎪⎭⎫⎝⎛-=θθθθθcos sin sin cos )(R 是把A在两坐标中的表示⎪⎪⎭⎫⎝⎛''21A A 和⎪⎪⎭⎫⎝⎛21A A 联系起来的变换矩阵。
量子力学的矩阵形式与表象变换

练习,求证U是么正矩阵。
么正变换小结
基矢变换: (e 1 ,e 2 ) (e 1 ,e 2 )U ()
基矢变换:Ψ´=ΨS-1,<- Ψ a = Ψ ´ a´ = Ψ ´ Sa
Δ 有关矩阵知识 (参考周世勋书P250-255)
1.对角矩阵 Anm=amδnm. 2. 转置矩阵 (A ~)nmAmn
3.厄米共轭矩阵 (或称共轭矩阵) (A )nm (A ~ ) nm A m 运算规则:(AB) BA (A) A
A 1 A A2
A 3
A1 A A2
A3
以二维坐标系间变换为例。
设新坐标系 (e1,e2)相对原坐标系 (e1,e2) 顺时针 转过θ角。则
e1 c1e1c2e2,
e2 d1e1d2e2,
r (r )(r r )
动量表象
i
p x
px,
, i p
p
Fˆ(ip, p)
r (p )(12)3/2e ip r
p (r )(12)3/2e ip r
p (p )(p p )
(列矩阵的本征矢正交定义: XiXj 0 .)
C. 厄米矩阵的本征矢的正交归一完备。XiXj ij
(若简并情况下k个本征矢不正交,可以通过线性 组合,变为正交的k个本征矢).
Δ.本征矢的归一化: XiXi 1
1
Δ.未归一的归一化系数C:
C
X
i
X
i
Δ.任意列矩阵X可用厄米矩阵的本征矢展开
第7章 量子力学的矩阵形式与表象变换

这组数(a1,a2, … an, …)就是态ψ在Q表象中 的表示。可用列矩阵表示。设ψ是归一化的, 那么就有
* * d a a u m n mun d 2 mn
a an mn a an 1
* m * n mn n
9
由此可见,|an|2是ψ所描述的态中测量力学量Q所
ˆ 的共同本征态un(n代表 的任何一个力学量完全集 Q
一组完备的量子数,并先考虑分立谱情况)可以用
来构成此态空间的一组正交归一完备基矢,称为Q
表象。基矢满足正交归一性
(u m , u n ) mn
8
按态叠加原理,体系的任何一个态ψ可以用它们 展开
an u n
n
其中an (u n , )
为λ。可见,幺正变换不改变算符的本征值。
ˆ 自身的表象, 如果F' 是对角矩阵,即B表象是 F ˆ 本征值的问题归结为寻找一个幺正变换把算符 F
ˆ 的本征值。于是求算符 那么F' 的对角元素就是 F ˆ 自身的表象,使 F ˆ 的矩阵 从原来的表象变换到 F 表示对角化。解定态薛定谔方程求定态能级的问
ˆ 在A表象中的本征值方程为Fa=λa。λ为本 设F
征值,a为本征矢。通过幺正变换将F和a从A表 象变换到B表象,则有
F ' SFS ; b Sa
1
在B表象中有
F ' b (SFS1 )Sa
SFa Sa b
即 F'b b
19
ˆ 在B表象中的本征值仍 这个本征值方程说明算符 F
am ' u m ' an u n
第八章 量子力学的矩阵形式与表象变换 2 量子力学教学课件

xnn
当 m n 时,非对角元为:
xmn
2 a a 2 nx x sin dx a 0 a 2
2 a mx nx (sin ) x(sin )dx a 0 a a
x dx
1 a (m n) (m n) x cos x cos 0 a a a
j j , S j j j j k k
ˆ Lkj k , L j
L
ˆ , L
, k S k
ˆ S L S ( SLS ) S k S 得 L , L j k j k kj j kj kj
Qm为Q在自身空间中的的本征值
Qnm u ( x)Qum (x)dx u ( x)Qmu m (x)dx
n n
m u ( x)u m (x)dx Qm nm
n
结论:算符在自身的表象中是一个对角矩阵
15
例:一维谐振子的坐标x,动量p和Hamilton量H在能量表象中 的矩阵表示。 谐振子的能量本征函数记为ψn (n=0, 1, 2, ……)
第16页
第17页
例: 求一维无限深势阱中粒子的坐标算符 ˆ 在能量表象中的矩阵表示。 H 解:
ˆ 及哈密顿算符 x
一 维无限深势阱能量的本征函数基矢为:
n
2 n x sin a a
2 2 2
n 能级 En 2 2 a
n=1,2,3,…..
18
坐标算符x
当m=n时,对角元为:
即变换矩阵S是么正矩阵, 所以变换也称为么正变换。
10
§ 2.力学量(算符)的矩阵表示
第4章 量子力学的矩阵形式与表象变换

第4章 量子力学的矩阵形式与表象变换§1 量子态的不同表象态的表象 量子力学中态和力学量的具体表示方式研究表象的意义 根据不同问题选择不同表象,还可以进行表象变换。
一、坐标表象波函数ψ(x ,t ) 1、ψ(x ,t )2、dx t x 2),(ψ——表示体系处在ψ(x ,t )所描述的态中,在x →x +d x 范围内找到粒子的几率,也就是说,当体系处在ψ(x ,t )所描述的态中,测量坐标x 这个力学量所得值在x →x +d x 这个范围内的几率。
3、2(,)1x t dx ψ=⎰4、动量为x p '的自由粒子的本征函数 xp ip e x ''=2/1)2(1)(πψ5、x 在坐标表象中对应于本征值x '的本征函数)(x x '-δ, 即,)()(x x x x x x '-'='-δδ 二、动量表象波函数 动量本征函数:pxip e x2/1)2(1)(πψ=组成完备系,任一状态ψ可按其展开(,)(,)()p x t c p t x dp ψψ=⎰ (1) 展开系数*(,)()(,)pc p t x x t dx ψψ=⎰ (2) ψ(x ,t )与c (p ,t )互为Fourier (付里叶)变换,一一对应关系,所不同的是变量不同。
认为c (p ,t )和ψ(x ,t )描述同一个状态。
ψ(x ,t )是这个状态在坐标表象中的波函数,c (p ,t )是同一个状态在动量表象中的波函数。
1、),(t p c ——状态波函数2、dp t p c 2),(表示体系处在c (p ,t )所描述的态中测量动量这个力学量p 所得结果为p →p +d p 范围内的几率。
3、1),(2=⎰dp t p c命题:假设ψ(x ,t )是归一化波函数,则c (p ,t )也是归一。
(在第一章中已经证明) 4、x p '的本征函数(具有确定动量x p '的自由粒子的态)若ψ(x ,t )描写的态是具有确定动量 p'的自由粒子态,即:1/21()(2)ip xp x eψπ''=则相应动量表象中的波函数:*(,)()(,)pc p t x x t dx ψψ=⎰()p i E te p p δ'-'=-所以,在动量表象中,具有确定动量p' 的粒子的波函数是以动量p 为变量的δ函数。
量子力学讲义IV.表象理论(矩阵表述)

量⼦⼒学讲义IV.表象理论(矩阵表述)IV. 表象理论 ( 矩阵表述 )1.如何⽤矩阵表⽰量⼦态与⼒学量,并说明理由?答:矩阵表⽰⼀般⽤于本征值为离散谱的表象(相应的希尔伯空间维数是可数的)。
具体说,如果⼒学量的本征⽮为,相应本征值分别为。
假定⼀个任意态⽮为,将它展开For personal use only in study and research; not for commercial use则态⽮在表象中波函数便可⽤展开系数的⼀列矩阵表⽰其意义是:在态中,取的概率为,这与表象中波函数意义是类似的。
⼒学量⽤厄⽶⽅阵表⽰,。
显然,⼀列矩阵和⽅阵维数与希尔伯空间维数是相等的。
⽤矩阵表⽰⼒学量,有如下理由:第⼀可以反映⼒学量作⽤于⼀个量⼦态得到另⼀个量⼦态的事实。
设,式中,。
取,两端左乘,取标积得,即第⼆矩阵乘法⼀般不满⾜交换率,这恰好能满⾜两个⼒学量⼀般不对易的要求。
第三厄⽶矩阵的性质能体现⼒学量算符的厄⽶性。
对于本征值为连续谱的表象(希尔伯空间维数不可数),也可形式的运⽤矩阵表⽰,这时可将矩阵元素看成式连续分布的。
2.量⼦⼒学中,不同表象间:基⽮、波函数、⼒学量是如何变换的?答:量⼦⼒学中由⼀个表象到另⼀个表象的变换为⼳正变换,它类似于欧⽒空间中坐标转动。
设表象中的基⽮为表象中的基⽮为(1) 基⽮变换关系为式中,(为⼳正矩阵)。
设有任意态,则态在及表象中波函数分别为矩阵。
(2) 波函数变换规则为:矩阵。
(3) ⼒学量变换规则为:。
(式中与为⼒学量在、表象中矩阵)3.正变换有什么特征?答:⼳正变换特点:(1⼳正变换不改变态⽮的模,这⼀特征相当于坐标旋转变换;(2⼳正变换不改变⼒学量本征值;(3)⼒学量矩阵之迹 TrF与矩阵⾏列式 dgtF亦不因⼳正变换⽽改变.4. 学量在其⾃⾝表象中如何表⽰?其本征⽮是什么 ?答:如果⼒学量本征值为离散谱,那么,它在其⾃⾝表象中表⽰式为对⾓矩阵,为诸本征值。
本征⽮为单元素⼀列矩阵如果⼒学量本征值为连续谱,则它在其⾃⾝表象中为纯变量其本征⽮为函数。
量子力学的矩阵形式及表示理论.

第六章量子力学的矩阵形式及表示理论第六章目录§6.1 量子体系状态的表示 (3)§6.2 Dirac符号介绍 (4)(1)量子态、Ket矢,Bra矢(Bracket) . 5(2)标积 5(3)算符及其表示 (7)(4)不可约张量算符的矩阵元计算简介 (12)(5)投影算符 15§6.3 表象变换,幺正变换 (17)(1)同一状态在不同表象中的表示间的关系 (17)(2)两表象的基矢之间关系 (18)(3)力学量在不同表象中的矩阵表示之间的关系 (18)(4)幺正变换 19§6.4平均值,本征方程和薛定谔方程的矩阵形式 (20)(1)平均值20(2)本征方程 21(3)薛定谔方程 (25)§6.5 量子态的不同描述 (26)(1)薛定谔绘景 (27)(2)海森堡绘景 (28)第六章 量子力学的矩阵形式及表示理论§6.1 量子体系状态的表示现在来讨论体系状态的“坐标”—状态表示如果有一组力学量Mˆ构成一力学量完全集,其共同本征函数构成一正交,归一和完备组,并有封闭性。
()mn n m ,δ=ϕϕ)r r ()r ()r (*m mm '-δ='ϕϕ∑于是,任一波函数⎰''ψ'-δ=ψr d )r ()r r ()r (⎰∑''ψ'ϕϕ=r d )r ()r ()r (m*m m∑ϕ=mm m a )r (。
⎰ψϕ=''ψ'ϕ=),(r d )r ()r (a m *m m2m a 是在)r (ψ中测得力学量M ˆ取值为m 的几率(若)r (ψ是归一化的)。
显然,当选定一组力学量完全集Mˆ 后,则集合 {}m a 是与 )r (ψ 完全等价的,它完全确定了体系的状态。
我们将会看到,{}m a 与)r (ψ一样,提供给我们同样多的信息。
状态表示的定义:若力学量的完全集M ˆ的共同本征函数组为m ϕ,则),(a m mψϕ=的全体{}m a ,被称为体系所处态ψ在Mˆ表象中的表示,也可以看作态矢量ψ在m ϕ作为基矢所张的“坐标系”中的“坐标”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ห้องสมุดไป่ตู้
V(x))un (x)
Enun (x)
令 则
un (x) Rn (x) iIn (x) ( (Rn (x), In (x) 都是实函数)
(
2 2m
d2 dx 2
V(x))Rn (x)
EnRn (x)
(
2 2m
d2 dx 2
V(x))In (x)
EnIn (x)
这表明 R n 和 I n 都是能量为 E 的解。但对束缚态,没有简并,所以只有一个解,因而 R n 和 I n
1
(1) 湮灭算符 aˆ 的本征态 ...... 错误!未定义书签。 (2) 相干态的性质 .............. 错误!未定义书签。
第三章 一维定态问题
现将所学得的原理和方程应用于最简单的问题:一维、不显含时间的位势,即一维定态问
题。
当
V(r,t) V(r)
则薛定谔方程 i (r,t) Hˆ (r,pˆ )(r,t) 有特解 t E(r,t) uE(r)eiEt /
§3.1 一般性质
设粒子具有质量 m,沿 x 轴运动,位势为 V(x) 。于是有
(
2 2m
d2 dx 2
V(x))uE (x)
Eu E (x) 。
由于 uE (x) 是满足一定条件或边条件下的解,所以不是所有 E 都有非零解。
(1)定理 1:一维运动的分立能级(束缚态),一般是不简并的
简并度(degeneracy):一个力学量的测量值,可在 n 个独立的(线性无关的)波函
而 uE (r) 满足 Hˆ (r,pˆ )uE(r) Eu E(r)
事实上,当 V(r) 有一定性质时,如 V(r) V(x) V(y) V(Z) 或 V(r) V(r) 时,三维
问题可化为一维问题处理,所以一维问题是解决三维问题的基础。
在解一维问题之前,先介绍一些解的性质。
需要指出,现讨论的 V(x) 是实函数,从而保持不含时间的 S.eq 中 E 为实数。
从而有
u2u1(x) u1u2(x) 0
若 u2(x)u1(x) 不是处处为零,则有
u2 u2
u1 u1
(ln u2 )
(ln u1 )
从而有
u1(x) Au 2(x) 。
二者仅差一常数因子,所以是同一波函数。也就是说,一个 E 只对应一个独立的波函数,
因此,是不简并的。
应当注意 ⅰ. 分立能级是不简并的。而对于连续谱时,若一端 u 0 ,那也不简并。但如
第三章
一维定态问题
第三章 目 录
§3.1 一般性质....................................... 2 (1)定理 1:一维运动的分立能级(束缚态),一般是不简 并的...................................... 2 (2)不同的分立能级的波函数是正交的。 .......... 4 (3)振荡定理 .................................. 4 (4)在无穷大位势处的边条件 .................... 5
§3.2 阶梯位势....................................... 6 §3.3 位垒穿透....................................... 8
(1) E<V0 ..................................... 9 (2) E V0 ................................... 10 (3)结果讨论 ................................. 11 §3.4 方位阱穿透.................................... 11 §3.5 一维无限深方位阱 .............................. 12 (1)能量本征值和本征函数 ..................... 12 (2)结果讨论 ................................. 13 §3.6 宇称,一维有限深方势阱,双 δ 位势.............. 14 (1)宇称 ..................................... 14 (2)有限对称方位阱 ........................... 15 (3) 求粒子在双 位阱中运动 ................... 18 §3.7 束缚能级与反射振幅极点的关系 ....错误!未定义书签。 (1) 半壁δ位阱的散射 .......... 错误!未定义书签。 (2)有限深方位阱 ............... 错误!未定义书签。 §3.8 一维谐振子的代数解法 ........... 错误!未定义书签。 (1)能量本征值 ................. 错误!未定义书签。 (2) 能量本征函数 .............. 错误!未定义书签。 (3)讨论和结论 ................. 错误!未定义书签。 §3.9 相干态 ......................... 错误!未定义书签。
(2)
u2 (1) u1 (2)
2
从而得
u2
d2 dx 2
u1(x)
u1
d2 dx 2
u 2 (x)
0
于是
u2u1(x) u1u2 (x) c (c 是与 x 无关的常数)。
对于束缚态 x ,ui 0
(或在有限区域有某值使 u2u1(x) u1u2 (x) 0 )
所以 c 0 ,
两端都不趋于 0(如自由粒子),则有简并。
ⅱ.当变量在允许值范围内(包括端点),波函数无零点,就可能有简并存在。
(因常数 c≠0)。
ⅲ.当 V(x) 有奇异点,简并可能存在。因这时可能导致 u2 (x)u1 (x) 处处为零。
推论:一维束缚态的波函数必为实函数(当然可保留一相因子)。
证
(
2 2m
d2 dx 2
数中测得,则称这一测量值是具有 n 重简并度。
(某能量本征值有 n 个独立的定态相对应,则称这能量本征值是 n 重简并的)。
证:假设 u1, u 2 是具有同样能量的波函数
(
2 2m
d2 dx 2
V(x))u1 (x)
Eu 1 (x)
(1)
(
2 2m
d2 dx 2
V(x))u 2 (x)
Eu
2 (x)
