凸轮解析法设计和M文件资料
凸轮解析法设计和M文件

ds 2 s s0 d d 2s ds ds s s0 d e 2 d e d 2 s s0
2 1.5
2.当凸轮理论廓线外凸时,凸轮实际轮廓曲率半 径 rT ,此时可能出现3种情况: ⑴当 rT 时,实际轮廓为一条平滑曲线; ⑵当 rT 时,实际轮廓上产生尖点; ⑶当 rT 时,实际轮廓已相交,产生运动失真。
理论轮廓最小曲率半径 CE可用作图方法确定: 如图5-27所示。 轮廓曲率半径计算公式
5.4.2 凸轮基圆半径的确定
设计凸轮机构时,基圆半径选的越小,所 设计的机构越紧凑。但基圆半径的减小, 会使压力角增大。压力角的正切
DP OP OD tan BD BD ds / d e ds / d e 2 2 s s0 s rb e
5.4.3 滚子半径的确定
等加速-等减速运动
2h s 2 2 ds 4h 2 d d 2 s 4 h 2 2 d
2h 2 s h 2 ds 4h d 2 d 2s 4h 2 d d 2s d 2 h 1 cos 2 h sin 2 2h cos 2 2
凸轮机构中,经常采用滚子从动件。选择滚子半 径时要考虑的因素较多。从滚子本身的结构设计 和强度方面考虑,滚子半径大些较好,这样有利 于提高滚子的接触强度,便于滚子的结构设计与 安装。但是滚子半径的增大也要受到一定的限制, 因为滚子半径的大小 将给凸轮实际轮廓带来较大 的影响。滚子半径与凸轮理论廓线的最小曲率半 径,及对应的凸轮实际廓线上的曲率半径,有如 图5-24所示的关系: 1.当凸轮理论廓线内凹时,如图5-26(a)所示凸 轮实际轮廓曲率半径,此时不论滚子半径大小如 何,均可作出内凹的凸轮实际轮廓。
凸轮轮廓设计—解析法

s
B’ h A o δ t t δs’ δ
一、从动件的常用运动规律 名词术语: 基圆半径、 推程、 基圆、 推程运动角、 远休止角、 回程、回程运动角、 近休止角、 行程。一个循环
D δs’
δh
r0
δt
δs δh
作者:潘存云教授
ω
B
δs
C
1.等速运动规律 在推程起始点:δ =0, s=0
3)偏置直动尖顶从动件盘形凸轮 已知凸轮的基圆半径r0,角速度ω 和从动件的运动规律和偏心距e, 设计该凸轮轮廓曲线。
7’ 5’ 3’ 1’ 1 3 5 78
e -ω
ω
k12 k11 k10 k9
8’
9’ 11’ 12’ 13’ 14’ 9 11 13 15
15’ 15 14’ 14 13’ 12’
y e rr s0 r0 ω e r0 y
O
-ω δ
x=x(δ ) y= y(δ )
B0
x
n θ x
偏置直动滚子推杆盘形凸轮机构
δδ
作者:潘存云教授
n
s
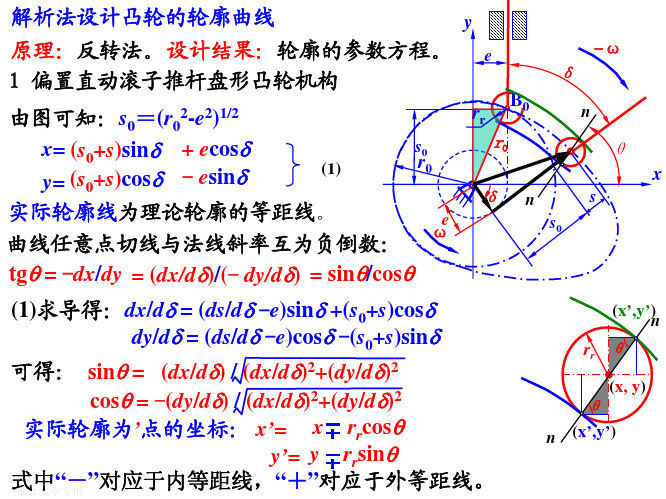
已知:r0、rr、e、ω、S=S(δ) 由图可知: s0=(r02-e2)1/2
x= (s0+s)sinδ y= (s0+s)cosδ
s0
+ ecosδ - esinδ
φ4
A4
φ6
A5
φ5
2.2.2
解析法设计凸轮的轮廓
图解法的缺点? 解析法的优点?
极坐标法求轮廓曲线的解析表达式--- 参数方程 偏置直动滚子推杆盘形凸轮机构 (反转原理+极坐标) 已知条件:e、rmin、rT、S2=S2(δ1)、ω1及其方向。 理论轮廓的极坐标参数方程:
齿轮凸轮组合机构解析法设计

齿轮凸轮组合机构解析法设计摘要:齿轮凸轮组合机构是一种常见的机械传动装置,广泛应用于各种机械设备中。
本文将采用解析法进行齿轮凸轮组合机构的设计,通过对齿轮凸轮组合机构的结构和原理进行分析,结合运动学方程和几何关系,以及相应的计算方法,可以得到齿轮凸轮组合机构的设计参数。
最后,通过实例验证了解析法的有效性和可行性。
1.引言齿轮凸轮组合机构是一种将齿轮和凸轮两种机构组合在一起的传动装置。
在齿轮机构中,利用互相啮合的齿轮来传递力矩和运动。
而在凸轮机构中,通过凸轮的凸起部分与从动件接触或离开来实现运动传递。
齿轮凸轮组合机构的设计涉及到几何形状、尺寸、齿轮齿数等多个参数,因此需要采用解析法进行设计。
2.齿轮凸轮组合机构的结构和原理齿轮凸轮组合机构由齿轮轴、凸轮轴和从动件组成。
齿轮轴上固定有一个或多个齿轮,凸轮轴上固定有一个凸轮。
从动件由凸轮的凸起部分与齿轮的齿啮合或分离来实现传动。
齿轮的齿数和凸轮的凸起部分的形状决定了齿轮和凸轮之间的运动规律。
3.齿轮凸轮组合机构的解析法设计步骤(1)确定齿轮和凸轮的齿数和凸起部分的形状。
齿轮和凸轮的齿数可以根据所需的传动比进行确定。
凸轮的凸起部分的形状可以通过给定的运动规律进行确定,比如简谐运动规律、等角速度运动规律等。
(2)建立齿轮凸轮组合机构的运动学方程。
运动学方程是描述齿轮凸轮组合机构各部件运动规律的方程。
通过建立从动件运动轨迹与凸轮轴的相对位置之间的关系,可以建立运动学方程。
(3)根据几何关系推导出相关参数。
通过几何关系,可以得到齿轮凸轮组合机构的相关参数,如齿轮的模数、分度圆直径、凸轮的基圆半径、凸起部分的形状参数等。
(4)根据计算方法计算设计参数。
根据所得到的齿轮凸轮组合机构的相关参数,可以利用计算方法进行具体的计算,如齿轮啮合位置的计算、齿轮啮合角的计算、齿轮模数的计算等。
(5)验证设计结果的可行性。
通过实例验证所得到的设计结果的可行性和有效性。
可以利用CAD软件进行设计和模拟仿真,通过调整设计参数,得到最佳的设计方案。
凸轮机构的分析和设计

3.滚子推杆滚子半径的选择 采用滚子推杆时,滚子半径的选择,要考虑滚子的结构、强 度及凸轮轮廓曲线的形状等多方面的因素。 (1)凸轮轮廓曲线与滚子半径的关系 1)当凸轮廓线内凹时,则ρa=ρ+rr。 此时,无论滚子半径大小如何,凸轮的工作廓线总是可以平 滑地作出来。 2)当凸轮廓线外凸时, 则ρa=ρ-rr。 若ρ=rr时, 则ρa=0,工作廓线出现变尖现象。 若ρ <rr时, 则ρa<0, 工作廓线出现交叉, 推杆运动规 律出现失真现象。
凸轮机构的分析和设计
一、 凸轮机构的应用和分类
1.凸轮机构的应用 (1)实例 内燃机配气凸轮机构 自动机床进刀机构 自动机床凸轮机构 (2)特点
适当的设计凸轮廓线可实现各种运动规律,结构简单,紧凑; 但易磨损,传力不大。
2.凸轮机构的分类 (1)按凸轮的形状分
1)盘形凸轮(移动凸轮)
2)圆柱凸轮 (2)按推杆形状及运动形式分 1)尖顶推杆、滚子推杆和平底推杆 2)对心直动推杆、偏置直动推杆和摆动推杆 (3)按保持高副接触方法分 1)力封闭的凸轮机构 2)几何封闭的凸轮机构
最大速度vmax (hω /δ0)×
1.00
最大加速度amax 2 2 (hω /δ0 )×
∞ 4.00
最大跃度jmax 2 2 (hω /δ0 )×
适用场合
低速轻载
∞ ∞ 39.5 60.0
2.00
1.57 2.00 1.88
中速轻载 中低速重载
中高速轻载 高速中载
余弦加速度 正弦加速度
5次多项式
(2)凸轮廓线设计方法的基本原理 在设计凸轮廓线时,可假设凸轮静止不动,时其推杆相对凸 轮作反转运动,同时又在其导轨内作往复运动,作出推杆在这种 复合运动中的一系列位置,则其尖顶的轨迹就是所要求的凸轮廓 线。这就是凸轮廓线设计的反转法原理。 2.用作图法设计凸轮廓线 (1)直动推杆盘形推杆凸轮廓线的设计 1)偏置直动尖顶推杆盘形凸轮廓线的设计 2)偏置直动滚子推杆盘形凸轮廓线的设计 3) 对心直动平底推杆盘形凸轮廓线的设计 结论 尖顶推杆盘形凸轮廓线的设计是滚子推杆和平底 推杆盘形凸轮设计的基本问题及方法。
用解析法设计凸轮廓线

廓线交叉被切
· · · · · · · · · · · · · · · · · · · · · = rr a = - rr =0
· · · ·· · · · · · · · · · · · · · < rr · · · · · a = - rr <0
结束
§ 9 - 4 凸轮机构基本尺寸的确定
1、压力角与基圆半径r0和偏置的关系
P 点为凸轮与推杆的相对瞬心
op
v
ds / dt ds d / dt d
OP e tan s0 s
d s / dt e r02 e 2 s
C
(1)压力角 与偏置的关系 (a)推杆偏于接触点处凸轮速度反向(速度瞬 心侧)— 正偏置 (b)推杆偏于接触点处凸轮速度同向—负偏置 (c)正偏置→ ↓;负偏置→ ↑ (d)正偏置时,e↑→ 推程 ↓,但回程 ↑
凸轮轮廓曲线的设计
三、用解析法设计凸轮廓线
1、偏置直动滚子推杆盘形凸轮机构
s0 r02 e 2
y
建立 B 点封闭矢量方程
s0
r e s0 s
向x 、y轴投影,得凸轮理论廓线:
r
x
x e cos ( s0 s) sin y e sin ( s0 s) cos
基本尺寸:基圆半径,滚子半径,平底长度,中心距……
四、推杆平底尺寸的确定
L 2lmax (5 ~ 7)
ds op l d
mm
lmax
max
lmax ds / d
另外,对于平底推杆凸轮,凸轮轮廓不 允许出现内凹和变化太快情况。
→ 可增大基圆或修改运动规律。
凸轮轮廓设计—解析法21页文档

15、机会是不守纪律的。——雨果
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
EHale Waihona Puke D凸轮轮廓设计—解析法11、战争满足了,或曾经满足过人的 好斗的 本能, 但它同 时还满 足了人 对掠夺 ,破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果, 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
第10章 凸轮传动解析法
θ
n (x’,y’)
2 对心直动平底推杆盘形凸轮 建立坐标系如图:反转δ后,推杆移动距离为s, P点为相对瞬心, OP = ds/dδ x= (r0+s)sinδ +(ds/dδ)cosδ y= (r0+s)cosδ -(ds来自dδ)sinδy -ω
δ
B0 s0
ω
r0 O
B P s0
x
δ
ds/dδ s
B
y A0 φ0 φ
φ0
δ -ω
A
δ ω
O
a
x
浙江大学专用
解析法设计凸轮的轮廓曲线 原理:反转法。设计结果:轮廓的参数方程。 1 偏置直动滚子推杆盘形凸轮机构 由图可知:s0=(r0 s0 x= (s0+s)sinδ + ecosδ r0 (1) y= (s0+s)cosδ - esinδ 实际轮廓线为理论轮廓的等距线。 e ω 曲线任意点切线与法线斜率互为负倒数: tgθ = -dx/dy = (dx/dδ)/(- dy/dδ) = sinθ/cosθ (1)求导得:dx/dδ = (ds/dδ -e)sinδ +(s0+s)cosδ dy/dδ = (ds/dδ -e)cosδ -(s0+s)sinδ
浙江大学专用
3 摆动滚子推杆盘形凸轮机构 理论廓线方程: x= asinδ - lsin(δ +ϕ +ϕ0) y= acosδ - lcos(δ +ϕ +ϕ0) 式中:a-中心距, l-摆杆长度 实际轮廓方程的求法同前。 对应点B’ 的坐标为: x’=x rrcosθ y’=y rrsinθ
B0 r0 l
2-e2)1/2
y
机械原理大作业凸轮设计

机械原理大作业凸轮设计1. 引言凸轮是一种通过凸起部分的形状变化驱动其他机械部件的旋转元件。
在机械系统中,凸轮被广泛应用于各种传动装置和运动控制系统。
本文档将讨论凸轮的设计原理和方法,并以一个具体的案例进行说明。
2. 凸轮设计原理2.1 凸轮的基本概念凸轮由凸起部分和基座两部分组成。
其中,凸起部分通常称为凸轮型面,它的形状决定了凸轮所能产生的运动规律。
基座是凸轮的固定部分,通常与主轴连接,使凸轮能够旋转。
2.2 凸轮设计的基本要求凸轮设计的目标是实现所需的运动规律。
在设计一个凸轮时,需要考虑以下几个方面:•运动规律:根据具体需求确定凸轮的运动规律,如线性运动、往复运动、旋转运动等。
•周期性:确定凸轮的运动周期,即凸轮的一次完整运动所需的时间。
•加减速:确定凸轮的运动加速和减速过程,以实现平滑的运动过渡。
•载荷和寿命:考虑凸轮所承受的载荷和使用寿命要求,选择适当的材料和结构。
2.3 凸轮设计的方法凸轮设计可以采用基于经验的方法或基于计算机辅助设计(CAD)的方法。
基于经验的方法通常适用于简单的凸轮系统,而复杂的凸轮系统通常需要借助CAD 软件进行设计和分析。
凸轮设计的关键步骤包括:•确定凸轮的运动规律和周期。
•根据凸轮的运动规律计算凸轮型面的形状。
•通过CAD软件创建凸轮的三维模型。
•进行凸轮的运动仿真和动态分析。
•对凸轮进行优化设计,以满足运动要求和结构要求。
3. 案例分析:凸轮驱动往复运动机构3.1 问题描述设计一个凸轮驱动的往复运动机构,要求满足以下条件:•机构的往复运动幅度为20mm。
•机构的往复运动频率为10Hz。
•机构的驱动电机转速为1000rpm。
•机构的凸轮型面应满足正弦形状。
3.2 设计步骤1.确定凸轮的运动规律和周期。
根据往复运动要求,选择正弦运动作为凸轮的运动规律,运动周期为0.1s。
2.计算凸轮型面的形状。
根据凸轮的运动规律和运动周期,计算凸轮型面的形状参数。
3.创建凸轮的三维模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ds / d e ds / d e
s s0
s rb2 e2
5.4.3 滚子半径的确定
凸轮机构中,经常采用滚子从动件。选择滚子半 径时要考虑的因素较多。从滚子本身的结构设计 和强度方面考虑,滚子半径大些较好,这样有利 于提高滚子的接触强度,便于滚子的结构设计与 安装。但是滚子半径的增大也要受到一定的限制, 因为滚子半径的大小 将给凸轮实际轮廓带来较大 的影响。滚子半径与凸轮理论廓线的最小曲率半 径,及对应的凸轮实际廓线上的曲率半径,有如 图5-24所示的关系:
解析法设计凸轮廓线主要适用于各种先进的 自动化加工方法,并要求加工精确的凸轮廓 线的场合,例如高速凸轮、靠模凸轮等。
偏置滚子移动从动件盘形凸轮轮廓 理论轮廓直角坐标方程式
x DN CD
(s0 s) sin e cos
y BN MN
(s0 s) cos e sin
s0 rb2 e2
h
1
2
sin
2
ds h 1 cos 2
d
d 2s
d 2
2h
2
s
in
2
5.3.3 凸轮机构的计算机辅助设计
用解析法设计凸轮轮廓的主要步骤有: ⑴输入已知的凸轮机构的结构参数(如凸轮基圆半
径、滚子半径、偏置移动从动件的偏距、从动件升 程、凸轮推程角、远休止角和回程运动角等),以 及运动和动力性能的许用值(如凸轮轮廓许用曲率 半径、推程许用压力角和回程许用压力角); ⑵校核凸轮机构在推程和回程最大压力角,以及理 论轮廓上最小曲率半径,使其不超过规定许用值; ⑶计算凸轮的理论轮廓坐标值和实际轮廓坐标值; ⑷计算从动件运动参数(位移、速度和加速度), 绘制从动件运动参数线图; ⑸计算凸轮轮廓坐标,绘制凸轮轮廓图形。
实际轮廓坐标方程式
x x rT
dy / d (dx / d)2 (dy / d)2
y y rT
dx / d (dx / d)2 (dy / d)2
理论轮廓坐标对凸轮转角的一阶导数
dx
d
ds
d
esin
s0
scos
dy
d
ds
d
e cos
s0
s sin
等速运动
s h
ds h
12.2 盘形凸轮机构设计和运动分析
用解析法设计凸轮廓线,就是根据给定的从 动件运动规律和某些机构尺寸参数,建立凸 轮轮廓的方程,并精确地计算出凸轮轮廓上 各点的坐标值。凸轮廓线方程的建立,仍然 按反转法的原理,将从动件自初始位置沿方 向连同机架转过任意角,然后建立从动件同 凸轮接触点的坐标方程(对于滚子从动件, 包括理论轮廓方程和实际轮廓方程)。
理论轮廓最小曲率半径 CE可用作图方法确定: 如图5-27所示。
轮廓曲率半径计算公式
s
s0
2
ds
d
2
1.5
s
s0
d 2s
d 2
s
s0
ds
d
e 2
ds
d
e
1.当凸轮理论廓线内凹时,如图5-26(a)所示凸 轮实际轮廓曲率半径,此时不论滚子半径大小如 何,均可作出内凹的凸轮实际轮廓。
2.当凸轮理论廓线外凸时,凸轮实际轮廓曲率半
径 rT ,此时可能出现3种情况:
⑴当 rT 时,实际轮廓为一条平滑曲线;
⑵当 rT 时,实际轮廓上产生尖点; ⑶当 rT 时,实际轮廓已相交,产生运动失真。
动件运动规律参考表5-1确定; ⑸以上公式运用中涉及到从动件位移方程及其一
阶和二阶导函数,需要根据给定的从动件运动规 律考表5-3确定。
5.4.2 凸轮基圆半径的确定
设计凸轮机构时,基圆半径选的越小,所 设计的机构越紧凑。但基圆半径的减小, 会使压力角增大。压力角的正切
tan DP OP OD
d
d2s 0
d 2
余弦加速度运动
s h 1 cos
2
ds
d
h
2
sin
d 2s
d 2
2h
2 2
cos
等加速-等减速运动
s 2h 2
2
ds
d
4h
2
d 2 s 4h d 2 2
s h 2h 2
2
ds 4h
d
2
d 2s 4h
d 2
2
正弦加速度运动
s
计算
机辅 助设 计凸 轮机 构的 程序 框图
能力训练案例5-2 :已知某偏置直动从动件盘形 凸轮机构的结构参数、运动规律和许用参数。 采用计算机辅助设计方法,计算凸轮机构的运 动参数和设计凸轮轮廓。
解:有关公式运用的说明 ⑴计算凸轮理论轮廓和实际轮廓的直角坐标分别
使用式(5-1)和式(5-2); ⑵计算凸轮机构的压力角使用式(5-6); ⑶计算凸轮理论轮廓的曲率半径使用式(5-7); ⑷计算凸轮机构的运动参数,需要根据给定的从
