中南大学大学物理练习册答案
大学物理练习册(下)答案解析
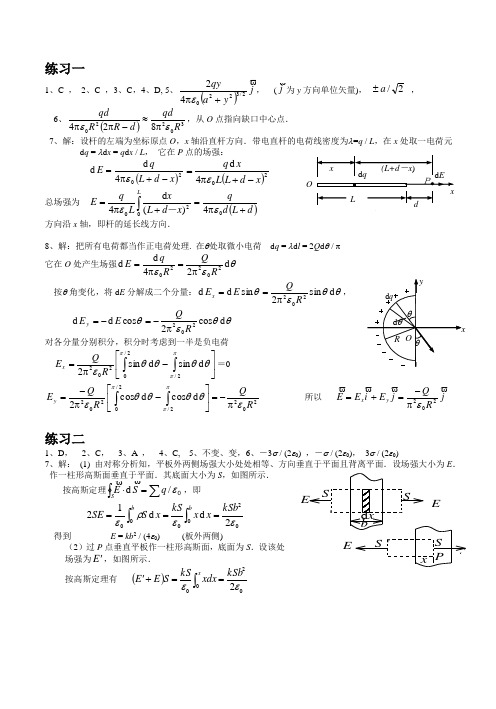
练习一1、C ,2、C ,3、C ,4、D,5、()j y a qy2/322042+πε, (j 为y 方向单位矢量), 2/a ± ,6、()30220824R qdd R R qd εεπ≈-ππ,从O 点指向缺口中心点. 7、解:设杆的左端为坐标原点O ,x 轴沿直杆方向.带电直杆的电荷线密度为λ=q / L ,在x 处取一电荷元d q = λd x = q d x / L , 它在P 点的场强: ()204d d x d L q E -+π=ε()204d x d L L x q -+π=ε总场强为 ⎰+π=Lx d L xL q E 020)(d 4-ε()d L d q +π=04ε 方向沿x 轴,即杆的延长线方向.8、解:把所有电荷都当作正电荷处理. 在θ处取微小电荷 d q = λd l = 2Q d θ / π它在O 处产生场强θεεd 24d d 20220RQR q E π=π=按θ 角变化,将d E 分解成二个分量:θθεθd sin 2sin d d 202R Q E E x π==,θθεθd cos 2cos d d 202R Q E E y π-=-=对各分量分别积分,积分时考虑到一半是负电荷⎥⎦⎤⎢⎣⎡-π=⎰⎰πππθθθθε2/2/0202d sin d sin 2R QE x =02022/2/0202d cos d cos 2R Q R Q E y εθθθθεππππ-=⎥⎦⎤⎢⎣⎡-π-=⎰⎰ 所以 j R Q j E i E E y x202επ-=+=练习二1、D ,2、C ,3、A ,4、C,5、不变、变,6、-3σ / (2ε0) ,-σ / (2ε0), 3σ / (2ε0)7、解: (1) 由对称分析知,平板外两侧场强大小处处相等、方向垂直于平面且背离平面.设场强大小为E . 作一柱形高斯面垂直于平面.其底面大小为S ,如图所示. 按高斯定理∑⎰=⋅0ε/d q S E S,即22d d 12εερεkSbx x kSx S SE bb===⎰⎰得到 E = kb 2 / (4ε0) (板外两侧) (2)过P 点垂直平板作一柱形高斯面,底面为S .设该处场强为E ',如图所示. 按高斯定理有 ()022εεkSbxdx kSS E E x==+'⎰xS P SEESSEd x b E 'd qR O xyθd θθPLdd q x (L+d -x )d ExO得到 ⎪⎪⎭⎫ ⎝⎛-='22220b x k E ε (0≤x ≤b ) (3) E '=0,必须是0222=-b x , 可得2/b x = 6、解:挖去电荷体密度为ρ 的小球,以形成球腔时的求电场问题,可在不挖时求出电场1E,而另在挖去处放上电荷体密度为-ρ的同样大小的球体,求出电场2E,并令任意点的场强为此二者的叠加,即可得 210E E E +=在图(a)中,以O 点为球心,d 为半径作球面为高斯面S ,则可求出O '与P 处场强的大小.ρε302113414d d d E S E S π⋅=π⋅=⋅⎰ 有 E 1O’=E 1P =d E 013ερ= 方向分别如图所示. 在图(b)中,以O '点为小球体的球心,可知在O '点E 2=0. 又以O ' 为心,2d 为半径作球面为高斯面S '可求得P 点场强E 2P()032223/)(4)(24d ερ-π=π⋅='⋅⎰'r d E S E S203212dr E P ερ-= (1) 求O '点的场强'O E. 由图(a)、(b)可得 E O ’ = E 1O’ =03ερd, 方向如图(c)所示.(2) 设空腔任一点P 相对O '的位矢为r ',相对O 点位矢为r则3ερr E PO =, 03ερr E O P '-=' , ∴ 0003'3)(3ερερερdOO r r E E E O P PO P=='-=+=' ∴腔内场强是均匀的.练习三1、D ,2、B ,3、C,4、C,5、q / (6πε0R )6、负,增加7、解:由高斯定理可得场强分布为:E =-σ / ε0 (-a <x <a ) E = 0 (-∞<x <-a ,a <x <+∞=E 1P ρ PE 2P E P 图(d) O O ' P E 1O’ ρ 图(a) O ρO ' d E O’=E 1 图(c)O P E 2P -ρ O 'r E 2O’=0图(b)E 1P由此可求电势分布:在-∞<x ≤-a 区间⎰⎰⎰---+==000/d d 0d aa xxx x x E U εσ0/εσa -=在-a ≤x ≤a 区间 00d d εσεσxx x E U x x =-==⎰⎰ 在a ≤x <∞区间 0000d d 0d εσεσax x x E U a a x x =-+==⎰⎰⎰8、解:设x 轴沿细线方向,原点在球心处,在x 处取线元d x ,其上电荷为x q d d λ=', 该线元在带电球面的电场中所受电场力为: d F = q λd x / (4πε0 x 2) 整个细线所受电场力为: ()l r r lq x x q F l r r +π=π=⎰+00024d 400ελελ 方向沿x 正方向.电荷元在球面电荷电场中具有电势能: d W = (q λd x ) / (4πε0 x ) 整个线电荷在电场中具有电势能: ⎪⎪⎭⎫ ⎝⎛+π=π=⎰+0000ln 4d 400r l r q x x q W l r r ελελ练习四1、D ,2、D ,3、B ,4、C ,5、U C C C C C q U C C C C C 21212221211)(,)(+-=+-,6、r εεσσ0,, 7、解:金属球的电势r d r d 221⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdrr Q εεε)11(π4210R R Q r r -+=εεε8、解:令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ∵ AB AC U U =,即-a +a O x UO R x r 0 r 0+ld xx∴ AB AB AC AC E E d d = ∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A=得 ,32S q A =σ Sq A 321=σ 而 7110232-⨯-=-=-=A C q S q σC C 10172-⨯-=-=S q B σ (2)301103.2d d ⨯===AC AC AC A E U εσV练习五1、πR 2c2、 5.00×10-5 T , 3、20d 4a lI πμ , 平行z 轴负向 ; 4、)11(4120R R I -μ,垂直纸面向外 ,2/122210)11(4R R I+μ ,12arctg R R +π21,5、)3231(40ππμ-+R I , 6、C, 7、解:因为金属片无限长,所以圆柱轴线上任一点P 的磁感应强度方向都在圆柱截面上,取坐标如图所示,取宽为l d 的一无限长直电流l R II d d π=,在轴上P 点产生B d 与R 垂直,大小为RI R R R I R I B 20002d 2d 2d d πθμ=πθπμ=πμ= RI B B x 202d cos cos d d πθθμ=θ=RI B B y 202d sin )2cos(d d πθθμ-=θ+π=∴ 520202221037.6)]2sin(2[sin 22d cos -ππ-⨯=πμ=π--ππμ=πθθμ=⎰RI R I R I B x T 0)2d sin (2220=πθθμ-=⎰ππ-RI B y∴ i B51037.6-⨯= T8、解:(1) 对r ~r +d r 段,电荷 d q = λ d r ,旋转形成圆电流.则 r dq I d 22d π=π=λωω 它在O 点的磁感强度rrr IB d 42d d 000π==λωμμ⎰⎰+π==b a a r r B B d 4d 000λωμa ba +π=ln 40λωμ 方向垂直纸面向内. r r I r p m d 21d d 22λω=π=⎰⎰+==ba am m r r p p d 21d 2λω 6/])[(33a b a -+=λω 方向垂直纸面向内.练习六1、B2、)2(120I I -μ3、320μI , 4、Rihπμ20,5、)2/(210R rI πμ ,0 6、解:取同轴闭合圆环r l π2= )(b r a <<则 ⎰π=⋅lr B l B 2d2222)(a b Ia r I ππππ--=∑∴ )(2)(22220a b r a r I B --=πμ 7、解:在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小, 由安培环路定律可得:)(220R r r R IB ≤π=μ因而,穿过导体内画斜线部分平面的磁通Φ1为⎰⎰⋅==S B S B d d 1 Φr r RIRd 2020⎰π=μπ=40I μ在圆形导体外,与导体中心轴线相距r 处的磁感强度大小为 )(20R r rIB >π=μ因而,穿过导体外画斜线部分平面的磁通Φ2为⎰⋅=S B d 2Φr r I R Rd 220⎰π=μ2ln 20π=Iμ穿过整个矩形平面的磁通量 21ΦΦΦ+=π=40I μ2ln 20π+IμOarbd r ω1、A ,2、B ,3、)/(cos 2eB m θv π, )/(sin eB m θv ,4、alB 2,5、铁磁质,顺磁质,抗磁质,6、 0.226 T ,300 A/m7、解: (1) 0=⨯=B l I F bcB l I F ab⨯= 方向⊥纸面向外,大小为866.0120sin ==︒IlB F ab NB l I F ca⨯=方向⊥纸面向里,大小866.0120sin ==︒IlB F ca N(2)IS P m =B P M m⨯= 沿O O '方向,大小为221033.443-⨯===B l I ISB M m N ⋅(3)磁力功 )(12ΦΦ-=I A∵ 01=Φ B l 2243=Φ ∴ 221033.443-⨯==B l IA J 8、解:在直线电流2I 上任意取一个小电流元dl I 2,此电流元到长直线 的距离为x ,无限长直线电流1I 在小电流元处产生的磁感应强度 xI B πμ210=21021060cos 22dxx I I dl x I I dF ⋅==πμπμ ab I I dxx I I F ba ln 60cos 22100210πμπμ=⋅=⎰1、D ,2、C ,3、A ,4、0.40 V , 0.5 m 2/s ,5、 5×10-4 Wb ,6、解:2IB xμπ=ln 22d adIl Id a ldx x dμμππ++Φ=⋅=⎰0l n c o s 2N I l d d a Nt dt dμωεωπΦ+=-=- 7、解: ⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m Φ∴ klvt tm-=-=d d Φε 即沿abcd 方向顺时针方向.练习九1、28/104.0s m ⨯顺时针 2、 πBnR 2 ,O 3、dtdBR221π, 4、等于零,不等于零;不等于零,等于零 5、RBfr 22π6、解: 作辅助线MN ,则在MeNM 回路中,沿v方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε= 又∵ ⎰+-<+-==ba ba MN ba ba Iv l vB 0ln 2d cos 0πμπε 所以MeN ε沿NeM 方向,大小为ba ba Iv -+ln 20πμ M 点电势高于N 点电势,即ba ba Iv U U N M -+=-ln 20πμ 7、解: ∵ bc ab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε=-=t abd d 2ΦεtB R B R t d d 12π]12π[d d 22=--∴ tBR R acd d ]12π43[22+=ε ∵0d d >tB∴ 0>ac ε即ε从c a →练习十1、C ,2、C ,3、0,4、 垂直纸面向里 , 垂直OP 连线向下 ,5、(4)(2)(1) 5、解:圆柱形电容器电容 12ln 2R R lC πε=12ln 2R R lUCU q πε== 1212ln ln 22R R r U R R r lU S q D εππε===∴ 12ln R R r ktDj ε=∂∂=6、如图10-17图所示,取r l S d d = 则 ⎰⎰-----=--=-+=ad aad aad da a d Il r r r Ilr l r Ir πI)ln (ln 2πd )d 11(π2d ))d (π22(0000μμμμΦ aad Il-=lnπ0μ ∴ aad lIL -==lnπ0μΦ练习十一1、A2、 B3、B ,4、D ,5、2π (n -1) e / λ , 4×103 ;6、解: (1)由λk d D x =明知,λ22.01010.63⨯⨯=, ∴ 3106.0-⨯=λmm oA 6000=(2) 3106.02.010133=⨯⨯⨯==∆-λd D x mm7、解:(1) ∆x =20 D λ / a =0.11 m(2) 覆盖云玻璃后,零级明纹应满足 (n -1)e +r 1=r 2设不盖玻璃片时,此点为第k 级明纹,则应有 r 2-r 1=k λ所以 (n -1)e = k λk =(n -1) e / λ=6.96≈7 零级明纹移到原第7级明纹处练习十二1、A ,2、 C ,3、C ,4、 1.40 ,5、0.6mm 。
中南大学大学物理实验报告答案大全+实验数据+思考题答案

(1) 按讲义中的电路原理图连接好实物电路图; (2) 测光电管的伏安特性曲线: ① 先使正向电压加至30伏以上,同时使光电流达最大(不超量程), ② 将电压从0开始按要求依次加大做好记录; (3) 测照度与光电流的关系: ① 先使光电管距光源20cm处,适当选择光源亮度使光电流达最大(不超量程); ② 逐渐远离光源按要求做好记录; 实验步骤 (4) 测光电管的截止电压: ① 将双向开关换向; ② 使光电管距光源20cm处,将电压调至“0”, 适当选择光源亮度使光电流达最大(不超量程),记录此时的光 电流I ,然后加反向电压使光电流刚好为“0”,记下电压值U ; ③ 使光电管远离光源(光源亮度不变)重复上述步骤作好记录。 数据处理
k
(a + b) sin ψ
k
如果人射光不是单色,则由上式可以看出,光的波长不同,其衍射角也各不相同,于是复色光将被分解,而在中央 k =0、 ψ =0 处,各色光仍重叠在一起,形成中央明条纹。在中央明条纹两侧对称地分布着 k=1,2,3,…级光谱 ,各级光谱 线都按波长大小的顺序依次 排列成一组彩色谱线,这样就把复色光分解为单色光。如果已知光栅常数,用分光计测出 k 级光谱中某一明条纹的衍射角ψ,即可算出该明条纹所对应的单色光的波长λ。 实验步骤 (1) 调整分光计的工作状态,使其满足测量 条件。 (2) 利用光栅衍射 测量汞灯在可见光范 围内几条谱线的波长。 ① 由于衍射光谱在中央明条纹两侧对 称地分布,为了提高测量的准确度,测量第k级光谱时 ,应测出 +k级和-k 级光谱线的位置,两位置的差值之 半即为实验时 k取1 。 ② 为了减少分光计刻度盘的偏心误差,测量每条光谱线时 ,刻度盘上的两个游标都要读数 ,然后取其平均值 (角 游标的读数方法与游 标卡尺的读数方法基本一致)。 ③ 为了使十字丝对准光谱线,可以使用望远镜微调螺钉12来对准。 ④ 测量时,可将望远 镜置最右端,从 -l 级到 +1 级依次测量,以免漏测数据。 数据处理 谱线 游标 左1级 (k=-1) 右1级 (k=+1) φ λ/nm λ /nm
中南大学大学物理实验预习答案

实验一迈克耳孙干涉仪的调整与使用【预习思考题】1.迈克尔孙干涉仪是利用什么方法产生两束相干光的?答:迈克尔孙干涉仪是利用分振幅法产生两束相干光的。
2.迈克尔孙干涉仪的等倾和等厚干涉分别在什么条件下产生的?条纹形状如何?随M1、M2’的间距d如何变化?答:(1)等倾干涉条纹的产生通常需要面光源,且M1、M2’应严格平行;等厚干涉条纹的形成则需要M1、M2’不再平行,而是有微小夹角,且二者之间所加的空气膜较薄。
(2)等倾干涉为圆条纹,等厚干涉为直条纹。
(3)d越大,条纹越细越密;d 越小,条纹就越粗越疏。
3.什么样条件下,白光也会产生等厚干涉条纹?当白光等厚干涉条纹的中心被调到视场中央时,M1、M2’两镜子的位置成什么关系?答:白光由于是复色光,相干长度较小,所以只有M1、M2’距离非常接近时,才会有彩色的干涉条纹,且出现在两镜交线附近。
当白光等厚干涉条纹的中心被调到视场中央时,说明M1、M2’已相交。
【分析讨论题】1.用迈克尔孙干涉仪观察到的等倾干涉条纹与牛顿环的干涉条纹有何不同?答:二者虽然都是圆条纹,但牛顿环属于等厚干涉的结果,并且等倾干涉条纹中心级次高,而牛顿环则是边缘的干涉级次高,所以当增大(或减小)空气层厚度时,等倾干涉条纹会向外涌出(或向中心缩进),而牛顿环则会向中心缩进(或向外涌出)。
2.想想如何在迈克尔孙干涉仪上利用白光的等厚干涉条纹测定透明物体的折射率?答:首先将仪器调整到M1、M2’相交,即视场中央能看到白光的零级干涉条纹,然后根据刚才镜子的移动方向选择将透明物体放在哪条光路中(主要是为了避免空程差),继续向原方向移动M1镜,直到再次看到白光的零级条纹出现在刚才所在的位置时,记下M1移动的距离所对应的圆环变化数N,根据,即可求出n。
实验二用动态法测定金属棒的杨氏模量【预习思考题】1.试样固有频率和共振频率有何不同,有何关系?固有频率只由系统本身的性质决定。
和共振频率是两个不同的概念,它们之间的关系为:式中Q为试样的机械品质因数。
中南大学版固体物理学习题及答案详解

第一章晶体结构1.试述晶态、非晶态、准晶、多晶和单晶的特征性质。
解:晶态固体材料中的原子有规律的周期性排列,或称为长程有序。
非晶态固体材料中的原子不是长程有序地排列,但在几个原子的范围内保持着有序性,或称为短程有序。
准晶态是介于晶态和非晶态之间的固体材料,其特点是原子有序排列,但不具有平移周期性。
另外,晶体又分为单晶体和多晶体:整块晶体内原子排列的规律完全一致的晶体称为单晶体;而多晶体则是由许多取向不同的单晶体颗粒无规则堆积而成的。
2.晶格点阵与实际晶体有何区别和联系?解:晶体点阵是一种数学抽象,其中的格点代表基元中某个原子的位置或基元质心的位置,也可以是基元中任意一个等价的点。
当晶格点阵中的格点被具体的基元代替后才形成实际的晶体结构。
晶格点阵与实际晶体结构的关系可总结为:晶格点阵+基元=实际晶体结构3.晶体结构可分为Bravais格子和复式格子吗?解:晶体结构可以分为Bravais格子和复式格子,当基元只含一个原子时,每个原子的周围情况完全相同,格点就代表该原子,这种晶体结构就称为简单格子或Bravais格子;当基元包含2个或2个以上的原子时,各基元中相应的原子组成与格点相同的网格,这些格子相互错开一定距离套构在一起,这类晶体结构叫做复式格子。
4.图1.34所示的点阵是布喇菲点阵(格子)吗?为什么?如果是,指明它属于那类布喇菲格子?如果不是,请说明这种复式格子的布喇菲格子属哪类?(a)(b)(c)(d)图 1.34(a)“面心+体心”立方;(b)“边心”立方;(c)“边心+体心”立方;(d)面心四方解:(a)“面心+体心”立方不是布喇菲格子。
从“面心+体心”立方体的任一顶角上的格点看,与它最邻近的有12个格点;从面心任一点看来,与它最邻近的也是12个格点;但是从体心那点来看,与它最邻近的有6个格点,所以顶角、面心的格点与体心的格点所处的几何环境不同,即不满足所有格点完全等价的条件,因此不是布喇菲格子,而是复式格子,此复式格子属于简立方布喇菲格子。
(完整版)中南大学物化课后习题答案9章可逆原电池

s e第9章 可逆原电池1.写出下列原电池中各电极反应、电池反应及E 的计算公式。
①② Pt,H 2(101325Pa)|KOH(a )|O 2(101325Pa),Pt③④解:(1) 负极 Pb(s)+(a) → PbSO 4(s)+2e正极 Cu 2+() + 2e →Cu(s)电池反应 Pb(s)+SO 4(a) + Cu 2+ (a Cu 2+) ==== PbSO 4(s)+Cu(s)(2) 负极 H 2( p Θ ) -2e → 2H + (a H +)正极 O 2( p Θ ) + H 2O +2e → 2OH -(a OH -)电池反应 H 2(p Θ)+ O 2(p Θ) → H 2O(l)(3) 负极 3H 2(p H2) - 6e → 6H +(aq)正极 Sb O (s) + 6e + 6H +(aq) → 2Sb(s) +3H O(l)电池反应 Sb2O3O(l)+3H2 (p H2) → 2Sb(s) + 3H2(4) 负极 Ag(s) + I -(a I -) → AgI(s) + e正极 AgCl(s) + e → Ag(s) + Cl - (a Cl-)-)电池反应 Agl(s) + I-(a I -) → Ag(s) + Cl - (a Cl2.试将下列化学反应设计成原电池(1)Zn(s) + H2SO4(a1) === ZnSO4(a2) + H2(p H2);(2)Ni(s) + H2O ==== NiO(s) + H2(p H2)(3)H2(p H2) + O2(p O2) ==== H2O(l);(4)H2(p H2) + HgO(s) ==== Hg(l) + H2O(l)解:(1)负极 Zn(s) -2e → Zn2+(a2)正极 2H+(a1) + 2e → H2(P H2)电池反应 Zn(s) +2H+(a1) ==== Zn2+(a2)+ H2(p H2)电池符号 Zn(s) | ZnSO4(a2) || H2SO4(a1) | H2(p H2),Pt(2) 负极 Ni(s) + 2OH -→NiO(s) + H2O +2e正极 2H2O + 2e →H2(p H2) +2OH -电极反应 Ni(s) + H2O==== NiO(s) + H2(p H2)电池符号 Ni(s),NiO(s) | KOH(稀) | H2(p H2), Pt(3)负极 H2(p H2) + 2OH -→ 2H2O + 2e正极 2H2O +2e → 2OH - + O2(p O2)电池反应 H2(p H2) + O2(p O2) ==== H2O(l)电池符号 Pt,H2(p H2) | NaOH(稀) | O2(p O2),Pt(4) 负极 H2(p H2) + 2OH -→2H2O +2e正极 HgO(s) + H2O +2e → Hg(l) +2OH -电池反应 H2(p H2) + HgO(s) ==== Hg(l) + H2O(l)电池符号 Pt ,H2(p H2) | KOH(稀) | HgO(s),Hg(l)3.工业上用铁屑加入硫酸铜溶液中以置换铜,试设计原电池;计算该反应在298.15K时的平衡常数,并说明此置换反应进行的完全程度。
大学物理I练习册参考答案

大学物理I练习册参考答案第一篇:大学物理I练习册参考答案大学物理I练习册参考答案力学部分:010004:(1)010011:(2)010014:(2)010016:(3)010044: B010057: D010095: B010098: C011002: 3t011009:011030:011039: 5m/s;17m/s011061: 4.8m/s;3.15rad22011012:ϖϖϖdv=ωRcosωtj-ωRsinωti;o011067: dt020003:(1)020012: C020015: B, D021002: 2g,0021016:(μcosθ-sinθ)g030023: B030028: D030038: D030061: D030069:(3)031005:031054: k/(mr);-k/(2r)2v0031062: 12J032046: h==4.25m;v=[2gh(1-μctgα)]1/2=8.16m/s 2g(1+μctgα)040001: A040011: B040020: C040030: B040032: C040054: A040064: D040070: C040076: C040090: C222040097: D040099: D041019: R1v1/R2;mvR/R112-1/2041043: Ma/2 ()041078: M/9042031: 156N;118N042005:电磁学部分1.B2.A3.C4.C5.2ε0A6.–2Ax,-2Byqd7.rλλ,ln02πε0r2πε0rUR1lnR2R1(2)Ek=4.8⨯10J , v=1.03⨯10m/s -778.(1)F=9.EP=0;UPC=⎰CPEdr=⎰rCRrλλdr=lnC 2πε0r2πε0R10.B11.B12.B13.C14.A15.D16.D17.q4πε0r2, 水平向左18.A19.εrC0,σ0,U0E0W0,εrεrεr20.看书P6721.看书P6722.C23.A24.D25.C27.μ0Iμ0IμI+=1.08⨯10-3T,垂直纸面向外28,0,垂直纸面向里2πR4R4πa29.μ0I, -2μ0I, ±2μ0I, ±2μ0I30, 2BIR,π/42;水平向右IaB,Ia2B34.πmga+b2μ0Ilna-b31,35.I1的磁场B=μ0I1,方向垂直向里,因此由安培定律(1)AD受I1的磁力FAD=I2aB 2πr=μ0I1I2a,方向向左。
中南大学物化课后习题标准答案-9--章-可逆原电池

第9章可逆原电池1 •写出下列原电池中各电极反应、电池反应及E旳计算公式.②Pt,H 2(101325Pa) | KOH@) I Q(101325Pa),Pt④I :I :l ・」:-:解:⑴负极Pb(s)+「(a-;J —PbSQ4(s)+2e............................................... .正极Cu2+(-丄'')+ 2e —Cu(s)2+电池反应Pb(s)+SQ4(aEM) + Cu (a C2+) ==== PbSO4(s)+Cu(s)⑵负极比(p® ) -2e —2H+ (a H+)正极Q( p® ) + H 2O +2e —2OH -(a OH -).. ........ — ..... —.... ......... .... ... 电池反应H2(p®) + O(l)O2( P®) —H2(3)负极3H2( P H2)- 6e —6H+(aq)正极Sb2Q(s) + 6e + 6H +(aq) —2Sb(s) +3H 20(1)............................................... 电池反应Sb2O3 +3H2 ( P H2)—2Sb(s) + 3H 20(1)⑷负极Ag(s) + I -(a i-) —AgI(s) + e_______________________________________________ 正极AgCI(s) + e —Ag(s) + Cl ( a ci-)电池反应Agl(s) + I -(a i-) —Ag(s) + Cl - ( a。
-)2. iJ:将下勿化学反应陵计成目电池(1) Zn(s) + H 2SQ(a": ===ZnSO4( ◎) + H2( P H2)(2) Ni(s) + H 2Q ==== NiQ(s) + H 2( P H2)(3) H2 (P H2) + Q( P Q2)= :===H 2OQ);(4)H2(P H2)+ HgQ(s)== ==Hg(l) + H 20(1)( 1)负极Zn (s) -2e2+ —Zn正极2H+( a i) + 2e —H2(P H2)----------------------------------------------- 电池反应Zn(s) +2H +(a i) ====Zn2+(a2)+ H 2( P H2)电池符号Zn(s) | ZnSO 4( a?) || H 2SO( a) | H 2( p H》,Pt(2) 负极Ni(s) + 20H -—NiO(s) + H 2O +2e正极2H2O + 2e —H2(P H2)+20H -.............................................. .电极反应Ni(s) + H 20 ==== NiO(s) + H 2伽)电池符号Ni(s),NiO(s) | KOH( 稀)| H 2(P H2), Pt(3) 负极H2(P H2) + 2OH -—2H2O + 2e正极2H2O +2e —2OH- + Q(p°2).............................................. 电池反应H 2( P H2)+ Q( P O2) ==== H2OQ)电池符号Pt,H 2伽)| NaOH(稀)| O 2(p°2>,Pt(4) 负极H2(P H2) + 2OH -—2HO +2e正极HgO(s) + H 2O +2e —Hg(l) +2OH ----------------------------------------------- 电池反应H2(P H2)+ HgO(s) ==== Hg(l) + H 2。
大学物理练习册(上册)答案

练习一 (第一章 质点运动学) 一、选择题 1、(D )2、(C )3、(D )4、(B )5、(D ) 二、填空题1、(1)A (2)1.186s(或4133-s) (3)0.67s (或32s ) 2、8m 10m3、(1)t e t t A βωβωωωβ-+-]sin 2cos )[(22 (2)ωπωπk +2( ,2,1,0=k ) 4、3/30Ct v + 400121Ct t v x ++ 5、(1)5m/s (2) 17m/s 三、计算题1、解:dxdvv dt dx dx dv x dt dv a ==+==262分离变数积分⎰⎰+=xvdx x vdv 020)62(得 )1(422x x v +=质点在任意位置处的速度为 )1(22x x v +=(由初始时刻的加速度大于零,可知速度的大小为非负)。
2、解:(1)第二秒内的位移为 m x x x 5.0)1()2(-=-=∆ 第二秒内的平均速度为s m txv /5.0-=∆∆= (2)t 时刻的速度为 269t t dtdxv -==第二秒末的瞬时速度为 s m s m s m v /6/26/292-=⨯-⨯=(3)令0692=-==t t dtdxv ,解得s t 5.1= 第二秒内的路程为 m x x x x s 25.2)5.1()2()1()5.1(=-+-=。
3、解:(1)由几何关系θθsin cos r y r x ==质点作匀速率圆周运动故dtd θω=,代入初始条件0=t 时0=θ,得 t 时刻t ωθ=,所以j y i x r+=)sin (cos j t i t rωω+=(2)速度为)cos sin (j t i t r dtrd v ωωω+-==加速度为)sin (cos 2j t i t r dt vd a ωωω+-==(3)r j t i t r dtv d a 22)sin (cos ωωωω-=+-==由此知加速度的方向与径矢的方向相反,即加速度的方向指向圆心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
=
2πrlE
=
Σ
i
qi
s
ε0
∑ (1)当 r < R1 时, qi = 0 ,∴E = 0 ;
i
∑ (2)当 r > R2 时, qi = 0 ,∴E = 0 ;
i
∑ (3)当 R1 < r < R2 时,
i
qi
=
λl
,∴ E
=
λ 2πε 0r
1
∫ ∫ 6.(1)过场点作同心球面,由高斯定理:
E ⋅ dS =
dq
σ rdr
du =
=
4πε 0 (x2 + r 2 )1/ 2 2ε 0 (x2 + r 2 )1/ 2
∴距盘心 x 处的电势为
∫ ∫ σ R
u = du =
rdr
σ =
(
x2 + R2 − x)
2ε 0 0 (x 2 + r 2 )1/ 2 2ε 0
(2)
E
=
−
du dxຫໍສະໝຸດ =σ 2ε 0⎛ ⎜⎜⎝1 −
∫ Ep =
0.2 λdl 0.05 4πε 0l 2
= λ ⎜⎛ 1 − 1 ⎟⎞ = 6.75×102V ⋅ m−1 ,方向向右 4πε 0 ⎝ 0.05 0.2 ⎠
6.在距长直导线为 x 处任取 dx ,其所带电量 dq = λdx ,又长直导线在 dx 处的场强为
E = λ , dq 受电场力 df = dqE = λ2 dx ,方向向右。由于 ab 上任意 dq 受力方向
感应强度 dB = µ0dI = µ0 Idx ,方向垂直纸面向里,因各细长条在 p 点的 dB 方向相同, 2πx 2πax
∫ 所以 Bp =
d+a µ0 I dx = µ0 I ln d + a ,方向垂直纸面向里。 d 2πa x 2πa d
�� � � � 6. B0 = Bab + Bbc + Bcd + Bda
L ⎟⎞ ⎠
,则 q0 从
P
→
Q
,
电场力的功
A
=
q0 (u p
− uQ )
=
q0q 4πε 0 L
ln
3(r 3r
+ +
L) L
电势能变化为 ∆W = − q0q ln 3(r + L) 4πε 0 L 3r + L
6 .( 1 ) 任 取 半 径 r 、 宽 dr 的 圆 环 , 其 所 带 电 量 dq = σ 2πrdr , dq 在 x 处 的 电 势 为
=
+0=
S 4πε 0 R 4πε 0r
8πε 0 R
(2)接地时,金属球电势为零
q
σ ′ds
q
q′
∫ U 0 = 4πε 0r +
=
+
=0
S 4πε 0 R 8πε 0 R 4πε 0 R
q′ = − q 2
练习二十九
1.2,1.6
2.600V
3.[2]
4.[3]
5.(1)∵ E = λ , w = 1 εE 2
x
⎞ ⎟
x2 + R2 ⎟⎠
2
练习二十八
1. 3F , 4F 89
2. σ 0 2
− ε0 E0 ,
σ0 2ε 0
− E0
3.[2] 4.[1] 5.(1)静电平衡时,电荷分布如图,按电势迭加原理,球和球壳的电势分别为
u球
=
1 4πε 0
⎛ ⎜⎜ ⎝
q r
−
q R1
+
Q+ R2
q
⎞ ⎟⎟ ⎠
u球壳
s
ρdV
v
/ε0
∫ 即: 4πr 2E =
r 0
ρ 0 e − kr r2
4πr 2dr
/
ε0
解得:
E
=
ρ0 ε 0kr 2
(1 − e−kr
)
(2)同理可求得球外任一点
E
=
ρ0 ε 0kr 2
(1 −
e −kR
)
练习二十七
1. q1 − q2 , − q1q2 2πε 0 R 4πε 0 R
2. R3 ρ ⎜⎛ 1 − 1 ⎟⎞ 3ε0 ⎝ d + r r ⎠
2πεr
2
Q2 dr ∴圆柱薄壳中的电场能量 dW = wdV = w2πrdrL = ln
4πεL r
b Q2 dr Q 2 b
∫ (2)介质中的总能量W =
= ln
a 4πεL r 4πεL a
3
(3)由W = Q2 ,得圆柱电容器的电容 C = 2πεL
2C
ln b
a
∫ 6.由高斯定理:
��
� Bcd
=
µ0I 8R
� i
� Bbc =
物理练习答案
练习二十五
1.水平向左, E = mgtgθ / q
2.2a 3.[3] 4.[2]
λdl 5.在 AB 上与 O 点相距为 l 处取 dl,其所带电量 dq = λdl 。 dq 在 p 点场强 dE = 4πε 0l 2 ,
方向向右。由于 AB 上任意 dq 在 p 点产生的场强方向相同,则
(r < R)
u = Q ⎜⎛ 1 − 1 ⎟⎞ +
Q
,
4πε 0ε r ⎝ r R + d ⎠ 4πε0 (R + d )
(R<r<R+d )
Q
u=
,
4πε 0r
(r >R+d )
练习三十
1. 0.21µ0 I / R ;垂直纸面向里
2. 2.2 ×10−6Wb
3.[3]
4.[4]
5.在与 p 点相距为 x 处,取一宽为 dx 的细长条,其中电流 dI = I dx ,它在 p 点产生的磁 a
3.[2] 4.[1]
5.(1)在棒上距 p 点为 l 处任取 dl ,其所带电量 dq = q dl , dq 在 p 点的电势为 du = qdl ,
L
4πε 0 Ll
∫ ∴ u p =
r+L qdl
q r+L
=
ln
r 4πε 0 Ll 4πε 0 L r
(2)同理 uQ
=
q 4πε 0 L
ln⎜⎛ 3r + ⎝ 3r
=
1 4πε 0
⎛ ⎜⎜ ⎝
q
+Q R2
⎞ ⎟⎟ ⎠
电势差
∆u
=
1 4πε
0
⎜⎜⎛ ⎝
q r
−
q R1
⎟⎟⎞ ⎠
(2)球壳接地,球与球壳间的场分布不变,所以电势差也不变,仍与上同。 (3)若用导线连接,则为等势体,所以电势差 ∆u = 0 。 6.(1)金属球是个等势体
q
σ ′ds q
q
∫ U 球
= U 0 = 4πε 0r +
2πε 0 x
2πε 0 x
∫ ∫ 相同,则 f =
df =
L+R λ2
dx =
λ2
ln L + R ,方向沿 ab 相互排斥。
R 2πε 0 x 2πε 0 R
练习二十六
1. EπR2
2.0, 5L2 , 6L2
3.略; 4.[4]
∫ 5.过场点作长为 l 的同轴圆柱面,由高斯定理得:
� E
⋅
� dS
D
s
⋅ dS
=
Σqi
,
E
=
D ,可知场分布为 ε
⎧
⎪ ⎪0
E
=
⎪⎪ Q ⎨ ⎪ 4πε 0ε r
r
2
⎪Q
⎪ ⎪⎩
4πε
0
r
2
r<R R < r < R+d
r >R+d
∞
∫ 由 u p =
Edr ,可得电势分布为
p
u = Q ⎜⎛ 1 − 1 ⎟⎞ +
Q
,
4πε 0ε r ⎝ R R + d ⎠ 4πε 0 (R + d )
