电路理论第8章
电路理论基础(第二版)潘双来,邢丽冬。。 PPT 第8章 8-1动态电路及其方程

§8-1动态电路及其方程
一、稳态和暂态
稳态:在前面介绍的电路中,外施激励源不管 是交流、直流还是非正弦周期变化的,我们 认为其作用在电路上已经很久,因此只要电 路的结构和参数一定,电路中的响应也是呈 交流、直流或非正弦周期规律变化。电路的 这种工作状态称为稳态。
暂态:
t
0 过渡期为零
电容电路
(t = 0)
i
R+
Us
K
uC
–
K未动作前,电路处于稳定状态
i = 0 , uC = 0
C K接通电源后很长时间,电容充电 完毕,电路达到新的稳定状态
(t →)
i
i = 0 , uC= Us
Us
R+
uC
C
U S uc
US
–
R?
i
有一过渡期
初始状态 0
t1 新稳态
过渡状态
t
电感电路
当电路的工作条件突然变更,如①开关动作(接通或 扳断); ②电路参数的变化; ③故障。
电路的原来的稳态遭到破坏,电路中的响应出现变动, 经过一段时间后,电路中电流、电压又会达到一个新 的稳定值,即达到新的稳态。
电路从一个稳态到另一个稳态之间的过渡过程称为暂态
S
R
R
uS (t)
uR
(t
)
uC (t)
(t = 0)
i
R+
Us
K
uL
–
K未动作前,电路处于稳定状态
i = 0 , uL = 0
L K接通电源后很长时间,电路达到 新的稳定状态,电感视为短路
(t →)
i
uL= 0, i=Us /R
第八章 测量电桥讲解

R2 R1 R3 R4 RR
R1 R1
R2
U0
R4+ R4
R3
E为等臂桥,或称全等桥:
E Uo 4R (R1 R2 R3 R4 )
R1 R1
U0
R2 R2
R4 R4
R3 R3
E
8.1.1 常用的几种电桥电路分析
K全 2K半 4K单
8.1.2 电桥的零位调整
在测量前应调整电桥致“平衡”状态(即R1R3 =R2R4 ),以提高测量精度、减小误差。 1 串联法
2 并联法 R4
R3 U0
R1
R2
Rp
E
R4
R3
R p U0
Rb
R1
R2
E
8.2 交流电桥
8.2.1 阻抗电桥 8.2.2 变压器电桥 8.2.3 紧耦合电桥 8.2.4 相敏整流电路
8.2.1 阻抗电桥 四个桥臂可以是电阻或阻抗元件。
Z1
I0 Z 2
U 0 Z L
Z4
Z3
E
U 0
Z1
Z 2 Z3
Z4
Z1Z3 Z 2 Z 4 E Z1Z 2 Z3 Z1Z 2 Z 4
Z1Z 3 Z 4
Z2Z3Z4
1 ZL
在测量前,电桥输出电压为零(U 0 0 ),可得电桥的
平衡条件: Z1 Z3 Z 2 Z 4 。
如各桥臂阻抗用复数表示为 Z i Ri jX i Z i e ji 则平衡条件分为幅值和相角两部分,写作
Z1 Z3 Z2 Z4
1 3 2 4
灵敏度 K全 2K半 4K单
《电路(一)》作业答案(08-09章)

& I
+
V1 Z1
& Us
V
-
Z2
V2
171 R +X = 4
2 1 2 1
求出: 求出:R1=15 , X1=±40 即:Z1= 15 ±j40
已知: = 续9–11 已知 V=100V, , V1=171V,V2=240V, , , I=4A,P1=240W。 = , 。 ∵
& I
+
V1 Z1
3
& U S = 10∠ 0° V
& I 1
结点电压方程
2
+
.
& US 1 1 1 & 1& 1& ( + + )Un1 − Un2 − Un3 = 1 1 1 1 1 1
1
1
1
3
-j10
US
-
+ & 2I -
j10
& & Un2 = 2I
1 1 1 & [ + + ]Un3 1 (− j10) ( j10) 1& 1 & Un2 = 0 整理 − Un1 − 1 (− j10)
& & 8–15 已知 I1= I2=10A,求: I、US ,
& 解:设 U = U ∠ 0 o V
& I
& 则: I1 = 10∠0o = 10 A & I 2 = 10∠90o = j10 A
+ & US - 10
j10
& I1
+ & U -
& I2
中南大学电路理论复习思考题

第1章复习思考题1-1.图1-1所示电路,试写出各电路所标出的未知电压和电流的数值。
图1-11-2.根据图1-2所示参考方向和数值确定各元件的电流和电压的实际方向,计算各元件的功率并说明元件是电源还是负载。
(a) (b) (c)图1-21-3.直流电路如图1-3所示,求电感电流和电容电压。
图1-31-4.如图1-4所示,电路中包含的各个元件的电压和电流参考方向如图所示,其中100P 1=W ,10P 2-=W ,50P 3=W ,20P 4=W ,求5P,元件5是电源还是负载?图1-41-5.求图1-5所示电路中的电压1u 和1i 。
图1-51-6.求图1-6所示电路中的电压u 。
3Ω2Ω4Ωi3 i10 V图1-61-7.求图1-7所示电路中的电压U 。
2ΩU4Ω+ -+ -+- +- 5V2V 5V 1Aa bde图1-71-8.图1-8所示电路中,已知5u ab -=V ,求电压源电压s u 。
图1-81-9.电路如图1-9所示,试求电压U X 。
图1-91-10.如图1-10所示的图,如果选1、2、3、4、8支路为树,则其基本回路组是什么?如果选择自然网孔为基本回路组,则其对应的树由哪些支路组成?②⑤1 2 3 4610 ④89 ⑥57 ③图1-10第2章复习思考题2-1.写出题2 1图所示各电路的端口电压电流的伏安特性方程。
(a) (b)图2-12-2.电路如图2-2(a)、(b)、(c)、(d)、(e)和(f)所示,试计算a、b两端的电阻,其中电阻R=8。
(a) (b)(c)(d)(e) (f)图2-22-3.利用电源等效变换,化简图2-3(a)和(b)的一端口网络。
(a) (b)图2-32-4.利用电源的等效变换求图示2-4电路中的电流I。
图2-42Ω6V+I2Ω2A7Ω6A2Ω2-5.求图2-5电路中的受控电流源的功率。
图2-5 2-6.求图2-6各电路的输入电阻R in。
图2-6第3章复习思考题3-1.用支路电流法求图3-1所示电路中各支路电流及各电阻上吸收的功率。
《电路理论基础》(第三版 陈希有)习题答案第八章
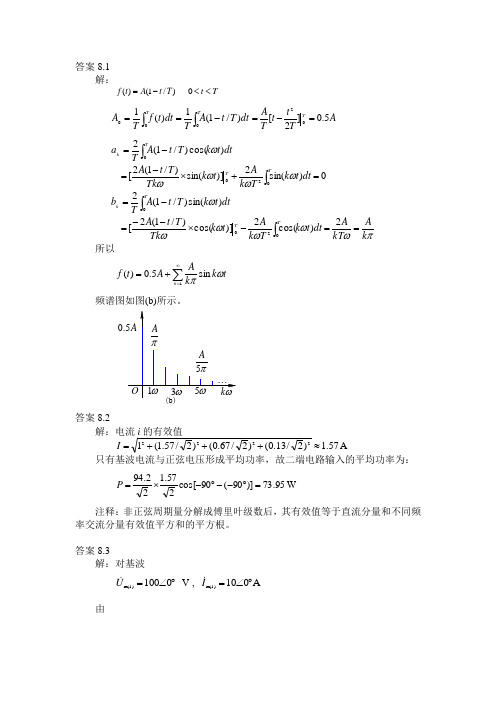
答案8.1解:)/1()(T t A t f -= T t <<0⎰⎰-==T T dt T t A T dt t f T A 000)/1(1)(1A T t t T A T5.0]2[02=-=⎰-=Tk dtt k T t A T a 0)cos()/1(2ω0)sin(2)]sin()/1(2[020=+⨯-=⎰T T dt t k T k A t k Tk T t A ωωωω ⎰-=Tk dtt k T t A T b 0)sin()/1(2ωπωωωωωk A kT A dt t k T k A t k Tk T t A T T==-⨯--=⎰2)cos(2)]cos()/1(2[020 所以∑∞=+=1sin 5.0)(k t k k AA t f ωπ频谱图如图(b)所示。
.0答案8.2解:电流i 的有效值57.1)2/13.0()2/67.0()2/57.1(12222≈+++=I A只有基波电流与正弦电压形成平均功率,故二端电路输入的平均功率为:95.73)]90(90cos[257.122.94=︒--︒-⨯=P W 注释:非正弦周期量分解成傅里叶级数后,其有效值等于直流分量和不同频率交流分量有效值平方和的平方根。
答案8.3解:对基波︒∠=0100m(1)U V , A 010m(1)︒∠=I 由Ω==-+=10)1(j )1(m )1(m )1(I U C L R Z ωω求得Ω=10R , 01=-CL ωω (1)对三次谐波︒-∠=3050m(3)U V , A 755.1im(3)ψ-∠=I又由Ω+︒-∠==-+=)30(5.28)313(j m(3)m(3))3(i I U C L R Z ψωω (2)所以2225.28)313(=-+CL R ωω (3)将式(1)代入式(3), 解得mH 9.31=L将mH 9.31=L 代入式( 1 ),求得F 3.318μ=C再将C L R 、、值代入式(2),有Ω︒-∠=Ω+=3028.5j26.7)10(i )3(ψZ 解得︒=45.99i ψ答案8.4解: (1) 电压有效值:V 01.80)225()250()2100(222=++=U电流有效值58.74mA )210()220()280(222=++=I (2) 平均功率 kW 42.345cos 210250cos 22050)45cos(280100=︒⨯+︒⨯+︒-⨯=PΩ︒∠=︒∠︒∠=Ω=︒∠︒∠=Ω︒-∠=︒∠︒-∠=k 455.2mA010V 4525k 5.2mA 020V 050k 4525.1mA 080V45100)3()3()2()1(Z Z Z 注释:非正弦周期量分解成傅里叶级数后,某端口的平均功率等于直流分量和不同频率交流分量单独作用产生的平均功率之和。
第八章 三相不对称短路分析

X 2 1.22 X d
无阻尼绕组同步发电机
X 2 1.45 X d
零序电抗:机端零序电压的基频分量与流入定子 的电流零序分量的比值。
" X 0 (0.15 ~ 0.6) X d
第8章 电力系统不对称故障的分析计算
二、异步电动机的各序电抗
异步电机的正序参数常用恒定阻抗表示
等值漏抗:正负零序相同。
励磁电抗:负序励磁电抗与正序相同。
结论:所有静止元件的正负序等值电路及其参 数完全相同。 零序励磁电抗:与变压器的铁芯结构密切相关。
第8章 电力系统不对称故障的分析计算
零序励磁电抗
对于由三个单相变压 器组成的三相变压器 组,每相的零序主磁 通和正序主磁通一样, 都有独立的铁心磁路。 对于三相四柱式变压 器,零序磁通也能在 铁芯形成回路。因此, 零序电抗很大。
(8 12)
式(8-12)表明:在三相参数对称的线性电路中,各序对称分量 相互独立,因此可对正负零序分量分别进行计算。 所谓元件的序阻抗,是指元件三相参数对称时,元件两端某一序 的电压降与通过该元件同一序电流的比值,即:
/I Z1 V a1 a1 /I Z 2 V a2 a2 /I Z 0 V a0 a0
3I0
Xn
3 I0
Xn
XI XII
3Xn
Xm0
第8章 电力系统不对称故障的分析计算
自耦变压器的零序阻抗及其等值电路
(1)中性点直接接地
其参数和等值电路,与外电路的联接,Xm0 ——与 普通变压器相同 中性点的入地电流为:
3( I I ) I n I0 II 0
图7-11
第8章 电力系统不对称故障的分析计算
潘双来第二版电路理论基础习题答案(完整版)
3-2. 155V. 3-3. 190mA. 3-4. 1.8 倍. 3-5. 左供 52W, 右供 78W. 3-6. 1 ; 1A; 0.75A. 3-7. 3A; 1.33mA; 1.5mA; 2/3A; 2A. 3-8. 20V, –75.38V. 3-9. –1A; 2A; 1A. 3-10. 5V, 20 ; –2V, 4 . 3-12. 4.6 . 3-13. 2V; 0.5A. 3-14. 10V, 5k . 3-15. 3-16.22.5V 3-17. 4/3 , 75W; 4/3 , 4.69W. 3-18. 3 , 529/12W.; 1 , 2.25W. 3-19 3-20. 50 . 3-21. 0.2A. 3-22. 1A. 3-23. 1.6V. 3-24. 4A; 3-25. 23.6V; 5A,10V. 3-26. 3-27 4V 3-28. ※ 第四章 o o o 4-1. 141.1V, 100V, 50Hz, 0.02s,0 , –120 ; 120 . o o o 4-2. 7.07/0 A, 1/–45 A, 18.75/–40.9 A. 4-3. U m 3 , 7.75mA . o o o 4-4. 10/53.13 A, 10/126.87 A, 10/–126.87 A, o 10/–53.13 A;各瞬时表达式略。 4-5. 67.08V, 30V, 25V; 12V, 0, 12V, 0; 0, 0, 12V. 4-6. 7.07A; 10A, 50A. 4-7. 173.2 . 4-8. 4 , 1.5H. 4-9.11V 4-10. 5 , 0.1F. o o 4-11. 5A; 20/–53.13 , 0.05/53.13 S. 4-12 4-13. 5 , 0.0577F; 3 , 29.33H; 3 ,0.125F; 0 ,0.02F 4-14.-Z 4-15. 4-16. 10A, 141V.
电路理论复习思考题期末复习题及答案
第1章复习思考题1-1.图1-1所示电路,试写出各电路所标出的未知电压和电流的数值。
图1-11-2.根据图1-2所示参考方向和数值确定各元件的电流和电压的实际方向,计算各元件的功率并说明元件是电源还是负载。
(a) (b) (c)图1-21-3.直流电路如图1-3所示,求电感电流和电容电压。
图1-31-4.如图1-4所示,电路中包含的各个元件的电压和电流参考方向如图所示,其中100P 1=W ,10P 2-=W ,50P 3=W ,20P 4=W ,求5P ,元件5是电源还是负载?图1-41-5.求图1-5所示电路中的电压1u 和1i 。
图1-51-6.求图1-6所示电路中的电压u 。
3Ω2Ω4Ωi10 V图1-61-7.求图1-7所示电路中的电压U 。
2ΩU4Ω+ -+ -+- +- 5V2V 5V 1Aa bde图1-71-8.图1-8所示电路中,已知5u ab -=V ,求电压源电压s u 。
图1-81-9.电路如图1-9所示,试求电压U X 。
图1-91-10.如图1-10所示的图,如果选1、2、3、4、8支路为树,则其基本回路组是什么?如果选择自然网孔为基本回路组,则其对应的树由哪些支路组成?②⑤1 2 3 4610 ④89 ⑥57 ③图1-10第2章复习思考题2-1.写出题2 1图所示各电路的端口电压电流的伏安特性方程。
(a) (b)图2-12-2.电路如图2-2(a)、(b)、(c)、(d)、(e)和(f)所示,试计算a、b两端的电阻,其中电阻R=8。
(a) (b)(c)(d)(e) (f)图2-22-3. 利用电源等效变换,化简图2-3(a)和(b)的一端口网络。
(a) (b)图2-32-4.利用电源的等效变换求图示2-4电路中的电流I 。
图2-42Ω6V+I2Ω 2A7Ω6A2Ω2-5.求图2-5电路中的受控电流源的功率。
图2-5 2-6.求图2-6各电路的输入电阻R in。
图2-6第3章复习思考题3-1.用支路电流法求图3-1所示电路中各支路电流及各电阻上吸收的功率。
电路理论基础总复习
四 主要内容的学习要点-- 回路电流方程
设法将电流源的 按“自阻”、“互阻”、“回路源电压”等规 源电流、待求电 则,列KVL方程。 互阻有正负 流、电流控制的 受控源按独立源处理,但最后需要补充方程。 受控源的控制电 对电流源支路,其端电压是未知的,适当选取 流选为回路电流 回路,使电流源只包含在一个回路中,若无需
ruriigulllulixirusrisisgususzsi直流电路交流电路动态电路第2章线性直流电路第3章电路定理第4章非线性直流电路第6章正弦交流电路第7章三相电路第8章非正弦周期电流电路第9章频率特性和谐振现象第10章线性动态电路暂态过程的时域分析第11章线性动态电路暂态过程的复频域分析第13章网络的图网络矩阵与网络方程第14章二端口网络介绍电路的简化分析方法各种电路定理图论稳态分析暂态分析现代电路理论电源
电流确定,电压和功率由外电路决定 受控源:VCVS,VCCS,CCVS,CCCS
VCR 变 化 多 样
一 电路的基本规律--
KCL : I 0 KVL : U 0
VCR R : U RI I GU
在直流电路中的表述
在上述方程 基础之上, 建立了电路 的各种分析 法方程,基 本定理,等 效变换
L : U L (s) sLI L (s) LiL (0 )
uC (0 ) 1 C : U C ( s) I C ( s) sC s
电源:U S ( s )
IS ( s)
二 电路课程的主要内容
直流电路
介绍电路 的简化、 分析方法、 各种电路 定理
稳态 分析
交流电路
第2章 线性直流电路 第3章 电路定理 第4章 非线性直流电路 第6章 正弦交流电路 第7章 三相电路 第8章 非正弦周期电流电路 第9章 频率特性和谐振现象 第14章 二端口网络
电路理论(湖南工程学院)知到章节答案智慧树2023年
电路理论(湖南工程学院)知到章节测试答案智慧树2023年最新第一章测试1.图示电路中,元件吸收的功率为-10W,则Uba=()。
参考答案:10V2.图中电流源的功率为()。
参考答案:吸收功率6W3.电压等于()V。
参考答案:4.如图所示,I=()A。
参考答案:75.如图所示,E=()V。
参考答案:46.图示电路中电流I=()A参考答案:7.图所示电路,电压U=()V。
参考答案:88.电路如图所示,1A电流源产生的功率Ps等于()W。
参考答案:19.在列某结点的电流方程时,均以电流的参考方向来判断电流是“流入”还是“流出”结点。
( )参考答案:对10.基尔霍夫电流定律是指沿回路绕行一周,各段电压的代数和一定为零。
()参考答案:错第二章测试1.电阻并联时,电阻值越大的电阻()。
参考答案:消耗功率越小2.在如图所示电路中,电阻增加时,电流I将()。
参考答案:增大3.如图所示电路,就外特性而言,则()。
参考答案:b、c等效4.等效变换过程中,待求量的所在支路不能参与等效。
()参考答案:对5.两电压不相等的理想电压源并联没有意义。
()参考答案:对6.两种电源模型等效时,对电源内部及内部功率是不等效的。
()参考答案:对7.图(a)所示电路与图(b)所示电路等效,则在图(b)所示电路中Us=()V ,R=()Ω。
()参考答案:6,28.试求下图所示电路左端的等效电阻=()Ω。
参考答案:39.计算图所示电路中两点间的等效电阻等于()Ω。
(保留两位小数)参考答案:1.7110.利用电源等效变换,求图所示电路中的电流I=()A。
参考答案:2A第三章测试1.下面关于用支路电流法求解全部未知的支路电流时,下列叙述正确的是( )参考答案:需要列写独立结点上的KCL方程和独立回路上的KVL方程2.对于含有n个结点b条支路的电路,下列有关回路电流法的看法正确的是()参考答案:回路(电流)必须选取b-n+1个,方程列写可少于b-n+1个3.下列有关结点电压法叙述正确的是()参考答案:结点电压是相对量,与参考节点选取相关4.下列有关标准结点电压法中自导、互导叙述正确的是()参考答案:自导永为正,互导永为负5.电路如图所示,试用支路电流法求各支路电流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8 章正弦稳态电路分析谭丹华中科技大学电气与电子工程学院8.1正弦量8.1. 1正弦量的三要素波形i (t )=I m cos(ωt +φ)i +_uφI mi(t)=I m cos(ωt+φ)waveformT ωti(2)角频率(Angular Frequency ) ω(3)初相位(Initial Phase Angle ) φ(1)幅值(Amplitude (or maximum value ))I m 12f ,2fT Tπωπ===T :周期f :频率工频:f =50Hz ,ω=2πf =314rad/sωt+ϕ=相位Phase Angle反映正弦量变化快慢。
反映正弦量的计时起点。
反映正弦量的大小。
iφ>00通常:|φ| ≤πψ=π/20φ=-π/20φ=008.1 正弦量的三要素tiφ<0t(3) 初相位(Initial Phase Angle ) φφI mi(t)=I m cos(ωt+φ)waveformT ωti同一个正弦量,计时起点不同,初相位不同。
注意8.2 同频率正弦量的相位差设u (t )=U m cos(ωt +φu )ϕ = (ω t +φu )-(ω t +φi )等于初相位之差规定:ωtu , iuiφuϕi (t )=I m cos(ωt +φi )1.同频率正弦量的相位差:ϕ = φu -φi180ϕ≤°ϕ >0,u 超前i ,或i 滞后u (u 比i 先到达最大值)。
ϕ <0,i 超前u ,或u 滞后i (i 比u 先到达最大值)。
2. 两同频率正弦量的超前、滞后关系:φi8.1.3 周期性电流、电压的有效值1.周期电流、电压有效值定义R直流I 2()d TW Ri t t=∫2W RI T=物理意义R交流i∫=Ttt i TI 02defd )(1均方根值∫=Ttt u TU 02defd )(1电流的有效值:电压的有效值:2. 正弦电流、电压的有效值m m 1 22U U U U==或8.2.0 相量-复数运算(P178)1.复数的表示形式zyReIm xOφr(cos jsin )z r =φ+φj z x y=+j e z r φ==∠φz r 22z r x y=+=arctan y xφ=cos x r =φsin y r =φ代数式指数式极坐标式三角函数式j e (cos jsin )j z r r r x yφ==φ+φ=∠φ=+模相除角相减z 1-z 28.2.0 相量-复数运算(P178)2. 复数运算①加减运算——采用代数式z 1±z 2=(x 1 ±y 2)+ j (x 1±y 2)z 1z 2ReImO ()i 1211221212z z r r r r ϕϕϕϕ=∠∠=∠+1111122222z r r ()z r r ϕϕϕϕ∠==∠−∠-z 2z 1ReImOz 1+z 2z 2模相乘角相加②乘除运算——采用极坐标式z 1-z 28.2.0 相量-复数运算(P178)j 111-e z r r φ==∠φ2. 复数运算③倒数运算④共轭运算z x jy∗=−3. 用相量表示正弦量的基础——欧拉公式cos sin j e j φ=φ+φcos Re ,sin Im j j e e φφ⎡⎤⎡⎤φ=φ=⎣⎦⎣⎦8.2.1 正弦量与相量的对应关系(P179)1. 问题的提出例:+_+_u s1u s2+_u s ()()V,=s1u t 2202sin 314t 试求:u s (t)及其有效值U S .解: 根据KVL()()()=−s s1s2u t u t u t ()()°=−−2202sin 314t 2202sin 314t 120()(()())°°⎡⎤=−−⎣⎦2202sin 314t sin 314t cos120cos 314t sin120()()°°⎡⎤=+⎣⎦2202sin 314t cos30cos 314t sin30()(V)°=+3802Sin 314t 30()()V°=−s2u t 2202sin 314t 120V∴=U 380u 3= u 1 +u 2ωtu , iu 1u 2O8.2.1 正弦量与相量的对应关系同频的正弦量相加仍得到同频的正弦量,所以,只需确定初相位和有效值。
因此采用变换的思想正弦量复数结论u 1u 1+u 2 →u 3u 2ωωω角频率U 1m U 2mU 3m 最大值(幅值)φ1φ2φ3初相位复常数-相量8.2.1 正弦量与相量的对应关系针对正弦量造一个复函数j()()et m F t U ω+φ=正弦量u (t )对应复数F (t )的实部j()()cos()Re[e ]t m m u t U t U ω+φ=ω+φ=cos()j sin()m m U t U t =ω+φ+ω+φ2. 正弦量的相量表示()cos()m u t U t =ω+φj j ()Re[e e ]tm u t U φω=j j ()Re[e ]Re[2e ]t t m u t U U ωω= =令,上式可写为j e m m m U U U φ=∠φ =mU U =2且8.2.1 正弦量与相量的对应关系任意一个正弦时间函数都有唯一与其对应的复数函数。
j ()cos( ) et m m u t U t U ω=ω+φ↔ 2. 正弦量的相量表示结论j j ()Re[e ]Re[2e ]t t m u t U U ωω= =正弦量与相量的对应关系:j j ()Re[e ]Re[2e ]t t m i t I I ωω= =旋转相量包含了三要素:U m 、φ、ω,相量包含了两个要素:U m , φ。
UU ∠φ =电路常选择有效值相量表示正弦量例题分析°°°=−=−+=−,12i 102cos(2t 30)A i 52cos(2t 30)A,u 1002sin(2t 135)V写出个正弦量所对应的相量,作出相量图,并比较它们之间的相位关系解:同一问题中,必须先统一函数用标准的余弦函数cosin 表示1I 1030A°=∠−i2I 5150A°=∠−iV V u 1002sin(2t 135)1002cos(2t 13590)1002cos(2t 225)1002cos(2t 225360)1002cos(2t 135)U100135°°°°°°°°=−=−−=−=−+=+=∠2i 52cos(2t 30)A 52cos(2t 30180)A 52cos(2t 150)A°°°°=−+=+−=− .I 2U V.I 1+1135º-150º-30º超前方向Leading direction滞后方向Lagging direction2115030120i i ()ψψ°°°−=−−−−=−113530165u i ()ψψ°°°−=−−=i 2 lags i 1120ºu leads i 1 165º例8-1 :例8-2-1(P179)8.2.2 正弦量运算的相量方法-相量法8.2相量法①同频率正弦量的加减j 1111j 2222()2cos( )Re(2e)()2cos( )Re(2e)ttu t U t U u t U t U ••ωω=ω+φ==ω+φ=U21U U U +=相量关系为:j j 1212j jj1212()()()Re(2e)Re(2e)Re(2e2e)Re[2()e]t tt t t u t u t u t U U U U U U ••••••ωωωωω=+=+=+=+i 1 ±i 2 = i 3123 I I I ±= 1122U U U ∠φ=∠φ+∠φ1122I I I ∠φ=∠φ±∠φj Re(2e )•ωtU.V∴=U 964例题分析例8-21o 2()62cos(31430) V ()42cos(31460) Vu t t u t t =+=+12()()()9.642cos(31441.9) Vu t u t u t t =+=+5.19j32j3.46=+++7.19j6.46=+12630 V460V U U =∠=∠ 9.6441.9 V=∠12630460U U U =+=∠+∠ +_u 1u 2+_u +_求u(t)及U12u u u =+12U U U =+8.2.2 正弦量运算的相量方法-相量法8.2相量法②正弦量的微分、积分运算()2cos( )i u t U t =ω+φj j j d d d Re 2e Re 2j e Re 2e d d ωωω⎡⎤⎡⎤⎡⎤===⋅ω=⎣⎦⎣⎦⎣⎦ t t t d u u U U U t tj j j i 1d Re 2e d Re 2e Re 2e j ωωω⎡⎤⎡⎤⎡⎤====⎢⎥⎣⎦⎣⎦ω⎣⎦∫∫t t t i u u t U t U U 微分运算积分运算d d d du u U j U t=↔=ω 1d =↔=ω∫ i iu u t U U j iU U =∠φ j j d 2e 2j eωω=ω t t U U dj =ω U U j j i 12e 2ej ωω=ωt t U U i 1j =ωU U 例题分析(P181 例8-2-4)8.2.3 基尔霍夫定律的相量形式相量形式时域ki(t )=∑k km k i (t )I cos(t )ωφ=+k j(t )j t k km km i (t )Re I e Re I e ωφω+⎡⎤⎡⎤==⎣⎦⎣⎦{}{}j t j t k km km i (t )Re I e Re I e ωω ⎡⎤===⎣⎦∑∑∑0j t km I e ω =∑km I =∑0k I =∑2 . KVL 相量形式时域k u (t )=∑k km k u (t )U cos(t )ωφ=+0km U =∑ 0k U =∑ km km kk k kU U U U φφ=∠=∠ 1. KCL1.电阻(Resistor )u R (t )i R (t )R +-R+-RU RI时域相量模型i R (t) = I Rm cos(ωt+φi ) u R (t) =U Rm cos(ωt+ φu ) u R (t)=Ri R (t)uR R i R R I I U U φφ=∠=∠ R RU RI = R u R iU RI φφ∠=∠U R =RI Rφu = φiωtiOu RRU Iφu =φiu R 与i R 是同相位Phasor diagramR R U I 与同相位Waveform diagram2. 电感(Inductor )L L iL L v I I U U φφ=∠=∠ L LU j LI ω= L u L iU j LI φωφ∠=∠u L 超前i L 90ºj ωL +-LU L I 相量图----相量模型U L =ωLI Lφu = φi +90ºLU LI 90ºφi2LL LU X L fL I ωπ===感抗(Inductor reactance)单位:Ω11==L LB L X ω感纳Inductor susceptance measured in siemens(S).ωX L(,,L L 0), X 0 ,X ωω==→∞→∞DC 短路开路3.电容(Capacitor )----相量模型C C iC C v I I U U φφ=∠=∠ = c cI j CU ω1∠=∠c v c iU I j C φφωi c 超前u c 90ºPhasor diagramcU cI 90ºψiIU+-1j Cω=cc1V I j C ωφv = φi -90º1=c cU I CωC U 1X I Cω==1==C CB C X ω容纳(Capacitor susceptance ) 单位:西门子(S).c , X 0, ω→∞=容抗(Capacitor reactance ),单位:Ω.c 0(), X , ω=→∞DC 开路短路8.2.4 电路的相量模型4. 线性时不变受控电源的相量模型1gu 1u 1i 2i 2u 1'12'21ri 1u 2i 2u 1'12'21i 1gU 1U 1I 2I 2U 1'12'21rI 1U 2I 2U 1'12'21ILCRu Si Li c i R+-8.2.4 电路的相量模型时域列写微分方程相量形式复数方程j ωL1/j ωCSU LI CI RI R+-电路的时域模型RC L i i i +=RC L I I I +=Sd d d L c i 1L i t u t C+=∫d R c 1Ri i tC=∫Sj L C 1j LI I U C ωω+= j = R c 1RI I Cω电路的相量模型8.3 阻抗与导纳I ZU+-N 0IU+-||z UZ Z φR j Imped nc :XIa e ==∠=+() |Z|R Xϕz阻抗三角形z u i ϕφφ=−UZ I=1. 阻抗•Z —复阻抗;R —电阻(阻抗的实部);X —电抗(阻抗的虚部);—复阻抗的模—阻抗角。
