理论力学第七章题解
(彩色版第七版)理论力学哈工大课后题答案
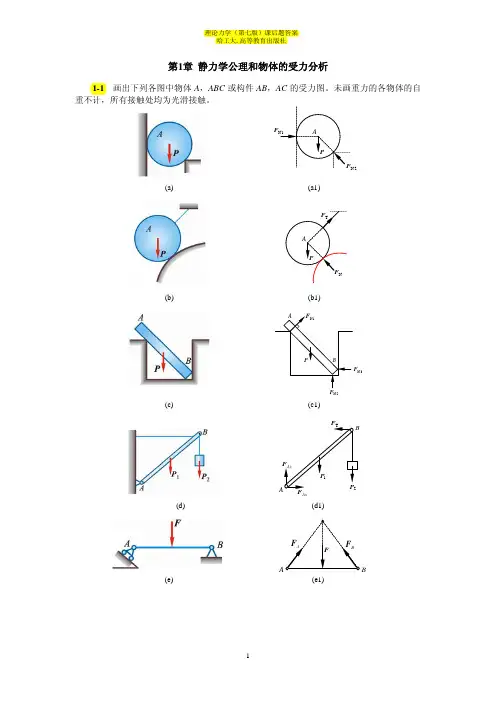
第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体A ，ABC 或构件AB ，AC 的受力图。
未画重力的各物体的自重不计，所有接触处均为光滑接触。
2F(a)(a1)(b) (b1)2N F 3N(c) (c1)Ax(d) (d1)B(e) (e1)Bq(f) (f1)(g)1F 2(h)(h1)Ax(i)(i1)(j)(j1)F(k) (k1)BA F FF ′ (l) (l2) (l3)图1-11-2画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计，所有接触处均为光滑接触。
22N(a1)2AxFAx(a2)3N(b)(b1)N3′(b2) (b3)1N2AxF(c)(c1)1N2N2Ax(c2)(c3)(d) (d1)CDy(d2)(d3)CxBxByF By′(e) (e1)(e2) (e3)ByBxAx(f) (f1)AxBx F′(f2)(f3)FB(g) (g1)BCx′F(g3)(h)(h1)FFAxC(i) (i1) (i2)F(i3)(i4)AyFFFCy (j) (j1)(j2) 2TFDx3TEyFCyEx′(j3) (j4) (j5)BBDECyF(k)(k1)BBCx (k2) (k3) DEA1F(l) (l1) (l2)A C E(l3) (l4)或CDxFEyFEy(l2)’(l3)’ (l4)’F′(m)(m1)EADFH2FAD′(m2) (m3)BN(n)q3N(n2)G(o)(o1)BADB(o2) (o3) (o4)图1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心A ，B 和C 处受3个力作用，如图2-1a 所示。
N 1001=F ，沿铅直方向；N 503=F ，沿水平方向，并通过点A ；N 502=F ，力的作用线也通过点A ，尺寸如图。
求此力系的合力。
(a)(b)图2-1解 （1） 几何法作力多边形abcd ，其封闭边ad 即确定了合力F R 的大小和方向。
理论力学7-2
z
M M '
rM z '
r'
O' x'
k ' rO ' i '
j'
y'
O
y
UNIVERSITY OF JINAN
第七章 点的合成运动
1. 动系做平移时 i 0, j 0, k 0
' k ' 0 2 x' i ' y ' j ' z
ve vr va ro
vB ve r O l l l
UNIVERSITY OF JINAN
第七章 点的合成运动
绝对加速度 相对加速度
n 2 aa aa O r
方向由A指向O
ar ?
n e 2 e
方向水平
2 O r2
v 牵连加速度 a l
l
方向由B指向D
v R vr aa R R 2 v R 2 r 2vr R
2 a 2
UNIVERSITY OF JINAN
第七章 点的合成运动
加速度合成定理(Theorem of composition of accelerations)
1. 动系做平移时
aa ae ar
2. 两个不相关的物体，求二者的相对速度。 根据题意, 选择所求相对运动速度的点为动点, 动系 固结于另一物体上。
UNIVERSITY OF JINAN
第七章 点的合成运动
3. 相对于运动物体在运动的物体上有一动点，求该点的绝 对运动。则取该点取为动点，动系固结于另一个运动物体 上。
理论力学第七章
例题
点的复合运动
例 题 7-1
3. 速度分析。
绝对速度va：va＝OA · ＝r ω ，方 ω 向垂直于OA，沿铅垂
方向向上。
牵连速度ve：ve为所要求的未知量， 方向垂直于O1B 。 相对速度vr：大小未知，方向沿摇杆 O1B 。 应用速度合成定理
va ve vr
13
例题
点的复合运动
2. 运动分析。 绝对运动－以O为圆心的圆周运动。 相对运动－沿杆BC直线运动。 牵连运动－平动。
24
ω0
O
30
C
例题
点的复合运动
例 题 8-10
3. 速度分析。
α
ω
60
绝对速度va：va = ω0 r，垂直于OA向下。
D A E 牵连速度ve： ve= vB，垂直于BD向右下。
B
vr vB v a
a
a
n ae sin 30 cos 30
2 3o l r 3l
所以杆BD的角加速度
t ae l
2 3 o r (l r )
3l 2
27
例题
点的复合运动
习题课
28
第七章
一、基本概念
点的合成运动习题课
1.一个动点，两个坐标系，三种 运动 2.速度合成定理
v2 B
v1
30
vr 与 va 的夹角 ve
60
M
β
ve sin 60 46 12 arcsin vr
va
vr
18
§7-３点的加速度合成定理
先分析 k’ 对时间的导数。
' drA rA rO k vA e rA dt ' ' drO dk e (rO k ) dt dt 因为 v drO r O e O dt
理论力学第七章摩擦课件
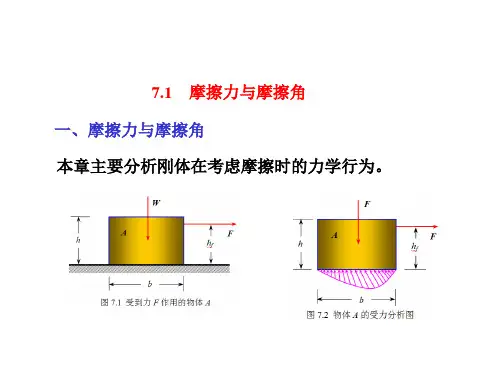
>>摩擦力与摩擦角
当物体A保持静止并且临界状态为先滑动时，只要保证所有主动
外力的合力与公法线的夹角小于等于摩擦角m，则无论外力多大，
全约束反力总可以与其形成平衡，而不会滑动。这种现象称为自锁 现象。如果主动力合力的作用线位于摩擦锥以外，则无论力多小， 物体都不能保持平衡。
7.2 考虑摩擦时物体系统的平衡
F
F4
b cos h sin a cos
W 2
1m cos20 2m sin20 200 kN
1.8m cos30
2
104 .2kN
综合以上四个结果，可得系统保持平衡时，拉力F的取值范围为
40.2 kN F1 F F4 104 .2 kN
>> 考虑摩擦时物体系统的平衡
例7-4 等厚均质矩形体A和B，如图7.14 所示。A重20kN，A与铅垂墙间是光 滑的，A与B和B与水平固定面间的摩 擦系数均为fs。试求系统平衡时fs至 少应为多大？B的重量W2至少应为多 少？
(2) 当物体处于向上滑动的临界状态时，摩擦力方向与图（b）所示的 摩擦力方向相反。
F
F2
sin cos
f f
cos sin
W
sin 20 0.2 cos 20 200 kN cos30 0.2 sin 30
109 .7 kN
(3) 当物体处于绕O点翻倒的临界状态时，此时有：x=0
Fy 0 FNB W 0 (c)
求解可得：
FNB
W cos 2 s in
Fs
W cos 2 s in
>> 考虑摩擦时物体系统的平衡
（2）这属于平衡的临界状态。首先
求角度的最小值，此时梯子的受力
理论力学第七章
B
M2
M
B
vr
M
va ve
A
M1
A
由各速度的定义：
MM va lim Dt 0 Dt
MM 1 ve lim Dt 0 Dt
M 1M MM 2 vr lim lim Dt 0 Dt 0 Dt Dt
理论力学
中南大学土木工程学院
28
va ve vr
wOC
C
va ve vr
ve va sin q v sin q
wOC
ve v sin q OA a
ab v sin q a
ve va
O
q
v A B
vr
vC OC wOC
理论力学
中南大学土木工程学院
38
[例]水平直杆AB在半径为r的固定圆环上以匀速u竖直下落。 求套在该直杆和圆环交点处的小环M的速度。 解：以小环M为动点，动系取在AB杆上， 动点的速度合成矢量图如图。 A 由图可得：
摆动推杆 凸轮机构
理论力学
中南大学土木工程学院
6
§7-1 绝对运动
绝对轨迹 绝对速度 va 绝对加速度 aa t n 或 aa ，aa ，
点的合成运动概念
动 点
点的运动
相对运动
相对轨迹 相对速度 v r 相对加速度 ar 或 art ，arn，
动系相对于定系的运动
定 系
固结于地面上的坐标系
（不需要画出）
中南大学土木工程学院
14
绝对加速度：aa
相对加速度：ar
牵连加速度：ae
理论力学
中南大学土木工程学院
15
动点：AB杆上的A点 动系：偏心轮
理论力学第七章课件
1第七章点的合成运动§7–1 点的合成运动的概念§7–2 点的速度合成定理§7–3 牵连运动为平动时点的加速度合成定理§7–4 牵连运动为转动时点的加速度合成定理2689M 0→Δt 时的极限，得取14由速度合成定理：r e a v v v +=由速度合成定理v= v固结于圆盘，而∴对t 求导：d d v v a O a ==′r e a 做出速度平行四边形,如图示。
002sin v v v v e r ===ϕϕϕnϕ注: 加速度矢量方程的投影是2730（2）速度分析re a v v v +=⊥CM⊥O 1A未知方向未知大小v rv ev a 速度根据点的速度合成定理，动点的绝对速度ϕ&r v A =s&cm/s π20)π41(2e ====t r r v v A ϕ&cm/s π4π2r ===t sv &解得采用几何法可得点v32∥AO 1a en M →Ca rn⊥CM⊥O 1A未知方向未知大小a rt a eta a 加速度（3）加速度分析rnrt en et a a a a a a +++=根据点的加速度合成定理有s &&rs2&2ϕ&r ϕ&&r33∥AO 1a en B →Ca rn⊥CB⊥O 1A未知方向未知大小a rt a et a a 加速度2t et cm/s π20)π21(====t r r a a A ϕ&&s,cm/ π22rt ==s a &&2222rn cm/sπ16)π4(===R s a &s&&rs 2&2ϕ&r ϕ&&r 22222n en cm/sπ20)π41(====t r r a a A ϕ&rnrt en et a a a a a a +++=其中34上式两端向y 轴投影得上式两端向x 轴投影得2rn rt en et a cm/s87.32 45sin 45sin 30sin 30cos −=°+°+°−°=a a a a a y rnrt en et a a a a a a +++=2rn rt en et a cm/s204.90 45cos 45cos 30cos 30sin −=°−°+°−°−=a a a a a x352a cm/s87.32−=y a rnrt en et a a a a a a +++=2a cm/s 204.90−=x a 点M 绝对加速度的大小和方向分别为22a 2a a cm/s 52.207=+=yx a a a 987.0)cos(a a −==a a xi ,a a 158.0)cos(aa −==a a y j ,a aα36α，方向如图示3841可表示为4243t瞬时在位置Ｉ牵连速度v其中:。
理论力学第7章答案
x′
a
n A
sin
θ
−
aAτ
cosθ= NhomakorabeaaBx
cos
θ
−
aBy
sin
θ
aAτ
=
−aBx
+
(a
n A
+ aBy )tgθ
=
−1cm/s 2
α OA
=
a
τ A
/ OA
=
−(1/ 40)rad/s2
7.13 滚压机构的滚子沿水平面作纯滚动如图示 曲柄 OA 长 r 连杆 AB 长 l 滚子 半径为 R 若曲柄以匀角速度 ω 绕固定轴 O 转动 计算连杆 AB 和滚子的角加速度
向
v A
垂直于
OA
杆
因此瞬心为 C
不难看出 C 点相对
AB 杆和定系的位置可分别以 (2r, ϕ) 和 (r,2ϕ) 表示 则动 定瞬心迹线分别是半径为 2r 和 r 的圆
7.9 图示反平行四边形机构中 AB = CD = 2a AC = BD = 2c a > c 求杆 BD
的动瞬心轨迹和定瞬心轨迹
b
杆速度瞬心在 点 vC = 0
∴ ωBC = vB / a = ω ωCD = 0
基点
aCτ = aBn + aCτ B + aCnB
x′ acτ cos θ = −aBn − aCnB
Q cos θ = sin ϕ = 7 / 4
aBn = ω2a
aCnB = ω2a
∴ aCτ = −8ω2a / 7
上二式中消去 ψ 得 (ρsin ϕ)2 + (2c − ρ cos ϕ)2 = (2a − ρ)2
理论力学第7章(点的合成运动)
点的速度合成定理是瞬时矢量式，共包括大小‚方向
六个元素，已知任意四个元素，就能求出其他两个。 二、应用举例
[例] 桥式吊车 已知：小
车水平运行，速度为v平， 物块A相对小车垂直上升 的速度为v。求物块A的 运行速度。
解：选取动点: 物块A 动系: 小车 静系: 地面 相对运动: 直线; 相对速度vr =v 方向 牵连运动: 平动; 牵连速度ve=v平 方向 绝对运动: 曲线; 绝对速度va 的大小, 方向待求。
由速度合成定理 va= vr+ ve ， 作出速度平行四边形 如图示。
v a v e tg 30 0 2 3 e 3 v AB 2 3 e ( ) 3
动点：AB杆上的A点 动系：偏心轮
绝对运动：直线 相对运动：圆周（曲线） 牵连运动：定轴转动
铰接四边形O1A=O2B=100mm， O1O2=AB，杆 O1A以等角速度 ω =2rad/s绕轴O1转动。 AB杆上有一套筒C，此套筒与杆CD相铰接 ，机构的各部件都在同一铅垂平面内。
）
[例3] 圆盘凸轮机构 已知：OC＝e , R 3e , （匀角速度） 图示瞬时, OCCA 且 O、A、B三点共线。 求：从动杆AB的速度。
解：动点取直杆上A点，动系固结于圆盘， 静系固结于基座。 绝对速度 va = ? 待求，方向//AB 相对速度 vr = ? 未知，方向CA 牵连速度 ve =OA=2e , 方向 OA
y
O C
x
x
合成运动：相对某一参考体的运动可由相对于其它参考 体的几个运动组合而成，称这种运动为合成运动
动点：要研究的点
两个参考系： 一般把固定在地球上的坐标系称为静参考系； 用 Oxyz表示； 固定在相对地球运动的参考体上的坐标系称为动参考系； 用 Oxyz 表示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
理论力学第七章题解
部门： xxx
时间： xxx
整理范文，仅供参考，可下载自行编辑
理论力学题解
第七章思考题
7.1. 建立适当的坐标系，单摆悬挂点A始终在轴上，摆锤为
B，摆长，则摆锤的约束方程为：，
，，。
可见，
摆锤受完整、双侧、非稳定约束。
是否受理想约束，要视悬挂点的约束情况而定。
b5E2RGbCAP
7.2. 轮I、II、III的转角可唯一确定力学系统的位置，
被确定后，轮I及绳的位置被确定，确定后，轮II轮III 的位置随之确定。
为系统的广义坐标。
系统的自由度为
3。
p1EanqFDPw
7.3. 由于约束方程可积，积分为：<为积分常
数），所以该约束属于完整约束。
7.4.
7.5.
7.6. <1）由于已知平板的运动规律，所以圆轮与平板的接触点的虚位移<相对固定平面）＝<相对平板）＋<平板牵连运动引起
的）中的。
又因圆轮作无滑滚动，因此。
于是圆轮所受
约束力的虚功之和，圆轮受理想约束。
<2）由于平
板运动规律没有预先给定，，，圆轮
受到非理想约束。
如果以圆轮和平板作为一个系统，约束力的虚功之和为零，系统受理想约束。
DXDiTa9E3d
7.7.
7.8.
7.9. 因<是质点1相对质点2的相
对虚位移）。
所以或，都会导致两约束力的虚功之和
为零。
7.10.
7.11.
第七章习题
7.1. 杆的自由度为1，以杆与水平方向的夹角作为广义坐标，根
据虚功原理，<y轴沿碗对称轴铅垂向下，原点在碗口中
心，是杆质心的坐标）而，
，因的任意性，使
，即，得
，。
RTCrpUDGiT
7.2. 系统自由度为1，建立坐标系。
选择曲柄与水平轴
轴得夹角为广义坐标。
虚功原理写成，是点的弧坐标，正方向沿逆时针
方向，坐标变换方程为：，将虚功原理的方
程写成,由于是任意的，所以得广义平衡方程
，。
5PCzVD7HxA
7.3. 系统自由度为1，以手柄的角坐标为广义坐标<逆时针方向为正方向），由虚功原理得<轴竖直向上），而
，得。
jLBHrnAILg
7.4. 弹簧圈自由度为1，选取弹簧圈面到圆锥体顶点的距离为广
义坐标，弹簧圈势能。
通过，得
，故弹簧圈平衡时。
xHAQX74J0X
7.5. ，以为广义坐标，水平面为重力势能零点，系统势能
，约束方程为，根据虚
功原理，得。
7.6. 将约束释放并以六个约束力、、、、、代替，将其作为主动力处理，选择一足与竖直直线的夹角为广义坐
标，由于系统结构与对称性，虚功原理写成，其中
为点在对称轴上的坐标，是两足端点距离，系统的约束方
程，，最后得到绳子的张力为。
LDAYtRyKfE
7.7. 解除约束并代以约束力、，取、点连线和杆的夹
角为广义坐标，建立原点在杆中点的直角坐标系，根据虚功
原理，，由坐标变换方程得，
，，考虑到的任意性，最后得。
Zzz6ZB2Ltk
7.8. 解除绳子的约束，将绳子张力、当作主动力处理，选择杆和竖直对称轴的夹角为广义坐标，以两钉的中间固定点为坐
标原点，建立轴水平向右、轴竖直向下的直角坐标系，由虚功原理，根据坐标变换方程，并考虑到的任
意性，得到广义平衡方程，进而得到绳子的张力。
dvzfvkwMI1
7.9. 用虚功原理，可求出质点的平衡位置为，。
利用不定乘子法，将约束方程求
变分，并乘以不定乘子，，与相
加，得，，求出，用，即
可求出：大小，方向从所在处指向圆环中心。
rqyn14ZNXI
7.10. 以滑轮、绳子、重物为系统，选择滑轮的角坐标为广义坐
标，系统的拉格朗日函数为，为重
物的初始未知坐标，作用量的变分
，应用分部积分和
的条件，，对于真实
运动，，且是任意的，因此，
，重物的加速度为。
EmxvxOtOco
7.11. ，，
，
进行分部积分并利用，且考虑到是任意的，进而
得到线性谐振子的运动微分方程。
7.12. 以小球的为广义坐标，，
，
即，
进行分部积分并利用的条件，由于的任意性，得到
质点的运动微分方程：
申明：
所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。